Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 5950–5955, May 1998
Colloquium Paper
This paper was presented at the colloquium “Computational Biomolecular Science,” organized by Russell Doolittle, J.Andrew McCammon, and Peter G.Wofynes, held September 11–13, 1997, sponsored by the National Academy of Sciences at the Arnold and Mabel Beckman Center in Irvine, CA.
Computer simulations of enzyme catalysis: Finding out what has been optimized by evolution
ARIEH WARSHEL† AND JAN FLORIÁN
Department of Chemistry, University of Southern California, Los Angeles, CA 90089–1062
ABSTRACT The origin of the catalytic power of enzymes is discussed, paying attention to evolutionary constraints. It is pointed out that enzyme catalysis reflects energy contributions that cannot be determined uniquely by current experimental approaches without augmenting the analysis by computer simulation studies. The use of energy considerations and computer simulations allows one to exclude many of the popular proposals for the way enzymes work. It appears that the standard approaches used by organic chemists to catalyze reactions in solutions are not used by enzymes. This point is illustrated by considering the desolvation hypothesis and showing that it cannot account for a large increase in kcatrelative to the corresponding kcagefor the reference reaction in a solvent cage. The problems associated with other frequently invoked mechanisms also are outlined. Furthermore, it is pointed out that mutation studies are inconsistent with ground state destabilization mechanisms. After considering factors that were not optimized by evolution, we review computer simulation studies that reproduced the overall catalytic effect of different enzymes. These studies pointed toward electrostatic effects as the most important catalytic contributions. The nature of this electrostatic stabilization mechanism is far from being obvious because the electrostatic interaction between the reacting system and the surrounding area is similar in enzymes and in solution. However, the difference is that enzymes have a preorganized dipolar environment that does not have to pay the reorganization energy for stabilizing the relevant transition states. Apparently, the catalytic power of enzymes is stored in their folding energy in the form of the preorganized polar environment.
Enzymatic reactions are involved in the acceleration and control of most biological processes. Thus, the understanding of the origin of the enormous catalytic power of enzymes is one of the important goals in molecular biology. Unfortunately, despite the enormous progress in structural and biochemical studies of enzymes, we still cannot use direct experiments to determine uniquely what are the most important factors in enzyme catalysis. It is quite obvious that enzymes reduce the activation free energies of their reactions, but, as will be shown in this work, it does not follow that evolution can do “everything” and that all possible mechanisms (e.g., entropy, strain, dynamic effects, etc.) can provide effective ways of catalyzing enzymatic reactions. Finding out what free-energy factors can help in catalysis is far from trivial because no current experimental technique can provide direct correlation between the structure of an enzyme substrate complex (ES) and the detailed contributions to its transition state energy. Such correlation can be established, at least in principle, by using computer simulation approaches.
This work will address the general problem of enzyme catalysis and the importance of using energy-based considerations for resolving this problem. It will be pointed out that many proposals about the catalytic power of enzymes cannot be addressed in a meaningful way without using the relevant thermodynamic cycles. This point will be illustrated by considering the desolvation hypothesis, showing that desolvation effects do not provide a useful catalytic advantage. We will also review energy considerations and computational studies of other catalytic proposals. Special attention will be given to electrostatic energies, emphasizing that such contributions appear to account for the catalytic effects of all of the enzymes that were examined by consistent computational studies. Finally, the nontrivial nature of the electrostatic catalysis will be discussed. It will be pointed out that enzymes stabilize transition states more than water does because their active sites contain dipoles that specifically have been ordered by the protein folding process. The presence of such preoriented dipoles in the enzyme active sites greatly reduces the destabilizing contribution of the so-called “reorganization energy” to the enzyme transition state binding energy.
Establishing the Key Problem in Understanding Enzyme Catalysis. To address the nature of enzyme catalysis, it is crucial to analyze the corresponding energetics in a clear way. In doing so, we start by considering the fact that most enzymes evolved to optimize kcat/Km. As shown in Fig. 1, this evolutionary constraint is equivalent to the requirement of reducing Δg≠, which corresponds to the difference between the energy of ES≠ and E+S. A part of this reduction can be accomplished by binding the parts of the substrate that are far from the reacting region, thus stabilizing ES and ES≠, the activated complex, by the same amount This binding effect has been obvious for a long time (see, e.g., refs. 1 and 2), but, in most instances, the binding contribution alone could not account for the large observed catalytic efficiencies of enzymes. It also has been obvious for >50 years (3, 4) that enzymes must reduce the activation barrier  by interacting differently with the substrate in the ES and ES≠ states. What was not clear and what is still one of the most fundamental problems in molecular biology is the actual mechanism for the reduction of
by interacting differently with the substrate in the ES and ES≠ states. What was not clear and what is still one of the most fundamental problems in molecular biology is the actual mechanism for the reduction of  and whether this reduction involves the ground state destabilization or the transition state stabilization.
and whether this reduction involves the ground state destabilization or the transition state stabilization.
©
PNAS is available online at http://www.pnas.org.
| Abbreviations: OMP, orotidylic acid; ODCase, orotidine monophosphate decarboxylase; ES, enzyme-substrate complex. |
† | To whom reprint requests should be addressed. e-mail: warshel@invitro.usc.edu. |
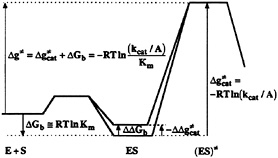
FIG. 1. A free-energy profile along a reaction coordinate for the enzymatic reaction in the regime of the low substrate concentration. The reaction involves the formation of the ES from the free enzyme (E) and substrate (S) in solution and the formation of the activated complex [(ES)≠]. The symbols ![]() Km and kcat, are, respectively, the activation, binding and apparent activation free energies, the equilibrium constant for the dissociation of the ES complex, and the second order rate constant for the enzyme-catalyzed reaction. The symbol A is the pre-exponential factor in the expression for the rate constant (5). The reason for using the lowercase “g” as a symbol for activation barriers is explained in ref. 5. The figure demonstrates that Δg≠ is independent of the magnitude of the ground state destabilization (ΔΔGb).
Km and kcat, are, respectively, the activation, binding and apparent activation free energies, the equilibrium constant for the dissociation of the ES complex, and the second order rate constant for the enzyme-catalyzed reaction. The symbol A is the pre-exponential factor in the expression for the rate constant (5). The reason for using the lowercase “g” as a symbol for activation barriers is explained in ref. 5. The figure demonstrates that Δg≠ is independent of the magnitude of the ground state destabilization (ΔΔGb).
The difficulty of finding logical explanations for the reduction of ![]() led‡ to many proposals that can be eliminated in hindsight by considering the evolutionary pressure on enzymes that evolved to optimize kcat/Km. That is, as seen from Fig. 1, no ground state destabilization (ΔΔGb) will help to reduce Δg≠. Thus, it is not useful, at least from an evolutionary point of view, to use ground state destabilization mechanisms. This point can be verified easily by going backward in evolution and considering the effect of mutations on Δg≠, kcat, and Km (see below).
led‡ to many proposals that can be eliminated in hindsight by considering the evolutionary pressure on enzymes that evolved to optimize kcat/Km. That is, as seen from Fig. 1, no ground state destabilization (ΔΔGb) will help to reduce Δg≠. Thus, it is not useful, at least from an evolutionary point of view, to use ground state destabilization mechanisms. This point can be verified easily by going backward in evolution and considering the effect of mutations on Δg≠, kcat, and Km (see below).
Before examining which mechanisms work and which do not work, it is important to realize that many of the outstanding questions in this field cannot be resolved uniquely by current experimental approaches. That is. enzyme transition states can-not be isolated experimentally and, although indirect experiments are very valuable, they cannot be interpreted without some model for structure-function correlation. In addition, it is important to realize that the issue of enzyme catalysis is an energy issue, and, as such, it cannot be resolved without the ability of dissecting the observed energy to the individual contributions. Finally, in analyzing the effect of enzymes on ![]() it is essential to focus on the proper reference state, thus avoiding considerations of irrelevant factors. One of the most effective ways of doing so involves comparison of the given assumed mechanism in the enzyme active site with the same mechanism in a solvent cage, where all of the reactants are at a contact distance (5) (Fig. 2). This definition allows one to avoid the rather trivial question associated with bringing the reactant to the same solvent cage (5) and to focus on the origin of the difference between kcat and kcage. In
it is essential to focus on the proper reference state, thus avoiding considerations of irrelevant factors. One of the most effective ways of doing so involves comparison of the given assumed mechanism in the enzyme active site with the same mechanism in a solvent cage, where all of the reactants are at a contact distance (5) (Fig. 2). This definition allows one to avoid the rather trivial question associated with bringing the reactant to the same solvent cage (5) and to focus on the origin of the difference between kcat and kcage. In
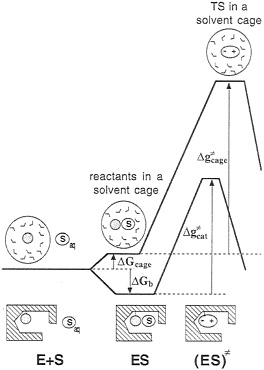
FIG. 2. A comparison of the free-energy profiles for an enzymatic reaction and for a reaction proceeding via an identical mechanism in a reference solvent cage. The symbols E, S, and Saq designate the enzyme, the substrate, and the substrate in the bulk solvent, respectively. The activation free-energy ![]() corresponds to the same reaction mechanism assumed for the given enzymatic reaction (i.e., it does not necessarily correspond to the actual reaction in solution). This
corresponds to the same reaction mechanism assumed for the given enzymatic reaction (i.e., it does not necessarily correspond to the actual reaction in solution). This ![]() can be determined by using experimental information for the related elementary reaction(s) or by using ab initio calculations.
can be determined by using experimental information for the related elementary reaction(s) or by using ab initio calculations.
other words, such an analysis forces one to focus on the true reason for the fact that kcat is much larger than kcage. The rate constant kcage can be evaluated from experimental information about elementary reactions in solutions (5, 6) and/or ab initio calculations in solution (7, 8), but such studies are not practiced by most workers in the field, in part because of the difficulties in estimating the energetics of some reaction intermediates in aqueous solution and the frequent reluctance to ask quantitative questions about energetics. Thus, in many cases, the discussion of the catalytic power of enzymes overlooks the most important question: How large is the effect of the enzyme environment? Instructive works documented the large acceleration of the reaction rate in different enzymes (9, 10) by comparing kcat/Km to the second-order rate constant in water. However, such a comparison includes the effect of the binding energy (ΔGbind) and does not tell us about the effect of the enzyme environment on ![]() For example, our recent analysis of the catalytic reaction of ribonuclease (T.M.Glennon and A.W., unpublished work) indicated that this enzyme provides the transition state stabilization,
For example, our recent analysis of the catalytic reaction of ribonuclease (T.M.Glennon and A.W., unpublished work) indicated that this enzyme provides the transition state stabilization, ![]() as large as ≈24 kcal/mol. This fact (which is not mentioned in the vast literature about ribonucleases) presents a major theoretical challenge because it is hard to see how simple environmental effects can lead to such a large free-energy change. Trying to address such problems quantitatively forces one to quantify the effects of different catalytic factors and to offer a concrete explanation for the overall reduction of
as large as ≈24 kcal/mol. This fact (which is not mentioned in the vast literature about ribonucleases) presents a major theoretical challenge because it is hard to see how simple environmental effects can lead to such a large free-energy change. Trying to address such problems quantitatively forces one to quantify the effects of different catalytic factors and to offer a concrete explanation for the overall reduction of ![]()
Finding Out What Was Not Optimized by Evolution-Desolvation and Other Proposals. Numerous seemingly reasonable proposals for the origin of the catalytic power of enzymes have appeared in the literature (see, e.g., refs. 1 and 11–23). However, some of these proposals turn out to be ineffective after one considers the relevant thermodynamic cycle and when one uses computer simulation approaches. As an example of this point, we will first consider the desolvation hypothesis. This hypothesis, as introduced by Cohen et al. (13) and Crosby et al. (14), suggested that enzyme active sites become basically nonpolar after the removal of water molecules and that such nonpolar sites help in accelerating enzymatic reactions. Realizing that a polar substrate would not bind in a nonpolar cavity, these authors pointed out that the binding energy of the nonreacting part of the substrate could be used as a driving force for the ground state destabilization by desolvation. By comparing activation energies measured for the reaction catalyzed by lyophilized hydrogenase in dry state and in solution (24), they estimated the desolvation contribution to kcat to be ≥103. Later, Jencks (1, 25) included the desolvation mechanism in the family of enzyme mechanisms that are based on the ground state destabilization concept. The “geometric destabilization” (strain, substrate distortion) and “induced destabilization” were considered to belong in the same class. The common denominator of these mechanisms was that they increased kcat by destabilizing the ground state (ES in Figs. 1 and 2) for the given enzymatic reaction (1, 25). Recently, large desolvation contributions to kcat were predicted by quantum mechanical calculations (26–29) that considered enzymatic reactions involving reactive ionized groups in their ground state. This finding led several research groups to the proposal that enzyme proficiency primarily is caused by the nonpolar enzyme active sites evolved to stabilize the gas-phase transition states (26–29).
Although it is possible that small ground state destabilization accompanied with the strong binding of a distant part of a substrate could in principle increase kcat by up to three orders of magnitude, it is unclear how the ground state destabilization could lead to the increase of kcat/Km and, consequently, to any evolutionary advantage. In addition to this general point, which pertains to all ground state destabilization mechanisms, there are problems related specifically to the desolvation hypothesis. These points were established clearly by the quantitative analysis of the reaction profile of amide hydrolysis in gas-phase, in aqueous solution, and in the enzyme (30). Here, we reiterate general problems associated with the idea of catalysis by nonpolar enzyme active sites and illustrate these concepts for the particular case of decarboxylation of orotidylic acid (OMP) to uridylic acid by orotidine monophosphate decarboxylase (ODCase) (28) and the hydrolysis of alkyl halides by haloalkane dehalogenase (29).
To explain the enormous proficiency of ODCase (10), which participates in the biosynthesis of pyrimidine nucleotides. Lee and
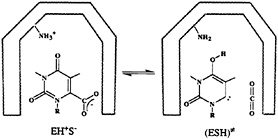
FIG. 3. The mechanism for the enzymatic decarboxylation of the OMP suggested by Lee and Houk (28). The ground and transition states for this reaction are denoted as EH+S– and ESH≠, respectively. The –NH3+ and –NH2 groups belong to the catalytic lysine residue in the hypothetical nonpolar active site of ODCase.
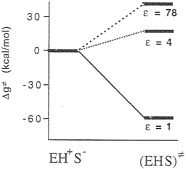
FIG. 4. An inconsistent free-energy diagram for the decarboxylation of OMP by ODCase in hypothetical active sites characterized by different values of the dielectric constant (ε), Note also that, in deriving this diagram, Lee and Houk modeled the EH+S– ground state as EH+ +S– (infinitely separated ions).
Houk suggested that the enzymatic reaction involves a transformation from a ground state composed of a lysine +–OMP– ion pair to a neutral transition state (Fig. 3) (28) “in a nonpolar enzyme environment” (28). In the absence of the experimental structure of this enzyme, the proposal of Lee and Houk was based on the results of the ab initio calculations that modeled the enzyme environment by a dielectric continuum model. To be more specific, they found that the decarboxylation reaction is barrierless in the gas phase and that the experimentally observed magnitude of kcat is reproduced by a model that considers the enzyme as a uniform medium with a dielectric constant, ε=4 (Fig. 4). Consequently, they concluded that the ODCase works by providing a nonpolar environment for the decarboxylation reaction.
Unfortunately, the energy of the EH+S– state in ε=1 and ε =4 is not identical at all to the corresponding energy at ε=78.§ For example, the gas-phase energy should be pushed up by the corresponding absolute value of the solvation free energy. Considering the uninteracting enzyme and substrate molecules in aqueous solution as a correct reference state (or simply using any single correct reference state), one obtains a qualitatively different reaction profile (Fig. 5). Here, the highest barrier corresponds to the formation of the R–NH3+ +S– ion pair in a vacuum-like environment. This barrier and the related barrier at ε=2 reflect the fact that ion pairs are less stable in a nonpolar environment (32). In addition, the uncharged transition state (EHS≠) has now the same energy in all three environments. Thus, the transition state stabilization of Fig. 4 disappears. Furthermore, the proposal of Lee and Houk (28) is undermined by the unrealistically low ε needed to obtain the experimental kcat (Fig. 5) and the fact that the NH3+ group will be deprotonated in such a nonpolar environment. This unprotonated alternative (NH2 +S–) reference state is denoted in Fig. 5 as E+S–. In fact, even the NH3+S– ion pair will become a neutral pair (NH2SH) in a nonpolar environment (for the sake of simplicity, this neutral pair is not shown in Fig. 5). At any rate, the enormous catalytic effect found by Lee and Houk will disappear once fully consistent thermodynamic and electrostatic considerations are invoked.
|
§ |
Note that using macroscopic concepts in describing electrostatic effects in proteins is an inadequate approach (see. e.g., ref. 31). For example, the use of a uniform dielectric constant is inadequate as a measure of the polarity of the enzyme active site because an active site containing fixed dipoles is polar, but its dielectric coast ant can be rather small. However. Lee and Houk (28) clearly meant the low dielectric active site to be an homogeneous, nonpolar environment analogous to the nonpolar solvents used by organic chemists to accelerate chemical reactions. Here, we will invoke macroscopic concepts (i.e., dielectric constants) just to show that enzyme active sites do not use such an environment. |
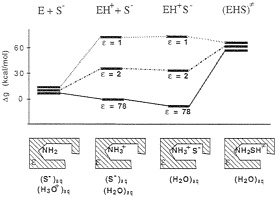
FIG. 5. A consistent free-energy diagram for the decarboxylation of OMP by ODCase. Note that the free energies of the ground state (EH+S–) in each environment involve the contribution of the corresponding solvation free energies. [The magnitude of this contribution was determined by the polarized continuum model (PCM HF/6–31G*) implemented in the Gaussian 94 program (59). The default Pauling’s atomic van der Waals radii scaled by 1.2 were used. The calculated solvation free energies for orotate. CH3NH3+, carbene-methylamine complex, and CO2 were –68, –76, –13.8, and –1.3 kcal/mol, respectively. For the EH+S– state, in which the orotate and CH3NH3+ ions were assumed to lie 6 Å apart, solvation free energy was estimated by using the generalized Born formula, in which the gas phase interaction energy of –55 kcal/mol was assumed. In addition, experimental binding free energy of the ODCase-OMP complex of –9 kcal/mol was taken into account.] As is clear from the figure, the ground state energies are very different at different values of ε (in contrast to the free-energy diagram presented in Fig. 4). Now the transition state energy is nearly identical in different environments, and the experimental value of kcat of 16 kcal/mol is obtained for ε as low as 1.5 (this value is unrealistic and will not support an ionized NH3+ group).
Without having the crystal structure of this protein, we can only point out major inconsistencies in the model of Lee and Houk; we cannot show how the enzyme stabilizes its transition state in this specific case. However, any single case that was examined by us (see also below) was found to involve transition state stabilization by a very- polar active site. In this respect, it is very Instructive to consider the pioneering work of Lienhard and coworkers (14), who introduced the desolvation idea in their study of pyruvate decarboxylase (14). These authors postulated that the active site of the enzyme must be nonpolar, and this view was later adopted (1) as a major support of the desolvation hypothesis. Recently, the crystal structure of pyruvate decarboxylase (33) revealed that its active site contains many polar residues. In particular, the substrate binding site is located in the region of the contact of the a and b domains of the protein and contains the Glu91 His92, Cys221, and Cys222 residues. Although a part of the thiamin cofactor for this reaction is surrounded by nonpolar amino acid residues, the activation of this cofactor occurs via the general base catalysis involving the water molecule and several polar residues. Moreover, the current mechanism of the substrate activation by the cofactor (34), which is supported by the available structural information (33), differs from the mechanism using the formation of the neutral pyruvic acid in the nonpolar environment, as suggested by Crosby et al. (14). Although the overall pyruvate decarboxylation reaction involves several steps for which the structures of the relevant intermediates in the enzyme were not yet determined by x-ray crystallography, it is clear that the enzyme active site is very heterogeneous with the numerous preoriented polar and ionic groups.
Another theoretical study that invoked the desolvation hypothesis is a recent investigation of the SN2 displacement of Cl– from dichloro ethane in the active site of haloalkane dehalogenase by Bruice and coworkers (29). In this case, unlike the ODCase
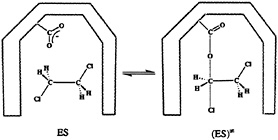
FIG. 6. The proposed (29, 36) mechanism for the enzymatic dehalogenation of the dichloroethane. The ground and transition states for this reaction are denoted as ES and (ES)≠, respectively. The –COO– group belongs to the catalytic Asp residue in the active site of the haloalkane dehalogenase (29, 36).
discussed above, it was possible to base the theoretical analysis on the known crystal structures (at 1.9- and 2.4-Å resolution, respectively) of this enzyme (35) and its complex with dichoroethane (36). The assumed reaction mechanism involves the nucleophilic attack of the ionized aspartate residue (Asp124) on the carbon atom of the substrate, which results in the displacement of the Cl– ion and formation of the alkyl ester intermediate (Fig. 6). In the next reaction step, the product (chloro ethanol) is formed by the nucleophilic attack of the water molecule on the alkyl intermediate, recovering the aspartate residue. The nucleophilic Asp124 is, together with the nearby His289 and Asp260 residues, situated in a cavity that also contains two Trp residues that form hydrogen bonds with the displaced chlorine ion. The structure of the corresponding transition state was calculated by the semiempirical PM3 method for the reaction occurring in the gas phase, in a dielectric continuum (ε=80), and in the enzyme active site (29). The enzyme active site was modeled by 14 amino acids, including the Trp125 and Trp175 residues, and a catalytic water molecule. As in the case of ODCase, the nonenzymatic reaction (37) was calculated to be extremely slow in aqueous solution, and the gas-phase reaction was found to be very fast. Moreover, the geometry and the relative energy of the transition state inside the enzyme active site was found to be similar to the transition state energy and geometry obtained at the same computational level for the gas phase reaction. Lightstone et al. (29) concluded that the hydrogen bonds of two Trp residues are important for stabilizing the transition state [note that such hydrogen bonds are the dipoles considered in our early studies (5, 22)). They also pointed out the importance of small reorganization energy that will be discussed below. However, restoring the arguments of Dewar and Storch (26), Lightstone et al. (29) also concluded that the enzyme operates by a desolvation mechanism, destabilizing the reactants in a gas-phase-like environment.
Although the above proposal contains correct elements, it has several problems. First, a detailed examination of the active site of haloalkane dehalogenase reveals a very polar environment at the chemically relevant sites.¶ In fact, this environment is already entirely obvious from the inspection of the x-ray structure where two dipoles (two hydrogen bonds)
|
¶ |
The statement that the active site is polar may sound unreasonable in view of the fact that the active site was found to contain mostly hydrophobic residues (35) However, considering the residue type without proper computational tools for structure-function correlation may be quite deceiving. As is clear now to most workers who are involved in studies of electrostatic effects in proteins (see e.g., refs. 31 and 38), even hydrophobic residues have very polar main-chain dipoles. Thus, the main-chain dipoles of hydrophobic groups and the side-chain dipoles of a few selected residues are sufficient to create high polarity in the proper places. Thus, the decision whether the active site environment is polar should be determined by calculating the interaction energy of this environment with the particular substrate and not by counting amino acids. |
are provided by Trp125, Trp175, two dipoles by the main chain peptide bonds of Glu56 and Trp 125, and two by the end of the α-helix (36). Second, the same energy considerations applied above for ODCase can show that the desolvation hypothesis does not work in the present case. To be more specific, if the active site of haloalkane dehalogenase really was nonpolar, the nucleophile Asp 124 would not be ionized in the ground state. An attack by the neutral Asp on the dichloro ethane [not considered by Lightstone et al. (29)]—which is, in principle, possible—will involve a zwitterionic transition state, and, as such, it will proceed more slowly in the nonpolar than in the polar environment. Third, the low activation barrier calculated for the gas-phase reaction reflects the assumption that the ground state of this system involves the ionized Asp124. Although Asp124 probably is ionized in the real enzyme, using an ionized nucleophile in the gas-phase calculation amounts to starting the reaction from a high energy intermediate (30). Finally, the correct inclusion of some of the active site dipoles (e.g., Trp125 and Trp175 dipoles) amounts to a study of the given reaction in a polar environment and not in the gas phase. Saying that the enzyme works by using the gas-phase environment plus hydrogen bonds to stabilize the transition state is problematic. In the same way, one might include the entire enzyme explicitly while neglecting the solvent and state that the system works like a gas-phase system.
Apparently, the desolvation hypothesis reflects the realization that organic chemists can accelerate chemical reactions by moving them from polar to nonpolar solvents (thus, one would assume that enzymes can accomplish the same trick). However, what is missing in this analysis is the energy of moving the reactants from a test tube with a polar solvent to the test tube with a nonpolar solvent. This energy contribution is equivalent to the energy lost when the substrate is moved from water to the hypothetical nonpolar active site. Another point that is missing is the lack of an evolutionary constraint to use binding energy in distant regions in destabilizing the reacting parts in their ground state. To be more specific, one may design a catalytic antibody that will gain some increase in kcat by a desolvation mechanism, but enzymes do not have the incentive to do so (this mechanism will not help in reducing kcat/Km). Furthermore, as was mentioned above, enzymes cannot destabilize the ionized form of natural amino acids and still use them as nucleophiles because such ionized groups will become unionized in nonpolar sites.
In addition to the desolvation hypothesis, there are other mechanisms for reducing ![]() that can be excluded by using energy considerations and computer simulations. These include the following mechanisms: (i) the strain mechanism (1, 11). This mechanism involved a ground state destabilization caused by steric strain. However, force field calculations (5, 39, 40) have established that such a mechanism cannot account for a large reduction in
that can be excluded by using energy considerations and computer simulations. These include the following mechanisms: (i) the strain mechanism (1, 11). This mechanism involved a ground state destabilization caused by steric strain. However, force field calculations (5, 39, 40) have established that such a mechanism cannot account for a large reduction in ![]() (ii) The orbital steering mechanism (16). Such a mechanism requires that the approach of the reacting molecules is restricted to a very narrow angular range by a steep potential energy surface in the direction perpendicular to the reaction coordinate. This proposal can be excluded once the actual energetics is estimated (5, 41). (iii) The low-barrier hydrogen bond mechanism (20, 21). This mechanism implies that hydrogen bonds catalyze reactions by forming partial covalent bonds to the corresponding transition state. This proposal has been shown to be anticatalytic (relative to the corresponding regular hydrogen bond) by considering the relationship between the solvation energy and charge delocalization (42). (iv) The idea that enzyme catalysis involves significant dynamic effects (17, 18) has been excluded by computer simulation studies (5, 43). Other proposals, such as the idea that ground state destabilization by entropic effects is the origin of the reduction in
(ii) The orbital steering mechanism (16). Such a mechanism requires that the approach of the reacting molecules is restricted to a very narrow angular range by a steep potential energy surface in the direction perpendicular to the reaction coordinate. This proposal can be excluded once the actual energetics is estimated (5, 41). (iii) The low-barrier hydrogen bond mechanism (20, 21). This mechanism implies that hydrogen bonds catalyze reactions by forming partial covalent bonds to the corresponding transition state. This proposal has been shown to be anticatalytic (relative to the corresponding regular hydrogen bond) by considering the relationship between the solvation energy and charge delocalization (42). (iv) The idea that enzyme catalysis involves significant dynamic effects (17, 18) has been excluded by computer simulation studies (5, 43). Other proposals, such as the idea that ground state destabilization by entropic effects is the origin of the reduction in ![]() (1, 12), cannot be excluded yet by computer simulation studies because of convergence problems. However, qualitative estimates (5) do not support this idea (see also ref. 44). Of interest, none of the suggestions that involve ground state destabilization are supported by mutation experiments. That is, the ground state destabilization mechanisms require that at least some of the mutations that change the activity of the enzyme in a significant way will involve large ground state stabilization (this means that the native enzymes evolved by using the specific group to induce ground state destabilization). However, mutations that lead to a large loss in catalysis (see, e.g., refs. 45–47) involve mainly large reduction of kcat accompanied by small changes in Km, (small changes in the ground state free energy) or in the increase in Km and no change in kcat (equal destabilization of the ground and transition state).
(1, 12), cannot be excluded yet by computer simulation studies because of convergence problems. However, qualitative estimates (5) do not support this idea (see also ref. 44). Of interest, none of the suggestions that involve ground state destabilization are supported by mutation experiments. That is, the ground state destabilization mechanisms require that at least some of the mutations that change the activity of the enzyme in a significant way will involve large ground state stabilization (this means that the native enzymes evolved by using the specific group to induce ground state destabilization). However, mutations that lead to a large loss in catalysis (see, e.g., refs. 45–47) involve mainly large reduction of kcat accompanied by small changes in Km, (small changes in the ground state free energy) or in the increase in Km and no change in kcat (equal destabilization of the ground and transition state).
Using Computer Modeling To Determine How Enzymes Really Work. As clarified in the previous section, it is possible to exclude some major catalytic proposals by simple energy considerations. Doing so, however, is not sufficient when one likes to determine the real origin of enzyme catalysis. It seems to us that the only way of resolving this issue is to take crystal (or solution) structures of different enzymes and to reproduce the observed ![]() Once this is accomplished, it is simple to examine which energy contributions are responsible for the overall effect. The selection of the proper computational strategy is not completely obvious. In principle, one can use the hybrid quantum mechanical/molecular mechanics approach introduced by Warshel and Levitt (40). However, despite the recent popularity of this approach (48–50), it does not yet provide sufficiently quantitative answers. The problems are that (i) current semi-empirical molecular orbital models are not accurate enough; (ii) most quantum mechanical/molecular mechanics approaches do not treat properly the complete enzyme substrate environment; and (iii) ab initio quantum mechanical/molecular mechanics approaches are too time consuming and, with the exception of one approach (51), do not involve calculation of activation free energies.
Once this is accomplished, it is simple to examine which energy contributions are responsible for the overall effect. The selection of the proper computational strategy is not completely obvious. In principle, one can use the hybrid quantum mechanical/molecular mechanics approach introduced by Warshel and Levitt (40). However, despite the recent popularity of this approach (48–50), it does not yet provide sufficiently quantitative answers. The problems are that (i) current semi-empirical molecular orbital models are not accurate enough; (ii) most quantum mechanical/molecular mechanics approaches do not treat properly the complete enzyme substrate environment; and (iii) ab initio quantum mechanical/molecular mechanics approaches are too time consuming and, with the exception of one approach (51), do not involve calculation of activation free energies.
At present, the most effective and consistent way of using computer simulations in studies of enzyme catalysis is provided by the empirical valence bond method (5, 52, 53). This method does not try to evaluate from a first principle the energy surface of the substrate but rather focuses on the change in this free energy on moving from the reference solvent cage to enzyme active site. Thus, this method focuses directly on ![]() Extensive empirical valence bond studies of many enzymatic reactions have been reported in the literature (5, 6, 53–56). Many of the above simulation studies provided quantitative or semiquantitative results, reproducing frequently the overall catalytic effect of the enzyme. The most significant finding of all the above studies is that the largest catalytic effect always is associated with electrostatic contributions. In other words, the electrostatic stabilization of the transition state is larger in the enzyme active site than in water.
Extensive empirical valence bond studies of many enzymatic reactions have been reported in the literature (5, 6, 53–56). Many of the above simulation studies provided quantitative or semiquantitative results, reproducing frequently the overall catalytic effect of the enzyme. The most significant finding of all the above studies is that the largest catalytic effect always is associated with electrostatic contributions. In other words, the electrostatic stabilization of the transition state is larger in the enzyme active site than in water.
The finding that enzymes provide large electrostatic stabilization is far from trivial and, in fact, seems at first sight to be inconsistent with all studies before the emergence of computer modeling. For example, studies of model compounds in solutions have not reproduced large electrostatic effects even with covalentty linked ionized groups that are aligned properly to stabilize ionic transition states (57). This fact can be rationalized by saying that electrostatic effects cannot be large in aqueous solution because the dielectric constant is large in such an environment even at a short interaction distance (22). It thus can be argued that protein active sites with low dielectric constant should be able to enhance electrostatic effects (58). However, ionized groups that were supposed to be the source of electrostatic effects in enzymes would not be ionized in low dielectric sites. Of course, the argument that electrostatic effects are small in high dielectric environments and cannot exist in low dielectric environments (which is the best that could have been concluded before the emergence of crystal structures of enzymes) is not correct. Protein active sites are neither homogenous low dielectric nor homogeneous high dielectric media. They are usually very polar heterogeneous sites (22, 31). This fact, however, cannot explain the finding that protein active sites provide larger stabi
lization to ionic transition states than water does. Here, the most puzzling problem is associated with the fact that the actual average electrostatic interaction between the transition states of an enzyme and the surrounding dipoles ![]() is not larger than the corresponding interaction with the dipoles of the reference solvent cage
is not larger than the corresponding interaction with the dipoles of the reference solvent cage ![]() The solution to this problem has been given before in a work (22) that pointed out that, in polar solvents, about half of the charge-dipole interaction is spent on dipole-dipole interaction (<Vμμ>) so that
The solution to this problem has been given before in a work (22) that pointed out that, in polar solvents, about half of the charge-dipole interaction is spent on dipole-dipole interaction (<Vμμ>) so that
In proteins, however, a significant part of ⟨ΔVμμ⟩ (or the corresponding reorganization energy) already is paid during the folding process, in which the folding energy is used to compensate for dipole-dipole repulsion and to align the active site dipoles in away that will maximize ΔGsol. The preoriented environment allows the protein to minimize the reorganization energy associated with the formation of the charged transition state (see Figure 9.7 of ref. 5).
The idea of preorganized dipoles as the source of the catalytic power of enzymes explains what really was done by evolution in optimizing enzymes. That is, the active site has to interact with the changes that occur in the substrate during the formation of the transition state to reduce ![]() The structural changes of the substrate during the given reaction could not be used effectively because enzymes are rather flexible; changes in entropy were not useful because they can only help in ground state destabilization. Thus, the most effective way was to interact with the changes in charges during the reaction. Here, a requirement of providing a large stabilization to the transition state charges forced the enzyme to be a better “solvent” for the transition state than aqueous solution (22), which can be accomplished by preorienting the active site dipoles. Note that the resulting environment is exactly the opposite from the nonpolar environment envisioned as a source of catalytic energy in the desolvation models above. Finally, the reason for the difficulty in realization that enzymes use preorganized dipoles can be traced in part to the fact that the catalytic energy is already in the folding process and not in the enzyme substrate interaction.
The structural changes of the substrate during the given reaction could not be used effectively because enzymes are rather flexible; changes in entropy were not useful because they can only help in ground state destabilization. Thus, the most effective way was to interact with the changes in charges during the reaction. Here, a requirement of providing a large stabilization to the transition state charges forced the enzyme to be a better “solvent” for the transition state than aqueous solution (22), which can be accomplished by preorienting the active site dipoles. Note that the resulting environment is exactly the opposite from the nonpolar environment envisioned as a source of catalytic energy in the desolvation models above. Finally, the reason for the difficulty in realization that enzymes use preorganized dipoles can be traced in part to the fact that the catalytic energy is already in the folding process and not in the enzyme substrate interaction.
This work was supported by National Institutes of Health Grant GM24492.
1. Jencks, W.P. (1987) Catalysis in Chemistry and Biology (Dover, New York).
2. Fersht, A.R. (1985) Enzyme Structure and Mechanism (Freeman, New York).
3. Haldane, J.B.S. (1930) Enzymes (Longman, New York), p. 182.
4. Pauling, L. (1946) Chem. Eng. News 24, 1375.
5. Warshel, A. (1991) Computer Modeling of Chemical Reactions in Enzymes and Solutions (Wiley, New York).
6. Fuxreiter, M. & Warshel, A. (1998) J. Am. Chem. Soc., 120, 183–194.
7. Florián, J. & Warshel, A. (1997) J. Am. Chem. Soc. 119, 5473–5474.
8. Florián, J. & Warshel, A. (1998) J. Phys. Chem. B 102, 719–734.
9. Radzicka, A. & Wolfenden, R. (1996) J. Am. Chem. Soc. 118, 6105–6109.
10. Radzicka, A. & Wolfenden, R. (1995) Science 267, 90–93.
11. Phillips, D.C. (1966) Sci. Am. 215, 78–90.
12. Page, M.I. (1977) Angew. Chem. Int. Ed. Engl. 16, 449–459.
13. Cohen, S.G., Vaidya, V.M. & Schultz, R.M. (1970) Proc, Natl. Acad. Sci. USA 66, 249–256.
14. Crosby, J., Stone, R. & Lienhard, G.E. (1970) J. Am. Chem. Soc. 92, 2891–2900.
15. Menger, F.M. (1985) Acc. Chem. Res. 18, 128–134.
16. Storm, D.R. & Koshland, D.E. (1970) Proc. Natl. Acad. Sci. USA 66, 445–452.
17. Careri, G., Fasella, P. & Gratton, E. (1979) Annu. Rev. Biophys. Bioeng. 8, 69–97.
18. Gavish, B. & Werber, M.M. (1979) Biochemistry 18, 1269–1275.
19. McCammon, J.A., Wolynes, P.G. & Karplus, M. (1979) Biochemistry 18, 927–942.
20. Frey, P.A., Whitt, S.A. & Tobin, J.B. (1994) Science 264, 1927–1930.
21. deland, W.W. & Kreevoy, M.M. (1994) Science 264, 1887–1890.
22. Warshel, A. (1978) Proc. Natl. Acad. Sci. USA 75, 5250–5254.
23. Cha, Y., Murray, C.J. & Klinman, J.P. (1989) Science 243, 1325–1330.
24. Yagi, T., Tsuda, M., Mori, Y. & Inokuchi, H. (1969) J. Am. Chem. Soc. 91, 2801–2807.
25. Jencks, W.P. (1975) in Advances in Enzymology and Related Areas of Molecular Biology, ed. Meister, A. (Wiley, New York), Vol. 43, pp. 219–410.
26. Dewar, M.J.S. & Storch, D.M. (1985) Proc. Natl. Acad. Sci. USA 82, 2225–2229.
27. Dewar, M.J.S. & Dieter, K.M. (1988) Biochemistry 27, 3302–3308.
28. Lee, J.K. & Houk, K.N. (1997) Science 276, 942–945.
29. Lightstone, F.C, Zheng, Y.J., Maulitz, A.H.& Bruice, T.C. (1997) Proc. Natl. Acad. Sci. USA 94, 8417–8420.
30. Warshel, A., Åqvist, J. & Creighton, S. (1989) Proc. Natl. Acad. Sci. USA 86, 5820–5824.
31. Warshel, A. and Russell, S.T. (1984) Q. Rev. Biol. 17, 283–421
32. Warshel, A. (1981) Biochemistry 20, 3167–3177.
33. Arjunan, P., Umland, T., Dyda, F., Swaminathan, S., Furey, W., Sax, M., Farrenkopf, B., Gao, Y., Zhang, D. & Jordan, F. (1996) J. Mol. Biol. 256, 590–600.
34. Metzler, D.F. (1977) Biochemistry (Academic, New York).
35. Verschueren, K. R G., Franken, S.M., Rozenboom, H.J., Kalk, K.H. & Dijkstra, B.W. (1993) J. Mol. Biol. 1993, 856–872.
36. Verschueren, K.H.G., Seljee, F., Rozenboom, H.J., Kalk, K.H. & Dijkstra, B.W. (1993) Nature (London) 363, 69–698.
37. Maulitz, A.H., Lightstone, F.C, Zheng, Y.-J. & Bruice, T.C. (1997) Proc. Natl. Acad. Sci. USA 94, 6591–6595.
38. Sharp, K.A. & Honig, B. (1990) Annu. Rev. Biophys. Biophys. Chem. 19, 301–332.
39. Levitt, M. (1974) in Peptides, Polypeptides and Proteins, eds. Blout, E.R., Bovey, F.A., Goodman, M. & Lotan, N. (Wiley, New York), pp. 99–113.
40. Warshel, A. & Levitt, M. (1976) J. Mol. Biol. 103, 227–249.
41. Bruice, T. C, Brown, A. & Harris, D.O. (1971) Proc. Natl. Acad. Sci. USA 68, 658–661.
42. Warshel, A. & Papazyait, A. (1996) Proc. Natl. Acad. Sci. 98, 13665–13670.
43. Warshel, A., Sussman, F. & Hwang, J.-K. (1988) J. Mol. Biol. 201, 139–159.
44. Lightstone, F.C & Bruice, T.C. (1996) J. Am. Chem. Soc. 118, 2595–2605.
45. Wilks, R M., Hart, K.W., Feeney, R., Dunn, C R., Muirhead, H., Chia, W.N., Barstow, D.A., Atkinson, T., Clarke, A.R. & Holbrook, J.J. (1988) Science 242, 1541–1544.
46. Leatherbarrow, R.J., Fersht, A.R. & Winter, G. (1985) Proc. Natl. Acad. Sci. USA 82, 7840–7844.
47. Carter, P. & Wells, J.A (1990) Proteins 7, 335–342.
48. Waszkowycz, B., Hillier, I.H., Gensmantel N. & Payling, D.W. (1990) J. Chem. Soc. Perkin Trans. 2, 1259–1264.
49. Bash, P.A., Field, M.J., Davenport, R.C, Petsko, G.A., Ringe, D. & Karphis, M. (1991) Biochemistry 30, 5826–5832.
50. Mulholland, A.J., Grant, G.R & Richards, W.G. (1993) Protein Eng. 6, 133–147.
51. Bentzien, J., Muller, R.P., Florián, J. & Warshel, A. (1998) J. Phys. Chem B, 102, 2293–2301.
52. Warshel, A. & Weiss, R.M. (1980) J. Am. Chem. Soc. 102, 6218–6226.
53. Åqvist, J. & Warshel, A. (1993) Chem. Rev. (Washington, D.C) 93, 2523–2544.
54. Åqvist, J. & Fothergill, M. (1996) J. Biol. Chem. 271, 10010–10016.
55. Fothergill, M., Goodman. M.F., Petruska, J. & Warshel, A. (1995) J. Am. Chem. Soc. 117, 11619–11627.
56. Hwang, J.K. & Warshel, A. (1996) J. Am. Chem. Soc. 118, 11745–11751.
57. Dunn, B.M. & Bruice, T.C. (1973) Adv. Enzymol. Relat. Areas Mol. Biol. 37, 1–60.
58. Fife, T.H., Jaffe, S.H. & Natarajan, R. (1991) J. Am. Chem, Soc. 113, 7646–7653.
59. Frisch, M.J., Trucks, G.W., Schlegel, H.B., Gill, P.M.W., Johnson, B.G., Robb, M.A., Cheeseman, J.R., Keith, T., Petersson, G.A., Montgomery, J.A., et al. (1995) Gaussian 94, Revision C.2 (Gaussian. Pittsburgh).






