5
School Quality, Student Achievement, and Fertility in Developing Countries
Paul Glewwe
Introduction
Investments in education are increasingly viewed as essential for economic growth in developing countries (World Bank, 1990; United Nations Development Programme, 1990; Becker, 1995). Education also has nonmarket effects, such as better health and lower fertility, that may not be captured in income numbers at the national or individual level (Haveman and Wolfe, 1984). Parents' decisions regarding their children's education depend in part on the characteristics of local schools, most of which are public schools. Unfortunately, in many countries the low quality of schools severely limits households' opportunities for educating their children. Examples of countries with school-quality problems are Brazil (Harbison and Hanushek, 1992), Ghana (Glewwe, 1998), and Pakistan (World Bank, 1995). Many more developing countries also have poor school quality; these three examples simply illustrate that the problem exists in each region of the developing world.
Low school quality can take various forms; recent studies have shown that schools in developing countries suffer from many deficiencies that lead to reduced learning among students (Lockheed and Verspoor, 1991; Hanushek, 1995). While remedying these deficiencies should raise school quality and lead to substantial increases in student learning, much remains to be discovered about which policy options are most effective in achieving this goal. Moreover, evidence is incomplete concerning the likely impacts of improved school quality on fertility and other socioeconomic outcomes.
This chapter examines the relationship between school quality and fertility in developing countries. A large amount of research has shown convincingly that the quantity of schooling in those countries is associated with significant reductions in fertility (Schultz, 1993), but very little research has examined the relationship between school quality and fertility. Given the low levels of school quality in many developing countries and increasing recognition of the need for improvement, two questions arise: First, do we really know how best to improve school quality? Second, what impact will increased school quality have on fertility? To answer these questions, the chapter first provides a critical assessment of the literature on the determinants of school quality in developing countries. It then examines the likely impact of improved school quality on fertility. Particular attention is given to the role played by cognitive skills, such as literacy and numeracy, and on the need to address a host of statistical estimation problems and data inadequacies that, regrettably, often receive insufficient attention in the literature.
The chapter is organized as follows. The next section begins by presenting a simple economic model of the determinants of educational outcomes, focusing on the role of school quality, and uses this model to draw implications for empirical work. The third section provides a critical review of the current state of knowledge on the impact of school quality on learning. The following two sections address the relationship between school quality and fertility, reviewing, respectively, what economic theory says about the impact of school quality on fertility and the scant empirical evidence that is available. The final section presents concluding remarks.
A Simple Economic Model Of Educational Outcomes
Overview of the Issues
Schooling provides children with many benefits. Most obvious are the skills taught explicitly as a part of the curriculum, such as literacy, numeracy, scientific knowledge, and advanced thinking skills. Schooling also provides social skills and values that can help children succeed in the adult world. Finally, a certain prestige may be associated with completing particular levels of education, so that one may be able to obtain better employment or a ''better" spouse (see Basu, this volume). The present discussion focuses on the basic cognitive skills school curricula are designed to impart, but occasional reference is made to other benefits of schooling as well.
The cognitive skills acquired by a child per year of schooling depend on the characteristics of the child, of his or her household, and of the school attended. The variation in acquired cognitive skills that is due to school characteristics can serve as an indicator of school quality. In particular, school quality can be defined as those school (and teacher) characteristics that increase the cognitive
skills children acquire per year of schooling. This concept of school quality is fairly intuitive. As discussed below, however, much remains to be learned about which school characteristics lead to the acquisition of cognitive skills.
The cognitive skills children acquire in school can play a very important role in determining their standard of living as adults. The best example is the role played by those skills in determining income, with better-educated individuals generally having higher incomes. At the same time, however, the exact relationship between cognitive skills and income is poorly understood and probably quite complex because different skills are likely to have different effects on income, and there has been very little research in either developed or developing countries on which skills are most important in this regard. Cognitive skills also affect individuals' living standards by helping to determine many other socioeconomic outcomes, such as health status, marriage prospects, and fertility. Yet almost nothing is known about which skills have the most important effect on these outcomes. Knowledge of the impact of different skills on income and on other socioeconomic outcomes could have implications for school curriculum. For example, if literacy skills were identified as much more important than, say, scientific knowledge in determining future income, it might be desirable to reduce some of the classroom time devoted to science while increasing the time devoted to language skills.
Figure 5-1 provides a visual framework for conceptualizing the relationships among school quality, school attainment, cognitive skills, and socioeconomic outcomes. At the top of the diagram, school, child, and family characteristics influence both schooling and other socioeconomic outcomes. One can think of these characteristics as exogenous (beyond the control of the child and the family), at least initially.1 Given these exogenous characteristics, parents (perhaps considering their child's wishes) decide how long to send their child to school. School quality may influence this decision (arrow a in Figure 5-1) because higher-quality schools should provide more benefits per year of schooling, making additional years of schooling more attractive. In contrast, school costs (arrow b) will tend to reduce years of schooling. Many child characteristics can affect years of schooling (arrow c); on the positive side, more talented children are likely to go to school longer, while on the negative side, children with greater potential to contribute to household income may receive less schooling. Finally, several family characteristics can affect years of schooling (arrow d); two examples are household income and parental tastes for their children's schooling, both of which may increase educational attainment.
Once a child enters school, the acquisition of cognitive skills begins. Time spent in school should increase skill acquisition (arrow f in Figure 5-1 ), as should
school quality (arrow e). In addition, child and family characteristics can play important roles (arrows g and h, respectively); for example, child ability should increase learning, holding other factors constant, and parents' education can do the same if they help their children with schoolwork. Note that school costs have no impact on learning once years of schooling are accounted for; there is no reason that school fees paid should affect skills acquired beyond their role in determining years of schooling.2
The bottom of Figure 5-1 shows the impact of schooling and other factors on socioeconomic outcomes, of which fertility is one example. The cognitive skills a child acquires in school should have substantial effects on many socioeconomic outcomes (arrow i). Family and child characteristics may have separate effects (arrows j and k, respectively). For example, children with more motivation or a better work ethic may be more successful even after controlling for cognitive skills, and parents may use social connections to help their children obtain better jobs. School quality and years of schooling may also affect socioeconomic outcomes beyond the direct effect of cognitive skills (arrows I and m). For example, years of schooling may signal employers about traits they seek in workers (e.g., innate ability, motivation, work ethic) that are difficult to measure.3 Similarly, enrollment in a higher-quality school may improve a child's socioeconomic prospects because of the prestige attached to that particular school.
Although the direction of causality in Figure 5-1 generally flows from top to bottom, some reverse causality is possible. These effects are indicated by dashed lines. For example, cognitive skills may determine years of schooling (arrow n) if schools prevent students from advancing to the next grade until they pass a standardized test; a child who fails such tests two or three times may be forced to drop out of school. As another example, one socioeconomic outcome that could affect years of schooling (arrow o) is pregnancy among female students; pregnant students may be forced to leave school because schooling is thought to be incompatible with their childcare responsibilities.
Obviously, the simple scheme presented in Figure 5-1 could be made more realistic through the addition of more detail. However, it is intended only to provide a basic framework, not a complete picture. The next subsection presents a formal economic model of the determinants of school quality, school attainment, and the acquisition of cognitive skills that will prove useful in the literature assessment presented in the next section.
The Model
This chapter, while somewhat eclectic, approaches education issues from a (neoclassical) economic perspective. In particular, it takes the position that a model of rational behavior is needed to ensure that proper statistical procedures are used in attempting to estimate the impact of school characteristics and school policies on educational outcomes and of schooling and cognitive skills on socioeconomic outcomes. The argument is quite simple. Explicit models of human behavior provide significant insight into whether assumptions underlying specific statistical methods are satisfied. If a plausible theory suggests that some assumptions are not satisfied, the empirical results based on those methods may be invalid. The model may also suggest how to test to determine whether the statistical assumptions hold and what statistical procedure should be used if they fail to hold. Note that this is not intended to be the definitive model on schooling, only a plausible model that can illuminate several statistical issues.
To formulate the model, it is assumed that parents make decisions for their children and that their objective is to maximize a utility function that has two arguments: household consumption (of goods and services) and child cognitive skills. More specifically, it is assumed that there are only two time periods. In time period 1, a child may attend school, work, or both (if both, the child first goes to school and works only after schooling is completed). In time period 2, the child becomes an adult and works.4 Whenever the child works in time period 1 or 2, part or all of the child's earnings may be given to his or her parents. The following simple utility function takes consumption in both time periods (C1 and C2) and child cognitive skills (A) as its arguments:
(5.1)
Note that δ is effectively a discount factor for future consumption, and σ is a parameter indicating tastes for educated children (higher values indicate a greater desire for educated children). Thus parents may value educated children for two distinct reasons: (1) educating children may increase the parents' levels of consumption, and (2) educating children directly affects utility (through σ).
The next step is to explain how cognitive skills, A, are produced. The following simple production function keeps the mathematics at a relatively elementary level:
(5.2)
where a is the "learning efficiency" of the child, Q is school quality, and S is
years of schooling. Increases in either Q or S should increase the cognitive skills produced, so f( ) and g( ) are increasing functions of Q and S, respectively. The learning efficiency of the child, α, can represent several different factors, such as innate (i.e., genetically inherited) ability, child motivation and tastes for schooling, and parents' motivation (and capacity) to help their children with their schoolwork. For simplicity, these different factors are combined into a single parameter, α.
The model is completed by specifying the relationships between consumption and child schooling and between child schooling and child income. Consumption levels in each time period are given by:
(5.3)
(5.4)
where p is the price of schooling (e.g., annual tuition); Y1 and Y2 are (exogenous) parental income in periods 1 and 2, respectively; Yc is the income of the child when he or she works in either time period; and k is the fraction of that income given to the parents.5The last term in equation (5.3), (1 - S)kYc, requires some explanation. For convenience, S has been rescaled to represent the fraction of time spent in school by the child in time period 1. The remaining time during that period, 1 - S, is spent working. This rescaling is purely for notational convenience and has no effect on the results; however, to keep the vocabulary simple, S is still called "years of schooling."
Finally, equation (5.5) relates the child's cognitive skills to employment income in either time period:
(5.5)
where π can be thought of as the productivity of cognitive skills in the labor market.
By substituting equation (5.2) into equation (5.5), then equation (5.5) into equations (5.3) and (5.4), and finally equations (5.2), (5.3), and (5.4) into equation (5.1), parents' utility is expressed as a function of years of schooling (S):
(5.6)
One can show (see the appendix) how the optimal (utility-maximizing) value of years of schooling is affected by changes in the model's various parameters. The findings are all intuitively plausible. Years of schooling increases when the following increase: (1) children's learning efficiency (α), (2) school quality (Q), (3) the weight (δ) parents give to future relative to current consumption, and (4) parents' tastes for schooling (σ). Years of schooling decreases when the price of schooling (p) rises. Finally, years of schooling is likely, though not certain, to rise when parents expect to receive a larger proportion (k) of their children's income from working and when the value of cognitive skills in the labor market (π) is higher.
Sometimes parents can choose not only years of school, but also school quality. The model can easily be extended to the case in which both years in school (S) and school quality (Q) are choice variables. To make the model more realistic, assume that the price of a school depends on its quality6:
(5.7)
where po is the "base" price of schooling. Thus high-quality schools have higher costs (p rises as Q increases). Equation (5.7) may at first seem to have an arbitrary functional form: If one school has a level of quality twice as high as that of another, why should the price be exactly twice as high, as opposed to less or more than twice as high? In fact, equation (5.7) is simply a normalization; Q should be interpreted as an index of expenditures on quality. Whether or not, say, doubling expenditures doubles the impact of school quality on learning (i.e., doubles f(Q)) depends on the functional form of f(Q).
After replacing p with poQ in equation (5.6), one obtains the following expression, which is to be maximized with respect to both S and Q:
(5.8)
Without further assumptions about the functional forms of f( ) and g( ), one cannot determine how changes in the various parameters, such as po, α, δ, and σ, affect S and Q. For ease of exposition, assume that f(Q) = Qß, where ß > 0, and g(S) = Sg where γ > 0. Differing values of ß and γ allow for a wide range of the shapes of both f( ) and g( ). Both ß and γ must be greater than zero to guarantee that f( ) and g( ) increase as Q and S, respectively, increase. Using these func-
tional forms, one can show (see the appendix) that parents' utility as given in equation (5.8) is maximized by setting S and Q as follows:
(5.9)
(5.10)
where the asterisk indicates the utility-maximizing (optimal) level for each variable. The optimal level of cognitive skills (A) is obtained by inserting equations (5.9) and (5.10) into equation (5.2).
Note that the optimal levels of S and Q in equations (5.9) and (5.10) are intuitively reasonable. Both years of schooling (S) and school quality (Q) are higher when parents give higher weight (δ) to future relative to current consumption, and parents have higher tastes for schooling (σ). School quality (Q) increases as learning efficiency (α) increases, but decreases as the base price of schooling (po) increases. A less plausible result is that years of schooling depends on neither the base price of schooling nor the innate ability of the child. This result admittedly is due to the functional forms used for f( ) and g( ), but it is not as unreasonable as it may first appear to be. What happens is that parents, in response to a lower base price or higher child learning efficiency, shift to higher quality, which raises their children's cognitive skills without changing years of schooling. By opting for higher quality instead of more years of schooling, parents avoid a cost associated with the latter—a reduction in the length of time a child works during time period 1 (see equation (5.3)). If school quality were not a choice variable, greater learning efficiency (α) or a lower price would lead to increased years of schooling, as explained above.
A final result that also appears counterintuitive is that an increase in the propensity of children to give money to their parents (k) or in the market return to cognitive skills (π) decreases years of schooling. Here again intuition suggests that the best response to such changes is to increase school quality and reduce time spent in school, which will increase the time the child spends working in time period 1.7
Implications of the Model for Statistical Analysis
The model presented above is useful for discussing several statistical issues involved in measuring the impact of school quality on learning. Most empirical studies of the impact of school characteristics on the acquisition of cognitive
skills are based on linear statistical models, an approach that simplifies estimation. Taking the logarithm of both sides of equation (5.2) and assuming exponential functional forms for f( ) and g( ) yields an equation that is linear in the logarithms of the variables.8 For ease of exposition, assume this latter equation is linear in the original variables; this assumption can be made because the following line of reasoning also applies to the linear-in-logarithms case. Thus the equation of interest is:
(5.2')
where the µ coefficients are unknown parameters to be estimated. The residual term e is added to account for the fact that in empirical work, no data fit the model perfectly.
Equation (5.2') can be estimated using simple statistical methods, but its specification of school quality is oversimplified. It is more realistic, and more useful for policy analysis, to decompose school quality into a function or index of the different school characteristics that promote learning. Doing so yields:
(5.2")
In equation (5.2"), Q has been replaced by an index of n different school characteristics (Q1, Q2 etc.) that affect the acquisition of cognitive skills. What policy makers want to know, and analysts need to estimate, is the magnitude of the various τ's. These estimates can be combined with data on the costs of the different school characteristics to assess the cost-effectiveness of each characteristic in promoting learning.
Equation (2") implicitly assumes that learning efficiency, α, can be observed. In fact, there are often few data on the factors determining learning efficiency, so equation (5.2") must be rewritten as:
(5.11)
where α (and its coefficient) is combined with e to produce u, a residual term that represents both random "noise" from imperfectly fitting data and the impact of unobserved aspects of learning efficiency (α) on cognitive skill acquisition (A). Examples of learning efficiency variables that are difficult to observe are the child's innate ability and motivation and the parents' motivation (and ability) to help children with schoolwork.9
Equation (5.11) is commonly estimated using ordinary least squares (OLS) regression. OLS provides unbiased estimates of all parameters (the µ's and τ's) in equation (5.11) only if the residual term, u, is uncorrelated with S and the various Q's. However, the simple model presented earlier shows that such correlation is very likely; in equation (5.10), higher learning efficiency (α) increases school quality (Q), implying that u, which represents (in part) variation in α, is positively correlated with the various Q's. The result in general will be overestimation of the associated parameters (τ's). Few empirical studies do anything to avoid this statistical problem.
If school quality is not a choice variable, the estimation problem discussed above can be avoided. In rural areas of many developing countries, school quality may well be exogenous because each village has only one school, and villages are too far apart for children to attend school in a neighboring village. In such cases, the Q variables in equation (5.1 1) may not be correlated with the error term, u. Yet even under this scenario, parents may still be able to influence school quality. First, they may directly affect quality at the sole local school by participating in the parent-teacher association (PTA) or using political connections to obtain better educational services. Second, they may send their children to live with relatives or at a boarding school, thus allowing them to attend a nonlocal school.10 Third, families with higher tastes for educated children may migrate to areas with better schools, a common occurrence in the United States.
Since parents may affect school quality even in rural areas, then, overestimation is possible. Yet it is also possible that endogenous school quality leads to underestimation. Even if parents cannot affect school quality, it could be correlated with the error term because governments may provide better schools to areas with unobserved education problems (Pitt et al., 1993). These unmeasured problems would again be relegated to u in equation (5.11), producing negative correlation between the error term and the school quality variables (Q's) and thus underestimating the impact of school quality.
Even when school quality is completely uncorrelated with the error term in equation (5.1 1), years of schooling (S) may be correlated. Note that in equation (5.9), parents with higher tastes for schooling (σ) send their children to school longer. These tastes are rarely measured, and any effect they have on learning efficiency (e.g., such parents help children more with schoolwork) would be reflected in the error term u, leading to positive correlation with S. This in turn
|
|
one can measure all of them. Indeed, it is not even clear that innate ability can be measured; any test that purports to do so (in the sense of genetic endowment) is likely to reflect environmental factors (American Psychological Association, 1995). One possible way to get around this problem is to use data on twins (see Behrman et al., 1994). However, such data are very rare in developing countries. |
would lead to biased estimates of the coefficient on S, as well as of the other estimated coefficients, both µ's and τ's. Instrumental variable techniques, such as two-stage least squares, may correct this problem. One possible instrument for years of schooling is the price of schooling, which should affect learning only by affecting years of schooling. Another approach is to estimate equation (5.11) for a single grade to remove variation in S.
Three additional problems merit attention. First, if some children in the relevant age range are not in school, the remaining children (whether in one or several grades) are not a random sample of the population. Intuitively, communities with high-quality schools will keep children in school longer, leading to a student population with lower average learning efficiency (because more ''less-efficient" children stay in school). This implies that u in equation (5.11) will be negatively correlated with school quality, resulting in underestimation of the impact of school quality on learning. Second, no data set includes every determinant of school quality, and observed aspects of quality may be positively correlated with unobserved aspects (because "good" schools are often good in many ways, only some of which are measured). Again, unmeasured aspects of school quality are, by default, part of the residual term in equation (5.11), causing u to be positively correlated with observed school quality variables and causing the τ parameters to be overestimated. A final difficulty in empirical work is measurement error in the explanatory variables, both S and the various Q variables. If these variables are not measured precisely, random measurement error will cause underestimation of the impact of both S and Q on the acquisition of skills. Nonrandom measurement error could lead to either underestimation or overestimation.
In summary, there are at least six ways in which uncritical application of common statistical methods can lead to biased estimates of the impact of school quality on learning. Some lead to underestimation and others to overestimation, while still others could go either way. These potential problems must be considered in assessing the findings of existing research, which are addressed in the next section.
What Is Known About The Impact Of School Quality On Learning And Years Of Schooling?
The simple model presented in the previous section suggests that the impact of school quality on students' cognitive skills operates in two ways—raising years of schooling attained and increasing learning per year of schooling. Building on the preceding discussion, this section assesses the literature on the determinants of cognitive skill attainment in developing countries, focusing on the role of school quality. It is argued that much remains to be learned, and several suggestions for future research are made.
Assessment of the Recent Literature
There is a large literature for developed countries and a growing literature for developing countries on the determinants of educational attainment and cognitive skill acquisition. The discussion here focuses on the developing-country literature; for recent reviews of the developed-country literature, see Hanushek (1986) and Hanushek et al. (1994).
Most of the literature on the determinants of learning in developing countries has focused on the impact of school quality on skills learned per year of schooling. Less work has addressed the impact of school quality on educational attainment. Comprehensive reviews of the literature since 1990 include Lockheed and Verspoor (1991), Harbison and Hanushek (1992), Velez et al. (1993), Fuller and Clarke (1994), Strauss and Thomas (1995), and Hanushek (1995). These reviews usually assemble a large number of studies and then tally, for many different school and teacher characteristics (or policies), (1) the number of studies that examined a particular characteristic and (2) the number of those studies that found a statistically significant effect of that characteristic on achievement test scores. Only one review, Strauss and Thomas (1995), seriously criticizes the statistical methods used. The others tend to accept results at face value even though, as Hanushek (1995:231-32) points out, "the standards of data collection and analysis are so variable that the results . . . are subject to considerable uncertainty."
Table 5-1 summarizes the findings of four reviews that follow the "typical" approach.11 The Strauss and Thomas study is excluded because it examines only five studies and draws few specific conclusions (see pp. 1956-59), and the later Hanushek study is excluded because it is based on Harbison and Hanushek (1992). Table 5-1 reveals three consistent findings: (1) class size has no effect, (2) teacher salaries have no effect, and (3) textbooks have a positive effect. A few other school or teacher characteristics look promising, but their effect is less certain because it is based on only two of the four reviews (radio instruction, school library, nutrition and feeding program, teacher's cognitive skills) or because the results for that characteristic are mixed (teacher education, physical facilities). However, meta-analysis techniques can be used to form judgments on many, if not most, of the ambiguous cases; for example, Kremer (1995) shows how the apparently ambiguous results in Harbison and Hanushek (1992), as reported in Hanushek (1995), can provide definitive answers.12
|
11 |
Table 5-1 does not include all the findings presented in each literature review. In particular, it excludes findings unrelated to school quality or considered by only one of the four reviews. Note that the table sometimes imputes values of "yes," "no," or "maybe" when the authors were reluctant to be so explicit. |
|
12 |
See Hedges et al. (1994) for an application of meta-analysis techniques to U.S. data, and Hanushek (1995) for a somewhat skeptical interpretation of the results. |
TABLE 5-1 Summary of Findings on Determinants of Cognitive Achievement from Four Recent Literature Reviews
|
Characteristic |
Lockheed and Verspoor (1991) |
Harbison and Hanushek (1992) |
Velez et al. (1993) |
Fuller and Clarke (1994) |
|
Class Size |
No |
No |
No |
No |
|
Expenditure per Pupil |
— |
Maybe |
— |
Yes |
|
Teacher Salaries |
— |
No |
No |
No |
|
Textbooks |
Yes |
Yes |
Yes |
Yes |
|
Radio Instruction |
Yes |
— |
— |
Yes |
|
School Library |
— |
Yes |
— |
Yes |
|
Nutrition/Feeding Program |
Yes |
— |
— |
Yes |
|
Teacher Training |
Yes |
Maybe |
No |
Yes |
|
Teacher Skills (test scores) |
— |
— |
Yes |
Yes |
|
Teacher Education |
— |
Yes/Maybe |
Yes |
Maybe |
|
Teacher Experience |
— |
No |
Yes |
Maybe |
|
Physical Facilities |
— |
Yes |
Maybe |
Yes |
|
Number of Studies Analyzed |
Large number, but not specified |
96 |
18 |
Over 100 |
Unfortunately, the greater clarity offered by meta-analysis techniques must be balanced against the fact that most of the results discussed in these literature reviews should not be taken at face value. In particular, it is not clear whether the regularities found indicate real phenomena or simply reflect inappropriate use and interpretation of commonly employed statistical methods. The statistical problems raised at the end of the previous section are rarely considered in the literature.13 Moreover, even with a rich set of data and careful use of sophisticated statistical methods, it is almost impossible to eliminate completely all potential sources of bias. In principle, the best method for overcoming almost all sources of bias is randomized trials of specific educational interventions. Such trials randomly divide a set of schools into a treatment group that receives a particular educational input or enacts a particular policy and a control group that receives no inputs and enacts no new policy. Very few such studies have been done in developing countries,14 though some new studies are under way at the
World Bank. Such studies are rare because they are very expensive and because they can examine only one or two policy changes at a time.
Finally, two other gaps remain in the literature. First, as noted by Fuller and Clarke (1994), cost-effectiveness calculations are rarely done. Improvements in cognitive achievement per dollar spent is the ultimate concern of policy makers. For example, consider the use of computers; Lockheed and Verspoor (1991) point out that although computers increase learning in developing countries, they are much more expensive (in terms of learning per dollar spent) than several other policies to the same end. Unfortunately, some school policies, such as changes in instructional techniques, are difficult to price. The study by Glewwe et al. (1995) was explicitly designed for cost-effectiveness calculations, but in the end could not achieve this purpose because almost no effective school policies could easily be priced. A second gap in the literature is that studies rarely examine the impact of school quality on learning through its effect on years of schooling.15 This may be an important pathway for increasing human capital in developing countries. Glewwe and Jacoby (1994) show that it can account for a third, or even more, of the total impact of particular school quality improvements on learning.
In summary, the existing literature on the impact of school quality on learning in developing countries suffers from many deficiencies. Some results are found so consistently that one can probably subscribe to them, but many more have less solid support. Even the findings with apparently solid support can be questioned because they are based on uncritical use of statistical methods. The most serious statistical problems are (1) omission of many important school and teacher variables from analyses because of data limitations and (2) measurement error in school quality variables. Problems of endogeneity and sample selectivity are less salient because studies that attempt to address them rarely find that the main results change.16 Recall that omitted-variable bias generally leads to overestimation, while random measurement error generally leads to underestimation. Given these effects in opposite directions, it is unclear how much confidence one can have in the existing literature. Yet in fairness to the literature, one must recognize that education is a highly complex process and that the data for analyzing it have typically been inadequate. A final complication is that the true determinants of learning may vary widely across developing countries. Nothing can be done about this, and sizeable variation should be expected given the vast differences in the school systems in developing countries.
Recommendations for Future Research
The pessimistic assessment of the current literature given above raises the question of what can be done to improve the state of knowledge in this area. Three broad recommendations are offered here.
First, statistical and econometric techniques need to be used more cautiously, with more rigorous testing of the underlying assumptions. In the econometric literature, this is known as specification testing (see Godfrey, 1988). Economists have only recently begun to do rigorous specification tests, and such tests are even rarer in research on education in developing (and developed) countries. The need to examine statistical methods critically also applies to literature reviews. There is an urgent need for a literature review that separates insufficiently rigorous findings (which may predominate in the literature) from findings based on careful statistical analysis and then applies meta-analysis techniques to the latter to assess what really works.
Second, much better data need to be collected. Education researchers often use school-based data that include little information on students' home characteristics. Moreover, in countries without universal school enrollment, school-based samples are nonrandom samples of the population. Other researchers use household survey data that provide little information on school and teacher characteristics. Future data collection should combine household surveys with detailed data on schools and teachers, and should also include more collection of panel data, which may avoid several estimation problems. Regrettably, panel data are rare in the developing-country education literature. Finally, many developing countries do not regularly collect data on student performance (Lockheed, 1995). These countries urgently need national testing of cognitive skills to see what students are really learning. These assessments can also lower the cost of collecting data for research purposes, since testing children is a major cost of such research.
Third, more randomized trials of educational interventions are needed. Such trials are one way to address the statistical problems that cast serious doubt on most existing studies. In addition, their results are fairly easy to explain to policy makers. Major multilateral and bilateral agencies that fund educational interventions should incorporate randomized trials in all major projects to assess project effectiveness and build a better information base on what really works. Of particular interest are comparisons of results from randomized trials with results produced by more conventional studies, which may indicate when the latter results are reliable. At the same time, it should be borne in mind that despite these advantages, randomized trials are no panacea; they can suffer from a variety of design and implementation problems, as pointed out by Heckman and Smith (1995).
Possible Impact Of Improvements In School Quality On Fertility
This and the next section focus on the impact of school quality on fertility. As noted earlier, while a fair amount of work has been done on the impact of school quantity on fertility, there is almost no theoretical or empirical work that specifically addresses the impact of improvements in school quality. However, what little work there is on the latter does provide some insights. This section reviews what economic theory can say about the likely impact of improvements in school quality on fertility, while the following section reviews the limited empirical literature that addresses this issue.
Changes in school quality can affect fertility in two distinct ways. First, when today's parents are making current childbearing decisions, they may take into account the quality of local schools. If school quality changes, parents may revise their childbearing plans, and if they do so, there will be an immediate effect of school quality on fertility. Second, even if today's parents make no significant changes in their childbearing plans, improved school quality will probably lead them to provide more education to each of their children, as was shown in the model presented earlier. When children, particularly daughters, reach childbearing age, their increased levels of schooling and higher cognitive skills per year of schooling may well lead them to have fewer children (see also Chapter 2). This effect of school quality on fertility will not manifest itself until many years after school quality changes. The following subsections address each of these pathways in turn.
Impact of School Quality on Current Fertility Decisions of Today's Parents
The standard reference for economic models of fertility is Becker (1981), particularly Chapter 5. The basic model is not presented here, but its essence is quite simple. Parents' utility is determined by three factors: (1) consumption of goods and services; (2) the number (quantity) of children they have; and (3) the average quality of their children, as measured by cognitive skills and schooling. All three factors have associated prices; note in particular that the price of child quality is primarily the cost of a year of schooling. This utility function is a generalization of the parental utility function presented earlier in equation (5.1), in which utility depends on consumption and child quality, but not on the number of children (which is assumed to be exogenous).
In virtually all discussions of Becker's model, it is assumed that the price of schooling refers to the quantity of schooling. However, there is no reason price cannot also be interpreted as referring to school quality. In particular, recall equation (5.7), and note how it enters the utility function in equation (5.8). The expression poQS rises if either Q or S rises; it can be interpreted as the price of S
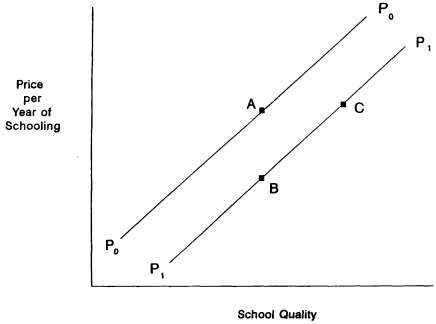
FIGURE 5-2 Price per year of schooling and school quality.
when Q is fixed or the price of Q when S is fixed.17 This point is made more intuitively by Figure 5-2, which shows the price of a year of schooling as a function of school quality. The line P0P0 shows the initial set of prices for different levels of school quality, and the line P1P1 shows a reduction in that price that is equivalent to a reduction in po in equation (5.7). One can think of this price reduction as either a reduction in the price of a year of schooling for a fixed quality (movement from A to B) or an increase in school quality for the same price per year of schooling (movement from A to C).
The implication of the above discussion is that models that examine the impact of the price of school quantity on fertility can also be used to assess the impact of changes in the price of school quality on fertility. This is possible because there is really only one price, changes in which can be interpreted as either changes in the price of quantity or changes in the price of quality. The
question then arises of what those models can tell us about the impact of the price of schooling on fertility. While Becker does not explicitly address this question, it is examined by Rosenzweig (1982), who shows that the impact of a decrease in the price of schooling on the fertility decisions of today's parents is ambiguous. The reason for this is simple: a decrease in the price of schooling is effectively a decrease in the price of child quality. Price effects suggest that parents will buy more child quality and less child quantity and fewer consumption goods. However, income effects suggest that parents will buy more of all three goods. Thus a decrease in the price of school will clearly raise the average schooling of children (since the price and income effects move in the same direction), but the effects on the number of children and consumption of other goods will be ambiguous.18
In summary, there has been no theoretical work examining the impact of changes in school quality, or more generally the price of school quality, on the current fertility decisions of today's parents. However, one can derive such results from economic models of fertility because there is really no difference between the price of school quantity and the price of school quality. The impact of a decrease in the price of schooling, which is essentially the same as a decrease in the price of school quality (or an exogenous increase in school quality), has an ambiguous effect on fertility because the income and substitution effects work in opposite directions: the former effect raises fertility (assuming child quantity is a normal good), while the latter effect reduces it. This theoretical ambiguity means one must examine the empirical evidence, which is done in the next section.
Impact of School Quality on Future Fertility Decisions of Today's Children
The previous subsection focuses on the impact of school quality on the fertility decisions made by today's parents, but it also explains that parents are likely to increase the average education levels of their children if school quality improves. When these children become adults, they will make their own fertility decisions, which will be influenced by the higher levels of human capital they have as a result of past improvements in school quality. There is now a fairly large literature on the determinants of fertility in developing countries, and one of the almost universal findings is that higher education leads to reduced fertility (Schultz, 1993; United Nations, 1995; Ainsworth et al., 1996; see also Chapter 2). Thus, improved school quality today will lead to reductions in future fertility when today's children become adults. Of course, the mechanisms by which this
comes about are quite complicated; Figure 5-3 depicts the various mechanisms involved.
For simplicity, Figure 5-3 does not distinguish between school quality and years of schooling. Together with other household and child characteristics (recall Figure 5-1), school quality and years of schooling affect children's values (arrow a), fertility knowledge (arrow c), and cognitive skills (arrow d).19 Fertility knowledge will be acquired directly in school only if it is part of the curriculum, such as a family-life course.20 Such knowledge can also be acquired indirectly through cognitive skill attainment; literacy acquired in school gives women (and men) the means to acquire fertility knowledge by reading various forms of written information (arrow f). These three direct products of schooling—values, fertility knowledge, and cognitive skills—have implications for young women in two different markets: the marriage "market" (arrows i, j, and k, respectively) and the labor market (arrow o).21 Cognitive skills also affect women's ability to promote child quality, that is child health and schooling (arrow p).
A woman's value in the marriage market can be thought of as her marriage prospects (see also Basu, this volume). In general, better-educated spouses are more valuable as wives, though some men may prefer less-educated wives because they are thought to be more subservient. A woman's value in the marriage market, as well as her own values, will determine her spouse's characteristics and her age at marriage (arrows h and q, respectively). In the labor market, the impact of cognitive skills, and possibly years of schooling (arrow e), on the value of a woman's time is almost always positive; that is, education raises the woman's productivity in the labor market. Similarly, cognitive skills increase her ability to raise high-quality children (arrow p). In a penultimate step, a woman's fertility knowledge, her cognitive skills, the value of her time, her ability to raise high-quality children, and her spouse's characteristics will determine the woman's bargaining power in marriage (arrows m, n, s, t, and v, respectively).22 The last step in Figure 5-3 shows how a woman's values, her spouse's characteristics and her age at marriage, her fertility knowledge, the value of her time, her bargaining
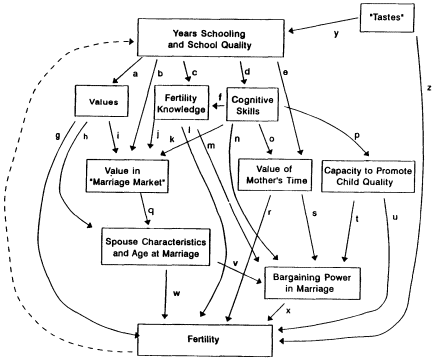
FIGURE 5-3 Relationship between schooling and fertility.
power within her marriage, and her ability to raise high-quality children (arrows g, w, l, r, x, and u, respectively) determine her fertility. A final point, noted earlier, is that it is also possible for fertility to affect schooling outcomes; a female student who has a child while in school may have to leave school. This arrow is dashed to indicate reverse causality.
The above discussion of Figure 5-3 is not intended to be an all-encompassing description of how education affects fertility. Indeed, the figure could be made even more complex.23 However, the discussion does demonstrate the complexity of the impact of schooling, in terms of both years of schooling attained and school quality, on the future fertility of today's children. Yet there is one more aspect of the relationship between education and fertility that deserves mention because the connection is not causal at all. One can imagine that young women vary in their tastes for different choices to be made during their lives. These
tastes can play a role in determining both schooling and fertility (arrows y and z).24 In particular, women who are less family oriented and more career oriented will tend to have both higher levels of schooling and lower fertility, even in the absence of a causal link from the former to the latter; rather, the causality operates through a third factor, tastes. Because such tastes are not easily observed, this possibility further complicates attempts to understand the relationship between schooling and fertility in both developed and developing countries.
Empirical Evidence On The Impact Of School Quality And Fertility
Impact on Current Decisions of Today's Parents
The present review revealed no empirical work that explicitly addresses the impact of school quality on the current fertility decisions of today's parents in developing countries. However, one can get at this issue by examining empirical work on the impact of school prices on fertility. While no studies were found that explicitly examine the impact of school prices, two studies examine the impact of availability of local schools, which can be interpreted as a price effect. The first is that of Rosenzweig (1982), which uses household survey data from India. It finds no significant impact of the availability of a local primary school on fertility rates. The second is that of Pitt et al. (1993), which uses district-level data from Indonesia. It finds that the presence of middle and high schools has no significant effect on fertility, while the presence of primary schools does have a small but significantly positive effect.
Of course, both of these studies can be criticized. Rosenzweig does nothing to control for the possible endogeneity of the presence of schools in a village; although the problem is noted, the conclusion is that nothing can be done to address it. In addition, variation in tastes for child quality and quantity are ignored. If some households or villages favor quantity while others favor quality, the results will be biased in favor of showing a negative effect of school availability on fertility. The implication is that an ambiguous result may mask a genuine positive relationship. Measurement error may also be a problem because the availability of a local school is a very crude indicator of school prices. The Pitt et al. (1993) study also has shortcomings. The data used include no information on household income or nonland assets, leading to possible omitted-variable bias (perhaps wealthier communities have more children, other things being equal, and also are able to lobby the government to build local schools). In addition, the fixed-effects estimates presented assume no interaction effects between observed variables and the fixed effects that are differenced out during estimation.
In summary, there is a small amount of evidence on the impact of school quality on the fertility decisions of today's parents, which can be inferred by looking at the impact of school availability on fertility. One study finds an insignificant effect of primary schools, while another finds a small but significant effect of primary schools, but no significant effect of middle or high schools. While these studies constitute a sample size of two and can be criticized on methodological grounds, they are relatively careful as compared with the literature reviewed earlier. Thus the little evidence available suggests no sizeable effects of school quality on the fertility decisions of today's parents. Of course, school quality may affect fertility in the future. This possibility is examined in the next subsection.
Impact on Future Decisions of Today's Children
We turn now to the impact of improvements in school quality on the future fertility decisions of today's children. Figure 5-3 shows that the relationship between education and fertility, while complex, must work through one of the following four pathways: (1) changes in values brought about by schooling, (2) changes in fertility knowledge, (3) cognitive skills learned in school, and (4) a noncausal relationship whereby an individual's tastes determine both schooling outcomes and fertility. Knowledge of the relative importance of these pathways and of the distinct contributions (if any) of specific types of cognitive skills would provide a much clearer picture of the role played by school quality in affecting future fertility, and might even demonstrate how changes in school curriculum could lead to reductions in fertility.
There appear to be only three studies that attempt to disentangle the various pathways through which schooling leads to reduced fertility. The first, Lam and Duryea (1999), uses Brazilian data to look at the impact of years of schooling on both fertility and labor force participation. At low levels of schooling, the authors find strong effects of years of schooling on fertility, but only weak effects on labor supply. They also find strong effects of low levels of schooling on child health. While many studies have examined the impact of schooling on both fertility and labor force participation, the Lam and Duryea study is distinctive in that it uses the results to say something about the pathways by which schooling affects fertility. In particular, the authors interpret the evidence, especially the effects of low levels of schooling, as indicating that the effects of schooling on fertility work, at least in part, through pathways other than those based on the value of a mother's time in the labor market.
Although the analysis of Lam and Duryea is intriguing, some of the findings can be criticized. First, their regressions on the determinants of fertility assume that a mother's schooling and that of her spouse are exogenous, which can be questioned. In particular, the positive relationship between higher schooling and lower fertility may reflect, at least in part, the impact of tastes as depicted in
Figure 5-2. Second, part of the impact of mother's schooling may work through spouse's schooling, in that a better-educated woman will choose a better-educated spouse (see also Basu, this volume). Third, many other variables that may determine fertility, such as local family planning or health services, are not included in the regression. Fourth, the authors ignore the possibility that part of the causality underlying the relationship between schooling and fertility may run from the latter to the former as a result of pregnancy forcing young women to drop out of school.
A second study addressing the pathways by which schooling leads to reduced fertility is by Oliver (1997). It uses data on women's cognitive skills to understand the relationship between education and fertility. In particular, it uses the 1988-1989 Ghana Living Standards Survey to show that a woman's level of literacy, but not her level of mathematical ability, leads to reduced fertility.25 In addition, it finds that years of schooling has a strong negative effect over and above the effect due to literacy. This finding suggests that either values, fertility knowledge, or perhaps cognitive skills other than literacy and numeracy can play a role in reducing fertility beyond the role played by the acquisition of basic cognitive skills.
Oliver's findings can be interpreted in terms of Figure 5-3. She shows that improvements in school quality reduce fertility by raising cognitive skills (arrow d in Figure 5-3). In addition, she shows that more years of schooling reduces fertility even after controlling for the effect that works through cognitive skills. This could occur because schooling changes students' values, their value in the marriage market, or their fertility knowledge (arrows a, b and c, respectively). Unfortunately, the data used by Oliver cannot distinguish among these alternative pathways.
Another intriguing aspect of Oliver's study is that it relates the impact of literacy and years of education on fertility to specific components of school quality. In particular, the study presents estimates of the impact of six middle school quality improvements on the number of children ever born, and for three of those a cost-effectiveness ratio is given. These results are shown in Table 5-2. The total impact of the different school improvements varies from a fertility reduction (measured in terms of children ever born) of 0.04 due to providing textbooks to a reduction of 0.64 due to providing blackboards. Note that much of this effect comes about because these schooling improvements also raise years of schooling (see column 2 of Table 5-2). Of the three schooling improvements for which cost-effectiveness figures are calculated, provision of blackboards is by far the least expensive avenue to reduce fertility. Repair of leaking classroom roofs is more expensive, and the costliest of the three is provision of textbooks. It would be interesting to compare these cost figures with the cost of reducing
TABLE 5-2 Impact of Middle School Improvements on Children Ever Born in Ghana
|
|
Impact on Children Ever Born |
|
|
|
|
Middle School Improvement |
Reading Scores |
Years of School |
Total |
Cost-Effectivenessa |
|
Reducing travel time from 2 to zero hours |
0.121 |
0.171 |
0.292 |
— |
|
Raising average teacher experience from 2 to 10 years |
0.112 |
0.158 |
0.270 |
— |
|
Providing a school library |
0.066 |
0.094 |
0.160 |
— |
|
Repairing classrooms that cannot be used when it rains |
0.288 |
0.153 |
0.441 |
1,273-2,545 cedis |
|
Providing blackboards in schools where none exist |
0.440 |
0.200 |
0.640 |
100-200 cedis |
|
Providing 50 textbooks per room in schools that now have 25 per room |
0.044 |
— |
0.044 |
36.364-60.605 cedis |
|
a These figures indicate the cost of reducing total predicted (future) children ever born to students in the improved classroom by 1. Note that the data presented here were collected in 1988-1989, at which time the exchange-rate value of the Ghanaian cedis was about 200 cedis per U.S. dollar. SOURCE: Oliver (1997). |
||||
fertility through typical family planning programs; unfortunately, Oliver does not do this in her study.
Oliver's study does suffer from some methodological shortcomings. The schooling of the mother is assumed to be exogenous, which ignores the possible role of tastes in determining the relationship between schooling and fertility. It is also likely that omitted-variable bias is present because several variables that may determine fertility are not included, such as the availability of family planning and health services. Third, the possibility that fertility could reduce schooling because pregnant girls quit school is not considered. Finally, although the attempt to relate fertility reduction to specific changes in school quality is particularly valuable, the study does not address aspects of school quality that are likely to change a child's values. This is an admittedly difficult task, and it is questionable whether any existing data could be used to investigate this aspect of schooling and fertility.
A final study that sheds light on the impact of school quality on fertility is that of Thomas (see Chapter 6), who uses recent household survey data from South Africa to examine how schooling affects fertility. In particular, Thomas examines the effect of years of schooling and of scores on mathematics and reading comprehension tests on children ever born. His findings are similar to those of Oliver. Reading comprehension has an important effect, but mathematics skills have no significant effect, and even when both of these variables are included in the regression, years of schooling still has a strong independent effect. Unfortunately, Thomas' South African data cannot be used to examine how specific aspects of school quality determine the acquisition of cognitive skills.
As with the other two studies, Thomas' work suffers from several shortcomings, most of which cannot be corrected with the available data. The role of tastes in determining both schooling and fertility may seriously bias the estimates, or at least reduce what can be inferred from them. The possibility of reverse causality, that is, of women dropping out of school because of pregnancy, is not considered. Finally, the general problems of omitted-variable bias and measurement error are not addressed.
In summary, these three studies support the common finding that schooling is associated with reduced fertility. The studies of Oliver and Thomas show that reading comprehension skills, but not mathematics skills, directly affect fertility, and Oliver's paper shows the association between specific changes in school quality and reduced fertility. Finally, the results of all three studies imply that the impact of schooling on fertility is not just a matter of attaining mathematics and reading skills. However, much more remains to be learned. What can be done about this need is briefly discussed in the following subsection.
Recommendations for Future Research
The most obvious recommendation for future research on the impact of school quality on fertility is that much more of such research should be done. First, more research is needed on the impact of school quality on the current fertility decisions of today's parents. This work should examine the impact of school quality directly, as opposed to relying on the price of schooling or the availability of a local school. Second, much more can be done to examine the impact of current changes in school quality on the future fertility decisions of today's children. As in the study by Oliver (1997), this work can be divided into two parts: the impact of a variety of cognitive skills, knowledge, and even attitudes on fertility, and the impact of improvements in school quality on all of those determining factors. While some initial work has been done on the most basic cognitive skills, almost nothing has been done on other cognitive skills or on knowledge and attitudes.
As with the literature on the determinants of school quality, another obvious
recommendation is that more useful data should be collected. Data are needed on school quality, fertility, and cognitive skills, plus attitudes and fertility knowledge (and other knowledge as well, such as health knowledge), from the same households. If data that follow young women over several years can be collected, a link can be made between specific schooling outcomes and subsequent fertility outcomes. Alternatively, if only cross-sectional data can be collected, the data should include the skills of adult women (determined by administering achievement tests) to see how those skills are related to fertility. Both types of data go well beyond what is usually collected in developing countries, which explains the paucity of research on the pathways by which school quality affects fertility.
Finally, the call for more randomized evaluations of education policies made earlier also applies here. Although this section has not gone into detail on the statistical problems that complicate attempts to estimate the impact of school quality on fertility (see Strauss and Thomas, 1995, for a discussion of this issue), many such problems do arise that are difficult to solve. Randomized evaluations can, in principle, get around almost all of these problems.26 There have apparently been no randomized trials relating schooling to fertility in developing countries, perhaps because the time lag between a schooling intervention and the future fertility outcomes of today's children may be many years. Again, bilateral and multilateral aid agencies need to take the lead on this matter by building randomized evaluations into their development projects.
Conclusion
The main message of this chapter is that very little is known about what determines school quality in developing countries, and even less is known on how school quality affects fertility. This state of affairs exists even though a large number of studies have been done on the first topic—the relationship between school quality and learning. There are two main reasons that little is known about this relationship: (1) statistical tools have not been used very carefully, and (2) the data available are usually inadequate for the task. Both of these problems need to be addressed in future work. In addition, randomized evaluations of schooling interventions hold promise for addressing some of the more intractable statistical problems. Given the apparent inefficiencies in the way schools operate in developing countries, improving the general state of knowledge on which interventions are most cost-effective has the potential to bring about sizeable increases in learning, and eventually in the standard of living, in those countries.
While the relationship between the quantity of schooling and fertility has
been documented numerous times, the effect of school quality on fertility has rarely been examined. Better knowledge of the various pathways involved in the latter could lead to policy recommendations that would ultimately help bring about further reductions in fertility. For example, the little evidence produced thus far suggests that spending more class time on reading skills and less on mathematics may reduce fertility. However, much more must be learned before such broad policy recommendations can be made, and one must bear in mind that fertility reduction is only one of many different schooling outcomes to be considered when contemplating such changes.
Finally, since this chapter was written from an economist's perspective, there is one more difficult question to raise: Why should the government concern itself with trying to alter households' fertility decisions? There is a tendency among many demographers to assume at the outset that fertility levels in developing countries are too high. This may be so, but it should be demonstrated instead of merely assumed. If demographers want to win the support of economists on this issue, more theoretical and empirical work may be needed.
Acknowledgments
The findings, interpretations, and conclusions expressed in this paper are entirely those of the author. They do not necessarily represent the views of the World Bank, its executive directors, or the countries they represent. I would like to thank Andrew Foster, Bruce Fuller, Hanan Jacoby, Emmanuel Jimenez, the editors of this volume, and two anonymous referees for very useful comments on and/or discussion of previous drafts.
References
Ainsworth, M., K. Beegle, and A. Nyamete 1996 The impact of women's schooling on fertility and contraceptive use: A study of fourteen sub-Saharan African countries. World Bank Economic Review 10(1):85-122.
Alderman, H., J. Behrman, S. Khan, D. Rose, and R. Scott 1995a Public schooling expenditures in rural Pakistan: Efficiently targeting girls and a lagging region. In D. van de Walle and K. Nead, eds., Public Spending and the Poor: Theory and Evidence. Baltimore, Md.: The Johns Hopkins University Press.
Alderman, H., P.A. Chiappori, L. Haddad, J. Hoddinott, and R. Kanbuv 1995b Unitary versus collective models of the household: Is it time to shift the burden of proof? World Bank Research Observer 10(1): 1-19.
American Psychological Association 1995 Intelligence: Knowns and Unknowns. Report of a task force established by the Board of Scientific Affairs of the American Psychological Association. Washington, D.C.: American Psychological Association.
Becker, G. 1981 A Treatise on the Family. Cambridge, Mass.: Harvard University Press.
1995 Human Capital and Poverty Alleviation. HRO Working Paper No, 52. Human Resources Development and Operations Policy Vice Presidency. Washington, D.C.: The World Bank.
Behrman, J. 1997 Intrahousehold Distribution and the Family. In M. Rosenzweig and O. Stark, eds., Handbook of Population and Family Economics. Amsterdam: North Holland.
Behrman, J., M. Rosenzweig, and P. Taubman 1994 Endowments and the allocation of schooling in the family and in the marriage market: The twins experiment. Journal of Political Economy 102(6)1131-1174.
Cox, D., and E. Jimenez 1991 The relative effectiveness of private and public schools: Evidence from two developing countries. Journal of Development Economics 34:99-121.
Fuller, B., and P. Clarke 1994 Raising school effects while ignoring culture?: Local conditions and the influence of classroom tools, rules and pedagogy. Review of Educational Research 64(1)119-157.
Gertler, P., and P.Glewwe 1990 The willingness to pay for education in developing countries: Evidence from rural Peru. Journal of Public Economics 42:251-275.
Glewwe, P. 1998 The Economics of School Quality Investments in Developing Countries: An Empirical Study of Ghana. London: Macmillan.
Glewwe, P., M. Grosh, H. Jacoby, and M. Lockheed 1995 An eclectic approach to estimating the determinants of achievement in Jamaican primary school. World Bank Economic Review 9(2):231-258.
Glewwe, P., and H. Jacoby 1994 Student achievement and schooling choice in low income countries. Journal of Human Resources 29(3):843-864.
Glewwe, P., M. Kremer, and S. Moulin 1998 Textbooks and Test Scores: Evidence from a Prospective Evaluation in Kenya. Draft paper. Washington, D.C.: The World Bank.
Godfrey, L.G. 1988 Misspecification Tests in Econometrics. Cambridge: Cambridge University Press.
Hanushek, E. 1986 The economics of schooling: Production and efficiency in public schools. Journal of Economic Literature 25:1141-1177.
1995 Interpreting recent research on schooling in developing countries. World Bank Research Observer 10(August):227-246.
Hanushek, E., C. Benson, R. Freeman, D. Jamison, H. Levin, R. Maynard, R. Murnane, S. Rivkin, R. Sabot, L. Solomon, A. Summers, F. Welch, and B. Wolfe 1994 Making Schools Work: Improving Performance and Controlling Costs. Washington, D.C.: Brookings Institution.
Harbison, R., and E. Hanushek 1992 Educational performance of the poor: Lessons from rural northeast Brazil . New York: Oxford University Press.
Haveman, R., and B. Wolfe 1984 Education and economic well-being: The role of non- market effects. Journal of Human Resources 19:377-407.
Heckman, J., and J.A. Smith 1995 Assessing the case for social experiments. Journal of Economic Perspectives 9(2):85110.
Hedges, L., R. Laine, and R. Greenwald 1994 Does money matter? A meta-analysis of studies of the effects of differential school inputs on student outcomes. Educational Researcher 23:5-14.
Heyneman, S.P., D.T. Jamison, and X. Montenegro 1984 Textbooks in the Philippines: Evaluation of the pedagogical impact of nationwide investment. Educational Evaluation and Policy Analysis 6(2): 139-150.
Jamison, D., B. Searle, K. Galda, and S. Heyneman 1981 Improving elementary mathematics education in Nicaragua: An experimental study of the impact of textbooks and radio on achievement. Journal of Educational Psychology 73(4):556-567.
Jimenez, E., M. Lockheed, E. Luna, and V. Paqueo 1991 School effects and costs for private and public schools in the Dominican Republic. International Journal of Education Research 15:393-410.
Jimenez, E., M. Lockheed, and N. Wattanawaha 1988 The relative efficiency of public and private schools: The case of Thailand. World Bank Economic Review 2:139-164.
Kagitcibasi, C., D. Sunar, and S. Bekman 1993 Long-Term Effects of Early Intervention. Department of Education, Bogadzdi University, Istanbul, Turkey.
Kremer, M. 1995 Research on schooling: What we know and what we don't, a comment on Hanushek. World Bank Researcher Observer 10:247-254.
Kremer, M., S. Moulin, D. Myatt, and R. Namunyu 1997 Textbooks, Class Size and Test Scores: Evidence from a Prospective Evaluation in Kenya. Cambridge, Mass.: Department of Economics, Massachusetts Institute of Technology.
Lam, D., and S. Duryea 1999 Effects of Schooling on Fertility, Labor Supply, and Investments in Children, with Evidence from Brazil. Journal of Human Resources.
Lockheed, M. 1995 Educational assessment in developing countries: The role of the World Bank. In T. Oakland, ed., International Perspectives on Academic Assessment. Norwell, Mass.: Kluwer Academic Publishers.
Lockheed, M., and A. Verspoor 1991 Improving Primary Education in Developing Countries. New York: Oxford University Press.
Oliver, R. 1997 Fertility and women's schooling in Ghana. In P. Glewwe, ed., The Economics of School Quality Investments, in Developing Countries: An Empirical Study of Ghana. London: Macmillan.
Pitt, M., M. Rosenzweig, and D. Gibbons 1993 The determinants and consequences of the placement of government programs in Indonesia. World Bank Economic Review 7(3):319-348.
Rosenzweig, M. 1982 Educational subsidy, agricultural development and fertility change. Quarterly Journal of Economics 97(1):67-88.
Schultz, T.P. 1993 Returns to women's education. In E. King and A. Hill, eds., Women's Education in Developing Countries: Barriers, Benefits, and Policies. Baltimore, Md.: The Johns Hopkins University Press.
Strauss, J., and D. Thomas 1995 Human resources: Empirical modeling of household and family decisions. In J. Behrman and T.N. Srinivasan, eds. Handbook of Development Economics, Volume IIIA. Amsterdam: North Holland.
United Nations 1995 Women's Education and Fertility Behavior: Recent Evidence from the Demographic and Health Surveys. New York: Department for Economic and Social Information and Policy Analysis, United Nations.
United Nations Development Programme 1990 Human Development Report. New York: Oxford University Press.
Velez, E., E. Schiefelbein, and J. Valenzuela 1993 Factors Affecting Achievement in Primary Education. HRO Working Paper No. 2. Washington, D.C.: The World Bank.
World Bank 1990 World Development Report. New York: Oxford University Press.
1995 Improving Basic Education in Pakistan: Community Participation, System Accountability and Efficiency. Washington, D.C.: The World Bank, South Asia Region.
Appendix A Simple Two-Period Model Of School Choice
To determine how the optimal (utility-maximizing) value of years of schooling is affected by changes in the parameters of the model given in the main text, assume first that school quality is given exogenously. As given in equation (5.6) in the text, the expression to be maximized with respect to S is:
(A-1)
The first and second derivatives of U with respect to S are:
(A-2)
(A-3)
Totally differentiating the first-order condition (the condition that equation (A-2) = 0) yields:
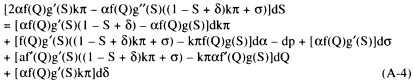
(A-4)
It is immediately clear that the coefficient associated with dp (i.e., -1) is negative and that the terms associated with dσ and dδ are positive. The fact that the second-order condition, (A-3), must be negative implies that the term associated with dS is positive. The fact that the first-order condition, (A-2), equals zero implies that the terms associated with dα and dQ are positive. Since k and π always appear together, their product can be treated as a single variable, denoted by kπ. The term associated with dkπ cannot be signed unambiguously, but it will be positive if σ is relatively small.
Now turn to the case where school quality, Q, is a choice, and higher school quality implies a higher tuition fee. As given in equation (5.8) in the text, under the assumption that f(Q) = Qß and g(S) = Sg, the expression to be maximized with respect to S and Q is:
(A-5)
The first and second derivatives of (A-5) with respect to S are:
(A-6)
(A-7)
The first and second derivatives of (A-5) with respect to Q are:
(A-8)
(A-9)
Note that the requirement that both second derivatives equal zero implies, by (A-9), that ß < 1, so that Qß is a concave function of Q. Setting (A-6) and (A-8) equal to zero, dividing (A-6) by Q and (A-8) by S, and substituting (A-6) into (A-8) (i.e., substituting out Po) yields:
(A-10)
Dropping Qß-1 from both sides of (A-10) and multiplying both sides by S1-γ yields the following optimizing solution for S:
(A-11)
Clearly, this solution is only plausible if y> ß. Substituting (A-11) into (A-7) and noting that y > ß implies that (A-7) is negative, which means that the second-order condition for maximization is satisfied. Setting (A-8) equal to zero, solving for Q, and replacing S with (A-11) yields the optimizing solution for Q:
(A-12)
The impact of most of the parameters in (A- 12) is clear. The exceptions are k and π , which again can be treated as a single variable kπ. Differentiating Q with respect to kπ yields:
(A-13)
The expression in (A- 13) will be positive if (1 + δ) + (1 - γ)σ/kπ > 0, and negative otherwise. Thus the impact of k and π on Q will depend on the values of δ, γ, σ, k, and π. Note that if σ is sufficiently small, this term will be positive even if αγ > 1, which is a similar condition for the case when Q is exogenous.


































