8
Excess Fertility, Unintended Births, and Children's Schooling
Mark R. Montgomery and Cynthia B. Lloyd
Introduction
Consensus prevails as to the benefits of education: it is believed to promote economic development, speed the completion of the demographic transition, and enhance individual well-being. Where the determinants of education are concerned, however, no similar consensus has yet taken shape. The process by which individuals acquire education is exceedingly complex, involving their motivations and abilities, the goals and resources of their families, and the actions taken, or not taken, by the state. Among the many factors that may affect children's schooling, few have emerged in the literature as clearly decisive, and the role of demographic determinants has yet to be fully understood. In this chapter, we consider two demographic determinants of children's schooling: unintended and excess fertility within the family. Our analysis is empirical in nature and relies on Demographic and Health Survey (DHS) data for four developing countries. To our knowledge, this research is the first to combine data on children's schooling with data on excess fertility and the intendedness status of recent births. We show that in two of the four countries studied—the Dominican Republic and the Philippines—unintended and excess fertility have sizeable negative impacts on children's schooling. In the other two countries—Kenya and Egypt—we do not find such effects. It appears that these fertility effects can be important, but vary in strength according to socioeconomic context.
Our focus on fertility can be understood as follows. Developing-country parents, who face resource constraints in much of their behavior, may find their plans for children's schooling disrupted or compromised by the arrival of unin-
tended births. Moreover, as the broader macroeconomic context changes, parents may find themselves situated in new and possibly unanticipated circumstances. In the light of these circumstances, current family size may be revealed to be excessive and may then present an obstacle to desired educational investments. Thus we consider two conceptually distinct measures of fertility: (1) unintended fertility, or the birth of children whom the mother reports were either unwanted at the time of conception or whose conception was reported to be mistimed; and (2) excess fertility, or the birth of a larger number of children than is implied by the mother's expressed family-size ideal. The essence of our approach is to compare the schooling achieved by children in families with and without such fertility.
For developing countries, the gap between desired and actual fertility is surprisingly large, with recent estimates suggesting that as many as one birth in five is unwanted (Bongaarts, 1990) and an even greater fraction unintended. As Bankole and Westoff (1995) demonstrate, in many middle-income developing countries, declines in desired family size now appear to be outpacing declines in fertility. The long-term educational implications of these trends deserve consideration.
Viewed from a broader perspective, our research addresses the individual welfare rationale that supports family planning programs. That rationale is based on the costs imposed by imperfect fertility control on women and their families. Our findings show that in some settings, at least, the rationale can be strengthened: effective family planning may improve the prospects for investment in children's human capital. It follows that if the fullest advantage is to be gained from public-sector investments in schooling, parents must have the means to limit their fertility to the levels they desire.
The remainder of the chapter is organized as follows. The next section provides a conceptual overview of the linkages among family size, excess fertility and unintended births, and human capital investments in children. It also reviews the rather meager literature that has addressed such questions. The third section presents a descriptive overview of the fertility and schooling environments in the four countries studied. The fourth section outlines the statistical model that motivates our empirical work; the results derived from that model are then given. The final section presents conclusions and suggestions for further research.
Review Of Concepts And Literature
Children with many or closely spaced siblings are often thought to be disadvantaged with respect to their schooling in comparison with other children. The disadvantages are believed to be due mainly to resource constraints, with children in larger families receiving smaller shares of total family resources. Economists have written about such issues under the rubric of the quantity,-quality tradeoff (see, among others, Becker and Lewis, 1973; Hanushek, 1992; Parish and Willis,
1993). As used in this literature, the term tradeoff refers not to any fixed or mechanistic causal relationship between fertility and children's schooling, but rather to the often-found negative association between the two.
A tradeoff—a systematic negative association—between fertility and children's schooling is evident in many settings, but there are important exceptions to the general rule. In recent reviews, Lloyd (1994) and Kelley (1996) document a considerable range of empirical associations between fertility and children's schooling at the family level. The associations are usually negative, but they are not always statistically significant or quantitatively large, and positive associations appear as well (Hermalin et al., 1982; Parish and Willis, 1993; Montgomery et al., 1995a, 1995b; see also Diamond et al., this volume).
When the results of many studies are summarized, the relationship between fertility and children's education is seen to vary over time and among countries according to several factors: the stage of economic development, the role played by the state, the phase of demographic transition, and the nature of the family system (Lloyd, 1994). It appears that some threshold level of development must be attained before fertility comes to be strongly negatively associated with children's schooling. If the surrounding environment is one of few schools and few skilled jobs, parents will have neither the opportunity nor the incentive to invest in their children's education, irrespective of whether resources are to be spread over many children or only a few (Desai, 1995). Another consideration is the role played by the state in school provision and finance. In countries in which a high proportion of the money costs of schooling are borne by parents, parental resource constraints are more important in determining which children attend school than is the case in countries in which education is provided free by the state. If the benefits of schooling are substantial, then it is the former situation, with parents responsible for the money costs of schooling, in which one would expect a negative association between fertility and children's education to emerge. Finally, in family systems involving sibling chains of support or child fostering, parents can distribute the costs of schooling and childrearing among a network of relatives, thereby escaping the constraints imposed by their individual family budgets.
Consequences of Unintended and Excess Fertility
Economic models are built on the premise that fertility and children's schooling are jointly determined outcomes of a common set of exogenous determinants. According to this way of thinking—see Appendix A for an extended discussion—a negative association between fertility and schooling is only one of any number of associations that might emerge from family productive and reproductive strategies. Fertility is not, in itself, a causal determinant of children's schooling, nor is schooling a causal determinant of fertility. It is therefore not meaningful to ask how desired fertility might affect desired children's schooling. The
question is ill defined; it confuses association with causation. It is appropriate, however, to ask how the exogenous determinants of desired fertility might affect desired schooling. When the issue is posed in these terms, there is a proper causal linkage to be considered.
In short, it is only the unintended or excess aspects of fertility that can act as causal determinants of children's schooling. An unintended birth imposes new and unanticipated demands on the resources that can be marshaled for schooling. Parents of unintended or excess children may be less able, and perhaps less willing, to increase the total resources devoted to their children or to reallocate resources among children on a particular child's behalf.1
To approach this issue more formally (see Appendix A for further discussion), let us imagine that parents make decisions so as to maximize a unitary utility function V(C, N, S, H), in which C refers to the level of parental consumption, N to the number of their children, S to the children's schooling, and H to the children's health or some other dimension of human capital investment.2 Parents face a budget constraint and must restrict their total expenditures to no more than Ω, the level of their exogenous income. The decision problem yields a set of optimal or desired values C*, N*, H*, S*, where N* represents the desired number of children. These optimal values yield utility level V*.
Now suppose an unintended birth occurs, so that family size exceeds the optimal value N*. Actual fertility is then N = N* + 1. All else being equal, this additional birth must reduce parental well-being, causing actual utility to fall below V*. How are we to gauge the magnitude of the impact? One approach is to ask what increment in income, DW, would be required to restore utility to V*, that is, to just compensate the parents for the additional child. The required compensation will depend on numerous factors: the initial level of income Ω; the many childrearing prices and constraints faced by the parents; and the nature of the utility function V, in particular its curvature in the neighborhood of N* with respect to the number of children.
This theoretical framework suggests an empirical model of the consequences of unintended fertility. In such an empirical model, the actual level of schooling S is a function not of actual fertility N = N* + U, where U is unintended fertility, but rather of U itself,
This specification isolates the unintended, exogenous component of fertility. The coefficient γ associated with U thus measures the direct consequences of unintended fertility for children's schooling.3 The set of other covariates X includes all exogenous factors (such as income Ω) that affect the desired level of schooling S* and, likewise,0 the desired level of fertility N*. Although not shown in this formulation, interactions of U and X could also enter the empirical model.
These concepts are easily generalized to the situation in which parents have, say, two life-cycle periods in which they can bear children. In period 1 they might desire to have N1* children and in period 2, N2* children. Associated with these fertility desires are the desired levels of schooling for the different sets of children, that is, S1* and S2*. (The subscripts on S* refer to the period of the child's birth.) These educational investments are planned to take place in periods 2 and 3. Among other things, optimal choices about fertility and schooling depend on the anticipated sequence of parental incomes, Ω1, Ω2, and Ω3.
Suppose that the parents succeed in having Nl* births in period 1, but in period 2 have U2 unintended births, so that N2 = N2* + U2. The unintended births may then affect the schooling of both older and younger children, as indicated in the following pair of equations:
Although the model as first written required that the effects of unintended or excess fertility be the same for all children in the family, differential effects among siblings, as shown in this expanded version, are perhaps more plausible. Going further, one might distinguish effects felt mainly by the unintended child herself (or himself) from those felt by other children in the family, as when an
older child is withdrawn from school to help care for a younger sibling whose conception was unintended.
The effects considered here may also be produced by changes in circumstances that render the parents' initially desired levels of fertility nonoptimal. Other than the arrival of an unintended birth, this is the primary reason for excess fertility as we have defined the term. Suppose that, anticipating life-cycle income levels of Ω1, Ω2 and Ω3, parents initially desire to have N1* and N2* children. Imagine that they succeed in meeting exactly these fertility goals. Upon entering period 3, however, the parents encounter an unanticipated shortfall in their income. This shortfall in Ω3 imposes new constraints on the remaining schooling investments they can afford and find it rational to make. Had the actual level of income been known in advance, the parents' desired fertility levels might well have differed from N1* and N2*. Our point is that although births N1* and N2* may have been fully desired at the time of their conception, later events may bring about revisions in desired family size and force a rethinking of educational investments. Viewing the situation in retrospect, the parents might well say in response to a survey question that the number of children they actually bore exceeded their ideal number. They would thus experience excess fertility even though, strictly speaking, no birth was unintended.
Consequences of Unintended or Excess Fertility
Remarkably little research has examined directly the consequences of unintended or excess fertility for developing-country families and children. This is surprising in view of the central role played by the elimination of such fertility in the rationale for family planning and in the emerging literature on unmet need. For example, much of the work on the health implications of birth spacing (see Montgomery and Lloyd, 1996, for a review) draws no distinction between intended and unintended fertility, although it can be assumed that very short birth intervals must generally be unintended.
Much of the research on the consequences of imperfect fertility control is concerned with the developed-country situation.4 For instance, the vast literature on the consequences of teenage pregnancy and birth (see Brown and Eisenberg,
1995, for a review) is dominated by studies of the United States. This literature has been concerned mainly with the consequences of teen births for the mothers, although a number of studies have examined effects on young children as well. Relatively few efforts have been made to distinguish intended from unintended births, as it has been assumed, quite plausibly, that the great majority of teen births in the United States are unintended.
A handful of studies in a variety of settings have documented negative effects for unwanted children, whether in terms of heightened mortality risks (Frenzen and Hogan, 1982, for Thailand), poor social development (Baydar and Grady, 1993; Baydar, 1995), poor psychological development (David et al., 1988), or greater risks of physical abuse and neglect (Zuravin, 1991).5 Yet we are aware of only one study, from Finland, that explores the consequences of a child's wantedness for educational attainment (Myhrman et al., 1995). This study is based on a unique longitudinal design that began in 1966 with interviews of women who were then in their sixth or seventh month of pregnancy.6 At the time of the first interview, the wantedness of each woman's pregnancy was ascertained. Some 63 percent of the pregnancies were reported to have been wanted at that time, 12 percent unwanted, and 25 percent mistimed. The study continued to monitor the women (all of whom gave birth) and their children, with assessments taking place in 1980-1981 and 1990, at which point the children were age 24. Myhrman et al. found that the children who were unwanted during pregnancy were subsequently less likely than their wanted counterparts to progress beyond the basic 9 years of education. The education of children who were mistimed fell between that of the other two groups. Among the young men surveyed in 1990, differentials in schooling by wantedness status were apparent only in larger families (those with three or more children). However, young women born into smaller families (two or fewer children) following an unwanted pregnancy had a particularly high risk of stopping after 9 years of compulsory schooling.
We know of no similar studies in the developing-country context. On occasion, however, ingenious efforts have been made to tease out the effects of unintended fertility by indirect means. In the case of India, Rosenzweig and Wolpin (1980) examined the educational consequences stemming from twin births, whose simultaneous arrival was clearly unintended. These consequences were negative, if not especially large, although one wonders whether an analysis focusing on unwanted fertility as well as spacing might have found more substantial impacts. In another interesting study, Rosenzweig and Schultz (1987) estimated levels of fecundability among Malaysian mothers, this being one of the
exogenous factors that might lead to unintended or excess births, and found a modest negative association between fecundability and children's schooling.
Fertility And Schooling In The Study Countries
The countries examined for this study—the Dominican Republic, Egypt, Kenya, and the Philippines—would seem to form an eclectic group, and one might wonder what features unite them. Four general criteria guided their selection. First, we required that several types of data be available: on the educational levels and enrollment of school-age children, on the fertility preferences of their mothers, and on access within the community to family planning and schooling. Surprisingly few DHS surveys gather this range of data, with data on children's schooling the most likely to be lacking. Second, these are countries in which the proportion of unwanted births is relatively high, in the range of 20-35 percent (Bankole and Westoff, 1995). Third, the study countries exemplify settings in which abortion is illegal.7 And fourth, taken together, these countries represent each of the major regions of the developing world.
Fertility
In these four countries, total fertility rates (TFRs) for the 3 years before the respective DHS survey dates range from a low of 3.7 in the Dominican Republic to a high of 5.2 in Kenya, with the TFR for the Philippines being 4.1 and that for Egypt 4.7. In each of the surveys, women of reproductive age were asked about the intendedness of all pregnancies resulting in live births during the 5 years preceding the survey. Women were asked whether, at the time they became
pregnant but before they gave birth, they wanted the birth then, later, or not at all. If a woman said she wanted the birth later, she was asked how much longer she would like to have waited.8 These retrospective data provide the basis for our measures of unintended fertility. The measurement of excess fertility is based on the difference between cumulative fertility and the woman's report of her ideal family size, both being measured at the date of the survey.
Appendix B examines at some length the conceptual and empirical differences between measures of unintended and excess fertility. Our view is that although these measures have certain elements in common, each presents distinctive features. The differences between the two are sufficient, we believe, to justify separate analyses. Both measures suffer from incomplete information on timing, that is, on the dates at which the attitudes in question were held. For instance, no data were collected on the intendedness of births that occurred before the 5-year retrospective window adopted by the DHS. Thus, the wantedness status of children over age 5 cannot be assessed by the same means as that applied to younger children. Likewise, information on a woman's current family-size ideal is solicited by the DHS, but no inquiries are made about how long she has maintained that ideal or about the nature of the ideals that were previously held. Moreover, the attitudes measured are those of the women respondents. Independent questions were not asked of fathers, and it cannot be determined whether the views women express are uniquely their own or reflect a consensus forged between spouses (and perhaps involving others).
Table 8-1 presents summary statistics on the extent of unintended fertility among the births occurring in the 5 years before the DHS surveys. The percentage of such births that were unwanted at conception varies from 15 percent in the Dominican Republic to 22 percent in Egypt. Because of ex post rationalization, this is likely to be an underestimate of the actual level of unwanted childbearing at the time of pregnancy (see Bankole and Westoff, 1997, for longitudinal evidence from Morocco). However, the children still labeled as unwanted as of the survey date are those that were probably most intensely unwanted at the time of conception. Another 13 to 35 percent of births are reported to have been mistimed, with 8 to 24 percent mistimed by more than 2 years. The total percentage of recent births that were unintended ranges from 52 percent in Kenya, to 45 percent in the Philippines, to 38 in the Dominican Republic, to 35 in Egypt. Kenya, with the highest fertility overall, also has the highest percentage of unintended pregnancy.
Table 8-2 presents these data from another perspective, that of the women who might experience either unintended or excess fertility. A substantial percentage of women in each country (from 41 to 63 percent) had no births during
TABLE 8-1 Intendedness Status of Births in 5 Years Before Survey
|
Wantedness at conception |
Dominican Republic (1991) |
Egypta (1988) |
Kenya (1993) |
Philippines (1993) |
|
Number of births |
4,216 |
8,716 |
6,115 |
9,152 |
|
Wanted at conception |
61% |
65% |
49% |
55% |
|
Mistimed 2 years |
16 |
13b |
11 |
10 |
|
Mistimed >2 years |
8 |
13b |
24 |
19 |
|
Unwanted |
15 |
22 |
17 |
16 |
|
Total |
100% |
100% |
100% |
100% |
|
n.a. = not available a Based on ever-married women only. b Desired time to next birth not asked. |
||||
TABLE 8-2 Incidence of Unintended and Excess Fertility Among Women
|
Variable |
Dominican Republic (1991) |
Egypta (1988) |
Kenya (1993) |
Philippines (1993) |
|
Number of women |
7,318 |
8,911 |
7,540 |
15,029 |
|
Number of births in last 5 years (Percent) |
||||
|
0 |
63 |
41 |
48 |
61 |
|
1 |
21 |
30 |
27 |
21 |
|
2 |
13 |
22 |
21 |
14 |
|
3 |
3 |
7 |
4 |
4 |
|
Of women with births in last 5 years |
||||
|
At least 1 unwanted birth At least 1 unwanted or |
18 |
28 |
20 |
21 |
|
mistimed by more than 2 years |
28 |
n.a.a |
48 |
40 |
|
For all women, ideal family size and fertility |
||||
|
Number of births at survey > |
||||
|
Ideal family size |
22 |
52 |
30 |
20 |
|
Surviving children at survey > |
||||
|
Ideal family size |
19 |
42 |
25 |
16 |
|
n.a. = not available a Only ever-married women interviewed; no data on desired time to next birth. |
||||
the preceding 5 years. Among those who did give birth, 18 to 28 percent had at least one unwanted birth; 28 to 48 percent had either one or more unwanted births or one birth mistimed by more than 2 years. From 43 to 59 percent of women (not shown) had at least one unintended birth. Egypt had the highest incidence of recent unwantedness and the Dominican Republic the lowest. Mistimed pregnancies were most prevalent in Kenya and least prevalent in the Philippines.
With regard to excess fertility, two measures are shown in Table 8-2, one based on children ever born and the other on surviving children.9 Egypt displays the highest levels of excess fertility, with 42 or 52 percent of women reporting a number of children that exceeded their current family-size ideal. The figure for Egypt is more than double that shown for the Dominican Republic and the Philippines.
Schooling
Our analyses are focused on children of school age—those aged 6 or 7 to 18, with the lower end of the range depending on the normal age for starting the first grade of primary school. The DHS surveys gather limited information, through their household rosters, on current educational status. Unfortunately, no educational histories are available for children. Thus we cannot determine the ages at which children passed important educational milestones, and issues related to age at first enrollment, dropout and reentry, or grade repetition can be studied only indirectly.
To understand school enrollment and educational attainment in the four study countries, one must be familiar with certain structural aspects of their educational systems, such as school starting ages, grade-to-grade promotion policies, the duration of primary and secondary levels, and the critical transition points at which performance on national exams may limit opportunities for advancement. Each of the countries is distinctive with regard to such structural features.
Table 8-3 summarizes the main elements of the educational systems of the four countries, not only at the time of the DHS surveys, but also for the relevant school years of all children in the sample aged 6-18.10 Egypt and Kenya have
TABLE 8-3 National Educational Systems, Four Study Countries
|
Level |
Dominican Republic (1991) |
Egypt (1988) |
Kenya (1993) |
Philippines (1993) |
|
Primary |
||||
|
Starting age |
7 |
6 |
6 |
7 |
|
No. of grades |
6 |
6 |
8 |
6 |
|
Promotion from grade to grade |
Teachers' evaluations, internally administered |
Local exams at end of grades 2, 4, 6 |
Automatic |
Cumulative rating system; pass grade = 75%, internally administered |
|
Secondary |
||||
|
Entry requirement |
Primary completion (certificado de suficiencia) |
Passing score on locally administered grade 6 exam |
Passing score on national KCPE exam |
Primary graduation certificate |
|
No. of grades |
Traditional Plan: 2 + 4 |
Preparatory: 3 |
4 |
4 |
|
|
Reform Plan: 4 + 2 |
Secondary: 3 |
|
|
|
Promotion from grade to grade |
Teachers' evaluations, internally administered |
Exam for basic education completed at end of grade 9; minimum score required for academic secondary |
Automatic |
Teachers' evaluations, internally administered |
|
University placement |
Secondary completion (bachillerato) |
National exam |
National exam |
National exam |
|
Total Grades |
||||
|
Preuniversity |
12 |
12 |
12 |
10 |
|
SOURCES: Postlethwaite (1992) and Kurian (1988). |
||||
starting ages of 6, whereas children do not normally begin primary school until the age of 7 in the Dominican Republic and the Philippines. Six grades of primary schooling characterize all the school systems except that of Kenya, where primary school lasts 8 years. Neither the Dominican Republic nor the Philippines imposes national exams during the primary and secondary years; to determine pass rates, they rely instead on internal exams administered separately within each school. The Kenyan system is rather different, allowing students to progress automatically from grade to grade until the end of standard 8, at which point students sit for a national exam that determines eligibility to enter secondary school. Roughly 44 percent of those completing primary school in Kenya are able to enroll in secondary school (UNESCO, 1994).11 In Egypt, the critical transition points occur more frequently, in that local exams are administered at all schools in a district at the end of grades 2, 4, and 6. A national exam for basic education is administered at the end of grade 9 (the last year of the preparatory level). Results on this exam determine whether a student can proceed to the secondary level on an academic track or is eligible only for technical school. All systems except that of the Philippines have a total of 12 years of primary and secondary schooling; the Philippines is unusual in having only 10 years of schooling prior to university.
Current status data are used to show patterns of educational progress for each country.12 The horizontal axes begin with the age at which children are meant to start grade 1 of primary school.13 The children who are currently enrolled are divided into two groups: those whose age is appropriate to the grade (labeled ''okay") and those who are over age because of either a late start or grade repetition ("behind").14 Students who have been but are not currently enrolled in school are labeled "dropped."
|
11 |
This figure is based on the ratio of the number of students enrolled in the first grade of secondary school (1992) to the number of students in the last year of primary school (1990). This figure is likely to be an overestimate. Data for 1991 are not yet available (UNESCO, 1994). |
|
12 |
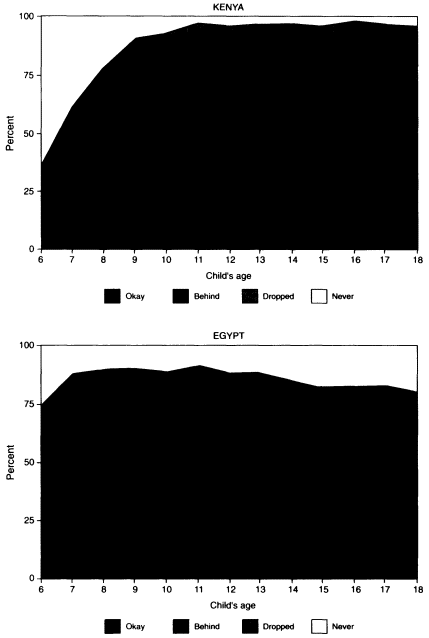
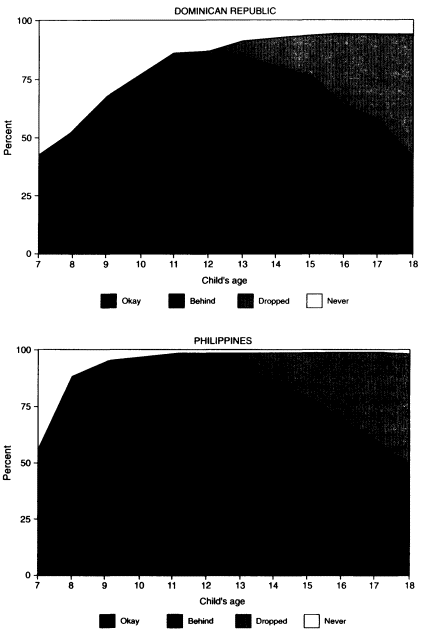
Figure 8-1. which compares children of different ages at a particular point in time, reflects both secular trends and life-cycle changes. Although we would like to use the data to depict a profile of school participation for the current cohort of school-age children, we know that patterns of school participation had been changing over the decade preceding the DHS surveys. As overall enrollment rates rise, we would expect to see the trends reflected in declining proportions of children never in school at younger ages. Interestingly, among our sample of countries, this pattern is clearly apparent only in Egypt. Indeed, the picture for the Dominican Republic suggests a deteriorating situation, with 6 percent of those aged 18 never having attended school, but as many as 14 percent of those aged 11. This deterioration is confirmed by a recent World Bank (1995) assessment. |
|
13 |
School participation can begin before the first grade of primary school in preprimary, nursery, or kindergarten. The prevalence of preschool attendance varies from country to country, as does its content. Because so little is known about preschool, it has been excluded here so that all the figures can be presented on a comparable basis. |
|
14 |
This approach follows that used by Lloyd and Blanc (1996) in their analyses of children's schooling in Africa. Children are classified as behind grade level if their number of grades com |
In Figure 8-1a, we compare Egypt and Kenya; both countries have a normal starting age of 6 for the primary level. The patterns reveal a striking contrast. In Kenya, starting ages are flexible, with children continuing to enter primary school until age 11.15 Late entry is evidently the major factor causing children to be behind grade for their age. With 8 grades of primary schooling and automatic promotion from grade to grade, dropout becomes significant only when children reach the end of primary school and sit for the national Kenyan Certificate of Primary Education (KCPE) exam. Given the limit on places in the first form of secondary, only the top-scoring 40 percent of Kenyan students can continue into secondary school. On the positive side of the ledger, relatively few students have never been to school.
In Egypt, a heavily bureaucratized school system enforces a strict age of school entry. Students who have not gained a place in school by age 7 are therefore unlikely to have the opportunity to attend later. As a result, enrollment in primary school is exceptionally high by age 7 (87 percent enrolled, in comparison with 61 percent in Kenya at the same age), but begins to drop off by age 9. The percentages never enrolled are noticeably higher than in Kenya, and dropout begins to occur at a steady rate at age 10, when students sit for a series of standard exams at the end of grades 2, 4, 6, and (most important) 9. Relatively few students appear to be behind grade for their ages, suggesting that those who are not able to keep up are more likely to drop out.
Figure 8-1b compares the Philippines and the Dominican Republic. In the Philippines, almost all children enter school eventually, and most have entered by age 9. Most children are able to complete the 6 primary grades, but participation begins to fall off during the 4 years of secondary. Late entry and repetition do not appear to be important problems. By contrast, late entry is evidently common in the Dominican Republic, with children behind grade representing almost half of all enrolled students aged 11-16.
Table 8-4 shows the distribution of children in each of our samples by educational status at the time of the survey and summarizes their performance on
|
|
pleted is less than the number of years that would have been completed if they had started school within 2 years of the recommended starting age in the country according to UNESCO (1994) and attended continuously from that age onward. Specifically, a child is behind grade level if completed years of education < current age - (recommended starting age + 2). The 2-year adjustment is made because children in any given grade may be observed at one of two ages (for example, a child starting school at age 6 will turn 7 during first grade) and coupled with an additional adjustment to produce a conservative estimate of the proportion of children behind grade level given possible age and grade misreporting. Thus in a country with a school starting age of 6, enrolled children who had completed grade I by age 8 would be classified as "at grade level." |
TABLE 8-4 Education and Fertility Measures: Samples of School-Age Children
|
Characteristic |
Dominican Republic (1991) |
Egypt (1988) |
Kenya (1993) |
Philippines (1993) |
|
Number of childrena |
5.475 |
13,521 |
8,765 |
14,296 |
|
Educational status measures (percent): |
||||
|
Never attended |
20 |
12 |
17 |
8 |
|
Dropped out |
8 |
10 |
5 |
10 |
|
Enrolled but behind schedule |
25 |
6 |
43 |
8 |
|
Enrolled, on schedule |
48 |
72 |
35 |
74 |
|
Total |
100 |
100 |
100 |
100 |
|
Years completed (mean) |
3.4 |
4.1 |
2.8 |
4.5 |
|
Percent Completing 1 Year Secondary Schooling, Among Those in Relevant Age Groupb |
46 |
66 |
10 |
72 |
|
Unwanted and excess fertility measures (percent): |
||||
|
1 unwanted sibling born in last 5 years |
9 |
22 |
17 |
15 |
|
2 or more unwanted siblings born in last 5 years |
3 |
8 |
7 |
4 |
|
At least I sibling unwanted or mistimed by more than 2 years |
14 |
36 |
38 |
27 |
|
In family with excess fertility |
57 |
83 |
72 |
53 |
|
a Age range 7-18 for the Dominican Republic and the Philippines, 6-18 for Egypt and Kenya. b Age groups: 14 and above for the Dominican Republic and the Philippines, 13 and above for Egypt, 15 and above for Kenya. |
||||
two indicators—mean grades of schooling completed and percentage completing I year of secondary school. The latter is a critical transition point in all countries. Interestingly, the Dominican Republic has the highest percentage of children never in school (20 percent). Egypt and the Philippines have the highest percentages currently enrolled and on schedule (72 and 74 percent, respectively).
Unintended and Excess Fertility in the Families of School-Age Children
The lower portion of Table 8-4 summarizes unintended and excess fertility in the samples of school-age children; Tables 8-1 and 8-2 presented similar figures for children born in the past 5 years and for women. The summary statistics in
Table 8-4 represent the incidence of such fertility from the perspective of the children whose educational attainment we are investigating. Note that the general rankings of the study countries resemble those shown in the previous tables, with the Dominican Republic and the Philippines having the lowest levels of both unintended and excess fertility and Kenya and Egypt the highest. In all four countries, well over 50 percent of school-age children reside in families with excess fertility. The incidence of unintended fertility is considerably lower, although it should be borne in mind that this measure is restricted to events occurring in the past 5 years.
In summary, the study countries offer considerable diversity with respect to levels of fertility overall, the extent of unintended and excess fertility, and the levels and age patterns of schooling. With this background, we now turn to a discussion of the methods applied to determine whether unintended and excess fertility affect children's schooling.
Model Specification And Estimation
To understand the implications of unintended and excess fertility for children's schooling, one must first ask who experiences such fertility. Our analysis is therefore set forth in terms of a two-equation system, in which one equation specifies the likelihood of unintended or excess fertility, and the second equation (or set of equations) focuses on the consequences of such events for children's schooling. In thinking along these lines, we are mindful of the possibility that unmeasured factors may at the same time affect exposure to the risk of unintended fertility and the levels of investment in children's schooling. Such unmeasured "common causes" could make it appear as if unintended fertility itself affects schooling, even if no such causal relationship exists. This possibility has been an important theme in the literature on consequences of teenage pregnancy in developed countries, motivating the use of longitudinal data and the application of a variety of appropriate statistical techniques, such as sister comparisons. Unfortunately, the data available to us are cross-sectional and provide only a single measure of each of the key variables—children's schooling, excess fertility, and recent unintended fertility. This fundamental data constraint must be kept firmly in mind as our statistical methods are developed and applied in this section and the next.
Our system is represented in latent-variable form in the equations below:
(8.1)
(8.2)
In this system, U* represents the parents' propensity either to (1) have an unwanted or mistimed conception leading to a birth in the 5 years before the survey
or (2) report excess fertility, as measured by the difference between the number of births at the time of the survey and the woman's ideal family size. We specify separate U* equations for these different indicators. Note that women who experienced no unanticipated events in the past 5 years, whether they had no births or only intended births, are treated identically in this estimation, an approach that is consistent with our theoretical framework.16 Note, too, a fundamental measurement difficulty: because the angle of vision on the past provided by DHS data is only 5 years, we risk grouping women who had an unintended event before the 5-year window of observation with those who did not. The likely consequence is to dilute the estimated effects (Wolfe et al., 1996).
The propensity for unintended or excess fertility U* is determined by a set of exogenous factors, denoted by Z, and by access to family planning services, FP. Using the DHS service availability surveys that complement the individual-level surveys, we assembled a number of measures of access to family planning and reproductive health services. These access variables are assumed to influence the likelihood of unintended or excess fertility, but not otherwise to influence children's schooling. Thus, the family planning access measures serve as excluded or instrumental variables in the equation system.
The second set of equations, with latent dependent variables Si*, has to do with the schooling of children in the family. Their schooling may be affected by the occurrence of an unintended birth or excess fertility (denoted here by U without an asterisk), as well as by a set of child-specific, family-specific, and community-specific variables Xi. As just mentioned, the family planning access measures are excluded from Xi. The schooling propensity for child i has an observed counterpart in either a binary indicator of school enrollment or an ordered index of educational attainment.
Figure 8-2 may help explain the essentials of our approach, showing how the analyses and implications may differ for unintended as compared with excess fertility. The time line in the figure depicts the 5-year window of the DHS surveys, the window within which data on intendedness were gathered. Child 1, shown in the upper portion of the figure labeled "Unintended," reached the minimum starting age for school before the date of the DHS survey and therefore must have been born before the 5-year window opened. Although this child's educational status is known, at least as of the survey date, the circumstances of his or her conception are not known. Child 2, by contrast, was born within the 5-year window, and in the case shown in the figure is reported to have been unintended. The educational consequences of this unintended birth may be evident if child 1 is affected, but because child 2 is still too young to have attended school, the consequences for him or her cannot be determined. Thus when we study the
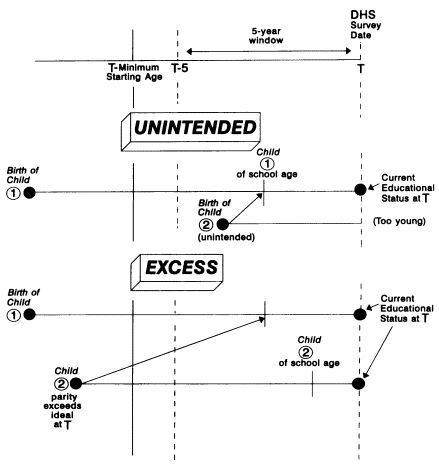
FIGURE 8-2 DHS data on children's schooling, unintended and excess fertility.
educational consequences of unintended fertility using DHS data, we are necessarily considering cross-sibling effects. For both children, these potentially negative consequences can be summarized only using the educational status data gathered at the time of the DHS survey, which reflect the cumulative effects of delays in school entry, repetition of grades, temporary withdrawal, and premature dropout up to the time of the survey. The longer-term effects of having an unintended sibling cannot be assessed because the window of observation is only 5 years.
Situations involving excess fertility, one example of which is depicted in the lower panel of Figure 8-2, are somewhat different. The family-size ideals measured in the DHS refer to an ideal as of the survey date. In the case shown in the
figure, the parity of child 2 exceeds the survey date ideal, and in a sense it is this child who brings about a situation of excess fertility for the family as a whole. Of course, the mother is not asked to single out and thereby label child 2 in her survey response on ideal family size. If child 2 is old enough to have attended school as of the survey date—this is the case shown in the figure—the educational consequences of excess fertility may be evident for both children. That is, where excess fertility is concerned, we can consider both own and cross-sibling effects. The situation is greatly complicated, however, by the possibility of change over time in family-size ideals. For example, the parities of both child 1 and child 2 might initially have been below the family-size ideal, but the ideal itself might then have declined in the interim between the birth of child 2 and the survey date. These possibilities cannot be explored using DHS data; the required information on the timing of events and attitude change is not available.
Data Construction
The estimation of equation (8.1) is based on individual data from women of reproductive age, supplemented by service availability data for their communities collected in each DHS sample cluster. To estimate equation (8.2), we constructed a sample of the school-age children (those aged 6-18) of these women. To link a child's educational status (recorded in the household roster) with information on fertility (collected from the mother), we had to match children from the birth histories to their records in the household roster using the mother's identifier code. We recognize that these are selective samples, yet they nontheless display educational distributions that are similar to those of all children aged 618.17
Estimation and Endogeneity Bias
If the disturbance terms εu and εi,s of the above equations are jointly normally distributed, the system can be viewed as a joint probit, ordered-probit system. The probit equation is equation (8.1), having to do with the incidence of unin-
tended or excess fertility; the ordered-probit equation is equation (8.2), which is estimated using ordered indices of educational attainment.18
A full implementation of the statistical model presents challenges in several dimensions. The main difficulty concerns the possibility of correlation between the disturbance terms in the fertility equation (8.1) and the children's schooling equation (8.2). If it were not for this correlation, the system could be neatly separated into two equations and the children's schooling model then considered on its own. It is quite important, therefore, to test for such cross-equation correlation before embarking on an ambitious exercise in joint estimation.
We carried out such endogeneity tests using generalized residuals from the fertility equation (Hausman, 1978; Guilkey et al., 1992; Bollen et al., 1995). The results, summarized in Appendix C, provide no evidence of cross-equation correlation in either the Dominican Republic or Kenya. There is a suggestion of endogeneity bias in the results for the Philippines and clear statistical evidence of bias, although this is not readily interpretable in substantive terms, for Egypt.
With these results in mind, the next section presents the findings from models that do not incorporate corrections for endogeneity bias. For the Dominican Republic and Kenya, we are on solid statistical grounds in doing so; the approach is less defensible for the Philippines, and the case of Egypt will require additional research.
Results
We now proceed to the multivariate analyses. Three measures of unintended and excess fertility are considered: (1) the occurrence of no, one, or two or more unwanted births in the 5 years preceding the DHS survey; (2) the occurrence of at least one unwanted birth or at least one badly mistimed birth, where the birth in question was desired more than 2 years after it occurred; and (3) the presence of excess fertility, defined earlier as having more births at the survey than the ideal family size reported by the woman. Many alternative measures and combinations of measures, including interactions with the child's sex, were examined in
preliminary analyses.19 We restrict our attention to these three measures because they seem to capture the main empirical features of interest.
The incidence equation—equation (8.1), in which the dependent variable is a measure of unintended or excess fertility—is estimated separately using each measure of unintended or excess fertility. These dependent variables are yes-no dummy variables for which we employ a probit model, with the exception of the first measure, indicating 0, 1, or 2+ unwanted births, for which we use an ordered-probit model.
With regard to measures of children's educational attainment, we have likewise restricted our attention to two dependent variables. The first represents the grades of schooling completed. For this variable we adopt the ordered-probit estimation method, a choice that allows us to capture in a flexible manner the irregular features of a years-of-schooling distribution. A second dependent variable is also defined-a dummy variable taking the value 1 if a child has completed any years of secondary schooling. To study this variable, we must limit the admissible age range of the children who enter into the analysis. The lower end of this age range is defined such that given first entry to primary school at the appropriate starting age and steady progression thereafter from grade to grade, the first year of secondary school should have been completed.
Incidence of Unintended and Excess Fertility
Given that the fertility equation of our system is estimated with three dependent variables for four countries, we choose to present here a summary qualitative assessment of the findings rather than the extensive details. Table 8-5 displays the main features of the results for each country.
As can be seen, in three of the four countries the likelihood of unintended and excess fertility is significantly reduced by the schooling of the woman. This finding is indicative of one of the important ways in which education affects fertility. Other things being equal, it is the children of less-educated mothers who
TABLE 8-5 Incidence of Unintended or Excess Fertility: Summary of Results
|
Characteristic |
Dominican Republic |
Egypt |
Kenya |
Philippines |
|
Woman's education |
Negative and significant |
Negative and significant |
Positive and significant to mixed |
Negative and significant |
|
In union |
Positive and significant |
Positive and significant |
Positive and significant |
Positive and significant |
|
Spouse's education |
Mixed and weak |
Weak and negative |
Mixed and weak |
Weak to positive |
|
Standard of living significant |
Negative and significant |
Weak and not |
Positive at low levels, then negative |
Negative and significant |
|
Urban residence |
Positive and significant to mixed |
Not significant |
Nairobi negative and significant; otherwise not significant |
Weak and mixed |
are more likely to bear the consequences of unintended or excess fertility. Kenya provides the exception to the rule, and we find this exception intriguing. It may be that the Kenyan woman who labels a particular conception as unwanted or who says that her current number of children is greater than her ideal is in some respects atypical in a social setting that has historically emphasized spacing rather than numbers as the key dimension of fertility control. In preliminary work focused specifically on detailed measures of spacing (not reported here), both the determinants and the consequences of mistimed fertility in Kenya appeared to differ from fertility described as unwanted or excessive.
Returning to Table 8-5, we find the expected result that being in union (married or living with a partner) is associated with a higher incidence of unintended or excess fertility. No doubt this association is due mainly to the elevated risk of exposure to conception in general. The education of the spouse, a variable defined in the DHS as referring to either the current or the most recent spouse/ partner, shows a somewhat erratic relationship to fertility, being in some cases positive, but usually weak. A standard-of-living index, defined as the summation of a number of socioeconomic items,20 is generally associated with reduced
incidence of both unintended and excess fertility. The effects are weakest in Egypt, but then Egypt is the case in which the education of the spouse exerts the strongest effect, and the spouse's education variable may in this case function as the better measure of living standards. Residence in an urban area (different coefficients were estimated for residence in towns, small cities, and the capital city) exhibits somewhat modest but usually negative effects on unintended and excess fertility.
Not shown in Table 8-5, but of great importance on both substantive and scientific grounds, is the role of access to family planning services in reducing unintended and excess fertility. To explore the effects of access, we incorporated in the models the numerous indicators of access that are available in the DHS family planning and health services questionnaires. These indicators are not at all standardized across countries, and in one case (Egypt) the service questionnaires were fielded only in rural areas. (For Egypt, we devised additional measures of access for urban areas by aggregating individual measures of knowledge of family planning method sources up to the community level.) The results clearly indicate that access to family planning services is a statistically important influence on unintended and excess fertility. This finding supports our research strategy, in which access measures are employed as instrumental variables. But it is less clear what dimensions of access matter in which settings, and we are not yet able to offer any summary assessments that could help guide program interventions. This is a high-priority area for future research.
Effects of Unintended and Excess Fertility
We now come to the heart of the matter—the effects of unintended and excess fertility on children's schooling. These effects are summarized in two ways: first with respect to an index of the number of grades of schooling completed, and second with an analysis that focuses on attainment of at least I year of secondary schooling for children in the relevant age range. The first analysis is conducted using the method of ordered probit, which, as will be shown, allows us to capture the main features of the distribution of completed schooling; the secondary schooling analysis employs simple probits.
We should repeat here the caution issued above regarding the statistical endogeneity of unintended or excess fertility. We have tested for this and found no cause for concern in the cases of Kenya and the Dominican Republic. For the Philippines the situation is less clear, and standard tests clearly indicate the presence of cross-equation correlation in Egypt. Thus, less confidence should be placed in the results for the latter two countries.
Table 8-6 presents estimates of a baseline model for all four countries in which no measures of unintended or excess fertility are included. This table establishes a set of benchmarks against which the models including fertility can be assessed. The coefficients shown here are not greatly affected by the inclusion
of the fertility measures, and after Table 8-6 we do not again report their estimates.
The findings in Table 8-6 reaffirm the central role played by the mother's education in furthering the educational achievements of her offspring. Likewise, we see evidence that the education of the spouse is also important. The coefficients on spouse's education (recall that the variable refers to current or most recent spouse) do not in general display the strength of the mother's education, although Egypt in some ways presents an exception. The standard-of-living indices function much as expected (the squared term needs to be taken into consideration in interpreting these coefficients, as does the range of the index, which runs from 0 to 9), with higher values of the index being associated with greater educational attainment for children. Urban residence is associated with greater educational attainment in most cases, particularly if the family lives in the capital city, but there are examples of weak or inconsistent results, such as for the Philippines.
For three of the four countries (Kenya is the exception), community-level measures of travel time to the nearest primary and secondary school are available. In some cases, the community informant could not supply an estimate (this occurred for both primary and secondary schooling in the Philippines and for secondary schooling in the Dominican Republic and Egypt). We therefore included dummy variables indicating knowledge of travel time, together with the estimated time itself. These access-to-schooling measures fall well short of what would be ideal, but regrettably, the DHS surveys collect no additional information on schools. It is interesting that in the Philippines and Egypt, longer travel times are associated with reductions in educational attainment. The effects are statistically significant, but within the range of travel times in the data, of only modest substantive importance.
The coefficients from these ordered-probit and probit models require some translation if they are to be understood in substantive terms. To aid in this interpretation, we present Figure 8-3, which summarizes the implications of the years-of-schooling model for children's educational attainment and may facilitate cross-country comparisons. Figure 8-3 shows, for each year of schooling, the predicted proportion of children who would achieve that year or more. To generate the curves, we apply the coefficient estimates of Table 8-6 to a hypothetical child aged 18, whose education should be complete or nearly so. The left-most curves indicate the countries with the lowest levels of educational attainment—Kenya and the Dominican Republic—with the Philippines and Egypt showing higher levels of attainment.
Table 8-7 presents our estimates of the consequences of unintended and excess fertility. The results are striking and, in some respects, unexpected. In the Dominican Republic and the Philippines, unintended and excess fertility are associated with clear reductions in the educational attainment of children. In Egypt and Kenya, by contrast, no such effects appear. At first glance, this pattern
TABLE 8-6 Baseline Estimates of Children's Schooling Models
|
|
Dominican Republic |
|
|
Characteristic |
Years of Schooling (ordered probit) |
Any Secondary (probit) |
|
Children's Characteristics |
||
|
Girl |
.353* |
.370* |
|
(z statistic) |
(12.16) |
(5.46) |
|
Age |
.540* |
-7.277 |
|
|
(2.49) |
(-.49) |
|
Age, squared |
.001 |
.520 |
|
|
(.05) |
(.55) |
|
Age, cubed |
-.000 |
-.012 |
|
|
(-.87) |
(-.61) |
|
Parental Characteristics |
||
|
Mother, primary schooling |
.540* |
.494* |
|
|
(10.99) |
(3.94) |
|
Mother, secondary schooling |
.973* |
1.098* |
|
|
(14.66) |
(6.30) |
|
Mother, higher schooling |
1.209* |
1.474* |
|
|
(14.38) |
(5.19) |
|
Mother, age |
.008* |
.016* |
|
|
(2.86) |
(2.21) |
|
Currently in union |
-.001 |
-.091 |
|
|
(-.02) |
(-1.01) |
|
Spouse, primary schooling |
n.a. |
n.a. |
|
Spouse, secondary schooling |
.254* |
.246* |
|
|
(5.59) |
(2.15) |
|
Spouse, higher schooling |
.344* |
.457* |
|
|
(5.22) |
(2.13) |
|
Standard of living index |
.240* |
.145 |
|
|
(6.53) |
(1.53) |
|
Index, squared |
-0.00 |
.010 |
|
|
(-.10) |
(1.03) |
|
|
Egypt |
|
Kenya |
|
Philippines |
|
|
|
Years |
Secondary |
Years |
Secondary |
Years |
Secondary |
|
Children's Characteristics |
||||||
|
Girl |
-.267 |
-.275 |
.165* |
.199 |
.261* |
.455* |
|
(z statistic) |
(-14.57) |
(-6.80) |
(6.97) |
(1.92) |
(15.00) |
(9.81) |
|
Age |
2.179* |
19.569* |
1.241* |
37.29 |
1.792* |
.217 |
|
(20.40) |
(4.37) |
(9.01) |
(.59) |
(12.70) |
(.02) |
|
|
Age, squared |
-.142 |
-1.194 |
-.044 |
-2.219 |
-.081 |
.036 |
|
|
(-15.34) |
(-4.09) |
(-3.65) |
(-.58) |
(-6.92) |
(.06) |
|
Age, cubed |
.003* |
.024* |
.001 |
.044 |
.002* |
-.002 |
|
(13.58) |
(3.85) |
(1.96) |
(.58) |
(4.89) |
(-.12) |
|
|
Parental Characteristics |
||||||
|
Mother, primary schooling |
.183* |
.238* |
.355* |
.507* |
n.a. |
n.a. |
|
(8.46) |
(5.07) |
(12.57) |
(3.99) |
|
|
|
|
Mother, secondary schooling |
.251* |
.774* |
.719* |
.848* |
.268* |
.426* |
|
(5.64) |
(4.82) |
(16.39) |
(4.16) |
(11.9) |
(7.22) |
|
|
Mother, higher schooling |
.216* |
.952* |
n.a. |
n.a. |
.281* |
.676* |
|
(3.06) |
(3.52) |
|
|
(8.79) |
(6.29) |
|
|
Mother, age |
-.001 |
.001 |
.019* |
.048* |
.007* |
.008 |
|
(-.32) |
(.32) |
(8.96) |
(4.22) |
. (3.85) |
(.15) |
|
|
Currently in union |
.074* |
.147* |
-.089 |
.217 |
.076 |
.177 |
|
(2.05) |
(2.20) |
(-2.43) |
(1.25) |
(1.85) |
(1.80) |
|
|
Spouse, primary schooling |
.323* |
.346* |
n.a. |
n.a. |
n.a. |
n.a. |
|
(14.60) |
(7.57) |
|
|
|
|
|
|
Spouse, secondary schooling |
.443* |
.914* |
.264* |
.336* |
.217* |
.471* |
|
(12.46) |
(9.19) |
(8.56) |
(2.61) |
(9.52) |
(7.88) |
|
|
Spouse, higher schooling |
.479* |
.620* |
n.a. |
n.a. |
.254* |
.577* |
|
(10.07) |
(5.03) |
|
|
(8.26) |
(6.18) |
|
|
Standard of living index |
.352* |
.224* |
.154* |
-.025 |
.271* |
.251* |
|
(11.09) |
(3.28) |
(6.49) |
(-.24) |
(16.55) |
(5.79) |
|
|
Index, squared |
-.025 |
-.005 |
-.003 |
.025* |
-.016 |
-.006 |
|
(-6.15) |
(-.54) |
(-.77) |
(2.03) |
(-8.59) |
(-1.19) |
|
|
|
Dominican Republic |
|
|
Characteristic |
Years of Schooling (ordered probit) |
Any Secondary (probit) |
|
Cluster characteristics |
||
|
Town |
-.072 |
-.055 |
|
(-1.25) |
(-.40) |
|
|
Small city |
.063 |
.115 |
|
(1.58) |
(1.26) |
|
|
Capital city |
.210* |
.226 |
|
(3.74) |
(1.77) |
|
|
Travel time to primary school known |
n.a. |
n.a. |
|
Primary travel time (minutes) |
.000 |
.003 |
|
(.031) |
(1.01) |
|
|
Travel time to secondary school known |
n.a. |
n.a. |
|
Secondary travel time (minutes) |
-.001 |
-.001 |
|
(-1.89) |
(-.78) |
|
|
χ2 (d.f.) |
5,785 (18) |
620 (18) |
|
p-value |
|
0.00 |
|
N |
5,428 |
1,798 |
|
n.a. = not available * denotes significance at the 5 percent level. |
||
|
|
Egypt |
|
Kenya |
|
Philippines |
|
|
Characteristic |
Years |
Secondary |
Years |
Secondary |
Years |
Secondary |
|
Cluster characteristics |
||||||
|
Town |
|
|
-.002 |
.327 |
-.020 |
.176* |
|
|
|
(-.02) |
(.83) |
(-.74) |
(2.43) |
|
|
Small city |
|
|
.323* |
-.236 |
-.033 |
-.079 |
|
|
|
(3.24) |
(-.54) |
(-1.46) |
(-1.34) |
|
|
Capital city |
|
|
0.94 |
.742* |
.016 |
.243* |
|
|
|
(1.45) |
(3.32) |
|
|
|
|
Travel time to primary school known |
|
|
n.a. |
n.a. |
.218 |
-.220 |
|
|
|
|
|
(1.24) |
(-.40) |
|
|
Primary travel time (minutes) |
|
|
n.a. |
n.a. |
-.010 |
-.001 |
|
|
|
|
|
(-10.4) |
(-.66) |
|
|
Travel time to secondary school known |
.235* |
.308* |
n.a. |
n.a. |
-.011 |
.214* |
|
(3.78) |
|
(2.40) |
|
(-.27) |
(2.21) |
|
|
Secondary travel time (minutes) |
-.015 |
-.017 |
n.a. |
n.a. |
-.001 |
-.001 |
|
(-11.19) |
(-6.26) |
n.a. |
n.a. |
(-3.84) |
(-2.13) |
|
|
χ2 (d.f.) |
13,657 (18) |
1,373 (18) |
11,817 (14) |
266(14) |
20063 (19) |
1286(19) |
|
p-value |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
|
N |
13,481 |
5,154 |
8,763 |
1,500 |
14,290 |
4,481 |
|
n.a. = not available * denotes significance at the 5 percent level |
||||||
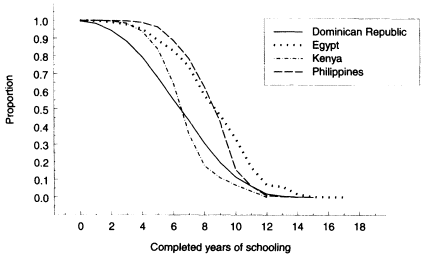
FIGURE 8-3 Predicted proportion with given years of schooling or more: Baseline
model results for a child at 18 years of age.
of results is disconcerting: Why should the countries with the lowest levels of unintended and excess fertility show the greatest impact of such fertility on education? We believe at least six factors may account for this pattern of results.
First, it may be that in an environment in which parents are generally more effective in controlling the timing of births and achieving their desired number of children, an unintended birth is perceived to be less likely, so that when it occurs, it may be more disruptive to family-building strategies. Note that the Dominican Republic and the Philippines are the lowest-fertility countries in the group. The point applies better to the case of the Dominican Republic, where some 34 percent of women use modern contraceptive methods, than to the case of the Philippines, in which only 15 percent use such methods.
Second, it is reasonable to expect that the disruption occasioned by an unintended birth may be greater where three conditions obtain: the returns to education are perceived to be considerable, the (direct) costs of education are also considerable, and there exist reasonably strong preferences for equalizing educational investments across children. In such an environment, parents might feel compelled to make across-the-board adjustments, so to speak, when faced with an unanticipated birth. (On these points, see Appendix A.)
Third, recall that the reports of unintended and excess fertility are those of women rather than their spouses. In the case of Egypt, women are said to cede much decision-making authority to their spouses, and in such settings a woman's own views of whether a birth was wanted or fertility is excessive might have little
to do with household resource allocation. If the man were to declare a birth unwanted, the implications might be quite different.
Fourth, a closely related point is that in none of these countries is there available a measure of the intensity of preferences, that is, of the degree of motivation to avoid excess family size or unintended births. It is plausible that in Egypt and Kenya, countries still in the early stages of demographic transition, such motivations may often be superficial or clouded by ambiguity and second thoughts.
Fifth, in all countries the possibility of random, nonsystematic measurement error in preferences deserves consideration.21 Such errors would tend to bias the estimated effects downward, and it may be that the measurement error variance is itself a function of a country's stage of demographic transition.
Finally, a point that bears in particular on the case of Kenya, we have not fully explored measures of birth mistiming. In a society in which birth spacing has been a dominant concern, with the possibility of and desires for limiting fertility a more recent development, the impact of poor spacing deserves further attention.
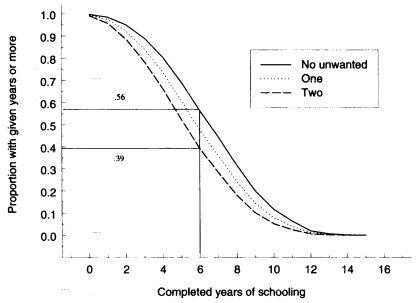
How important in substantive terms are the effects of unintended and excess fertility? To address this question, we consider the years-of-schooling estimates for the Dominican Republic and translate the parameter estimates into predicted years of schooling for a hypothetical child aged 18. (Of the two countries where effects were found, we choose the Dominican Republic case because these results are better justified in statistical terms than are those for the Philippines.) The calculations used here apply to unwanted fertility, but the nature of the results would be similar had we chosen to illustrate the estimated consequences of excess fertility. We generate three predictions—one for the case in which no unwanted birth occurred, another in which one such birth occurred, and a third in which two such births occurred. The range in predictions then illustrates the role of this particular covariate, other things being held constant. To provide a sense of relative strength, we then compare the predictions with those generated by the single strongest socioeconomic covariate in our models—mother's education.
The comparison in substantive terms can be seen in Figures 8-4 and 8-5. Figure 8-4 graphs the results when unwanted fertility is varied as just described, and Figure 8-5 carries out the analogous exercise for mother's education. These estimates do not include the indirect effects of mother's education that operate through unintended fertility, only the direct effects. To understand the figures, it may be helpful to focus attention on grade 6, which is the end of primary schooling in the Dominican Republic. The predicted proportion of children achieving at least this level of schooling is .56 in the case of no unwanted births, .48 in the case of one unwanted birth, and just .39 in the (extreme) case of 2 or more
TABLE 8-7 Selected Coefficients on Measures of Unintended or Excess Fertility
|
|
Dominican Republic |
|
Egypt |
|
|
Measure of Unwanted or Mistimed Fertility |
Completed Years |
Secondary Schooling |
Completed Years |
Secondary Schooling |
|
Model I |
||||
|
One unwanted birth in last 5 years (z value) |
-.280* |
-.249 |
.000 |
.009 |
|
(-5.22) |
(-1.66) |
(0.02) |
(0.18) |
|
|
Two or more |
-.550* |
-.340 |
-.032 |
-.121 |
|
(-6.16) |
(-1.22) |
(-0.92) |
(-1.50) |
|
|
|
.00 |
.12 |
.64 |
.29 |
|
Model II |
||||
|
At least one unwanted birth or birth mistimed by 3 or more years |
-.322* |
-.245 |
-.023 |
-.049 |
|
(-7.22) |
(-1.89) |
(-1.15) |
(-1.09) |
|
|
Model III |
||||
|
Number of births > Ideal family size at survey |
-.219* |
-.259* |
.031 |
-.088 |
|
(-6.87) |
(-3.49) |
(1.12) |
(-1.21) |
|
|
* Significant at p<.05. |
||||
unwanted births, a total difference of some 17 percentage points. This is a substantively important difference. Similar results can be derived from the other measures of unintended and excess fertility. Had we chosen the Philippines for our example, the differences would not have been quite as large (and recall the potentially contaminating role of statistical endogeneity in those results).
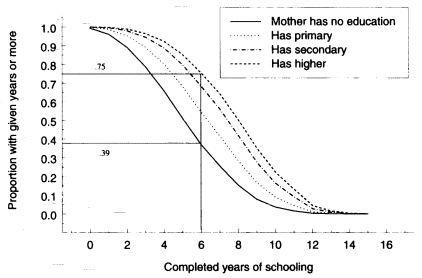
To be sure, the difference produced in children's education in the Dominican Republic by varying the incidence of unwanted childbearing (in a 5-year period) is not as large as what would be generated by variations in the educational level of the mother. Figure 8-5 shows that the predicted proportion of children having 6 or more completed years of schooling ranges from .39 in the case when mothers have no schooling to .75 when they have post-secondary schooling. The conceptual experiment in this figure, however, involves a great range for mother's education (from none to post-secondary), and it is not obvious what policy instruments could effect such a change.
|
|
Kenya |
|
Philippines |
|
|
|
Completed Years |
Secondary Schooling |
Completed Years |
Secondary Schooling |
|
Model I |
||||
|
One unwanted birth in last 5 years (z value) |
.006 |
.139 |
-.033 |
-.081 |
|
(0.20) |
(1.01) |
(-1.33) |
(-1.24) |
|
|
Two or more |
-.073 |
-.126 |
-.129* |
-.190 |
|
(-1.49) |
(-0.56) |
(-2.99) |
(-1.76) |
|
|
|
.30 |
.46 |
.01 |
.12 |
|
Model II |
||||
|
At least one unwanted birth or birth mistimed by 3 or more years |
-.058 |
.058 |
-.075* |
-.141* |
|
(-2.29) |
(0.48) |
(-3.69) |
(-2.62) |
|
|
Number of births > Ideal family size at survey |
-.008 |
-.256 |
-.124* |
-.203* |
|
(-0.29) |
(-1.81) |
(-6.73) |
(-4.17) |
|
Conclusions
Our empirical results suggest that in the middle to latter phases of a fertility transition, the positive effects of mother's education on children's education are likely to be reinforced by reductions in the incidence of unintended or excess fertility. The consequence is a ''virtuous circle" linking mothers and their children. The children of women who are able to avoid unintended fertility benefit in terms of their schooling; one assumes that as adults, they will be better equipped to manage their own fertility and to make appropriate provision for the children of the next generation. This phase of the fertility transition is exemplified by the cases of the Philippines and the Dominican Republic, where the TFR lies between 3.7 and 4.1. The full extent of these effects cannot be estimated with DHS data given the 5-year window of observation. These longer-term effects are potentially greater than those estimated here.
At an earlier phase of the fertility transition, as illustrated here by the case of Kenya with a TFR of 5.2, women with more education are among the first to
reduce their family-size desires, a change that induces an initial positive association between mother's education and unintended and excess fertility. In a setting where birth spacing has traditionally been important, but family-size preferences remain high, a child's schooling appears to suffer, if it suffers at all, only when siblings are mistimed. The gap between actual and desired fertility does not otherwise seem to hinder children's schooling. This result is consistent with research suggesting that the relationship between fertility and education may become significant and negative only after certain development and demographic thresholds have been passed. Also, in Kenya as in much of sub-Saharan Africa, there are possibilities for meeting unanticipated childrearing costs through sibling chains of support and networks of relatives. Furthermore, the direct costs of schooling may be sufficiently low, in this early phase of transition, that an unintended birth can be accommodated without serious disruption to planned investments. In Egypt, where the fertility transition is in a more intermediate phase (a TFR of 4.7 at the time of the 1988 survey), our results are not easily interpreted, although again the direct costs of schooling may not be sufficiently high for an unintended birth to present difficulties.
One implication of these findings is that as the transition reaches its later phases, differences among women in the ability to meet, yet not exceed, their reproductive goals may be an important factor generating social inequalities among their children. Access to family planning services for women of all socioeconomic levels is important, and our findings underscore the continuing need for investment in family planning services for the disadvantaged.
Acknowledgments
We gratefully acknowledge the support of the Rockefeller Foundation through its grant to the Population Council, "Interrelationships Between Fertility and Child Investment: New Research Frontiers." Edmundo Paredes and Jie Wang provided invaluable research assistance throughout the project. We also acknowledge, with thanks, comments from Dennis Ahlburg, John Bongaarts, John Casterline, Deborah DeGraff, Jane Guyer, and two anonymous reviewers.
References
Appleton, S. 1995 Exam Determinants in Kenyan Primary School: Determinants and Gender Differences. Washington, D.C.: Economic Development Institute, World Bank.
Bankole, A., and C.F. Westoff 1995 Childbearing Attitudes and Intentions. DHS Comparative Studies No. 17 . Calverton, Md.: Macro International, Inc.
Bankole, A., and C.F. Westoff 1997 The Consistency and Validity of Reproductive Attitudes: Evidence from Morocco (unpublished manuscript).
Baydar, N. 1995 Consequences for children of their birth planning status. Family Planning Perspectives 27(6):228-234.
Baydar, N., and W. Grady 1993 Predictors of Birth Planning Status and Its Consequences for Children. Seattle, Wash.: Battelle Public Health Research and Evaluation Center.
Becker, G., and H.G. Lewis 1973 On the interaction between the quantity and quality of children. Journal of Political Economy 81(2 Part II):S279-S288.
Behrman, J. 1988 Intrahousehold allocation of nutrients in India. Oxford Economic Papers 40:32-54.
Bollen, K.A., D.K. Guilkey, and T.A. Mroz 1995 Binary outcomes and endogenous explanatory variables: Tests and solutions with an application to the demand for contraceptive use in Tunisia. Demography 32(1): 111-131.
Bongaarts, J. 1990 The measurement of wanted fertility. Population and Development Review 16(3):323-334.
Brown, S., and L. Eisenberg, eds. 1995 The Best Intentions: Unintended Pregnancy and the Well-Being of Children and Families. Committee on Unintended Pregnancy, Division of Health Promotion and Disease Prevention, Institute of Medicine. Washington, D.C.: National Academy Press.
Casterline, J., A. Perez, and A. Biddlecom 1996 Factors Underlying Unmet Need for Family Planning in the Philippines. Research Division Working Paper. New York: The Population Council.
David, H., Z. Dytrych, Z. Matejcke, and V. Schuller, eds. 1988 Born Unwanted: Developmental Effects of Denied Abortion. New York: Springer Publishing.
Desai, S. 1995 When are children from large families disadvantaged? Evidence from cross national analyses. Population Studies 49(2): 195-210.
Frenzen, P.D., and D.P. Hogan 1982 The impact of class, education and health care on infant mortality in a developing society: The case of rural Thailand. Demography 19(3):391-408.
Guilkey, D.K., and J.L. Murphy 1993 Estimation and testing in the random effects probit model. Journal of Econometrics 59:301-317.
Guilkey, D.K., T.A. Mroz, and L. Taylor 1992 Estimation and Testing in Simultaneous Equations Models with Discrete Outcomes Using Cross Section Data. The Evaluation Project Working Paper Document #IM-01-01. University of North Carolina at Chapel Hill.
Hanushek, E. 1992 The trade-off between child quantity and quality. Journal of Political Economy 100( 1 ):84-117.
Hausman, J. 1978 Specification tests in econometrics. Econometrica 46(6): 1251-1271.
Hedeker, D., and R.D. Gibbons 1994 A random-effects ordinal regression model for multilevel analysis. Biometrics 50:933-944.
Hermalin, A., J. Seltzer, and C.-H. Lin 1982 Transitions in the effect of family size on female educational attainment: The case of Taiwan. Comparative Education Review 26(2):254-270.
Jensen, E., D. Ahlburg, and M. Costello 1996 The Impact of Wantedness and Family Size on Child Mortality and Health-Care Allocations Within Filipino Families. Williamsburg, Va.: The College of William and Mary.
Kelley, A. 1996 The consequences of rapid population growth on human resource development: The case of education. In D. Ahlburg, A. Kelley, and K. Mason, eds., The Impact of Population Growth on Well-Being in Developing Countries. Berlin: Springer-Verlag.
Kurian, G.T., ed. 1988 World Education Encyclopedia. New York: Facts on File Publications.
Lightbourne, R.E. 1985 Individual preferences and fertility behaviour. In J. Cleland and J. Hobcraft, eds., Reproductive Change in Developing Countries: Insights from the World Fertility Survey. Oxford: Oxford University Press.
Lloyd, C.B. 1993 Family and Gender Issues for Population Policy. Population Council Research Division Working Paper No. 48. New York: The Population Council.
1994 Investing in the next generation: the implications of high fertility at the level of the family. In R. Cassen, ed., Population and Development: Old Debates, New Conclusions. Washington, D.C.: Overseas Development Council.
Lloyd, C.B., and A.K. Blanc 1996 Children's schooling in sub-Saharan Africa: The role of fathers, mothers, and others. Population and Development Review 22(2):265-298.
McClelland, G.H. 1983 Family-size desires as measures of demand. In R. Bulatao and R. Lee, eds., Determinants of Fertility in Developing Countries. Volume 1: Supply and Demand for Children. New York: Academic Press.
Mensch, B., M. Arends-Kuenning, A. Jain, and M. Garate 1995 Meeting Reproductive Goals: The Impact of the Quality of Family Planning Services on Unintended Pregnancy in Peru. Population Council Research Division Working Paper No 81. New York: The Population Council.
Montgomery, M.R., and C.B. Lloyd 1996 The effects of family planning programs on maternal and child health. In D. Ahlburg, A. Kelley, and K. Mason, eds., The Impact of Population Growth on Well-Being in Developing Countries. Berlin: Springer-Verlag.
Montgomery, M. R., A. Kouamé, and R. Oliver 1995a The Tradeoff Between the Number of Children and Child Schooling. Living Standards Measurement Study Working Paper No. 112. Washington, D.C.: The World Bank.
1995b The Tradeoff Between the Number of Children and Their Schooling: Evidence from Côte d'Ivoire and Ghana. Population Council Research Division Working Paper No. 80. New York: The Population Council.
Myhrman, A., P. Olsen, P. Rantakallio, and E. Laara 1995 Does the wantedness of a pregnancy predict a child's educational attainment? Family Planning Perspectives 27(3): 116-119.
Parish, W., and R. Willis 1993 Daughters, education and family budgets: Taiwan experiences. Journal of Human Resources 28(4):863-898.
Postlethwaite, T.N., ed. 1988 The Encyclopedia of Comparative Education and National Systems of Education. Oxford: Pergamon Press.
Rosenzweig, M., and T.P. Schultz 1987 Fertility and investments in human capital: Estimates of the consequences of imperfect fertility control in Malaysia. Journal of Econometrics 36:163-184.
Rosenzweig, M., and K. Wolpin 1980 Testing the quantity-quality fertility model: The use of twins as a natural experiment. Econometrica 48( ):227-240.
1993 Maternal expectations and ex post rationalizations. The Journal of Human Resources 28(2):205-229.
UNESCO 1994 Statistical Yearbook. Paris: UNESCO.
United Nations 1992 Abortion Policies: A Global View. Volume 1: Afghanistan to France. New York: United Nations.
1993 Abortion Policies: A Global View. Volume 2: Gabon to Norway. New York: United Nations.
1995 Abortion Policies: A Global View. Volume 3: Oman to Zimbabwe. New York: United Nations.
Varian, H.R. 1984 Microeconomic Analysis. Second edition. New York: W.W. Norton & Company.
Westoff, C.F., N. Goldman, and L. Moreno 1990 Dominican Republic Experimental Study: An Evaluation of Fertility and Child Health Information. Columbia, Md.: Institute for Research Development/Macro Systems, Inc.
Wolfe, B., R. Haveman, D. Ginther, and C.B. An 1996 The 'window problem' in studies of children's attainments: A methodological exploration. Journal of the American Statistical Association 91(435):970-982.
World Bank 1995 Staff Appraisal Report, The Dominican Republic. Second Basic Education Development Project. Report No. 14963-DO. Washington, D.C.: The World Bank.
Zuravin, S.J. 1991 Unplanned childbearing and family size: Their relationship to child neglect and abuse. Family Planning Perspectives 23(4):155-161.
Appendix A A Parental Utility Maximization Model For Fertility And Children's Schooling
In this appendix, we develop a formal decision model in which parents choose the number of their children and the level of educational investment in each child, taking into account the implications of alternative choices about children for their own consumption levels. The model is primarily a vehicle for illustrating in a formal manner the theoretical points made in the main text. It is therefore a highly simplified representation of the decision problem. In particular, the model is set in a one-period decision framework, in which both fertility and education choices are made at the outset of the reproductive life cycle. A more realistic and interesting approach, as discussed in the main text, would be to allow for multiple decision periods, so that parents would have the opportunity to learn about the educational abilities of their children and might adjust subsequent fertility and consumption in light of the accumulated information. Such dynamic decision models are extremely complex to analyze, however, and as our purpose is mainly to illustrate key points, we do not pursue this generalization here.
There are conceptual benefits to be gained from a formal mathematical approach, even if this representation is understood to be no more than a stylized and simplified depiction of the decision problem. Perhaps the principal benefit is in showing that parental desires-as expressed in their wanted fertility levels, their desired pattern of educational investments in children, and their preferred level of own consumption-are jointly determined by a common set of exogenous factors. These factors include the level of parental income, the prices and related resource constraints parents face, and the fixed features of parental preferences. We therefore think of wanted fertility and wanted education as being joint outcomes of a common decision process: they each depend on the exogenous determinants, but do not depend, in any causal sense, on each other. The level of wanted fertility is not a causal determinant of the level of wanted children's schooling, nor is the level of wanted schooling a causal determinant of wanted fertility.
In this framework, it is not meaningful to ask how wanted fertility affects wanted levels of children's education, nor is it appropriate to put the question the other way. The dimensions of wanted fertility and wanted children's education are closely associated, to be sure, but this association is not, in itself, a causal one. Rather, the association reflects the joint dependence of fertility and education on the exogenous causal determinants mentioned above. Where unwanted fertility is concerned, however, one can ask about the causal consequences. This is because unwanted fertility can be regarded as an exogenous shock that displaces parental consumption and human capital investment strategies from what would otherwise have been optimal.
In a more complex, dynamic decision framework, one could investigate the
consequences of unwanted fertility (or other exogenous shocks) during the reproductive life cycle on subsequent fertility and subsequent child investments. These consequences might well depend on the level and age pattern of the wanted births that had already occurred at the time of the exogenous shock. Such earlier births (likewise, earlier child investments) would function as predetermined constraints (or sunk costs) that could limit the scope and nature of any post-shock adjustments on the part of parents. Moreover, in a dynamic decision problem in which the spacing and arrival of wanted births is not fully controllable by parents, it becomes conceptually appropriate to ask how the timing of wanted births affects subsequent fertility, child schooling, and parental consumption. Likewise, one can ask how imperfectly predictable factors, such as a child's educational abilities, might affect the parents' fertility as these factors become known.
Given that this chapter is mainly empirical in nature and based on cross-sectional data sets, we have chosen not to pursue the theoretical possibilities afforded by dynamic modeling. The empirical concerns are indeed difficult to address. If lagged, predetermined values of ex ante choice variables are to be included in the empirical model, a means must be found to protect the estimates against the effects of persistent omitted variables, which would be expressed first in the lagged values of the choice variables and again in the current values being modeled. Thus, demanding data requirements must be met to permit consistent estimation of such models. Longitudinal data are required, at a minimum, and the DHS data used here simply do not meet these requirements. With richer data, one could begin to ask a richer set of causal questions.
Elements of the One-Period Model
We begin by separating the one-period parental utility function into two factors. The first factor, denoted here by U, measures the utility that parents derive from the number of children and their education. We follow Behrman (1988) in using the constant elasticity of substitution (CES) specification, that is,
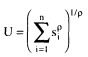
in which i is a subscript for child i, and si is the education of that child. Here n is the total number of children. The parameter p of this subutility function serves to index the degree of parental aversion to inequality in the distribution of resources among their children. It ranges from -∞ to 1, with the case of ρ = 1 representing no aversion to inequality and, at the opposite end, the case of p →∞ representing no tolerance of inequality, that is, Leontief preferences.22
In addition to U, the utility of the parents is affected by their own consumption C. We assume that the full utility function can be expressed in a Cobb-Douglas form,
V = UCa
where the parameter α gives the subjective weight parents attach to their own consumption. The full parental utility function is therefore a composite in which a CES factor, having to do with child services, is nested within a Cobb-Douglas function in which the two arguments are the child services aggregate U and parental consumption C.
The budget constraint for this problem allows for both discretionary and exogenous components of expenditure on children. Each child is assumed to require a fixed amount w in childrearing expenditures; in addition, a child-specific net price pi is associated with each unit of education si. The rationale for making the net price of education child-specific is to account for differences across children in the expected future benefits of schooling. We could accomplish the same goal by elaborating the model in the time dimension, with the nature of the future benefits made explicit, but the current specification should suffice for the purposes of illustration.
The budget constraint can then be expressed as
where W is total parental income.
Solving the Utility Maximization Problem
The utility maximization problem can now be divided into discrete stages that correspond to the alternative numbers of children that parents could contemplate having. For any given number of children n, parents face the task of optimally dividing their discretionary income, Ω - wn, between child services U and their own consumption C. The Cobb-Douglas specification for the full utility function implies that with n given,
|
|
additional children receive a strictly positive amount of schooling. In future work, we will study more general specifications that do not impose this requirement. |
and what remains of household resources is then available to be distributed among the n children for their schooling.
The properties of the CES framework (see Varian, 1984, for details) imply that each child will receive
in education, where r = ρ/(ρ - 1) and Y = (Ω- wn)/(1 + α) is the total amount of discretionary income available for schooling. We refer to this as the schooling demand equation, where by demand we mean demand that is conditional on a particular fertility level n. The conditional indirect utility derived from child services is then
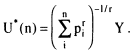
We can now summarize the overall parental utility derived from n children as
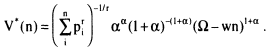
This is a conditional indirect utility function, giving maximum parental utility as a function of the number of children, which is itself a choice variable. Using this expression, the task that remains is to search over discrete values of n to find the optimal value—the level of fertility that maximizes parental utility. In the main text, we refer to the optimal value of n as wanted fertility. Since n is discrete, no analytic expression for wanted fertility is available, but for given parameter values, it is straightforward to find the level of wanted fertility by numerical means.23
Let n* denote the level of wanted fertility. The wanted level of children's education, which will in general differ across children, is then determined by substituting n* for n in the denominator of the schooling demand equation above. Likewise, the optimal level of parental consumption is given as C = α/(1 + α) (Ω - wn*). Since n* is a function only of the set of exogenous factors (Ω, p, w, ρ, α), wanted schooling and consumption are also fully determined by these factors. It is in this sense that wanted fertility and schooling are jointly determined.
Some Properties of the Solution
As Behrman (1988) demonstrates in a related context, parental aversion to inequality has a potentially important role to play in allocating educational investments among a set of children. This role emerges in situations in which the net price of schooling, pi, differs across children, so that there is an economic incentive to invest differentially. The extent to which such differential investment takes place depends on ρ, the utility parameter that expresses whether parents are indifferent to inequality (ρ = 1) or would tend to resist allocating resources in an unequal manner (ρ < 1), other things being equal. When parents are wholly indifferent to inequality, educational resources are concentrated in the child whose net price of schooling pi is lowest. When they resist such a concentration of resources, by contrast, educational investments tend to be spread more equally among children, although the child with the lowest net price will generally continue to receive more in the way of parental investment (apart from the extreme case of Leontief preferences).
The discrete nature of fertility also influences patterns of child investment. To see this, consider the comparative statics of the response to a change in parental income Ω. Suppose that Ω is reduced. In addition to reducing their own consumption, parents faced with lower income have the option to adjust to the situation in two ways that affect their children: on the extensive margin, by reducing the desired number of children, and on the intensive margin, by leaving the number of children unchanged and reducing educational investments. For certain combinations of parameters, as income Ω falls, parents will adjust first by cutting back on children's schooling. After a certain point, however, income will be low enough that parents will find it necessary to reduce fertility. A one-child reduction in fertility frees an amount w in exogenous childrearing expenses. Once that fertility reduction has been made, a portion of the freed w can be used to increase children's schooling, that is, to increase it relative to what it was before the fertility reduction took place. Thus, if we were to graph the relationship between Ω and children's schooling, the graph could exhibit a sawtooth pattern whose shape would reflect both the intensive and the extensive margins of adjustment. A similar pattern could characterize the parental response in own consumption as Ω varies. As far as we are aware, these potentially complex responses have not been much studied, whether from a theoretical or an empirical perspective.
Parental Responses to Unwanted Fertility
The conceptual approach developed here can be used to study the consequences of unwanted fertility for parental consumption and children's educational investments. As above, let n* denote the level of wanted fertility. If an unwanted birth occurs, actual fertility is then n' = n* + 1. Returning to the
expressions above concerning children's education, we can determine the education response to unwanted fertility by inserting n' in the demand equation where n* had appeared; we can do likewise for parental consumption. The implied adjustments in education and consumption will depend on a number of factors: the level of exogenous childrearing costs w, the child-specific net prices for education pi, the level of income Ω, and so on.
The full welfare cost for parents can be summarized in terms of compensating variation, that is, in terms of the additional level of income Ω that would be required to leave the parents as well off with n' children as they would have been with the number of children they actually wished to have, or n*. It is possible to calculate the required compensation by using the conditional indirect utility function V*(n) shown above. This compensation can then be interpreted as a summary measure of parental motivation to avoid unwanted fertility. Alternatively, it can be interpreted as the monetized welfare costs (again from the parents' point of view) that are imposed by unwanted fertility.
Appendix B Measurement Of Unintended And Excess Fertility
In the main text, we focus on two distinct concepts—excess fertility and unintended fertility. As noted, the former is measured by the extent to which a woman's cumulative fertility exceeds her expressed ideal family size at the time of the survey. Reports on ideal family size are elicited by the following DHS question: ''If you could go back to the time you did not have any children and could choose exactly the number of children to have in your whole life, how many would that be?" Unintended fertility, by contrast, is typically measured with reference to the 5-year window of time ending at the survey. Within that window, the intendedness of each birth is determined by asking the mother to think back to her feelings at the time she was first pregnant with the child and to report whether she wanted the pregnancy at that time. If the pregnancy was wanted, she is asked whether it was wanted then or later.
Concerns about the measurement of unwantedness have focused primarily on the problem of ex post rationalization. Rationalization is a potential problem when respondents who already have children are asked questions about desired or ideal family size or about the unwanted status of specific surviving children (McClelland, 1983). In particular, the questions on unintended fertility are asked on a child-by-child basis, and in answering them, the woman may feel that she is being required, in effect, to affix a label to each child. Yet a child whose conception was unwanted might have grown up to become a loved and much "wanted" member of the family. The woman might therefore feel some reluctance to label the child's conception as unwanted, and the approach might produce underreports of unwanted conceptions. (No similar bias would be expected to distort estimates of birth timing.) The DHS questions were worded so as to minimize ex post rationalization, and there is some evidence from experimental studies in Peru and the Dominican Republic (Westoff et al., 1990) that the emphasis on feelings at the time of conception helps reduce the problem. The fact that substantial numbers of women report excess fertility and unwanted births appears to be ample proof that family-size desires represent considerably more than rationalization.
Another form of rationalization could lead to biases in the opposite direction. Rosenzweig and Wolpin (1993) have conjectured that women may be overly optimistic at the time of pregnancy about the endowments of their unborn children. They suggest that retrospective reporting of unwantedness at the time of pregnancy may produce an overestimate rather than an underestimate of the actual level of unwantedness prior to birth. The possibilities for ex post revisionism, regardless of the direction of the possible bias, are what make the kind of longitudinal data available in the Finnish survey ideal for the study of the consequences of unwantedness.
Apart from considerations of recall error and ex post rationalization, a woman's reports on the intendedness of a particular child's conception should not change over time. Such reports are based on the memory of feelings held at a particular fixed point in the past. We do, however, expect to observe changes over time in measures of excess fertility for an individual woman, even if her actual fertility remains unchanged. A woman's desire for children, as expressed in her ideal family size, can be altered by changes in economic, marital, or health circumstances, or by the receipt of new information or knowledge, even if her underlying preferences are held constant (McClelland, 1983). Thus a woman could report her last birth as being wanted at the time of conception and during the same survey interview report excess fertility in the present. She might do so if, in the interim, she faced deteriorating economic conditions, gained new skills in the labor market that increased the opportunity costs of childbearing, absorbed new ideas about the advantages of small families from the media, or lost a husband through death or divorce. Similarly, a woman who reports not having wanted a particular pregnancy in the past could report no excess fertility in the present for a variety of reasons, including an improvement in her own or her community's economic circumstances that allows her to afford more children than previously, the arrival of a new husband who is eager for her to have children with him, or a change in government policies. It is therefore quite difficult to determine from the survey questions themselves whether a woman is inconsistent in her responses. The fact that a woman currently views her family size as excessive does not necessarily mean that any particular child was unwanted at the time of conception, nor does it mean that any particular child is unwanted now. Excess fertility indicates only that the woman now sees her family size as being too large in relation to current ideals.
Of course, if fertility ideals and intentions are wholly transitory, their measurement as of a particular point in time will not provide a reliable guide to either past or future behavior. Recent evidence from Peru suggests that desired fertility is reasonably stable in the short run (Mensch et al., 1995). In this study, over 80 percent of women reinterviewed after 3 years provided consistent responses to a question about future fertility intentions. When responses to the question about future childbearing desires from the 1991-1992 DHS were compared with responses to the same question in the 1994 follow-up survey, 72 percent of women gave the exactly the same response. Of those who did not want more in 1994 but had wanted more in 1991-1992, roughly half had had a child in the interval or had experienced a marital disruption; thus an additional 7-8 percent gave consistent answers. Therefore, roughly 80 percent of women gave consistent answers between the two surveys. This provides some evidence to suggest that women's fertility desires do not change wholesale over 3 years. Casterline et al. (1996) examined changes in the Philippines over a shorter reinterview period—6 weeks—and also found considerable evidence of stability.
Although Bankole and Westoff (1995) consider recent births, the aggregate
measures of unwanted fertility reported elsewhere in the literature are not based on reports on the wantedness status of particular births, but rather on measures of ideal family size (Lightbourne, 1985) or the desirability of the next birth (Bongaarts, 1990). In the terms we have employed, the Lightborne measures are measures of excess fertility. Bongaarts (1990) compared such excess fertility measures with alternative, forward-looking measures based on the desirability of a next birth. He found strong correlations between these two alternatives, but much weaker correlations between the desire for a next birth and the wantedness status of recent births. Evidently, the alternative measures must tap different concepts; in addition, they are differentially affected by changing events and by recall or misreporting error.
To obtain a sense of the empirical overlap between measures of excess and unintended fertility, we examined the DHS data from our four study countries. We investigated whether women who say they currently have excess fertility also report as unwanted at conception those recent births whose parity exceeds the mother's current ideal. The proportion of such recent births reported to be unwanted at the time of conception ranges from 35 percent in the Philippines to 65 percent in the Dominican Republic.
In light of the above discussion, it should be clear that such differences in the fertility measures can be interpreted in various ways. One possibility among many is that ideal family size may have declined over the 5 years preceding the survey (Bankole and Westoff, 1995), perhaps as economic circumstances changed. Thus some children who were wanted prior to their birth may now be found in a family that is larger than their mother would view as ideal under her present circumstances.
In summary, it appears reasonable to proceed with the excess and unintended fertility measures, each taking a place in the analysis. These measures are fundamentally different in character, and as just shown, they are sufficiently different empirically to warrant separate consideration.
APPENDIX C Endogeneity Tests Using Generalized Residuals in Schooling Equations
|
Measure of Unwantedness |
χ2 on family planning access in incidence equation (p-value) |
Generalized residual coefficient, years equation (z stat.) |
Generalized residual coefficient, secondary school equation (z stat.) |
|
Dominican Republic |
|||
|
0, 1, or 2+ unwanted births in last 5 years |
23.6 |
0.022 |
0.354 |
|
(0.07) |
(0.15) |
(0.79) |
|
|
Any unwanted births or births or more years mistimed by 3 |
17.6 |
-0.109 |
0.752 |
|
(0.29) |
(-0.66) |
(1.50) |
|
|
Number of births exceeds family-size ideal |
31.0 |
0.170 |
0.100 |
|
(0.01) |
(1.08) |
(0.57) |
|
|
Egypt |
|||
|
0, 1, or 2+ unwanted births in last 5 years |
50.5 |
-0.173* |
-0.327* |
|
(0.00) |
(-3.23) |
(-2.37) |
|
|
Any unwanted births or births mistimed by 3 or more years |
61.2 |
-0.175* |
-0.384* |
|
(0.00) |
(-2.68) |
(-2.21) |
|
|
Number of births exceeds family-size |
85.9 |
-0.141 |
-0.447 |
|
(0.00) |
(-1.94) |
(-1.98) |
|
|
Measure of Unwantedness |
χ2 on family planning access in incidence equation (p-value) |
Generalized residual coefficient, years equation (z stat.) |
Generalized residual coefficient, secondary school equation (z stat.) |
|
ideal |
|||
|
Kenya |
|||
|
0, 1, or 2+ unwanted births in last 5 years |
21.8 |
-0.238* |
0.218 |
|
(0.02) |
(2.57) |
(0.46) |
|
|
Any unwanted births or births mistimed by 3 or more years |
17.5 |
-0.172 |
0.093 |
|
(0.06) |
(-1.26) |
(0.12) |
|
|
Number of births exceeds family-size ideal |
27.2 |
-0.162 |
0.438 |
|
(0.00) |
(-1.89) |
(0.71) |
|
|
Phillippines |
|||
|
0, 1, or 2+ unwanted births in last 5 years |
27.0 |
-0.059 |
-0.129 |
|
(0.04) |
(0.71) |
(0.20) |
|
|
Any unwanted births or births mistimed by 3 or more years |
29.3 |
-0.202* |
-0.001 |
|
(0.02) |
(-2.18) |
(-0.01) |
|
|
Number of births exceeds family-size ideal |
34.7 |
0.324* |
0.440 |
|
(0.01) |
(3.17) |
(1.22) |
|
|
* Significant at p < .05. |
|||