B A Model for Diffusion of Radon Through the Stomach Wall
The primary functions of the stomach in the gastrointestinal system are to dissolve ingested foods and pass the contents to the small intestine, where nutrients are transferred to the bloodstream. Those functions are facilitated by the production and secretion of acid and enzymes that eventually dissolve the contents. The wall of the stomach contains the cells that generate the acid. The epithelial surface of the stomach wall is coated with a mucous layer that serves as a barrier between the acidic lumen and the tissues surrounding the stomach. Adjacent to the mucous layer is a region of tissue consisting of crypts that contain proliferating stem or progenitor cells that eventually reach the surface to perform the necessary functions. These cells are radiosensitive and are believed to be responsible for initiation and promotion into stomach cancer.
The failure of most materials in the lumen of the stomach to penetrate into the wall in effect serves as a protective measure for stem cells, in that alpha particles originating in the stomach contents cannot reach the stem cells. However, alcohol, aspirin, and inert gases, such as carbon dioxide and the noble gases, are known to penetrate into and pass through the wall of the stomach and to enter the blood stream. The mechanism of this process is assumed to be molecular diffusion, but blood flow can influence clearance through the stomach wall. It is thought that some of the radon ingested with water will also diffuse through the contents to the wall and then through the stomach wall; this presents an opportunity for alpha particles from radon decay to deposit energy at the location of radiosensitive cells.
The objective of this modeling exercise was to estimate the transport of radon through the stomach wall by diffusion. It was not designed to give a
complete description of the very complicated geometry and dynamics of the stomach. However, it was created to provide indications of the concentration and duration of radon in regions that may contain radiosensitive cells. These efforts were necessary because no other theoretical or experimental information is available. By varying the parameters, it was possible to obtain a range of results and to identify extreme values that could serve as bounds for radon concentrations in the stomach wall.
For simplicity, the lumen of the stomach was considered to be a sphere. The sphere was surrounded by concentric spherical shells representing the mucous layer and the wall. The stomach was filled with water containing a unit concentration of radon at time t = 0. The radon concentration in the mucous and wall was zero at t = 0. The radon concentration at the outer surface of the wall was considered to be zero at all times because of the removal of radon by blood flowing through the stomach wall.
The time-dependent equation describing the concentration of radon can be derived from Fick's law:
where
C = the concentration of radon,
D = the effective diffusion coefficient, ![]() 2 = the Laplacian operator, and
2 = the Laplacian operator, and
λ = the radioactive-decay constant associated with 222Rn.
Since the intervals associated with events in the stomach are generally much less than the half-life of 222Rn, radioactive decay is neglected. Using spherical symmetry, the Laplacian operator can be expressed in terms of only the radius, r:
One procedure for solving the equation is to separate C into the product of two components, one in radius only, R(r), and another in time only, T(t) (Andrews 1986). Thus,
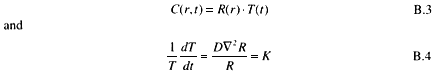
where K is referred to as a separation constant. Initial and boundary conditions are expressed as
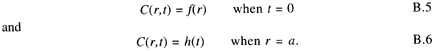
Substituting U = r R into the spatial part of the equation transforms the spherical Laplacian operator into a simple second-order differential equation:
That is identical with the equation for one-dimensional diffusion through a slab, provided that the initial and boundary conditions reflected in U are
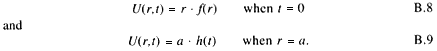
If a solution for U can be found, then the corresponding solution for the sphere is:
The first example is that for a homogeneous sphere and shell. The shell has no radon at time t = 0. The purpose of this calculation is to show how fast radon would escape from an undisturbed sphere and through a shell by diffusion only. The dimensions and initial and boundary conditions are as follows:

A solution that satisfies those conditions is:
Figure B.1 shows a graph of C(r)/Co as a function of radius from the center of the sphere with a diffusion coefficient for radon in water of D = 1 × 10-5 cm2s-1 (Tanner 1964). The radon concentration decreases near the boundary of the sphere but is almost unchanged at a radius less than 3 cm. Even after 1 h, there is considerable radon remaining in the sphere. This illustrates that diffusion alone is not sufficient to transfer all the available radon through the stomach wall in the amount of time corresponding to normal residency in the lumen.
The model was then revised to take into account removal of radon from the lumen by means other than diffusion. The contents of the stomach are considered
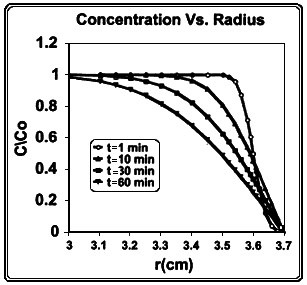
Figure B.1
Concentration of radon, C/C0, vs. radius, r, within a sphere of water with radius rs = 3.6 cm. The interior of the sphere is surrounded by a spherical shell of water with a thickness 0.1 cm and a radon concentration C(r) = 0 at t = 0. The diffusion coefficient for radon in water is D = 1 x 10-5 cm2 s-1.
to be well mixed, but the concentration is decreasing exponentially with a half-time of 20 min. For simplicity, the volume of the lumen remains constant such that any material leaving the stomach is replaced with water that dilutes the radon.
The basic differential equations are unchanged. However, the interior surface of the stomach wall is driven by the function h(t) that is controlled by the concentration in the lumen. A solution can be obtained with Duhamel's theorem where the concentration in the wall is the convolution of the time derivative of a solution after a unit step function at t = 0 (Carslaw and Jaeger 1959).
The dimensions corresponding to the boundary conditions following an intake of 250 mL of water are as follows (see fig. B.2):

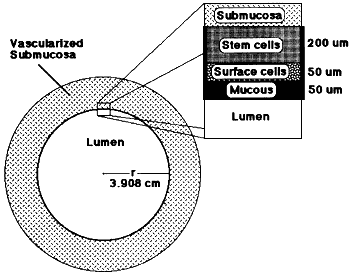
Figure B.2
Diagram showing the geometry used in the model for diffusion of radon through the stomach wall.
The wall consists of mucous (50 µm), surface cells (50 µm) and tissue with crypts that contain the radiosensitive stem cells (200 µm) (E. Robbins 1998, personal communication). The stem cells are centered at a depth of 200 µm below the surface. It is assumed that blood flow removes all radon at a depth of 300 µm.
A solution for that situation is
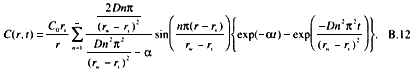
The results depend on the selection of a diffusion coefficient for radon in the mucous and wall. The effective diffusion coefficient includes a retardation factor that accounts for absorption in the medium. There are no published values in the literature for the effective diffusion coefficient of radon in tissue. For this report, we have adopted a value obtained for xenon and assume a nominal value of D = 5 × 10-6 cm2 s-1 for both the mucous and the stomach wall. The exact location of the radio-sensitive cells is also unknown. For this calculation, the absorbed dose is estimated at a depth of 200 µm which is 150 µm below the mucous.
Figure B.3 shows the results from the model with the concentration C(r)/Co plotted at various times after intake. It can be seen that the concentration in the
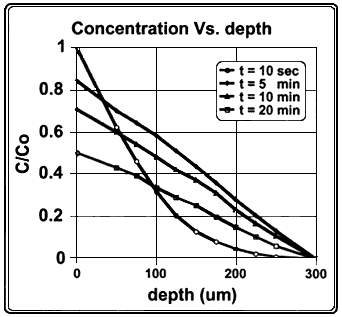
Figure B.3
Concentration of radon, C/Co, as function of depth in the stomach wall. The radius of stomach lumen is 3.908 cm, corresponding to a volume of 250 mL. The concentration in the lumen is considered to be uniform and is assumed to decrease exponentially with a half-time of 20 min. The depth of the mucous layer is 50 µm, and that of the stem cell population is 200 µm.
wall becomes linear with distance from the surface when t is greater than 5 min. Figure B.4 shows the results of the model with the concentration C(t)/Co plotted as a function of time at various distances (in micrometers) from the inner surface of the wall.
The flow rate of radon through the stomach wall can be obtained from the following relationship:
where φ(r,t) is the flow rate of radon per unit area, often referred to as the flux density. Because radioactive decay has been neglected, one would expect the time-integrated flux to yield the total radon flowing through the wall and this should be independent of r:
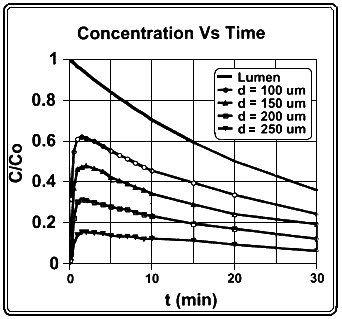
Figure B.4
Concentration C/Co in the stomach wall as a function of time after intake. The radius of the stomach lumen is 3.908 cm, corresponding to a volume of 250 mL. The concentration in the lumen is considered to be uniform and is assumed to decrease exponentially with a half-time of 20 min. The depth of the mucous layer is 50 µm and that of the stem cell population is 200 µm.
For the conditions described here, the fraction of radon released to the blood stream due to diffusion through the stomach wall is 20%.
The absorbed dose to the cells at a depth, r, is related to the time-integrated radon concentration at this same depth. The integrated concentration, relative to that in the lumen is
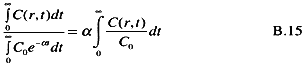
For conditions described here, the time-integrated concentration at the location of the stem cells (depth = 200 µm) was approximately 30% of the integrated concentration in the lumen. As seen from figure B.3, the time-integrated concentration
varies linearly with depth through the stomach wall. The results do not change significantly when the diffusion coefficient is varied from 10-5 to 10-7 cm2 s-1. The number of radon atoms that decay in the vicinity of the stem cells can be obtained by
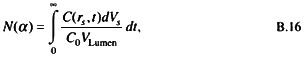
where
N(α)= the number of nuclear transformations of 222Rn occuring in the volume element dV per ingested Bq,
dVs = the volume of a spherical shell surrounding the assumed location of stem cells in the stomach wall (4φr2dr),
r = 3.928 cm, at a depth of 200 µm, and)
dr = 100 µm.
The result of this integration yields four nuclear transformations per becquerel of 222Rn after ingestion of 250 mL of water. That indicates that energy deposition by alpha particles in the vicinity of the radiosensitive cells will certainly not be uniform. Absorbed dose obtained by averaging energy deposition over the volume of interest for this situation should be interpreted with caution.
The model presented here assumes that there is no capillary involvement in the first 250 µm of tissue below the mucous layer in the stomach wall. If such capillaries were present in the region between the surface cells and the crypts containing the stem cells, the capillary blood flow would reduce radon penetration into the wall.
It must be emphasized that this is a very naive representation of the actual conditions in the stomach after an intake of water containing 222Rn. However, these simplifications can increase our understanding of the processes associated with the ingestion of radon by illustrating how assumptions about diffusion could influence internal dosimetry. These results can also provide a basis for the development of more-representative models.








