3
Transfer of Radon from Water to Indoor Air
The estimation of the increment of airborne 222Rn in a dwelling that arises from the use of water that contains dissolved radon is a complex problem. It involves the solubility of radon in water, the amount of water used in the dwelling, the volume of the dwelling, and the ventilation rate. The amount of waterborne radon escaping into the air is different throughout a dwelling but is higher in areas of active water use such as bathrooms and kitchens. It also depends on the radon concentration in the water and the activities that are taking place. However, it is common to estimate the average incremental concentration throughout the dwelling (![]() a) and derive a transfer coefficient as the ratio of that average concentration in water
a) and derive a transfer coefficient as the ratio of that average concentration in water ![]() w:
w:
The relationship used to estimate the transfer coefficient has been derived by Nazaroff and others (1987) on the basis of the assumption that a house is a single well-mixed volume. The transfer function can then be described by:
where W is the time-averaged water use rate; e is the use-weighted transfer efficiency of 222Rn from water to air; λ is the air-exchange rate, which is assumed to be uncorrelated with the water use rate; and V is the volume of the dwelling.
This chapter reviews published transfer-coefficient measurements. In addition, it performs a distributional analysis in the same manner as Nazaroff and others (1987) and compares the results.
Measurements Of Transfer Coefficients
There are only a few measurements of transfer coefficients (from water to air) in the literature, and most of them refer to a limited number of geographic areas. Thus, there is considerable uncertainty in the extrapolation of the resulting distribution to the entire housing stock of the United States. The earliest reports of the measurements of the transfer coefficient were made by Gesell and Prichard (1980) and Castrèn and others (1980). They assumed that all the indoor radon was due to radon in the water, so the transfer coefficient was overestimated. Gesell and Prichard took measurements in apartments, where soil-derived radon is likely to contribute little to measured values. Castrèn's measurements, taken in houses in Finland, made the same assumption and are thus not likely to be useful. The actual values for the dwellings in Finland were not reported, and the data are no longer available (Castrèn, private communication, 1997).
McGregor and Gourgon (1980) measured Ca and Cw in six conventional residences, five trailers, and two schools in Nova Scotia, Canada. Only upper limits for the transfer coefficients can be estimated, because ventilation rates and water-use patterns were not determined. They found values of 0.032–0.24 × 10-4 for the trailers and 0.038–0.52 × 10-4 for the dwellings. The values are lower than many of the reported coefficients. Because the ventilation and water-use rates are not available, it is not possible to know whether the values are low as a result of high ventilation rates, low water use, or some combination of the two. Owing to the uncertainty in separating the contributions of soil gas and drinking water to the indoor radon concentrations, the transfer-coefficient values only for the five trailers have been included in the committee's estimated distribution of values.
During the late 1970s and throughout the 1980s, Hess and coworkers (1990; 1987b; 1987a; 1982) measured the transfer coefficients in a series of houses across Maine. In all, measurements were made in about 70 houses. They have used an approach that they term the ''burst method.'' Measurements are made during a 2-h period when a series of water-use activities are performed. The idea is to use as much water during this 2-h period as would typically be used over a 24-h period. Radon is also monitored over a second 24-h period during which the residents use water according to their normal daily routine. The water-use activities during the second 24-h period were recorded. Ventilation rates were also measured directly.
As part of a study of the effectiveness of radon-mitigation methods (Deb 1992), concentrations of radon in air and water were measured before and after the initiation of a water treatment to reduce the concentration of radon in the
water. Measurements of radon in air and water use were made in each of 119 houses before and after treatment. In two homes one measurement was unavailable; therefore, values for only 117 homes were used. In two of the communities, concentrations of radon in water were generally below 185,000 Bq m-3; thus, the increment of airborne radon was small and difficult to measure accurately. In addition, not all of the before-and-after measurements were made in comparable seasons, so there might be substantial errors in many of the measurements. However, in a number of the homes, the measurement after treatment of the water was higher than the measurement before the reduction in waterborne radon. It is possible to estimate the transfer coefficient from the before-and-after radon concentration measurements appropriately weighted for the measured water use. However, some of the values are negative and therefore invalid. To incorporate all of the data into the distribution of values, the measurements for each home were averaged. Examination of the transfer coefficient as a function of the radon concentration in water before treatment suggested that choosing homes where the untreated-water concentrations were greater than 81,000 Bq m-3 would avoid most of the invalid results. Use of this criterion resulted in 31 values, which included only three negative ones.
Lawrence and others (1992) made a series of measurements in 29 homes in Conifer, Colorado. The air volume of each home and the volume of water used were determined, and the air and water 222Rn concentrations were measured. However, ventilation rates were not measured, so the authors only estimated the minimum and maximum values of airborne radon resulting from release from the water used in the homes. Thus, minimum and maximum values of the transfer coefficients could be calculated from the results given in their paper. To use the resulting information in the overall distribution of measured transfer coefficients, a best estimate of the transfer coefficient was calculated by taking the square root of the product of the maximum and minimum values.
Chittaporn and Harley (1994) have measured the water-use contribution to airborne radon in an energy-efficient home in New Jersey. They estimate a transfer coefficient for the home at 1.7 × 10-5.
The resulting distribution of values of the measured transfer coefficient is shown in figure 3.1. The median is 4.5 × 10-5, and the average is 8.7 × 10-5 with a standard deviation of 1.2 × 10-4. When plotted on a logarithmic scale, the central portion of the distribution is fairly linear and thus the geometric properties have also been calculated. The geometric mean is 3.8 × 10-5 with a geometric standard deviation (GSD) of 3.3.
Modeling Of Transfer Coefficient
The model of Nazaroff and others (1987) is used here to estimate the central values of the distribution of transfer coefficient. As in that report, it is assumed that the underlying distributions of the house volumes, ventilation rates, water
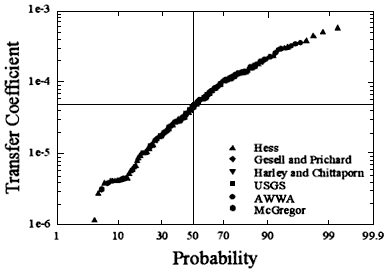
Figure 3.1
Cumulative probability distribution of measurements of transfer coefficient.
use, and use-weighted transfer efficiency are lognormal and so can be combined as done by Nazaroff and others (1987). There are new data on these input variables since the Nazaroff and others estimation, and they are summarized in the following sections.
House Volumes
A new survey of US dwelling volumes has recently been reported by Murray (1997). Two sets of values are reported; one is based on a 1993 survey of dwelling area conducted by the US Department of Energy (DOE) (1995), and the second is based on volumes obtained from a large number (over 4,000) of measurements of air-exchange rates using perfluorocarbon tracers between 1982 and 1987. Murray reports that the values fit a lognormal distribution well. Because the DOE survey represents a substantially larger number of homes (7,041), the geometric mean of 320 m3 and a GSD of 1.8 derived from those data is used. The committee obtained the DOE database and extracted the area and the number of occupants per dwelling. Assuming a ceiling height of 2.44 m, house volumes per occupant were calculated. Figure 3.2 shows the distribution of dwelling volumes per occupant for each number of occupants and the overall distribution of dwelling volume per occupant. For the overall distribution, the geometric mean is 115 m3 of volume per occupant with a GSD of 2.0.
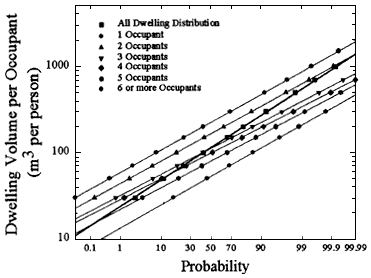
Figure 3.2
Cumulative probability distribution of volume of dwelling per occupant derived from 1993 DOE Residential Energy Consumption Study.
Ventilation Rates
Murray and Burmaster (1995) made a similar analysis of ventilation rates, based on the Brookhaven perfluorocarbon-tracer measurement database containing data on 2,844 dwellings. A geometric mean of 0.53 air changes per hour with a GSD of 2.3 was calculated. This value is somewhat lower than had been used by Nazaroff and others (1987). As Murray and Burmaster indicate in their paper, the houses used in the studies that constitute the database were not chosen on any statistical sampling basis. Most of the measurements were made in the northeastern United States or California and during the winter. Although the authors have made an effort to stratify the data and project the data to the entire United States, they may not have been able to fully represent the variability inherent in the US housing stock. The authors themselves indicate that they have concerns about the representativeness of their results. If the ventilation rate is negatively biased, its use in the model would tend to overestimate the transfer coefficient.
Alternatively, a modeling study by Sherman and Matson (1997) that used the larger DOE Residential Energy Consumption Study (DOE 1995) estimated a mean value of 1.1 air changes per hour. This study provided mean ventilation rates for each county in the country. Sherman and Matson estimate the number of houses of various types and sizes in each county in the United States by using data from the 1990 national census and the same DOE survey used to estimate
house volumes. Sherman and Dickerhoff (1994) present the leakage rates of various types of US homes. Combining the data with average county weather, they calculate the distribution of residential ventilation rates for the population of US dwellings. The arithmetic and geometric means of these data are essentially the same: 1.1 air changes per hour with a GSD of 1.1. Thus, although the values might represent the central tendency in the data, they do not provide a good representation of the variability over housing types.
To combine the modeled ventilation rates into a transfer coefficient, it is necessary to be able to reflect the variability of the values for individual dwellings in the same way that the variability in water use, housing volume per occupant, and use-weighted transfer efficiency are reflected in their distributional parameters. Nazaroff and others (1987) looked at several smaller data sets of measured ventilation rates. They report geometric means of 0.90 and 0.53 air changes per hour and GSDs of 2.13 and 1.73, respectively. Those values are similar to the GSD of 2.3 estimated by Murray and Burmaster. Thus, it appears that a reasonable GSD for the underlying distribution of individual dwellings should be around 2. Because the Murray and Burmaster approach was to estimate the distribution over the entire housing population, the committee adopted their GSD to propagate into estimates of the geometric mean and standard deviation of the transfer coefficient. Using the Sherman and Matson model arithmetic mean and a GSD of 2.3 implies a geometric mean of about 0.77 air changes per hour. The committee also considered using the calculated geometric mean of 1.07 from the Sherman and Matson data with the higher GSD. That ventilation rate would yield a geometric mean transfer coefficient of 3.9 × 10-5 and an average 8.8 × 10-5.
There is thus a disparity in the estimated geometric means between the available measurements and the results of modeling. The committee was concerned about the relatively few measurement data on ventilation in some areas of the country and in seasons other than winter. The model looks as though it might better represent the distribution of housing and the seasonality of ventilation rates across the United States. Clearly, neither source of information is fully satisfactory in providing the needed input to the estimation of the transfer coefficient.
Water Use Per Occupant
Residential water use in five cities was reported by Bowen and others (1993). The cities were Altamonte Springs, FL; Nashua, NH; Norman, OK; Portland, OR; and Tucson, AZ. Those authors reported average per capita use in two seasons and as a function of flow rates. There was no separation of indoor use from outdoor uses, such as watering lawns and filling pools. Only water used indoors will contribute to the indoor radon concentration, so these data are not helpful unless it is possible to estimate the indoor use fraction, and there is not direct information available to do so. Thus, the data are not directly useful in
estimating water use per occupant without assuming the fraction of indoor water use.
However, additional data from an ongoing residential water-use measurement program were made available by the American Water Works Association (DeOreo, private communication, 1997). This study has provided information on detailed daily amounts of use for a number of specific activities (clothes-washing, dishwashing, toilets, showering, baths, faucets, etc.) for 595 houses and permits a determination of the indoor use rates. It was conducted in Boulder; CO, Denver, CO; Eugene, OR; Seattle, WA; and San Diego, CA. Systems were installed in the homes to provide a log of each water use, its duration, and the total volume of water used. For some of the days being monitored, water use was extremely low, suggesting that the occupants were not home and so were not using water in the normal manner. By carefully reviewing the various records, it is possible to eliminate those values from the database. That results in the distribution observed in figure 3.3. Although there was a wide variation in total water use among the locations, there was much less variation among the indoor use rates; the average was 0.28 ± 0.20 m3 per person per day, and the geometric mean was 0.23 with a GSD of 1.8.
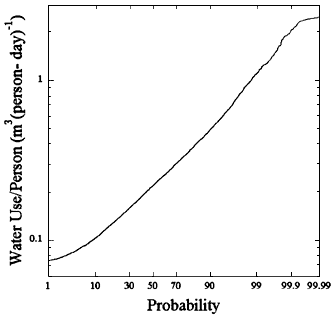
Figure 3.3
Cumulative probability distribution of water use per day per person based on data from Boulder, CO; Denver, CO; Eugene, OR; Seattle, WA; and San Diego, CA.
Use-Weighted Transfer Efficiency
The transfer efficiency is the fraction of the radon in the water that is released to the air during the activities that use water (showering, clothes-washing or dishwashing, and so on). The earliest values of the transfer efficiencies have been previously reported by EPA (Becker III and Lachajczyk 1984) and Nazaroff and others (1987). The transfer efficiency of showerheads has been measured by Fitzgerald and others (1997) and by Bernhardt and Hess (1996), who found values quite similar to those used by Nazaroff and others. The transfer efficiency for each activity was combined with the water use data to yield a use-weighted transfer coefficient. A geometric mean of 0.52 with a GSD of 1.3 was obtained.
Transfer-Coefficient Model Results
The new input values and the earlier values of Nazaroff and others are compared in table 3.1. Both the dwelling volume and the water use per occupant are greater in the committee's analysis. The transfer efficiency has remained essentially the same. The resulting geometric mean value of the transfer coefficient has risen to 0.55 × 10-4 with a GSD of 3.5. The arithmetic average transfer coefficient is estimated at 1.2 × 10-4, it is considerably higher than the geometric mean value because of the high degree of skewness of the distribution.
Conclusions
There is reasonable agreement between the average value of the transfer coefficient estimated by the model and the value calculated from the measured data.
Table 3.1
Lognormal Distributions of Parameters in Transfer-Coefficient Calculation
|
|
Nazaroff and others (Nazaroff and others 1987) |
Committee |
||
|
Parameter |
GeometricMean |
Geometric Standard Deviation |
Geometric Mean |
Geometric Standard Deviation |
|
Dwelling volume per occupant (m3 person-l) |
99 |
1.9 |
115 |
2.0 |
|
Ventilation rate |
0.68 |
2.0 |
0.77 or 1.07 |
2.3 |
|
Transfer efficiency water to air |
0.55 |
1.1 |
0.52 |
1.3 |
|
Water use per capita (m3 person-1 h-l) |
7.9 × 10-3 |
1.6 |
9.4 × 10-3 |
1.8 |
|
Geometric mean transfer coefficient |
6.5 × 10-5 |
2.8 |
5.5 × 10-5 or 3.9 × l0-5 |
3.5 |
The average of the measurements was 8.7 × 10-4 with a standard error of 1.0 × 10-4. With a modeled geometric mean ventilation of 1.07 air changes per hour, the transfer coefficient is calculated to have the same value as the measurements. However, if the committee uses the estimate of the geometric mean of the ventilation rate of 0.77, the resulting estimate of the transfer coefficient is 1.2 × 10-4. The committee feels that there are problems with both the measurements and the model results. Considering the problems with both the measurements of the transfer coefficient and the measurements that are the input values for the model, the committee recommends that the Environmental Protection Agency continue to use 1.0 × 10-4 as the best central estimate of the transfer coefficient, based on the available data.
Because of the uncertainty in the value of the ventilation rate and its distributional characteristics, the committee recommends assuming that the transfer coefficient is between 0.8 and 1.2 × 10-4. The committee is not assigning a specific uncertainty to the central estimate, but rather assumes that the central estimate has the highest likelihood of lying within that range.









