5
Dosimetry of Inhaled Radon and its Associated Risk
Inhalation Of Radon And Its Short-lived Decay Products
The occurrence of bronchogenic lung cancer after inhalation of 222 Rn and its short-lived decay products is well established from follow-up studies of underground miners (Lubin and others 1995; 1994; UNSCEAR 1993; National Research Council 1988, 1999; NCRP 1984a). There is convincing evidence that occupational exposure has produced excess lung cancer. The bronchial airways are the location of most lung tumors (Saccomanno and others 1996). The only quantitative risk estimates available are those from underground-miner studies. The evaluation of lung-cancer risk in miners is summarized later in this chapter.
Risk Posed By Inhalation Of 222Rn Decay Products
The assessment of risk in miners did not rely on internal dosimetry but was based on the air exposure to decay products in units of potential alpha energy concentration (PAEC) in the mines. The unit of exposure was the working level month (WLM) and was an easy measurement to make in mine air by simply taking a filtered air sample and counting total alpha particles (NCRP 1988). For domestic (i.e., residential) exposures, 1 WLM is equivalent to an indoor radon concentration of exposure at 185 Bq m-3 for a full year with 70% of time spent in the home (Harley and others 1991). The SI unit of exposure replacing PAEC is the joule hour per cubic meter (J hr m-3); 1 WLM equals 0.0035 J h m-3. However, because the original miner studies and all of the subsequent analyses and
models refer to exposures in units of WLM, we have preserved that formalism in this discussion.
Excess lung cancer in underground miners was evident after exposures to radon decay products of several hundred to several thousand WLM that would equate to long-term exposure to 222Rn in the home at very high concentrations. The health effects of average home concentrations are less certain, and current residential epidemiologic studies are attempting to measure the risk (as discussed later in this chapter). However, risk estimates based on these studies are not currently available.
The exposure assessment for miners was related to the potential energy concentration in air. However, it is the actual bronchial dose that confers the lung cancer risk. Therefore, it is necessary to know whether the bronchial dose in miners per unit PAEC in air in mines yields an equivalent bronchial dose per unit PAEC in homes. If the dose per unit exposure is equal in both situations then the derived miner risk estimates may be applied directly to home exposure.
The projection of risk from the mines to other environments, particularly for domestic exposures and for the entire lifetime, also makes 222 Rn decay product bronchial dosimetry a necessity. That requires not only physical models to evaluate the dose per unit exposure in mines relative to that in other exposure situations but also biological risk models to compare short-term with whole-life exposure. Occupationally exposed miners were exposed for 2 y to about 20 y. As described in the BEIR VI report (National Research Council 1999), there are factors that compensate for differences in exposure conditions between mines and homes, such as unattached fraction and breathing rate. Therefore, the miner risk estimates were used directly to estimate the risk from radon and its decay product exposure in domestic environments (National Research Council 1999).
Lung Dose From 222Rn Gas
The alpha dose delivered to target cells in bronchial epithelium arises mainly from the short-lived decay products deposited on the bronchial airway surfaces. The alpha dose from radon gas itself is smaller than that from its decay products because of the location of radon as it decays in the airway; there is a low probability that an alpha particle will interact with a cell. The decay products, however, are on the airway surfaces within about 20 to 30 µm of these target cells, and thus have a higher probability of hitting a target-cell nucleus.
The annual weighted equivalent dose from radon gas decaying in the lung has been calculated by the International Commission on Radiological Protection (ICRP 1981) and the National Council on Radiation Protection and Measurements (NCRP 1987a; 1987b) (see Table 5.1). The gas dose itself is 7 × 10-3 mSv y-1 per Bq m-3 (ICRP 1981) or 5 × 10-3 mSv y-1 per Bq m-3 (NCRP 1987a). The dose from 222Rn gas is lower by about a factor of 10 compared to the bronchial dose from the decay products deposited on the airways.
Table 5.1
Annual Weighted Equivalent Dosea to the Lung from 222Rn Gas Exposure
|
Organ |
mSv y-1 per Bq m-3 |
Reference |
|
Whole lungb |
7 × 10-3 |
ICRP (1981) |
|
Bronchial surfacesc |
5 × 10-3 |
NCRP (1975) |
|
a Weighted using ICRP values of Wr and Wt b Dose calculated from 222Rn solubility in tissue and radon in airways. c Dose calculated to bronchial surfaces from 222Rn decay in airways. |
||
Dose to Organs Other than the Lung from Inhaled 222Rn
Any inhaled gas, including radon, is slightly soluble in body tissues. Radon in the lung diffuses to blood and is transported to other organs, where the gas and the decay products that build up in the tissue deliver a radiation dose. Harley and others (1958) in a study of inhaled radon, determined the solubility of radon in the body. Two persons were in a controlled, relatively high-radon atmosphere for about a day. Sequential exhaled-breath samples were used to infer retention times in the five major body-compartments—lung, blood, intracellular and extracellular fluid, and adipose tissue. The data were used in the metabolic modeling of the dose to other organs from inhaled radon (Harley and Robbins 1992). The dose to organs other than the lung had been calculated previously by Jacobi and Eisfeld (1980). The dose per unit exposure for organs other than the lung are shown in table 5.2, where it can be seen that the dose to other organs is lower than the dose to the bronchial epithelium, in most cases by a factor of about 100.
222Rn Decay-Product Dose During Showering
The most important variables in the alpha dose to cell nuclei in the bronchial airways are aerosol size distribution, breathing rate, and location of the target-cell nuclei.
The most extensive activity-weighted size distributions that have been measured in homes were reported by Hopke and others (1995a). Figure 5.1 shows the average values of the activity fractions for each of the decay products and for PAEC for the homes in which no smokers are present; figure 5.2 presents similar data on homes with smokers.
When a home is supplied by radon-bearing groundwater, the radon that is released into the air during water use becomes another source of indoor radon decay products. To evaluate the significance of this contribution to the overall radon risk, it is necessary to examine each instance of water use (such as in the kitchen, bathroom, and laundry room) and to look at both the steady-state (long-
Table 5.2
The Weighted Equivalent Dose to Tissues Other Than the Lung for Continuous Exposure to 1 Bq m-3 of 222Rn in Air
|
Tissue |
mSv y-1 per Bq m-3 |
Reference |
|
Livera |
5.1 × 10-5 |
Jacobi and Eisfeld (1980) |
|
Kidneysa |
5.6 × 10-5 |
Jacobi and Eisfeld (1980) |
|
Spleena |
5.2 × 10-5 |
Jacobi and Eisfeld (1980) |
|
Red Bone Marrowa |
9.6 × 10-5 |
Jacobi and Eisfeld (1980) |
|
Bone Surfacesa |
2.5 × 10-5 |
Jacobi and Eisfeld (1980) |
|
Soft Tissueb |
3.0 × 10-5 |
Harley and Robbins (1992) |
|
Adipose Tissueb |
9.0 × 10-5 |
Harley and Robbins (1992) |
|
Skinb |
50 × 10-5 |
Harley and Robbins (1992) |
|
Normal Marrowb |
6.3 × 10-5 |
Harley and Robbins (1992) |
|
Adipose Tissue Marrowb |
16 × 10-5 |
Harley and Robbins (1992) |
|
Bone Surfaces (Normal Marrow)b |
1.5 × 10-5 |
Harley and Robbins (1992) |
|
Bone Surfaces (Adipose Tissue Marrow)b |
3.0 × 10-5 |
Harley and Robbins (1992) |
|
0.01 |
Harley and Robbins (1992) |
|
|
Alveolar Capillariesb |
20 × 10-5 |
Harley and Robbins (1992) |
|
a Weighted using ICRP (1977) weighing factors. b Weighted using IRCP (1990) values of Wr and Wt. c T lymphocytes located in bronchial epithelium. |
||
term) and the dynamic (short-term) components of the exposure. The potentially most important source of short-term exposure is the release of radon from water during showering and the subsequent inhalation of its decay products. The steady-state component has been studied in considerable detail (Fitzgerald and others 1997; Bernhardt and Hess 1996) and is described in chapter 3. Only recently have there been studies of the time-varying exposure. The exposure assessment of waterborne radon includes both its contributions to long-term average indoor radon concentrations and the short-term, perturbed conditions that exist as a result of showering.
Showering Conditions
It is necessary to provide the radon-progeny activity size distribution as a function of time during and after showering. There have been two recent studies of the increments in exposure and dose that arise from showering with radon-laden water (Fitzgerald and others 1997; Bernhardt and Hess 1996).
Exposure conditions are quite different during showering because radon is transferred from water to air with little or no direct release of decay products from the water. As a result, there might be a high local concentration of 222Rn, but it takes time for the decay products to grow into equilibrium concentrations. Because the ingrowth of the activity will occur with an effective half-life of about 30 min, the highest concentrations of decay-product activity occur after the person
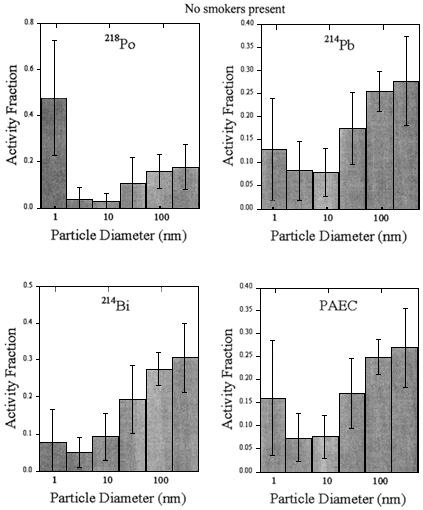
Figure 5.1
Average values of the activity fractions for each of the decay products and for PAEC (no smokers present). The error bars indicate the standard deviations of the 20 distributions that comprise the average.
has left the area. Thus, exposure to the 222Rn decay products is much lower than would be expected based on radon itself.
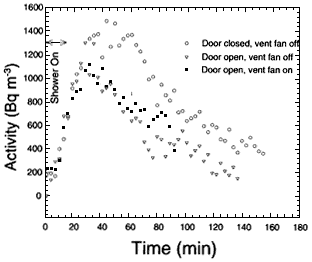
The Fitzgerald and others (1997) study used a normally occupied dwelling that was supplied with water from a well; the water contained radon at 518,000–555,000 Bq m-3. The dwelling was a one-story wooden house of a type common in northern New York state. Details of the measurement methods for radon and
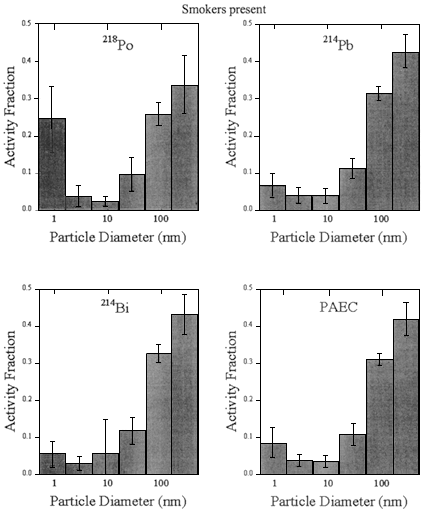
Figure 5.2
Average values of the activity fractions for each of the decay products and for PAEC (smokers present). The error bars are as in figure 5.1.
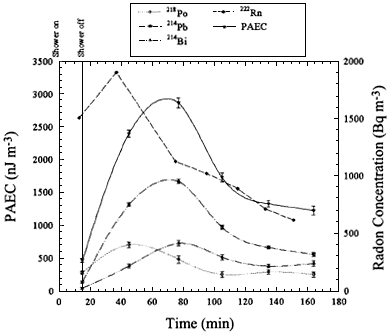
its decay products are provided by Fitzgerald and others (1997). Figure 5.3 shows the radon concentration as a function of time under several ventilation conditions. Figure 5.4 shows the evolution of PAEC as a function of time in one experiment.
The growth of the aerosol particles means that any calculations of dose must allow for the possibility of hygroscopic growth of the particles, such that the aerosol size spectrum and hence the activity-weighted size spectrum might shift
size before, during, and after a shower. If an aerosol particle can grow, the increase in size will result in a larger decay-product attachment rate. If the particles can grow in the high humidities during showering, they can grow in the respiratory tract (George 1993). However, measurements show that this growth is minimal (Dua and Hopke 1996).
Changes in particle size will have two effects. First, the changes will affect the deposition of the particles onto the room surfaces, thereby affecting the amount of aerosol decay product available for inhalation. Second, the changes will alter where the aerosol particles deposit in the respiratory tract, and so affect the dose delivered to the lung (National Research Council 1991a). Furthermore, depending on how close the bathroom humidity is to 100%, the amount of possible growth when the particles enter the lungs is reduced, further altering deposition patterns in the lung. Figure 5.5 presents a series of number-weighted particle size distributions based on measurements with a scanning electrical mobility spectrometer. From the number-weighted size distributions, activity-weighted distributions can be calculated by using the attachment coefficients of Porstendörfer and others (1979). Figure 5.6 shows the estimated activity-weighted size distributions. Tu and Knutson (1991) have shown that this method provides a reasonable approximation of the directly measured activity-weighted distributions.
It is possible to make direct activity-weighted size distribution measurements (Ramamurthi and Hopke 1991; Tu and others 1991). However, the system available for such activity-weighted size distribution measurements draws 90 L
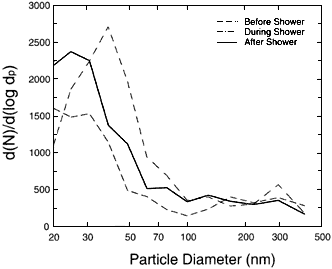
Figure 5.5
A series of number-weighted particle size distributions based on measurements with a scanning electrical mobility spectrometer.
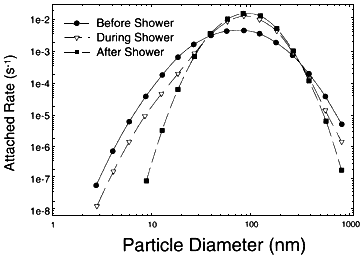
Figure 5.6
Calculated activity-weighted size distributions.
of air per minute and so would substantially alter the aerosol size distribution in a volume as small as a bathroom. Since it is not feasible to make direct measurements of activity-weighted size distributions, they have to be calculated. For initial work with the field data, a series of simplifying assumptions were made. From the measured number-weighted size distributions, the activity-weighted size distributions could be calculated as follows. Using the equations given by Porstendörfer and others (1979), the attachment coefficients for 222Rn decay products to any size of particle can be calculated. With these coefficients and the experimental particle data, the attachment rates can be calculated; and with the steady-state equations given by Knutson (1988), the activity-weighted size distribution can be calculated (see figure 5.6). The steady-state approximation gives an upper bound to the calculated values, whereas a dynamic-model calculation (Datye and others 1997) gives results that are likely to be more representative of typical showering conditions.
Figure 5.6 clearly shows how the activity-weighted size distribution shifts during showering toward larger particles that are less efficient at delivering a dose to the bronchial tissues. Thus, although the activity suspended in the air increases because of enhanced attachment of the activity to the larger particles, the dose does not increase as sharply because the larger particles are less effectively deposited in the lung. The period during which the peak is shifted is short—around 5 to 10 min—and the particles return to their original size within about 15 min. The asymmetry in the peaks can in some measure be attributed to the variable nature of the particle size spectra over the sampling period and to the
relatively poor counting statistics in the particular experiment. For dosimetric calculations, the particle size distribution during showering is therefore essentially the same as the normal house particle size distribution. This is not unexpected, because as radon gas is released from water droplets and decay products form, they interact with the normal home aerosol particles.
Integrated Measured 222Rn Concentration in the Shower
The 222Rn released to a shower from water was monitored in an ultra-high energy efficiency home with a private well (N. Harley, private communication). Integrated measurements spanned two 6-mo periods and indicate the average shower concentration. Data from this example home is presented.
The home monitored was in northern New Jersey and occupied by two adults and three children. The duration of all five morning showers was measured to be 60 minutes per day. The 222Rn concentration was measured at the bathroom cold-water tap and in water at showering temperature that was collected from the showerhead but near the tub surface to determine 222Rn loss. The long-term data are shown in table 5.3. The mean concentration in cold tapwater was 60,000 Bq m-3; on the average, 6,000 Bq m-3 remained in the drain water after spray from the showerhead.
The showerhead normally delivers water at 0.0053 m3 min-1 with a mean 222Rn concentration of 60,000 Bq m-3. The fraction of 222Rn lost (table 5.3) by the water to the air was 90% (the water concentration decreases from 60,000 Bq m-3 to 6,000 Bq m-3) as the water fell from the showerhead to the tub floor. Thus, the shower released to the air at an average of about 290 Bq 222Rn min-1.
Table 5.4 shows the time-integrated 222Rn concentration in the ventilator duct directly above the shower as measured with a passive, alpha-track detector. A small exhaust fan in the vent outlet operates during showering to remove water vapor from the home. The duct concentration approximates the concentration in the shower. The concentration over the two 6-mo intervals varied somewhat, as expected, because of different conditions in the shower.
From the preceding description of the aerosol particle size distribution as a result of showering, it is clear that the aerosol characteristics in showers are not substantially different from those found in the rest of the house in terms of particle number or size.
The annual dose to the bronchial airways of a person can be calculated from three factors:
- A knowledge of the 222Rn concentration in the shower.
- The estimated time spent in the shower per year (about 1% for illustrative purposes).
- The central value of the 222Rn bronchial dose factor, given the equilibrium factor in the shower (0.05) is 0.004 mGy yr-1 per Bq m-3. This dose factor takes
Table 5.3
Measured 222Rn Concentration in Cold Water and Water from Shower at Normal Showering Temperature (Shower Water Collected Near Tub Splash Surface)
|
Date |
Cold Water (222Rn Bq/L) |
Shower (222Rn Bq/L) |
% Loss |
|
Jun 94 |
67.34 |
29.60 |
|
|
Mar 95 |
64.38 |
9.62 |
|
|
Mar 95 |
57.72 |
3.55 |
|
|
Apr 95 |
63.27 |
5.07 |
|
|
Apr 95 |
56.24 |
1.78 |
|
|
Apr 95 |
55.13 |
2.55 |
|
|
May 95 |
67.34 |
2.41 |
|
|
May 95 |
59.57 |
4.14 |
|
|
May 95 |
53.28 |
4.81 |
|
|
Jun 95 |
59.94 |
3.40 |
|
|
Aug 95 |
64.75 |
10.10 |
|
|
Aug 95 |
74.74 |
11.06 |
|
|
Aug 95 |
66.97 |
10.58 |
|
|
Aug 95 |
62.16 |
6.81 |
|
|
Sept 95 |
46.99 |
3.61 |
|
|
Oct 95 |
52.91 |
1.49 |
|
|
Dec 95 |
53.65 |
1.55 |
|
|
Jan 96 |
55.87 |
4.07 |
|
|
Feb 96 |
57.35 |
4.07 |
|
|
Apr 96 |
54.58 |
3.85 |
|
|
Jul 96 |
47.73 |
5.14 |
|
|
Average |
60.00 |
6.00 |
90.00 |
- into account the average particle size distribution observed in indoor air (Harley 1996). This is compared with the normal home equilibrium of 0.40 and a bronchial dose factor of 0.032 mGy yr-1 per Bq m-3.
For typical home conditions, the annual shower exposure is a few percent of the whole house exposure attributed to water use. For this reason, the transfer factor is assumed to include both the whole house and showering exposure when calculating dose. The detailed factors given above permit the showering dose and whole house dose to be calculated separately for a specific case.
Table 5.4
222Rn Air Concentration Measured in the Shower Using Passive Alpha Track Detectors
|
Date |
222Rn (Bq m-3)in Shower |
|
Mar–Aug 95 |
4400 |
|
Aug 95–Jan 96 |
3500 |
Lung-Cancer Risk Posed by Inhalation of 222Rn Decay Products
There are five models for transporting lung cancer risk from the underground-mining studies to exposure in the environment: the historic NCRP (1984b; 1984a) model, the ICRP (1987) model, the model developed by the fourth National Research Council (National Research Council 1988) Committee on Biological Effects of Ionizing Radiations (BEIR IV), the National Cancer Institute model (Lubin and others 1994) derived from the pooling of 11 underground mining studies, and the model developed by the sixth National Research Council (National Research Council 1999) Committee on Biological Effects of Ionizing Radiations (BEIR VI). The BEIR VI model is similar to the NCI model, with updated data from the same 11 underground miner cohorts.
Although the 222Rn decay-product exposure data are universally weak in all the miner epidemiologic followup studies, they are the only human data available from which one can derive numerical estimates of occupational and domestic lung-cancer risk. Some generalizations are possible and necessary to quantitate this risk.
NCRP Model
NCRP was the first to propose a model for environmental lung-cancer risk based on the miner data (NCRP 1984a). The model accounted for the fact that miners exposed for the first time when over 40 y old appeared to have higher lifetime risk of lung cancer than miners exposed for the first time in their 20s. The apparent lower lifetime risk for those exposed at young ages was assumed to be due to a reduction in risk with time since last exposure. Thus, earlier exposure was assumed to diminish because of cell death or repair of cells transformed by earlier exposure. The half-life for repair (or loss) was assumed to be 20 y.
One key factor noted by NCRP was that lung cancer is a rare disease before the age of 40, regardless of the population considered. Miners exposed when young did not generally appear as lung-cancer cases until the usual cancer ages were attained (50–70 y). That would account for an apparent increase in lifetime lung-cancer risk at higher ages because there would be a shorter time for transformed cells to be lost compared with the situation in persons exposed at lower ages. Miners were exposed, on the average, for less than 10 y in the Colorado, Ontario, and Czech cohorts. The total time for followup was 20 y or more, so the apparent reduction in risk with time after exposure could be observed.
The NCRP model took the form of an exponential reduction with time after exposure, with the stipulation that there was a minimal latent period of 5 y. Also, lung cancer could not appear before the age of 40. This model is known as a modified absolute-risk model. Risk is expressed after exposure without regard to
other risks of lung cancer, such as smoking, but risk is modified by time since exposure.
To express lifetime risk after a single exposure, it is necessary to sum the risk over the number of years of life after exposure, taken as age of exposure to age 85. The lifetime risk, TR, posed by continuous exposure was expressed as the sum of lifetime risk for a single year's exposure over the total exposure interval considered.
When the model was developed, there was not enough information on the risk associated with smoking and 222Rn exposure combined to separate an additional effect from this carcinogen. It was stated that the risk coefficient, C, could be modified when sufficient data were available.
Numerical values of lifetime risk for different models are shown in table 5.5.
Table 5.5
Lung Cancer Risk for Continuous Whole-Life Exposure to 4 pCi/L (148 Bq m-3 or 0.56 WLM/ yr at Indoor Conditions) as Predicted by Various Models of Domestic Exposurea
ICRP Model
ICRP (1987) developed its models for environmental risk on the basis of both a constant-relative-risk model and a constant-absolute-risk model. ICRP assumed that the risk expressed over the years that cancer occurs would be increased if exposure occurred in childhood. It assumed that the risk was 3 times as great for exposure at ages 0–20 than for exposure at ages over 20. There is little justification for that assumption, as later information suggests that those exposed as children might have no different risk than those exposed as adults (Lubin and others 1995; Xuan and others 1993). This is discussed further later in this chapter.
The constant-absolute-risk or constant-relative-risk model is no longer considered appropriate for lung cancer. The best models use modifications of the parameters to account for a risk reduction with time since exposure. Although not biologically correct, risk estimates calculated with a constant-relative-risk model are within a factor of 3 of those calculated with other models.
Values of lifetime risk for the ICRP model are shown in table 5.5.
BEIR IV Model
The fourth National Research Council Committee on Biological Effects of Ionizing Radiations (BEIR IV) prepared a report, Health Risks of Radon and other Internally Deposited Alpha-Emitters (National Research Council 1988). The committee was given the raw data or selected parts of the original data from four mining cohorts: the US (Colorado), Canadian (Ontario and Eldorado), and Malmberget (Swedish) cohorts. Reanalysis was performed with the AMFIT program developed for analysis of the Japanese atomic-bomb survivor data. The program uses Poisson regression to estimate parameters.
With AMFIT the data were analyzed with both internal and external cohorts for a control population. The BEIR IV committee stated that a relative-risk model fit the observed mortality well. The relative-risk model assumes that radon decay product exposure increases the age-specific lung-cancer mortality rate in the population by a constant fraction per WLM of exposure. However, in all cohorts, there was an obvious reduction in lung-cancer relative risk with time after exposure. The relative-risk model was modified to reduce risk with time since exposure. The BEIR IV committee called its modified relative-risk model a time-since-exposure (TSE) model.
Smoking was examined as a confounder. The only study with complete smoking history on the miners was the Colorado study. The effect was tested with a hybrid relative-risk model that incorporated a mixing parameter for smoking. A parameter value of zero fit an additive effect of smoking and 222Rn interaction; a value of 1 fit a multiplicative model best. A maximum log-likelihood test was applied to the data, and it was found that the best parameter fit was between 0 and 1. This indicated that combined risk was more than additive but less than multi-
plicative. That is, the lifetime risk of lung cancer posed by radon exposure did not simply add to the lifetime risk of lung cancer associated with smoking, but neither did the risks multiply. The risk related to radon and smoking appeared to be between the two extremes.
The exposure data on the Eldorado cohort were not considered carefully by the BEIR IV committee. A reported Eldorado mining exposure of 1 WLM gave a 50% excess lung-cancer mortality—clearly an erroneous value. It is known that the miners had prior exposure in other mines, but the additional exposure is not known (Chambers and others 1990). The exaggerated risk per WLM in this study for the 1-WLM exposure cohort is important in controlling the overall BEIR IV model. This exposure category included a large number of person-years. Therefore, when the four cohorts were combined to yield a ''best estimate'' of the relative-risk coefficient, the 1-WLM group carried substantial weight. If this data point were omitted, the risk coefficient in the model would be less than the 0.025/WLM used in the final BEIR IV model. That possible effect should be carefully considered in any future models that use the Eldorado cohort. Thus, considering that inaccuracies might be incorporated into the BEIR IV model, the calculated risk estimates for both smokers and nonsmokers at environmental exposures are likely to be overestimates.
The values of lifetime risk as calculated by the BEIR IV TSE model are also shown in table 5.5.
NCI Model
The National Cancer Institute coordinated an effort to pool the epidemiologic data from 11 underground-mining studies. The authors from the various countries pooled results, and these were reported by the National Institutes of Health (Lubin and others 1995; 1994). The report Radon and Lung Cancer Risk: A Joint Analysis of 11 Underground Miners Studies , is the most complete analysis of the health detriment to underground miners. For the pooled analysis, there were 2,701 lung cancer deaths among 68,000 miners who accumulated about 1.2 million person-years of exposure.
In all 11 cohorts, the excess relative risk (ERR) of lung cancer (the fractional increase in lung cancer) was linearly related to the cumulative exposure estimated in working level months (WLM). Thus, although other carcinogens might be present in the mine atmosphere, a clear exposure-response relationship was associated with 222Rn decay products. Smoking history was complete only in the Colorado mining cohort. Because of the lack of smoking information the combined risk for smoking and radon could only be inferred qualitatively.
The Colorado uranium-miner data are shown as a typical example of the 11 cohorts in figure 5.7. The ERR/WLM for all 11 studies is shown in figure 5.8. Parts a and b of figures 5.8 show the ERR for all the cohorts combined, and for all cohorts with exposure under 600 WLM.
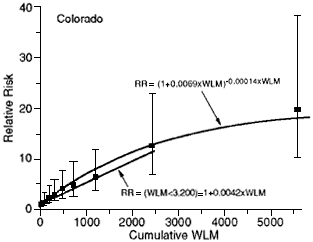
Figure 5.7
Relative risk (RR) of lung cancer in the Colorado Miner Cohort as a function of cumulative WLM exposure and fitted model. Fitted linear model shown < 3200 WLM. (NIH 1994).
One important aspect of the data is shown in figure 5.7—that the ERR at high exposures tends to flatten out. That observation is erroneously called the inverse-exposure effect. It is usually stated that the increase in lung-cancer risk per unit exposure is higher for low exposures than for high exposures. The flattening of the response curve is probably the result of cell-killing due to multiple traversals of cell nuclei. At low exposures, even a single traversal of a cell nucleus by an alpha particle is rare. Therefore, the effect is actually a reduced response at high exposure that is due to sterilization, not an increased response at low exposure.
The terminology has caused considerable confusion because it implies that domestic exposure can somehow be "more dangerous" than mine exposure. That is not the case, and it has been demonstrated that no additional risk above the linearity shown in all the cohorts is posed by domestic exposures.
The main features of the lung-cancer risk model derived from the jointly analyzed data are as follows:
- There is a reduction in risk after cessation of working in the mines. It is called the time-since-exposure effect (the TSE factor).
- There appears to be no clear age-at-start-of-exposure effect; that is, the age at the start of mining is not an obvious factor. However, the age attained after the start of mining is a factor, and risk decreases with age (the AGE factor).
- Longer duration (the DUR factor) or lower 222Rn concentration (the WL
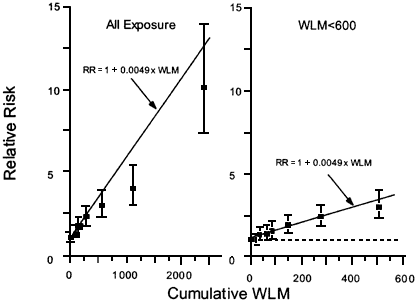
Figure 5.8
Fitted exposure response model (left side) and relative risk (RR) of lung cancer (right side) in all 11 cohorts of miners for all exposures, and for exposures < 600 WLM (Lubin and others 1995).
- factor) gives rise to larger risk. Because this is how the model parameters are derived, it gives rise to the reason for the so-called inverse-exposure effect.
- There is a higher lung-cancer risk per unit of 222Rn exposure for smokers than for nonsmokers.
The two models derived from the joint analysis are considered equally likely to fit the observations.
- TSE/AGE/WL model (time since exposure, age, and concentration):
where
w5-12, W15-24 = exposure in WLM 5-14 years before the end of mining, and so on.
- TSE/AGE/DUR model (time since exposure, age, and duration):
The estimated parameter values derived for these two models are given in table 5.6. The combined effect of smoking and 222Rn exposure could not be
determined quantitatively. The pooled analysis showed a linear increase in risk of about a factor of 3 for smokers over never-smokers. This value is a decrease from the BEIR IV estimate of 10 to I for smokers over never-smokers. A striking feature of the data is the time-since-exposure effect. With three time windows in the model, the joint analysis showed a reduced risk with time, compared with two time windows included in the BEIR IV model, which did not show this effect.
BEIR VI Model
In 1999, the National Research Council published the BEIR VI report (National Research Council 1999), a revision and update of the BEIR IV report. The BEIR VI models to project lung-cancer incidence from 222Rn decay-product exposure produce equations that are identical with that reported by NIH (Lubin
Table 5.6
Parameter Estimates from BEIR VI (National Research Council 1999) Models Based on Original (Lubin and Others 1994) and Updated Pooled (Lubin and Boice 1997) Miner Data
|
Exposure-Age-Duration Modela |
Exposure-Age-Concentration Modela |
||||
|
|
Original Data |
Updated Data |
|
Original Data |
Updated Data |
|
Βb × 100 |
0.39 |
0.55 |
Β × 100 |
6.11 |
7.68 |
|
Time-since-exposure windows |
|||||
|
θ5-14 |
1.00 |
1.00 |
θ5-14 |
1.00 |
1.00 |
|
θ-24 |
0.76 |
0.72 |
θ15-24 |
0.81 |
0.78 |
|
θ25+ |
0.31 |
0.44 |
θ25+ |
0.40 |
0.51 |
|
Attained age |
|||||
|
ϕ<55 |
1.00 |
1.00 |
ϕ<55 |
1.00 |
1.00 |
|
ϕ55-64 |
0.57 |
0.52 |
ϕ55-64 |
0.65 |
0.57 |
|
ϕ65-74 |
0.34 |
0.28 |
ϕ65-74 |
0.38 |
0.29 |
|
ϕ75+ |
0.28 |
0.13 |
ϕ75+ |
0.22 |
0.09 |
|
Duration of exposure |
Exposure rate (WL) |
||||
|
γlt;5 |
1.00 |
1.00 |
γlt;0.5 |
1.00 |
1.00 |
|
γ5-14 |
3.17 |
2.78 |
γ0.5-1.0 |
0.5 1 |
0.49 |
|
γ15-24 |
5.27 |
4.42 |
γ1.O-3.0 |
0.32 |
0.37 |
|
γ25-34 |
9.08 |
6.62 |
γ3.0-5.0 |
0.27 |
0.32 |
|
γ35+ |
13.6 |
10.2 |
γ5.0-15.0 |
0.13 |
0.17 |
|
|
|
|
γ15.0+ |
0.10 |
0.11 |
|
a Parameters estimated on the basis of the model RR=1+βw*Φaγz fit using the two-stage method where w*=w5-14+θ15-24w15-24+θ25+w25+. Here the subscript a denotes categories of attained age and the subscript z denotes categories of either exposure duration (in years) or radon concentration in WL. b Units arc WLM-1. |
|||||
and others 1994). The BEIR VI analysis used updated versions of the 11 miner cohorts, so the model results are quite similar. The parameters estimated by the BEIR VI committee are also provided in table 5.6.
The NCI report summarized the calculated deaths in the US population from the assumed average exposure of 46 Bq m-3. Its calculated value was 15,000 deaths, consisting of 10,000 deaths in smokers and 5,000 in nonsmokers. This estimate of the attributable risk is derived from the model of lung cancer risk, a distribution of radon exposures, and the lung cancer and overall mortality rates (National Research Council 1999; NIH 1994).
Epidemiology of Childhood Exposure and Lung-Cancer Risk
It is apparent that leukemia and breast cancer are more frequent in people exposed to radiation in childhood than in those exposed as adults (National Research Council 1990a). Concern has been expressed that the same might be true for lung cancer that results from exposure to radon and its decay products at early ages.
Some data are available on occupational exposure to high radon concentrations in childhood. Lubin and others (1990) analyzed data on Chinese tin miners in the Yunnan province. Of exposed workers, 37% started employment under the age of 13; in this group, the risk coefficient for lung cancer was 1.2% WLM-1. For those first employed over the age of 18, the risk coefficient was 2.9% WLM-1. Later and more complete information on the entire cohort (Xuan and others 1993) showed heterogenous results with no pattern that would support the notion that children are at higher risk. It appears that children are not a particularly sensitive population.
Tentatively, the lower risk coefficient for children than for adults reported by Lubin and others (1990) suggests that the reduction in lung-cancer risk with time after exposure might be effective in children. The fact that lung cancer does not appear at a substantial rate in any population before the age of 40, permits a substantial interval for risk reduction for exposure in childhood.
Environmental and Domestic Epidemiology
Lung-cancer excess (above that expected from smoking) in the underground-miner populations has been demonstrated conclusively. Combining that and the knowledge that some homes have radon and daughter concentrations near or above those found in historical mines, it seems virtually certain that environmental radon is responsible for some lung cancer in the general population.
There are more than 20 environmental epidemiologic studies of radon exposure to determine whether health effects can be documented directly (National Research Council 1999; Neuberger and others 1996; Neuberger 1989, DOE/CEC
1989; Borak 1988). Most domestic studies show either a slight positive or slight negative correlation between measured radon in the home and lung-cancer mortality.
Many studies are ecologic exercises that relate lung-cancer mortality in a region with indoor radon concentration (Cohen 1992; 1990). In some cases the radon is not measured, but rather is estimated as high or low, depending on the type of house. The ecologic studies are ambiguous because no attempt is made to determine actual exposure to individuals in the area of study and no correction can be made for smoking, the strongest confounder for lung cancer (Stidley and Samet 1994; Cohen 1989). The ecologic study of Cohen (1995) is the most comprehensive. It encompasses about 300,000 radon measurements in 1,601 counties in the U.S. The trend of county lung cancer mortality with increasing home radon concentration is strikingly negative, even when attempts are made to adjust for smoking prevalence, and 54 socioeconomic factors. The measured average county radon concentrations do not exceed 300 Bq m-3, thus the typical low home exposure region is studied. This finding contradicts the existing risk estimates at low exposure, and a sound reason for the significant negative trend should be sought.
To date, there are 8 published case-control studies that compare the relative risk of lung cancer between high-and low-exposed groups. An attempt is made to measure the 222Rn exposure in the home. The largest case-control study to date was performed in Sweden (Pershagen and others 1994). There were 1,360 cases and 2,847 controls, and exposure was assessed with 3-mo measurements during the heating season, retrospectively for homes lived in for more than 2 y after 1947 up to 3 y before diagnosis of cancer. The lung-cancer excess was not statistically significant even for smokers or nonsmokers with over 400 Bq m-3 in the home for over 32 y.
A meta-analysis was performed with results of the eight published domestic studies. The lung-cancer excess is not statistically significant, but the trend with increasing concentration in the homes is significant (Lubin and Boice 1997). The graph of the eight studies from Lubin and Boice (1997) is shown in figure 5.9.
All that can be said about domestic risk is that it is low and difficult, if not impossible, to detect given the high background lung-cancer mortality in the populations studied. Although a pooling of data from the largest current and past case-control studies from all countries will be performed at NCI by the year 2000, it is unlikely to provide quantitative domestic risk estimates. Because of the poor precision of the individual studies. Lung cancer from environmental exposure might eventually be documented, but it is most likely that numerical risk estimates for lung cancer from 222Rn and decay-product exposure will rely on projection models from the underground-miner experience.
The difficulty in pooling the domestic studies is described by Neuberger and others (1996.).

Figure 5.9
Relative risks (RR) from eight lung cancer case-control studies of indoor radon levels. Dashed line is extrapolation of risk from miners for a 25 y exposure. Dotted line is a relative risk of 1 (Lubin and Boice 1997).
Epidemiology Of Cancer Of Organs Other Than Lung
Two followup studies of the cancer risk in organs other than the lung were performed. One cohort was uranium miners in West Bohemia, and the other was iron miners in Sweden. In the West Bohemia study of 4,320 uranium miners, 28 sites of cancer mortality were evaluated. No statistically significant cancers other than lung cancer occurred. The authors state that the possible exception is cancer of the gallbladder/extrahepaticducts, with 12 deaths (ratio of observed to expected (O/E), 2.26; and confidence interval (CI), 1.16–3.94), but they state that such cancers would have to be studied further to prove that radon was causal (Tomasek and others 1993).
In the Swedish study, the mortality of 1,415 iron miners was studied, and 27 sites of cancer were evaluated Darby (1995). There were no statistically significant increases in gallbladder or extrahepatic duct cancers, but a marginal excess of stomach cancers was found (O/E=1.45; CI=1.04–1.98). The authors state that the stomach cancer was probably due to the considerable number of Finns in the workforce; stomach cancer in males, especially in northern Finland, is considerably higher than in Sweden, the population used for reference.
Stomach cancer in the United States has been qualitatively linked to smoking habits in some studies though no analytic study has yet been mounted to attempt to derive risk estimates. Data in the United States (NIH 1996) generally show an increasing mortality risk ratio for stomach cancer with increasing smoking rates, but the data are inconclusive. The two studies of other cancers provide reasonable support for the conclusion that the dosimetric significance of inhaled 222Rn and decay products for the induction of cancer in other organs is absent or minimal.
Evaluation Of Risk Per Unit Exposure From Inhaled 222RN in Air
The lifetime risk of lung cancer associated with indoor radon concentration of 150 Bq m-3, calculated from the various models, is summarized in table 5.5. The most recent estimate of risk of lung cancer in the United States due to inhalation of radon decay products is from the model published in the BEIR VI report.
The BEIR VI calculated estimates of lung cancers per year in the United States from the two models are 15,000 and 21,000. These result from an average exposure of the population to 46 Bq m-3; the exposure distribution was documented from the national residential radon survey by the Environmental Protection Agency (Marcinowski and others 1994).
The lifetime risk can be calculated per unit Bq m-3 directly from the relative risk tables given in BEIR IV, NCI and BEIR VI for smoking and nonsmoking males and females. The fractional values used by the BEIR VI committee for ever-smoking males and females are 0.58 and 0.42, respectively. The values for the lifetime base risk of lung cancer in ever-smoking males, never-smoking males, ever-smoking females, and never-smoking females are 0.116, 0.0091, 0.068, and 0.0059, respectively (J. Lubin, personal communication).
The lifetime inhalation risks per unit of exposure to 222Rn in air and in air from water use are shown in table 5.7. The risk is estimated for ever-smokers and never-smokers and men and for women with the average of the two BEIR VI preferred risk models. The lifetime risks are derived as a product of the BEIR VI preferred relative risk estimates and the baseline lung cancer risks given above. The lifetime risk per unit of exposure to 222Rn in air derived from water use is the risk in air multiplied by the average water transfer coefficient.
All the risk computations described above are based on up to 11 cohorts of underground miners. The atmospheric characteristics in the various mines have a wide array of values with regard to unattached fraction, decay product equilibrium, etc. The absorbed dose delivered to the target cells in bronchial epithelium differs somewhat among mines and among different homes. The various factors such as higher unattached fraction in homes versus mines and lower breathing rates in homes versus mines compensate, in such a way that the application of the
Table 5.7
Lifetime Risk of Lung Cancer for Lifetime Exposure to 1Bq m-3 Calculated from the BEIR IV, NCI, and BEIR VI Lifetime Relative Risk Tables
|
|
Lifetime Lung Cancer Risk per Bq m-3 in Air (in Water) |
||
|
Model |
Men |
Women |
Population |
|
BEIR IV (National Research Council 1988) |
|
|
1.0 × 10-4 (1.0 × 108) |
|
Lubin and others (1994) |
|
|
1.2 × 10-4 (1.2 × 108) |
|
BEIR VI (National Research Council 1999) |
|
|
|
|
Ever-smokers |
3.1 × 10-4 (3.1 × 10-8) |
2.0 × 10-4 (2.0 × 10-8) |
|
|
Never-smokers |
0.59 × 10-4 (0.59 × 10-8) |
0.40 × 10-4 (0.40 × 10-8) |
|
|
Population weighted average of ever-smokers and never-smokers |
|
|
1.6 × 10-4 (1.6 × 10-8) |
models for exposure in homes derived directly from the mines is considered valid for predictive purposes (National Research Council 1999).
The population estimate, 1.6 × 10-4, for the lifetime risk of lung cancer for lifetime exposure in the home to 1 Bq 222Rn m-3 in air, as derived from BEIR VI, is the value adopted by this committee. It can be seen that the BEIR VI estimate of lifetime risk is higher than that for the domestic studies (see table 5.5) which support a lower risk estimate for 222Rn (table 5.7).