4
Matter at Extreme Densities
Introduction
The completion of the Relativistic Heavy Ion Collider (RHIC) in 1999 will open a new window on matter at the highest energy densities. RHIC will collide beams of heavy nuclei traveling at nearly the speed of light, with energies of 100 GeV per nucleon. The collisions will produce large regions of matter at unprecedented energy densities in the laboratory. One of the new phenomena expected in this regime is the deconfinement of quarks. At low energies the quarks that make up neutrons, protons, and other hadrons are always confined in groups of two or three. However, when nuclear matter is sufficiently excited by compression or heating, or both, the quarks should no longer be bound together, but should be able to move freely through the excited volume. Matter is believed to have existed in this form, a quark-gluon plasma, for the first few microseconds after the Big Bang.
The questions driving theory and experimental studies are these:
- What is the nature of matter at the highest densities?
- Under what conditions can a quark-gluon plasma be made?
- What are the basic rules governing the evolution and the transition to and from this kind of matter?
Subatomic particles, the hadrons, are composed of quarks and gluons confined within the volume of the hadron according to quantum chromodynamics (QCD). The nature of this confinement, which is a crucial aspect of the quark-gluon
description of matter, is inadequately understood. At RHIC, such high-energy densities will be created that the quarks and gluons are expected to become deconfined across a volume that is large compared to that of a hadron. By determining the conditions for deconfinement, experiments at RHIC will play a crucial role in understanding the basic nature of confinement and shed light on how QCD describes the matter of the real world. These experiments are complementary to the studies of the structure of the nucleon described in Chapter 2.
An exciting theoretical challenge in studying high-energy-density matter is to understand chiral symmetry. Massless quarks possess a handedness (i.e., right-handed or left-handed); this chirality is a fundamental symmetry of QCD. In the everyday world, particles have mass. How the massless quarks turn into particles with mass is not completely understood, but the process spontaneously violates the chiral symmetry of QCD. By probing the transition between states where chiral symmetry holds and where it is broken, insight can be gained about how particles acquire their masses. Although the connection between chiral symmetry and quark deconfinement is not well understood at present, chiral symmetry is expected to hold in the quark-gluon plasma.
Information gathered from high-energy heavy-ion collisions is potentially also important in astrophysics. It will help constrain the equation of state, the equation that relates the density of matter in neutron stars and supernovae, as well as in the first microseconds of the early universe, to pressure and temperature. This information will place stronger theoretical constraints on the maximum mass of a neutron star, improving the ability to distinguish neutron stars and black holes.
A transition from normal hadronic matter to a quark-gluon plasma at high densities or temperatures is expected because, generally, as matter is heated or compressed its degrees of freedom change from composite to more fundamental. For example, by heating or compressing a gas of atoms, one eventually forms an electromagnetic plasma in which the nuclei become stripped of electrons, thereby forming an electron gas. Similarly, when nuclei are squeezed (as happens in the formation of neutron stars in supernovae, where the matter is compressed by gravitational collapse) they merge into a continuous fluid of neutrons and protons—nuclear-matter liquid. Likewise, a gas of nucleons, when squeezed or heated, should turn into a gas of uniform quark matter, composed of quarks, antiquarks, and gluons.
The regions in temperature and baryon density where the transition to a quark-gluon plasma is expected are shown in Figure 4.1. Baryons are protons, neutrons, and other particles made up of three quarks. At low temperatures and baryon densities, the system can be described in terms of hadrons, nucleons, mesons, and internally excited states of nucleons. In the high-temperature (~ 150 MeV or 1012 K), high-baryon-density (~ 5-10 times the density of nuclear matter) region, the appropriate description is in terms of quarks and gluons. The transition between these regions may be abrupt, as in the boiling of water—with a
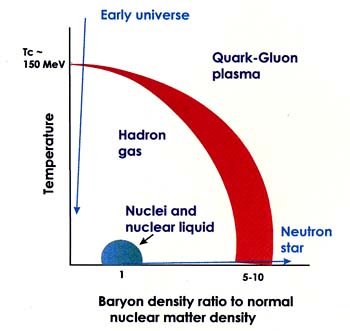
FIGURE 4.1
Phase diagram of hadronic matter. The figure shows regions of temperature and baryon density in which matter exists as a nuclear liquid, hadron gas, or quark-gluon plasma. The path followed by the early universe as it cooled from the quark-gluon plasma phase to normal nuclear matter is shown as the arrow on the left. The arrow near the bottom traces the path taken by a neutron star as it forms. Heavy-ion collisions follow a path between these two extremes, increasing both the temperature and the baryon density.
latent heat (first-order transition), without a latent heat (second order), or only a smooth but rapid crossover. The smoothness of the transition with three quarks, the realistic case, is still unclear, but the calculations show a strong change within 10 MeV of the transition temperature, 150 MeV. Under any circumstances, the physics changes strongly between the low- and high-temperature regimes.
Figure 4.1 also shows a second transition, between normal nuclei, which are liquid, to a gas of nucleons. Theory indicates that macroscopic quantities of nuclear material undergo this transition at densities below that of normal nuclear matter. The two phases should coexist at temperatures below a critical temperature of approximately 15-20 MeV. As in ordinary matter, there should be latent heat required as the system goes from the vapor, through a mixed phase of vapor and liquid, to the liquid phase. Density fluctuations and the abundances of
nuclear droplets (small nuclei with nucleon number A in the range 6 to 50) should increase with temperature in the mixed-phase region. These phenomena have been studied experimentally, as described in Box 4.1.
From the time of the Big Bang, the early universe cooled as it expanded. For the first microseconds, the temperature was at least hundreds of MeV and matter existed as a quark-gluon plasma. Figure 4.1 shows the evolution of the early universe as a downward trajectory practically along the vertical axis of the phase diagram. The matter of the early universe had a much smaller net number of baryons than photons, about one in a billion. As the universe cooled below the critical temperature for deconfinement, the primordial plasma coalesced into hadrons. The quarks found partners and became confined into nucleons and mesons and eventually into the nuclei we observe today. If the transition is first order, droplets of hadrons formed in the middle of the plasma similar to the way water precipitates into rain drops.
Such density inhomogeneities could have enhanced the abundance of the elements Be or B. They may even have led to formation of strange quark matter nuggets or planetary-mass black holes, which could account for some of the sofar-unobserved dark matter in the universe. If the transition is relatively slow cosmologically, then the hadron formation process could contribute to the entropy, or disorder, observed as the number of photons in the universe. These features of the universe depend on how the transition from the quark-gluon plasma to hadronic matter took place.
In neutron stars the properties of matter under extreme conditions also play a crucial role. For example, our present lack of knowledge of the properties of matter at densities beyond twice that of nuclei is reflected in uncertainty about the maximum mass of neutron stars. RHIC experiments, by providing information on the equation of state, should help us determine possible states of matter in neutron stars. For example, neutron stars may, at a density as low as a few times nuclear-matter density, contain a mixed state consisting of droplets of quark matter immersed in ordinary hadronic matter fluid. If their central density rises to five to ten times that of nuclear matter, they may have quark-matter cores in their deep interiors. One cannot even definitely rule out, without further data, the possibility of a distinct family of quark stars with higher central densities than those of neutron stars.
Ultrarelativistic Heavy-Ion Collisions
To date, experiments to study matter at very high energy density have been performed at several beam energies. High baryon density can be achieved by colliding nuclei at an energy where they just barely stop one another, as recent experiments have shown. The Brookhaven AGS accelerator has been an optimal tool for studying extremely dense matter. The CERN SPS, with higher energy, provides somewhat lower baryon density but higher energy density, making additional
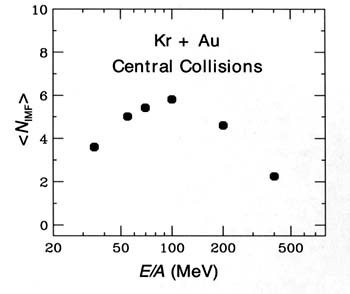
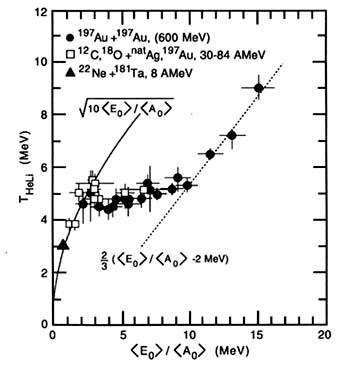 FIGURE 4.1.2 The “caloric curve" of nuclear matter. The temperature of the system created in the collision of heavy ions at intermediate energy is plotted as a function of the excitation energy available. Both quantities are inferred rather than directly measured—the temperature from the relative abundances of different nuclear isotopes, and the excitation energy from the number and energy of observed particles. Because the temperature and excitation energies are derived and rely upon theoretical assumptions, there remain large uncertainties on their values. Nevertheless, the initial rise, followed by a region of constant temperature with increasing excitation energy, ultimately followed by a second temperature rise, is the behavior of a system undergoing a first-order phase transition. More sophisticated experiments will show whether this trend actually occurs in nature or is an artifact of the way the temperature and excitation energy are currently inferred from the data. occurs should allow extraction of the thermodynamic properties of the liquid-gas phase transition. Some of the experimental evidence for the phase transition is shown in Figure 4.1.1, which illustrates the yield of light nuclei in collisions of Kr beams of different energies on a stationary Au target. At energies between 50 and 100 MeV per projectile nucleon, light nuclei are abundantly produced. Careful analysis of the data indicates that the excited systems decay in less than 3 × 10-22 sec. a time much less than that required for sequential emission of light nuclei, with equilibrium being reestablished between each successive step. Other intriguing evidence that the mixed phase may be prepared in the laboratory is shown in Figure 4.1.2. For excitation energies of 2 to 10 MeV, the temperature remains nearly constant at 4.5 MeV (about 5 × 1010 K), suggesting an enhanced specific heat as in a phase transition. This figure is a encouraging step toward observing the phase transition; however, experimental uncertainties in the determination of the temperature and excitation energy scales are significant and must be improved before thermodynamic quantities can be reliably extracted. |
observables accessible. The RHIC collisions will have ten times the energy of the collisions at the SPS. A very high energy density with a net baryon density of nearly zero is expected.
Experiments have been performed with beams of light (sulfur and silicon) and heavy (lead and gold) nuclei. These experiments have mapped how the collisions evolve in time and change character with changing energy. They have shown which observables must be measured and how such measurements are best done, given the large number of particles produced. The program has included careful comparisons to proton-proton and proton-nucleus collisions to guide the search for evidence of new physics. These experiments have revealed several surprises, as discussed below.
Collisions at increasingly higher energies create increasing numbers of mesons, as the incoming energy of the projectile is transformed into the mass carried by these mesons. Eventually the bombarding energy becomes high enough that the nucleons can no longer completely stop each other. Then the nuclei pass through one another, becoming highly excited internally, and leave the physical vacuum between them with a great deal of energy. This excited vacuum contains quarks, antiquarks and gluons (see Box 4.2). Such nuclear transparency becomes important in the highest-energy collisions. The nuclear fragmentation regions. which recede from each other at nearly the speed of light, contain essentially all the baryons of the original nuclei. The central region with very few baryons is of special interest, because it resembles the hot vacuum of the early universe. Although the hot, dense phase of the collision does not live long, the initial temperature and density reached are very high indeed.
RHIC offers a unique opportunity—the matter created in RHIC collisions will redefine the energy density and temperature frontiers. The matter is expected to exist much longer than the hot matter studied in experiments to date.
Stopping
The degree to which colliding nuclei stop each other determines the energy available to excite the central region between the nuclei. The excitation energy heats the matter and produces particles. If a large number of particles is produced in a small volume, this high density creates pressure, causing the blob of matter to expand collectively. Experimental data on nucleon distributions and the amount of energy produced transverse to the beam direction allow one to infer the extent of stopping in collisions. Data at 14 GeV/nucleon for the heaviest nuclei are consistent with the maximum possible energy deposition, or "full stopping." At the SPS, the collisions are more than three times as energetic, and a considerable fraction, but not all, of the available energy is found to be transferred to other degrees of freedom.
Calculations that reproduce the experimentally observed stopping indicate maximum baryon densities about 10 times that of normal nuclear matter in
14 GeV/nucleon collisions, and up to 6 times at the SPS. The corresponding energy densities are about 10 times that of normal nuclei and 2 to 5 times the energy density inside a hadron. Although a smaller fraction of the incoming energy is stopped in the higher-energy collisions, the energy density is higher and the baryon density lower than at the AGS. These estimates indicate that collisions that are being studied at existing facilities may be reaching the threshold of the deconfinement transition, and signatures of the new phase may be observable. These signatures and experiments looking for them are described below. At RHIC, the stopping of the nucleons will be much less, but because the collision starts out with 10 times as much energy as current collisions at CERN, the heating and energy density achieved will, it is predicted, be at least twice that in present collisions. Consequently, experiments will no longer need to peer across the threshold but will be able to study a deconfined state thoroughly.
Evolution of Collisions
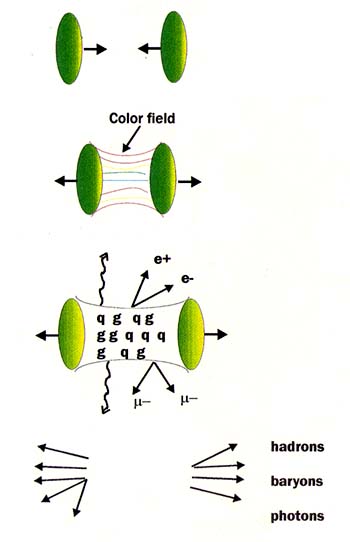
Very high-energy heavy-ion collisions proceed through a number of different stages, shown schematically in Figure 4.2. In the first stage, the two colliding nuclei penetrate one another. The quarks and gluons composing the nuclei collide and transfer a large amount of energy from the projectile to the vacuum, energy later observed as new particles (Figure 4.3). This stage of the collision, lasting about 3 × 10-24 sec, is short because of the relativistic contraction of nuclei moving nearly at the speed of light.
From the very energetic or "hard" collisions among the quarks and gluons, additional gluons and light and heavy quarks are produced. These new quarks and gluons, along with those present initially, undergo a cascade of further collisions, which slows down or stops the nuclei, as discussed above. The techniques of perturbative QCD, developed to describe e+ - e- and proton-antiproton collisions, have been applied to describe this cascade. The calculations predict very high initial temperatures, 2 to 3 times that required for deconfinement, and copious gluon production. These gluons should thermalize in less than the time required for the nuclei to interpenetrate, sharing their energy equally among themselves. This process would produce a quark-gluon plasma in local thermal equilibrium that lives long enough to generate detectable signals. The hot and dense stage of the collision, where the plasma is expected to exist, lasts only about three times as long as the interpenetration stage; experiments will have to sample this stage for evidence of the existence and properties of the quark-gluon plasma. The predicted signatures are described below, along with some intriguing results from existing lower-energy experiments.
The hot and dense phase then cools and expands, and below the deconfinement temperature and density the quarks and gluons condense into a gas of hadrons. The hadronization transition is expected to take place around 10 to 30 × 10-24 sec after the nuclei began to collide. It is at this point that most
|
BOX 4.2 Probing the Vacuum Although one usually thinks of the vacuum as space with nothing in it, quantum theory tells us that the vacuum is not really completely empty. It contains a "sea" of quark-antiquark pairs. However, these particles are present in the vacuum only fleetingly, as fluctuations of the fields generated by other particles. Normally, but not always, these fluctuations are too small to be observed. Nuclear physicists will explore the vacuum by heating it up to an extremely high temperature (some 1,500 billion degrees!) by colliding pairs of heavy ions at very high energies. The vacuum becomes polarized by the large energy density, making the sea of quark-antiquark pairs visible as discussed in the section describing the structure of hadrons. When two nuclei collide, they pass through each other, converting some of their energy to heat, heating themselves as well as the tiny piece of vacuum between the two retreating nuclei. Theory predicts that such heating will create conditions comparable to those in the first millionth of a second after the Big Bang. The first panel in Figure 4.2.1 shows two heavy nuclei approaching each other at velocities near the speed of light. At these speeds they appear flattened because of the Lorentz contraction. Immediately following the collision, the two nuclei have formed a hot region between them, as shown in the second panel. In this hot region, there will be fluctuations of the color field that governs the interactions of quarks and gluons. A number of interesting phenomena should take place. The color field will produce quark-antiquark pairs, converting collision energy into particles. Because of the high temperature, a very high density of quarks and antiquarks, as well as the gluons they exchange when they interact, will build up. At high densities, the quarks should no longer be confined in the particles we normally observe. Instead, they will roam freely over the hot zone, forming a quark-gluon plasma. The plasma will radiate photons and lepton pairs, such as electron-positron or muon-antimuon pairs, as indicated in the third panel. The leptons and photons are not affected by the strong force among the quarks as they escape from the quark-gluon plasma; thus, they serve as messengers carrying information about the plasma's properties. Following the collision, the quark-gluon plasma cools and changes back to the usual hadronic phase of matter. A large number of particles, primarily hadrons (baryons and mesons), emerge from the collision. The hot vacuum cools back to its usual, seemingly empty state. However, the particles produced in the collision are left over, as shown in the bottom panel, allowing experiments to "peek" into the structure of the vacuum. |
of the particles shown in Figure 4.3 come into existence. The matter is still highly excited, and the density of the hadrons is large. The hadrons scatter from one another, maintaining the pressure and causing further expansion and cooling. The multiple scatterings of the particles tend to partition the available energy equally among them and keep the system in equilibrium. Eventually, the system is sufficiently dilute that the hadrons cease colliding and travel outward without further disturbance.
The number of particles at the end reflects the energy deposited in the collision.
This energy rises with the energy of the beam, as illustrated by Figure 4.3. The thousands of particles emerging from the space normally subtended by one nucleus indicates an extremely high energy density in that space. The detection of this large number of particles requires sophisticated and ingenious detectors with high granularity. The complexity of the detectors is comparable to that of the largest existing detectors in high-energy physics: however, the nuclear experiments must identify a larger range of particles, and they must retain sensitivity to rather low-energy particles. The requirements of measuring high-energy
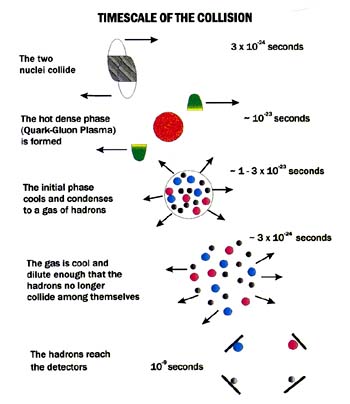
FIGURE 4.2
Schematic illustration of the different stages in a heavy-ion collision. The stages include (a) initial interpenetration of the colliding nuclei; (b) the hot dense phase where the quark-gluon plasma should exist; (c) the hot hadron gas phase; (d) freezeout of the hadrons, where they no longer scatter among themselves; and (e) the point when the hadrons reach the detectors. The time scale for each stage is indicated on the right side of the figure.
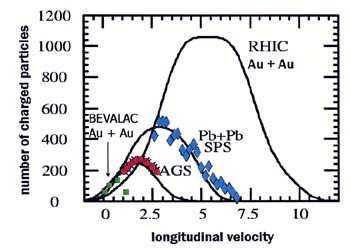
FIGURE 4.3
The number of charged particles produced in Au + Au (or Pb + Pb) collisions is plotted as a function of the longitudinal velocity of the particles. The increase in the number of particles produced from modest energy (1 GeV/nucleon beam) at the Lawrence Berkeley National Laboratory Bevalac through the AGS at Brookhaven National Laboratory and the CERN SPS is dramatic. The uppermost curve shows the number of particles predicted to be produced with the very high energy at BNL's Relativistic Heavy-Ion Collider.
collisions of very heavy ions have driven new developments in detectors, readout electronics, and data acquisition technology.
Hot Dense Initial State
The arrangement of the quarks and gluons making up the nucleons inside a nucleus has been studied with energetic electron, positron, and proton beams. New results from the HERA electron-proton collider in Germany show an abundance of gluons carrying a small fraction of the nucleon momentum. These results indicate that in addition to the quark collisions, an even larger number of collisions among gluons will occur at RHIC, causing a hot gluon gas to be formed. A hot gluon gas has never before been created, and RHIC will offer the first glimpse of such matter. The dominance of gluons causes special signatures, which can be looked for experimentally. The temperature and corresponding
energy density should be significantly larger at RHIC than for AGS or SPS collisions, and the lifetime of the hot dense state should be longer.
The gluons participate in a rapid cascade of subsequent collisions. The cascade drives the central region toward thermal equilibrium on a time scale comparable to the interpenetration time of the colliding nuclei, producing exactly the conditions needed to form a quark-gluon plasma in local thermal equilibrium. Such equilibrium is unlikely in isolated nucleon-nucleon collisions because the density of gluons is not sufficient to produce the fast cascade. The hot, gluon-rich initial state should produce thermal photons, which survive the subsequent stages of the collision and enter the detectors unchanged. Heavy-ion collision experiments look for these photons. Another result of the gluon-rich initial state is the fusion of gluon pairs to produce many charmed quark-antiquark pairs, which are observable at the end of the collision via the charmed mesons they form.
In the higher energy heavy-ion collisions planned for at the LHC at CERN, the gluon densities are predicted to be even greater. Though this density should further increase the temperature and lifetime of the plasma, the LHC energy causes production of quarks and antiquarks very early in the collision as well. The initial state is thus quite complex, and the number of particles that must be detected in the final state is correspondingly higher.
Hadronic Rescattering and Freezeout
The quark-gluon plasma is expected to exist in the hot, dense stage of the collision, and this stage is consequently of primary interest. However, the evolution to the finally observed hadrons must be understood in order to interpret the results of the experiments.
After the hot dense region expands sufficiently, the hadron gas becomes so dilute that scattering among the components ceases and the hadron gas "freezes out." Following this freezeout, the various particles freely fly out of the collision region, reaching the detectors nanoseconds later.
The freezeout volume can be studied by measuring the correlations of the momenta of identical particles. This technique, which relies on quantum wave mechanics, is borrowed from astronomers, who developed the use of intensity correlations to measure the size of distant stars; the spatial range of the observed correlations is related to the size of the emitting star. Similarly, in nuclear collisions, the correlations between pairs of mesons carry information about the size of the region emitting the mesons, as shown in Figure 4.4. The source sizes inferred exceed the size of the incoming nuclei. Furthermore, the dependence of the correlations on the momenta of the particles indicates that the system is expanding. Detailed measurements of both the two-particle correlation functions and the momentum spectra of single hadrons at RHIC energies should pin down the expansion velocities and the temperatures at which the hadronic phase freezes out.
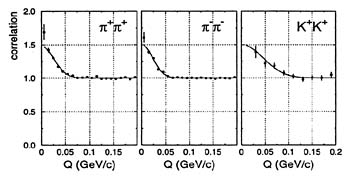
FIGURE 4.4
The rate of detecting identical meson pairs from a high-energy collision of two gold nuclei as a function of their relative momentum Q. The technique can measure a diameter of about one-trillionth of a centimeter by using the uncertainty principle to convert the width in Q of the measured peak into the size. (Courtesy of E877 collaboration.)
Thermal Description of the Final State
The latter phase of the collision, after the quarks coalesce into hadrons, appears to behave as a system of hadrons in thermal equilibrium. The equilibrium is unlikely to span the entire central region in the collision, as the hadrons scatter primarily with nearby neighbors. Consequently, equilibration is local rather than global; however, the size of the equilibrated region is large enough to include many particles.
Experimental measurements that characterize the hadronic system include average momenta of the particles transverse to the beam. Measurement of the spectral slope, or falloff in the number of particles with increasing transverse momentum, as a function of the collision centrality—how nearly head-on the nuclei collide—permits determination of the temperature and the extent of chemical equilibrium. From such measurements, a large latent heat associated with a first-order phase transition should be observable experimentally.
In the data available at present, the production rate of different particle types is consistent with a system in local thermal and chemical equilibrium. It is possible to fit the data with this assumption and determine the point at which the particles cease to interact. The fit indicates that freezeout in collisions at 14 GeV/nucleon occurs in the temperature range 120 to 140 MeV, with baryon density 30-40 percent that of normal nuclear matter. Analysis of higher-energy data reveals freezeout at similar temperature and baryon density. One of the first
experimental results awaited from RHIC is how the higher initial temperature affects the freezeout.
Signatures of Quark-Gluon Plasma Formation
Determining the nature of high-density matter and identifying the formation of a quark-gluon plasma are the major experimental challenges at RHIC. Ideally, the experiments must show that some features of the data cannot be present without a quark-gluon plasma. A number of such signatures have been predicted and are listed in Table 4.1. This section describes several of the table entries in more detail and summarizes what is known from experiments thus far.
Typically, an experiment looks for multiple signatures as a correlated change in the observables, such as those shown schematically in Figure 4.5. Varying the conditions of the collisions (energy and size of the colliding nuclei, for example) will allow experimental determination of the energy density required for the deconfinement transition and will allow its properties to be studied. Putting together information from the different signals will shed light on how confinement works and how chiral symmetry is restored. Even short-lived or partially equilibrated plasma should exhibit properties different from normal hadronic matter and, thus, be detectable.
The first five signatures in Table 4.1 are detectable by measurement of electrons and muons emitted from the collisions. These leptons are frequently emitted in pairs, one positive and one negative; the invariant mass of the pair is calculated from the measured energy of the two leptons. As leptons and photons interact electromagnetically, they exit the colliding system virtually unaffected by the surrounding hadronic matter. This allows them to provide information about the early stages of the collision. Figure 4.6 shows schematically how the dilepton mass distribution would be modified, should all of these predicted signals occur.
A striking signature of quark-gluon plasma existence is the suppression of J/psi labeled region 4 in Figure 4.6. The interaction between quarks is screened by other quarks in the deconfined state, so quark bound states such as the J/psi cannot survive in the plasma. Bound states with a large radius are dissociated first, while the small ones, like the upsilon (at a mass of about 9.5 GeV, beyond the range shown in Figure 4.6), consisting of the heavier b-quarks, should not be suppressed. The psi' state is less tightly bound and has a larger radius than the J/psi, so it should disappear first.
The observed J/psi production is currently under intense theoretical and experimental study to see whether it indicates plasma formation. A good cross-check would be to observe that the upsilon production probability is little changed. However, data on upsilon production in heavy-ion collisions will not be available until RHIC runs. Because the upsilon production cross section is very small, a high beam energy is required to create a significant number of upsilons.
TABLE 4.1 Predicted Signatures of Quark-Gluon Plasma Formation
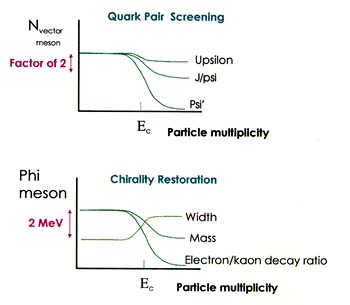
FIGURE 4.5
Quark-gluon plasma and chiral symmetry signatures. This figure illustrates two different signatures of quark-gluon plasma formation and chiral symmetry restoration. The top plot shows the number of J/psi, psi', and upsilon mesons produced; J/psi and psi' production should be suppressed if a quark-gluon plasma is formed. The bottom illustrates modification of properties of the phi meson. If chiral symmetry is restored, the phi mass should decrease and width increase; the preferred decay channel should also change. Each is plotted as a function of the energy observed transverse to the beam direction, showing the expected correlated change as the energy density in the collision increases. The magnitude of differences between normal hadronic matter and quark-gluon plasma is indicated.
Copious production of gluons in the early stage of the collision should increase the likelihood for fusion of gluons to produce charmed quarks. This process would lead to an enhancement of charm compared to that in nucleon-nucleon collisions, though only a small fraction of this enhancement goes into the production of charm and anticharm quarks bound together, and this enhancement will not appreciably alter the J/psi suppression discussed above. Mesons incorporating charmed quarks decay before reaching the detectors. Leptons from these decays contribute to the observed lepton pair spectrum in the intermediate mass region labeled 3 in Figure 4.6. Enhanced production of lepton pairs in this region has been observed by two experiments.
Thermal radiation of real or virtual photons (which decay to charged lepton
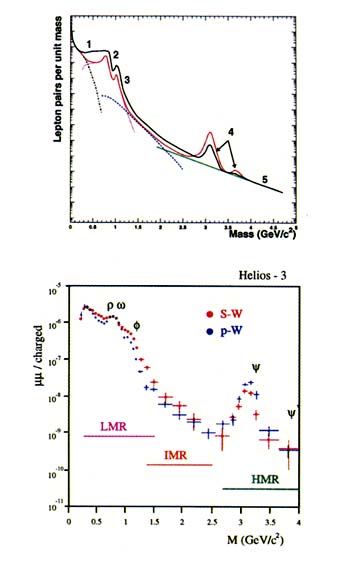
FIGURE 4.6
Lepton pair spectrum. The top panel shows a schematic view of the distribution of lepton pairs (either electrons or muons) as a function of invariant mass. The red line shows the lepton pair spectrum from normal hadronic matter. The dashed blue line indicates the expected spectrum when a quark-gluon plasma is formed. Five regions of the spectrum are of interest: (1) low-mass pairs in which enhanced production from thermal radiation from the plasma should be observable; (2) the phi meson, which should be broader in width as chiral symmetry is restored; (3) intermediate-mass pairs, which should be enhanced by decays of mesons containing charmed quarks formed by the plasma; (4) the J/psi and psi' mesons, which should be suppressed by the plasma; and (5) the high-mass pairs, Drell-Yan continuum. The bottom panel shows the measured distribution of muon pairs in collisions of sulfur and proton projectiles on a tungsten target. The muon-pair yield relative to the total number of charged particles is given; LMR and IMR indicate the low- and intermediate-pair-mass regions, while HMR shows the start of the high-pair-mass region. Significant differences between sulfur and proton projectiles are visible and may indicate onset of a new phase of matter.
pairs; labeled 1 in Figure 4.6) provides direct information on the thermal history of the collision. Such data are usually studied by looking at the production probability as a function of the total energy or momentum perpendicular to the beam direction carried by the pair of leptons. The highest-energy part of the distribution reflects the hottest, earliest stage of the collision. The mass range in the dilepton spectrum where such radiation appears and the number of dileptons radiated depend on the initial temperature. If very high temperatures are reached, copious thermal dileptons should be produced. Detection of such radiation would determine whether the initial temperature is sufficient for deconfinement.
Excess low-mass dileptons (labeled 2 in Figure 4.6) have been observed in heavy-ion collisions by the CERES and HELIOS-3 experiments. However, attempts to explain the excess as thermal radiation from the hot initial state have not been able to account for its mass dependence. Thermal radiation should decrease smoothly with increasing dilepton mass, but the experiments show a peak directly below the rho meson. This can be explained if the mass of the rho meson were to decrease during the hot, dense stages of the collision. These data have generated considerable excitement, as decreasing rho mass may indicate the onset of chiral symmetry restoration.
In proton-proton collisions, hadrons containing a strange quark are produced much less frequently than hadrons with light quarks only. The high temperature required for a quark-gluon plasma should make it much easier to produce the heavier strange quarks, enhancing strangeness. Indeed, experiments have found a doubling of the number of strange hadrons compared with proton-proton yields. An enhancement in the number of phi mesons, which are bound states of strange and antistrange quark pairs, has also been observed. The excess strange particles fall into two classes. The yields of the lighter strange particles, in particular the kaons and lambdas, can be accounted for by secondary collisions. If a sufficiently energetic pion collides with a nucleon, a strange and antistrange quark may be created (labeled 2 in Figure 4.6). These would get bound into an extra kaon and lambda. Models simulating the cascade of hadronic scatterings correctly reproduce the observed kaon and lambda excess in heavy-ion collisions. However, the other strange particles, phi mesons and strange antibaryons, which contain more than one strange quark or antiquark, are not so easily explained. Strange antibaryons are nearly impossible to produce in secondary collisions among the hadrons in the hadron gas phase of the collision. All of the existing models must invoke new physics (e.g., statistical decay of small quark matter clusters) to explain the experimental results. Consequently, production of strange antibaryons will be studied extensively at RHIC.
A quark-gluon plasma affects particles traversing it differently than does hadronic matter. A single quark, detected after hadronization and freezeout via the jet of particles it produces, should lose significantly more energy going through a deconfined plasma of quarks and gluons than if the quarks and gluons are bound into hadrons. The plasma will also affect the angular correlation
between pairs of jets. While the beam energy in experiments performed to date is too low for significant jet production, energy loss of jets is an important new signal to be studied at RHIC.
Unusual objects may be made when a quark-gluon plasma expands and hadronizes. We must remain prepared for nature to surprise us in the way she reveals the physics of this unexplored regime, as when first presenting neutron stars to us in the form of pulsars.
Chiral Symmetry
At high temperatures or densities, chiral symmetry may hold, and consequently the properties of hadrons may be modified with increasing density of the medium around them. For example, the mass of the kaons is predicted to decrease, an effect which would be manifested experimentally via a larger number of very low momentum kaons. The mass of the rho meson would decrease, modifying the lepton pair spectrum as illustrated in Figure 4.6; this may possibly already have been observed by the CERES collaboration. The mass and width of the phi meson would also be affected. Because the phi is close in mass to two kaons, a slight modification in the kaon mass could cause a measurable change in the likelihood of phi decay to two kaons versus (for instance) decay to an electron plus a positron.
A new signature for the chiral phase transition has been proposed, the formation of disoriented chiral condensates corresponding to different ways of going from a phase with full chiral symmetry back to symmetry of the kind found in normal matter. It is possible that this transition does not happen uniformly over the entire system, resulting in regions with different conditions. Such a state would have highly specific experimental characteristics, such as unusual ratios of charged to neutral pions, or charge correlations, as have in fact been reported in certain cosmic ray events. Searches at currently available energies have not yet produced evidence for such a condensate, but at the much higher energies of RHIC, a larger fraction of the collisions may be expected to reach the required conditions, substantially increasing the probability of observing these signatures.
Relativistic Heavy-Ion Collider
The heavy-ion collisions studied to date at Brookhaven National Laboratory's AGS and at CERN in Europe show hints of interesting new phenomena. However, we do not yet have firm evidence of the existence of a new phase of matter. RHIC at Brookhaven National Laboratory, on which construction is well under way, is expected to settle these questions. Beginning in 1999, RHIC will collide beams of Au ions at energies 10 times larger, in the center of mass, than have been available at the AGS or at CERN. Construction is proceeding on schedule, and, as of this writing, beam was successfully brought into RHIC from the AGS
(which will continue to run, primarily to serve as an injector for RHIC) and brought one-sixth of the way around the RHIC ring. For further information on this facility, see Chapter 8.
Experiments at RHIC
RHIC has six collision regions, four of which will be instrumented for data taking in 1999. The four experiments include two large, multipurpose experiments, STAR and PHENIX, and two small, focused experiments, PHOBOS and BRAHMS. This group of experiments was chosen to be complementary and allow full measurement of possible new phenomena when RHIC begins operation. The experiments were designed to cover the predicted signatures of new physics, as listed in Table 4.1. Complementary experiments are required, because it is not possible to measure all of the signatures in a single experiment; for example, detecting all the hadrons interferes with measurement of low-energy leptons.
STAR is optimized for large coverage for hadrons, and PHENIX for leptons and photons. Each one surrounds the collision area with a variety of detectors and catches as many of the emitted particles as possible. STAR and PHENIX are both international collaborations of 300 to 400 physicists. The two smaller experiments, PHOBOS and BRAHMS, are each approximately one-tenth the size and complexity of the large experiments. PHOBOS will measure the very low energy hadrons that do not penetrate the large magnetic fields and thicker detector layers in the large experiments. BRAHMS will reach angles much closer to the beam direction than any of the other experiments, thus providing a more kinematically complete picture than the other experiments, albeit with only a few particles from each event.
Figure 4.7 shows the layout of the PHENIX experiment at RHIC. The detectors in PHENIX measure as many of the predicted quark-gluon plasma signatures as possible, with an emphasis on leptons and photons. This will allow a search for correlated changes as the beam energy and size of the colliding system is varied.
Construction is currently under way in each of the collision areas in RHIC. All four detectors will be ready to collect data in 1999. Figure 4.8 shows the status of PHENIX construction as of September 1998, with the magnets and detector carriages shown in Figure 4.7 installed into the collision area.
The four experiments under construction for 1999 constitute a first survey of the physics of RHIC. They cover most, but not all, of the predicted signatures of the quark-gluon plasma. Analysis of early data will show which detector capabilities require upgrades to fully realize the physics potential of RHIC. The two uninstrumented beam intersections offer the possibility of entirely new experimental approaches. The two large experiments have both made compromises (driven by financial considerations) in their initial detectors, but upgrade paths to

FIGURE 4.7
The PHENIX detector for RHIC. Different components of the detector are labeled; each component provides information complementary to the others. Information from the components is combined to determine the momentum, type, and trajectory of the particles produced in the collision. The two beams enter from either side of the experimental hall and collide in the center of the detector. PHENIX has three magnets; the central magnet analyzes electrons and hadrons, while the forward and backward magnets measure muons emitted near the beam direction. Charged particles entering the central magnet are tracked by using three types of gas-filled detectors. Hadrons are identified by measuring their arrival time at walls of scintillator detectors. Electrons are identified in four ways: production of light in the ring-imaging Cerenkov counter, the distinctive amount of energy lost when they traverse the time expansion chamber, the unique shower of energy produced in the electromagnetic calorimeter, and matching of the shower energy with the momentum measured by the tracking system. Photons, which are neutral, are identified by the energy they deposit in the electromagnetic calorimeter and the absence of a charged track associated with that deposition. Muons are the only particles able to penetrate the central magnet pole face and the absorber layers at the ends of PHENIX. Their momentum is measured with tracking chambers located inside the muon magnets. (Courtesy PHENIX group.)

FIGURE 4.8
The PHENIX collision area in September 1998. The beams enter the area from left and right. In the picture, the central magnet and both muon magnets are installed. The other detector elements will be brought to the hall as they are completed. (Courtesy PHENIX group.)
extend their capabilities have been identified. The data and new discoveries will determine which further studies and upgrades are required.
Outlook
Intriguing experimental results show that the high-energy-density matter created in heavy-ion collisions is at (or may be just above!) the threshold to enter a new form. RHIC will come online in 1999, with 10 times higher energy than currently available, and will produce matter well over the threshold for the transition to deconfined matter. Theoretical descriptions of the quark-gluon plasma have predicted numerous signatures of its formation, and a suite of experiments is under construction to investigate the proposed signatures. The properties of high-energy-density matter will be extracted, and the data will improve the current understanding of how quarks are confined and how particles acquire mass
when the quarks coalesce into hadrons. As we begin to learn the nature of high-energy-density matter at RHIC, the experiments can be accordingly expanded and upgraded. Finally, there is a possibility that complete surprises await. The energy regime is totally new, and the potential for unexpected discoveries is exciting. The answers will begin to be known in the next several years.