1
Tests and the Challenge of Linkage
Why does it matter to anyone other than testing experts whether the results of different achievement tests can be placed on a common scale? Given the vast and diverse array of educational tests used in American schools today, what purposes would be served by developing an equivalency scale to compare their results? Proponents of procedures to compare ("link") test scores argue that many Americans need more information about how individual students in the United States are performing in relation to national and international benchmarks of performance, information that is not readily available from existing tests. Moreover, they claim that parents, students, and teachers would profit from knowing how individual students' performance on key subjects compares with the performance of students in other schools, other states, and even other countries, where different tests and assessments are used. Existing tests, including the federally funded National Assessment of Educational Progress (NAEP), can now be used to compare the performance of groups of students, but they do not tell how individual students are performing relative to national and international standards. Finally, many people believe that such comparisons could spur improvements in schooling at the state and local levels (e.g., Achieve, 1998), although many other educators, testing experts, and policy makers are less enthusiastic about the utility of this type of information as a tool for genuine improvements in teaching and learning (e.g., Jones, 1997).
Arguments over the utility and feasibility of test score comparability, which had been limited to relatively few measurement researchers, have recently come to public attention during the debate triggered by President Clinton's proposed Voluntary National Tests (VNT). One stated goal of that initiative is to provide parents, students, and teachers with clear information about the performance of individual students as measured by national standards; one aspect of the debate centers on whether there is a need to develop a new test or an equivalency scale to link existing tests. The debate led Congress to ask the National Research Council (P.L. 105-78, November 1997), to evaluate the feasibility of developing a common scale to link scores from existing commercial and state tests to each other and to NAEP.1
Under the auspices of its Board on Testing and Assessment, the National Research Council established the Committee on Equivalency and Linkage of Educational Tests in January 1998. The primary focus of the committee's study is linkage among the tests currently used by states and districts to measure individual students' educational performance. We examined a substantial amount of data about selected tests that would be likely candidates for the kinds of linkage suggested in the legislation. We focused in particular on common uses of such tests, their diversity in content and format, their measurement properties, the degree to which they change over time, the extent to which state and local school policies can affect the uses and interpretations of test results, and specific properties of NAEP that enable or hinder links to other tests. We have concentrated on tests of 4th-grade reading and 8th-grade mathematics, the subjects proposed for the VNT.
Background
Educational testing in the United States is an increasingly diverse and complex enterprise. To a large extent this situation reflects the nation's decentralized system of educational governance and the variety of choices that states and local districts have made about curriculum and assessment.
Over the past decade, many states and local districts have moved rapidly to revise their curriculum goals to reflect high expectations for student learning, to design customized tests aligned with those curricula, and to adopt new, test-based accountability systems aimed at bringing classroom teaching into alignment with curricular goals in order to spur improvements in teaching and learning. States are developing more content-based assessments to match curriculum goals, and those assessments differ substantially from state to state, both in content and in form. The variation occurs in part because the movement for high standards brings with it more articulation of specific content. Even within states, there is much tension over content and governance between the state and the local level. Reforms in Title I of the Improving America's Schools Act, passed in 1994, reflected and reinforced the trend toward greater state and local innovation in standard-setting, testing, and accountability. Similar patterns were articulated in the Goals 2000-Educate America Act, also passed in 1994, and the Individuals with Disabilities Education Act, passed in 1997.
At the same time, the tension of standardization versus diversity and local innovation has become manifest through the public's demand for increasingly uniform and systematic information about student performance. Educators, parents, policy makers, and others want to know more than existing tests can show about the performance of individual students. In particular, they want to know how students measure up to national and international benchmarks.
Existing tests, including NAEP, can compare the performance of groups of students in one state with the performance of groups of students in other states. International comparative assessments, such as the Third International Mathematics and Science Study (TIMSS) tell us how U.S. students as a group are doing compared with those in other nations. But these national programs are not designed to tell how individual students are performing relative to national and international standards. Despite large investments of public and private dollars in tests and testing, current tests do not readily tell us whether Leslie in Louisiana is performing as well as or better than cousin Maddie in Michigan or whether either has attained the level of mathematics skills and knowledge of Kim, who lives and attends school in Korea.
These competing trends in the testing arena—greater reliance on state and local initiatives and increased demands for national indicators of individual student performance—reflect long-standing tensions in the
American experiment with public education. The Constitution does not authorize any specific federal role in education, and the conduct of education has almost always been left to states and localities. Nonetheless, the federal government has promoted education in various ways since the founding of the republic. For example, the Northwest Ordinances of 1785 devoted public lands for the purpose of supporting education; the Morrill Act of 1862 granted land to establish "land-grant" colleges; and in 1867 Congress established a federal Office of Education to gather statistics and monitor the progress of education.
Although the concept of national education goals that are codified in law is quite recent, the federal government in the twentieth century—particularly at times of perceived international or economic crisis—has frequently turned to education as an instrument of national interests and to promote the general welfare of the nation. Often these initiatives have been controversial, causing debate over what, if any, is the proper role of the federal government in education. Today's education policy debates are in many ways a continuation of the historical experiment. Seeking ways to reconcile local variation and national standards is a manifestation of the quintessentially American ideal to build unity from respect for differences, to balance uniformity with heterogeneity—in essence, to have the best of both worlds.
Viewed through this lens of our unique experiment in pluralism and federalism, the question motivating this study is both predictable and sensible. Given the rich and increasingly diverse array of tests used by states and districts in pursuit of improved educational performance, can information be provided on a common scale? Can scores on one test be made interpretable in terms of scores on other tests? Can we have more uniform data about student performance from our healthy hodgepodge of state and local programs? Can linkage be the testing equivalent of "e pluribus unum?"
Committee's Approach
In approaching our charge, the committee made a number of key assumptions. First, the question motivating this study manifests a long-standing tension in the American educational system that curriculum, instruction, and assessment are best designed and managed at the state and local levels, but that there is also a need for greater uniformity in the
reporting of information about student achievement in our diverse system.
Second, though Congress was not explicit about the purposes of linkage, we recognize that the study originated in the debate over the VNT; however, we understand our charge as limited to the specific and fairly technical aspects of linkage. Though our work has some implications for possible links between the VNT and NAEP, we take no position on the overall desirability of the Voluntary National Tests. Our conclusions should not be read as either endorsing or opposing them.
Third, we adopted a definition of "feasibility" that combines validity and practicality. Validity is the central criterion for evaluating any inferences based on tests and is applied in this report to inferences based on linkages among tests. By practicality we mean not only whether linkages can be calculated, in the arithmetic sense, but whether the processes necessary to collect the data and conduct the empirical studies are reasonable and manageable.
This is the second and final report of the committee. In our interim report, published in June, we presented two important conclusions: (1) it is not feasible to develop a single scale to link the "full array" of existing tests to one another, and (2) it is not feasible to link the full array of existing tests to NAEP and report results in terms of the NAEP achievement levels. The committee reached these negative conclusions with some reluctance, given our appreciation of the potential value of a technical solution to the dual challenges of maintaining diversity and innovation in testing while satisfying growing demands for nationally benchmarked data on individual student performance.
In this final report we extend our analyses and conclusions in a number of ways. First, we consider a somewhat relaxed definition of the problem and explore issues surrounding linkages among subsets of existing tests. Given the apparent similarity in content, format, and purpose of at least some of the major tests used in schools today, it is reasonable to ask whether valid links among them would provide useful and accurate information to parents, students, and others. Furthermore, it is useful to consider criteria that might be applied by educators and school officials who are considering linkages across particular tests or types of tests. We also consider specific issues pertaining to NAEP, again by focusing on the validity of links between any achievement test (rather than the full array of existing tests) and the NAEP scale and achievement levels. (The NAEP achievement levels are standards that classify performance in four
categories: below basic, basic, proficient, and advanced; see Chapter 3 for details.) Finally, this report provides greater detail about contextual issues that influence the feasibility of linkage, as well as elaboration of key methodological problems originally flagged in our interim report.
The rest of this chapter provides a primer on educational testing and a blueprint of the logic underlying methodological issues in test equating and linking. Chapter 2 expands the discussion of linkage by examining statistical methods, validity of links under various conditions, issues of aggregation, and criteria by which to evaluate the quality of linkages. Chapter 3 examines special issues regarding links to NAEP and the NAEP achievement levels. Chapter 4 returns to the broader policy context of this study and addresses three overlapping features of the testing "landscape" in the United States that together determine the feasibility of linkages: diversity in testing technology (test designs, formats, etc.), diversity in content emphasis across tests, and diversity in the intended and actual uses of tests in the states and districts. Chapter 5 is a synopsis of our key findings and conclusions and a brief overview of unanswered questions that may warrant further research.
Drawing Inferences from Tests
To evaluate the validity of inferences from scores on a given test of educational achievement—call it test A—one asks how well one can infer, from a test taker's performance on test A, the proficiencies or knowledge it is designed to measure. When scores on test A are linked to scores on a second test—call it test B—the quality of the linkage hinges on how well one can infer from performance on test B the proficiencies that test A is designed to measure. To understand what is required to create a valid linkage among tests, it is first necessary to understand the nature of tests.2
Tests are constructed to assess performance in a defined area of knowledge and skill, typically called a domain. In some cases, a domain may be small enough that a test can cover it exhaustively. For example, there are only a few rules governing the capitalization of nouns in English, and one could assess proficiency with them in the space of a fairly short test. Teachers frequently administer tests that cover small parts of broader
domains. The achievement tests of interest to policy makers and the public, however, generally attempt to measure much larger, more diverse domains, say, 4th-grade reading or 8th-grade mathematics.
Because the time available to assess students is limited, broad domains have to be tested with small samples of those domains. Consequently, performance on the test items themselves is not as important as is the inference the scores support about mastery of the broader domains the tests are designed to measure. Missing 10 items out of 20 on a test of general vocabulary is important not because of the 10 words that were misunderstood, but because missing half of the items justifies an inference about a student's level of mastery of the thousands of words from which the test items were sampled.
Tests of the same domain can differ in important ways. In order to build a test that adequately represents its domain, a number of decisions must be made. It is helpful to think of the process as three stages leading from the domain to the final test, which can be called "framework definition," "test specification," and "item selection" (see Figure 1-1). The choices made at each stage constrain the assessment, while making it more definite.
First, the developers of an assessment must delineate, from the entire domain of the subject being assessed, such as mathematics, the scope and extent of the subdomain to be represented in the assessment. A test framework provides a detailed description of how the domain or subdomain will be represented. (As we describe in Chapter 4, differences between frameworks lead to somewhat different tests.)
Second, choices at the stage of test specification determine how a test will be built to represent the subdomain defined by the framework. Test specifications, which are sometimes called the test blueprint, specify the types and formats of the items to be used, such as the relative number of selected-response items and constructed-response items. Designers must also specify the number of tasks to be included for each part of the framework. For example, a reading test blueprint would specify the number of passages students will read. In mathematics, a blueprint would indicate that the test will include items that are best answered with the use of a numerical calculator: NAEP includes such items, but TIMSS, given in many countries, does not. The NAEP and TIMSS mathematics frameworks are very similar, yet the two assessments have different specifications about calculator use.
Third, following domain definition and test specification, test makers
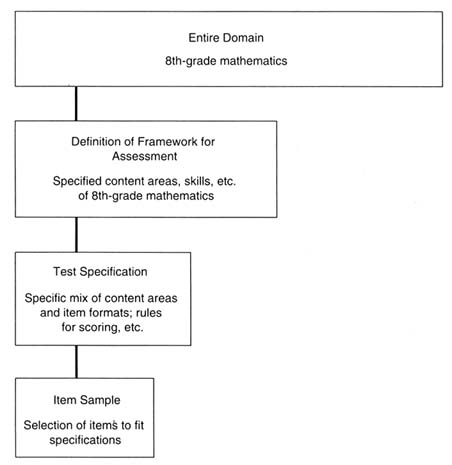
Figure 1-1 Decision stages in test development.
devise particular items that assess some part of the test specification. A set of items is chosen, for a given test, from a large number of prepared items, so that the selected set matches the test specification. Many testing programs have several equivalent forms of their tests in use and produce additional forms at regular intervals. For example, several forms of the Scholastic Assessment Test (SAT) are produced yearly, each of which matches the same framework and the same detailed blueprint.
Drawing Inferences from Linked Tests
The choices made at each stage of test development affect the validity of a test, by which is meant the ability to use test scores to estimate proficiency in an entire domain. Linking, which in general means putting the scores from two or more tests on the same scale, magnifies the challenges to validity because different tests reflect different choices made at each stage of the test development process. Choices made during test development (as shown in Figure 1-1) lead to three basic types of linkage.
The first type of linkage adjusts scores on different forms of a test that reflect the same framework and the same test specifications. This is the case of multiple forms of the same basic test, such as the Armed Services Vocational Aptitude Battery (ASVAB), the Law School Admissions Test (LSAT), or the SAT. There is little form-to-form variation in score meaning in these circumstances. Nevertheless, the different forms contain different items, differing slightly in difficulty, so some statistical adjustment is often necessary. A linking process called “test equating" is used to make statistical adjustments of scores on each new form so that the scores on that form are comparable in meaning to scores on the previous forms.
Score distributions can sometimes be aligned by a simple linear adjustment. This method, called linear equating, is analogous to converting temperatures between Fahrenheit and Celsius scales; see Box 1-1. Another method, equipercentile equating, adjusts for a given population the entire score distribution of one test to the entire distribution of the other. Equating permits valid inferences to be drawn from scores on any of the forms of linked tests that are built to the same specifications.
The second type of linkage is between two tests with the same framework but different test specifications. An example would be the linking of a new test, built from the NAEP frameworks but with a different mix of item types, and NAEP. The validity of inferences from such links is vulnerable to the possibility that performance of some students or groups might vary differentially across formats or other elements of the test specifications.
The committee's work has been concerned primarily with links between scores that differ in both framework and specifications. This third type of linkage is intended for tests designed to reflect different (though perhaps overlapping) perspectives of a domain.
Linking studies involving NAEP and TIMSS are examples of efforts to link assessments based on different frameworks. The potential variations
|
Box 1-1 Fahrenheit, Celsius, and Educational Tests There is a well-known formula for linking Fahrenheit and Celsius temperatures: F° = (9/5)C + 32°. Thus, if one reads that Paris is suffering from a 35-degree heat wave—which may not seem very hot—one needs to multiply 35 by 9 and divide that result by 5 to get 63 and then add 32 to get a very recognizably hot 95, in degrees Fahrenheit. This formula is an example of a linking function and is analogous to what is meant by linking two test score scales. Just as one placed the Celsius value of 35 on the Fahrenheit scale and got 95 (which may be more meaningful to some people), linking can allow one to place the scores from one test on the scale of another and interpret that score or to compare it to those of test takers who took the other test. Other uses of linking assessments are to estimate how schools or districts would have performed had their students taken an assessment, such as NAEP, that they did not take. Although the temperature measurement analogy is useful for understanding some aspects of tests, it is only a partial analogy because temperature measurement is very simple compared with the assessment of complex cognitive activities, such as reading or mathematics. |
in assessments point to an important criterion for evaluating test-based inferences: the extent to which results are reasonably consistent across alternative measures of the same domain. For example, a given score on the NAEP grade 8 mathematics assessment is intended to measure a level of mastery of the material specified in the NAEP mathematics framework, whereas a given score on TIMSS is intended to estimate a level of mastery of the material specified by the TIMSS framework, which is overlapping, but different from the NAEP framework. Therefore, the only thing one could say with confidence is that the NAEP scores reflect mastery of the NAEP framework, and the TIMSS scores reflect mastery of the TIMSS framework. It is understandable that a student might score better on one assessment than on the other, that is, find NAEP easier than TIMSS. In practice, however, these distinctions may blur. Many users of results from a given test will interpret both scores as representing degrees of mastery of the same general domain, such as "8th-grade mathematics" and will seem perplexed at the discrepancy. It is necessary to clarify the domain to which scores should generalize in order to evaluate the quality of any linkages among tests.
Matters of test design are not the only potential factors that affect the validity of linkage-based inferences, and in some cases, they might not be the most salient. Differences in test use can also affect the interpretation of a linkage. When a test is used in a low-stakes fashion—that is, if no serious consequences are attached to scores—teachers and students may have little incentive to focus carefully on the specific sample of content reflected in the test. In contrast, when stakes are high, teachers or students have reason to care a good deal about scores, and they may focus much more on the specific sample of knowledge, skills, task types, and response expectations reflected in the specifications for that test. Thus, introduction of a new high-stakes test may lead to an increase in mastery of that part of the domain, without a corresponding improvement in mastery of other parts of the domain that the assessment is supposed to represent but does not. This narrowed instructional focus may produce inflated scores on that high-stakes test. Whatever this focus might imply for the validity of the measured gains, however, it is likely to throw into question the stability over time of any linkage between the high-stakes test and any low-stakes test of the same domain.
Since all tests are small samples from broad and complex domains, a possible lack of consistency across measures is an omnipresent threat to linkage that warrants careful, case-by-case evaluation; see Box 1-2 for a discussion of linking methods.
|
Box 1-2 Linking Methods Equating. The strongest kind of linking, and the one with the most technical support, is equating. Equating is most frequently used when comparing the results of different forms of a single test that have been designed to be parallel. The College Board equates different forms of the Scholastic Assessment Test (SAT) and treats the results as interchangeable. Equating is possible if test content, format, purpose, administration, item difficulty, and populations are equivalent. In linear equating, the mean and standard deviation of one test is adjusted so that it is the same as the mean and standard deviation of another. Equipercentile equating adjusts the entire score distribution of one test to the entire score distribution of the other for a given population. In this case, scores at the same percentile on two different test forms are equivalent. Thus, if a score of 122 on one test, A, is at the 75th percentile and a score of 257 on another test, B, is also at the 75th percentile for the same population of test takers, then 122 and 257 are linked by the equipercentile method. This means that 75 percent of the test takers in this population would score 122 or less on test A or would score 257 or less on test B. The linked scores, 122 and 257, have the same meaning in this very specific and widely used sense, and we would place the A score of 122 onto the scale of test B by using the value of 257 for it. By following this procedure for each percentile value from 1 to 99, tests A and B are linked. Two tests can also be equated using a third test as an anchor. This anchor test should have similar content to the original tests, although it is typically shorter than the two original tests. Often the anchor test is a separately timed section of the original tests. Sometimes, however, the items on the anchor test are interspersed with the items on the main tests. A separate score is computed for the responses to those items as if they were a separate test. An assumption of the equipercentile equating methodology is that the linking function found in this manner is consistent across the various populations that could be chosen for the equating. For example, the same linking function should be obtained if the population is restricted only to boys or only to girls. However, the research literature shows that this consistency is to be expected only when the tests being linked are very similar in a variety of ways that are discussed in the rest of this report. Calibration. Tests or assessments that are constructed for different purposes, using different content frameworks or test specifications, will almost always violate the conditions required for equating. When scores from two different tests are put on the same scale, the results are said to be comparable, |
|
or calibrated. Most of the statistical methods used in equating can be used in calibration, but it is not expected that the results will be consistent across different populations. Two types of empirical data support equating and calibration of scores between two tests. In one type, the two tests are given to a single-group of test takers. When the same group takes both tests, the intercorrelation of the tests provides some empirical evidence of equivalent content. In a second design, two tests are given to equivalent-groups of test takers. Equivalent-groups are often formed by giving both tests at the same time to a large group, with some of the examinees taking one test and some the other. When the tests are given at different times to different groups of test takers, equivalence is harder to assert. Two tests can be equated or calibrated using a third test as an anchor. This method requires that one group of students takes tests A and C, while another group takes tests B and C. Tests A and B are then calibrated through the anchor test, C. For this method to be valid, the anchor test should have the same content as the original tests, although it is typically shorter than the other tests. One relatively new equating procedure, used extensively in NAEP and many other large testing programs, depends on the ability to calibrate the individual items that make up a test, rather than the test itself. Each of a large number of items about a given subject is related or calibrated to a scale measuring that subject, using a statistical theory called item response theory (IRT). The method works only when the items are all assessing the same material and requires that a large number of items be administered to a large representative set of test takers. Once all items are calibrated, a test can be formed from a subset of the items with the assurance that it can be automatically equated to another test formed from a selection of different items. Projection. A special unidirectional form of linking can be used to predict or "project" scores on one test from scores on another test without any expectation that exactly the same things are being measured. Usually, both tests are given to a sample of students and then statistical regression methods are applied. It is important to note that projecting test A onto test B gives different results from projecting test B onto test A. Moderation. Moderation is the weakest form of linking. It is used when the tests have different blueprints and are given to different, nonequivalent groups of examinees. Procedures that match distributions using scores are called statistical moderation links, while others that match distributions using judgments are called social moderation links. In either case, the resulting links are only valid for making some very general comparisons (Mislevy, 1992; Linn, 1993). |













