Page 95
5
Measuring the Consequences of Climate Variability and
Forecasts
Although the potential benefits of improved seasonal-to-interannual climate forecasts are not known precisely, they are widely believed to be substantial. Government agencies spend money to improve the skill of climate forecasts, presuming that society will benefit and that markets may not allocate scarce resources to supply useful forecast information. Agencies have an implicit interest in measuring the effects of climate variations and the potential and actual benefits of climate forecasts in order to direct research to where the potential benefit is greatest, evaluate past research and communication efforts, and improve the delivery of forecast information. This chapter examines the concepts, data, and analytical methods needed and available for assessing the effects of climate variability and the value of improved climate forecast information. It considers how to define and measure the effects of climatic variations and estimate the value of improved forecasts, examines the state of scientific capability to make such estimates, and considers the availability of the data needed to estimate the actual and potential benefit of improved forecasts.
It is useful to distinguish two related analytical tasks: estimating the effects of climatic variation and estimating the value of climate forecasts. Climatic variations alter the outcomes for actors engaged in activities that are sensitive to weather or other climate-related environmental conditions, such as fires and floods, in ways that depend on the coping systems those actors use. Climate forecasts can have value by allowing these
Page 96
actors to use their coping systems differently in order to improve their outcomes relative to what they would have been without the forecast.
Estimating the Effects of Climate Variations
An effect of climatic variations in a particular time period for a particular actor, activity, or region can be defined as the difference between an outcome for that period and the long-term average of similar outcomes, net of nonclimatic influences and of longer-term changes in average climate. According to this definition, each region or activity has climate-induced good and bad years, compared with long-term averages.
Using this definition to measure the effects of climatic variations is not a simple matter. It requires first that the effects of climatic variability on a range of outcomes be identified and measured for each sensitive activity in each region. Monetary effects and deaths and serious injuries from extreme weather events are relatively easy to identify and measure, but many other effects are not. For extreme events, they include uninsured injuries and property losses, as well as other effects that are harder to quantify, such as increased community cohesion in the immediate period of disaster recovery and in the longer term, community recognization and shifts in employment patterns, with some people benefiting and others losing.
The effects of nonextreme climatic variations can be particularly difficult to measure. Although many extreme negative events are routinely tallied, few nonextreme events are. The effects of such climatic variations are often subtle or distant in time from their causes, and, for these reasons, causality may be hard to establish. Some effects are deleterious and others are beneficial. It is necessary to model many of these effects rather than measuring them directly, as can be done with storm damage. Econometric models have been used in attempts to value commonplace weather events (e.g., Center for Environmental Assessment Services, 1980), but with mixed success.
Estimating the effects of climatic variation requires that data be developed on the various outcome variables and on things that may affect them, both in the time periods of interest and over a long enough past to establish historical averages. In any weather-sensitive sector, many outcome variables may be affected by climatic variability either directly or indirectly. In agriculture, for example, weather-sensitive outcomes include not only crop yields and income from crop sales, but also the costs (in money and time) of crop selection, water management, crop hazard insurance, participation in the futures market, government disaster payments, and so forth. Each of these activities may be affected by climatic
Page 97
variation or the anticipation of it, and each may benefit from appropriate kinds of climate forecast information.
It is important to have data available at sufficient levels of disaggregation and resolution to examine the effects of climatic variations and of forecasts on particular sectors, types of actors or activities within sectors, and geographic regions. For example, agriculture's gain from improved forecasts might be the insurance industry's loss, if farmers gamble by adopting seed varieties that will do well under forecast climatic conditions, in the expectation that insurance will pay if the crop fails. Or, as with the 1997-1998 El Niño, the costs of a climatic event along the U.S. Pacific coast may be tied to benefits in the Northeast. There is need to understand the regional and sectoral effects as well as the aggregate effects. Even if the aggregate effect of a set of climatic events is zero, better prediction might improve outcomes in every region.
The distribution of costs and benefits of climatic variations within a sector is also important to recognize and measure. A major climatic event may affect people very differently depending on whether they have access to disaster insurance, on precisely where they are located in a flood plain, on their previous economic condition, or on other specific factors.
A major difficulty in estimating the effects of climatic variations is constructing appropriate baselines. Baselines are intended to capture important social and environmental outcomes that may be altered by climatic variability. It is important that the defining characteristics of such baselines be described to reflect outcomes in the absence of the climatic variability being examined, in order to provide a benchmark against which to compare the outcomes after particular climatic variations.
Choosing the appropriate temporal scale of baselines is critical. Social and environmental outcomes must be corrected to take into account longer-term climatic change and various nonclimatic factors that have influenced them and that are likely to be different in the present and the future from what they were in the past. But a baseline period can be too long. Episodic tastes and preferences, technological eras, and stages of economic development often distinguish societies temporally. It is important to capture in a baseline the elements of society that are most homogeneous over time scales of seasonal-to-interannual climate variability. In sum, estimating the effects of any one season's climate on a particular activity or region requires significant efforts to conceptualize the relevant outcomes and the range of climate-related and other factors that affect them, to measure all these variables, to develop data bases, and to build and validate models.
Page 98
A Conceptual Model of the Effects of Climate Variability
To model the effects of climatic variability, one must simplify a very complex system of human-environment interactions. Numerous conceptual modeling schemes have been previously proposed to portray the interactions of human systems and climate variability. We rely here on a scheme modified from one proposed by Kates (1985). Kates's general scheme is shown in Figure 5-1, and our scheme, which focuses on the major factors affecting the human consequences of climatic variations and forecasts, is in Figure 5-2. Our scheme differs from the more general one in providing more detail on particular kinds of human activity and human-environment relationships and in omitting some of the feedbacks in the general model for a more focused presentation.
Most analyses of the human consequences of climatic variability include one or more elements of the scheme in Figure 5-2, with some parts better represented than others. Climatic averages and variations affect various biophysical systems on which people depend; they also influence human activities designed to cope with climate. The human consequences of climatic variations are shaped by climatic, biophysical, and social factors, including both the coping activities and more general social forces. For example, farm income is affected not only by climatic events and their biophysical consequences, but also by the coping behaviors of farmers
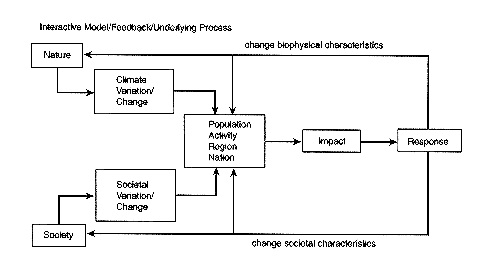
FIGURE 5-1 A schematic model of factors
responsible for the human consequences
of climatic variability. Source: Kates (1985). Reprinted by
permission of SCOPE.
Page 99
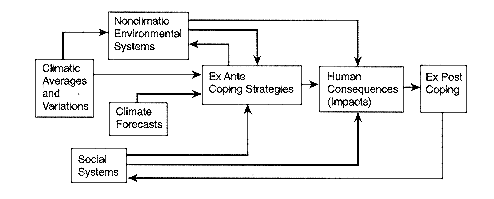
FIGURE 5-2 A schematic model of the human
consequences of climatic variability
emphasizing the roles of coping mechanisms and of climate
forecasts.
and the institutions that support them (reviewed in Chapter 3) and by other social phenomena. Among them are those that respond directly to climatic events, such as the prices and availability of agricultural commodities, timber, and other climate-sensitive goods and services, and relatively climate-independent social phenomena, such as changes in food preferences and in society's willingness to underwrite the stability of farm income with transfer payments.
It is important to emphasize that, although climatic variations affect people directly (e.g., through the impacts of temperature on human health and the demand for energy), many of the most important effects operate indirectly through biological systems (e.g., water supplies, agricultural ecosystems). In fact, the first indications of climatic variability of consequence to human systems are environmental: for instance, changes in streamflow, reservoir levels, incidence of fire, water in soils and plants, and crop yields. These environmental systems are also influenced by human coping mechanisms, such as management of flood-control dams, choices of crop species and cultivars, soil management choices, and so forth. Moreover, the effects of climate-induced biophysical changes are shaped by human coping mechanisms and other social phenomena (e.g., food and insurance prices and availability, emergency preparedness, income distribution). Thus, the consequences or impacts attributed to climatic variability are in fact dependent not only on climatic processes but also on their interactions with other biophysical processes, human coping mechanisms, and various other social phenomena.
Of special interest for the present purpose is the fact that people typically intervene in valued biophysical systems when they believe that climatic events may adversely affect them. Thus, each of these systems is
Page 100
human-managed to some extent, as indicated in Figure 5-2 by the arrow from ex ante coping to nonclimatic environmental systems. Climate forecasts, through their influence on ex ante coping, can be expected to induce people to intervene in biophysical and social systems to increase their well-being under expected climatic conditions. Consequently, it is important for analyses of the impacts of climatic variations and forecasts to recognize that forecasts may affect ecological and other biophysical systems through human interventions initiated in response to the forecasts. When forecasts are skillful and provide decision-relevant information, acting on them can improve social well-being.
A key to understanding the consequences of climatic variability for society lies in understanding the dynamic interplay of people's preferences and the constraints on those preferences, and how climate variability affects this interplay. These preferences and constraints influence human behavior in the face of uncertainties, such as those related to climatic variability. Preferences matter because, for example, decision makers' aversion to absorbing risk will affect what they do in risky environments. Constraints matter because they bound the set of possible actions by which people exercise their preferences. Among the major kinds of constraints are the biophysical (e.g., the amount of rainfall affects seed growth), the technological, ''income'' constraints (e.g., the ability of the decision maker to borrow or to obtain formal or informal insurance), and constraints imposed by societal institutions.
Current Scientific Capability
We presume, for purposes of discussion, that the ideal model of the effects of climatic variability on society is one that explicitly represents all the structural elements shown in Figure 5-1 based on knowledge obtained from observation. With knowledge of these fundamental elements and their relationships, and assumptions about decision making (e.g., the assumption of economically rational behavior), it is possible for researchers to predict what decision makers will do given particular technological capabilities, amounts and types of information, and institutional regimes (e.g., insurance). Use of data to construct and validate their models lends credibility to the resulting predictions. Current scientific capability reflects progress in understanding key structural elements of decision making in response to climate variability, but we are a long way from understanding all aspects of the problem and are particularly deficient in modeling based on direct observation. Some models and analytical approaches contain little or no information about structural elements of decision making. Many such models rely on reduced-form statistical relations. Some models are little more than assumption-driven simula-
Page 101
tions with no connection to observations. In the following section, we review examples of research progress, pointing out strengths and weaknesses of different approaches to estimating the societal effects of climatic variability. Our review first considers research on how climatic variability affects other biophysical systems that impose constraints on human systems. We turn our attention to research on decision making based on observation and then consider research that simulates decision making in the absence of observation.
Estimating Biophysical Impacts That Constrain Human Systems
The biophysical impacts of climatic variability pose a formidable constraint on decision making. A considerable amount of modeling research has focused on estimating the biophysical effects of climatic variability and change. The modeling approaches used in this research fall into two broad classes: reduced-form and deterministic. Reduced-form modeling has relied on correlations between highly aggregate climatic and other biophysical data and has used them to predict biophysical outcomes of a range of climate scenarios. Deterministic modeling specifies causal relations linking climate variability to biophysical outcomes, sometimes deriving the causal relations from theoretical principles, such as well-understood mechanisms in plants that partition sensible and latent heat fluxes to maintain viable internal temperatures in the presence of stressful external temperatures.
Most reduced-form studies establish correlations between observed climatic elements and observed measures of biophysical system performance. For example, historical time series of observed temperature and precipitation may be related to time series of crop yields using regression techniques (Thompson, 1969; Bach, 1979). The resulting regression coefficients are then used to predict the effects of current climate variability on crop yields. A similar approach can be used to analyze streamflow and ecosystem zonation (e.g., Holdridge, 1967). In a National Research Council report, Waggoner (1983) used such an approach to predict a 2 to 12 percent decline in yields of major U.S. Midwest crops (corn, soybeans, wheat) relative to their current averages as a result of an assumed 1°C increase in annual temperature and a 10 percent decline in summer precipitation. Such approaches are also being used to examine the possible effect of El Niño outbreaks on crop yields. Cane et al. (1994) found that maize yields in Zimbabwe seemed to vary regularly with El Niño cycles.
Reduced-form models bypass obtaining information characterizing the structure underlying decision making and examine instead the empirical relationship between changes in one or another dimension of the biophysical environment—e.g., variations in rainfall—and the outcomes
Page 102
of decisions. The chief advantage of reduced-form approaches is that they greatly simplify the relationship between climate and biophysical outcomes. They are practical when data limitations are large. However, collinearity among explanatory climate variables is often large. Also, the climatic variations used to force the models are often outside the range of climatic observations from which the model coefficients were estimated. Spurious relationships between climate predictors and their predicted outcomes, and statistical overfitting of the data, are frequent (Katz, 1977). Because such models do not specify many variables that may affect the relationship between climatic variables and human outcomes, they are not useful for making predictions about what would happen if the missing variables (e.g., seed technology, forecasting skill) changed over time.
Deterministic models of plant growth and other ecological processes permit detailed estimates of the effects of climate variability to be made under a wide range of climate conditions. Examples include mathematical simulation models of forest growth and composition (Botkin et al., 1972; Shugart, 1984) and agricultural crop growth and yield (Williams et al., 1984; Jones and Kiniry, 1986). Such models realistically couple climatic determinants (e.g., temperature, precipitation, solar radiation, humidity, wind speed) with biophysical processes (e.g., plant water use, photosynthesis) that regulate biophysical outcomes (e.g., crop yields). For example, forest composition models have simulated the retreat of maple forests poleward in northeastern North America in response to climate change (Davis and Zabinski, 1992). They have also been used to estimate the impact of sustained drought on timber productivity in the central United States (Bowes and Sedjo, 1993). In the Missouri-Iowa-Nebraska-Kansas (MINK) study (Rosenberg et al., 1993; Easterling et al., 1993), a crop model simulated a contemporary crop response to a recurrence of the Dust Bowl droughts of the 1930s. MINK researchers found that such droughts, absent human intervention, would reduce current yields of maize, soybeans, and wheat by as much as 30 percent below current averages. The model revealed that crop development rates were abnormally increased by the high heat of the droughts, which led to premature termination of grainfill.
Deterministic approaches are richly detailed in causal explanation of biophysical impacts. They provide detailed diagnostic information on why a certain type of outcome was predicated. However, they require massive amounts of data and are highly location-specific, which requires the scaling of results to represent surrounding regions. Acquisition of the necessary data to run the models can be difficult, especially in nations and regions with less developed scientific infrastructure.
Modeling can be improved by joining together the strengths of reduced-form and deterministic models. Promising work on this front seeks
Page 103
to use a geographic information system to organize data sets spatially for use in deterministic crop growth models (Lal et al., 1993). This will facilitate realistic aggregation of the results from multiple modeling sites into regional estimates of crop response to climate variability. However, in regions where reliable data for running the models are too sparse or even nonexistent—including many developing countries—there is little prospect for using deterministic models to estimate large-area response to climate variability.
Neither of the above approaches adequately takes into account human coping with climatic variability. They must be coupled with social and economic analyses based on observations to make the effects of human intervention explicit and realistic. For example, data on how farmers adapt to climatic variations by changing crop production practices are necessary to model the phenomena that make outcomes for farms less sensitive to climatic events than outcomes for individual plants or farm animals.
Research Based on Observations of Decision Making
A basic research challenge is to obtain adequate knowledge of human decision making to allow for empirically based assessments of the consequences of climatic variations that take into account human adaptations. Recent advances in computer power and the availability of data that track decision makers over time have led to a number of studies of the structure of individual decision making in a variety of contexts. These studies, which have looked at such decisions as the replacement of bus engines, the purchases and sales of bullocks by farmers, the adoption of new seed varieties, and teenagers' decisions to leave school, assume particular functional forms for preferences, technological changes, and income constraints. They also assume that individuals are forward-looking, taking into account that their current decisions will affect future outcomes. The basic approach is to start with initial values of the parameters characterizing preferences and constraints, solve the model using well-known solution techniques for dynamic stochastic models, and compare the dynamic decisions (outcomes) predicted by the model with what is observed in the data. This process is repeated until a set of parameters characterizing the structure is found, providing the best fit between the model outputs and the observational data.
One example of this technique, applied to longitudinal data on poor Indian farmers, looked at how variations in rainfall, under conditions of borrowing constraints and the absence of insurance, affected the decisions of farmers to buy and sell bullocks. The structural estimates of the model—which among other things revealed how risk-averse the farmers
Page 104
were—were used to assess how farmers' welfare would have been improved and stocks of bullocks increased if farmers had had weather insurance or increased capabilities to borrow.
Such models can also incorporate learning. A standard method for doing this is to incorporate Bayesian learning. Model estimation then reveals, along with preference parameters and standard technology parameters, how fast learning takes place and how it is affected by the underlying uncertainty of the economy. Such estimable dynamic models have shed new light on behavior and reveal, among other results, how important it is to achieve an understanding of the consequences of technological change to understand the constraints facing decision makers. Because the techniques involve iterative estimation and model solution, obtaining estimates of the structure underlying dynamic decisions requires a great deal of computing power. To obtain estimates in realistic time frames, the number of parameters characterizing the structure is kept to a minimum, so that a common criticism of such models is that they are too simple. Absent substantial innovations in dynamic solution techniques or computing power in the near future, hybrid estimable models that take estimates of biophysical processes from other studies and fix them for purposes of estimation may be a promising technique in coming years.
Input-output models have been used to trace flows of costs and revenues among linked sectors of regional and national economies. Such models (e.g., Bowes and Crosson, 1993) fully replicate interindustry exchanges of capital and labor costs embodied in producer and consumer goods and show how such exchanges are affected by changes in final demand for goods and services. They enable climate-induced changes in supplies of basic materials (e.g., agricultural production, fish harvests) to ramify throughout the connected industries in an affected economy. In the MINK study mentioned above, an input-output model was used to compute the overall effect of a recurrence of the Dust Bowl droughts of the 1930s on the MINK region's economy. Absent adjustments to on-farm production, the droughts prompted a 9.7 percent ($29.9 billion) decrease in total regional production.
The main strength of input-output models is their ability to track interindustry exchanges in great detail. Intersectoral linkages are realistic—that is, they are based on observation. The main disadvantage of input-output models is their static nature. The coefficients used to represent interindustry exchanges are constants, with the result that the models are unable to represent the reinvestment of underused resources induced by climatic events (e.g., unemployed agricultural labor) in other sectors of the economy. Consequently, input-output models tend to overstate the negative impacts of climatic events.
Page 105
A wide spectrum of retrospective, case-study-based methods is available to estimate the societal impacts of climate variability. Past climatic variations create natural experiments that allow for a quasi-experimental case-control design for studying the effects of climate fluctuations. For example, regions experiencing localized climate fluctuations can be compared with adjacent regions with similar physiographic and socioeconomic characteristics that experience average climatic conditions. Riebsame (1988) studied a decade-long period of high precipitation in northern California that was preceded and followed by periods of normal precipitation. Nearby regions experienced no noticeable change in precipitation. Operating rules on major reservoir impoundments in the affected area were systematically altered to avoid flood risk at the expense of maintaining water supplies for summer irrigation needs. No such altered behavior was evident in the control region. Such methods provide a way of systematically separating social and economic impacts of climate variability from the vast array of nonclimate-related influences on social and economic behavior.
Comparative case studies employing carefully coordinated field survey methods and documentary analysis provide key insights into the causal mechanisms that determine the adaptations and vulnerability of populations, regions, and sectors to climatic variability. Survey methods may include implementation of detailed questionnaires, participant interviews, and participant observation. A key to the success of such case studies is the orchestration of research questions, assumptions, data sets, and analytical approaches to provide comparability among case studies and make generalization possible. Comparative case studies are being used in the International Geosphere-Biosphere Program's Land Use/Cover Change core project (Turner et al., 1995) to parse out proximate causes and driving forces of land use change in a variety of locations globally. An illustration of an exemplary use of the comparative case study approach for the study of the consequences of climatic variability is provided in Box 5-1.
Liverman (1992) argues that the "political economy" approach offers an alternative to mechanistic methods of gauging climate impacts. Drawing from Marxist social theory, the political economy approach seeks to understand the impacts of climate in the larger context of political, social, and economic conditions of society. Those conditions either ameliorate or exacerbate climate vulnerability, which is defined as the degree to which different classes of society are at risk from climate variability. The trappings of underdevelopment (flows of resources out of a region, political oppression, land expropriations, exploitative labor practices) combine to force the impoverished into unsustainable environmental management, which leads often to greater vulnerability to drought and other climate
Page 106
|
variations. Liverman (1992) showed that land reform in Mexico—specifically, the creation of the ejido land tenure system characterized by communal land holding—led to higher agricultural losses from drought compared with privately held land.
Simulations of Decision Making
Firm-level economic decision models have been used to track the effects of climatic variability on economic agents' expectations of climate risk. Such models use discrete stochastic sequential programming, a
Page 107
mathematical programming technique that treats a decision-making process as multistage and sequential. Decisions made in the present time, such as when to plant crops, depend on decisions made at previous times, such as when to prepare crop seedbeds, and on outcomes of previous random (e.g., climate) events. Kaiser et al. (1993) used such a model to examine farm-level decision making in response to climate change in a selection of upper midwestern U.S. locations. They found that, in a risk-neutral situation (defined as profit-maximizing), certain crops currently grown in the region (e.g., sorghum) would never be planted because they would never be profitable. The percentage of area planted in maize would always exceed that of soybeans because of price inducements and longer growing seasons under climate change. Although the application here was for long-term climate change, the technique could easily be applied to shorter time-scale climatic events such as individual droughts, prolonged rainy spells, and the like.
The strength of firm-level decision models lies in the explicit structure they provide for estimating decision making under climate risk. They illustrate outcomes when economic agents act perfectly rationally. The greatest shortcoming of the approach is the tendency to optimize decision making for the risk-neutral case (profit maximization). Other views of risk, including noneconomically motivated ones (e.g., preservation of environmental values), may also be on an agent's list of priorities. Lack of empirical validation of the individual structural components of the model is also a problem. Comparison of ex post studies of farmer decision making throughout a period of climate variability with projections from a decision model focusing on the same climate event could greatly enhance the interpretation of such a model.
Computable general equilibrium economic models attempt to simulate the effects of climatic variation on economies by balancing supply and demand so that a new equilibrium state is achieved in the wake of climatic perturbation to resource supplies (e.g., Adams et al., 1990; Kane et al., 1992). These models use optimization procedures that reallocate labor and capital throughout the economy in the face of climate-disrupted supplies of resources until supply and demand balance at a new market-clearing price for affected commodities. Reallocations are deemed to be at a new equilibrium state when producer and consumer surplus are jointly maximized. Economic impacts of climatic variability in computable general equilibrium models are often expressed as changes in prices or in some aggregate economy-wide measure such as net social welfare. Such models have been used widely to estimate the economic impacts of future climate change (Rosenzweig and Parry, 1994; Kane et al., 1992; Adams et al., 1990), but are only now being applied to estimate costs of seasonal-to-interannual climate variability.
Page 108
The main strength of the computable general equilibrium approach is the ability to illustrate the potential economic costs and benefits of climate variability under conditions in which resources are fully allocated throughout the economy (e.g., labor left unemployed by climatic events is reemployed where economically optimal). A major weakness is the inability to estimate how climatic impacts are distributed among different sectors, populations, and regions. Effects of climatic variability on interindustry purchases of inputs and sales of outputs (see discussion of input-output models) are not explicit. And, like the firm-level approaches noted above, the structural elements of computable general equilibrium models are rarely evaluated in light of observed human behavior.
Challenges in Estimating the Impacts of Climate Variability
Considerable attention has been devoted to estimating the effects of climatic variability on ecosystems and society. Food and fiber production has been the subject of most of the recent progress in understanding owing to their great sensitivity to climate. Water resources and energy have received somewhat less attention. The direct effects of climate variability on food, fiber, water, and energy can be analyzed with a high degree of precision and confidence in most developed countries, although knowledge is much more limited with regard to the other links that determine human consequences (see Figure 5-2). The situation is not as good in developing countries due to shortages of scientific infrastructure. Basic knowledge and modeling capacity for other sensitive sectors, including health, industry, transportation, and environmental amenities, are weak. Lack of data is a major hindrance to progress in understanding the effects of climate variability in these less studied sectors (see discussion below). The lack of an identifiable research community dedicated to understanding and predicting the effects of climatic variability in these sectors is a problem everywhere, but especially in developing countries.
Estimating the Value of Climate Forecasts
What Kinds of Benefit Can Climate Forecasts Provide?
As Chapter 4 makes clear, climate forecasts are beneficial only if they provide timely information people can use to modify the actions they take to cope with climatic variations. This information may concern a variety of weather and climatic events about which forecasts can provide useful early warning, including hurricanes and some other major storms, droughts, floods, wildfires, and subtle variations from climatic averages. Some climatic events cannot now be forecast with measurable skill, how-
Page 109
|
ever, and the forecasts that can be skillfully made are not always in the necessary time frame for coping. The information that is useful is specific to the users (see Box 5-2).
Despite these difficulties, climate forecasts have the potential to improve net social welfare across a broad range of activities and sectors and at various scales (households and firms, industries, regions, nations). In principle, skillful climate prediction can improve outcomes in both good years and bad, thus raising the long-term average outcomes for future years above the baseline of the past. Skillful forecasts can help individuals and organizations prepare better both for extreme negative climatic events and for less dramatic but more common climate variations, both negative and positive. Preparedness for the latter climatic variations can be quite valuable because the consequences of nonextreme and positive climatic events can be very large in the aggregate. For example, in addition to the well-publicized damage wrought by the violent storms attributed to the El Niño event of 1997-1998, it also brought significant benefits. These probably include savings in expenses for winter heating throughout the Northeast, lower oil prices, a longer season for the construction industry in many regions, fewer storm- and cold-related deaths in the Northeast, and replenishment of soil moisture on arid agricultural lands in the Southwest. El Niño may also have been responsible for the absence of significant hurricane damage in the Eastern United States during the 1997 hurricane season—an economic savings of $5 billion compared with an average hurricane year (Pielke and Landsea, 1998). Farmers, builders, homeowners, and managers of municipal emergency response operations who took optimal action on the basis of climate forecasts for 1997-1998 would probably have been considerably better off than those who did not.
Page 110
The potential benefits of climate forecasts may take many forms. Generally, individuals and organizations can benefit by planning and preparing for the climatic events that are forecast rather than doing what they usually do, which is to rely on historical average climate and perhaps folk forecasting methods to make their preparations. They may benefit by minimizing the cost of disasters, but also by various ex ante preparations that take advantage of climate-generated opportunities or reduce the costs of preparedness for extreme events that are less likely than usual to occur. In the case of the 1997-1998 El Niño forecasts, the potential value may have included insurance benefits for those in disaster-prone areas who increased their coverage in time, freeing of municipal funds normally used for snow removal in the Northeast, increased income for farmers who hedged against floods or planted winter crops to take advantage of increased soil moisture, and more stable employment for construction workers.
The potential rise of a climate forecasting industry may have value beyond any particular climate forecast. It may expand the service sector that makes forecast information readily available to particular kinds of users, and it may lead to beneficial changes in the coping systems used in weather-sensitive sectors. In short, climate forecasts may bring a variety of kinds of benefits to different kinds of actors. A full catalogue of the possible benefits, such as would be desirable for quantifying them, does not yet exist.
Skillful climate forecasts are not likely to benefit everyone equally, however, and some may even lose. When forecasts influence the way money changes hands, there are bound to be winners and losers. Valuation of forecasts must be sensitive to the full range of costs and benefits from their use.
A Conceptual Approach to Estimating the Value of Forecasts
The value of a climate forecast, like the effects of climate variability, can be conceptualized as a difference between outcomes. The value of a climate forecast can be defined as the difference between the outcomes experienced by actors in weather-sensitive sectors with and without the forecast, or the difference between their outcomes with forecasts of different levels of skill. The value of a forecast might also be estimated by the expenditures made for it: public expenditures for climate forecasting research, mass media time devoted to presenting forecast information, private-sector expenditures on climate forecasts, and so forth. We do not believe such an approach to estimating value would give a meaningful result for climate forecasting at this time, because the enterprise is not yet well enough developed for people to know what they are purchasing, so
Page 111
their expenditures do not provide a reliable proxy for the value of the forecasts. Moreover, one of the reasons for estimating the value of forecasts is as a guide to public policy decisions to invest in improved forecasts in anticipation of their future value.
One might estimate the value of a climate forecast for improving human outcomes by comparing the outcomes actually experienced by actors who have access to a forecast with the outcomes they might have experienced without it; conversely, one might compare the outcomes experienced by actors having no access to a forecast with what their outcomes might have been with the forecast. These two approaches may give systematically different results because estimates of what outcomes might have been can be biased by assumptions about the degree to which recipients make optimal use of forecast information. Glantz (1986) offers examples of situations in which forecast recipients ignored accurate forecasts for understandable reasons. He reports that the Peruvian government kept the anchoveta fishery open in 1972 and again in 1977, overruling the recommendations of Peruvian scientists, because of the extreme dependence of the country on the fishing industry and a wishful hope that elevated sea temperatures would not damage the fishery.
Both methods of estimation compare actual experience with a hypothetical, or counterfactual, situation, and both can conclude that the value of a forecast may be negative as well as positive: people who act on erroneous forecasts and people who choose not to act on accurate ones are often worse off. Thus, like the effects of climate variability, the value of a climate forecast cannot be directly measured. It can only be modeled, based on assumptions for estimating what the outcomes might have been in the counterfactual situation. The modeling task is complicated by the fact that forecasts are probabilistic, so it may make sense to estimate their value across a range of possible realizations.
Current Scientific Capability in Valuing Climate Forecasts
To shed light on the potential usefulness of climate forecasts, basic understanding is needed of how agents perceive the forecasts, the sorts of decisions the forecasts might influence, and the specific attributes required of the forecasts by agents. Such understanding requires data measuring fundamental attributes of both agents who might benefit from forecasts and do and those who might benefit but do not, including information on climate-sensitive decisions, characteristics of decision makers, and affected resource streams. It also requires consideration of the effects of different ways of disseminating forecast information on the responses of different kinds of recipients. Empirical analysis of such issues can provide insights into how decision makers actually use climate forecasts and
Page 112
other uncertain information. Lack of data is a major hindrance to valuing forecasts, as we discuss next. We then review research on the usefulness of climate forecasting in decision making. As above, we divide our review into that research based on observation and that based on assumptions absent observation.
To assess the value of a climate forecast, it is important to understand the kinds of information the forecast provides in relation to the kinds of forecast information that can benefit forecast users. The users, of course, desire information of relevance to their decisions. As Chapter 3 suggests, the information they want is a function of the kind of weather-sensitive activity they are engaged in, the coping strategies they use, the time horizon for decisions, and other particular factors. What they want to know may or may not be possible for climate science to provide from current knowledge, but it is nevertheless worth comparing with the information that is in fact provided (see Box 5-2). The value of a climate forecast depends in part on the extent to which it includes the kinds of information that are relevant to users' decisions and presents that information in ways users understand.
Weather-sensitive activities are sensitive in many ways, and the quality of the data varies greatly. The most detailed data on the costs of events such as floods, storms, and wildfires come from insurance carriers, which collect such data in the course of doing business. However, these data cover only insured costs. In the past five years, the U.S. insurance industry's ability to provide reasonable estimates of insured costs of extreme events has improved dramatically. The industry's data bases of property and property values are extensive, thus allowing predictions of hurricane or extreme weather tracks to be translated into reasonable estimates of property damage. The best source of estimates on insured losses from floods is the Federal Emergency Management Agency, using data on flood insurance coverage and payments for residential structures under the National Flood Insurance Program. Insurance industry sources can and do make estimates of damage associated with extreme events for individual events as well as probable annual losses and currently use this information for rating risks associated with properties as well as for analyzing the financial exposure status of each company. Clearly, improvements in the estimation and prediction of extreme events would improve the overall quality of the industry's estimates.
The availability and quality of similar data in other countries are unknown. It is reasonable to expect, however, much lower data quality for uninsured losses in countries that lack a well-developed property casualty insurance industry or where few people participate in insurance markets. Moreover, as already noted, data on costs and benefits are harder
Page 113
to find when the outcomes result from nonextreme climatic events and when the outcome variables are difficult to quantify.
Social and economic data are widely collected, however, on outcomes that are affected by seasonal-to-interannual climate variation and that might therefore be improved by skillful forecasts. For example, most countries collect data on agricultural production, human morbidity and mortality from various causes, streamflows in important rivers, yields from fishing and lumbering, and various other phenomena that are sensitive to weather and climate. Such data can be used to model the effects of climate variability and the value of forecasts. However, their usefulness for this purpose depends on the extent to which sufficiently long time series are available, data are comparable across time and geographical regions, measurement procedures are constant, and other such factors. There is reason to believe that the data available in many countries on many of these variables fall short of the necessary quality and comparability. However, the extent of this shortfall is not well understood.
Research Based on the Use of Actual Climate Forecasts
Empirical decision studies attempt to shed light on how decision makers actually use (or fail to use) and value forecasts. These studies examine the ways actual forecasts are received, interpreted, and applied, drawing lessons about forecast value from actual experiences. The ledger on such studies is thin, but there are a few deserving of mention here. Stewart (1997) divides empirical studies of forecast use and valuation into the categories of: (1) anecdotal reports and case studies; (2) user surveys; (3) interviews and protocol analysis; and (4) decision experiments. We add a fifth category of empirical modeling studies.
Case studies on the value of climate forecasts are common in government publications (e.g., Aber, 1990) and agricultural cooperative extension circulars. A typical case may recount how farmers used forecasts to improve the efficiency of operations. A grain grower might be interviewed and asked how valuable the forecasts are in managing the crop and may provide a dollar estimate of how much was saved by using the forecast. The problem with such reporting is that the information given is subjective and apt to be unreliable.
Ex post case studies of actual forecasts provide important insights into how decision makers actually apply climate forecasts. Stewart cites a case study by Glantz (1982) of the ramifications of using a faulty streamflow forecast in the Yakima valley in the state of Washington as an example. As previously noted, Glantz detailed the costs in terms of the value of legal claims brought by farmers who, at great cost, had undertaken preemptive actions to avoid loss due to the erroneously forecast
Page 114
water shortage. Though such case studies give some basis for estimating the value of climate forecasts, they do not separate climate forecast-related behavior from behavior that may be determined by other factors.
User surveys ask representative samples of respondents to value climate forecasts (Easterling, 1986; McNew et al., 1991). Hence, they are really studies of the perceived value of such forecasts (Stewart, 1997). Stewart argues that user surveys are reliable instruments for gauging subjective forecast value.
Several investigators have relied on interviews and closely related protocol analysis to gain knowledge about how valuable climate forecasts are to decision makers (e.g., Changnon, 1992; Sonka et al., 1992). Stewart describes these techniques as the characterization of forecast users' decision-making protocols based on extensive interviews. For example, Glantz (1977) interviewed a wide range of decision makers in Sahelian Africa to determine what they said they would have done differently had they had available a perfectly accurate forecast of the recently experienced drought of 1973. He learned that, given the lack of effective possible response strategies, most Sahelian decision makers were skeptical that even a perfect forecast would have caused them to do anything differently. Like most of the other descriptive techniques reviewed above, interviews and protocol analysis lack a compelling experimental design that enables causal relations to be unambiguously defined.
Decision experiments take a gaming approach to eliciting information about the value of forecasts to decision makers. Actual decision makers are asked to participate in the experiments. Participants are presented with detailed forecast scenarios and requested to explain in detail what their actions and thoughts would be under each scenario. A regression model is then developed to ''predict'' participants' hypothetical behavior with respect to forecast use. Sonka et al. (1988) used decision experiments to model the behavior of two managers responsible for production planning in a major seed corn manufacturing company. The main problem with decision experiments is that behavior in actual situations may differ systematically from behavior in the simulation.
Easterling and Mendelsohn (in press) used a Ricardian-based econometric approach to estimate the cross-sectional relationships of climate, agricultural land values, and revenues in the United States. Assuming that this relationship is conditioned by cropping systems that are strongly, though not perfectly, adapted to their local average climatic resources (including variability and frequencies of extreme events), the econometric model provides a baseline from which to quantify imperfect adaptation to widespread climate events marked by extreme departure from historic averages. Easterling and Mendelsohn argue that the revenue differences between the baseline and drought conditions, net of input substitutions
Page 115
and market adjustments, is the theoretical aggregate value of a perfect forecast of drought.
The approach used in this study has been criticized by Antle (1996) and must be viewed in light of fundamental criticisms. It uses reduced-form relationships between climate and aggregate decision making and thus does not make the structural elements of decision making explicit. The approach requires the assumption that the underlying conditions embedded in the reduced-form model, such as agricultural policy, must be assumed to be constant between the period of the data used to generate the model and the period being simulated. It also requires invariance in the model structure over time and space (Schneider, 1997). Moreover, the farmers in each region use coping mechanisms (e.g., hedging against risk, using seeds that are resilient to climatic fluctuations) based on the lack of skillful forecasts; thus, unless they are completely insured, they have lower profits on average than they would if skillful forecasts were available. This last consideration calls into question the validity of the assumption that the baseline condition equates with having a perfect forecast because technologies and other coping mechanisms will be different with better forecasts. For instance, farmers with good forecasts will use seeds that are more sensitive to weather (such as water-dependent varieties if the forecast is for lots of rain).
Despite the criticisms, Easterling and Mendelsohn (in press) illustrate some of the defensible approaches to estimating the value of climate forecasts using the general concept of differences in outcomes. One value of the concept is that it makes possible a distinction between the potential value of a forecast and its actual value: for example, actors who do nothing with forecast information receive no value from it. The concept also allows for the possibility that a skillful forecast can have negative value. This may occur in at least two ways. Actors may do things with the expectation that the forecast average will be realized, but, because of residual error in the forecast, their outcomes might have been better if they had followed normal routines. Or some actors may take advantage of forecast information in ways that benefit them at great cost to others, so that the aggregate value of the forecast is negative.
Simulations of Climate Forecast Value
Johnson and Holt (1997) state that the theoretical basis for valuing forecast information lies in Bayesian decision theory. Bayesian theory treats information as a factor in the decision process to be used by agents to reduce uncertainty. According to Bayesian theory the following assumptions hold: (1) prior to having a forecast available, economic agents have subjective "prior" probability estimates of a set of possible future
Page 116
states of climate based on historical experience; (2) they attach a set of actions to each of the states of climate, and each combination of action and state of climate has a consequence; (3) they have a ranked preference for certain consequences over others that may be expressed in an expected utility function; and (4) climate forecast information is assumed to modify agents' subjective prior probabilities by creating a set of "posterior" probabilities.
The value of the additional information provided by the forecast is based on the expected utility resulting from decisions made after the forecast has been received and before the forecast climate event occurs compared with the expected utility resulting from the decision that would be made at the same time without the forecast information. The agent is faced with choosing from among two optimal choices, one being to choose the optimal action given only prior subjective probabilities and the other being to choose the optimal action given the posterior probabilities.
According to Johnson and Holt (1997), solving the value-of-information problem for individual decision makers in a strictly theoretical sense using the above procedures is relatively straightforward. However, determining the market value of such information is much more difficult for two reasons. First, establishing a market equilibrium condition and understanding how that equilibrium is modified by the introduction of additional information is problematic. Second, aggregating individual responses to construct market-level supply and demand relations necessary for information pricing is equally problematic. A commonly accepted way to deal with these two problems is to adopt the hypothesis of rational expectations—the hypothesis that all individuals possess perfect knowledge of the underlying structure of the market and act on that knowledge accordingly. This opens the way to treat the simple case of an individual decision maker as representative of all decision makers comprising the market. It forms a benchmark of ideal agent behavior against which to evaluate other, less ideal behaviors.
Most applications of Bayesian decision theory to weather and climate forecast valuation are agricultural ones. Wilks (1997) reviewed several such applications. Specific examples include the application of forecasts to the decisions on whether to convert grapes to raisins versus selling them for juice (Lave, 1963); on whether to take steps to protect orchard crops from potential frost damage (Katz et al., 1982); on how much hay to store as feed for the following year (Byerlee and Anderson, 1982); on which crops to plant in the upcoming year (Tice and Clouser, 1982; Adams et al., 1995); and on the amount and timing of fertilizer applications (Mjelde et al., 1988). Examples of applications of climate forecasts to sectors other than agriculture include, in forestry, the decision on how to allocate firefighting resources between two forest fires (Brown and
Page 117
Murphy, 1988) and, in transportation, the decision on how much to invest in snow removal equipment (Howe and Cochrane, 1976).
The two crop choice studies cited above (Tice and Clouser, 1982; Adams et al., 1995) are illustrative of the issues concerning rational expectations raised by Johnson and Holt (1997). Tice and Clouser (1982) examined the use of a seasonal climate forecast by a farmer to determine relative area planted to corn versus soybeans. The forecast was assumed to be perfectly accurate. Two allocations of crops are computed by using historical climatic averages and by using forecast information. The simple arithmetic difference between average net revenues per hectare using climatic averages and that dictated by the forecast was computed. Use of the forecast to allocate areas planted in corn and soybeans was shown to increase revenues by $3.65 per hectare per year beyond revenues using historical climate.
Adams et al. (1995) investigated the use of climate forecasts to determine allocations of areas planted to cotton, corn, sorghum and soybeans in the southeastern United States. The chief difference between their study and that of Tice and Clouser (1982) was that they computed forecast value in terms of total net social welfare (combined producer and consumer surplus) for the nation rather than revenues for the individual farmer. Using a general equilibrium economic model, they computed welfare using forecast-assisted crop allocations under an assumption that all southeastern farmers would plant accordingly. Furthermore, they explicitly considered the case in which forecast accuracy is imperfect. They found that the use of a perfect forecast increased social welfare by $145 to $265 million per year. The use of an imperfect (though still skillful) forecast increased welfare by $96 to $130 million per year.
Several research problems remain unsolved for Bayesian decision theory applications to climate forecasts. These applications do not address how forecast information available in an invariant, and possibly irrelevant, format is made relevant and incorporated into individual decision makers' information requirements, which differ considerably from one decision maker to the next. They do not adequately explore the possibility that decision makers' utility functions are nonlinear. Most applications do not estimate the distributional effects of the use of forecasts (i.e., winners versus losers). Finally, the lack of data and empirical techniques for clearly valuing forecasts precludes the testing of Bayesian models against the real world.
Challenges in Estimating the Value of Forecasts
There remain some significant challenges in applying the general concept of the value of forecasts. One is in addressing the imperfections in
Page 118
existing forecasts and the uncertainty about precisely how skillful they are for specific geographic regions, time horizons, and climate parameters. Part of this challenge is to develop acceptable indicators of the concept of skill. Another challenge is to address users' perceptions of forecast skill, which certainly affect their willingness to act on forecasts and are probably shaped by various factors in addition to forecast skill itself (for example, the most recent forecast's accuracy, trust in the sources of forecast information, nonclimatic events that affect users' outcomes in the forecast period).
Yet another challenge for modeling the value of forecasts is to take into account the ways improved forecast skill may change existing systems for coping with climate variability. Weather-sensitive actors act under the presumption of weather uncertainty, which improved forecasts reduces. Farmers, for example, choose seeds and make capital investments assuming the unpredictability of climate variations. They are likely to use skillful forecasts that arrive with sufficient lead time to invest differently in insurance and in futures markets to increase profitability. They may also shift from planting seed varieties that are tolerant of a variety of climatic conditions—a traditional strategy for coping with unpredictable growing seasons by trading some potential for increased yield for a hedge against disastrous crop failures—to planting more weather-sensitive varieties, to take advantage of the conditions predicted for each growing season.
One might estimate the effects of climate predictability by comparing the profitability and behavior of actors in environments with different natural degrees of climate variation to suggest how they would respond to different levels of predictive skill. It might also be useful to compare farmers facing different average weather characteristics (e.g., rainfall levels) who, because of good insurance mechanisms, took little ex ante action to mitigate risk. This comparison would provide information on the gains from optimal adjustments to predicted changes in weather because it compares farmers in different climate regimes who have set in place the best arrangements for maximizing profits from given average rainfall levels without regard to risk, which perfect forecasts would eliminate.
Ideally, models of the value of climate forecasts should treat coping mechanisms as endogenous variables, to reflect the possibility that improved predictions may induce innovations throughout weather-sensitive sectors of the economy. They may even affect outcomes in a sector by inducing innovation in another sector. For example, better forecasts may affect agriculture not only by changing farmers' strategic behavior, but also by inducing change in the crop insurance and seed industries and even by creating new industries, for example, climate consulting. We are suggesting that the theory of induced innovation be employed in some
Page 119
efforts to model the effects of improved climate forecasts. For summaries of the literature on induced innovation, see Thirtle and Ruttan (1987) and Ruttan (1997).
Several of the challenges that have been mentioned in connection with estimating the effects of climate variability are equally relevant to estimating the value of improved forecasts. One of these is estimating the effects on outcome variables that are hard to quantify. For example, decreasing the amount of uncertainty about next month's or next season's weather may facilitate vacation planning for some people. It may relieve anxiety about possible extreme events—or, depending on the content of the forecast—it may produce anxiety. Improved forecasts will, at least at first, cause people engaged in weather-sensitive activities to rethink their usual methods of coping—a rethinking that may bring long-term benefits but that has short-term costs, at least in time and effort. It may be difficult even to identify all the important nonfinancial effects, and it is always difficult to weigh them against each other and against monetary outcomes.
It is also important but difficult for models to disaggregate the estimates of net value and to consider the distributional effects of improved forecasts. Models should address the likelihood that some groups may benefit from improved forecasts at the expense of others. We have already noted some of the possibilities, such as that commodities speculators, farmers, and consumers are to some extent competitors in how they use forecasts. There is also the possibility revealed by the experience of the Green Revolution—that to the extent that there are fixed costs of interpreting forecast information, larger operators will benefit more by spreading those costs over a larger output, leaving smaller and less economically successful operators at a relative disadvantage. It is important to estimate the value of climate forecasts both throughout entire economies and disaggregated by sector, region, and type of actor.
Addressing many of the challenges alluded to above is made difficult by a glaring lack of appropriate data sets. Long-time-scale, comprehensive data sets archived at appropriate geographic scales (household/firm, local, regional, national) are nonexistent or not readily accessible to the broader research community. Data on particular attributes are often of dubious quality and not comparable over space and time. Moreover, there is no general agreement about which data are most important to collect for the purposes of estimating the effects of climate variations or the value of forecasts.
Because the quality of the relevant data is probably far short of what is needed for good analysis, it is important to set priorities for improving the data base. In doing this, it makes sense to consider at least these factors:
Page 120
|
Finally, it is important to begin to calculate all social costs in valuing forecasts. The true net value of a forecast is not only its worth to an individual actor or set of actors; it also includes the costs to society of its development and dissemination to actors, including the costs of incorrect forecasts. In addition, the value of the entire forecasting enterprise may be different from the sum of the value of individual forecasts because public reactions to some forecasts, such as early and well-publicized ones, may affect the response to subsequent forecasts. Estimating the value of forecasting within a systems approach is fraught with complications and uncertainties, such as how to properly weight and value the opportunity costs of investing in the development of forecasts and how to estimate the effect of one forecast on the use of future ones. Such challenges must be confronted before such a systems approach will be feasible.
Findings
Scientific capability to measure and model the effects of seasonal-to-interannual climatic variability is well developed in some sectors (e.g., agriculture, water resources) and only beginning to be developed in others (e.g., human health, environmental amenities). Scientific capability to judge the value of climate forecasts is in its infancy. The ability to predict the ways people cope with climatic variability, with or without a climate
Page 121
forecast, is limited by a number of factors, including lack of data on the factors affecting decision making. The state of the science of impacts of climatic variability and the value of climate forecasts can be summarized in terms of these findings:
|
|||||||||
Page 122
|
|||||||||||||||||||||||||||
Page 123
|
||||||





























