Appendix C
Accounting for Forest Assets
While adjustment in an asset account is conceptually similar to net investment of ''made assets," it is more precise for forests to call the change in asset values "net accumulation" to reflect the fact that, even at constant prices, the asset value of a forest can either increase or decrease. Most generally, net accumulation is defined 1 as
where N(t) is the net accumulation in period t, and V(t) is the asset value in period t (present value of rents). As Hartwick and Hagemann (1993) have shown, net accumulation can also be written as:
where r = discount rate (or the difference between the nominal interest rate and the rate of growth of log prices, p is the price of logs, q(t) is the harvest level in period t, and C[q(t)] is total extraction costs. While these definitions are both general and precise, they are generally impossible to implement empirically: V(t + 1) cannot be directly observed in period t.
Instead, economists infer the value of the asset from assumptions about intertemporal market equilibrium. Three cases have been examined.
The first is identical to the literature on nonrenewable resources, appropriately treating the exploitation of primary, old-growth forests as timber mining. Since it is generally uneconomic to replace primary forests with forests of a similarly old age, this analogy is not as odd as it might seem. Under these circumstances,
where C'[q(t)] is marginal extraction costs. This model of net accumulation (pure depreciation) is generally called the Hotelling model to emphasize the connection between mining old growth that will not be replaced and mining minerals that cannot be replaced.
While the Hotelling model may be appropriate for the case of pure depreciation, it misses several important aspects of the forest sector. An alternative approach is transition models, which account in part for these problems by recognizing that forest growth offsets harvests. Assuming constant prices and a forest inventory recognized only by total net growth, this model suggests that net accumulation is
where g(t) is the net forest growth in period t.
By recognizing forest growth, such a formulation improves on the ordinary Hotelling approach, but still suffers the defects of (1) ignoring endogenous price changes in the sector and (2) characterizing the forest only by net growth and not its more complex underlying age-class structure. Economic theory suggests that once the transition between old- and second-growth forests is complete, timber prices will stabilize and the economic return to holding forests will arise solely from forest growth. Vincent (1997) has developed the appropriate measures of net accumulation for optimally managed second-growth forests. Depreciation associated with the harvests equals
where h is values per unit area, v(τ) is the timber yield at age τ, and τ* is the economically optimal rotation age. Accumulation associated with the growth of subrotation-age forests is
Net accumulation is simply the sum of unit-area depreciation or accumulation weighted by the area in the particular age class:
where A(t,τ) is the area in age-class τ in period t. Note that if A(t,τ) = ΣA(τ)/τ* for all τ (the so-called "normal forest" with an equal area in each age class), then N(t) = 0. This approach improves upon both the Hotelling and transition approaches. It assumes that forest owners cut their trees at the economically optimal time and that timber prices are in intertemporal market equilibrium.
The three cases discussed above require assumptions of intertemporal price equilibrium, optimal management, and constant prices and costs. These are strong assumptions. With the data that exist for U.S. forests, it is possible to develop a practical approach for measuring timber accumulation that improves upon the methods used in most countries and requires less restrictive assumptions.
Ideally, one would like transaction data on a representative sample of timberland. Because timberland is an extremely heterogenous product traded in dispersed markets, assembling such data is quite difficult. 2 It is therefore necessary to compute V(t) and V(t + 1) directly and to estimate net accumulation using equation (C.1). One possible approach, following Vincent (1997), begins by summing per-acre values weighted by area across all age classes (subscripts for other important value descriptors, such as region, ownership, species, and site quality, are suppressed for ease of reading).
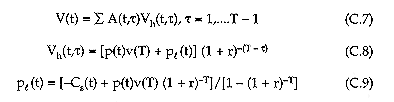
where T is actual cutting age, p(t) is net price (stumpage price), pl (t) is bare-land value, and Cs(t) is full rotation management costs in period t.
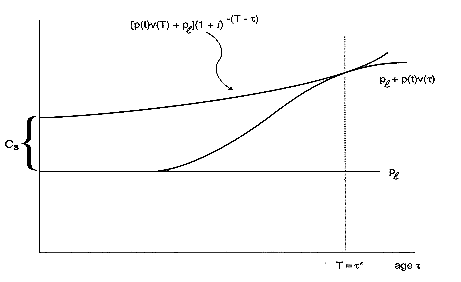
Figure C-1
Valuation of Forest Stands of Differing Ages.
The above are the basic valuation equations for forests of different age classes. Figure C-1 shows the approach graphically. The value of an acre of age-class τ timber is simply the value of the timber at the harvest age T (which may or may not be the economically optimal harvest age), discounted by the number of years until harvest. Note that p(t) in this formulation is net price, not price gross of extraction costs. This definition is used because the net price (called the stumpage price) is commonly recorded in forestry. While net prices differ across regions and among species, some evidence suggests that within a region, extraction costs may be constant (Adams, 1997). In this formulation, net rent = A(t,T)v(T)p(t) and is already accounted for in the National Income and Product Accounts for marketed timber. If desired, net accumulation can be divided into separate revaluation, growth, and depletion accounts in the usual way.
How would such an approach be implemented? The forest inventory and analysis work of the U.S. Department of Agriculture's Forest Service maintains data on A(t,τ), v(τ), T, and Cs(t) by eight regions in the United States, ownership, and site quality; unfortunately, the data on the national forests are not as comprehensive as those on private and other public lands. The Forest Service's ATLAS model is designed to update the inventory on an annual basis and to project it into the future. Data on p(t) by region and species (or species group) are available from the Forest
Service (the value of timber harvested in a year, or so called "cut prices") and from commercial price reports for some regions.
The primary difficulty with this valuation approach is selecting the discount rate (r) to be used. Similar difficulties arise in minerals accounting when the net present value approach is introduced. No valuation method escapes this difficulty, except with strong and unrealistic assumptions about intertemporal price paths. A practical approach is to reestimate the discount rate periodically on the basis of an asset pricing model for timberland. The discount rate is then treated in the same manner as timber prices, with a separate revaluation account to reflect changes in the discount rate.





