Page 168
4
Nonequilibrium Physics
The term ''nonequilibrium physics'' means "the study of physical systems that are not in mechanical and thermal equilibrium with their surroundings." In some cases, these are systems spontaneously approaching equilibrium, such as a molten metallic alloy being allowed to cool and solidify. In other cases, they are systems changing their shapes or properties as forces are exerted on them, heat applied to them, or their states of repose are otherwise disturbed. Examples include flowing fluids driven by thermal or pressure gradients, solid materials deforming or breaking under the influence of external stresses, or quantum systems—atomic spins, perhaps—being driven by oscillating electromagnetic fields.
As a field of research, nonequilibrium physics is simultaneously very new and very old. The natural origins of complex patterns such as dendritic snowflakes or chaotic motions such as those of turbulent fluids have puzzled human beings since the dawn of history, but it is only in the last decade or so that we have begun to understand these phenomena in any depth. This field is also simultaneously very pure and very applied. The processes used to produce industrial materials—for example, casting alloys for jet engines or fabricating microscopically small features of computer chips—are all applications of nonequilibrium physics. In many cases, however, the fundamental research needed to predict and control these processes with the precision necessary for advanced technologies has yet to be done.
It is in this area of research, also, that condensed-matter and materials physics interact especially strongly with other scientific disciplines. Nonequilibrium physics is inherently interdisciplinary. It has involved engineers, mathematicians, and chemists in addition to physicists since it emerged as a recognized
Page 169
specialty about a generation ago. In recent years, the same nonequilibrium concepts being tested in the design of alloys are also being applied to galaxy formation in the cosmos, climatic changes on the Earth, and the growth of forms in biological systems.
The Brinkman report1 was remarkably prescient in its discussion of nonequilibrium physics. Its authors recognized the growing importance of topics such as pattern formation, chaotic behavior, turbulence, and fractal geometries. Understandably, they missed today's emerging interests in friction, fracture, and granular materials and the speculations that some of these spatially extended chaotic phenomena might be exhibiting previously unanticipated collective behaviors. They also could not have predicted the invention of the scanning-probe microscopes and optical tweezers that are only just now beginning to open the world of biological phenomena to first-principles physical investigations.
In the last decade or so—the period since the Brinkman report—important progress has been made in many of these areas. We now understand in much more systematic ways how complex patterns emerge from simple ingredients in hydrodynamic, metallurgical, and chemical systems. Notable progress has been made in sorting out the mechanisms that control pattern formation, for example, in convecting liquid crystals, on the surfaces of vibrating fluids, in chemical reaction-diffusion systems, and in some biological phenomena such as cellular aggregation and membrane morphology. New understanding of spiral waves in active media has found application in the analysis of cardiac arrhythmia. We are beginning to understand how complex systems—for example, those in which fluid flow and chemical reactions are occurring simultaneously—sometimes become intrinsically self-organized, sometimes exhibit large critical fluctuations, sometimes become chaotic, and sometimes do all three of those things at the same time.
Nonequilibrium physics has grown into a major enterprise, one that cannot be described fully in this report. The committee has therefore selected a special set of topics as illustrative examples of the themes and issues to emphasize. The first of these topics is pattern formation and turbulence in fluid flow. The next two are in the areas of processing and performance of structural materials, specifically, microstructural pattern formation in solidification and a group of topics in solid mechanics: friction, fracture, granular materials, and polymers and adhesives. The final section includes some brief remarks about nonequilibrium phenomena in biology and in the quantum domain. Each of these topics, in different ways, illustrates the four themes listed below:
1. Much of the most important progress in recent years has consisted simply of recognizing that fundamental questions remain unanswered in the physics of
1National Research Council [W.F. Brinkman, study chair], Physics Through the 1990s, National Academy Press, Washington, D.C. (1986).
Page 170
familiar situations. We regularly see turbulent fluids in the atmosphere and in our kitchen sinks, as well as in a wide variety of less obvious but equally important engineering applications. Snowflake-like solidification patterns are familiar to us and are even more common than most of us realize because they occur on microscopic scales within most structural metals and alloys. We deal with friction, fracture, and the mechanical performance of solid materials in essentially every action that we take in our daily lives. Yet, as we shall point out in this chapter, our basic scientific understanding of these phenomena remains incomplete and is inadequate for many practical purposes.
2. Nonequilibrium systems that form patterns or exhibit complex, perhaps chaotic, behaviors are especially sensitive to small perturbations; thus their detailed behavior may be extremely difficult to predict or control. As a general rule, complex patterns form in simple systems when they undergo instabilities. For example, smoothly flowing fluids become turbulent, or smooth solidification fronts sprout branches. In a technical sense, the term "instability" is synonymous with extreme sensitivity; a system is said to be "unstable" when it requires only an infinitesimally small perturbation to cause a qualitative change in its behavior. Turbulent eddies and dendritic branches are triggered by tiny fluctuations in their surroundings, and their subsequent development is also controlled sensitively by those fluctuations. It is in this sense that the properties of these systems are often extremely difficult to predict. One of the biggest challenges to condensed-matter and materials physics in the next decade may be to understand the intrinsic limitations, if any, on the quantitative scientific analysis of such phenomena.
3. Progress in nonequilibrium physics will depend in many cases on our ability to bridge length scales and timescales. For example, solidification is controlled both by mechanisms of molecular attachment at crystal surfaces and by heat diffusion across large ingots. Fracture is controlled both by breaking of molecular bonds at crack tips and by the macroscopic flow of elastic energy in solids. In general, we need to understand the interrelations between phenomena at scales ranging from atomic and molecular all the way up to fully macroscopic.
4. Progress in nonequilibrium physics, as in all of condensed-matter and materials physics, will depend on our ability to bridge cultures. We shall have to understand the importance of, and the impediments facing, our efforts to bring new science to bear on technology and to take advantage of new technologies to advance basic science.
Pattern Formation And Turbulence In Fluid Dynamics
Nonequilibrium Phenomena in Fluids
When a fluid system is driven far from mechanical or thermodynamic equilibrium, it has a spontaneous tendency to form patterns and defects. Some examples are the spiral waves and ordered oscillations in reaction-diffusion sys-
Page 171
tems; rolls, hexagons, and plumes in thermal convection of fluid layers; turbulent "spots" in the transition from the laminar state to turbulence in a boundary layer; and large-scale circulation patterns in the atmosphere. It is likely that, at least to some extent, living organisms are the result of this tendency for nonequilibrium systems to self-organize. This pattern-forming tendency owes its existence to nonlinearities that dominate the dynamics under conditions of strong forcing.
Although patterns found in nonequilibrium systems are varied in character and combine an astonishing labyrinth of order and disorder, they do share some common features. For example, the details of pattern formation are generally sensitive to small perturbations. In small systems, boundary conditions determine the positions and orientations of patterns. The nonlinearities in pattern-forming systems often produce intermittency; that is, such systems may undergo irregular, large excursions away from their most probable states.
It is only natural, then, to think that these common features might imply a deeper layer of truth, and that there might exist a general theory of nonequilibrium phenomena. Such a theory, if it exists, is still outside our reach; but we have made substantial progress in developing special theories for some particularly simple cases. Examples include liquid-crystal hydrodynamics, Rayleigh-Benard convection, Taylor-Couette flow, and fully developed turbulence in boundary layers. The main advantage of studying simple-fluid systems, as opposed to more complex-fluid systems such as those used in industrial processes, is that the laws of motion for the simple fluids are well known. If there exist common underlying principles, they will be most easily discovered in simpler systems. Specific examples will continue to provide useful insights, and the methods of analysis that they generate will find broad utility. What is unclear is whether a deep general theory will emerge from the knowledge acquired by studying special systems; whether nonequilibrium phenomena, like thermodynamic critical phenomena, fall into a small number of universality classes; and whether a broad-based understanding will eventually enable us to predict and control complex, technologically important processes.
Pattern Formation
Consider the simple case of Rayleigh-Benard convection. When a fluid, initially at rest between two horizontal plates, is heated from below, it experiences a temperature gradient. For small gradients, the heat transfer from the bottom to the top occurs purely by conduction—that is, by molecular collisions. When the gradient exceeds a certain threshold, however, the conductive state becomes unstable and yields to convective states involving bulk motion of the fluid. If the system is confined so that the fluctuations are correlated across the entire system, or if the system is modulated externally, the convective dynamics is largely temporal rather than spatial in character; one then observes a variety of universal properties associated with temporal chaos of low-dimensional systems.
Page 172
Universality here pertains to quantitatively identical dynamics in apparently dissimilar systems.
Most systems are loosely confined, or unconfined for all practical purposes, and so the dynamics has a strong spatial complexion. This appears in the form of cellular structures such as squares, hexagons, rolls, and traveling waves whose properties depend on features such as boundary conditions or the strength of the forcing. In principle, these features of "collective behavior" are fully described by the Navier-Stokes equations. Unfortunately, the latter are rather complex and cannot be used directly for studying the conformation and dynamics of patterns. Much recent progress has come via the study of relatively simple, so-called "amplitude equations" that accurately approximate the full Navier-Stokes equations near the onset of instability where the nonlinearity is weak.
The amplitude equations are closely related to the Ginzburg-Landau equations that describe the behavior of order parameters in transitions from one state to another. They have been used successfully to describe major features of pattern formation, including defects, that occur in weakly nonlinear regimes. For systems where the initial instability is a traveling wave, as in binary mixtures, the dynamics can be described by means of the complex Ginzburg-Landau equation. This equation is rich in character; features such as "defect mediated turbulence" also appear to be contained in it. However, not all of its facets have yet been explored. Other complexities arise in spatially extended systems where, for example, the phases of the patterns may vary slowly in time and space. Equations for this kind of dynamics have been written and their outcome verified for special cases where the basic patterns are known and their shapes do not change. Again, much work remains to be done.
One of the grand unifying principles in equilibrium statistical mechanics is the minimization of free energy. Much thought has been expended on possible analogies in nonequilibrium phenomena. Although a suitable integral of the amplitude function and its gradient serves as an approximate free energy in some cases, this is not a viable procedure in general. A class of pattern formation problems that has not been fully explored is the nucleation and growth of turbulent "spots" in boundary layers (or "slugs" and "puffs" in pipe and channel flows). A spot is a compact object of well-defined shape; it moves in the flow direction at a specific speed; the flow within the spot is turbulent; and the distinction between its inside and outside is generally unambiguous. The spot preserves its characteristic shape as it grows, and the growth rate increases as the Reynolds number (a measure of the flow strength) grows beyond a critical value. A suitably defined length scale seems to diverge at the critical Reynolds number. Although there is a random element to the initiation of the spot in space and time, morphological characteristics such as its shape and growth rates seem universal. These and some other facets of turbulent spots bear superficial resemblance to critical phenomena and to growth processes like diffusion-limited aggregation or directed percolation. How to bring these similarities to bear quantitatively on the
Page 173
formation of spots has eluded us so far. Although there is a large body of engineering literature on this problem, very little of it is motivated by the more general considerations of nonequilibrium physics.
Turbulence
More complexities develop as one increases the stress applied to a fluid system at its boundaries, for example, by increasing the heat flux or the shear rate. ("Increasing the stress" means increasing the Reynolds number.) Among the complexities are the decay of the long-range order of the patterns, the development of new length scales, and the appearance of a strong flux of energy across the range of length scales (the "inertial range") on which turbulent motion is occurring. The scale range increases with the Reynolds number and is bounded, on the one hand, by the characteristic size of the system (the "large scale") and, on the other, by the small "dissipation scale'' at which viscous effects become dominant. The flow is said to be fully turbulent when the scale range is large.
Well-developed turbulence has some interesting and important features. A tracer substance such as a dye, when injected into a turbulent flow, is mixed efficiently and diffused at unusually high rates; isosurfaces of the dye concentration are fractal; the small scales are spatially intermittent and amenable to multifractal description and modeling; correlations and fluctuations are anomalously large; and externally imposed perturbations decay slowly. These features are characteristic of phenomena far from equilibrium.
A quantitative theory of turbulence is likely to be valuable in the study of other nonequilibrium phenomena. This is why turbulence merits some attention and discussion here; indeed, until the 1960s, fluid turbulence was the clearest example of a phenomenon in which a large range of length scales are simultaneously important (see Box 4.1). The successful application of scaling, universality, and renormalization group theory to thermodynamic critical phenomena has altered this situation, but turbulence still offers one of the cleanest examples of scaling behavior in nonequilibrium physics.
Physicists generally like to focus on "universal" aspects of the phenomena they are studying. The conventional wisdom in turbulence theory is that small-scale turbulence possesses universal properties that are independent of specific large-scale flows. However, the notion of absolute universality, initiated brilliantly by Kolmogorov and others, is not strictly valid for turbulence, let alone for all nonequilibrium systems. Universality may pertain, at best, only to certain scaling exponents. The universality of scaling exponents is a compelling notion-one that clearly invites comparisons with other nonequilibrium problems—and principal questions regarding them are just beginning to be resolved. There are lingering impediments. For example, at present there is no theory in turbulence for effects of finite Reynolds number or finite shear. Despite advances in modern experimental methods, properties of turbulence continue to be probed
Page 174
| BOX 4.1 Length Scales in a Turbulent Jet |
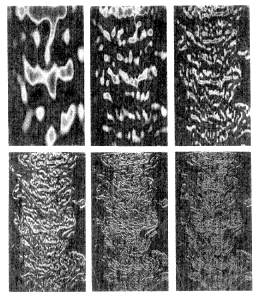
| Figure 4.1.1 illustrates one essential feature of turbulent flows—namely, the coexistence of many superimposed length scales. The present example is a turbulent jet in which a small amount of fluorescent dye has been mixed. The dye concentration has been mapped by the so-called "laser-induced fluorescence" technique. Different scales of the dye concentration field have been extracted by convolving the data with wavelets of different sizes. That is, from top left to bottom right, we see pictures of the same flow pattern in which the size of the features being resolved has been reduced by a factor of 2 from frame to frame. Note that, the smaller the structure, the more string-like it becomes. There is no apparent self-similarity and, in contrast to earlier ideas, individual structures do not become more isotropic at smaller length scales. Note, however, that the anisotropy of individual structures does not necessarily preclude statistical isotropy. |
| The jet shown here has a Reynolds number of about 4000. This is rather low, and so the scale range is not large. In Earth's atmosphere at a height of 30 m, the scale range is about 105, yielding 1015 degrees of freedom in three dimensions. If the equations of motion are to be solved explicitly on a computer, the memory requirements grow roughly as the cube of the Reynolds number. This feature limits the Reynolds numbers at which turbulent solutions can be obtained by numerical techniques. There are also inherent complications such as sensitivity to initial conditions, but the statistical averages are believed to be independent of them. |
|
|
| Figure 4.1.1 |
Page 175
only partially at high Reynolds numbers, and quantities of theoretical interest can be measured only approximately. A major advance in this regard is the use of powerful computers to solve the equations of motion explicitly and thus elucidate spatio-temporal details of turbulent solutions. The Reynolds numbers of the numerical solutions are approaching the range of interest for addressing important issues.
An interesting question is whether the coherence of the small-scale motion, in the form of elongated and anisotropic vortex structures, is consistent with the universal scaling presumed to exist in fully developed turbulence. In an anisotropic ferromagnet near its critical point, for example, the critical indices do not depend on the magnitude of the anisotropy (although they are different for isotropic and anisotropic cases). In turbulence, however, the critical indices may, in some instances, depend on the magnitude of the anisotropy. The relation between scaling, which emphasizes the sameness of various scales, and structure, which becomes better defined and topologically more anisotropic for larger amplitudes, is at present quite obscure.
In summary, the issues considered here are the changes occurring in a fluid flow that is increasingly stressed at its boundary. The stresses may be applied by mechanical, thermal, or other means. The changes include instabilities, bifurcations, temporal chaos, pattern formation, phase modulations, defects, growth of localized structures, interactions among dissimilar length scales and timescales, universal and anomalous scaling, intermittency, anomalous transport, and the like. These phenomena have strong similarities to those that are seen in other nonequilibrium systems. If these similarities can be exploited intelligently, there will be many new opportunities for understanding turbulence better. Conversely, turbulence poses a rich variety of problems and has an array of tools of analysis that should be useful to other branches of nonequilibrium physics.
Fluid turbulence is a difficult problem with a long history, but the pace of progress has accelerated in recent years. Much of the recent progress is the result of a powerful combination of modem experimental methods, computer simulations, and analytical advances. The present picture of turbulence is generally self-consistent despite lingering uncertainties, and recent advances have further improved our qualitative and quantitative understanding. That the qualitative understanding should impact practical and industrial problems is substantially an article of faith; much remains to be bridged between the fundamental developments of recent years and practical problems of industrial relevance. To some extent, this is a problem of bridging cultures. To a larger extent, however, this is a reflection of the difficulties of strongly nonlinear problems that occur far from equilibrium.
What matters in turbulence is the ability to quantify properly the mix of the universal and system-specific aspects and to describe that mix economically. Such an understanding will propel forward not merely the study of fluid turbulence but the entire subject of nonequilibrium physics.
Page 176
Processing And Performance Of Structural Materials: Metallurgical Microstructures
The nature of nonequilibrium physics in condensed-matter and materials physics—its intellectual vitality, its technological potential, and some of the difficulties it faces—is concisely illustrated by the history of our understanding of dendritic solidification patterns and their relevance to the microstructural properties of metallic alloys. In more familiar terms, this is the "snowflake" problem. Only in the past few years have we finally learned how these elegant dendritic crystals emerge literally out of thin air, and why they occur with such diversity that no two seem to be exactly alike.
Much of the research on dendritic crystal growth has been driven not only by our natural curiosity about such phenomena, but also by the need to understand and control metallurgical microstructures. The interior of a grain of a freshly solidified alloy, when viewed under a microscope, often looks like a collection of overly ambitious snowflakes. Each grain is formed by a dendritic (tree-like) process in which a crystal of the primary composition grows out rapidly in a cascade of branches and sidebranches, leaving solute-rich melt to solidify more slowly in the interstices. The speed at which the dendrites grow and the regularity and spacing of their sidebranches determine the observed microstructure which, in turn, governs many of the properties of the solidified material such as its mechanical strength and its response to heating and deformation.
One logical and possibly realistic goal for research in this area might be the development of quantitative methods for predicting the metallurgical microstructures that emerge in the processing of industrial materials. An especially important class of examples includes the materials used for high-temperature applications such as gas turbines and jet engines. It would be useful to be able to develop predictive models for forging turbine disks, or for casting complex shapes such as turbine blades, or for the vapor deposition processes used to apply thermal barrier coatings to those blades. In principle, industrial laboratories could benefit greatly if they were able to design such processes cheaply and quickly by computer rather than by expensive, time-consuming trial-and-error methods. We now have in hand some of the conceptual bases for such calculations, and our computational capabilities continue to grow exponentially. Let us ask, therefore, what will be needed—what new experiments, new theory, new mathematics—in order to write usefully predictive computer codes to design and control such manufacturing processes.
Because many of these processes involve dendritic crystal growth, we know that one starting point must be an understanding of the dynamics of isolated, freely growing dendrites. Box 4.2 describes some of the remarkable progress made in the last few years. The free-dendrite problem is most easily defined by reference to the xenon dendrite shown in the figure in Box 4.2, a pure single crystal growing into its liquid phase. The speed at which the tip advances, the radius of curvature of the tip, and the way in which the sidebranches emerge
Page 177
behind the tip are all determined uniquely by the degree of undercooling—that is, by the degree to which the liquid is colder than its freezing temperature. The question is, How? (An equivalent problem is one in which the dendritic behavior is controlled not by the temperature but by the degree of chemical supersaturation.)
As described in Box 4.2, a rich understanding of the behavior of isolated dendrites has been found in theories of morphological instability and the discovery that very weak forces—crystalline anisotropy of surface energies, for example, or even atomic-scale thermal fluctuations in some cases—an completely control the patterns that emerge from these instabilities. These new conceptual developments, however, still leave us very far from being able to predict metallurgically relevant microstructures. Current simulations of casting, for example, include heat flow and fluid convection in complex geometries but succeed in only very rudimentary ways in coupling those effects to the formation of dendritic microstructures.
Perhaps the most important theoretical challenge is a quantitative understanding of what is called the "mushy zone"—the region between the fully formed solid and the molten fluid where the dendrites are forming and interacting among themselves. Within this region, the thermal, chemical, and hydrodynamic degrees of freedom of the system are all active. Even if each dendrite is behaving according to the rules already discovered, it is doing so in an environment where the local growth conditions are determined by its neighboring dendrites and their associated diffusion and flow fields. This behavior is almost certainly chaotic, and therefore most likely will have to be described in probabilistic rather than deterministic terms. We know that the mushy zone has its own collective instabilities that can produce fatal structural defects in the solidified materials.
The situation in the real world is even more complicated. In many casting processes, new dendrites nucleate at impurities throughout the molten fluid as it cools. Thus these processes are highly sensitive to the purity of the materials. Moreover, heterogeneous nucleation of this kind is extremely difficult to predict or control, even under ideal conditions. Other complications arise from the fact that, in welding, for example, the molten fluid itself is turbulent.
Can such behavior be modeled in a usefully predictive way? Can the relevant dynamics be described with sufficient accuracy by some coarse-grained, many-dendrite theory; or will there be such sensitivity to details and such a huge variety of possibilities that this problem will forever be beyond our reach? And even if we can make substantial progress, will we be able to translate our theoretical understanding into decision-making tools that will be applicable to real-life manufacturing?
These questions regarding intrinsic limits of predictability are unavoidable. Nevertheless, we should be able to do better than we can at present. We already know enough about these systems to recognize that a coordinated experimental
Page 178
| BOX 4.2 The Free Dendrite Problem |
| Under most metallurgical processing situations, dendritic growth is controlled by diffusion—either the diffusion of latent heat away from the growing solidification front or the diffusion of chemical constituents toward and away from that front. These diffusion effects very often lead to shape instabilities; small bumps grow out into fingers because, like lightning rods, they concentrate the diffusive fluxes ahead of them and therefore grow out more rapidly than a flat surface. The key to understanding pattern formation in such situations is understanding the nature of these instabilities. |
| Today's prevailing theory of free dendrites is generally known as the ''solvability theory" because it relates the determination of dendritic behavior to the question of whether there exists a sensible solution for a certain diffusion-related equation that contains a singular perturbation. The term "singular" means that the perturbation, in this case the surface tension at the solidification front, completely changes the mathematical nature of the problem whenever it appears, no matter how infinitesimally weak it might be. |
| This theory has been worked out in detail for many relevant situations, such as the xenon dendrite shown here (Figure 4.2.1). It predicts how pattern selection is determined, not just by the surface tension (itself a very small correction in the diffusion equations), but by the crystalline anisotropy of the surface tension—an even weaker perturbation in this case. It further predicts that the sidebranches are produced by secondary instabilities near the tip that are triggered by thermal noise and amplified in special ways as they grow out along the sides of the primary dendrite. The latter prediction is especially remarkable because it relates macroscopic features—sidebranches with spacings on the order of tens of microns—to molecular fluctuations whose characteristic sizes are on the order of nanometers. |
| Each of those predictions has been tested in the xenon experiment, quantitatively and with no adjustable fitting parameters. They have also been checked in less detail in experiments using other metallurgical analog materials. In addition, |
(Box continued on next page)
and theoretical investigation of mushy-zone dynamics in relatively simple situations would yield useful new information.
Yet here is another example of today's widening gap between fundamental research and applied technology in the United States. Few if any materials manufacturing companies in this country continue to support research in this area, and most no longer even maintain technical staffs that could take advantage of new developments. Some serious efforts are being made at governmentsupported laboratories to remedy this situation, but the university-industry-government consortia that exist in Europe and Asia do not exist here at present.
Processing And Performance Of Structural Materials: Solid Mechanics
Solid mechanics, by necessity, has been a very well studied part of engineering and the applied sciences. We depend on experts in this field to design
Page 179
(Box continued from previous page)
| the theory has been checked in numerical studies that have probed its nontrivial mathematical aspects. As a result, although we know that there must be other cases (competing thermal and chemical effects, for example, or cases where the anisotropy is large enough that it induces faceting), we now have reason to feel confident that we understand at least some of the basic principles correctly. |
|
|
| Figure 4.2.1 /Xenon dendrite (Courtesy of ETH, Switzerland.) |
structures—buildings, automobiles, airplanes, connections in electronic devices, and so on—that will be strong, safe, and reliable.
Although some of the basic principles of modem solid mechanics were established by physicists (for example, the dislocation theory of plastic deformation in crystals), the field has developed largely outside of mainstream physics throughout the last half of the twentieth century. The experts in solid mechanics have been engineers, applied mathematicians, materials scientists, geologists, and so on, but seldom physicists.
That situation is changing. In just the last few years, there has been a healthy revival of interest in this area within the physics community, and interdisciplinary activities have been expanding. Perhaps the most important reason for this change is that many of the most challenging modem problems in solid mechanics involve nonequilibrium phenomena and therefore pose novel fundamental questions. Another important reason is that, for the first time in history, we have the experimental and computational tools needed to answer those questions.
Page 180
Brittle and Ductile Solids
As an introduction to some of these issues, consider the distinction between brittle and ductile solids. A brittle solid breaks when enough stress is applied to it, whereas a ductile material deforms plastically. Remarkably, we do not yet have a truly fundamental understanding of the distinctions between these two behaviors; we do not even have a sharp definition of "brittleness" and "ductility." The conventional theory says that dislocations form and move more easily through ductile materials than brittle ones, thus allowing deformations to occur in one case and fracture in the other. But this picture is incomplete and far too simple.
One difficulty in the standard picture emerges when we realize that all solids deform plastically under very high stresses, such as those in the neighborhood of a crack tip. Those stresses, by definition, must be high enough to break the bonds between neighboring molecules; thus they ought to be high enough to rearrange the molecules and thus cause plastic deformations that blunt the tip or limit the stresses in its neighborhood. How, then, can cracks propagate through any material? Do some materials spontaneously harden in regions of concentrated stress? If so, why? Or might they sometimes fail to deform plastically if the stresses change too rapidly? These are fundamental nonequilibrium questions that lie at the very heart of solid mechanics.
Another equally fundamental difficulty is that the concept of "dislocation" is meaningful only for crystalline solids; but noncrystalline materials such as glasses and amorphous metals can also be brittle or ductile. What is happening in such systems? Materials scientists have speculated for many years about an amorphous analog of dislocation motion, but we do not yet have a clear idea of what that might be, and we are very far from being able to describe such mechanisms quantitatively.
In fact, we still have no satisfactory understanding of the equilibrium properties of the glassy state; we do not even know whether it makes sense to use the term "thermodynamic equilibrium" for such systems (see Box 4.3). Perhaps glassy materials exist only as long-lived metastable or unstable states. If so, where do they fit into our classification of solid-like materials? What language do we use to describe their properties? Questions of this kind will become even more urgent and difficult when, later in this chapter, we talk about granular materials, biomaterials, materials in constrained geometries, or a variety of other states of matter whose unconventional mechanical properties have yet to be explored and understood.
Instabilities in Dynamic Fracture
The field of fracture mechanics is among the most elegant and important in all of the engineering sciences. In the last several decades, its practitioners have developed powerful mathematical theorems and numerical algorithms that permit
Page 181
| BOX 4.3 Glassy States of Matter |
| It is quite remarkable that, despite literally centuries of scientific study, we still do not have a fundamental understanding of glassy states of matter. This gap in our knowledge looks even more remarkable when we realize that the category of glassy materials—i.e., amorphous, noncrystalline solids, includes a very large fraction of the substances that we encounter in everyday life. It includes window glass, of course, and metallic glasses; and it includes many polymeric materials. Indeed, very many simple substances—even ice—can exist with great stability in glassy states. Condensed-matter physicists accurately use the term "glass" to describe yet other strongly disordered systems. For example, "spin glasses" are magnetic systems in which the interactions between the atomic spins are randomly distributed in sign, thus frustrating any tendency toward long-range order. The term "vortex glass'' refers to the tangle of field-carrying vortices that occurs in certain kinds of superconductors. |
| For ordinary practical purposes, glassy materials become solids when cooled below their so-called "glass temperatures." They acquire immeasurably large viscosities and they support shear stresses. The uncertainties are whether these materials might continue to behave like liquids if only we could measure their properties over sufficiently long times or whether, on the other hand, this solid-like behavior is characteristic of some new, intrinsically nonliquid state. This is not an academic question. If we need to predict the structural or thermal properties of amorphous materials, then we need to know what fundamental concepts are relevant. |
| A great deal of progress has been made in the study of glassy materials during the last decade or so. That progress has consisted of many new phenomenological insights about a wide variety of different kinds of glasses and also some careful new experiments that seem to point to the need for unconventional descriptions of the ways in which molecules move and interact in glassy systems. In addition to new understanding of the behavior of glasses themselves, the concepts that have emerged in these investigations have generated novel ideas in fields as far from condensed-matter physics as numerical mathematics and psychology. "Simulated annealing," for example, is a powerful numerical strategy for solving optimization problems. It is based on a model of how a glass-forming material finds its state of (near) equilibrium when it is cooled at a controlled rate through its glass temperature. "Neural network" models of associative memory originally were developed in conjunction with studies of the properties of spin glasses with different kinds of couplings between the spins. It seems likely that this deep and subtle field of research will continue to generate new concepts of far-reaching impact. |
them to compute stress distributions and failure criteria for highly complex solid objects. With the help of modern computers, they are now able to predict with confidence the mechanical properties of structural materials in a wide variety of engineering applications.
Almost all of this progress, however, pertains to static—or very nearly static—phenomena. Roughly speaking, conventional fracture mechanics has been concerned primarily with predicting when materials will break and much less
Page 182
with understanding what happens after failure occurs. The latter topic, "fracture dynamics," remains largely unexplored. It is fundamentally more challenging than its static counterpart because it involves very deep issues in nonequilibrium physics. Some of the most important outstanding questions are, How fast do cracks move? What mechanisms limit their growth? How is energy dissipated in fracture? What determines the various kinds of fracture patterns that we see in nature?
One of the most important recent developments in fracture dynamics has been the experimental demonstration that fast brittle cracks undergo material-specific instabilities (see Figure 4.1). Fracture surfaces frequently are rough; they may even be fractal. We now know that this roughness often occurs because fast cracks are unstable with respect to bending away from their directions of propagation or dissipating energy in the form of tip-splittings or sidebranches. High-speed fracture is frequently a complex, chaotic, pattern forming process. But instability is not a universal phenomenon. Since our ancestors first made stone tools and later learned how to "cut" diamonds, it has been clear that sharp, smooth fracture surfaces can be made by producing cleavage cracks in glassy or crystalline solids. Apparently the trajectories of those cracks are stable.
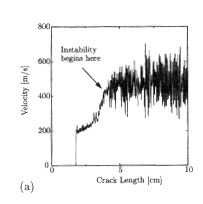
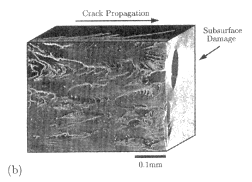
Figure 4.1
Unstable fracture in a polymeric glass. This figure illustrates an experiment in
which a crack was observed with high precision as it moved along the center
line of a long strip of the polymer. (a) The graph of crack speed versus crack
length. We see that the initial crack in the unstressed sample was about 2 cm
long. The stress applied to the sample was increased until the crack suddenly
started moving at a speed of about 200 m/s. The crack then accelerated
smoothly up to a critical speed of about 400 m/s, at which point an instability
occurred that shows up on the graph as a rapid and irregular oscillation of the
crack speed. (b) Photograph of the fracture surface left by the unstable crack.
The front face is the fracture surface itself, with visible roughness on the scale
of 0.1 mm. The top and right faces show that the instability also generated
sidebranching cracks and subsurface damage as the main crack moved
through the system. (Courtesy of University of Texas, Austin.)
Page 183
Despite literally thousands of years of familiarity with these phenomena, we still do not know what mechanisms control fracture stability. There exist some candidate ideas, a few of which have yet to be tested; but there is as yet no theory that is sufficiently plausible and well developed that it can serve as a guide to experiment. One hint, known for about 30 years, is that the stresses in the neighborhood of a crack tip moving at an appreciable fraction of the speed of sound transform in a way that might cause bending. But this observation does not address crucial questions pertaining to the dynamics of deformation and decohesion near the crack tip, which must surely be relevant. The situation is further complicated by the lack of a good theory of ductile yielding in situations where stresses and strains are varying rapidly in both space and time.
In some respects, the present state of the theory of dynamic fracture resembles that of dendrite theory almost half a century ago, before scientists had identified the diffusive instability that underlies pattern formation in crystal growth. To be sure, elastodynamics, plasticity, and decohesion in solids are much more complex phenomena than diffusion. Also, it is quite possible that there are many qualitatively different mechanisms that cause instability in fracture. Perhaps this additional complexity explains why progress has been so slow in this field. With modem tools and interdisciplinary modes of research, we should be able to do better in the future.
Polymers and Adhesives
As discussed elsewhere in this report, an increasing fraction of the structural materials used in modem technological applications are polymers or polymeric composites. Nonequilibrium phenomena are involved both in the chemical and thermal processing of these materials and in the way they respond to stresses during use. These materials occur both as structural elements by themselves and as the adhesives that bind different kinds of structural components in complex applications.
Many structural polymeric materials are alloys of two immiscible polymers, consisting typically of micron-sized droplets of one polymer dispersed in a matrix of another. The mechanical behavior of such a composite is not some simple average of the properties of its constituents. Rather, it depends crucially on the shapes of the droplets and the properties of the interfaces between the droplets and the matrix. Common examples are rubber-toughened glassy polymers used to produce materials that resist high-speed impact damage and, in recent applications, three-phase blends consisting of one rubbery, one glassy, and one semicrystalline phase. Control of both the particle morphology and the fracture toughness of the internal interfaces depends on so-called "compatibilizers," copolymers usually produced in situ by reaction during a mixing flow in the molten state. Besides promoting the breakup of particles into a fine dispersion by their action
Page 184
as polymeric surfactants and inhibiting particle coarsening by preventing coalescence, these compatibilizers help strengthen the interfaces between the phases.
Some progress has been made in understanding how these connectors work, in large part because we now have instrumental probes that allow us to see what is happening on submicron length scales or smaller. Techniques for using copolymers to strengthen interfaces between immiscible glassy polymers are now fairly well established. However, it is still far from clear how to ensure entanglement between polymers, and thus achieve fracture toughness, at interfaces without connectors. The rules for strengthening interfaces involving semicrystalline polymers are especially important for practical purposes but as yet remain undiscovered. Consider polyethylene, the most common semicrystalline polymer, as an example. Outstanding questions include, How long do polyethylene connectors at an interface have to be to allow a zone of plastic deformation to form ahead of a crack tip? If parts of such connectors are incorporated into crystals, is that sufficient to lock them into place, or do they have to be both entangled and run through the adjacent crystals for effective anchoring? What role does crystallization play in the strengthening or weakening of such interfaces? Such evidence as exists suggests that the influence of crystallization is significant. Do the answers to the above questions depend on crack growth rate?
Most adhesives are polymeric, and these play increasingly significant roles in a wide variety of technologies. Adhesives span the range from the very rigid materials used in structural applications to very soft solids such as the pressuresensitive adhesives used in adhesive tape. In all cases, the performance of the adhesive joint is determined by a complex interplay between the bulk mechanical properties of the participating materials, including the adhesive itself, and the detailed microstructural features of the interface. As in the case of the polymer alloys, these molecular-scale features are becoming accessible to physical probes such as secondary-ion-mass spectrometry, ion-beam analysis, and neutron reflectometry. Thus, while adhesives traditionally have been developed by time-consuming, empirical approaches, the prospect now exists for rational design based on molecular-scale information.
Friction
Another classic part of materials research that is enjoying a resurgence of interest among physicists is the science of friction. This topic has much in common with dynamic fracture and adhesion. Two interacting solid surfaces sliding past each other look in many ways like a dynamic shear crack. Mechanisms such as cohesion and decohesion, energy dissipation, elastic deformation, and so on are all relevant. But friction is an even larger and more complex topic than fracture because it occurs in such a wide variety of circumstances and, apparently, with an equally wide variety of underlying physical mechanisms.
The conventional goal of research on this topic is to determine frictional
Page 185
forces as functions of the relative state of motion of two solid surfaces and the stress holding the surfaces in contact with each other. Real friction, however, is far more interesting and complex than this conventional statement would make it seem.
Much of the recent progress in this area has been based on novel techniques for visualizing the microscopic processes that take place during friction-controlled sliding. Several atomic-scale probe microscopies have been used, as well as some relatively simple and direct methods for following the motions of larger features such as contact points and asperities. Numerical simulations, especially via molecular dynamics, are now beginning to provide very valuable insights; and good use also is being made of analog systems for making accurate observations of slipping events. A recent example of the latter technique involves layers of carefully characterized granular substances confined between sliding plates.
Friction problems fall very roughly into three different categories: friction between molecularly flat crystalline surfaces, friction between deformable rough surfaces, and, in a very general sense, lubricated friction—that is, friction controlled by the dynamic behavior of substances constrained to move between the surfaces that are sliding across one another. In the first of these categories, the clean crystalline surfaces, it is possible to make plausible models that involve only atomic-scale degrees of freedom. Although such models still must include assumptions about irreversible behavior, they are relatively well posed and, in some cases, they are now beginning to produce credible agreement between theory and experiment.
The other two categories of friction problems are fundamentally more challenging because they involve two or more widely separated length scales and timescales. They may also be of broader practical importance.
In dry friction between polycrystalline, noncrystalline, or otherwise imperfect surfaces, the actual area of contact is much smaller than the nominal area of the surfaces. The behavior of the small contact regions is crucial in determining frictional forces and dissipation rates, but there is as yet no clear understanding of the physical mechanisms that occur there. The problem seems to have issues in common with fracture; the behavior is governed by cohesion and decohesion at atomic-scale contacts that are strongly coupled to larger-scale elastic and plastic modes of deformation. One useful way of dealing with systems of this kind is to describe them not just by the relative positions and speeds of the sliding surfaces but also by "state variables" that might represent, for example, the density and strength of the contacts, and that obey equations of motion of their own. Such "rate and state dependent" friction laws have been developed especially by seismologists.
The ostensibly most complex problems in this field are those in which a "lubricant"—that is, some extraneous substance—is present in the space separating the sliding surfaces and transmits the frictional forces from one surface to the other. In some of the most interesting recent experiments, the lubricant
Page 186
is confined to a very small region, just a few molecular diameters across, and thus its properties—especially under shear—may be quite different from those of the same substance in bulk. Now the use of state variables is absolutely essential. The lubricant may respond to changes in the shear rate by changing its state, perhaps from liquid-like to solid-like, and such variations may occur on many different space scales and timescales. The challenge is to identify the essential degrees of freedom for these complex systems and to understand the interrelations between the relevant microscopic and macroscopic phenomena.
One of the most interesting and characteristic kinds of behavior seen in friction experiments is stick-slip motion. In many circumstances, surfaces in contact with one another will stick together until the applied shear stress reaches some threshold, and then will slip past each other in accord with a rate-dependent friction law until, under the influence of external forces perhaps, they come to rest and restick. Familiar examples include squeaky door hinges and the motion of a violin string driven by a bow.
It is easy to imagine how stick-slip motion can occur at a localized asperity, that is, at a point where irregularities on opposite surfaces are attached to each other via contact forces or molecular bonds. Slipping begins when the bond breaks and stops when a new bond is established. On macroscopic scales, friction-limited slipping may be the average of very many uncorrelated microscopic stick-slip events. Macroscopic motions also may have a stick-slip character, as in the case of the squeaky hinge. Such behavior occurs when the combined action of dynamic friction and external loading induces some kind of mechanical instability.
One interdisciplinary research topic that combines many of these ingredients—stick-slip friction plus fracture—is earthquake dynamics. Earthquakes, by definition, are stick-slip events. They are triggered when some piece of a fault is brought to its slipping threshold by the tectonic forces in the Earth's crust. They have the additional features that they occur on large length scales and have an extremely broad range of sizes, even on single fault segments. Both physicists and seismologists have been interested recently in the discovery that models of earthquake faults consisting simply of elastically coupled stick-slip slider blocks are deterministically chaotic systems that exhibit some of the characteristic behavior of real faults. Of course, these models do not account for the geometric complexity of real seismic phenomena; but the qualitative picture that they provide, in which large events occur intermittently as cascades of small events, is at the least an intriguing caricature of many kinds of self-organized phenomena. It might even prove to be useful in seismology.
Page 187
Granular Materials
Granular substances such as sand provide an especially clear example of a familiar class of materials whose properties have yet to be understood from a fundamental scientific point of view. These materials have been studied empirically for centuries in civil engineering, geology, soil mechanics, etc., because they are essential ingredients in a wide variety of natural phenomena and have many practical applications. But we do not know how to answer some of the most basic questions about their behavior.
There are several clear distinctions between granular materials and the other, superficially comparable, many-body systems that are more familiar to physicists. Because they have huge numbers of degrees of freedom, they clearly need to be understood in statistical terms. However, individual grains of sand are enormously more massive than atoms or even macromolecules; thus thermal kinetic energy is irrelevant to them. On the other hand, these grains also have infinitely many internal degrees of freedom; thus they may—or may not—be highly inelastic in their interactions with each other or with other objects. They also may—or may not—have irregular shapes; arrays of many grains may achieve mechanical equilibrium in a wide variety of configurations and packings. It seems, therefore, that the concept of entropy must be relevant. We shall need some way of deciding which are the statistically most probable states under various constraints. But is there any analog of temperature or internal energy? What other quantities might be necessary for describing the states of these substances?
The questions become even more interesting when we consider the analogs of nonequilibrium properties for granular materials. What happens to sand when it is made to vibrate? Or when it is exposed to shear stresses? In some circumstances it behaves like a solid; close-packed sand can support limited shear stresses. In other circumstances—strong shaking in an earthquake, for example—it flows like a liquid. In yet other circumstances, granular materials behave in ways that we do not yet know how to characterize (see Figure 4.2). Their free surfaces spontaneously form regular patterns when shaken in special ways; their internal stresses organize themselves into chain-like structures under certain kinds of loading; flow patterns sometimes look roughly like localized shear bands.
Granular materials are only the simplest examples of states of matter that are unfamiliar and relatively unexplored from a fundamental point of view, yet appear in many ordinary circumstances. To change the granular system just a little, we might consider cases in which the grains cohere to each other. If the coherence is weak, such substances may behave like viscous fluids—wet sand or clay, for example. If it is strong, then we have materials like concrete or sandstone which, for the most part, behave like ordinary solids. They support shear stresses, and they can be brittle or ductile in their failure modes. In both cases, however,
Page 188

Figure 4.2
Localized standing wave in a vertically vibrated layer of 0.2 mm diameter bronze
balls. (Courtesy of Center for Nonlinear Dynamics, University of Texas, Austin.)
when we try to understand the nonequilibrium properties of these materials, we find ourselves in uncharted territory.
We find ourselves even further afield when we consider the nonequilibrium physics of yet more dynamically complex materials such as foams, or the colloidal suspensions, gels, and so on discussed in Chapter 5. Foams, for example, are close-packed collections of bubbles separated by fluid films. They may be simi-
Page 189
lar in some respects to granular materials; their fluid-like properties may be controlled by local rearrangements of the bubbles.
Such considerations lead us inevitably to think about the nonequilibrium behavior of biological materials. Cellular membranes, for example, are double layers of large phospholipid molecules (see Chapter 5). These membranes obviously have a high degree of structural integrity; they do not pull apart easily and they resist bending. Yet the molecules rearrange themselves easily within the layers, which behave in many ways like two-dimensional fluids. There has been substantial progress in the last decade in understanding the properties of these basic biological materials. But it is only very recently, with the advent of new experimental techniques, that the outstanding questions in this immense field are beginning to become well-posed problems in nonequilibrium materials physics.
Length Scales, Complexity, and Predictability
There is a growing consensus among seismologists that it is impossible, even in principle, to predict earthquakes. By this, they mean that they may never be able to tell us, say a month or a year in advance, that an earthquake will occur at a certain time and place. They have good reasons to be optimistic that, with new scientific techniques, they will be able to make increasingly accurate estimates of seismic hazards; and they may even be able to identify some precursory phenomena that, in special circumstances, are warnings of imminent seismic events. But earthquake faults are extremely complex, unstable, dynamical systems. When near their slipping thresholds, they are highly sensitive to everything from large-scale motions of the Earth's crust down to the detailed friction laws governing the motions of rocks at the points where failure might occur. Even if we had an arbitrarily large computer and a complete understanding of the physics at each of the relevant length scales and timescales, it seems highly unlikely that we could ever determine the state of such an immensely complex system with enough accuracy to be able to make event-specific predictions.
Are there similar in-principle limitations in other areas of solid mechanics? In the foreseeable future, we ought to be able to determine from first principles the elastic-plastic response and fracture toughness for single-crystal copper or silicon, or perhaps even for some amorphous materials. As we have seen, these are challenging but potentially solvable problems. Is there any hope, however, of being able to make such determinations for multicomponent, polycrystalline, structural alloys, or for multiphase polymeric composites, and then go on to predict how those materials will perform in service over extended periods of time? Or are such predictions as difficult as predicting earthquakes?
As seen from the perspective of the last decade of the twentieth century, it appears that the next decades of research in nonequilibrium solid mechanics should be characterized by a diversity of goals and modes of inquiry. It seems clear that we must continue to move in certain well-established and productive
Page 190
directions—ab initio calculations of dislocation dynamics in crystals, for example, or experimental tests of such theories using synchrotron radiation. The results of those investigations should provide data and new insights that will be essential for a wide range of related research and applications, and they should point the way to new research in directions that we cannot now anticipate.
In pursuing these investigations, however, we must recognize that making the transition from stomistic theories of single-crystal plasticity to engineering design of large-scale, complex, structural materials is not just a matter of building bigger computers. We are almost certain to find new physics problems that need to be solved at each of the many stages of this process. If the analogy of earthquake prediction is accurate, then many of these problems will have to be solved in ways that are not now familiar to us.
Further Prospects For The Future
Nonequilibrium Phenomena in the Quantum Domain
Modem technological advances in mesoscopic and atomic systems, described elsewhere in this report, have made it imperative that we extend the study of nonequilibrium phenomena to the quantum domain. The inclusion of quantum mechanics makes an already difficult task even more difficult. In addition to having to understand which microscopic details are relevant to observed macroscopic effects, quantum mechanics forces us to consider the idea of ''coherence," that is, the degree to which quantum mechanical wavefunctions preserve not just their amplitudes, but also their phases during dynamical processes. We have to think carefully about the physical meanings of both classical statistical fluctuations and quantum uncertainties. Not only do we have only partial information about the relative probabilities of various atomic or electronic configurations, but now we must take into account that we have only partial information about the quantum phases.
Such considerations become yet more challenging when we consider the problem of "quantum chaos"—the quantum mechanics of systems whose classical behavior is chaotic. In classically chaotic systems, we lose predictability as the system evolves in time. What happens to such systems in the quantum domain? Until just a few years ago, such a question seemed to be more important philosophically than practically; but that situation has changed dramatically with recent developments in mesoscopic physics. The electronic orbits in artifically structured nanosystems are often chaotic, and the control of these systems is now so precise that the electronic states can remain coherent long enough for the chaotic behavior to be relevant. Thus, what had previously been an abstract problem in quantum measurement theory is now becoming a practical problem in the design of advanced electronic devices.
An even more advanced example of the growing importance of quantum
Page 191
dynamics in nonequilibrium phenomena is the current effort to develop quantum computers. Here, as in the mesoscopic devices, we are dealing with systems far from equilibrium coupled to an external environment and a ''classical" measurement apparatus. But, in this case, the whole concept depends on the possibility of maintaining systems with many degrees of freedom in quantum mechanically coherent states for times long enough actually to perform useful computations. Related questions have been raised by the production of Bose-Einstein conden-sates by evaporative cooling in atom traps. We are only beginning to understand how to describe the dynamics of the formation of a coherent condensate in a quasi-isolated system driven out of equilibrium by evaporative cooling.
Yet another example of the importance of dissipation and decoherence can be found in the study of quantum critical phenomena such as the metal-insulator transition. The dynamics of critical phenomena are often best studied using both linear and nonlinear response to applied external probe fields. It is often the case that "external" dissipation (due to phonons, for example) is irrelevant to the equilibrium-critical behavior because the effective electron-phonon coupling vanishes at low temperatures. However, this coupling can be "dangerously irrelevant" to the nonlinear transport because the external dissipation is the only mechanism available to carry away the Joule heat. Hence, the less relevant the phonons are to the equilibrium properties, the larger the bottleneck they represent for energy dissipation in the nonequilibrium case. This can lead in some cases to a singular temperature rise that obscures the underlying singular response of the quantum critical fluctuations.
In short, there continues to be a host of deep and largely unresolved philosophical questions in quantum measurement theory, forced on us by the development of systems at the interface between the quantum and classical domains. These questions may well be of growing practical importance in the next decade.
Nonequilibrium Phenomena in Biology
Living systems are, by definition, in states that are far from thermodynamic equilibrium. They are very different from any of the examples that we have discussed so far, however. The most obvious difference is that they are highly complex in their basic ingredients. Even the simplest biological materials are composed of large multicomponent molecules that, individually, perform specific chemical and mechanical functions. More important, the selection of these molecular constituents, and the ways in which they are assembled to make living organisms, has taken place not according to some global optimizing principle of the kind cherished by physicists, but rather according to the incremental and perhaps chaotic processes of evolution. In dealing with systems of this kind, physicists are learning to make basic changes in their research strategies.
Biology always has been a far more empirical and phenomenological science
Page 192
than physics. Until very recently, there has been little room in biology for what physicists call "theory." The complex phenomena being observed and interpreted by biologists are taking place in systems whose fundamental properties are not understood in the way we understand, for example, the physics of solid xenon or the mechanical properties of grains of sand. Physicists usually have not had the information they need for developing quantitative theories of biological phenomena or the tools they need for testing those theories.
As described in more detail elsewhere in this report, that situation is now beginning to change. Laser tweezers, atomic-force microscopes, and the like are permitting us to see what individual molecules are actually doing during biological processes. It is now possible, for example, to measure forces between cellular membranes, to watch those membranes change their shapes in response to various kinds of stimuli, or to see how proteins are formed and transported from one place to another within cells. From the wealth of information just now becoming available, we are beginning to understand that large biological molecules often function as machines, absorbing energy from their chemical environments, dissipating energy, and doing biologically useful work—all in accord with the basic principles of nonequilibrium physics.
There seems little doubt that, so far, we are seeing only a very small part of the huge world of biological materials and biophysical phenomena. The near-term challenges for physicists working in these areas will be to identify those biological systems that are ripe for quantitative investigation, to develop the instruments and techniques for data analysis that will be needed to characterize those systems, and to induce quantitative and predictive theories that can serve as guides for further experimentation. Ultimately, the goal is to acquire a deep, detailed understanding of the most extraordinary of all nonequilibrium phenomena: life itself.
Future Directions And Research Priorities
In summary, the committee draws the following conclusions regarding recent developments and future directions for research in the nonequilibrium physics of condensed matter and materials.
1. Fluid dynamics, in addition to being relevant to a wide range of topics in science and technology, remains a uniquely valuable laboratory for the study of complex, nonequilibrium phenomena that emerge in relatively simple, easily characterized systems.
2. Very significant progress has been made in the last decade in understanding dendritic pattern formation in crystal growth. That progress, however, has yet to have a major impact on efforts to predict and control solidification microstructures in industrially important materials. In part, the difficulty is that there remain some challenging scientific problems to be solved, such as the problem of
Page 193
the "mushy zone." Another part of the difficulty is that there is relatively little effort in this area in the United States, especially in industrial laboratories.
3. Recent developments in scientific instrumentation, especially atomic-scale resolution in probe microscopy, plus extraordinary advances in computing power, mean that long-standing problems in solid mechanics should now be solvable. These are fundamentally challenging problems that involve non-equilibrium statistical physics, nonlinear dynamics, and the like. They are also, essentially without exception, directly relevant to modern technology. Among those problems are the following:
a. The origin of dynamic instabilities in brittle fracture;
b. The fundamental distinction between brittleness and ductility in both crystalline and amorphous solids;
c. The relation between molecular and mesoscopic structure and mechanical properties, especially fracture toughness, in composite materials containing, for example, varieties of polymeric constituents;
d. The relation between molecular and mesoscopic structure and the dynamics of friction in an extremely wide variety of situations, ranging from atomically flat surfaces interacting across molecularly thin layers of lubricants, to tectonic plates interacting across earthquake faults; and
e. The relation between elementary interactions between grains and the macroscopic mechanical behavior of granular materials.
4. In all probability, the next major frontier for research in nonequilibrium physics will be in the area of biological materials and phenomena.
5. The same recent advances in scientific instrumentation and computing power that portend both major advances and major surprises in nonequilibrium materials research also force us to face fundamental issues in the physics of complex systems. The problem of understanding the limits of predictability in these systems must be addressed with every bit as much skill and objectivity as the more familiar problems of understanding specific properties of specific systems. These issues lie, not just at the interface between different scientific disciplines, but also at the interface between science and public affairs.