D Logistics Productivity of Aircraft
LtGen Philip Shutler, USMC (Ret.), Senior Fellow, Center for Naval Analyses
Introduction
One of the first considerations when planning military operations is to position superior force to overcome the threat with minimum losses to friendly units. Within the concepts of maneuver warfare, this is a dynamic process that responds to the uncertainties of combat with movement and directed fire on the threat, and continues until the threat has been overcome. The commander must use available transportation assets to make initial deployments of troop units, fighting vehicles, support vehicles, and supplies, and then readjust the deployments to defeat the threat while, at the same time, moving replacements and resupply materiel into position. As envisioned in Operational Maneuver From the Sea and Ship-to-Objective Movement, the bases for most of the force and materiel will be ships up to 25 miles at sea, and the objectives will be as far as 200 miles inland.
The transportation vehicles will include landing craft (air cushion) (LCAC) for ship-to-shore movement and trucks for overland movement, but, if fighting units are to be positioned and sustained at distances of 225 miles from the ships, and the safety of trucks on the road is uncertain, most of the unit movement and resupply must come from aircraft. The V-22 and CH-53E are capable of carrying limited loads to those distances and, more important, can land anywhere a zone can be established. The questions that need to be answered are as follows:
- What quantity of materiel can these aircraft deliver to selected distances?
- How long will it take to complete the initial delivery?
- What is the rate of resupply in tons per day?
Specific transportation planning to answer these questions is quite complex and depends on many variables. It is possible, however, if certain assumptions are made, to assess the transportation feasibility of a particular plan of action. The purpose of this appendix, then, is to present a simplified method for calculating productivity in tons/day accurately enough to determine feasibility. The way the calculations are structured also shows how the process can be adjusted to accomplish achievable results.
Logistics Productivity
Logistics productivity is measured in tons per day and is dependent on three primary factors: (1) the number of mission aircraft that can be kept functioning throughout the day; (2) the mission load that can be carried on each round trip or sortie; and (3) the number of mission sorties each aircraft can make in a day. The general formula is

Mission Aircraft
The number of mission aircraft that can be kept functioning is the number of aircraft assigned adjusted by the average availability factor:
mission aircraft = assigned aircraft x % availability. [1]
Mission Load
For helicopters and tilt-rotor aircraft, there is a direct trade-off between useful load and fuel. Configured with a fuel-only maximum load, the aircraft can fly to the so-called "ferry range." The maximum round-trip range, with near-zero useful load, is here termed the "no-load distance," approximately half the ferry range. One could think of the no-load distance also as the maximum distance that a single passenger could be delivered under emergency conditions, and the aircraft returned without refueling. As shown in Figure D.1, the maximum useful load ≅ maximum "mission fuel" (≈ one-half the maximum all-fuel load). The fuel consumption per mile can be estimated as

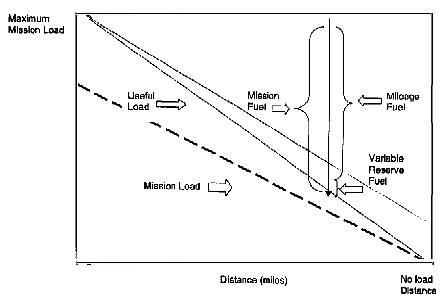
FIGURE D.1
Mission load derivation.
Figure D.1 illustrates that if the fuel weight is reduced to the minimum needed for fixed reserves, the aircraft can carry a useful load for very short distances. Figure D.1 also indicates that there may be an additional variable fuel reserve proportional to the "mileage fuel." The fuel carried on a mission is typically the mileage fuel plus variable and a minimum fixed reserve. Figure D.1 shows that mission fuel is proportional to distance:
mission fuel = fuel consumption per mile x mission distance. [3]
As shown in Figure D.1, useful load = maximum useful load - mission fuel. Using [3], useful load = maximum useful load - fuel consumption per mile x mission distance, and substituting from [2]:
One can also observe that in practice the full useful load often cannot be achieved because some cargo takes up the full space but does not weigh enough, or the particular mission does not require a full load. A mission load is defined as useful load adjusted by a percent efficiency factor:
So,

Sorties Per Aircraft Per day
Sorties per aircraft per day can be calculated by dividing total available flight time per aircraft per day by the flight time per sortie:
Available flight time is determined by outside factors such as spare parts, maintenance technician availability, and air crew manning levels, as well as daylight and dark as missions dictate. Flight time per sortie is determined by dividing total round-trip distance flown by cruise speed. It is assumed here that the hours/sortie is mostly due to the actual flight time to a single destination.1
Thus
and
Here, again, it is useful to use the construct of no-load distance. The number of sorties that could be flown to the no-load distance is
If it is assumed that the total available flight time remains constant regardless of the number of sorties flown, then the number of sorties is inversely proportional to distance, as shown in Figure D.2. That is to say, if you fly half as far, you can fly twice the number of sorties. This assumption is reasonably accurate for distances from one-eighth of the no-load distance to three-fourths of
|
1 |
The figures for cycle times (equivalent to hours/sortie) in Tables C.2 and C.3 in Appendix C allow for appreciable extra time over and above actual round-trip flight times. |
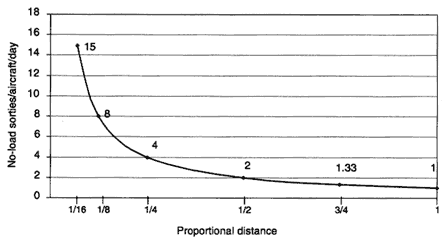
FIGURE D.2
Mission sorties per aircraft per day.
the no-load distance. At less than one-eighth of the no-load radius, turnaround and queue times can preclude maintaining fixed flight time. The curve may also be less useful at distances greater than three-fourths of the no-load distance because auxiliary fuel cells may use up cargo space.
Starting from the value at no-load distance in Figure D.2, since the mission distance is œ the no-load distance, the sorties will be increased by the proportion of
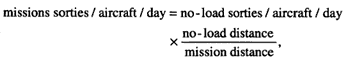
and
Returning to the original formulation:

Substituting the values from equations [1], [5], and [6] for terms highlighted by brackets, and rearranging terms:

The first term ![]() consists of three elements of aircraft design that remain constant for a particular aircraft configuration.
consists of three elements of aircraft design that remain constant for a particular aircraft configuration.
The second term [% availability x % efficiency x hours/aircraft/day] is determined from assumptions of future availability, efficiency, and flight time/ aircraft/day. This term can vary from a high of 12 (100% availability x 100% efficiency x 12 hours/aircraft/day) under ideal conditions, with excess flight crews, to a low of 1 (50% availability x 50% efficiency x 4 hours/aircraft/day) under poor conditions, as might prevail at the end of prolonged surge activity.
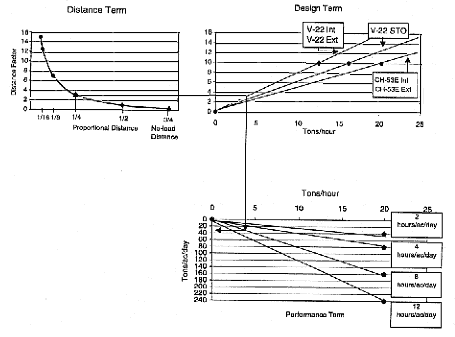
The third term ![]() represents the diminishing effect of distance on productivity when both mission load and sortie rates are reduced with distance. A plot of this term is shown in the upper left-hand corner of Figure D.3.
represents the diminishing effect of distance on productivity when both mission load and sortie rates are reduced with distance. A plot of this term is shown in the upper left-hand corner of Figure D.3.
Applications
Payload Versus Mission Distance
There are five major aircraft configurations to be considered:
- V-22 short takeoff, internal load (V-22 STO);
- V-22 vertical takeoff, internal load (V-22 int);
- V-22 vertical takeoff, external load (V-22 ext);
- CH-53E vertical takeoff, internal load (CH-53E int); and
- CH-53E vertical takeoff, external load (CH-53E ext).
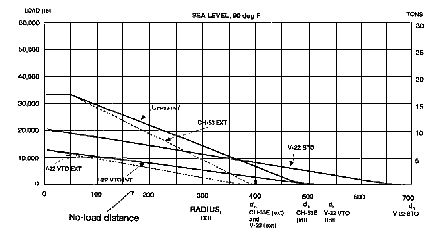
A plot of useful payload vs. mission distance is shown in Figure D.4. The information regarding V-22 STO, V-22 int, and CH-53E int is derived from briefing charts provided by the Naval Surface Warfare Center, West Bethesda,
Maryland. The information regarding V-22 ext and CH-53E ext is estimated in accordance with the following methodology.
Effective Cruise Speed
An aircraft carrying an external load would go out at external-load cruise speed and return at internal cruise speed. Thus, the mission time for the out and in legs is
The effective round-trip cruise speed, then, is round-trip distance divided by mission time:
Or
''External No-load Distance"
As discussed above, the rotary-wing aircraft no-load distance for internal loads is the maximum round-trip distance. A "no-load distance for external loads" can be defined as the extrapolation, to zero load, of a linear fit to data for finite loads. These data and extrapolations can vary for different types of external loads, but this is ignored here. An approximate value of an "external no-load distance" can be obtained by assuming that the hourly fuel consumption rates, and so the times of flight for internal and external loads, are about the same.2 Then the
"external no-load distance" = (external no-load time of flight ≈ internal no-load time of flight) x (effective external cruise speed).
And substituting from [8],
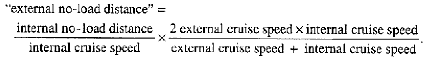
So,
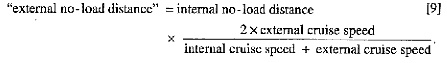
Thus, if V-22 cruise speed with external load = 130 knots, and V-22 cruise speed with internal load = 230 knots, and V-22 internal no-load distance = 550 nautical miles, then from [9]:
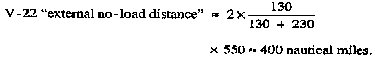
Similarly, if CH-53E cruise speed with external load = 90 knots, and CH-53E cruise speed with internal load = 130 knots, and CH-53E internal no-load distance = 500 nautical miles, then from [9]:

Calculating Productivity
It is, of course, possible to use formula [7] as stated in a straightforward fashion to calculate productivity. It is, however, much simpler and more instructive to use a nomograph similar to the one shown in Figure D.3 to relate the many factors involved in the calculation.
The nomograph is constructed as follows: (1) the distance term is plotted in the upper left corner of Figure D.3, (2) the aircraft design term
TABLE D.1
TABLE D.2
|
% Availability |
% Efficiency |
Flight/Time/ Aircraft/Day |
% Availability x % Efficiency x Flight Time/Aircraft/Day (approximate values) |
|
1.0 |
1.0 |
12 |
12 |
|
.9 |
.9 |
10 |
8 |
|
.7 |
.7 |
8 |
4 |
|
.6 |
.6 |
6 |
2 |
|
.5 |
.5 |
4 |
1 |
An important problem that often must be solved is this: Can the number of aircraft available position and support the size force necessary at a stated distance from base to objective?
Solution:
Step 1. Divide distance by the no-load distance for the configuration and enter at the proportional distance. (In the marked example, configuration is V-22 ext, distance is 100 miles, no-load distance is 400 miles, and proportional distance is one-fourth). Read up to distance factor. (Example: Distance factor is 3.)
Step 2. Move to the right to the appropriate design configuration line. Note: the no-load distance and the design line must be for the same configuration. (Example: The line chosen is for V-22 ext. Value is 3.75 tons/ hour.)
Step 3. Move downward from the design line to the appropriate performance line. (Example: Performance assumed is 8 hours/aircraft/day.)
Step 4. Move to the left and read tons/day/aircraft. (Example: 30 tons/day/aircraft.)
Step 5. Divide total planned tons/day by tons/day/aircraft to estimate the number of assigned aircraft required.
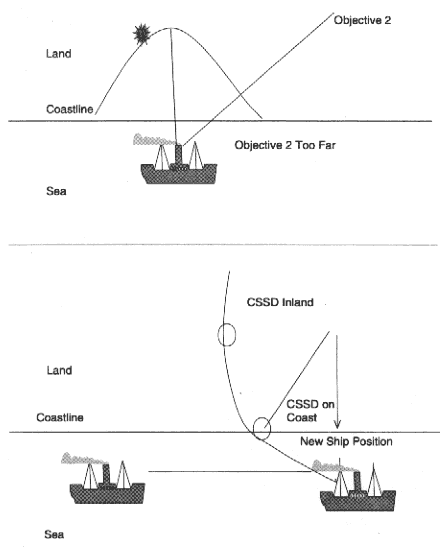
If the aircraft assigned are inadequate, the process can be reversed to estimate the distance to which the aircraft could sustain the force, or, alternatively, to estimate the distance from the objective where a temporary combat service support detachment (CSSD) should be positioned to support the second step to the final objective area. As seen in Figure D.5, the location of the temporary CSSD could be on land or at the coastline or at sea. If on land, the logistics flow to the CSSD site would be by air; on the coastline, by surface craft or air; and, if at sea, the ship itself could move to the location.
The stated purpose of this appendix is to provide a simplified method for estimating logistics feasibility of various courses of action in OMFTS and STOM. Figure D.4 satisfies that requirement, but it should be used with caution. Logistics requirement estimates are notorious for inaccuracy. Aircraft availability and efficiency of the loading process are often overestimated, particularly for the later stages of operations. The effects of night, weather, battle damage, and the fog of war further diminish the ultimate performance of the transportation systems.
Those cautions having been noted, however, the distances that can be reached by ground forces (up to 500 miles when returning to home base, and to a total flying mileage of 1,000 miles if fuel is available closer to the objective) and the time to accomplish the insertion (21/2 hours to 500 miles) gives ground forces such as Marine reconnaissance, Army rangers, and small combat teams of all Services an operational reach approaching that of tactical aircraft. The vertical takeoff and landing characteristics permit basing, or at least refueling, at a wide variety of ships and small, hideable facilities ashore.
It is true for these operations, as it has always been, that a plan that is logistically infeasible is, in fact, not feasible, but the ways in which logistics support can be accomplished through temporary combat service support detachments, or forward arming and refueling points, or fuel caches ashore or at sea, or aerial refueling, have increased manifold. The operational reach of land forces, whether starting from sea or from shore, has been increased and response times decreased to such an extent that land operations of all types must be reexamined and adjusted.