Computational and Theoretical Techniques for Materials Science (1995)

The algorithms employed in computational materials science vary in the ease and completeness with which they can be parallelized. Additionally, arrays or operations to be spread across the nodes of a parallel computer must clearly be more numerous than the nodes. This often implies a trade-off between programming effort and scalability. Another consideration is Amdahl's Law. For example, if an application spends 95 percent of its time in matrix diagonalization, the maximum speed increase attainable from parallelization of diagonalization alone is a factor of 20—regardless of the number of computer nodes used. With these considerations in mind, the panel comments below on the relative amenability to parallelization of several representative algorithms.

One of the striking successes of parallel computing can be seen in molecular dynamics of classical systems characterized by long-range forces. This effort has been led by astrophysicists modeling galactic dynamics driven by gravity. The fundamental N² scaling seemingly implied by the long-range forces is reduced to N scaling by the use of the fast multipole method. Simulations exploiting this technique frequently involve more than 10⁶ particles. The parallelization of molecular dynamical simulations characterized by short-range forces also has been successful, but scaling to large numbers of processors is often difficult because the ratio of computation to communication is small for simple models.

The great success of parallel classical molecular dynamics simulations of very large systems illustrates another general aspect of parallelization in the context of local interactions. If the calculation is decomposed spatially, computation can be thought of as a volume effect and interprocessor communication as a surface effect. Thus, the fractional time consumed by communication can be thought of as the surface-to-volume ratio and can be made arbitrarily small by increasing the total size of the system. This effect often acts to diminish or delay the impact of Amdahl's Law. Of course, our ability to simultaneously obtain both long time scales and large systems sizes remains a challenge to parallel algorithm development.

Quantum molecular dynamical simulations, such as those employing the Car-Parrinello method, have been successfully parallelized, despite the fact that these methods make extensive use of the communication-demanding fast Fourier transform. These applications share with the larger class of nonlinear optimization methods, such as those based on functional gradients, the important distinction between the parallelization of inner and outer loops. The greatest scalability is often attainable from the inner loops over spatial grid points, for example, but parallelization of the outer loops frequently makes more efficient use of the memory and processing power of individual computer nodes while offering less scalability.

Parallelization of quantum chemical methods is possible, but because of the size and complexity of most quantum chemical codes, progress has been relatively slow. An aspect of quantum chemical and Gaussian-based density-functional calculations is dominance of integral evaluation. The required integrals are, in general, independent and represent an entry path for parallelization.

Computational materials science presents many problems, some of which relate to parallel computation in unique ways. Within the field there is a hierarchy of time and length scales extending from the most accurate and elaborate treatments of electronic correlations through local-density and molecular dynamics calculations to continuum theories of macroscopic materials. Additionally, each of these elements often offers a variety of formulational and algorithmic approaches, such as plane-wave and real-space formulations of local-density calculations.

The potential for effective parallelization of each of these component problems involves three principal factors: (1) the interprocessor communication requirements of algorithmic alternatives; (2) the exploitation of the enormous memories provided by parallel computers; and (3) the exploitation of existing serial code components, often highly optimized and representing large investments of time and effort. The importance of communication requirements stems from the fact that the time required to retrieve data from the memory of another processor is very much longer than from local memory. Some algorithms, such as the fast Fourier transform, require extensive interprocessor communication. Such communication can often be hidden, that is, caused to occur simultaneously with productive computation. Thus, it becomes very important to exploit, wherever possible, mathematical and communications routines optimized for specific machines by their vendor.

The very large memories often available with parallel supercomputers permit the replication of data, thereby permitting local retrieval during execution. For example, if the individual states of an electronic-structure calculation are evolved by different processors, replication of the effective potential permits the states to be evolved without additional communication. This example can also be used to illustrate the value of executing optimized serial code in individual nodes. If individual states are evolved in individual nodes, the implied fast Fourier transforms and any optimizations of the serial evolution code are preserved. Such a conversion provides a relatively simple approach to parallelization, although it will not yield ultimate performance and scalability.

Formulational alternatives can also differ in their amenability to parallel execution. For example, the description of long-range forces in molecular dynamics simulations using logarithmic tree algorithms reduces the computational scaling from N² to N log (N). The effectiveness of these methods has been extensively demonstrated in the context of gravitational forces in galaxy modeling. Their use for the description of Coulomb interactions is being developed. This scaling improvement is, in principle, independent of parallel execution; however, the system-size crossover beyond which such methods are advantageous often calls for parallel computers.

Scaling and system-size crossover enter similarly into the discussion of “order-N” methods of electronic structure. There has been much progress on this front, including the development of a variety of alternatives within this context. Application of the Lanczos method to the kinetic energy operator on a mesh, density-matrix methods, and methods restricting the optimization of the occupied subspace are all presently under study, and all lend themselves to parallel execution.

In the context of Monte Carlo calculations, the large systems calling for parallel execution focus attention on the selection of cluster moves. When such a system is distributed over the nodes of a parallel computer, identification of effective cluster moves becomes a special challenge. Significant progress has been made in this area.

Massively parallel processors (MPPs) seem destined to become the mainstream of scientific supercomputing. The impact of MPPs can already be easily gauged in many fields from the number of publications whose results were obtained on such machines, ranging from weather forecasting to quantum chromodynamics, molecular dynamics, and the evolution of the universe. This trend is certain to continue at accelerated rates, assisted by the increasing number of such machines coming on line and by the increasing maturity of the software and hardware.

Computational materials science is one of the fields already benefiting from this increase in computational power available at national sites. A summary of some of the current and future developments in MPPs follows.

For the past few years processor speeds have doubled every 18 months or so, and this trend is projected to continue until the end of the century and beyond. This means that in the next five years or so, processor speeds will increase by about an order of magnitude. At the same time, network bandwidths also are increasing, albeit at a slower rate. Furthermore, the dollar cost per Mflops is on the decline. Currently, the figure is about $200/Mflop, which is expected to drop to about $20/Mflop by the year 2000, probably sooner, and this cost is roughly independent of the size of the system, ranging from workstations to MPPs.

In addition, dynamic random access memory (DRAM) involves a technology closely related to that driving microprocessor evolution. Thus, the memory associated with individual microprocessors has grown to multiple gigabytes, making the total memory available in a parallel computer a significant fraction of a terabyte.

A related trend in the context of technical computing is the shift from “trickle down” to “trickle up” as the fundamental source of new technologies. Until quite recently, new technology was introduced at the “high end” of the market and was often supported by federal agencies and national laboratories.

Subsequently, these technologies trickled down to the rest of the economy. One measure of the reversal of this trend is the fact that 1994 was the first year in which more money was spent on desktop computing systems than all other types of computing combined. The extent to which this inexorable trend will drive all computing, including supercomputing, to the personal computer price scale is a matter of intense speculation. Related questions, such as the role to be played in technical computing by desktop-related software, like Microsoft 's NT operating system, will also play out in the coming half decade.

Demands on the interprocessor communication system vary widely among applications. Of the two principal performance characteristics of these systems, bandwidth and latency, it is more often latency that is the bigger bottleneck. This latency has been dramatically reduced in recent years, from the tens of milliseconds characteristic of local area networks (LANs) to the range of microseconds. However, the newest microprocessors perform floating point operations in about 10 microseconds. This very large ratio of communication to computation dictates the granularity of parallel computations. The pace of advances in microprocessor design and fabrication is so great, coupled with the slower evolution of interconnection performance, that the granularity of parallel computation is likely to increase through the rest of the decade.

All this makes it economically and technologically attractive for MPP suppliers to ride the technology curve (see Figure 3.1) and use off-the-shelf commodity chips and subsystems, something most have decided to do.

These trends in technology curves and the economies of scale associated with commodity system components (order-of-magnitude increase in speed and order-of-magnitude decrease in cost in the next five years or so) will hasten the arrival of teraflops performance. Such machines are expected to be available in

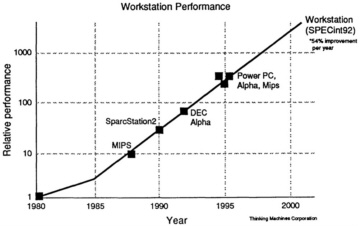
Figure 3.1 Time dependence of workstation speeds.

Source: Thinking Machines Corporation.

the next three to four years, and at reasonable cost. It is worth restating that this big increase in computational power is due not only to using more processors but also to an order-of-magnitude increase in the speed of individual processors. It is important to keep this in mind since a large number of problems of interest in computational materials science (e.g., many using molecular dynamics) are limited by the problem of time scales. Increasing the raw power of an MPP by adding more processors (and more memory) allows the study of much larger problems but not longer time scales. However, the order of magnitude increase in processor speed should give a concomitant order-of-magnitude increase in accessible time scales, and this starts getting into physically interesting regions.

The question of how many teraflops per user will be available will be less of a technological question and more of an economic and policy one. In addition to policy and economics, the pace of conversion to parallel computing will be accelerated by the ongoing development of the environment in which parallel applications are developed and executed. This environment includes operating systems, languages, compilers, debuggers, libraries, visualization aids, and parallel input/output (I/O). Each of these is considered below.

Operating Systems. The operating system of choice is currently Unix and its many relatives as implemented on various platforms. The trend toward using off-the-shelf chips makes it natural and economical to use this operating system, which is what most users are familiar with from their workstations. This at least eliminates the operating system as an obstacle to migration to MPPs.

Languages and Compilers. Certainly one of the biggest concerns of users of MPPs is the portability issue. Few users are willing to spend the time to port codes to one specific MPP platform knowing that this same code will not run on other such platforms. MPP vendors, in collaboration with university researchers, have recognized the need for standards that will guide the development of parallel languages and programming models.

One such set of standards is the Message Passing Interface (MPI), which is a voluntary set of standards agreed upon by most vendors and a large number of university researchers and developers. MPI attempts to standardize the message passing programming model by standardizing the functionality of and the calls to message passing routines. Implementation of MPI on the various platforms will be optimized by the vendors and will not be the concern of users whose codes will be portable. The MPI standard is available, and some of its implementations by the various vendors are beginning to appear. So the message-passing environment is quickly becoming standardized, which will give users more flexibility in writing their codes and in running them on a wider range of available MPPs. It is worth stressing that an important virtue of MPI is its clean separation of hardware specifics from the programming interface. This provides portability of applications and protects the often large development investment represented by complex applications.

In addition to MPI, the standard for highly parallel Fortran (HPF) has been agreed upon, and vendors have all committed to it. HPF will be very useful for users who favor the global programming model because, among other

things, it provides for the very convenient array syntax. Clearly, however, its utility extends to the message-passing domain, where Fortran 77 is currently used. Currently, HPF is in different stages of implementation by various vendors. C is also supported on most platforms and when used with MPI will provide portable C message-passing codes. A standard for parallel C (based on Thinking Machines Corporation 's C*) also has been approved and will be implemented.

A development that now plays a central role in developing commercial applications and systems software is the use of object-oriented programming techniques. C++, the most widely used object-oriented programming language, is available on a variety of MPPs. Object-oriented programming has had less impact on scientific applications programming, partly because of the large existing base of (mostly Fortran) software and partly because of concerns about obtaining maximum efficiency on vector, superscalar, and scalable parallel platforms. Nevertheless, the possibility of using object-oriented methods in developing new applications should receive some consideration. The difference between Fortran 77 and Fortran 90 is considerable, with many new constructs being introduced into the latter; the extension to HPF introduces even more constructs. It may be that the work involved (for Fortran 77 users) in developing a new program in HPF would not be substantially less than developing it in C++. The possibility of exploiting the advantages of object-oriented programming should be borne in mind when new applications are being developed.

These developments in HPF, C/C++, and MPI will make user codes less platform specific and should encourage a rapid migration of codes to MPPs. In addition to these language and compiler developments for MPPs, the same developments will be proceeding for workstations and networks of workstations. In other words, the same HPF code can be compiled and run on a single workstation, on a network of workstations, or on an MPP. The portability along such a vertical hierarchy of parallelization, the constancy of the cost per Mflop, and the advent of high-bandwidth LANs and network connections to remote sites should significantly simplify the parallel computing model. Codes can be developed, debugged, and tested on workstations available locally; small production runs can possibly be done on networks of workstations that could also be available locally; and, as computational and memory needs grow, production runs could be done remotely on MPPs. Such a parallel computing model would resemble the current scalar or vector model and would open channels of flexibility that could make parallelization attractive, or even hard to resist. However, as is currently the case for vector supercomputers, codes will require fine-tuning to realize optimal performance on specific platforms.

Development Environment. Another factor that will greatly facilitate the migration of codes to MPPs is the improving and stabilizing development environment, in the form of debuggers and parallelization aids. To aid in the parallelization of codes, preprocessors such as Forge have been developed to translate serial code to parallel code. Such preprocessors are certainly not an automatic solution and should always be approached with caution. However, when used carefully and judiciously, they can certainly aid in the conversion process. In the long term, however, achieving the ultimate performance will generally require fundamental rethinking of the algorithm being used, since some algorithms are better suited for parallelization than others.

Debuggers for both data parallel and message passing codes are currently available from several vendors. The most sophisticated debuggers are integrated graphical programming environments within which users can develop, edit, execute, debug, and profile the performance of programs written either in message passing or for global parallel execution. Features such as the visual display of timing, bottlenecks, and so on greatly facilitate the optimization of parallel code.

Execution Environment. Equally important is the availability of a good, and scalable, scientific and mathematical library. Several vendors are currently or will soon be providing

such libraries, each optimized for that vendor's MPP, thus providing optimal performance. Such calls to platform-specific library routines and functions will be easy to change (if needed) to run on different platforms. These libraries include such widely used routines as fast Fourier transforms, linear algebra, various solvers, random-number generators, and communication primitives.

Visualization. Visualization is an important part of code development, debugging, and data analysis and is, therefore, crucial for migration of code to MPPs. One reason for going to MPPs is to treat much bigger problems much faster, and by the very nature of this goal, immense data sets will be generated. Visualization of these data sets will not only be desirable but in fact vital to understanding the phenomena being studied. This presents some large problems that vendors are addressing. One such problem is the communication rate. Shipping huge data sets to graphics workstations is already becoming impractical because the transfer rates tend to be low, the available memory insufficient, and the processing speed of the workstations too slow to process such huge data sets in a timely way. Therefore, the tendency will be to do the visualization on the MPPs themselves, which will require parallel graphics packages. These packages will of course need high-bandwidth parallel I/O, which is already available from some vendors and will be available from others. Parallel I/O allows the user to access the data rapidly and the nodes of the MPP to start the visualization. For some remote users who may have difficulty transferring the full three-dimensional rotatable visualization to their screens (because of the network connection to the MPP), data reduction will be the way to solve this problem. They can, for example, transfer one isosurface at a time, or even (if the data set is exceedingly large) a single two-dimensional slice at a time. Such reduced data sets will allow remote users to benefit from the power and versatility of MPPs and parallel visualization over the network. The arrival of very fast network connections will alleviate many of the connection problems faced by remote users and the data transfer problems among computers.