Chapter 4
Implications and Opportunities for NRL
Existing materials research activities at the Naval Research Laboratory (NRL) encompass many of the fields discussed in Chapter 2 of this report. In the Condensed Matter Division a dozen or more scientists are engaged in computational and theoretical materials research, including the large Complex Systems Group. There are also scientists in the Chemistry Division active in this area. All of these researchers are trained in physics or chemistry, and the unifying theme in their research is the use of quantum mechanics. This concentration of expertise is well placed to explore the opportunities the panel identifies below.
Among the areas of computational and theoretical materials research represented at NRL are electronic structure calculations, growth phenomena, strongly correlated systems, ferroelectrics, clusters, defects, transport properties, free-energy calculations, phase changes, optical properties, many-body theory, algorithm development work on simulations of larger systems, and order-N tight-binding methods. In addition, the Chemistry Division pursues research in chemical vapor deposition, reactions at surfaces, simulation of detonations and of friction, and algorithm development in density-functional methods.
In this chapter the panel looks at the intersection of the three fundamental components of the study: (1) the technical opportunities of the coming decade, (2) the capabilities of the NRL staff, and (3) the Navy's needs. The hierarchy of theoretical approaches depicted in Figure 4.1 summarizes many of the technical opportunities. The anticipated dramatic increases in computing power affect the boundaries of the theoretical approaches. For example, increased computing power coupled with algorithmic advances, such as order-N methods, will allow phenomena
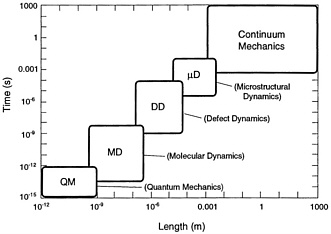
Figure 4.1 The “food chain” of theoretical descriptions refers to the use of output from calculations appropriate to one time/distance scale as input to calculations appropriate to larger time/distance scales
conventionally considered to be mesoscopic in scale to be treated quantum mechanically. One such opportunity stands out among many others in its relevance to Navy needs; it is the simulation of detonations. In addition to its technical timeliness and its Navy relevance, this topic enjoys the special virtue of not requiring the extended time scales characteristic of diffusion and polymer folding, for example. Much of this discussion can be captured in the following formula:
Computational Resources = C × N × t (4.1)
where t is the time scale of the phenomenon of interest, N is the number of particles, and C is the complexity of the theoretical description. Equation 4.1 is, in general, an oversimplification. For example, the complexity C often contains additional dependence on the system size N. Rendering C independent of N is the objective of the so-called order-N methods of electronic structure.
It is often possible to trade resource allocation between C and N—for example, the number of atoms against a classical versus quantum mechanical description of their interaction. It is seldom possible to dramatically lengthen the duration of the simulation. This allocation rule (Eq. 4.1) also highlights the limited ability of parallel computation to affect the duration t. The intrinsic serial character of molecular dynamics can be avoided only by using Monte Carlo and other intrinsically statistical approaches. The impact of computing technology on molecular dynamics simulations is suggested by the history of the size and duration of such simulations as shown in Figure 4.2 Although the extremes of time and length scales cannot yet be reached simultaneously, a large-scale molecular dynamics simulation of fracture in a short-range pair potential model has already been carried out at Los Alamos for 108 particles and 250 vibrational periods. The “food chain” of theoretical descriptions depicted in Figure 4.1 and further summarized in Equation 4.1 provides a useful framework for characterizing the opportunities for NRL in the coming decade. The food chain process requires a usefully succinct summarization of calculational output, such as fitting classical pair and many-body potentials to output from quantum mechanical calculations. These summarization links among the members of the food chain are not known in general and represent one of the foremost challenges in computational materials science. NRL enjoys competence across the entire food chain of theoretical descriptions, from the details of many-particle correlations to continuum theories of chemistry and mechanics. The synthesis of these competencies and expansion of their scope by exploiting parallel computation are the dominant themes of this report. Specific opportunities under this umbrella are identified and elaborated on in the following sections.
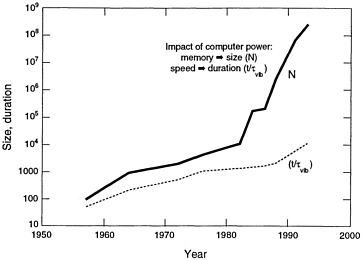
Figure 4.2 Historical growth of molecular dynamics calculations over four decades. The number of particles correlates with the growth of available memory, whereas simulation times correlate with processor speed. The particle number evolution appears to exhibit two breaks: the first in the early 1980s reflects the advent of vector supercomputers, and a second in the late 1980s reflects the advent of parallel computers.
CODE PARALLELIZATION
Opportunity 1: Parallelizing code will benefit from the consolidation of existing scalar methods. The possibility of establishing contacts with commercial firms to support such codes should be explored.
An important statement to make at the outset is that parallelization of code is a time-consuming venture and can be carried out only in an environment that has a firm, long-range commitment to this activity and to the research studies that will follow naturally from this code development.
Development of scalable code for massively parallel processors will greatly increase performance and the size of the system that can be studied. Porting an existing code to run on parallel machines is only the first step, although it still offers a computing and memory advantage, even if it does not fully exploit the hardware and software. A more significant challenge is the rethinking of algorithms and code structures. This may require a nontrivial investment of time, but the gains can be large.
To help this parallelization and optimization process, a long-term institutional commitment to parallel computing is needed. In addition, the hardware and software developments, discussed earlier, will help parallelization efforts. These developments can be simply summarized as vendor efforts to consolidate parallel languages (e.g., highly parallel Fortran [HPF]), communications interfaces (e.g., massively parallel interface [MPI]), and so on. In other words, the programming environment is being consolidated, thus making codes more parallelizable, portable, and flexible. An equally important consolidation that should take place is that of the various scalar codes that run the same applications, such as the three gaussian local density approximation (LDA) codes developed and used at NRL. It is clearly more cost-effective to parallelize a single, consolidated, streamlined code than to have various individuals do that separately, each for his or her own code. There are other benefits to such consolidation of codes. The collaboration needed to effect it will undoubtedly lead to enhancements and improvements of the scalar code itself, perhaps even to conceptual advances. Another benefit is that a consolidated scalar and/or parallel code simplifies the task of establishing contacts with software firms and the commercialization of these codes. Clearly, this will benefit users at large, in academia and industry, and would be one way to transfer technologies from government laboratories. Another benefit is that NRL would no longer need to spend resources to maintain these codes—that would be done by software companies. It is therefore important for the NRL and other government agencies to encourage and facilitate the establishment of such contacts.
INTERACTION WITH EXPERIMENTALISTS
Opportunity 2: The ability to treat more complex problems will enhance the importance of interactions with in-house experimental programs.
One of the common limitations in applying theoretical and computational results to experimental situations is the degree to which large-scale systems must be abstracted for theoretical study. The ability to treat larger systems will alleviate this, especially in the context of modeling extended systems and in the use of embedding methods. For example, in reactions at a surface a much larger region of the surface can be represented accurately, making the description more realistic. However, treating larger systems more accurately may be less important than the ability to treat more complex phenomena atomistically for the first time. Physical phenomena involved in making and breaking chemical bonds, such as fracture and the study of crack propagation and tribology, are the focus of intense interest experimentally but can be studied using molecular dynamics, for example, only for a system large enough to realistically display such effects.
The ability to treat larger systems, and to describe systems more realistically, should greatly increase the synergism between a theoretical group and experimentalists. More realistic models and fewer assumptions can substantially improve the quality and strength of interaction between theory and experiment. This is especially valuable in the NRL context, given the extensive experimental work conducted in many aspects of materials science and technologies critical to the Navy.
INCORPORATION OF CHEMISTRY INTO MATERIALS CALCULATIONS
Opportunity 3: A dramatic increase in computing power will permit enhancement of the incorporation of chemistry (thermochemical accuracy) into materials calculations.
The incorporation of chemistry into materials calculations will be enhanced by dramatic improvements in computer power and algorithmic advances. NRL can continue to serve the Navy's need to understand detonation chemistry at the molecular hydrodynamic level,
as well as tribo-chemistry (reactions at surfaces induced by interfacial friction). At present, reactive empirical bond order (REBO) potentials are used to describe, in a generic sense, the reactions under both condensed-matter detonation and friction and wear conditions. As further improvements are made to this kind of empirical potential approach, from fitting of fully quantum mechanical methods or as direct on-the-fly quantum mechanical methods become more amenable to inclusion in large-scale molecular dynamics simulations, it will be possible to expand the repertoire of chemically interesting materials for these applications. Moreover, in the area of materials failure or corrosion, a challenge (and opportunity) exists in treating chemistry that occurs at the crack tip, as well as interactions of crack tips and dislocations with impurities. The existing capabilities in tribology and detonation chemistry (experimental and theoretical) at NRL merit encouragement in terms of both staff levels and computing facilities.
ADVANCES IN THE TREATMENT OF ELECTRON CORRELATIONS
Opportunity 4: Theoretical advances in the treatment of electron correlations are an important problem with broad implications for algorithmic development and the enhancement of computer codes.
In addition to new methods and algorithms and more computing power for treating increasingly realistic and complex systems, the issue of accuracy is a critical one for many applications in materials research. Even the qualitative behavior of materials such as the cuprous oxides requires accurate treatment of the effects of many-electron correlations because of the relatively stronger Coulomb interaction in these systems. Although standard electronic structure calculations based on the local density functional approximation yield highly accurate structural properties for many systems, they often have difficulty in describing the properties and phase diagram of highly correlated magnetic systems such as the d- and f-electron materials. Moreover, LDA cohesive energies and energy surfaces (e.g., along reaction paths) are generally not given to the level of chemical accuracy. This is an issue of particular concern in molecular dynamics simulations in which accurate dynamic and thermodynamic quantities, such as defect diffusion or melting of solids, are desired.
Much effort and progress were made recently in improving the treatment of electron correlations in materials computation. Advances have been and are continuing to be made along several directions. One direction is to remain within a self-consistent field density functional formalism but to go beyond the LDA for ground-state properties. Another is to use many-body perturbation theory for excited-state properties such as photoemission and optical properties. Yet another is to deal directly with the many-body wave function by using correlated wave functions and quantum Monte Carlo techniques. Theories going beyond LDA are aimed at improving the description of the electron exchange-correlation hole using various schemes such as the generalized gradient approximation and the weighted-density approximations. For example, although there remain problems in general applications, the generalized gradient approximation has recently attracted considerable attention because of its improved results on molecular properties and on cohesive and magnetic properties of selected solids. The GW approximation discussed under optical properties earlier in this report is an example of a successful use of many-body perturbation theory for treating electron correlations in excitation energy calculations. Among the different approaches, quantum Monte Carlo methods are perhaps the most involved computationally and conceptually but probably the most accurate, because the many-electron wavefunction and various correlation properties are computed directly in the simulations.
These recent advances in the treatment of electron correlations thus provide some unique opportunities and challenges for computational
materials research. Methods with chemical accuracy would provide the needed predictive power for materials designed by using computers. Past work in this area has been mostly on theoretical developments and tests of the validity of approximations. Efforts on algorithmic efficiency and adaptation to new machine architectures remain to be carried out in most cases. NRL researchers are actively involved in many of these developments. In view of the significance of this subject to the theoretical foundation of materials theory and applications, it is important that NRL continues to participate in this most basic component of materials research.
BRIDGING THE ATOMIC AND MESOSCOPIC SCALES
Opportunity 5: Dynamic properties of materials will become amenable to study using system sizes that bridge the gap between atomic- and mesoscopic-size scales.
Our ability to model the dynamical properties of materials is limited by the fact that with the current generation of computers it is essentially impossible to achieve the system sizes and time scales relevant to experiments. The most interesting dynamical problems involve the emergence of large-scale structures that show subtle dependence on the smallest scales in the problem. To see these structures, simulations must involve large numbers of atoms evolving over long periods of time. For example, in fracture dynamics it remains an open question to understand the emergence of subsonic propagation speeds of the crack tip and micron-scale pattern formation on the crack surface. In molecular dynamics simulations, the current state of the art involves the simulation of large two-dimensional systems and considerably smaller three-dimensional systems. The applied stress is often much larger than that used in experiments in order to generate results in computationally observable times. For example, irregular patterns are generated in these simulations that emerge at significantly smaller wavelengths than observed experimentally. The connection between the numerical observations and the experiment remains unclear for many of these features. Similar problems arise in modeling other dynamical phenomena, such as growth, tribology, cavitation, and surface reconstruction. In each case the underlying forces are local, so advances in parallel computing will have a significant impact. In addition, each increase in performance and memory capability will allow more realistic simulations.
Because the behaviors involve such a wide range of scales, modeling of the dynamical properties of materials involves a range of numerical techniques. For example, in modeling growth, ab initio calculations lead to interatomic potentials. These are then used in molecular dynamics simulations to obtain rate constants for different categories of interactions. Finally, kinetic Monte Carlo simulations incorporate those rates into larger-scale simulations of atomic motion. Expertise in all of these areas currently exists at the NRL. The challenge will be for researchers to work effectively together to bridge the gap between different length and time scales.
STRENGTH OF MATERIALS
Opportunity 6: Dramatic improvement in code performance will permit study of the strength of materials across a broad front.
The strength of materials is intimately related to the creation and propagation of extended defects (e.g., edge and screw dislocations), as materials that contain few dislocations (such as whiskers) can approach the theoretical yield strength limit. An issue closely related to the ultimate strength of a material is crack propagation. For example, metals will exhibit plastic deformation via dislocation mechanisms before failure, whereas ceramics will not exhibit plastic deformation before failure by crack propagation.
Clearly, the microscopic description of extended defects and crack tips is an important,
but complex and challenging, issue. While continuum theories of crack and dislocation propagation are useful, they are severely limited in providing quantitative theories of materials strength (e.g., they cannot describe atomistic details of the crack tip). For this reason, microscopic descriptions are becoming increasingly important for predicting and describing real materials. Since a microscopic dynamical description of crack formation and dislocation generation may involve hundreds of thousands of atoms, there are few quantitative approaches to this problem. Techniques such as the embedded atom method can be used for many-body interactions in simulations of crack and dislocation propagation in metals, but these procedures are computationally intensive when millions of atoms are involved. Moreover, the time scales for dynamical simulations are often incommensurate with experimental time frames.
An additional two orders of magnitude in computing power should result in realistic descriptions at an atomistic level. Many more atoms could be handled. For shock and impact simulations the time frames of the theoretical simulation may be in registry with the experimental circumstances. NRL researchers possess sophisticated capabilities in the area of atomistic simulations and are well positioned to take advantage of such computational advances. It is reasonable to expect that the next generation of parallel computers will result in dramatic improvements in predicting the strength and failure of materials, especially metallic alloys. On the other hand, a fully quantum mechanical description of extended defects and crack propagation is probably not forthcoming with an additional two orders of magnitude of computing power. Nonetheless, it will probably be possible to extract key interatomic interactions via quantum calculations on salient subunits of the systems of interest.
PREDICTING THE OPTICAL PROPERTIES OF MATERIALS FROM FIRST PRINCIPLES
Opportunity 7: Linear and nonlinear optical properties of a wide variety of materials will become amenable to study.
The prediction of the optical properties of materials is a particularly challenging task because standard electronic structure methods are typically ground-state theories that afford poor descriptions of electronic excitations in materials. Nevertheless, determination of the optical properties of materials is of critical importance in several technological areas (high-speed communications, solid-state lasers, display technologies, and so on) and global security activities (detectors and sensors for nonproliferation monitoring and intelligence, underwater communication, and so on). Recent theoretical and computational developments in the area of ab initio calculations of quasi-particle energy eigenvalue spectra indicate that optical transitions in materials can be accurately predicted from first principles. In addition, these ab initio quasi-particle methods can serve as the basis for accurate calculation of energy levels of point defects in materials that are of central importance in several technological applications, such as scintillators and phosphor materials used in display technologies. In light of these recent theoretical advances, as well as the importance to the Navy of optical detectors and sensors, several oportunities exist for NRL to enhance its current core competencies in the area of ab initio determination of the optical properties of materials. Given the costly and time-intensive investments needed to synthesize, characterize, and manufacture novel materials with desirable optical properties, the development and implementation of theoretical methods that afford predictive capabilities of the optical properties of materials are likely to have a significant impact on optical materials research and development. Moreover, extension of NRL's materials theory program in the area of ab initio description of the optical properties
of materials would provide an opportunity to develop synergism with experimental groups at NRL currently involved in the optical properties of quantum-confined structures.
The development of detector and sensor materials is of central importance to the Navy's missions. These include detection in both the visible and nonvisible electromagnetic spectrum. As a result, augmentation of NRL's current theoretical and computational materials physics capabilities to encompass prediction of the optical properties of materials would be of direct programmatic relevance to the Navy' s missions and programs.
Calculation of the optical properties of materials from ab initio quasi-particle methods is currently limited to approximately 100-atom systems, including complex systems such as surfaces and interfaces, fullerenes, and color centers in alkali halides. The emergence of massively parallel computing environments offers unprecedented opportunities to apply current ab initio methods to materials systems of increasing structural and chemical complexity. These applications will require substantial effort in order to efficiently implement current ab initio quasi-particle methods on emerging massively parallel platforms. At the same time, effort should be expended in the areas of algorithms and formalism development, such as the implementation of efficient real-space formulation of quasi-particle methods. These formalisms would allow substantial improvement with respect to the number of possible materials systems that can be treated.
ALLOY PHASE DIAGRAMS
Opportunity 8: Phase diagrams and kinetic properties near phase transitions for a wide variety of systems will be possible with vastly improved accuracy.
The ground-state properties of many elemental and binary systems can now be calculated to obtain heats of formation to chemical accuracy (0.01 eV atom) or better. This includes distinguishing between various competing crystallographic structures and the deviations from linearity in binary systems owing to electronic interactions and relaxation. From atomically fully relaxed calculations for various ordered configurations, accurate numerical values (no longer adjustable parameters) can be extracted to be used in truncated but otherwise exact cluster expansions or Monte Carlo simulations. This expansion converges fairly rapidly and provides the link between statistical, mechanical, and ab initio quantum mechanical electronic structure studies. A prominent opportunity in this context is the use of electronic structure calculations to contribute to the databases utilized by semiempirical theories of material-phase diagrams, such as CALPHAD.
Accurate phase diagrams of coherent alloys with line compounds, narrow phase fields, miscibility gaps, and wide homogeneity regions without artificial symmetries about specific compositions are capable of being correctly produced, including accurate solidus-liquidus temperatures and compositions. Systems that have already shown great promise are binary combinations of s-p metal-transition metals, transition metal-noble metals, and transition metal-transition metal and semiconductor alloys. The extension to ternary systems is, in principle, straightforward albeit time consuming; it is in fact what computers do best. For coherent alloys the conceptual framework is sound and the extension of this theory to more complex systems would increase its relevance to the Navy's needs. The capability exists at NRL to make a significant contribution to this area, since parallelized codes allow a large number of systems to be treated in a reasonable time frame. The correlation of alloy stability with alloy properties should affect the mechanical properties and strength issues.
Inclusion of the effects of magnetic phenomena and pressure on the phase diagram and properties is a relatively unexplored area awaiting both computational and theoretical advances. Similarly, the treatment of a
geometrically general random alloy is still very much an open issue.
DETERMINATION OF PHENOMENOLOGICAL INTERACTIONS FROM ELECTRONIC STRUCTURE CALCULATIONS
Opportunity 9: Substantial improvements in the determination of phenomenological potentials from electronic structure calculations will be accelerated.
The abstraction of phenomenological parameters (i.e., both their formulation and extraction of actual values) from detailed calculations at one time/distance scale to be used at the next higher level remains one of the outstanding challenges of this field. Phenomenological interactions pass information from the lowest time and distance scales in the hierarchy of Figure 4.1 , speeding up the calculations by not dealing with the finer-scale complexity and by increasing the realism in the larger scale. This process is based on the fact that the larger scales average over many of the details of the smaller scale. An important issue to remember is that since the approaches used for the larger-scale problems only incorporate part of the detail of the finer scale, it must be ensured that the proper details are represented correctly. Electronic structure calculations can now reliably determine the electronic properties of tens of atoms (including transition metals), and this can be extended easily to hundreds. Approximate replacements for the self-consistency process can extend this even further. Another tactic that can extend the range of electronic calculations is to calculate accurate results for a region of importance surrounded by a medium of lesser significance. Such embedding schemes that deal with the properties of clusters in a medium have been partially successful with improvements “on the horizon” for years. A real problem remains in the determination of a parameterization. However, although the extraction of parameterizations for coherent alloys has been demonstrated, even the formulation of a chemically and geometrically general formulation of parameterization is a largely unsolved problem. To expand the scale further means proceeding from quantum-level treatments to atomic-level simulations. The basis of this step is to characterize the electronic structure properties in terms of approximate systems such as cluster expansions, embedded atoms, potential induced breathing models, and tight-binding representations. A significant limitation of such schemes is the issue of charge transfer. Nonetheless, they have a wide range of applications. To treat longer-range interactions, albeit with reduced accuracy, polarizable atom-type models can be applied for nonmetallic systems.
Such interchanges between the time and distance scales shown in Figure 4.1 are exemplified by dislocation mesoscale dynamics. The interactions in question include core repulsions, attractions between opposite-sign dislocations on the same slip system, and creation and annihilation mechanisms. All of these can be obtained from large-scale molecular dynamics simulations. They then provide the interaction laws for dislocation dynamics, where the fundamental “particles” are defects rather than atoms. In turn, the behavior of a large number of dislocations under various loading conditions provides information for microstructural continuum models. Finally, these latter simulations allow constitutive laws (or models) to be constructed for use in continuum engineering simulations at the macroscopic level. Occasionally, there are phenomena that are already able to be modeled by a continuum description on the time and distance scales accessible to molecular dynamics, but usually the links between overlapping parts of the chain shown in Figure 4.1 must all be used to obtain practical (macroscopic) modeling information.
Epilogue
Given the rapid pace of change in the computer industry today, it is clear that the details of the computer-related issues in this report will continue to evolve quickly. Advances made in algorithmic design will inexorably lead to scientific progress that will then bring other challenges to the forefront. The panel has thus attempted to articulate only general strategies that relate largely to machine-independent issues and that are based on today's scientific standard. The opportunities outlined in this report indicate possible future directions, each of which involves many intricacies that will become clear only as progress is made. Thus, any specific actions taken as a result of this document must be reviewed and adapted on a continual basis.










