3  The Research Endeavor
The Research Endeavor
The brief story told in Part 2 illustrates how much the world has changed in recent years and the enabling role that condensed-matter and materials physics is playing in modern technology. We turn now to a closely related topic, the fundamental scientific challenges of research in this field. Once again, the capitalized words in the main text link to sidebars that provide more information on a few selected topics.
What is “condensed-matter and materials physics”? Fifty years ago, the transistor emerged from this area of physics. High-temperature superconductivity was discovered by condensed-matter physicists, as were the fascinating low-temperature states of superfluid helium. Scientists in this field have long-standing interests in essentially all aspects of magnetism and magnetic materials. They investigate the properties of glasses, polymeric materials, granular materials, and composites in which diverse constituents are combined to produce entirely new substances with novel properties. They are reaching out to researchers in the earth and atmospheric sciences because they share interests in topics such as friction, fracture, and fluid flow. The outreach to biology and the study of biological materials are now beginning in a serious way.
Hardly any other field of science so seamlessly spans the whole range between the most basic research and the most applied. Advances in basic research inspire new ideas for applications, and application-driven technological advances provide tools that enable new fundamental investigations. At the same time, technological problems raise questions that demand new fundamental insights. For example, with new fundamental understanding of NONEQUILIBRIUM PHENOMENA, we may soon see a qualitative improvement in our ability to predict and control complex properties of the structural materials used to manufacture everything from airplanes and bridges to electronic devices. Technological advances provide tools such as synchrotrons, neutron sources, electron microscopes, high magnetic field facilities, COMPUTERS, and
|
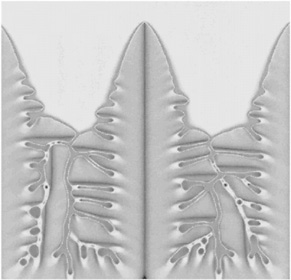
NONEQUILIBRIUM PHENOMENA The processes that are used to produce industrial materials—casting alloys for jet engines or fabricating microscopically small features of computer chips—are all exercises in what we call “nonequilibrium physics,” the study of systems that are changing their shapes or properties as we exert forces on them, freeze them, or otherwise disturb their states of equilibrium. Predicting and controlling these processes with the precision that will be needed for applications requires fundamental understanding of the nonequilibrium phenomena underlying them and is a challenge for physicists. For example, snowflakes form by a branching process that is called “dendritic crystal growth.” Research in this area has been driven not only by our natural curiosity about snow-flakes, but also by the need to understand and control metallurgical microstructures. The interior of a grain of a freshly solidified alloy, when viewed under a microscope, often looks like a collection of overly ambitious snowflakes. Each grain is formed by a dendritic mechanism in which a crystal of the primary composition grows out rapidly in a cascade of branches and side branches, leaving solute-rich melt to solidify more slowly in the interstices. The speed at which the dendrites grow and the regularity and spacing of their side branches determine the observed microstructure, which in turn governs many of the properties of the solidified material such as its mechanical strength and its response to heating and deformation. We cannot yet predict microstructures accurately, but much progress has been made in the last decade. Figure 3.1 shows one of the best new theoretical efforts in this direction. Much of the most important recent progress in nonequilibrium physics has consisted simply of recognizing that fundamental questions remain unanswered in many familiar situations. The recent growth of interest in fracture and friction, for example, has led us to realize that we need to establish first-principles understanding of the difference between brittleness and ductility, especially in noncrystalline materials. We are learning about the dynamics of granular materials, systems that are like liquids in some respects, like solids in others, and unlike either in many of the most important ways. And we are just beginning to learn which questions to ask in a search for understanding the dynamics of fracture at crack tips, failure at interfaces between different solids, or rupture on earthquake faults. |
SCANNING PROBE MICROSCOPES. These tools, in turn, provide unprecedented opportunities to investigate materials on the atomic scale, leading to fundamental discoveries that drive both science and technology. The new physics of THE FRACTIONAL QUANTUM HALL EFFECT, for example, was made possible by new materials fabrication technology. The study of MATTER UNDER EXTREME CONDITIONS has led both to fundamental and practical breakthroughs.
Several of the most profound conceptual developments in science have occurred in CMMP in the last two decades. The so-called “renormalization-group ” theory of critical fluctuations in condensed matter has helped us understand phenomena as varied as phase transformations, the interactions between elementary particles, and the fluctuations of the stock market. Chaos, turbulence, and pattern formation are other core concepts in this field that have had wide-ranging implications across the world of science. The historic role of condensed-matter physicists, ever since the emergence of quantum electronics and the transistor, has been to discover new concepts and phenomena and to develop their new knowledge in ways that are meaningful for fundamental advances in many fields and for practical applications.
|
SCANNING PROBE MICROSCOPY Although the atomic picture of the world was formed over a century ago, it is only in the last few decades that compelling visualization of atoms has become possible. Since there are only 92 stable elements, the diverse materials known to us derive their complexity for the most part from the patterns of their atoms' arrangement, in molecules and in solids. Direct atomic-scale visualization of these patterns allows us to develop new materials and better understand old ones. It has been used to look at the action of semiconductor devices, the workings of chemical reactions, and the structure of genes. Many new visualization tools emerged from condensed-matter and materials physics. One such advance was the invention of scanning probe microscopy. In this class of techniques, a sharp needle-like tip is moved around (scanned) near a surface. A map of the surface is then constructed in real time by measuring some response of the surface to the tip —the force of the surface on the tip, for example, or the electric current that flows between the tip and the surface. Using precision actuators called piezoelectrics, a tip can be moved up and down or sideways by less than the size of an atom. Scanning the tip across the surface in this way while measuring the response allows an atomic-level image to be built up, much as a blind person can acquire a mental picture of an object by feeling its shape. 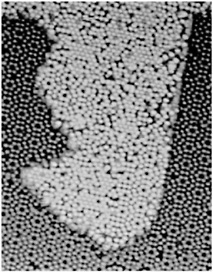 FIGURE 3.2 A scanning tunneling microscope image showing a snapshot of the growth of germanium on a silicon surface. Each bright spot is a single atom. (Courtesy of IBM Research.) The first suggestion of a super-resolution microscope can be traced back as far as 1928 to the British scientist E.H. Synge, but the first working scanning probe microscope with atomic resolution was not invented until 1981, at IBM's research laboratory in Zurich, Switzerland. In the decade and a half since then, a wide variety of related visualization techniques have been developed. Scanning probe techniques now exist that allow atomic-scale sensing and mapping of electrical, optical, and magnetic properties, surface forces, and other phenomena. A particularly important recent innovation has been the possibility of using a scanning tip not just to study a sample but also to manipulate atoms actively. The “quantum corral” shown on the front cover and in Figure 1.3 was made in this way. This microscopic atom-by-atom “engraving”makes even microsurgery look like the metaphorical bull in the china shop. |
What does the future hold for condensed-matter and materials physics? There must be many surprises in store for us. Consider the fact that essentially none of the most important discoveries in this area made in the last decade were anticipated in the 1986 National Research Council report Physics Through the 1990s. And the pace of scientific change, especially when viewed on an international scale, is now accelerating.
A particularly dramatic surprise was the discovery in 1986 of HIGH-TEMPERATURE SUPERC0NDUCTIVITY, which disproved a consensus then growing among scientists that superconductivity could exist only at temperatures very near absolute zero. Now, just over a decade later, we are beginning to see commercially marketed devices based on superconductivity at easily accessible liquid-nitrogen temperatures, and we can look forward to decades of new developments. Even more important, condensed-matter and materials physicists have learned that chemically complex materials, like the new superconductors, can have extraordinarily interesting properties. The study of such complexity in solids is emerging as a whole new style of inquiry.
|
HIGH-TEMPERATURE SUPERCONDUCTIVITY By the mid-1970s it seemed that the limiting temperature for superconducting materials was near 25 K, a temperature still requiring expensive liquid helium cooling. Theoretical calculations based on the mechanism that controlled electron pairs in known superconductors indicated a maximum temperature for superconductivity of less than 40 K. In 1986 a totally unexpected, even shocking, discovery was made. A class of copper oxide ceramic materials was found to become superconducting at temperatures much higher than 25 K. We now have many complex materials that become superconducting at temperatures well above the boiling point of inexpensive liquid nitrogen, 77 K. The occurrence of superconductivity in a totally unexpected class of materials, and the potential for its practical use above the temperature of liquid nitrogen, have motivated a wide range of research and development efforts over the past decade. Superconductivity has now been observed in specially prepared ceramics at temperatures as high as 135 K. Despite extensive worldwide efforts, however, an understanding of the mechanism for superconductivity in the new oxide materials is still lacking. For example, physicists cannot reliably predict whether a material could exist that would superconduct at room temperature. These new materials are brittle ceramics, with properties completely different from those of the ordinary metals in which low-temperature superconductivity occurs. Paradoxically, in their pure state, these oxides do not conduct electricity at all—they are magnetic insulators. Even when charge carriers are introduced by chemical doping, they are poor conductors at room temperature. 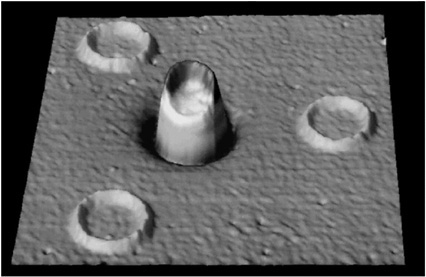 FIGURE 3.5 This magnetic image shows four high-temperature superconducting rings, each 60 microns in diameter, fabricated on at a constant elevation above the substrate. The volume of each structure thus represents the magnitude of the magnetic flux trapped within that ring. The trapped flux in the center ring is exactly half the unconventional electron pairing. (Courtesy of IBM Research.) The superconducting state itself appears to have pairs of electrons orbiting around each other in an unconventional manner. (See Figure 3.5.) The sensitivity of this state to magnetic fields presents technological challenges that must be overcome for certain practical applications; but on the positive side, it has also led to exciting new fundamental scientific ideas. The discovery of high-temperature superconductivity has focused attention on the enormous variety of complex oxide materials. In addition to superconductivity, many of these materials exhibit other novel magnetic and electrical properties. |
A different kind of unanticipated complexity is emerging in ARTIFICIALLY STRUCTURED MATERIALS, engineered with features so small that they behave like artificial atoms. These structures are candidates for the next generation of computing elements, but their potential uses in both science and technology go far beyond computing as we know it. As we learn how to assemble increasingly complex structures from more and more complex building blocks, perhaps even from biological molecules, we can anticipate a whole new world of scientific phenomena and practical applications.
Other completely unexpected discoveries of the last decade include FULLERENES, and carbon nanotubes—spherical and cylindrical arrangements of carbon atoms that have remarkable chemical and structural properties. Even more glimpses of the future have recently been provided by observations of intrinsically quantum mechanical behavior in systems so large that they had been thought to be outside the realm where such effects could occur. Such macroscopic quantum phenomena include Bose-Einstein condensation of collections of large numbers of atoms and the excitonic laser. Suddenly, deep philosophical questions about the meaning of observations in quantum mechanics are becoming relevant to the development of entirely new kinds of electronic devices, perhaps even the development of ultrafast quantum computation.
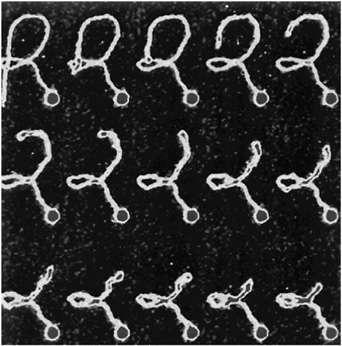
Surely one of the most significant developments on the horizon is the movement of condensed-matter and materials physics into the biological and medical sciences. Here, in parallel with advances in materials, communications, and information technologies, is the other scientific revolution that has profoundly changed our world in recent decades. Modern medical techniques such as magnetic resonance imaging and laser surgery were made possible by research in physics, and THE PHYSICS OF MACROMOLECULES is a well-established area of research at the intersection of physics, chemistry, and biology. Nevertheless, physics laboratories so far have played only relatively minor roles in mainstream biological research.
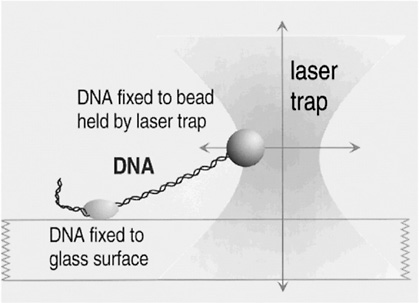
That situation is about to change. Although we could hardly have imagined such possibilities a decade ago, we now have instruments such as scanning probe microscopes and OPTICAL TWEEZERS that allow us actually to see what large molecules are doing inside biological cells and even to measure the forces that they exert on one another. In centers around the world, scientists are just beginning to use these new tools to solve critical problems involving the physics of biological systems. These problems are posing entirely new intellectual challenges; the implications of their solutions are likely to be immense.
As these examples illustrate, condensed-matter and materials physics is a vital field at the very crossroads of the scientific enterprise. It combines the intellectual stimulation of investigations at the frontiers of human knowledge with the satisfaction of providing insights and capabilities that can improve all our lives. ![]()