invariably they were better. The new program ran faster on the examples given in the first paper. However, it was never clear how much of the speedup was due to a faster machine, better programming, or tuning of the algorithm to the specific examples in the first paper. In fact, it was not clear whether if one ran both programs on some new instances of the problem, the original program might not be faster.
To overcome this problem, researchers set out to develop a science base for algorithm design. They adopted a mathematical criterion for determining the goodness of an algorithm, namely, asymptotic complexity. This allowed one to talk about the quality of algorithms, to develop techniques such as divide-and-conquer, which often yielded asymptotically optimal algorithms, and to organize and codify the knowledge of algorithms and algorithm design. Today our knowledge in this area has grown tremendously; textbooks have been written and practitioners have been educated far beyond the knowledge and state of the art in programming as it existed in the 1960s. It is this kind of development that we are seeking when we try to develop a science base for modeling and simulation and for information capture and access.
In this lecture I will select a number of examples from my institution to illustrate points. I use these examples because I am familiar with the technical details. They also are representative of the type of research going on today at many institutions across the United States and around the world.
MODELING AND SIMULATION
Figure 1 shows a model of an antenna. The antenna is 150 feet across but folds up into a space of approximately 1 cubic foot. Before deploying such an antenna in space, it is important to verify that it
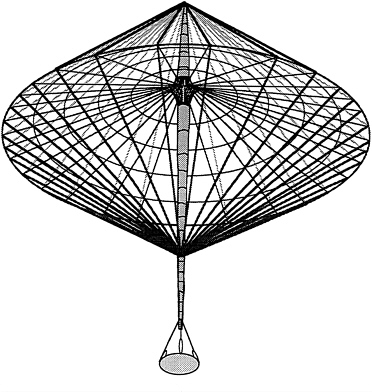
FIGURE 1 Space antenna.
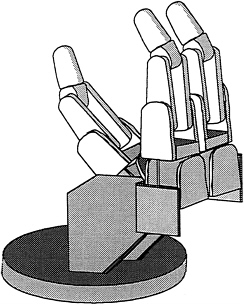
FIGURE 2 3-finger JPL gripper.
will deploy properly. Doing this by building a physical prototype of the antenna is impossible. The antenna is made primarily of cables and will not support its own weight under gravity. Even if one could build a physical prototype, one would be reluctant to test a dejamming procedure because if the antenna should jam in deployment, the procedure might destroy the prototype. In this situation, computer modeling and simulation are an essential tool, allowing one to electronically simulate deployment and dejamming without risk.
Figure 2 is a picture of an electronic prototype of the 3-finger JPL gripper. We wanted to experiment with gripping and rotating objects and selected this particular gripper to prototype electronically because we had access to the engineering drawings. The prototype is more than just a solid model of the gripper. The model has properties such as mass and inertia and the ability to represent forces on the cables in the fingers. The modeling system, NEWTON (Cremer, 1989), takes a description of an object such as this gripper and allows one to program the gripper to grasp or manipulate an object and to view the simulation on a workstation. What is novel about NEWTON is the automatic creation of a simulation from a physical description of an object, and the capability of an event handler to detect if a collision takes place during a simulation. If a collision does take place, NEWTON also appropriately modifies the equations governing the simulation to account for the new constraints.
Since the model of the gripper is only a computer file, one can edit it. Figure 3 shows a 4-finger version. One quickly realizes that one has the ability to explore finger placement, length and number of fingers, size and shape of gripped objects, and so on. Thus, a designer could explore a large design space, which would be impossible if he or she were dealing with a physical gripper. One can try out designs by simulating actual situations in which a dextrous gripper would be used. This ability to design and test objects by simulation will facilitate the creation of new, better, and less expensive objects for all.
Daniela Rus, a graduate student at Cornell University, used the electronic prototype of the gripper in her Ph.D. thesis on manipulation of objects (Rus, 1991). Her work extends earlier research on grasp
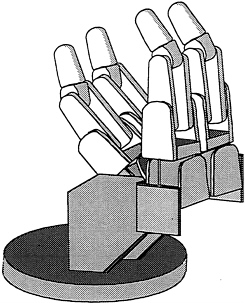
FIGURE 3 4-finger JPL gripper.
closure to actual manipulation and is the start of a science base for dexterous manipulation. One expects to see very general theorems about manipulations, theorems such as the following:
This algorithm will rotate any convex object whose ratio of maximum diameter to minimum diameter is less than two.
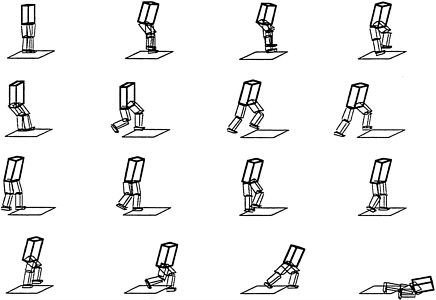
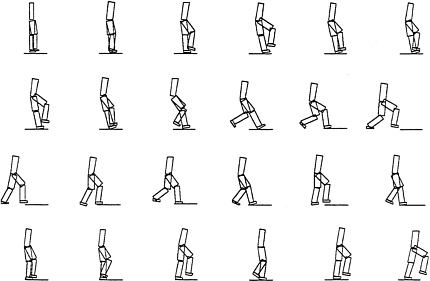
Several researchers have created simple models of humans and walking devices and have used the model-driven simulation system (NEWTON) to study walking. Examples of such use are illustrated in Figure 4a and Figure 4b.
Previously, research in these areas was restricted to a small number of well-funded institutions that could afford to build and operate mechanical walking devices. Now, a number of researchers at diverse institutions are studying robust algorithms for walking. Another advantage of simulation is the ability to handle rough terrain, reduced gravity, heavy winds, and other such parameters. Once an algorithm for walking fails and the device crashes, electronic models do not need to go into the machine shop for repair of mechanical breakage.
Today, computing power is cheap enough that we can simulate simple devices. The important issue is what is the science base that will support this activity? I will discuss two of the technical areas where work is needed. The first has to do with solid modeling.
Reliability in Solid Modelers
One of the major problems that arose during this work on simulations was the lack of a reliable solid modeler. At the time this work was started, many commercial solid modelers were available. However, all of them seemed to have a problem with reliability. The modelers had been constructed to work with objects in general position. In our environment, objects were almost never in general position; they were
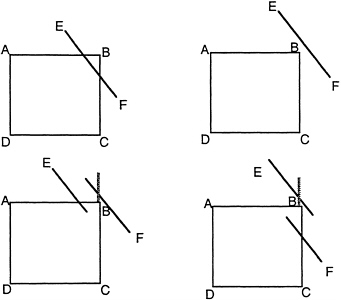
FIGURE 5 Intersecting squares.
in degenerate position. For example, if a gripper was going to grasp a cube, at the time of contact the side of the cube would be parallel with the side of the gripper and the modeler would fail. On careful examination the cause of failure became apparent.
To see what was happening, consider Figure 5, which illustrates the situation where one is trying to determine if two squares intersect. Suppose that the squares are so close to intersecting that one cannot tell by numerical computation on which side of the line EF the vertex B lies. That is, B is closer to EF than the numerical accuracy of the original data. One might ask if line segment EF intersects AB between A and B and then determine by a numerical computation that the answer is yes. Next, one might ask if line segment EF intersects BC between B and C, and due to numerical round off, one would get the answer no. In this case, one is left with the inconsistent situation illustrated in the bottom right corner of Figure 5. Clearly, the solution in this case is to rearrange the computation so that only one numerical computation is done, and the answer to both of the above questions is derived from it. The example given is simple enough that this is possible. However, in a three-dimensional solid modeling, the problem is more complex (Stewart, 1991).
What we learned is that there are basically two types of computation:
-
Symbolic or discrete computation involving exact logical quantities, such as graphs, discrete structures, text, and so on, and
-
Numerical or engineering computation involving floating-point numbers that approximate values of physical entities.
If one is dealing solely with symbolic computation, then one can write a provably correct program, and indeed these programs are reliable. Similarly, if one is dealing solely with numerical approximations, one can again write programs that work reliably. In fact, if the initial approximations are sufficiently close and careful numerical techniques are applied, the results will be close to the true
FIGURE 6 Irrational object.
answers. The difficulty occurs when one tries to combine both numerical and symbolic computation. If one does a single conversion from numerical data to symbolic data, then no difficulty is likely to occur. The reason for this is that there is probably numerical data close to the actual numerical data that is consistent with whatever decision is made in the conversion to symbolic data. However, if one does multiple conversions, then there is a possibliity of making inconsistent decisions in the sense that there is no numerical input data that is consistent with those decisions.
An engineer might try to solve this problem by using double-precision arithmetic. However, double-precision arithmetic only hides the problem. A mathematician might suggest arbitrary precision arithmetic or symbolic computation. Neither of these methods provides a solution since data is not always exact to start with and may even be inconsistent. It is necessary to solve the underlying problem. If we can do that, then single precision is adequate. In fact, we can use faster, but numerically less stable, algorithms.
Some authors have proposed using rational arithmetic. Clearly, this is not satisfactory, since, as Figure 6 shows, an arrangement of lines can be drawn in the plane but cannot be drawn if one is restricted to rational arithmetic. That is, the coordinates of at least one intersection point must be irrational.
One solution for creating a reliable solid modeler would be to rearrange the computations so that only an independent set of conversions from numeric to symbolic data is made. Then no difficulty will arise. It is surprising that, for many problems, it is possible to arrange the computation so that all conversions are logically independent. This can be done, for example, with the problem of interesecting two polygons in a plane. Similarly, it can be done for intersecting convex three-dimensional objects (Hopcroft and Kahn, 1992). However, such a solution is not known for intersecting arbitrary three-dimensional solids.
One test of a solid modeling system is to take an object such as a cube and rotate it by an angle theta about each of its axes, and then intersect the rotated version with the original for small angles of theta. At the time we were testing solid modelers, most modelers worked for theta above 2 degrees and some even for 1/2 of a degree. Using the principle of making decisions as independent as possible, we were able to construct a modeler such that one could reduce theta to 1/10, 1/100, 1/1,000, and 1/10,000 of a degree. We did not go below 1/10,000 of a degree since at that point the modeler concluded that the two objects were identical and returned the original object as the intersection.
What happens as theta is made smaller is the following. For theta equal to 2 degrees or greater, modelers return the true intersection of the two cubes, a figure with 20 vertices. For theta equal to 1/10,000 of a degree, we get the original cube with 8 vertices. For angles in between, the modeler begins to identify various pairs of vertices in the true intersection that are very close together. The reason modelers crash in this region is that the decisions made in these identifications are made inconsistently. Our modeler always made these decisions in a consistent fashion, and as theta decreased, the output went through a series of consistent topologies until that of the original cube was reached. To further test the reliability of the modeler, we selected two small values for theta for which the output topologies were different. Then by divide-and-conquer, we shrank the interval until we found a and b such that a and b gave rise to different output topologies, but (a + b)/2 = a in the precision used. The algorithm still worked (Hopcroft et al., 1989).
SimLab
One of the lessons learned from NEWTON was that one should raise the level of abstraction even higher. The Xerox Corporation, in an effort to increase the flow of information between universities and companies, set up a small laboratory called the Design Research Institute and located it on the engineering campus at Cornell University. The Xerox employees in this laboratory have appointments as visiting scientists at Cornell and interact closely with faculty and students. A serendipitous output of this relationship occurred one day when our modeling and simulation group looked at a simulation that some Xerox employees had done. The simulation was that of some particles moving in an electric field around a wire onto a charged piece of material. The simulation had required a fair amount of time to assemble the required software packages and to get them to operate with each other. We immediately recognized that NEWTON could have done the simulation, if NEWTON were slightly more general. After all, the simulation involved the integration of partial differential equations, just exactly what NEWTON did. The only difference was that the partial differential equations were different since there was an electromagnetic field.
We had built Newtonian mechanics into NEWTON. However, had we abstracted out the laws of Newtonian mechanics and built a simulator generator that took as input the physical equations and produced as output a simulator that itself took as input a description of a physical scene and produced as output a simulation, then we could have switched domains from dynamics to dynamics plus electrostatics. This situation is illustrated in Figure 7.
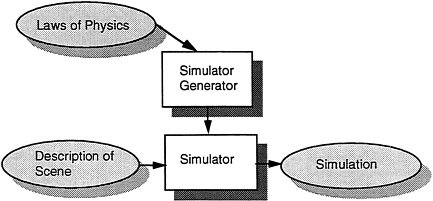
Figure 7 SimLab.
The important lesson learned is that symbolic manipulation systems can be used to transform physics, as presented in a textbook, to a running FORTRAN program. The higher conceptual level allows small groups to write, in a few weeks, codes that previously required long periods of time and person-years of effort. It should also allow one to retarget codes more easily to a new architecture. In the past, there was a single model of computation, the von Neumann model. Each new generation of computer, with its increased speed, caused all programs to execute faster. Today, as parallel architectures evolve, we can no longer expect a program coded for one architecture to automatically execute on a newer machine with a different parallel architecture. Recoding promises to be a major impediment, particularly if the time to recode an application is several years and thus comparable to the lifetime of a given machine architecture. Moving to a higher conceptual level of programming will become a necessity.
Triangulations
As our work on modeling and simulation progressed to fluids and other branches of physics, a need for meshes arose. In two dimensions, we faced the problem of triangulating a planar region, making sure that no triangles had small angles. Triangles with small angles are undesirable in that they lead to larger error in certain iterations. A method developed by Paul Chew was very effective and had the advantage that it provided guaranteed lower bounds on the size of angles in the triangulation (Bern and Eppstein, 1992). The method is based on Delaunay triangulations.
The method developed by Chew is to start with a set of points with no two points closer than one unit. A triangle is formed from each set of three points that defines a circle not containing any additional points. Such a triangulation is called a Delaunay triangulation ( Figure 9). If the radius of any circle formed by three points of a Delaunay triangulation was greater than one unit, Chew added a point at the center of the circle and repeated the process of creating a Delaunay triangulation. Note that the point at the center of the circle is at least one unit away from any other point, and thus that property is preserved. The process is repeated until we have a Delaunay triangulation with no large circles (radius greater than one) and no two vertices closer than one.
At this point we have a Delaunay triangulation in which no triangle has any angle less than 30°. To
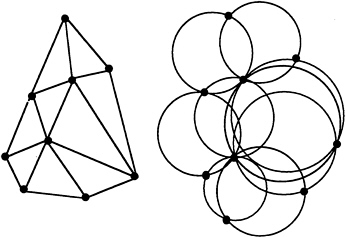
FIGURE 9 Delaunay triangulation argument.