3
Development of a Dosage-Response Relationship
The weight of additional survey information, more consistent interpretations of reported physical measurements, supplementary laboratory findings, and limited theoretical understanding all suggest that the dosage-response relationship recommended by CHABA (1981) warrants revision. The following sections develop a rationale for constructing dosage-response relationships from the information currently available. Although these relationships are preferable to that recommended in 1981 (which was based on even less information), they too are intended as interim recommendations only.
LIMITATIONS OF UNDERSTANDING
A dosage-response relationship implies that variability in the quantity plotted as the independent variable on the abscissa is wholly and uniquely responsible for variability in the quantity plotted on the ordinate. Ideally, a dosage-response relationship is a product not merely of a regression analysis conducted on a few data sets, but also of a well-founded theoretical understanding of the relationship between the predictor and predicted variables. Understanding of this sort generally arises only after a thorough competition among differing theoretical accounts for a large body of detailed, methodologically sound empirical findings.
The reality of the present case is far from ideal. No large body of field studies exists, but only a sparse set of correlational observations of uneven quality and comparability. Fundamental understanding of the source of community response to impulsive noise exposure remains rudimentary at best, since only a
few formal theoretical treatments have been attempted. However, a small body of laboratory judgments of the immediate annoyance of high-energy impulses provides some guidance in interpreting the findings of survey data on community response to high-energy impulsive sounds.
In these circumstances, selection of variables for dosage-response relationships is of necessity somewhat arbitrary, and proximity to data points is not necessarily the principal consideration in formulating a relationship useful for environmental assessment purposes. The predictor variable must also be a simple, plausible, and preferably causal one that can be readily explained and understood, easily calculated, and conveniently manipulated for environmental planning and other comparative purposes.
PURPOSE AND APPROACH TO PREDICTION
The purpose of a dosage-response relationship in the current circumstances is to enable useful predictions to be made of a covert attitudinal variable (annoyance) from an empirically measured (or predicted) acoustic variable. Individuals and communities are undoubtedly sensitive in some degree to essentially all aspects of noise exposure: its level, spectral composition, and variability (in level, time, and space) not to mention its origins, history, novelty, predictability, tonality, onset time, timing, duration, and, of course the interactions of all such factors. The history of quantitative prediction of community response to noise exposure has been a continuing effort to find the smallest subset of these factors that in combination can account for useful amounts of variance when applied to disparate communities.
Ever since the pioneering work of Rosenblith and Stevens (1972), “community response”—construed for present purposes as the prevalence of annoyance—has been predicted from some type of integration of noise exposure. This is not the only possible strategy for predicting community response, but it is at least an expedient one that has proven serviceable in the case of nonimpulsive noise. The approach is useful not only because it works tolerably well for practical purposes, but also because it permits simple manipulation of exposure variables and analysis of impacts of noise environments that may vary widely along several dimensions.
It is difficult to argue on the basis of empirical evidence, however, for a strong causal relationship between any metric of noise exposure and community response. The fact that useful estimates of community response may be made for some purposes over a 20 dB range from about Ldn = 55 to 75 dB does not mean that annoyance is uniquely caused by a time-weighted average of sound levels. Oddly, the very utility of DNL as a predictor variable has contributed to confusion over the root causes of community response to noise exposure. DNL em
bodies a number of assumptions (about frequency weighting, time of day of exposure, and the fungibility of level, duration, and number of events as determinants of annoyance) that may have little to do with the factors that actually generate annoyance in residential populations.
Because the relationship between DNL and community response is not known to be a causal one, challenges to the assumptions of DNL (notably the equal-energy hypothesis) are not necessarily challenges to the predictability of community response. The arguments advanced in the rest of this chapter lead to two alternate means for predicting the annoyance of impulsive noise exposure. Until a better understanding of the origins of community response to impulsive noise exposure arises, both of these interim approaches should be viewed as expedients rather than as tacit theories about the origins of annoyance. Briefly, these two approaches may be summarized as:
Method 1: Adaptation of Green and Fidell (1991) Model. The Green and Fidell (1991) model of community response to nonimpulsive noise exposure may be adapted to the impulsive noise case by a minor change in the value of a single parameter.
Method 2: Level-Dependent Summation. Schomer's (1994) nonequal energy summation model accounts for the contribution of each impulsive noise event to long-term annoyance in a level-dependent manner.
CHOICE OF METRICS
The working group that produced CHABA (1981) selected the prevalence of a consequential degree of annoyance as the predicted variable of its recommended dosage-response relationship, in part for the sake of consistency with the metric selected by Schultz (1978), and in part for lack of any clearly superior metric. Annoyance remains the most robust and well-documented effect of noise exposure on communities (Fields, 1993). No information developed since 1981 suggests a need for revisiting this decision.
CHOICE OF FREQUENCY WEIGHTING AND INTEGRATION METHOD
Confusion persists about the implications of annoyance prediction schemes adopted by earlier CHABA working groups in part because previous reports have not fully discussed the rationale for their choices. Since further study by CHABA of the problem of current interest is unlikely in the foreseeable future, this rationale is discussed at greater length below.
Frequency Weighting
The use of C-weighted sound exposure level and C-weighted day-night average sound level for describing the noise environment produced by high-intensity impulsive sounds was proposed first in CHABA (1977). Two reasons were cited:
-
The use of C-weighting provides a reasonable measure of the low-frequency sound pressures associated with high-energy impulses of the type under consideration; and
-
The use of sound exposure level instead of peak sound level meets the need to incorporate a measure of signal duration, since perception of noisiness increases with signal duration.
CHABA (1981) retained C-weighted day-night average sound level as the predictor variable of its recommended dosage-response relationship. C-weighted DNL was selected not because of its high correlation with the metric selected for the ordinate, or because clear evidence showed that its correlation with annoyance was any greater than that of A-weighted DNL. Instead, CDNL was selected as a predictor variable for five other reasons:
-
The obvious precedent of dosage-response relationships synthesized for general transportation noise suggested that adoption of a similar time-weighted average predictor variable for an impulse noise relationship would facilitate its understanding and acceptance.
-
Environmental analyses conducted for purposes related to the National Environmental Policy Act of 1969 routinely require evaluation of a proposed action and various alternatives to it. A cumulative noise metric such as DNL permits ready comparison of the effects of different sets of noise sources and operating conditions. Thus, for example, the use of DNL as the predictor variable of a dosage-response relationship facilitates analyses of the environmental effects of alternate aircraft fleets, numbers and paths of flight operations, times of day of flyovers, and so forth.
-
C-weighting was preferred to A-weighting in part because A-weighted measurements may fail to discriminate among impulsive sounds with widely varying amounts of very low-frequency energy (e.g., sonic booms), and because A-weighted measurements do not correlate well with secondary emissions of structures.
-
C-weighting was preferred to A-weighting in part to preclude the erroneous inference that measures adequate for mitigating impacts of A-weighted noise exposure could be effectively applied to mitigating the effects of impulsive noises as well.
-
C-weighted sound exposure level is very stably related to peak overpressure for sonic booms. (The standard deviation of the differences between the two
-
only rarely exceeds 2 dB.) The difference between A-weighted sound exposure levels of sonic booms having the same peak overpressure may be as much as 20 dB or more. Since most predictive models for sonic booms calculate overpressures as their primary measure, the reliable predictability of CSEL is an important concern.
Nothing learned about the predictability of community response from noise metrics in the years since the 1981 working group recommended use of CDNL as a predictor variable is sufficiently compelling to merit consideration of a different frequency weighting for present purposes. Neither C-weighted nor A-weighted noise metrics are well enough correlated with annoyance to account for the bulk of the variance in the relationship between the predictor and predicted variables, and the differences in correlation between various metrics of high-energy impulsive noise and annoyance that have been reported in different data sets are neither consistent nor great enough to outweigh the five factors noted above.
Integration Method
It is well established that sounds of increasing duration are judged as increasingly more annoying (see Fidell et al., 1970, for a demonstration of this effect over a range of four decades in time). It is also well accepted that sounds of greater level are reliably judged more annoying than sounds of lesser level. Aggregation of a series of sounds by summing the mean-square values of their sound exposures, in accordance with what is commonly referred to as the equalenergy hypothesis, accords equal weight to both of these effects. In doing so, the hypothesis intentionally confounds the effects of level and duration on annoyance, such that annoyance is predicted to grow in direct proportion to increases in either the level or the duration of sounds.
Most schemes for predicting the annoyance associated with long-term exposure to a complex noise environment have been based on the integration of noise exposure in a manner consistent with the equal-energy hypothesis. Construction of such predictor variables from individual noise events occurs in three steps. First, the noise of individual events is converted to a sound exposure level to normalize the events to a reference duration of 1 second. Second, the level of the mean-square sum of sound exposure over a representative 24-hour day is formed (with or without more or less arbitrary adjustments for time of day of occurrence, depending on the predictor variable of choice). Third, the (weighted or unweighted) sum of sound exposure levels is normalized to a 24-hour time period by subtracting 49.4 dB (10 log [86,400], the number of seconds in 24 hours).
The equal-energy hypothesis plays two roles in the above process:
-
It justifies assignment of equal weight to duration and level in calculating sound exposure levels of individual noise events; and
-
It justifies assignment of equal weight in the summation of the sound exposure levels of individual impulsive noises that leads to an equivalent level value.
Schomer's laboratory and controlled-exposure studies suggest the possibility of achieving greater accuracy of prediction of community response to high-energy impulsive noise through a level-dependent summing of CSEL values of individual impulses into a variant form of CDNL. As described in Appendix B, it can be argued from the findings of Schomer's controlled-exposure studies that this summation into C-weighted impulsive DNL of CSEL values should give increasingly greater weight to CSEL values of greater magnitude. This approach is referred to henceforth as a “level-dependent summation process.” To differentiate C-weighted impulse DNL in which the summation of the SEL values is dependent on their magnitude from DNL, the resulting DNL is abbreviated CIDNL instead of CDNL. The letter symbol for CIDNL is LCIdn.
POSSIBLE FITTING FUNCTIONS
If the inference of a dosage-response function were simply a curve-fitting exercise, then the great variability of the primary data set (Figure 2) would provide little compelling basis for choice among various fitting functions. The sigmoidal form of the exponential fitting function adopted in CHABA (1981) was preferred to a linear fitting function not on the basis of a least-squares criterion or a logistic regression, but rather because it was unreasonable to permit predictions of the prevalence of noise-induced annoyance in a community to increase indefinitely. An informal weighting of the influence of each data point led to consensus decisions about the slope and the absolute position of the curve seen in Figure 1.
Since the data points available today still do not greatly constrain the choice of fitting functions, logical rather than purely curve-fitting grounds must still be sought for inferring a dosage-response relationship. The three most compelling considerations are those of first principles, whatever guidance the findings of controlled-exposure studies and limited theoretical understanding can provide, and expedience. Expedience alone suggests the importance of preserving some consistency with previous practice, minimizing the costs of physical measurement and exposure prediction, and ease of understanding.
Table 2 summarizes four plausible approaches to the prediction of the annoyance of impulsive noise exposure that could in principle be adopted for present purposes. (Yet others, such as a centile-based threshold method, are also possible, but were not pursued for pragmatic reasons.) As described in greater detail below, the working group considered that the disadvantages of the first two prediction methods described in Table 2 outweighed their advantages, and that the last two approaches were more appropriate in differing circumstances.
TABLE 2 Alternate Approaches to Predicting the Prevalence of Annoyance Associated with Exposure to High-Energy Impulsive Noise
|
Name of Approach |
Predictor Variable |
Nature of Variable |
Advantages of Prediction Scheme |
Disadvantages of Prediction Scheme |
|
Method 1 |
CDNL |
Equal energy sum of CSEL values of individual impulsive noises |
Simplicity (attributes annoyance exclusively to exposure); consistency with CHABA (1981) recommendation and direct comparability with standard prediction methods for nonimpulsive noise impacts; straightforward measurement of noise exposure |
Fails to account for bulk of variance; inconsistent with some laboratory findings; requires acceptance of equal energy hypothesis |
|
Loudness level-weighted DNL |
Energy sum of SEL values with nonstandard frequency weighting |
Consistent with equal energy hypothesis; would probably yield results similar to use of CIDNL as a predictor variable due to weight given to low-frequency energy |
Substantial increase in complexity of measurement and calculation of noise exposure; inconsistent with preferred frequency weighting for measurement purposes; unknown ability to account for variance |
|
|
Method 2 |
CDNL adjusted for nonacoustic factors |
Equal energy sum of CSEL values of individual impulsive noises, adjusted for response bias |
Reduction in variance of data set; straightforward measurement of noise exposure; consistency with prediction methods developed for nonimpulsive noise impacts |
Partial loss of consistency with standard approach to predicting annoyance of nonimpulsive noise exposure |
|
Impulsive Noise Day-Night Average Sound Level (CIDNL) |
Level-dependent summation of CSEL values based on differential rates of growth of annoyance for impulsive and nonimpulsive sounds |
Consistency with findings of a body of controlled-exposure studies; demonstrable reduction in range and variance of data set; systematic approach to prediction of annoyance of mixed (impulsive and nonimpulsive) noise environments |
Substantial increase in complexity of measurement and calculation; loss of consistency with standard approach |
Adaptation of Green and Fidell (1991) Model
Fidell et al. (1988) and Green and Fidell (1991) have shown that a simple one-parameter model can account for appreciably more variance in community response to general transportation noise than empirical data fits. This model considers noise exposure as a form of treatment administered to a community. The response of the community to the treatment is determined by applying a criterion for reporting annoyance to the average noise dose. The effective dose produced by exposure is assumed (as in the original CNR system) to grow at a rate similar to the growth of loudness with level (i.e., a twofold increase in dose for every 10 dB increase in signal level).
Variability in the prevalence of annoyance in communities that is not accounted for by a loudness-based transform on DNL is attributed to response bias. Among the many nonacoustic factors that may affect the prevalence of noise-induced annoyance in communities are various attitudes toward noise sources and their operators (approval, fear, distrust, etc.), socioeconomic levels of individuals, and economic dependence on the operation of noise sources.
This approach follows from recognition of two separable components in self-reports of annoyance: a component directly linked to noise exposure and an entirely independent component associated with individual willingness to describe oneself as annoyed to some degree. The latter component is referred to as response bias. The two components are confounded in a verbal report of the form “I'm very annoyed by that sonic boom,” since the self-report alone provides no way to distinguish the contributions of the acoustically related factors from the contributions of response bias to the expressed degree of annoyance. For lack of adequate means of distinguishing the two components, most interpretations of self-reports of annoyance tacitly assume that the contributions of response bias to annoyance are negligible.
Given that acoustic and nonacoustic determinants are confounded in individual self-reports, it follows that they are also confounded in the proportion of respondents in a neighborhood who describe themselves as highly annoyed by noise exposure. Two communities in which the same proportions of residents describe themselves as highly annoyed might have quite different noise exposures. Similarities of this sort in response to disparate noise exposures are attributed to difference in response biases among the residents of the two communities. Civic action groups, political or media attention, and other factors can make the residents of the quieter community more likely to describe themselves as highly annoyed even by relatively low noise exposures.
More specifically, reactions of individuals in the community to noise exposure are assumed to be exponentially distributed with a mean population value, m. The value of m in the case of nonimpulsive noise is assumed to be related to the day-night average sound level by:
10 log m = 0.3 Ldn. (4)
Thus, noise exposure creates a distribution of reactions within a community with a mean value that increases with the level of noise exposure. Individuals describe themselves as highly annoyed when their reactions to noise exposure exceed a fixed value of a criterion (A) for reporting annoyance. The net effect of the nonacoustic factors on the decision-making process is to shift a dosage-response function back and forth along the abscissa. The proportion of the population describing itself as highly annoyed is predicted as follows. Suppose
P = e−A/m (5)
where P is the probability of reporting high annoyance, m is defined as in Eq. 1, and A is the criterion value for reporting annoyance. As described above, the value of A may vary from neighborhood to neighborhood for any of a number of nonacoustic reasons.
The criterion value for reporting high annoyance, D, may be expressed in exposure-like units. If D is defined for the nonimpulsive case as
D = (1/0.3) 10 log A,(6)
then Eq. 4 may be rewritten as
10 log [−ln P] = 0.3 (D* − Ldn), (7)
or as
10 log D, or D*, is a decibel-like quantity that represents the average value of the criterion for reporting annoyance in units directly comparable with DNL values.
Schomer's (1991) comment on this approach, as well as the NASA data summarized in TABLE 1, suggest adoption of a value larger than 0.3 for the exponent to account for a more rapid growth of annoyance with level for impulsive sounds. A value of 0.45 is a reasonable summary of the data contained in Table 1. Thus, the proportion of a community highly annoyed by high-energy impulsive noise exposure would be predicted as shown in Eq. 9:
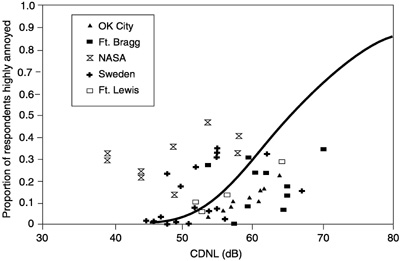
FIGURE 8 Dosage-response relationship of Method 1: Adaptation of Green and Fidell (1991) model.
where D* is the constant 61.1 chosen to minimize the variance of the set of available field observations of the annoyance of high-energy impulsive noise exposure.
Figure 8 shows a relationship developed from the rationale of this discussion that can be used for environmental assessment purposes to predict the prevalence of annoyance associated with exposure to high-energy impulsive noises (Method 1). Figure 9 compares the relationship of Method 1 with that recommended in CHABA (1981). Note that the new relationship predicts a greater prevalence of annoyance than the former relationship in the region above LCdn = 50 dB.
Level-Dependent Summation Approach
Many of the laboratory findings discussed in Chapter 2 show that: (1) a 1 dB increase in the CSEL of a blast sound corresponds to about a 2 dB increase in the ASEL of an equivalently annoying control sound and (2) test subjects are indifferent to the difference among the annoyance of a blast sound at a CSEL of 103 dB, a vehicle passby at an ASEL of 103 dB, and band-limited white noise at an ASEL of about 104 dB.
These two findings imply that it is possible to construct a method for predicting the prevalence of annoyance by defining an “annoyance unit” (abbreviated AU) numerically equivalent to a unit of sound exposure for nonimpulsive sounds
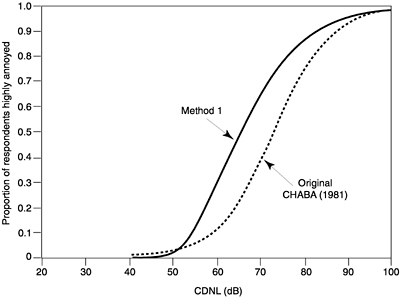
FIGURE 9 Comparison of dosage-response relationship recommended in CHABA (1981) with Method 1 (Adaptation of Green and Fidell (1991) model, using CDNL as the predictor variable).
measured in A-weighted units.1 Since the sound exposure unit is chosen to be equal to 1 pascal-squared second (per ANSI S12.8-1988), 10 times the logarithm to the base 10 of the numerical value of AU exactly equals ASEL. This convention respects and preserves all of the machinery for working with A-weighted exposures created by nonimpulsive sources. Thus, a 3 decibel change in level corresponds to both a doubling of A-weighted sound exposure and a doubling of annoyance units. Sound exposure and annoyance units would also double with each doubling in numbers of events of the same sound level. Equal trading between number of events and event magnitude (sound exposure or annoyance units) is also preserved. Note that this definition of annoyance does not require community response to increase linearly with sound exposure.
|
1 |
Although this new metric, annoyance unit, is obviously closely related to the corresponding sound exposure, the name was chosen to distinguish it as a measure of sound exposure modified to reflect the annoyance associated with this exposure. |
TABLE 3 Annoyance Units (AU) as a Function of SEL (Method 2)
|
Annoyance Units (AU) |
||
|
SEL (dB) |
A-weighted sounds |
C-weighted sounds |
|
88 |
0.25 |
0.0078 |
|
91 |
0.5 |
0.031 |
|
94 |
1 |
0.125 |
|
97 |
2 |
0.5 |
|
100 |
4 |
2 |
|
103 |
8 |
8 |
|
106 |
16 |
32 |
|
109 |
32 |
128 |
|
112 |
64 |
512 |
|
115 |
128 |
2,048 |
|
118 |
256 |
8,192 |
|
NOTE: This table is calculated using Eqs. 10 and 11. |
Annoyance from high-energy impulsive sound does not fit this model. For blast sounds, two incoherent events at the same sound level produce double the C-weighted sound exposure (+3 dB) and double the number of equivalent annoyance units. But a change of +3 dB in the CSEL of a single high-energy impulsive sound produces a much greater change in annoyance response than a doubling of equivalent annoyance units would indicate. For a relationship in which the slope is on the order of 0.5, a 3 dB change in high-energy impulsive sound level corresponds to about a fourfold increase in equivalent annoyance units. Put another way, four high-energy impulses, each creating a CSEL of X dB, correspond in terms of equal annoyance to one impulse creating a CSEL of about X + 3 dB. One A-weighted sound exposure unit would equal one annoyance unit, but for CIDNL the entries in Table 3 would be used to calculate level-dependent annoyance units from CSEL. For any high-energy impulsive sound CSEL (in Table 3), a level-dependent, C-weighted impulsive AU (symbolized as χCI) is given by:
where LCE is the letter symbol for CSEL. For nonimpulsive sounds measured in units of ASEL, AU equals the sound exposure (symbolized by χA) and is given by:
where LAE is the letter symbol for ASEL. The general form of Eq. 10 is given
below. Note that χCI and χA both equal 8 at an SEL value of 103 dB, but that χCI has a factor of 2 in its exponent. This factor of 2 provides the conversion to the high-energy impulsive sound model suggested by Schomer's laboratory data. When the SEL increases by 3 dB, annoyance units double for A-weighted sounds but increase fourfold in χCI units.
Eq. 10 is a specific case of the more general equation:
where LCE is the letter symbol for CSEL. The term LA = C-94 relates the equality level to the sound exposure level of 94 dB, which corresponds approximately to the sound exposure for a sound pressure of 1 Pa (pascal) and a duration equal to the reference sound-exposure duration of 1 s. In Eq. 10, with the equality level in Eq. 12 set equal to 103 dB, this term reduces to the number 8. Also, in Eq. 10 the slope, β, is 0.5.
Just as one may calculate ADNL from day-night A-weighted sound exposure (abbreviated ADNSE, symbol Edn), one could calculate day-night average annoyance unit level (AUDNL) from total day-night annoyance units (abbreviated DNAU, symbolized χdn). Simply,
where po is the reference pressure of 20 µPa and 86,400 is the number of seconds in a day. Eq. 13 can also be written as
where ![]() is the level of the average A-weighted sound exposure and n is the number of events. Thus,
is the level of the average A-weighted sound exposure and n is the number of events. Thus,
Following Eq. 14, Eq. 15 can also be written as
where ![]() is the letter symbol for the average level of the event annoyance unit exposure and n is the number of events. For example, if the annoyance units calculated from CSEL using Table 3 totaled 300 in some high-energy impulsive sound environment, then this environment would be equivalent to a common
is the letter symbol for the average level of the event annoyance unit exposure and n is the number of events. For example, if the annoyance units calculated from CSEL using Table 3 totaled 300 in some high-energy impulsive sound environment, then this environment would be equivalent to a common
sound environment in which the DNASE and the annoyance units totaled 300. From Eqs. 13 and 15, the area in which the DNASE or DNAU equals 300 corresponds to an area in which the ADNL is about 70 dB.
As an example, consider a single impulsive sound with a CSEL of 109 dB. From Eq. 10,
χC = 8 × 2[(109−103)/1.5]
= 8 × 24 = 128. (17)
From Eq. 15,
Lχdn = 10 log(128) + 54.6 = 75.7. (18)
Computing AUDNL is especially simple if the underflying distribution of CSELs comes from a Gaussian distribution, as is often the case (Sutherland et al., 1990; Schomer and Luz, 1994). Then, from the arithmetic median CSEL, L(50)CE, and standard deviation, σ, one can calculate the mean-square “annoyance” exposure level, LχE, by:
where β is the slope of the relation between the CSEL of a high amplitude impulse sound and an equivalently annoying control sound and LA=C is the equality point (the point at which the impulse sound CSEL and its equivalently annoying control sound ASEL are equal). For the case where β = 1, Eq. 15 reduces to the well known
LχE = L(50)CE + 0.115 σ2
= L(50)CE (20)
which, of course, is independent of LC=A. For LC=A equal to 103 dB and β equal to 0.5, Eq. 15 reduces to
LχE = 103 + (2) (L(50)CE − 103) + 0.115(2)2 σ2 . (21)
For example, consider a sonic boom distribution with mean CSEL of 100 dB and a standard deviation of 6 dB. For 8 booms per day, Eq. 21 yields the energy-average annoyance unit level of each boom as
LχE = 103 + (2)(100 − 103) + 0.115(2)262 (22)
= 103 − 6 + 16.6 = 113.6.
Then from Eq. 18
Lχdn = 113.6 + 10 log(8) − 49.4 = 72.6. (23)
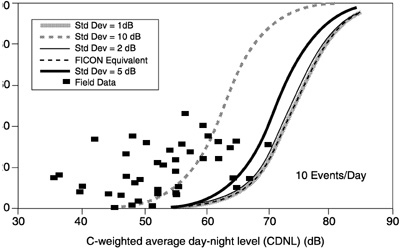
Figure 10 and Figure 11 show nominal dosage-response relationships produced by the level-dependent summation method for two cases: 10 and 100 high-energy impulsive sounds per day. Because the standard deviation of the distribution of impulsive sounds is used (in conjunction with an assumption of normality of distribution) to approximate the effect of the level-dependent summation process, the curves are parametric in the standard deviation of the distribution of impulsive sound levels. Under typical field conditions, the standard deviations of actual distributions of sonic booms propagating over long ranges at different times of day are probably closer to the higher values plotted than to the lower values.
Figure 12 shows the relationship between the available social survey data points and the dosage-response relationships for the level-dependent summation method. A comparison of the data points with the dosage response curves suggests that standard deviations greater than 10 dB must be assumed for reasonable agreement with the bulk of the field observations.
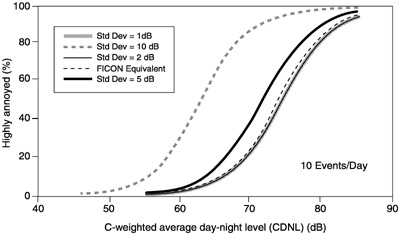
FIGURE 10 Dosage-response relationship of Method 2 (level-dependent summation) using CDNL for 10 events per day.