5
ANALYTICAL AND NUMERICAL MODELING
Quantification of the risk of failure, either progressive or catastrophic, open hole or cased, during drilling or production, requires the calculation of stress and/or deformation fields around the wellbore and a comparison with accepted criteria of failure. These calculations can be performed with varying degrees of sophistication and with varying predictive limitations.
Two major cases will be considered separately. The unsupported case, often referred to as the open hole situation in petroleum applications, will be discussed first.3 Then a section will be dedicated to the cased/supported circular openings.
Unsupported Openings
Most of the existing work on borehole stability is based on perfectly elastic/plastic models that are calibrated with test data taken from conventional triaxial compression experiments. Rupture is assumed to occur when the stresses reach the elastic limit that is usually set at the peak of the experimental stress-strain curve.
|
3 |
In the petroleum and drilling engineering fields, muds are very often present in the hole; hence, the wellbore is hydrostatically loaded to prevent the caving in of the walls. |
Elastic Analysis
The solution for the stresses and displacements due to an infinite circular hole in a homogeneous, isotropic, linear elastic medium is given by the superposition of Kirsch's solution (the antiplane solution), and the solution for an internally pressurized hole of arbitrary orientation (Fairhurst, 1968; Deily and Owens, 1969; Daneshy, 1973a; Bradley, 1979; Richardson, 1981; Hsiao, 1987; Yew and Li, 1987). Stress transformations and assessment in a local coordinate system are a routine mathematical exercise. The solutions at the borehole wall can be simplified, with little loss of accuracy, by assuming Poisson's ratio to be equal to zero (Li, 1986). As discussed earlier, the major difference between a borehole (horizontal or otherwise) drilled parallel to a principal axis and one noncolinear is that one of the shear components, τθz, remains finite at the borehole wall. Its magnitude affects the overall integrity of the borehole, and the principal stress tensor will be rotated in the neighborhood of the circular opening.
Knowing the stress field associated with a particular wellbore configuration, various failure mechanisms can be assessed.
-
Tensile failure. One This criterion states that tensile failure will occur when the minor principal stress4 reaches the tensile strength of the medium. Two generic kinds of tensile failure can be envisioned. The first occurs at or close to the borehole wall (Santarelli et al., 1986; Detournay and Cheng, 1988) and the fracture trace can theoretically be at an angle to the borehole axis; this has been experimentally observed by Kuriyagawa et al. (1988). The second kind does not intersect the borehole, is concentric, and by itself may be kinematically stable. The principal stresses at the wall of the borehole and the theoretical trace of the fracture on the borehole wall are given by Daneshy (1973b).
If these borehole pressurization tests are conducted at slow pumping rates, multiple fracture development is favored. At higher rates, fracture coalescence may occur almost instantaneously, potentially leading to a “quasilongitudinal” macroscopic fracture, aligned along the borehole axis (Baumgärtner et al., 1989), at least near the wellbore. Rationalization for such rate dependency and for micro- vs. macroeffects is not satisfactory. In addition to predictions of the initiation angle, the elastic theory discussed indicates an orientation dependency on the fracture initiation pressure.
|
4 |
By convention, compression is taken as positive. |
As the orientation of the wellbore changes, the pressure required for failure changes (either in tension as the wellbore is pressurized in hydraulic fracturing or in shear as the wellbore is produced). The initiation pressure is not necessarily a monotonic function of the orientation. There may be specific orientations, in 3-D space, where the pressures required for initiation and breakdown are maximized.
From a practical viewpoint, there is sometimes a misconception that once the in-situ stress tensor is known and one is contemplating a horizontal hole, it suffices to drill this hole parallel to the minimum horizontal stress component. Then, successive isolation and pressurization cycles should induce a series of transverse fractures. As Strubhar et al. (1975) asserted, such a generalization is risky, and laboratory experiments (Scott et al., 1953; Daneshy, 1973a) have shown that fractures preferably initiate parallel to the borehole axis. This is substantiated further by Baumgärtner et al. (1989), who conducted laboratory testing on large blocks subjected to true triaxial loading. Generalized plane strain elastic theory predicts that the fracture trace (initiation) on a deviated well makes an angle with the borehole axis. A multiplicity of such inclined en échelon features may therefore be initiated. Also, the theory of elasticity predicts that each fracture begins at the same circumferential location on the borehole, presuming no interaction. Except for the case of extremely small flow rates, these fractures may not have a chance to extend before a new en échelon fracture is initiated. The consequence on a macroscale is that these features may effectively coalesce to form a quasilongitudinal fracture.
On the contrary, Bjarnasson et al. (1988) and Ljunggren et al. (1988) pointed out that it is also feasible to induce large enough transverse stresses (generated by Poisson's effects) to cause failure perpendicular to the wellbore trajectory.
-
Shear failure. This mechanism can occur in an active mode (inward movement) during production or in a passive mode during pressurization. If wedges of rock are produced and fall inward, there is little consequence in wells that are not highly deviated from the vertical during drilling unless severe bridging has occurred. These offending pieces fall to the bitface and are reground. In wells deviated at least in excess of 60 to 75 degrees from the vertical, this debris is a potential source of future problems such as bridging and sticking (Tomren et al., 1983; Okrajni and Azar, 1985; Wilson and Willis, 1986). As with tensile failure, there are a number of criteria available for determination of the potential for shear failure. A Drucker-Prager criterion incorporating frictional characteristics, taking into account all
-
stresses acting on the medium (major, minor, and intermediate) (e.g., Bradley, 1979), is commonly used for oilfield stability assessment.
-
Matrix collapse. This is a colloquial description associated with volume reduction and densification of the medium. This can occur in poorly consolidated formations and in rocks that have an unusually large porosity (Ruddy et al., 1988). This failure is controlled by the hydrostatic compressive strength of the medium. When this parameter is exceeded by the mean stress, the porous matrix collapses.
It should be noted that although there are many published accounts of such elastic analyses being used, the predictions are likely conservative. Indeed, they cannot account for pseudo-stable states associated with progressive failure and redistribution of stresses due to nonelastic material properties. Furthermore, the failure mechanics in rock is more than just a routine strength-of-materials exercise. From a micromechanics point of view, a process zone will be inherent ahead of the fracture tips. To rationalize a marriage between initiation-related effects and propagation effects, e.g., represented by linear elastic finite elements, several minimum assumptions must be recognized, including scale conditions wherein the instantaneously initiated fracture is of sufficient length for a smooth transition between the two extreme disciplines of consideration (Ingraffea, 1987).
Inelastic Analysis
Despite the fact that the elastic approach is widely used in the design of circular openings, it is viewed as being insufficient to predict quantitatively failure and to describe various failure modes observed in underground excavations, as well as in instrumented hollow cylinder tests. The assumption of linear elastic behavior up to failure leads to excessive stress concentrations at the borehole wall. Cases of abnormal stability as compared to the theoretical stress concentration given by linear elasticity are frequently observed in situ or in hollow cylinder experiments. This point of view is emphasized in Guenot's (1987) review of experimental results from hollow-cylinder testing for a great variety of materials (sandstone, limestone, coal, marble, granite, etc.).
There may be justification for the presumption of brittle behavior. Ewy et al. (1988a, 1988b) cite failure of thick-walled cylinders of sandstone by brittle spalling. They offer the following scenario for the failure process around thick-walled cylinders, without invoking strain softening:
-
Progressive spalling occurs in which intact slabs of fairly uniform thickness are successively separated from the surrounding rock by fractures approximately parallel to the free surface.
-
This process starts as extensile spalling and potential propagation parallel to the maximum tangential stress.
-
These features turn to meet the free surface (pseudoshear) (Horii and Nemat-Nasser, 1988). The resultant stabilized triangular surface, characteristically seen in breakouts, may therefore not be shear-related (Pollard and Holzhausen, 1979; Nemat- Nasser and Horii, 1982).
There is ample evidence that the consequent behavior is a reflection of the intermediate principal stress, stress gradients and related geometric effects, the stress path, and likely the strain rate.
Guenot and Santarelli (1988) support this premise, citing Kaiser et al. (1985) who demonstrated the inability of strain-softening to describe failure initiation. Despite these observations, particularly in rock at extreme depth or in moderately unconsolidated formations, there is indisputable evidence that the medium may not respond in a completely elastic manner to the stress field associated with the introduction of a wellbore, and that a “plastified” region can develop around the borehole in which the stress distribution will be totally modified.
Examples of such behavior include squeezing, when the mud pressure in wellbores penetrating ductile rock does not prevent progressive inward movement, potentially resulting in ellipticity. Bradley (1979) reports occurrences in salt and shale. Fuenkajorn and Daemen (1988) cite examples in salt. Many other situations have been reported.
Elastoplastic analyses have been performed by a number of authors (Risnes et al., 1982; Detournay and Fairhurst, 1987; Fjaer et al., 1987; Gumusoglu et al., 1987; Santarelli and Brown, 1987). Such analyses were presented to determine the stress and displacement fields around a circular opening, taking into account the existence of intact (elastic) and failed (plastic) zones, using appropriate constitutive relations.
As another example, Shi (1988) proposed generic viscoelastic failure modes dependent on the magnitude and relative values of σrr, σθθ, and σzz and the mud weight.
Maury (1987) also specified plastic analysis for oil field operations, delineating various failure mechanisms as a function of mud weight, a wellbore pressure analog. The various modes of failure correspond to different stress regimes prevailing at the wellbore wall.
Detournay and Fairhurst (1987) emphasized the concept of obliquity and presented a methodology to determine the relationship between the far-field stress (vertical wellbore in an isotropic horizontal stress field) and the failure modes. Their discussion confirmed that if elastoplasticity is invoked, for statically determinate conditions, the greatest extent of failure should be expected in the direction of the least compressive stress (as also seen for elastic calculations and in laboratory testing).
A major drawback of the previously described classical procedures is the inadequacy to describe some surface rupture modes usually referred to as axial cleavage fractures or extension ruptures (Maury 1987). This deficiency is related to the ad hoc assumption that failure is an intrinsic property of the material that should naturally be associated with the elastic-plastic limit. An alternative way to describe rupture phenomena in rocks is based on the bifurcation theory, together with more realistic constitutive modeling.5 This approach to differentiates between the rheological behavior of the material and the various rupture phenomena. Furthermore, the bifurcation theory can be used to describe and predict the occurrence of the various observed failure modes.
Simplified Bifurcation Analysis
Vardoulakis and Papanastasiou (1988) considered borehole stability in a deep rock layer under a uniform stress field at infinity, s 8, as illustrated in Figure 10. Furthermore, they considered a deep section of the borehole. The creation of the hole was simulated by a gradual reduction of the support pressure s3at the borehole wall. The most severe loading case corresponds to zero support pressure, s3 = 0.
|
5 |
Bifurcation of a monotonous deformation process indicates that at some critical state, the deformation process does not follow its straight-ahead continuation but turns to an entirely different mode. Typical examples of bifurcation phenomena are buckling, barreling, necking, shear-banding and axial splitting observed in rock specimens. Mathematically, bifurcation means that the equations describing the equilibrium continuation do not provide a unique solution. Equilibrium bifurcation analyses in deformable solids are mostly based on the fundamental works of Hill (1958), Biot (1965), Mandel (1965), and Rudnicki and Rice (1975). |
Under these idealized loading conditions, one may examine the various deformation modes of the borehole in order to gain a better insight of the existing possibilities:
-
Cylindrical convergency of the borehole. As illustrated in Figure 11, this case corresponds to a uniform reduction of the borehole radius. This case can be reproduced mathematically with an isotropic, linear elastic model for the surrounding rock, and is known as the Lamé solution (Timoshenko, 1934). Other solutions can be easily constructed for more complicated constitutive models.
-
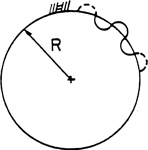
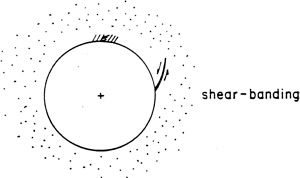
Warping of the borehole wall. This deformation mode is sketched in Figure 12. It should be emphasized that the majority of the existing solutions to surface warping is for the half-space problem and not to the borehole problem (Vardoulakis, 1984). The warping mode must be accounted for by the formation of shear-bands, as shown in Figure 13, or exfoliation at the borehole wall due to activation and subsequent unstable propagation of pre-existing cracks, as shown in Figure 14.
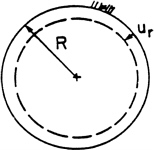
Figure 11. Cylindrical convergency of a borehole.
Figure 14. Exfoliation at the borehole wall.
Vardoulakis and Papanastasiou (1988) analyzed borehole stability using the finite element method, determining the lowest stress at infinity that causes warping of the borehole. This theory suggests that the critical bifurcation stress corresponds to the short wavelength limit that is affecting a vanishingly narrow ring of material in the vicinity of the borehole wall. Consequently, one can restrict the analysis to a small domain in the neighborhood of the borehole wall and neglect the stress-gradient. For the same reason, this domain can be replaced by a half-space of material loaded by the boundary stresses that may cause plane-strain surface instabilities. If surface instabilities are not possible, then the dominant failure mode is shear-band formation in the vicinity of the borehole wall.
Isotropic Far-Field Stresses
Vardoulakis and Papanastasiou (1988), Vardoulakis et al. (1988), and Sulem and Vardoulakis (1988) analyzed borehole stability for the case of isotropic far-field stress within the frame of a deformation
theory for rigid-plastic, pressure-sensitive materials. Papanastasiou and Vardoulakis (1989) and Papanastasiou et al. (1989) studied also the scale effect (i.e., the dependency of the borehole stability on the radius of the borehole) using a deformation theory for rigid-plastic material with microstructure (Cosserat material). These theoretical predictions have been recently validated experimentally by Ewy and Cook (1989) and Haimson and Herrick (1989).
Numerical Analysis of Localization Phenomena in Deep Boreholes
The previous results encouraged Papanastasiou (1990) and Papanastasiou and Vardoulakis (1991) to pursue the task of treating the borehole problem within a 2D, nonlinear finite element (FE) analysis to model the evolution of the rupture zone and the progressive failure of the structure. The rock was modeled by the elastoplastic constitutive equations of the J2 flow theory of plasticity for cohesive frictional/hardening softening, dilatant material. These constitutive equations were fitted on true stress-strain data from experiments on Carboniferous sandstone. The ill-posed boundary value problem of borehole stability in strain-softening rock was regularized by adopting a continuum with the Cosserat microstructure in which the individual grains possess, in addition to the translational degrees of freedom, a rotational degree of freedom as well. Grain rotation and its gradient give rise to a nonsymmetric stress tensor and couple stresses that introduce a length scale into the problem which improves the computational stability and allows for robust post localization computations. The results (Figure 15) clearly show a progressive failure mechanism; the computed failure modes are in a good qualitative agreement with the laboratory and field observations. Also, the existence of an internal length in the constitutive equations enables one to model the existence of the scale effect in the problem; thus, small holes fail at higher external stresses than large holes.
Nonlinear Effects
The introduction of nonlinear effects, such as stress-dependent elastic constants, adds further complications. Indeed, for certain
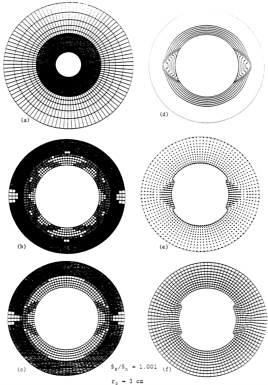
Figure 15. (a) Global picture of the plastic and elastic domains before localization. Detail of the plastic and elastic domains at (b) first step after localization and (c) after completion of localization. Detail of (d) isolines of accumulated plastic shear strain (e) incremental displacement field and (f) deformed mesh.
parameter combinations, failure can initiate inside the material (Santarelli et al., 1986; Santarelli and Brown, 1987; Guenot and Santarelli, 1988) at a finite distance from the borehole wall. Specifically, Santarelli and Brown (1987) used a numerical model incorporating an increase in stiffness with confining pressure. The motivation for this work included observations by Daemen and Fairhurst (1971) who showed that there were no indications of fracturing or loosening around hydrostatically (external) pressurized thick-walled cylinders, even when the tangential stress was four times the uniaxial compressive strength (Hobbs, 1966; Hoskins, 1969; Haimson and Edl, 1972), as well as observations (e.g., Kaiser et al., 1985) that linear elasticity inadequately predicted tunnel convergence near failure. Using a power law variation for Young's modulus as a function of the confining stress for a vertical wellbore in an elastic medium with isotropic horizontal stresses, a generalized representation of Hooke's law was presented. The observations were as follows:
-
The maximum tangential stress concentration occurs within the rock and not at the borehole wall for specific loading conditions.
-
The formulations do not take into account prepeak yield. The consequence is an overestimate of the tangential stress at the well and an underestimate of strains.
-
The representation could be improved by incorporating moduli relationships which do not imply that the modulus approaches zero as the confining stress approaches zero.
Improved recognition of the pre-yield behavior recognizes the occurrence of damage and the influence of microstructure. Mühlhaus (1987) described the microstructure using the generalized Cosserat continuum theory with microrotations and coupled stresses. Damage may be viewed as a radial variation of the shear modulus governed by the minor principal stress acting on an element. Using these concepts, surface instabilities can be delineated, where surface buckling of small finite columns occurs. Presuming surface instability of a half-plane on a local scale, the location where the maximum tensile radial stress occurs can be delineated. Such stresses occurring in the post-buckling range can cause latent cracks parallel to the surface to open, potentially promoting unstable crack growth and consequent spalling.
In a manner analogous to surface instabilities, other localized effects could be active. Localization of deformation can occur in shear bands. These can be understood as an instability in the macroscopic constitutive description of the rock, corresponding to weak discontinu-
ities of the displacement field. In terms of the Cosserat theory, the thickness of the shear bands is defined by certain material parameters depending on a length dimension, such as grain diameter. The concept of localization in shear bands diverges from standard plasticity concepts which presume that all slip surfaces are active and that there is pervasive failure.
Time-Dependent Effects
The integrity of a wellbore regime can be influenced by time-dependent material response (i.e., viscoelastic or viscoplastic behavior). It can be further affected by temporal variation of the stress field due, for example, to poroelastic effects. Fully coupled analyses mathematically acknowledge that transient changes in the pore pressure field around the wellbore—due to fluid permeation—modify the in-situ stress regime. The transcience may lead to failure away from the borehole wall. Such a limited equilibrium state does not necessarily appear during drilling but may possibly occur later in the life of the well, as delayed instabilities (Paslay and Cheatham, 1963; Haimson, 1968; Detournay and Cheng, 1988; Guenot and Santarelli, 1988)
Such applications of poroelasticity are complicated by the existence of filtercake from drilling fluids (Haimson, 1968; Hsiao, 1987; Roegiers et al. 1987; Guenot and Santarelli, 1988). A pseudo-impermeable cake provides a discontinuity between mud pressure in the well and pore pressure in the reservoir. Guenot and Santarelli (1988) quantify this as cake efficiency.
Analogous to poroelastic effects are thermoelastic effects. For example, during drilling or during waterflooding (Perkins and Gonzalez, 1984; Guenot and Santarelli, 1987), substantial cooldown around a wellbore can occur. Reservoir cooling will generate tensile stresses, which may stabilize or destabilize the near-wellbore region, depending on the interrelationship between the radial, the axial and the circumferential. During drilling, thermal effects may be transitory as the well is deepened because circulation cools the bottom of the well and heats upper portions.
Clay mineral hydration by water-base drilling fluids is well known in the oil and gas industry. It leads to tight holes in soft shales and to unstable walls with brittle breakouts in more indurated shales. In the latter case, clay hydration generates swelling stresses, leading to an actual brittle shear failure which is determined from the shape of the debris. There are two basic ways of controlling this phenomenon:
(1) to adapt the salinity and the pH of the water base mud, or (2) to switch to another type of mud (i.e., oil-base mud or emulsions).
However, it is interesting to realize that swelling does not have the same exact meaning for civil or mud engineers. In both cases, swelling of shale occurs when reactive clay minerals and water are in contact. In civil engineering, for swelling to occur, the rock must be unloaded at a stress level below a given stress value (called the swelling stress). The swelling of shale is stress-dependent; it is determined by the so called “Hüder-Amberg” test—the higher the stress, the less important is the swelling. Beyond a given value, the swelling phenomenon does not occur—no deformation, no swelling pressure. In civil engineering, values for this swelling stress have been measured to be of the order of the magnitude of a few MPa.
The mud engineer is interested in the original water content of the shale. A dry shale will adsorb water until an equilibrium is reached. The value of the water content corresponding to this equilibrium varies from one shale to another. Both fields have a separate approach to the same problem.
Scale Effects
The scale effects in the determination of rock mass strength and deformability have been extensively discussed by Heuzé (1980). The scale effect, as far as boreholes are concerned, was studied experimentally by Haimson and Herrick (1989) and numerically by Papanastasiou et al. (1989a, 1989b).
In the aforementioned bifurcation analysis of deep boreholes, rock was described by a classical continuum theory of plasticity for rigid-plastic, cohesive/frictional material. It was found under these constitutive assumptions, the critical diffuse bifurcation mode is surface instability. This finding was explained by the high stress gradient at the borehole wall. Surface instability corresponds to the infinitesimally small wavelength limit with respect to the borehole radius, i.e., to a bifurcation solution that is affecting only an infinitesimal ring of material close to the borehole wall. The short wavelength limit is an accumulation point of bifurcations. Consequently, almost all wavelengths of the warping mode are possible, and there is no influence of the borehole radius.
The pressure-sensitive character of the material behavior gives rise to solutions that can be used to explain the experimentally observed high resilience of model boreholes to external pressure (Guenot, 1987). However, experiments suggest also that small boreholes fail at higher
external stresses than large holes (Haimson and Herrick, 1986, 1989). This means that to achieve an accurate statement about borehole stability based on laboratory model tests (the dependency of the borehole stability on the borehole radius), the so-called scale effect must be also modeled.
Supported Openings
Many circular openings are lined, cased and/or cemented to (1) guarantee long-term access, (2) allow local remedial work, and (3) guarantee hydraulic isolation. As peviously indicated, any time-dependent deformation (i.e., deformation that has not been completed prior to casing) or deformation due to production or stimulation activities will transfer loads to the composite geometry. Such completions can be jeopardized by creep, differential consolidation, subsidence and mobilization of macrofeatures such as faults. Depending on the far-field stress tensor and the formation constitutive relations, the loading on the casing can be calculated with levels of accuracy parallel to those defined for openhole completions.
Elastic Analysis
As an approximation, oilfield calculations have often simplistically involved computing the stress concentration at the borehole wall, implementing these values as boundary loads on the cement sheath, and subsequently determining the loading applied to the casing as a thin-walled cylinder. The problem of fracture initiation from a cased/perforated completion is substantially more complicated and often more relevant.
Nonlinear or Time-Dependent Analysis
In a completely analogous manner to the open hole, casing integrity can be assessed assuming viscous and/or plastic effects. Risnes et al. (1982) show such calculations (presuming an elastoplastic behavior) and that the stability of the perforations may be the factor of overriding importance, particularly in poorly consolidated formations. The literature is replete with calculations, field measurements, and correlations addressing this issue (Cheatham and McEvar, 1964; Patillo
and Smith, 1982; Farenthold and Cheatham, 1986; Sulem et al., 1987; Fuenkajorn and Daemen, 1988).
Many analyses assume that the casing is instantaneously in-place; hence, the solution constitutes an upper bound (i.e., conservative design considerations). A more exact determination of the load transfer mechanism may be possible using the concept of the ground reaction curve (Ladanyi, 1980; Gill and Ladanyi, 1987), well-known in the geotechnical domain.
Intersections
As a first approximation, the stability of perforations can be assessed by assuming their cross section to be circular. The problem is then similar to the openhole configuration discussed earlier, with the exception that the loading conditions are dependent on the depth of the perforation. The perforation tunnel acts as a stress concentrator but in a stress field that is influenced by the borehole itself.
Bratli and Risnes (1981) extended perforation analysis further by presuming a spherical cavity in poorly consolidated material, behaving as an elastoplastic medium, with a Coulomb failure criterion. They account for steady-state fluid inflow into the wellbore through a perforation, representing local shell failure around the cavity as well as a total collapse, related to global plastic behavior. Flow guidelines to maintain stability are proposed for engineering applications.
As a well is produced, sand production problems need to be avoided by limiting the hydraulic gradient such that it never exceeds the stabilizing forces (i.e., gravity, shear strength, interlocking and capillarity) of the constitutive grains. This is well illustrated by Morita et al. (1987). These authors modelled ellipsoidal perforation tunnels using coupled finite-element models representing transient fluid flow and a modified kinematic model with a cap. There is a complex interaction between the morphology of the perforation and the structurally and permeability-damaged zone around a perforation, which is erodable with sand production. For example, Morita et al. (1987) indicate that:
-
Initially, a perforation may be a relatively thin elongated cavity, penetrating the formation, with a zone of damage surrounding it. When production starts, this will be an unstable feature because of high gradients through the damaged zone.
-
With production, the perforation shape will evolve to a more stable enlarged cavity. The rate at which formation particles are removed will stabilize with this shape evolution and the removal of the zone damaged by completion practices. If the production rate is varied (wells are often shut in for periods of time), sand production will likely temporarily increase when production starts again.
-
Once moderate quantities of water start to be produced, loss of capillary bonding might increase the production of sand unless plugging occurs.
-
When depletion of the reservoir occurs, the risk of substantial failure is increased.
-
Guidelines for perforation length, density, and phasing are given to optimize production and to minimize the potential for cavity interaction.
Slabbing and Exfoliation
Lippmann (1978, 1983) and Burgert and Lippmann (1981) examined the static and dynamic limit equilibrium of an imaginary block of perfectly elastic plastic material adjacent to the excavation. Slabbing and exfoliation then occur in circumstances where the resisting forces do not balance the lateral forces that tend to propel the block inside the cavity.
Salamon (1974), Pariseau (1979), Pietrusczak and Mróz (1980), and Zubelewicz and Mróz (1983) studied rock bursting in strain softening material. In this case, instability becomes possible at or beyond the peak strength of the rock. However, this mechanism can be questioned on the grounds that the softening observed in compression tests of brittle rock samples is, in reality, structural in nature, attributable to the specimen's failure mechanism rather than a case of real material (constitutive) softening. Softening in element tests is always associated with inhomogeneous deformation modes like shear banding or slabbing (Drescher and Vardoulakis, 1982; Read and Hegemier, 1984).
Experiments on rock specimens usually reveal that failure under the conditions of uniaxial compression or extension is manifested either in the form of shear bands or in the form of splitting and slabbing. Based on similar observations, Freudenthal (1977) viewed rock splitting near an opening and rock bursting as a result of crack initiation and propagation associated with the existence of radial tensile stresses around the excavation. The existence of such stresses was predicted on the basis of a non-linear elasticity theory with second-order terms to account for shear induced volume expansion (Reiner, 1949).
Vardoulakis (1984) and Vardoulakis and Mühlhaus (1986) based their analyses of near-surface rock bursting phenomena on the assumption that splitting and slabbing are the result of surface instabilities (Bazant, 1967). Surface buckling phenomena cause secondary tensile stresses, which for material points close to a free surface remain unbalanced in a direction normal to the free surface. These tensile stresses cause latent, surface-parallel cracks to open. These opened tensile cracks magnify the effect of the diffuse bifurcation, since under a field of uniaxial compressive stresses, parallel to the Griffith cracks, tensile stress concentrations are established at the crack tips. It is then assumed that this mechanism may result in an unstable growth of cracks and finally in splitting. Unstable crack growth and splitting correspond to some critical crack-surface density (distributed material damage) which manifests itself in the mean spacing of the forming plates. The split material is finally becoming much weaker than the intact material because of the lower buckling stress of the individual plates. Keeping this model in mind, it is considered that borehole breakouts are the result of the buckling of flaked rock surfaces, the flaking itself being triggered by surface instabilities.
The surface instabilities in elastic and viscoelastic half-spaces were first analyzed by Biot (1965, 1966) and Bufler (1965a, 1965b). Surface instabilities in homogeneously stressed half-spaces made of classical continua are independent of the wavelength of the buckling mode. In view of this fact and the close relation of surface instabilities to anisotropy, Mühlhaus (1985), Mühlhaus and Vardoulakis (1986) and Papamichos et al., (1989) considered the response of a Cosserat continuum (i.e., a continuum with bending stiffness) and validated this theory against analytical (Biot, 1965) or numerical solutions for periodically layered half-spaces. Doris and Nemat-Nasser (1980) analytically solved the stability of an elastoplastic layer on an elastoplastic half-space. Horii and Nemat-Nasser (1982) studied surface instabilities in geologic materials possessing internal friction and dilatancy. Vardoulakis (1984) and Vardoulakis and Mühlhaus (1986) related rock bursting in rigid plastic hardening solids having internal friction and dilatancy to surface instabilities, and demonstrated that rock bursting is more likely to happen in brittle rocks.
The influence of surface-parallel Griffith cracks on the critical buckling load and for linear elastic solids was analytically studied, for periodic arrays by Keer et al. (1982) and for isolated cracks by Nemat-Nasser and Horii (1982) and Nazarenko (1986). These studies showed that the critical bifurcation for surface buckling is dramatically
reduced by the existence of surface parallel Griffith cracks. For arbitrary surface-parallel crack arrays in anisotropic half-spaces Vardoulakis and Papamichos (1989) succeeded in numerically solving the corresponding bifurcation problem by applying the displacement discontinuity method (Crouch, 1983). Biot (1972) indicated first that in full space, the stress intensity factor of a Griffith crack in a stress field parallel to its extent drops to zero for values of initial stress corresponding to surface instability. This statement was found true also for the case of half-spaces and arbitrary crack arrays (Papamichos and Vardoulakis, 1989). These findings on the micromechanical level justify the use of bifurcation theory (in connection with phenomenological constitutive models that show distributed damage with hardening and softening branches) to study surface exfoliation phenomena.
Influence of Preexisting Discontinuities or Structure
In geomechanics one is concerned with materials that are inhomogeneous, although the scale where the nonhomogeneity becomes significant may be different from case to case. If the ratio of a characteristic fabric length of the material (grain or joint body diameter, etc.) to a characteristic structural length (tunnel or foundation diameter, etc.) is sufficiently small then, in general, conventional continuum methods can be applied for the modeling of each problem. There are exceptions as usual, e.g., in case of strain softening where width localization of the zone becomes the decisive structural length (M ühlhaus and Vardoulakis, 1987). In all other cases, the domain considered has to be subdivided in homogeneous subdomains or, as in the case of particulate materials, one has to apply one of the distinct (Cundall, 1976; Cundall et al., 1978; Cundall and Hart, 1983; Cundall and Strack, 1983; Cundall, 1987) or discrete (Hocking et al., 1985; Williams et al., 1985; Williams, 1987) element methods.
Discrete Element Method
From the physical point of view, the distinct and discrete element methods are equivalent. As in the finite element method, first assumptions are made on the distribution of the displacements within each sub-body. Then Newton law of motion is used to obtain the velocity and displacement amplitudes from the unbalanced forces. A characteristic feature of the method is that the equations of motion are
integrated by means of the central difference expressions so on diagonal mass and damping matrices the velocity amplitude of some sub-body or block is completely determined by the unbalanced forces and the velocity amplitudes of the previous time step of the same sub-body. Then each problem can be solved block-wise which makes the method particularly suitable for use on personal computers. Applications of the discrete element method to slope stability (steeply dipping foliation planes) and mining problems are found in Cundall (1987) and Lorig et al. (1989); applications of the discrete element method to the collapse of a soil embankment, and penetration of a projectile into a soil can be found in Williams (1987).
The most widely used distinct and discrete element code appears to be UDEC (Cundall and Hart, 1983). The computational effort in the application of the distinct/discrete element methods to practical problems is considerable. Alternative methods that are between the conventional continuum theory and the detailed discrete methods are therefore desirable.
Block Theory
This approach describes a series of theorems and application methods governing the 3D geometry of intersecting fractures (joints) and excavated surfaces (Warburton, 1981; Goodman and Shi, 1983; Lin and Fairhurst, 1988). By means of topological programs manipulating these relationships, all possible rock blocks are divided into a small number of types, each of which is analyzed for its support needs in a specific excavation. The underlying principle of block theory is that prevention of the movement of “keyblocks”6 assures the complete safety of the entire excavation. The input for the analysis has, as a minimum, the orientations of each of the joint sets and the shape and orientation of the excavation. The friction angles of each joint set are needed to quantify support requirements but optimum directions and shapes of excavations can be determined even without this knowledge. With these data, one program determines the supporting force needed per unit length of tunnel as a function of tunnel orientation. A recent development of block theory is the statistical simulation of the traces of intersection of the tunnel wall and the system of discontinuities, and
|
6 |
By definition, a key block is removable and unstable without support. |
their unrolling to produce a map of block faces on the tunnel surface. These are analyzed to determine the removable blocks.
Discontinuous Deformation Analysis
This numerical approach is fundamentally different from the discrete element method in that it couples a complete kinematic theory for block interactions with the equilibrium and strain compatibility relations of continuum mechanics. The minimization of potential energy associated with internal deformations and interblock contacts leads to an implicit formulation like that of finite element analysis.