Fully Nonlinear Water Wave Computations Using the Desingularized Method
R.F.Beck, Y.Cao, and T.-H.Lee
(University of Michigan, USA)
ABSTRACT
The use of Euler-Lagrange time stepping methods to solve numerically fully nonlinear marine hydrodynamic problems is discussed. The mixed boundary value problem that arises at each time step is solved using a desingularized approach. In this approach the singularities generating the flow field are outside the fluid domain. This allows the singularity distribution to be replaced by simple isolated singularities with a resultant reduction in computational complexity and computer time.
Various examples of the use of the method are presented including two-dimensional water wave problems, the added mass and damping due to sinusoidal oscillations of two-dimensional and axial symmetric bodies, and the wave pattern and wave resistance of a Wigley hull moving at constant forward speed. The results show excellent agreement with other published computations and good agreement with experiments.
INTRODUCTION
In recent years, there has been significant progress in solving marine hydrodynamic problems with fully nonlinear free surface boundary conditions. While some of the work has incorporated fluid viscosity and surface tension, the majority has assumed that the fluid is incompressible and inviscid and that the flow is irrotational. These assumptions lead to a boundary value problem for which the Laplace equation is valid everywhere in the fluid domain. This does not imply that viscous effects are unimportant and in certain situations they may dominate. However, the inviscid problem is an order of magnitude easier to solve and thus has been the basis of much of the research. Throughout this paper it is assumed that the fluid is incompressible and inviscid and that the flow is irrotational.
Fully nonlinear computations can be performed by a variety of methods. For steady forward speed, an iterative procedure can be used to satisfy the nonlinear free surface boundary conditions. In the work of Jensen, et al. (1989), and more recently Kim and Lucas (1990, 1992) and Raven (1992), a series of linearized boundary value problems based on the solution to the previous iteration and satisfied on the deformed free surface of that iteration are solved. The iteration is continued until convergence to the complete, nonlinear solution is obtained. Bai et al. (1992) also use an iterative procedure but employ a localized finite-element method to solve the boundary value problem at each iteration. For steady problems the iteration procedure may converge to the fully nonlinear solution faster than a time stepping method.
Longuet-Higgins and Cokelet (1976) first introduced the mixed Euler-Lagrange method for solving two-dimensional fully nonlinear water wave problems. This time stepping procedure requires two major tasks at each time step: the linear field equation is solved in an Eulerian frame; then the fully nonlinear boundary conditions are used to track individual Lagrangian points on the free surface to update their position and potential values. Variations of this method have been applied to a wide variety of two- and three-dimensional problems. Most of the variations involve how the linear field equation is solved at each time step. Among the researchers who applied the method to two-dimensional problems are Faltinsen (1977), Vinje and Brevig (1981), Baker et al. (1982) and more recently Grosenbaugh and Yeung (1988), Cointe et al. (1990) and Saubestre (1990). In three dimensions, the computations become much more difficult because of the large number of unknowns that are required. Results have been obtained by a number of researchers, including Lin et al. (1984), Dommermuth and Yue (1987), Kang and Gong (1990), Zhou and Gu (1990), Cao (1991), Cao et al.
(1990, 1991, 1992), and Lee (1992).
The successful implementation of an Euler-Lagrange method to solve fully nonlinear water wave problems requires a fast and accurate method to solve the mixed boundary value problem that results at each time step and a stable time stepping scheme. In our research, the mixed boundary value problem is solved using a desingularized boundary integral method. Similar to conventional boundary integral methods, it reformulates the boundary value problem into a boundary integral equation. The difference is that the desingularized method separates the integration and control surfaces, resulting in nonsingular integrals. The solution is constructed by integrating a distribution of fundamental singularities over a surface (the integration surface) outside the fluid domain. The integral equation for the unknown distribution is obtained by satisfying the boundary conditions on the surface (the control surface) surrounding the fluid domain.
A variety of problems have been solved by the desingularized approach. Webster (1975) was probably the first to apply the technique to panel methods. He used triangular patches of linearly distributed sources “submerged” within the body surface to study the steady flow past an arbitrary three-dimensional body. Schultz and Hong (1989) showed the effectiveness and accuracy of the desingularized method for two-dimensional potential flow problems. Cao et al. (1991) gave convergence rates and error limits for simple three-dimensional flows including a source-sink pair traveling below a free surface.
The desingularized method has been successfully applied to several free surface problems. Cao et al. (1993a) have investigated the formation of solitons propagating ahead of a disturbance moving in shallow water near the critical Froude number. The wave resistance, lift force and pitch moment acting on a submerged spheroid traveling beneath the free surface were computed by Bertram et al. (1991) and compared to linear theory results. Using an iterative technique, the wave resistance was computed by Jensen et al. (1986, 1989) and Raven (1992). The desingularized method has been applied to ship motion problems by Bertram (1990) and Lee (1992).
There are several computational advantages to the desingularized method. Because of the desingularization, the kernels of the integral equation are no longer singular and special care is not required to evaluate integrals over the panels. Simple numerical quadratures can be used to greatly reduce the computational effort, particularly by avoiding transcendental functions. In fact, for the source distribution method the distributed sources may be replaced by simple isolated sources. Higher order singularities such as dipoles can easily be incorporated. Isolated Rankine sources also allow the direct computation of the induced velocities on the free surface without further numerical integration or differentiation. The resulting code does not require any special logic and is thus easily vectorized. We have not yet installed the code on a parallel machine but the algorithm is straight forward and should not cause any difficulties. At present, the method is O(N2), but by using multipole expansions it could be reduced to an O(N lnN) method.
In the next section, the desingularized approach using isolated sources to solve fully nonlinear marine hydrodynamic problems will be discussed. The solution is developed in the time domain starting from rest. Following the theoretical development, some of the details of the numerical methods will be presented. Finally, numerical results will be presented and compared to experimental results where available.
FULLY NONLINEAR PROBLEM FORMULATION
An ideal, incompressible fluid is assumed and surface tension is neglected. The problem is started from rest so that the flow remains irrotational. This implies the existence of a velocity potential such that the fluid velocity is given by its gradient and the governing equation in the fluid domain is the Laplace equation.
A coordinate system Oxyz translating in the negative x direction relative to a space fixed frame is used. The time dependent velocity of translation is given by Uo(t). The Oxyz axis system is chosen such that the z=0 plane corresponds to the calm water level and z is positive upwards. The total velocity potential of the flow can then be expressed as
1
where ![]() is the perturbation potential. Both Φ and
is the perturbation potential. Both Φ and ![]() satisfy the Laplace equation
satisfy the Laplace equation
(2)
Boundary conditions must be applied on all surfaces surrounding the fluid domain: the free surface (SF), the body surface (SH), the bottom (SB) and the surrounding surface at infinity (S∞). A kinematic body boundary condition is applied on the instantaneous position of the body wetted surface:
(3)
where n=(n1,n2,n3) is the unit normal vector to the surface (out of the fluid domain) and VH is the velocity of the body relative to the moving coordinate system. The subscripts 1,2,3 refer to the x,y, and z axis directions respectively. There is also a kinematic condition applied on the bottom:
(4)
where VB is the velocity of the bottom relative to the Oxyz system. For an infinitely deep ocean equation (4) reduces to
(5)
Finite depth will increase the computational time because of the additional unknowns necessary to meet the bottom boundary condition but there is no increase in computational difficulty. In fact, the flatness of the bottom is immaterial. The only overhead relative to a flat bottom is computing the necessary geometrical parameters of a nonflat bottom. This contrasts with the typical Green function approach where a finite depth Green function is significantly harder to compute than an infinite depth Green function and a nonflat bottom can not in general be accommodated.
On the instantaneous free surface both the kinematic and dynamic conditions must be satisfied. The kinematic condition is
(6)
where z=η (x,y,t) is the free surface elevation. The dynamic condition requires that the pressure everywhere on the free surface equals the ambient pressure, Pa. The ambient pressure is assumed known and may be a function of space and time. Normally it would be set equal to zero. Using Bernoulli 's equation the dynamic condition becomes:
(7)
where ρ is the fluid density and g the gravitational acceleration.
Because we are solving an initial value problem with no incident waves, the fluid disturbance must vanish at infinity:
(8)
In addition, the initial values of the potential and free surface elevation must be specified such that
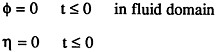
(9)
In the Euler-Lagrange method a time stepping procedure is used in which a boundary value problem is solved at each time step. At each step, the value of the potential is given on the free surface (a Dirichlet boundary condition) and the value of the normal derivative of the potential (a Neumann boundary condition) is known on the body surface and bottom surface. The potential and its normal derivative are updated at the end of each time step. The free surface potential and elevation are determined by integrating with respect to time (or time marching) the free surface boundary conditions. In our calculations, a Runge-Kutta-Fehlberg technique is used to do the time stepping. The body and bottom boundary conditions are prescribed for the forced motion problem. In the case of a freely floating body, the equations of motion must be integrated with respect to time in a manner similar to the free surface conditions.
On the free surface, the kinematic condition is used to time step the free surface elevation and the dynamic condition is used to update the potential. Many different approaches are possible to time march the free surface boundary conditions. The most common is a material node approach in which the nodes or collocation points follow the individual fluid particles. Another technique is to prescribe the horizontal movement of the node but allow the node to follow the vertical displacement of the free surface. The prescribed movement may be zero such that the node locations remain fixed in the x-y plane. Depending on the problem, one of the techniques may be easier to apply than the others.
It is convenient to rewrite the free surface boundary conditions, equations (6) and (7), in terms of the time derivative of a point moving with a prescribed velocity v relative to the Oxyz coordinate system. By adding ![]() to both sides of (6) and
to both sides of (6) and ![]() to both sides of (7) and after some algebraic manipulation, the kinematic and dynamic conditions can be put in the form
to both sides of (7) and after some algebraic manipulation, the kinematic and dynamic conditions can be put in the form
(10)
and
(11)
where
(12)
is the time derivative following the moving node. This is similar to the usual material derivative of fluid mechanics except the velocity is the given v rather than the fluid velocity.
If v is set equal to ![]() the node follows a prescribed path with velocity (U(t), V(t)) in the x-y plane and moves vertically with the free surface. Setting
the node follows a prescribed path with velocity (U(t), V(t)) in the x-y plane and moves vertically with the free surface. Setting ![]() results in the x-y locations of the nodes remaining fixed in the Oxyz coordinate system and equations (10) and (11) reduce to:
results in the x-y locations of the nodes remaining fixed in the Oxyz coordinate system and equations (10) and (11) reduce to:
(13)
and
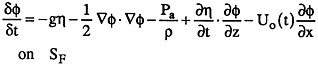
(14)
In the material node approach, the velocity is set equal to the fluid velocity such that ![]() , resulting in
, resulting in
(15)
and
(16)
where XF=(xF(t),yF(t),zF(t)) is the position vector of a fluid particle on the free surface and
(17)
is the usual material derivative.
The form of the free surface boundary conditions given by the above equations allows the value of the elevation and potential to be stepped forward in time. The left hand sides of equations (10)–(16) are the derivatives with respect to time of the potential and wave elevation moving with the node. The quantities on the right hand side are all known at each time step; the spatial gradient of the potential can be determined analytically after solving the boundary value problem and the wave elevation is known. The difficulty is the gradient of the free surface elevation (![]() in equations (10) and (13)) that must be evaluated numerically. This leads to increased computer time and numerical inaccuracies. However, this term is only needed in the prescribed horizontal node movement approach. In the material node approach no extra derivatives need to be evaluated and this probably explains why this is the approach most often used. With material nodes one must always be concerned that the nodes do not penetrate the body surface between time steps since they are unconstrained. In zero forward speed problems, material nodes or fixed nodes seem to be the most appropriate. In problems with forward speed, the material node approach has difficulties near the body because nodes tend to pile up near the bow and stern stagnation regions. The prescribed horizontal node movement approach does not have this difficulty since the node movement is constrained. An appropriate choice of v is one which parallels the body waterline and is close to
in equations (10) and (13)) that must be evaluated numerically. This leads to increased computer time and numerical inaccuracies. However, this term is only needed in the prescribed horizontal node movement approach. In the material node approach no extra derivatives need to be evaluated and this probably explains why this is the approach most often used. With material nodes one must always be concerned that the nodes do not penetrate the body surface between time steps since they are unconstrained. In zero forward speed problems, material nodes or fixed nodes seem to be the most appropriate. In problems with forward speed, the material node approach has difficulties near the body because nodes tend to pile up near the bow and stern stagnation regions. The prescribed horizontal node movement approach does not have this difficulty since the node movement is constrained. An appropriate choice of v is one which parallels the body waterline and is close to ![]() . In this case, the contribution of the
. In this case, the contribution of the ![]() term to the right hand side of (10) will be small and numerical inaccuracies will be minimized. Consequently, fast, simple numerical derivatives can be used to evaluate the
term to the right hand side of (10) will be small and numerical inaccuracies will be minimized. Consequently, fast, simple numerical derivatives can be used to evaluate the ![]() term.
term.
At each time step a mixed boundary value problem must be solved; the potential is given on the free surface and the normal derivative of the potential is known on the body surface and the bottom. In terms of a desingularized source distribution, the potential at any point in the fluid domain is given by
(18)
where Ω is the integration surface outside the fluid domain.
Applying the boundary conditions, the integral equations that must be solved to determine the unknown source strengths σ(xs) are
(19)
and
(20)
where xs=a point on the integration surface, Ω
xc=a point on the real boundary
![]() = the given potential value at xc
= the given potential value at xc
Гd=surface on which ![]() is given
is given
![]() = the given normal velocity at xc
= the given normal velocity at xc
Гn= surface on which ![]() is given
is given
The hydrodynamic forces acting on the body due to a prescribed motion are found by integrating the pressure over the instantaneous wetted surface. The generalized force acting on the body in the jth direction is thus given by:
(21)
where nj is the generalized unit normal into the hull defined as
(n1, n2, n3) = n
(n4, n5, n6) = r×n
(22)
n=unit normal to body surface (out of fluid)
![]()
![]() =body axis system
=body axis system
and j=1,2,3 corresponds to the directions of the ![]() axis respectively.
axis respectively.
The pressure in the moving coordinate system is given by Bernoulli 's equation:
(23)
where ![]() is the time derivation of the potential following a moving node on the body and v is the velocity of the node relative to the Oxyz system.
is the time derivation of the potential following a moving node on the body and v is the velocity of the node relative to the Oxyz system.
NUMERICAL TECHNIQUES
In the usual manner, the integrals may be discretized to form a system of linear equations to be solved at each time step. In the desingularized method, the source distribution is outside the fluid domain so that the source points never coincide with
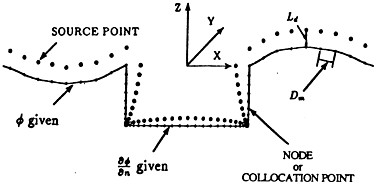
Figure 1: Schematic of source and node locations
the collocation or node points and the integrals are nonsingular. In addition, because of the desingularization we can use simple isolated sources, rather than a distribution and obtain the equivalent accuracy. This greatly reduces the complexity of the form of the influence coefficients that make up the elements of the kernel matrix. As shown in figure 1, nodes (the collocation points) are distributed on the free surface and body surface. The isolated sources are distributed a small distance above each of the nodes. The nondimensional desingularized distance is given by
(24)
where ℓd and ν are constants to be chosen by the user and Dm is a measure of the local mesh size (typically the square root of the panel area in three-dimensional problems). Cao et al. (1991) found values of ℓd=1.0 and ν=.5 to be about optimum. The accuracy and convergence of the solutions are relatively insensitive to the choices of ℓd and ν.
At each time step the mixed boundary value problem that must be solved is defined by equations (19) and (20). Using an array of isolated simple sources above the free surface and inside the body surface to construct the velocity potential, equation (18) becomes
(25)
where NF is the number of the isolated sources above the free surface,
![]() is the location of the jth source and
is the location of the jth source and
![]() is the strength of the jth source at
is the strength of the jth source at ![]()
Similarly,
NB, ![]() and
and ![]() are the number, location and strength of the sources inside the body surface.
are the number, location and strength of the sources inside the body surface.
The integral equations (19) and (20) are satisfied at the nodes on the free surface and body surface such that
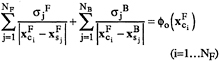
(26)
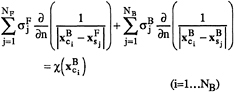
with N=NF+NB being the total number of unknowns. Equations (26) can also be written in matrix form as
A · Σ=B (27)
or
(28)
where
![]() i=1…NF, j=1…NF
i=1…NF, j=1…NF
![]() i=1…NF, j=(NF+1)…N
i=1…NF, j=(NF+1)…N
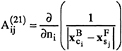 i=1(NF+1)…N, j=1…NF
i=1(NF+1)…N, j=1…NF
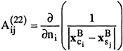 i=(NF+1)…N,
i=(NF+1)…N,
j=(NF+1)…N
![]() i=1…NF
i=1…NF
![]() i=(NF+1)…N
i=(NF+1)…N
![]() i=1…NF
i=1…NF
![]() i=1(NF+1)…N
i=1(NF+1)…N
where ![]() and
and ![]() are the node points on the free surface and body surface respectively.
are the node points on the free surface and body surface respectively.
Equations (27) are a system of (NF+NB) equations for the unknown source strength Σ. Once Σ is known, the velocity potential and fluid velocity can be analytically calculated anywhere in the fluid domain.
Equations (27) can be solved either by a direct or iterative solver depending on the size of the matrix. For most of the two-dimensional problems considered in this paper, we use a LU decomposition solver. For the three-dimensional problems, an iterative solver GMRES is used. For problems where different grid spacings are used on different parts of the domain boundary, solving equation (27) as a whole system may not be efficient. A domain-decomposition technique is often better. In this technique Σ(1) and Σ(2) are determined separately through an iterative procedure. Rewrite equation (28) as
A(11) · Σ(1)=B(1)−A(12) · Σ(2) (29)
A(22) · Σ(2)=B(2)−A(21)· Σ(1) (30)
Σ(1) is determined by solving (29) with Σ(2) known (or guessed), then Σ(1) is substituted into (30) to determine Σ(2). The new Σ(2) is then used in (29) to update Σ(1). The procedure repeats until both equations are satisfied to the given error tolerance.
After Σ is determined, the fluid velocity on the free surface can be computed so that the right hand sides of the free surface conditions (10) and (11) can be found. The free surface elevation and the potential are then updated by a time stepping procedure. In the free surface updating, if material nodes are used, the spatial derivatives of the free surface elevation, ![]() are not required. The use of generalized nodes moving with prescribed velocity v requires the spatial derivatives of η and central-differencing or cubic splines are used. The time-stepping of the free surface is done by using a fourth-order Runge-Kutta-Fehlberg scheme.
are not required. The use of generalized nodes moving with prescribed velocity v requires the spatial derivatives of η and central-differencing or cubic splines are used. The time-stepping of the free surface is done by using a fourth-order Runge-Kutta-Fehlberg scheme.
For forced body motion problems, the force acting on the body does not enter the time-stepping procedure. Therefore, the calculation of the forces acting on the body can be post-processed. Bernoulli 's equation (23) is used to compute the pressure on the body and the pressure is then integrated over the body surface to determine the forces. The pressure calculation requires the time-derivative of the potential on the body surface which is determined using central-differencing.
NUMERICAL RESULTS
In this section we shall present numerical results for a variety of cases including surface piercing bodies and a two-dimensional wave tank. The wave tank is useful to illustrate several properties of the calculations. Two-dimensional results are presented for a rectangular box in heave. Three-dimensional results are shown for axially symmetric cylinders and a Wigley hull.
Numerical Wave Tank
The two-dimensional wave tank consists of side walls, a wavemaker at one end and an absorbing beach at the other and a bottom at depth h. We have used several types of wavemakers including a paddle, a plunging wedge, and a variable pressure distribution on the free surface. The most effective beaches (cf. Cao, et al. 1993b) seem to be an energy absorbing layer on the free surface proportional to either ![]() or
or ![]() .
.
Figure 2 shows the waves generated by a pneumatic sinusoidal wavemaker started from rest. The tank has walls at each end and is .625 wavelengths deep. Two lines are shown: the dash line was computed using the traditional material nodes and the solid line is for fixed horizontal nodes. As can be seen the agreement between the two methods of calculation is excellent.
Figure 3 presents the comparison between two and three dimensional calculations. In this case, the wave tank is 12 units long, 4 units deep and the wavelength is 7.5 units. For the three-dimensional calculations the tank was 6 units wide. For the two-dimensional computations the fundamental singularity is ln(r) while in the three-dimensional calculations it is 1/r. As can be seen, the agreement is again very good; it is not perfect because of the panelization of the walls in the three-dimensional calculations. As more panels are used on the walls, the agreement continues to improve. For figure 3, only 8 panels were used at each section to divide the wall from the free surface to the bottom and the tank was less than one wavelength wide. The required number of panels needed to represent the walls is important because for a given total number of panels, the more panels on the walls the less will be available to represent the free surface and the body.
The conservation of energy in the wave tank with a pneumatic wavemaker and a beach proportional to ![]() is shown in figure 4. The solid line represents the energy build up with respect to time as the waves are made. The pneumatic wavemaker is forced to oscillate through one cycle with a period of
is shown in figure 4. The solid line represents the energy build up with respect to time as the waves are made. The pneumatic wavemaker is forced to oscillate through one cycle with a period of ![]() . Thus, we see that the energy in the tank, ET , builds up until
. Thus, we see that the energy in the tank, ET , builds up until ![]() and then remains constant until the waves start to be absorbed by the beach. EA represents the energy absorbed by the beach and it starts to build up at approximately
and then remains constant until the waves start to be absorbed by the beach. EA represents the energy absorbed by the beach and it starts to build up at approximately ![]() . The sum of ET+EA is the energy in the tank plus that absorbed by the beach. As expected the total energy remains constant. At the end of the run some energy remains in the tank because of wave reflection from the beach. The energy in the tank will decrease further if the simulation is allowed to run longer, but it would take a long time for the reflected waves to travel down to the wall at the wavemaker end and return back to the beach. The ratio of the energy remaining in the tank to the total energy is a measure of the reflection from the beach. This particular beach has not been optimized and it appears to absorb about 90% of the energy. One of the problems of fully nonlinear calculations is to find a means of measuring the effectiveness of a beach. The usual reflection coefficient is only valid for linear waves. We have tried several different measures, but none have been very satisfactory.
. The sum of ET+EA is the energy in the tank plus that absorbed by the beach. As expected the total energy remains constant. At the end of the run some energy remains in the tank because of wave reflection from the beach. The energy in the tank will decrease further if the simulation is allowed to run longer, but it would take a long time for the reflected waves to travel down to the wall at the wavemaker end and return back to the beach. The ratio of the energy remaining in the tank to the total energy is a measure of the reflection from the beach. This particular beach has not been optimized and it appears to absorb about 90% of the energy. One of the problems of fully nonlinear calculations is to find a means of measuring the effectiveness of a beach. The usual reflection coefficient is only valid for linear waves. We have tried several different measures, but none have been very satisfactory.
Dommermuth et al. (1988) showed excellent agreement between their fully nonlinear mixed Euler-Lagrange computations and experimental results. The experiments and numerical calculations were for a piston-type wavemaker programmed to produce wave breaking at mid-tank. To allow comparisons, the Fourier amplitudes and phases of the time history of the wavemaker's velocity are given in their paper. Figure 5 compares the computed wave elevation at five different locations with those presented in Dommermuth et al. (1988, figure 2). To within the accuracy of the graphics, the agreement is excellent. For our computations, the wave tank was 20 units long and 1 unit deep. A absorbing beach is placed at the far end. 501 nodes were placed on the free surface with 26 nodes on the piston wavemaker and 26 nodes on the far wall. The bottom was accounted for by using image sources for each desingularized source. Material nodes were used and the time step size was ![]() . A fourth-order Runga-Kutta-Fehlberg time stepping scheme is used. The running time on a CRAY-YMP was 1.6 hours.
. A fourth-order Runga-Kutta-Fehlberg time stepping scheme is used. The running time on a CRAY-YMP was 1.6 hours.
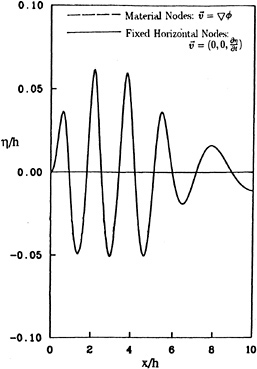
Figure 2: Comparison of fixed horizontal nodes versus material nodes.
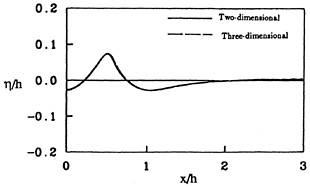
Figure 3: Comparison of two-dimensional versus three-dimensional computations
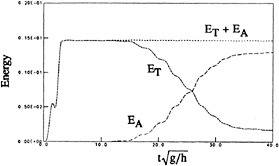
Figure 4: Energy in a wave tank as a function of time
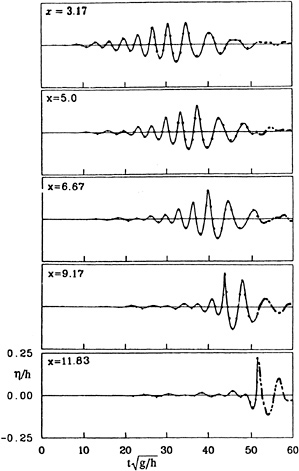
Figure 5: Free surface elevation at various distances from a piston-type wavemaker as a function of time.
Present calculations ——;
Dommermuth et al. (1988)
experiments---;
calculations •
Heaving two-dimensional rectangle
Two-dimensional computations have been performed on a rectangle in heave and sway; details of the calculations may be found in Lee (1992). The convergence of the numerical results and agreement with experiments are similar for both heave and sway. Because of space limitations only a sampling of the heaving results will be presented here.
Three node spacings on the body have been tried. The first is simple equal spacing between the nodes. The second is a cosine spacing in which the nodes are more closely packed around the sharp corner and the free surface. The third is a semi-cosine spacing that retains the cosine spacing on the bottom but uses only half a cosine on the sides. This keeps the closely packed spacing around the corner but increases the panel size near the free surface. The semi-cosine spacing is useful because for stability reasons the panels on the free surface near the body need to be approximately the same size as the body panels near the waterline. Thus, larger free surface panels can be used for a given number of body panels. Consistent with the findings of Cao et al. (1992) for a Karman-Trefftz airfoil, no node is placed at the corner in any of the spacing schemes in order to avoid a spike in the tangential velocity. Calculations have shown little variation in the numerical results with node spacing schemes.
Figure 6 shows the typical wave profiles generated by a heaving rectangle in infinite water depth. The beam of the rectangle, B, is two and the draft, H, is one. The nondimensional heaving frequency is ![]() and the motion amplitude is 10% of the draft (a/H=.1). Semi-cosine spacing of is used on the body and approximately 30 material nodes per wavelength were used on the free surface. Rather than a beach in the far field, Lee (1992) used an algebraically increasing panel size starting at four wavelengths from the body. The increasing panels are carried out for 80 more wavelengths with the last panel being many wavelengths long. This far field panel arrangement introduces significant numerical damping and greatly delays the significantly attenuated reflected waves from entering the near field of interest. As can be seen in the figure, there is essentially no reflected waves at the edge of the inner region for the time interval shown.
and the motion amplitude is 10% of the draft (a/H=.1). Semi-cosine spacing of is used on the body and approximately 30 material nodes per wavelength were used on the free surface. Rather than a beach in the far field, Lee (1992) used an algebraically increasing panel size starting at four wavelengths from the body. The increasing panels are carried out for 80 more wavelengths with the last panel being many wavelengths long. This far field panel arrangement introduces significant numerical damping and greatly delays the significantly attenuated reflected waves from entering the near field of interest. As can be seen in the figure, there is essentially no reflected waves at the edge of the inner region for the time interval shown.
Figure 7 shows the convergence of the numerical calculations to the experimental results of Vughts (1968). Vughts conducted experiments with an oscillating model and compared the results to linear theory calculations using both conformal mapping and Lewis forms. The fully nonlinear calculations converge to a value between Vugts' experimental and numerical results for a nondimensional frequency of π/3.
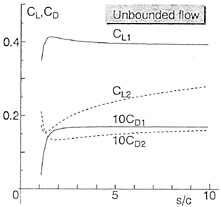
The comparisons between Vughts' results for both the added mass and damping coefficients over the entire frequency range are shown in figures 8 and 9. There figures are for a nondimensional amplitude of .15, the largest amplitude tested. The results for smaller amplitudes are similar. Analogous to the experiments, our results show very little sensitivity to motion amplitude. The variation of the added mass and damping coefficients with amplitude fall approximately within the circles used to plot the fully nonlinear results in figures 8 and 9. As can be seen from the figures, the fully nonlinear computations agree well with the experiments and with linear theory.
Heaving axially-symmetric bodies
The flow due to a heaving three-dimensional cylinder has also been studied, the details may be found in Lee (1992). Axially-symmetric problems ca n be reduced to a one-dimensional integral equation by employing ring sources such as used by Dommermuth and Yue (1987). Because the desingularized technique is being developed for general body shapes, ring sources were not used in our calculations. Instead, the calculations were performed using multiple planes of symmetry. The first calculations were done using two planes of symmetry so that the unknown sources were distributed over one quarter of the domain. More computational efficiency is gained by increasing the number of planes of symmetry. Figure 10 shows the waves produced at different periods for a circular cylinder (R/H=1.0) in heave. Two sets of results are shown corresponding to using two planes of symmetry and 60 planes of symmetry. The actual panelization of the free surface is very different for the two cases since in the two-plane case the number of nodes is increased as the distance from the origin increases and in the other it is constant. In both cases the number of nodes on the cylinder and at the waterline on the free surface are the same. The results are so close that only one line is apparent in the figure for each period shown.
A more accurate measure of the difference between the predicted wave elevation is given in table I. Table I presents the RMS difference between the wave elevations produced by the two calculations for the different periods. The RMS difference is a measure of the difference in predicted wave profiles at a total of 120 fixed wave probes. The probes were uniformly distributed over the computational domain of interest. Cubic spline interpolation is used to determine the wave elevation at each probe from the values of the wave elevation at the computational
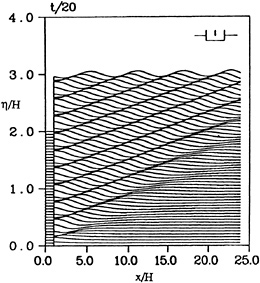
Figure 6: Time history of the free surface profile for a heaving two-dimensional rectangle in infinite water depth, B=20, H = 1.0, a/H = .1, ![]()
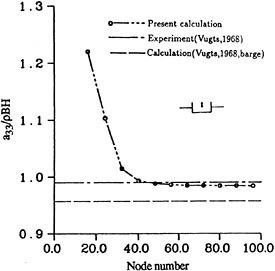
Figure 7: Added mass coefficient vs number of nodes on the ineer domain of the free surface for a heaving two-dimensional rectangle in infinite water depth, B = 2.0, H = 1.0, a/H = .15 ![]()
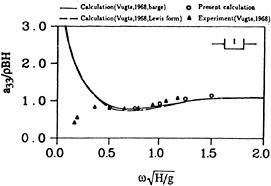
Figure 8: Added mass coefficient vs frequency for a heaving two-dimensional rectanglein infinite water depth, B = 2.0, H = 1.0, a/H = 0.15, panel size = λ/30
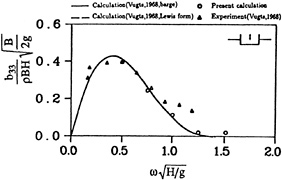
Figure 9: Wave demping coefficient vs frequency for a heaving two-dimensional rectangle in infinite water depth, B=2.0, H=1.0, a/H=0.15, panel size=λ/30
nodes. The nondimensional RMS difference between wave profiles 1 and 2 is defined as:
(31)
where
xi=the location of the ith wave probe
Nrms=the number of wave probes
η1(xi)=the wave elevation of the first profile at the ith wave probe
η2(xi)=the wave elevation of the second profile at the ith wave probe
a=the motion amplitude
As can be seen from table 1, the RMS difference in wave elevation between using two planes of symmetry and multiple planes of symmetry is less than 5.×10−6.
We have also examined the effects of using equal, cosine, or semi-cosine node spacing schemes on the body. The cosine and semi-cosine schemes are the same as described for the two-dimensional rectangle. As expected the equal spacing was the worst. For 90 planes of symmetry and equal numbers of nodes on the body and free surface, the cosine and semi-cosine spacings gave no significant difference between the predicted wave elevations. As previously stated, the semi-cosine spacing leads to a better distribution of panels on the free surface and was therefore used in most of the calculations.
Dommermuth and Yue (1987) considered the case of a cylinder with proportions R/H=2. heaving in shallow water. The draft to water depth ratio, H/h, is .5. The oscillation amplitude, a/H, is .5 and the forcing frequency corresponds to a linear wavelength of 2R. Their calculations were made using ring sources in a Green's theorem formulation to solve the boundary value problem at each time step and material nodes to do the time stepping. Figures 11 and 12 compare our desingularized calculations with the curves presented by Dommermuth and Yue for the time history of the nondimensional heave force (F3/ρgπR2a) and the wave elevation of the free surface at different periods.
The nonlinear forces computed by the desingularized method and Dommermuth and Yue agree very well considering the two completely different numerical techniques used. As can be seen, the nonlinear forces are significantly different from the linear predictions during the up-stroke but are fairly close on the down-stroke.
Figure 12 shows the comparison of the predicted wave elevations at different periods of motion. Again, the agreement is very good. The desingularized method did not show the slight irregularity near the intersection line experienced by Dommermuth and Yue.
The ability of the desingularized method to handle more complex shapes is illustrated by the results shown in figures 13 and 14. These figures show the nondimensional force and heave displacement of a cylinder (Rupper=1.0, Hupper=1.0) with an attached larger bottom cylinder (Rbottom=1.5, Hbottom=.5). In figure 13 the motion amplitude is a/Hupper=.25 and in figure 14 it is .5. In both figures the water depth is infinite. In figure 13 the nonlinear effects including the mean shift of the force are small because the amplitude of motion is modest. In figure 14, the amplitude of motion has been doubled; the nonlinear effects are
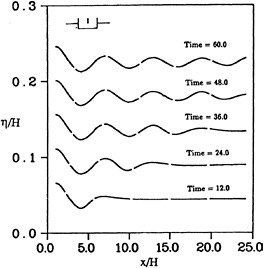
Figure 10: Comparison of the wave profiles using 2 and 60 planes of symmetry at the end of different periods for a heaving three-dimensional cylinder in infinite water depth, R=1.0, H=1.0, a/H=0.1, ![]()
Table 1: The RMS difference of the free surface elevation at the end of each period using 2 planes of symmetry and 60 planes of symmetry
|
Time |
2T |
3T |
4T |
5T |
6T |
7T |
8T |
9T |
10T |
|
RMS (×106) |
3.93 |
4.15 |
4.32 |
4.73 |
4.58 |
4.61 |
4.70 |
4.67 |
4.69 |
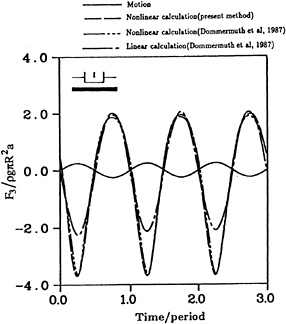
Figure 11: Time history of the vertical force for a heaving three-dimensional cylinder n finite water depth, h/H = 2.0, R = 1.0, H = 0.5, a/H = symmetry plane number = 60
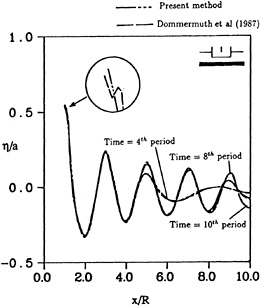
Figure 12: Comparison of instantaneous wave profiles for a heaving cylinder in finite water depth, h/H=2.0, R=1.0, H=.5, a/H=.5, symmetry plane number=60
now obvious and the mean shift is substantial. At the peak of the force curve, the vertical force is well in phase with the motion because the bottom of the cylinder is deeply submerged under the free surface. The force is almost a pure added mass effect. As the cylinder moves upward, however, the bottom is closer to the free surface and a phase difference appears between the curve of the force and the motion as a result of the wave damping.
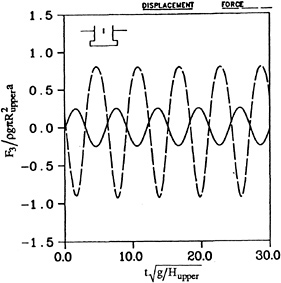
Figure 13: Time history of the heaving amplitude and vertical force on a double cylinder in infinite water depth,
Rupper=1.0, Hupper=1.0,
Rbottom=1.5, Hbottom=0.5,
a/Hupper=0.25
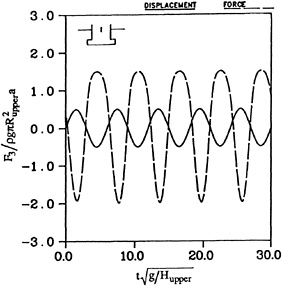
Figure 14: Time history of the heaving amplitude and vertical force on a double cylinder in infinite water depth,
Rupper=1.0, Hupper=1.0,
Rbottom=1.5, Hbottom=0.5,
a/Hupper=0.50
Wigley Hull Starting from Rest
Results for the free surface waves and wave resistance of a Wigley hull starting from rest have been computed using the desingularized approach. The results we are presenting must be considered as preliminary because all the convergence and other verification tests have not yet been completed. The Wigley hull is a mathematical form having a length-to-beam ratio of 10, a beam-to-draft ratio of 1.6 and the following equation for its hull surface:
(32)
where L=length
B/2=half-beam
H=draft
The velocity of the model at any time is given by:
(33)
The computations are made using moving nodes that travel with a velocity in the x-direction of Uo(t). The velocity in the y-direction is set so that the nodes move along prescribed paths around the hull. The prescribed paths and node placement may be seen in figures15 and 16. Having the nodes move along the prescribed paths eliminates the difficulty that must be overcome of material nodes crossing the hull surface between time steps. To avoid node pile up at the stagnation points, no nodes are distributed on the plane of symmetry. To allow unequal spacing in the x-direction, regridding is used after each time step. Regridding is also used on the body surface to reposition the nodes as the waterline moves vertically during the unsteady start-up phase. In the calculations to date, the model has been fixed in position. Since the program is in the time domain, allowing sinkage and trim is a simple addition but it has not yet been made.
On the upstream boundary it is assumed that both the potential and wave elevation are zero. The nodes are convected downstream so that no downstream boundary condition appears necessary. On the side boundaries no special conditions are imposed. This has been observed to lead to wave reflection at the side boundaries when the boundaries are too close to the vessel, but normally the reflected waves are outside the domain of interest
Figures 15 and 16 present the wave elevation contours for a Froude number .25 at time step ![]() for two different numbers of nodes.
for two different numbers of nodes.
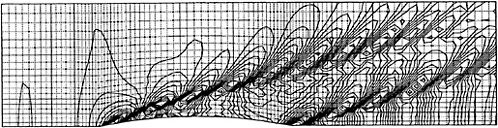
Figure 15: Wave contours for the Wigley Hull, Froude number = .25, coatse grid, NF = 1920, NB = 369, ![]()

Figure 16: Wave contours for the Wigley Hull, Froude number = .25, fine grid, NF = 2478, NB = 510, ![]()

Figure 17: Shaded rendering of the waves generated by the Wigley Hull, Froude number=.25, fine grid, ![]()
The coarse spacing used in figure 15 has 1920 nodes on the free surface and 369 nodes on the body. The fine spacing used for figure 16 has 2478 nodes on the free surface and 510 nodes on the body surface. As can be seen, the finer grid spacing yields more detail around the hull but basically the waves are quite similar. Note that there does not appear to be any visible wave reflection from the side boundaries. A shaded rendering of the contour plot in figure 16 is shown in figure 17.
The development of the wave system along the plane of symmetry and around the hull is seen in figure 18 for the fine grid. An expanded scale of the wave profile along the hull for the last time step is given in figure 19. Also plotted in figure 19 is the wave profile along Wigley hull as experimentally measured by the University of Tokyo (see Noblesse and McCarthy 1983 or Noblesse et al. 1991). It should be noted that the experimental measurements show a great deal of variation depending on model size. While the waves shown in figure 18 have not completely reached steady state (in particular the transverse wave system behind the model), the wave profile long the hull appears close to steady. The comparisons with the experimental results in figure 19 indicate that the bow wave height is underpredicted and that there is higher frequency noise around midship. However, in general the comparison is good. We are presently investigating the reasons for the bow wave discrepancy and methods to eliminate the noise around midship. No smoothing or low pass filtering has been done on the data in figures 15–19.
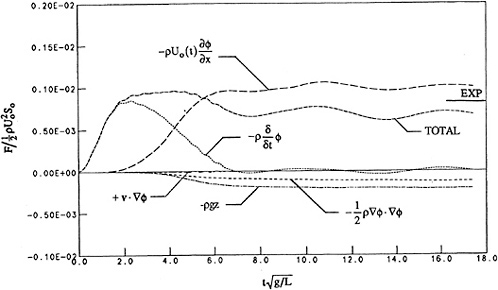
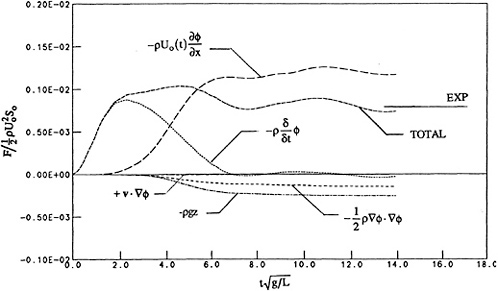
The wave resistance acting on the hull is shown in figures 20 and 21 for the course and fine grid spacings respectively. The contributions of the five individual components identified from equation (23) are also plotted in the figures. The resistance force components are nondimensionalized as ![]() where Uo is the final velocity and So is the nominal wetted surface (So=0.1487L2) The first component and largest during the initial start-up, is due to the time derivative of the potential following each individual node. The second term is the linear pressure due to the forward speed. This is the usual linear pressure component in steady forward motion problems. It is large and positive and dominates at large times. The remaining components are all nonlinear. The third is the gravity term due to the change in the integration of ρ gz over the wetted surface. This term is proportional to the wave elevation squared and is small and negative. The forth component is the velocity squared term which is also small and negative. The final component is the correction for the moving nodes. The node movement is due to the changing wave elevation along the hull and is consequently small, eventually going to zero. The net result is that this component is very small. For unsteady ship motion problems it could conceivably become much larger.
where Uo is the final velocity and So is the nominal wetted surface (So=0.1487L2) The first component and largest during the initial start-up, is due to the time derivative of the potential following each individual node. The second term is the linear pressure due to the forward speed. This is the usual linear pressure component in steady forward motion problems. It is large and positive and dominates at large times. The remaining components are all nonlinear. The third is the gravity term due to the change in the integration of ρ gz over the wetted surface. This term is proportional to the wave elevation squared and is small and negative. The forth component is the velocity squared term which is also small and negative. The final component is the correction for the moving nodes. The node movement is due to the changing wave elevation along the hull and is consequently small, eventually going to zero. The net result is that this component is very small. For unsteady ship motion problems it could conceivably become much larger.
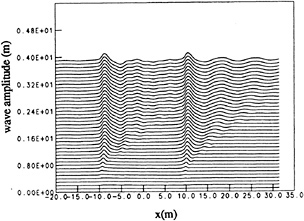
Figure 18: Development of wave system along Wigley Hull surface, Froude number=.25, fine grid
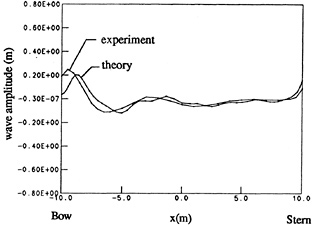
Figure 19: Wave amplitude along Wigley Hull, Froude number=.25, ![]()
The fine grid calculations shown in figure 21 have not been carried out further because of the unavailability of CRAY time. The horizontal line in both figures is the experimental wave resistance as measured by the University of Tokyo on the 2.5m model (cf. Noblesse and McCarthy 1983). Using different model scales or the wave pattern resistance would result in a slightly different experimental line. The oscillations in the total force curve are the τ=1/4 oscillations that occur in the wave resistance when starting from rest and their decay rate is proportional to 1/t.
The total wave resistance of the fine grid results (figure 21) is approaching the experimental value while the coarse grid is approximately 12 to 15% low. The reason the fine grid has higher wave resistance is due to a slightly higher bow wave and a small trough near the stern. Further computations are necessary to confirm the convergence.
Another difference between the coarse and fine grid results is the high frequency oscillations occurring in the coarse grid results during the nondimensional time range 3–4 and again in the range of 7–9. The oscillations seem to almost have disappeared in the fine grid calculations. Apparently, they are related to the lack of resolution in the coarse grid. The time step size was ![]() for both calculations.
for both calculations.
CONCLUSIONS
The desingularized method is a viable alternative for solving fully nonlinear water wave problems. The desingularization allows the use of simple isolated sources with little loss in accuracy. The resulting code is straight forward and easily vectorized. The use of generalized nodes on the free surface rather than always using material nodes can have computational advantages. For a given problem, it might be more beneficial to use material nodes, nodes fixed in a horizontal position relative to the body, or nodes following a prescribed path.
The method has been applied to a variety of problems in two and three dimensions. Comparisons with other numerical computations and with experimental results have shown very good to excellent agreement.
The results for the Wigley hull at a Froude number of .25 are promising but much more research needs to be done. Verificaton and convergence checks need to be completed and a complete range of Froude numbers investigated. The wave resitance is acccurately predicted when compared with experiments. The wave profile along the hull is generally well predicted, but the bow wave is slightly under predicted and there are small higher frequency waves near midship.
ACKNOWLEDGEMENTS
This research was funded by the Office of Naval Research Grant Number N-00014-70-J-1818. Computations were made in part using a CRAY Grant, University Research and Development Program at the San Diego Supercomputer Center.
REFERENCES
Bai, K., J.Kim and H.Lee ( 1992), “A Localized Finite-Element Method for Nonlinear Free-Surface Wave Problems,” Proceedings 19th Symposium on Naval Hydrodynamics, Seoul, Korea, pp. 90–114.
Baker, G.R., D.I.Meiron, and S.A.Orszag ( 1982), “Generalized Vortex Methods for Free-Surface Flow Problems,” J. Fluid Mech., 123, pp. 477–501.
Bertram, V. ( 1990), “Ship Motions by Rankine Source Method,” Ship Technology Research, Vol. 37, No. 4, pp. 143–152.
Bertram, V., W.W.Schultz, Y.Cao, and R.F. Beck ( 1991), “Nonlinear Computations for Wave Drag, Lift and Moment of a Submerged Spheroid,” Ship Technology Research, Vol. 38, No. 1, pp. 3–5.
Cao, Y., W.W.Schultz and R.F.Beck ( 1990), “Three-Dimensional, Unsteady Computations of Nonlinear Waves Caused by Underwater Disturbances,” Proceedings 18th Symposium on Naval Hydrodynamics, Ann Arbor, Michigan, pp. 417–427.
Cao, Y. ( 1991), “Computations of Nonlinear Gravity Waves by a Desingularized Boundary Integral Method,” Ph.D. Thesis, Technical Report No. 91–3, Department of Naval Architecture and Marine Engineering, The University of Michigan, Ann Arbor, Michigan, USA.
Cao, Y., W.W.Schultz and R.F.Beck ( 1991), “A Three-Dimensional Desingularized Boundary Integral Method for Potential Problems,” International Journal of Numerical Methods in Fluids, Vol. 11, pp. 785–803.
Cao, Y., T.Lee and R.F.Beck ( 1992), “Computation of Nonlinear Waves Generated by Floating Bodies,” 7th International Workshop on Water Waves and Floating Bodies, Val de Reuil, France, pp. 47–52.
Cao, Y., R.F.Beck and W.W.Schultz ( 1993a), “Numerical Computations of Two-Dimensional Solitary Waves Generated by Moving Disturbances,” accepted for publication in the International Journal for Numerical Methods in Fluids.
Cao, Y., R.F.Beck and W.W.Schultz ( 1993b), “An Absorbing Beach for Numerical Simulations of Nonlinear Waves in a Wave Tank,” 8th International Workshop on Water Waves and Floating Bodies, St. Johns, Newfoundland, Canada.
Cointe, R., P.Geyer, B.King, B.Motin, and M.Tramoni ( 1990), “Nonlinear and Linear Motions of a Rectangular Barge in a Perfect Fluid,” Proceedings 18th Symposium on Naval Hydrodynamics, Ann Arbor, MI, pp. 85–99.
Dommermuth, D.G. and D.K.P.Yue ( 1987), “Numerical Simulations of Nonlinear Axisymmetric Flows With a Free Surface,” Journal of Fluid Mechanics, Vol. 178, pp. 195–219.
Dommermuth, D.G., D.K.P, Yue, W.M.Lin, R.J.Rapp, E.S.Chan, and W.K.Melville, ( 1988), “Deep-Water Plunging Breakers: A Comparison Between Potential Theory and Experiments,” J. Fluid Mechanics, Vol. 189, pp. 423–442.
Faltinsen, O.M. ( 1977), “Numerical Solution of Transient Nonlinear Free-Surface Motion Outside or Inside Moving Bodies, Proceedings 2nd Conf. on Num. Ship. Hydro., U.C.Berkeley, (ed. J.V. Wehausen and N.Salvesen), pp. 347–357, University Extension Publications.
Grosenbaugh, M.A. and R.W.Yeung ( 1988), “Nonlinear Bow Flows—An Experimental and Theoretical Investigation,” Proceedings 17th Symposium on Naval Hydrodynamics, The Hague, Netherlands, pp. 195–214.
Jensen, G., H.Söding and Z.-X.Mi ( 1986), “Rankine Source Methods for Numerical Solution of the Steady Wave Resistance Problem,” Proceedings 16th Symposium on Naval Hydrodynamics, University of California, Berkeley, pp. 575–582.
Jensen, G., V.Bertram and H.Söding ( 1989), “Ship Wave-Resistance Computations,” Proceedings 5th International Conference on Numerical Ship Hydrodynamics, Hiroshima, Japan, pp. 593–606.
Kang, C.-G. and I.Y.Gong ( 1990), “A Numerical Solution Method for Three-Dimensional Nonlinear Free Surface Problems,” Proceedings 18th Symposium on Naval Hydrodynamics, Ann Arbor, Michigan, pp. 427–438
Kim, Y.-H. and T.Lucas ( 1990), “Nonlinear Ship Waves,” Proceedings 18th Symposium on Naval Hydrodynamics, Ann Arbor, Michigan, pp. 439–452.
Kim, Y.-H. and T.Lucas ( 1992), “Nonlinear Effects on High Block Ship at Low and Moderate Speed, Proceedings 19th Symposium on Naval Hydrodynamics, Seoul, Korea, pp. 43–52.
Lee, T.-H ( 1992), “Nonlinear Radiation Problems for a Surface-Piercing Body,” Ph.D. Thesis, Report No. 323, Department of Naval Architecture and Marine Engineering, University of Michigan, Ann Arbor, Michigan.
Lin, W.M., J.M.Newman and D.K.Yue ( 1984), “Nonlinear Forced Motions of Floating Bodies,” Proceedings 15th Symposium on Naval Hydrodynamics, Hamburg, pp. 33–49, Washington: National Academy Press.
Longuet-Higgins, M.S. and E.D.Cokelet ( 1976), “The Deformation of Steep Surface Waves on Water: I. A Numerical Method of Computation,” Proc. R. Soc. Lond., A350, pp. 1–26.
Noblesse, F., and J.H.McCarthy ( 1983), editors, “Ship Wave-Resistance Computations,” Proceedings of the Second DTNSRDC Workshop.
Noblesse, F., D.M.Hendrix and L.Kahn ( 1991), “Nonlinear Local Analysis of Steady Flow About a Ship,” Journal of Ship Research, Vol. 35, No. 4, pp. 288–294.
Raven, H.C. ( 1992), “A Practical Nonlinear Method for Calculating Ship Wavemaking and Wave Resistance,” Proceedings 19th Symposium on Naval Hydrodynamics, Seoul, Korea .
Saubestre, V. ( 1990), “Numerical Simulation of Transient Nonlinear Free-Surface Flows with Body Interaction,” Technical Report 90–52, Department of Mechanical and Environmental Engineering, University of California, Santa Barbara.
Schultz, W.W. and S.W.Hong ( 1989), “Solution of Potential Problems Using an Overdetermined Complex Boundary Integral Method,” J. Comput. Phys., No. 84, pp. 414–440.
Vinje, T. and P.Brevig ( 1981), “Nonlinear Ship Motions,” Proceedings 3rd International Symp. Num. Ship Hydro., Paris, pp. 257–268, Bassin d'Essais des Carenes, France.
Vughts, J.H. ( 1968), “The Hydrodynamic Coefficients for Swaying, Heaving and Rolling Cylinders in a Free Surface,” International Shipbuilding Progress, Vol. 15, pp. 251–276.
Webster, W.C. ( 1975), “The Flow About Arbitrary, Three-Dimensional Smooth Bodies,” J. Ship Research, No. 19, pp. 206–218.
Zhou, Z. and M.Gu ( 1990), “A Numerical Research of Nonlinear Body-Wave Interactions,” Proceedings 18th Symposium on Naval Hydrodynamics, Ann Arbor, MI., pp. 103–118.
Rankine Source Method in High Speed Range
K.Kataoka, J.Ando, K.Nakatake, and K.Oda
(Kyushu University, Japan)
ABSTRACT
The conventional Rankine source method (Low Speed Approximation, LSA) uses the double body flow as the basic flow. We propose a new Rankine source method (High Speed Approximation, HSA) which uses the inverse image above the still water surface in the high speed range. In order to show the availability of HSA, computations for 2-D point doublet are carried out and then the numerical results are compared with the analytical ones. And we introduce a new panel method named SQCM (Source panel with Quasi-Continuous Vortex Lattice Method), which represents the flow around a wing.
Next, applying LSA and HSA together with SQCM to the flows around circular cylinder, 2-D, 3-D mono and tandem hydrofoils in a wide range of speeds, the wave profiles, lifts and wavemaking resistances are obtained and compared with the analytical solutions or the experimental results.
According to these results, we show that HSA is more easily applicable to the tandem hydrofoil system in the high speed range.
NOMENCLATURE
|
|
: velocity potential/vector around hydrofoil |
|
|
: velocity potential/vector due to basic flow |
|
|
: velocity potential/vector due to wave flow |
|
|
: velocity potential/vector due to σF |
|
|
: velocity potential/vector due to source m |
|
|
: velocity potential/vector due to vortex γ |
|
qU |
: velocity vector of uniform flow |
|
Cp |
: pressure, coef. |
|
D |
: drag |
|
D1 |
: drag of fore/first foil |
|
D2 |
: drag of aft/second foil |
|
Fn |
: Froude number |
|
L |
: lift |
|
L1 |
: lift of fore/first foil |
|
L2 |
: lift of aft/second foil |
|
L∞ |
: lift of mono foil in unbounded flow |
|
Rw |
: wavemaking resistance |
|
SF |
: still water surface |
|
Sc |
: surface of circular cylinder |
|
Sw |
: hydrofoil surface |
|
V |
: uniform flow velocity at infinity |
|
c |
: hydrofoil chord length |
|
f |
: submergence of leading edge(fore foil) |
|
g |
: acceleration of gravity |
|
k0 |
: number of wave (=g/V2) |
|
m |
: source strength on body surface |
|
nx,ny |
: x and y components of external unit normal vector |
|
p |
: pressure in fluid |
|
p0 |
: pressure at upstream infinity |
|
s |
: stagger (distance of leading edges) |
|
s |
: hydrofoil span |
|
x,y,z |
: rectangular coordinate |
|
α |
: geometric angle of attack |
|
γ |
: vortex strength |
|
η |
: wave height |
|
μ |
: strength of point doublet |
|
ρ |
: fluid density |
|
σF |
: source strength on still water surface |
|
|
: velocity potential due to circular cylinder |
|
|
: velocity potential due to hydrofoil |
|
|
: basic flow effect component |
|
Δ |
: free surface effect component |
|
suffix j |
: value for j-th hydrofoil |
INTRODUCTION
Rankine source method presented by Dawson [1] has been applied widely as a practical method for calculating wave resistance and many improvements have been made. Most of Rankine source method uses double model flow as the basic flow in the limiting case of zero Froude number (Low Speed Approximation, LSA). It is considered that LSA is successful in case of ship wave calculation because Froude number based on the ship length in general is relatively small. However, when we try to solve the wave resistance problem in the high speed range by Rankine source method, it is doubtful whether we can use LSA to represent the basic flow in the same way as the low speed range [2] or not.
By the way, it is well known that the research and development of high speed marine vehicles have been performed all over the world. Among them, we can find many crafts which have hydrofoils to lift up the hulls [3]. A review of hydrofoils and hydrofoil craft was given by Acosta [4]. In recent studies of the hydrofoil problems, Lee et al. [5] treated the 2-D cavitating hydrofoil advancing under the free surface. Bai et al.[6] presented a localized finite-element method for nonlinear 3-D free surface ploblems.
It is clear that the free surface effect on the lift and drag of hydrofoil is not negligible. In case of hydrofoil, Froude number based on the chord length is much higher than Froude number of ship. So, if we use the conventional Rankine Source method for the free surface problem in high speed range, a question will arise whether we can use LSA or not. To clear this question, we present a new Rankine source method which uses inverse image above the still water surface to represent the basic flow (High Speed Approximation, HSA). At first, we discuss the free surface problem of 2-D point doublet in high speed range. Next, we show the calculated results of 2-D hydrofoil. And we describe a new panel method named SQCM, which represents the flow around a wing.
Hydrofoil craft has usually tandem foil system, that is, one foil is located at the front and the other is at the rear. The lift and drag of the tandem foil system advancing under the free surface may be affected by the advancing speed, the depth of immersion, the vertical and horizontal distance between two foils and so on. However, we can not find the papers which show the effects of these parameters on the performance of the tandem foil system. In this paper, we show the calculated results of the lift and drag of 2-D and 3-D tandem foil system by using of a numerical method which combines SQCM and the new Rankine source method. In addition, we compare these results with the experimental ones of 3-D tandem foil system, which was performed at Kyushu University.
FORMULATION OF TWO KINDS OF RANKINE SOURCE METHODS
2-D circular cylinder
At first, we derive the formulation of HSA and LSA for a circular cylinder located under the still water surface, and then we give some additional explanations to the case of a 2-D point doublet.
We take the x-axis in the direction of uniform flow with speed V and the y-axis in the vertically upward direction as shown in Fig. 1.
Let us consider a circular cylinder of diameter D(=2α) located at y=−f in a uniform flow (see Fig. 1). Here we distribute the source m on the surface of the circular cylinder Sc and the source σF on the still water surface SF. Then the velocity potential to express the flow field around the circular cylinder ![]() is given as
is given as
(1)
In Eq.(l), ![]() and are
and are ![]() the velocity potentials to express the basic flow and the effect of the free surface disturbance, respectively, and are given as
the velocity potentials to express the basic flow and the effect of the free surface disturbance, respectively, and are given as
(2)
In Eq.(2), ![]() and
and ![]() are the disturbed velocity potentials to express the basic disturbance due to the double model or the inverse image and the effect of the free surface on the cylinder, respectively. Denoting the combined disturbed velocity potential due to
are the disturbed velocity potentials to express the basic disturbance due to the double model or the inverse image and the effect of the free surface on the cylinder, respectively. Denoting the combined disturbed velocity potential due to ![]() and
and ![]() is represented by the following equation
is represented by the following equation
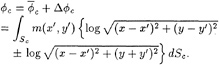
(3)
In the above equation, the sign+means the double model and the sign −does the inverse image. The source strength m is divided into ![]() used for the basic flow and Δm used for the free surface effect as
used for the basic flow and Δm used for the free surface effect as
![]() (4)
(4)
In Eq. (2), the disturbed velocity potential due to the free surface wave ![]() is represented by
is represented by
(5)
As described above, we obtained two kinds of velocity potentials for the flow field around the circular cylinder. Considering the facts that ![]() at y=0 in case of the double model flow and at y=0 in case of the
at y=0 in case of the double model flow and at y=0 in case of the ![]() inverse image flow, the linearized free surface condition is expressed as
inverse image flow, the linearized free surface condition is expressed as
(6)
where k0=g/V2 and g is the gravitational acceleration. Then the velocity potential ![]() must satisfy the boundary condition on the surface of the circular cylinder as
must satisfy the boundary condition on the surface of the circular cylinder as
(7)
Solving Eqs.(6) and (7) simultaneously, we can obtain m on the cylinder surface and σF on the still water surface. As to the radiation condition, we satisfy it by Kyushu University method [7] which shifts downwards the source loading mesh from the control point mesh by one mesh length.
Using the obtained m and σF, we calculate the wave height η and the wavemaking resistance Rw by the following equations,
(8)
![]() , (9)
, (9)
where ![]()
Next, we give some additional explanations to the case of a point doublet to express the circular cylinder. Denoting the strength of a point doublet with the axis in the −x direction, the disturbed velocity potential ![]() is expressed as
is expressed as
![]() , (10)
, (10)
where μ=Va2
In this case, ![]() 0 and
0 and ![]() 1 become
1 become
![]() (11)
(11)
In this formulation, only σF is unknown and is obtained by solving Eq.(6) making use of Kyushu University method. Then the wave profile is calculated by Eq.(8) and the wavemaking resistance Rw is obtained by Lagally's theorem, i.e.
(12)
The analytical wave height and wavemaking resistance are given by Havelock [8] as,
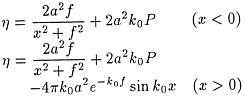
(13)
where
(14)
Hydrofoils
Here, we derive the formulation of HSA and LSA for the three cases, i.e. 2-D mono hydrofoil, 2-D and 3-D tandem hydrofoil-system problems, together. We call the fore foil the first one (j=1) and do the aft foil the second one (j=2) in tandem systems. But when the mono foil problem is considered, we use only the first/fore foil neglecting the terms of the second/aft one.
Let us consider a hydrofoil-system whose chord length is c and the leading edge of the first foil is located at y=−f in the inviscid incompressible and irrotational uniform flow (see Fig. 2). In our usual calculation method [9] for the 3-D wing section, we used the source distributing panels on wing surface and the vortex surface on which vortices distribute constantly in the chordwise direction. In the 3-D problem, we must solve the nonlinear simultaneous equations derived from the Kutta 's condition. In order to avoid this numerical difficulty, we use source distributions m1, m2 on the surface panels of both foils Sw1, Sw2 together with the vortices γ1, γ2 distributing discretely on the camber surfaces C according to the Lan's QCM [10] which expresses thin wing approximately. Then the number of the equations is increased but we can solve linear simultaneous equations at a time and reduce the computational time. We call this new QCM combined with the source panels SQCM (Source panels with QCM) briefly [11].
In the 3-D problem, free vortices flow along the camber surface and to the rear infinity parallel to the nose-tail line through the trailing edges. In addition to the sources m (m1, m2) on the hydrofoil surfaces and vortices γ (γ1, γ2) on the camber, the source σF is distributed on the still water surface SF, which expresses wave flow. These singularities induce the velocity vectors qS, qV and qF (cf. Appendix).
The source and vortex strength m, γ are divided into ![]() used for the basic flow and Δm, Δγ used for the free surface effect as
used for the basic flow and Δm, Δγ used for the free surface effect as
![]() (j=1,2) (15)
(j=1,2) (15)
Then the velocity vector q around hydrofoil-system can be also expressed by the sum of the basic flow velocity vector q0 and the wave flow velocity vector q1 as
q=q0+q1, (16)
where q0 is expressed by HSA in case of high speed and by LSA in case of low speed. Here q0 and q1 are shown as follows [2].
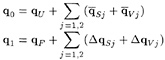
(17)
where qU is velocity vector of the uniform flow and ![]() are the disturbed velocity vectors to express the basic flow, i.e. the double model or the inverse image and ΔqSj, ΔqVj are the effects of the free surface on the flow field around each foil surface, respectively.
are the disturbed velocity vectors to express the basic flow, i.e. the double model or the inverse image and ΔqSj, ΔqVj are the effects of the free surface on the flow field around each foil surface, respectively.
To express qV by N vortex lattices, the loading point xk and the control point xi are selected as follows according to QCM.
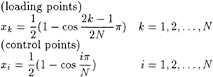
(18)
where chord length equals 1.
We can obtain vortices ![]() and sources
and sources ![]() simultaneously solving the boundary conditions, that is, there does not exist normal component of the velocity vector both at the camber surface elements and on the hydrofoil surfaces. At this time, the Kutta's condition is satisfied sufficiently according to QCM of itself.
simultaneously solving the boundary conditions, that is, there does not exist normal component of the velocity vector both at the camber surface elements and on the hydrofoil surfaces. At this time, the Kutta's condition is satisfied sufficiently according to QCM of itself.
Making use of HSA (inverse image) or LSA (normal image), the linearized free surface condition (A-15) is solved and σF is obtained. And then γ1, γ2 and m1, m2 influenced by σF are calculated and σF is obtained by solving the linearized free surface condition again. These procedures are repeated three or four times.
Wave profiles which hydrofoil system makes are calculated using these singularities γ1, γ2, m1, m2 and σF by Eq.(A-16), which satisfies the linearized free surface condition (A-15) and the radiation condition. As to the radiation condition, we satisfy it by Kyushu University method [7] as well as the circular cylinder problems.
Lift and drag are obtained by summing up of horizontal and vertical components of the pressure around hydrofoil surfaces. They are expressed for j=1, 2 as follows
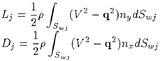
, (19)
where nx, ny show the x, y components of the external unit normal vectors on the foil surface, respectively. Then lift L and wavemaking drag D of the tandem hydrofoil system are
L=L1+L2 , D=D1+D2. (20)
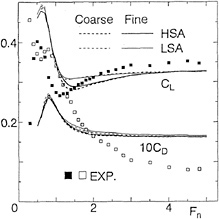
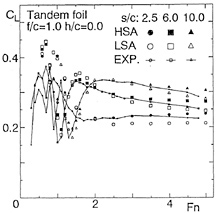
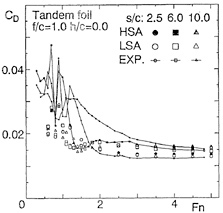
RESULTS AND DISCUSSION
Results of 2-D circular cylinders
We consider the wavemaking problem due to a circular cylinder (D=1.0m) located at a depth (f=1.0m).
Point Doublet
At first, we show some results of the case to use a point doublet for the circular cylinder. Calculation region on the still water surface and the panel size are almost ![]() and 0.20m, respectively, though they change a little with Froude number
and 0.20m, respectively, though they change a little with Froude number ![]() .
.
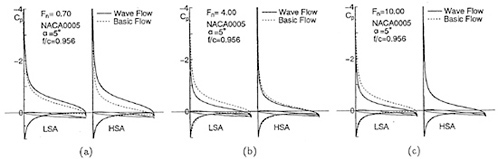
Figs. 3(a), (b) show comparisons of source distributions on still water surface due to the circular cylinder obtained by LSA and HSA at Fn=0.85, 10.0. At Fn=0.85, both numerical results by LSA and HSA are very similar to each other except right above the cylinder, however, at Fn=10.0 results of LSA are quite different from ones of HSA.
Figs. 4(a), (b) show comparisons of wave profiles obtained by LSA, HSA and analytical
method at Fn=0.85, 10.0. At Fn=0.85, both numerical results by LSA and HSA agree well with the analytical ones, however, at Fn=10.0 LSA gives quite different wave profile from results of HSA and analytical method. In Fig. 5, the wavemaking resistance coefficient Cw(= 2Rw/ρV2D) of a point doublet is shown in the speed range Fn=0.2~10.0. Though the wave profiles differ in case of LSA at high speed, we can not recognize the difference of Cw in the wide range of Froude number. We think that HSA gives more correct wave profiles at high speed than LSA compared with the analytical method.
Surface Source Distribution
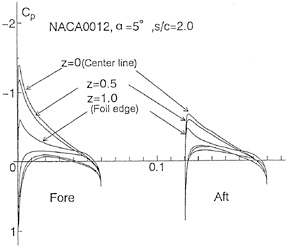
Next, we show some results of the case to use the surface source distribution for the circular cylinder. We divide the cylinder surface into 90 segments and do the still water surface as stated before. Figs. 6(a), (b) show comparisons of wave profiles obtained by LSA and HSA compared with the analytical method. At Fn=0.85 and 10.0, the wave profiles show nearly the same tendencies as Figs. 4(a), (b). Little difference may be due to the consideration of the boundary condition on the circular cylinder. In Fig. 7, Cw of the circular cylinder is shown. At Fn≈1.0, numerical results differ from the analytical ones, however, the values themselves do not differ so much. These tendencies are also same as the case of a point doublet. In order to confirm these behavior, we calculate the pressure coefficient Cp(=2(p−p0)/ρV2) and show them in Figs. 8(a), (b), (c) which indicate Cp around the circular cylinder at. Fn=0.20, 0.85, 10.0. We know that the pressure distributions becomes similar after satisfying the boundary conditions correctly even if the basic flows are different.
Results of Hydrofoils
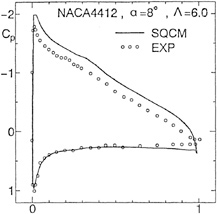
In order to confirm the program codes, using a 2-D wing NACA0012 in the unbounded flow, we calculate the pressure coefficient over the wing surface and compare the results by SQCM with one of the panel method in Fig.9. We divide the wing surface into 50 segments and the camber surface into 25 segments in the case of SQCM. The pressure distributions agree very well with each other and we confirm the availability of SQCM.
2-D Mono Hydrofoil
In the following calculations, NACA0005 symmetric wing section is used and chord length c=1m and angle of attack α=5°. We divide the hydrofoil surface into 90 segments around the wing section and the camber line into 45 segments and the division of the still water surface is similar to the case of circular cylinder.
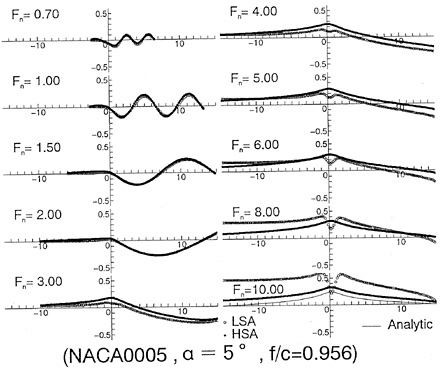
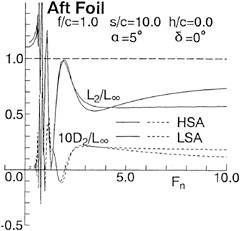
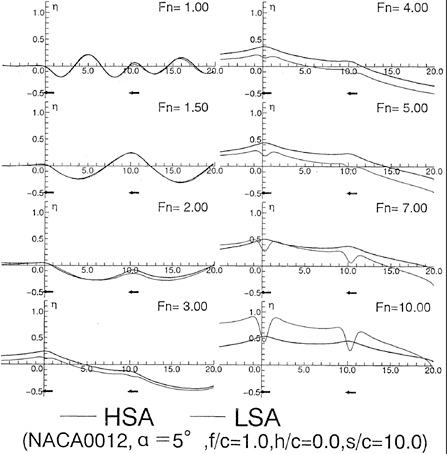
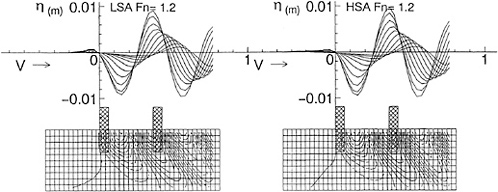
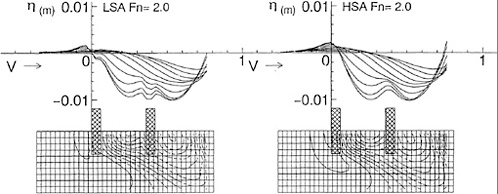
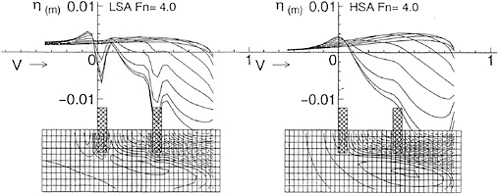
Fig. 10 shows wave profiles η varying with ![]() . At Fn=1.0 there is little difference between LSA and HSA, but above Fn=3.0 wave profiles by LSA show the depression above the foil and entire profiles are risen up unnaturally. On the other hand, HSA shows calm variation and seems to converge to a natural profile. This profile is very similar to the result of the experimental investigation [12]. In the case Fn=10.0, it is also shown the wave profiles in the high speed limit which is derived from Eq.(A-18) when the upstream end η=0. It looks like the result of HSA.
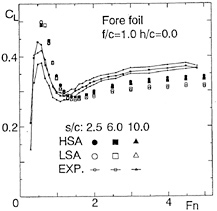
. At Fn=1.0 there is little difference between LSA and HSA, but above Fn=3.0 wave profiles by LSA show the depression above the foil and entire profiles are risen up unnaturally. On the other hand, HSA shows calm variation and seems to converge to a natural profile. This profile is very similar to the result of the experimental investigation [12]. In the case Fn=10.0, it is also shown the wave profiles in the high speed limit which is derived from Eq.(A-18) when the upstream end η=0. It looks like the result of HSA.
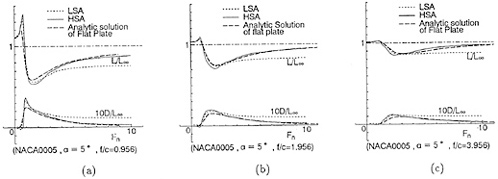
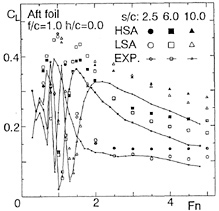
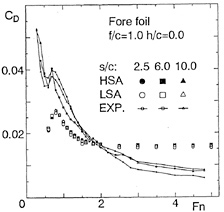
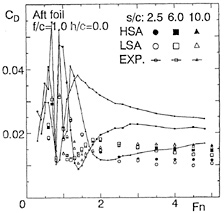
In Figs. 11 (a)~(c) lift L and drag D are shown for various Fn, as the ratios of them to the lift in unbounded flow (L/L∞, D/L∞). Additionally, the analytical solutions are shown for the lift and wavemaking resistance of 2-D flat plate obtained by Nishiyama [13]. Fig.11(a) shows the results in case of the depth f/c=0.956. It is seen that the values obtained by LSA are going to converge to each constant value, but both lift and drag by HSA are converging to the analytical solutions in high speed range (Fn>5.0). However, the results by both LSA and HSA are different from the analytical solution in relatively low speed range. This means that the effect of the free surface is large at the depth of the chord length level and the effect of the wing thickness 5% is clear, which is the difference between wing section and the flat plate. Then in the deeper cases, f/c=1.956 and 3.956 as Figs.11(b) and (c), the difference becomes small and they agree to the analytical solutions.
Figs.12(a)~(c) show in case of f/c=0.956 the pressure coefficients around the hydrofoil surface, comparing the results of LSA and HSA as well as the case of the circular cylinder (Figs. 8(a)~(c)). These broken and full lines mean the pressure distributions in the basic flow field and the wave flow field, respectively. It is not similar to the case of the circular cylinder. There exists remarkable difference in the wave flow between LSA and HSA and this can explain the difference of the lifts and drags in Fig.11(a). Especially in LSA, it does not change the pressure distribution around the hydrofoil surface in the high speed range (Fn >4.0).
2-D Tandem Hydrofoil-System
In the following calculations, the wing parameters are the same for the fore and aft foils, that is, NACA0012 symmetric wing sections is used, chord length c=1m and angle of attack α=5º. We divide the hydrofoil surface into 90 segments around the wing section and do the camber line into 45 segments and the division of the still water surface is similar to the case of the mono hydrofoil.
First we show the source distribution σF on the still water surface comparing HSA with LSA at the low speed (Fn=0.88), and at the high speed (Fn=5.0) in Figs.13(a), (b), where the two arrows mean the horizontal positions of the fore and aft foils. In this case s/c=10.0 and it is same in the following figures.
There is little difference of σF between HSA (thick line) and LSA (thin line) at the low speed (Fn=0.88), but at the high speed (Fn=5.0) there is a big difference. These σF create the wave profiles as Figs.14(a), (b). HSA and LSA make similar wave profiles to each other at the low speed (Fn=0.88), but very different at the high speed (Fn=5.0). It is seen that the wave profile by HSA rises up and the one by LSA shows the unnatural depressions just above each hydrofoil in the high speed range.
Figs.15(a), (b) show the lift and drag interference factors for the fore, the aft and combined system according to the distance between two foils. Here we define the interference factor as the ratio of forces to the value of mono foil in the unbounded flow. From Fig. 15(a), in case of high speed (Fn=5.0) and the stagger (s/c>5.0) it is seen that both lift L and drag D of tandem-system are almost invariant to the stagger s. But, these factors decrease due to the effect of the free surface in case of s/c less than 5.0. In Fig.15(b) we show the lift and drag interference factors for the fore, the aft and combined system in case of the low speed (Fn=0.88). Lift and drag of the aft foil are affected very much by the wave which is created by the fore foil, but those changes of the fore foil are not affected in case of s/c above 3.0. Then wave profile at the high speed (Fn=5.0) varies as Fig.16 and there is a convex part of the free surface above the aft foil. In Fig.16(b) we show the wave profiles in the low speed (Fn=0.88). Here these values of s/c are chosen so that they are corresponding to the maximal or minimal position of lift and drag in Fig.15(b). It is seen that the amplitudes of wave profiles in the downstream are corresponding to the maximal or minimal position of drag, and this tendency agrees well to the linear analytical solution of hydrofoil problem in stationary wave [14], in which the phase of wave is discussed corresponding to change of lift and drag. However, in case of lift, the position of lift maximal is different from the analytical solution. Though there is a possibility that the aft foil may vary the wave profile near itself, we do not know the true reason.
Figs.17(a)~(b) show the lift and drag interference factors for the fore and aft foils comparing the results of HSA and LSA against Fn. In case of the fore foil those are similar to the results of mono hydrofoil in Fig.11 and minus value of drag is shown in the high speed range. In case of the aft foil, it is seen that the wave effect is large, which is created by the fore foil. Here minus value of drag is also shown in low speed range, but in the tandem-system total drag never become minus value. We notice that the lift and the drag by LSA have a tendency to converge to each constant value and on the contrary by HSA, lift approaches the value in the unbounded flow and drag does zero in high speed range (Fn>5.0). In Fig.18 wave profiles are shown in the relatively high speed range (Fn>1.0) and it is seen that strange depressions above each hydrofoil by LSA in the high speed range (Fn>3.0). On the other hand, wave height by HSA is different but it is a common phenomenon that long, convex and smooth wave profiles are created in the high speed range. Then it can be understood that from these variations of wave profiles in the high speed range lifts and drags are not affected very much by the position of the aft foil as Fig.15(a).
3-D Tandem Hydrofoil-System
In order to confirm SQCM in 3-D problem, we compare the numerical result with experiment [15]. Fig.19 shows the pressure distributions on the mono hydrofoil surface along the midspan chord in the 3-D unbounded flow. We divide the hydrofoil surface into 50×7 segments around the wing section and along the half-span and do the camber surface into 25×7 segments along the chord and the half-span. Since the foil is symmetric to the midspan, we calculate the one side using the image. The smooth pressure distribution on the 3-D hydrofoil is obtained and the tendency agrees well with an experiment. Especially around the trailing edge it is seen that the Kutta's condition is satisfied well by SQCM.
In the following calculations and exper-
iments, both the fore and aft foils have the same principal dimensions, that is, they have NACA0012 symmetric wing sections, chord length c(=0.06m), span length s(=0.3m) and angle of attack α(=5º).
Fig.20 shows the pressure distributions around the tandem hydrofoil surfaces in unbounded flow. The distance between the trailing edge of the fore foil and the leading edge of the aft foil equals one chord length, that is s/c=2.0. Mesh sizes around the hydrofoil surfaces and on the camber surface are same as Fig.19. It is seen that the pressure distributions of both foils are smooth and the Kutta's condition is satisfied enough.
Fig.21 shows the lift coef. CL and the drag coef. CD for various stagger s/c and shows the interference between the fore and aft foils. When s/ c is small, the ratios of interference are large, and drags of each foil are changed according to s/c but average drag for tandem system is almost constant. This phenomenon is known as the Munk's theorem [16].
Using HSA and LSA, we obtain the wave profiles and the pattern contours per 1.0mm for mono hydrofoil whose depth is just chord length (f/c=1.0). Typical examples are shown in Figs.22(a)~(b), and the relation between wave profiles and wave patterns is one of the elevation and the plane figure. We divide still water surface area (![]() into 30×10 segments (coarse or single mesh). The mesh division and hydrofoil plane are also projected in the figure where thick line means still water level, and full and broken lines do crest and trough side, respectively. There is no extreme difference between LSA and HSA in the case of relatively low speed (Fn=0.8). But when Fn=4.0, it is seen that smooth wave profiles are obtained by HSA and sharp trench appears right above the hydrofoil by LSA as well as the 2-D problems. Then in order to confirm the effect of the division of still water surfaces we carry out the calculation on the same condition as Fig.22(b) using 60×20 double segments (fine or double mesh) and show the results in Fig.23. When Fn=4.0 in case of high speed, there are little differences in the results of HSA using the coarse mesh. On the contrary, it is shown the depression is reduced if we use fine mesh in LSA. Moreover, more fine mesh may erase the depression obtained by LSA. The trouble is that it appears the tremendous concave area afterwards the hydrofoil and the computational time increases rapidly. For example single mesh in Fig.22 needs 4 minutes and triple mesh does about 4 hours. Furthermore we calculate the 2-D doublet problem by LSA using very fine mesh of 250 times, it is confirmed that the depression becomes very small but never agree to the analytical solution.
into 30×10 segments (coarse or single mesh). The mesh division and hydrofoil plane are also projected in the figure where thick line means still water level, and full and broken lines do crest and trough side, respectively. There is no extreme difference between LSA and HSA in the case of relatively low speed (Fn=0.8). But when Fn=4.0, it is seen that smooth wave profiles are obtained by HSA and sharp trench appears right above the hydrofoil by LSA as well as the 2-D problems. Then in order to confirm the effect of the division of still water surfaces we carry out the calculation on the same condition as Fig.22(b) using 60×20 double segments (fine or double mesh) and show the results in Fig.23. When Fn=4.0 in case of high speed, there are little differences in the results of HSA using the coarse mesh. On the contrary, it is shown the depression is reduced if we use fine mesh in LSA. Moreover, more fine mesh may erase the depression obtained by LSA. The trouble is that it appears the tremendous concave area afterwards the hydrofoil and the computational time increases rapidly. For example single mesh in Fig.22 needs 4 minutes and triple mesh does about 4 hours. Furthermore we calculate the 2-D doublet problem by LSA using very fine mesh of 250 times, it is confirmed that the depression becomes very small but never agree to the analytical solution.
Next, we compare the lift coef. CL and the drag coef. CD with the experimental results and show them in Fig.24 for various Fn with broken line (coarse mesh, Fig.22) and full line (fine mesh, Fig.23). The difference of the results between the mesh size (full and broken lines) is very small, but the difference of CL between HSA and LSA (thick and thin lines) is large. And the results of HSA are very similar to the experiments. Here we can not make a quantitative comparison directly, because these experimental values involve the effect of viscous drag of two struts, and it seems this effect also affects qualitatively the drag coef. CD.
From the above discussions it may be clear that HSA is more useful to reduce the number of mesh and CPU time than the conventional method LSA. Then in the following calculations, we use coarse mesh and compare the calculated results between HSA and LSA.
In Figs.25(a)~(c) we show the wave profiles and the wave patterns of the tandem foil system comparing HSA with LSA. The conditions of tandem system are that the stagger s/c=6.0, the gap h/c=0 and the depth f/c=1.0, too. Calculation area and mesh on the still water surface are almost same as the case of mono hydrofoil, but we add another meshes afterwards corresponding to the stagger of each foils s/c.
In Figs.25(a)~(c), there is no extreme difference between LSA and HSA in the case of Fn=1.2, but in the cases of Fn=2.0 and 4.0, we notice that smooth wave profiles are obtained by HSA and sharp depressions appear right above each hydrofoil by LSA. On the other hand, we notice a little rise right above each hydrofoils by HSA. These are very similar results to those of the 2-D problems [17]and we think that HSA is also useful in the 3-D hydrofoil problems in the high speed range.
At last we show the variation of the lift coef. CL and the drag coef. CD for the fore, the aft foils and the combined hydrofoil system in the case of s/c=2.5, 6.0, 10.0 comparing the results of HSA and LSA with the experiments.
Figs.26(a) and (b) show the lift coef. CL of the fore and the aft foils, respectively. The results of the fore foil are very similar to ones of the mono hydrofoil and there is no difference
due to s/c. But the difference due to s/c is clear for the aft foil in high speed range (Fn>2.0). However, in relatively low speed range, it varies extremely according to the wave profiles created by the fore foil. And the numerical results agree well with the experiments.
Figs.27(a) and (b) show the drag coef. CD of the fore and the aft foils, respectively. Both results of HSA and LSA agree well with each other, but are different from the experiments. However, since the experimental results involve the effects of struts, it is difficult to compare them directly with the numerical one.
Figs.28(a) and (b) show the lift coef. CL and the drag coef. CD of the combined tandem hydrofoil system. That is an average of the values of the fore and the aft foils. We understand the effect of the aft foil is predominant and the lifts coincide with the results of experiments but the tendency of the calculated drags for s/c is contrary to the experiments.
Through Fig.26 to Fig.28 there exists a difference between HSA and LSA, but as to the force they are not so different as in case of wave profiles in the high speed range. These are similar to 2-D problem.
CONCLUSION
We introduced a new calculation method SQCM which combines the source distributing surfaces panels with QCM and satisfies well the Kutta 's condition. Since there needs no iteration, it is very effective calculation method of characteristics of 3-D wings.
We proposed a new Rankine source method named HSA which uses the inverse image above the still water surface in the high speed range. We carried out the numerical calculations for a circular cylinder and 2-D thin hydrofoil in the high speed range and confirm that both forces and wave profiles agree very well to the analytical ones. The wave profile obtained by HSA is smooth and shows a little rise above the hydrofoil.
On the contrary, wave profile calculated by LSA shows so big depression right above the hydrofoil, using usual mesh size of still water surface. In addition, the depression increases with Froude number and it seems to be very strange.
Next, applying LSA and HSA to the flows around 2-D and 3-D mono and tandem hydrofoils in a wide range of speeds, we obtain the wave profiles, lifts and wavemaking resistances and compare them with the experimental results.
According to these results, HSA seems more applicable than LSA in the high speed range, and is expected to be a useful tool to predict the wave flow around the high speed ship with hydrofoils.
Acknowledgment
Finally the authors wish to express gratitude to Mr. Ohmori T., Mr. Okada S., Mr. Shindo K. and Mr. Mizuno S. for their precise experiments and analysis.
This research is partly supported by the Grant-in-Aid for Cooperative Research of the Ministry of Education, Science and Culture. All the calculations in this paper have been carried out by using FACOM M1800/20, VP2600/10 at the Computer Center, Kyushu University and as well FACOM M1800/30, VP2600/20 at the Computer Center, Kyoto University.
REFERENCES
1. Dawson C.W., ”A Practical Computer Method for solving Ship Wave Problems”, Second International Conference on Numerical Ship Hydrodynamics, Berkeley, 1977
2. Ando J., Kataoka K., Nakatake K., ”Rankine Source Method in High Speed Range” (in Japanese), Transactions of the West-Japan Society of Naval Architects, , No.84. 1992, pp. 1–10
3. ”First International Conference on Fast Sea Transportation” , Norwegian Institute of Technology, Trondheim, Norway, 1991
4. Acosta A.J., ”Hydrofoils and Hydrofoil Craft” , Annual Review of Fluid Mechanics, Vol.5, 1973
5. Lee C.S., Lew J.M. and Kim Y.G., ”Analysis of a Two-Dimensional Partially- or Supercavitating Hydrofoil Advancing under a Free Surface with a Finite Froude Number”, Nineteenth Symposium on Naval Hydrodynamics, Seoul, 1992
6. Bai K.J.Kim J. and Lee H., ”A localized Finite-Element Method Froude Number”, Nineteenth Symposium on Naval Hydrodynamics, Seoul, 1992
7. Ando, J. and Nakatake, K., ”A Method to Calculate Wave Flow by Rankine Source” (in Japanese), Transactions of the West
Japan Society of Naval Architects, No.75. 1988, pp. 1–12
8. Havelock, T.H., ”Some Cases of Wave Motion due to a Submerged Obstacles”, Proc. Roy. Soc. London, vol. 93, 1917
9. Nakatake K., Komura A., Ando J., Kataoka K., ”On the Flow Field and the hydrodynamic Forces of an Obliquing Ship ” (in Japanese), Transactions of the West-Japan Society of Naval Architects, No.80 . 1990, pp. 1–12
10. Lan, C.E., ”A Quasi-Vortex-Lattice Method in Thin Wing Theory”, Journal of Aircraft, Vol.11, No.9, 1974, pp. 518–527
11. Kataoka K., Ando J., Nakatake K., ”On Characteristics of Three-Dimensional tandem hydrofoils” (in Japanese), Transactions of the West-Japan Society of Naval Architects, No.86. 1993, pp. 1–14
12. Parkin B., Perry B., Wu T., ”Pressure Distribution on a hydrofoil near the Water Surface”, Journal of Applied Physics, Vol. 27, No. 3, 1956, pp. 232–240
13. Nishiyama T., ”Linearized Steady Theory of Fully Wetted hydrofoils”, Advances in Hydroscience, Vol. 3, pp. 237–342, 1966
14. Nishiyama, ”Characteristics of the submerged hydrofoil among stationary waves. ”, J. Soc. Naval Arch. Japan, No.97, 1955, pp.1–8
15. Pinkerton, R.M., ”Calculated and Measured Pressure Distributions over the Midspan Section of the N.A.C.A. 4412 Airfoil”, NACA Report No. 563, 1936
16. Moriya T., ”An Introduction to Aerodynamics”, Baifukan Book Co., Tokyo, 1959
17. Kataoka K., Ando J., Nakatake K., ”On Characteristics of Two-Dimensional tandem hydrofoils” (in Japanese), Transactions of the West-Japan Society of Naval Architects, No.85. 1993, pp. 1–14
APPENDICES
Expression of Hydrofoil Using Potential
When we consider a hydrofoil-system in the inviscid incompressible and irrotational uniform flow, the flow field can be expressed by the velocity potential ![]() . Then
. Then ![]() satisfies the equation of continuity
satisfies the equation of continuity
(A-1)
and body surface condition
(A-2)
And ![]() is expressed by the sum of the potential
is expressed by the sum of the potential ![]() 0 expressing basic flow and the potential
0 expressing basic flow and the potential ![]() 1 expressing free surface effects as
1 expressing free surface effects as
(A-3)
where ![]() 0 is expressed by HSA in case of high speed or by LSA in case of low speed and
0 is expressed by HSA in case of high speed or by LSA in case of low speed and ![]() 0 and
0 and ![]() 1 are shown as follows
1 are shown as follows
(A-4)
respectively, where ![]() is the disturbed velocity potentials to express the basic disturbance to use the double model or the inverse image and
is the disturbed velocity potentials to express the basic disturbance to use the double model or the inverse image and ![]() expresses the effect of the free surface on the each foil surface, respectively. Then the disturbed velocity potential of the hydrofoil system
expresses the effect of the free surface on the each foil surface, respectively. Then the disturbed velocity potential of the hydrofoil system ![]() w is divided into the term
w is divided into the term ![]() S due to the source on the hydrofoil surface and
S due to the source on the hydrofoil surface and ![]() V due to the vortex on the camber surface
V due to the vortex on the camber surface
(A-5)
We express these ![]() S,
S, ![]() V,
V, ![]() F and the induced velocity in the following sections.
F and the induced velocity in the following sections.
Expression of qS and  S
S
Flow velocity vectors qS induced by the source distributions around the hydrofoil surfaces are given as
(A-6)
where ![]() S is the disturbed velocity potential due to the source and in the 2-D problem
S is the disturbed velocity potential due to the source and in the 2-D problem
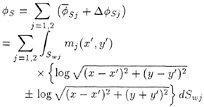
(A-7)
and in the 3-D problem
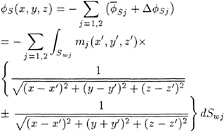
, (A-8)
where the sign+means LSA and the sign−does HSA.
Expression of qV and  V
V
The velocity vector qV induced by the vortex γj distributing on the camber surface is shown as
(A-9)
where ![]() V is in the 2-D problem
V is in the 2-D problem
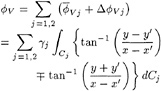
, (A-10)
and in the 3-D problem qV is shown directly as
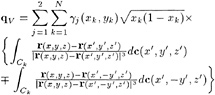
, (A-11)
where r(x,y,z) means the position vector.
In the above equation, the sign+means HSA and the sign−does LSA. The dc(x,y,z) means a line element vector of the k-th vortex line which is located discretely at (xk, yk) on the camber surface following QCM. The contour Ck is made of the three vortex lines, one is spanwise on the camber surface and the others start chordwise from both ends to the rear infinity through the trailing edges.
Expression of qF and  F
F
The velocity vector qF induced by source σF distributing on the still water surface is shown by the disturbed velocity potential ![]() F as follows
F as follows
(A-12)
where ![]() F is
F is
(A-13)
in the 2-D problem, and
(A-14)
in the 3-D one.
Expression of Linearized Free Surface Condition and Wave Profile
As above mentioned, two types of disturbed velocity potential are available. In the case of LSA (Normal Image) is used, ![]() , at y=0 and in the case of HSA (Inverse Image),
, at y=0 and in the case of HSA (Inverse Image), ![]() at y=0. Involving both cases, the linearized free surface condition and corresponding wave profile η are given as follows.
at y=0. Involving both cases, the linearized free surface condition and corresponding wave profile η are given as follows.
(A-15)
(A-16)
where g is acceleration of gravity, k0=g/V2 is the number of wave.
Using HSA, since there is no analytical solution for hydrofoils, we define the wave profiles in the limit of high speed analytically from the linearized free surface condition,
(A-17)
It is shown as
(A-18)
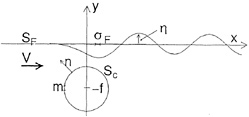
Fig.1 Coordinate system of circular cylinders
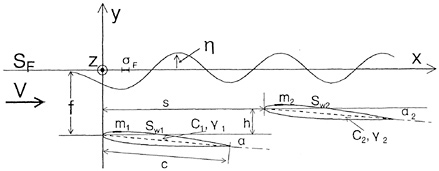
Fig.2 Coordinate system of hydrofoils
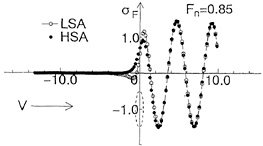
Fig.3(a) Source distribution on still water surface due to circular cylinder
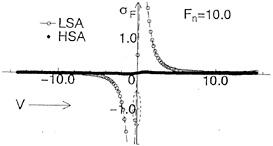
Fig.3(b) Source distribution on still water surface due to circular cylinder
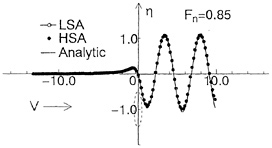
Fig.4(a) Wave profiles due to point doublet
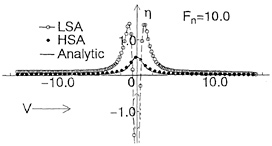
Fig.4(b) Wave profiles due to point doublet
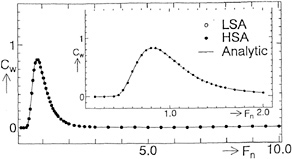
Fig.5 Wave making resistance coefficient Cw of point doublet
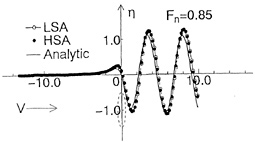
Fig.6(a) Wave profiles due to circular cylinder
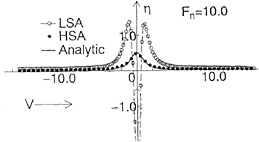
Fig.6(b) Wave profiles due to circular cylinder
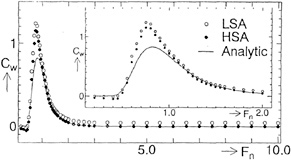
Fig.7 Wave making resistance coefficient Cw of circular cylinder
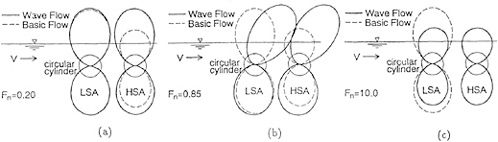
Fig.8 Pressure distribution on circular cylinder surface
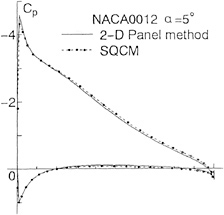
Fig.9 Comparison of 2-D panel method and SQCM
Fig.13(a) Comparison of source distribution between HSA and LSA
Fig.13(b) Comparison of source distribution between HSA and LSA
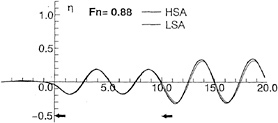
Fig.14(a) Comparison of wave profiles between HSA and LSA
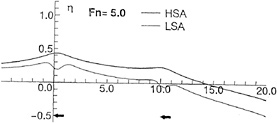
Fig.14(b) Comparison of wave profiles between HSA and LSA
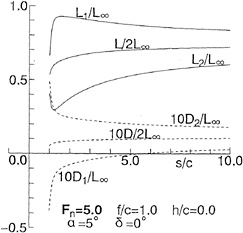
Fig.15(a) Change of interference factor versus stagger
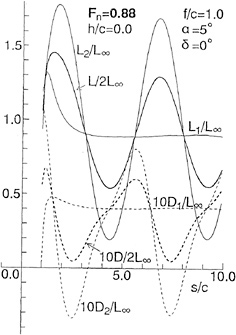
Fig.15(b) Change of interference factor versus stagger
DISCUSSION
by Dr. Spyros Kinnas, MIT
The authors should be congratulated for their extensive study of the Rankine Source Method. I have two questions concerning the so-called SQCM:
-
What is the theoretical basis of combining a QCM (an inherently linearized formulation) to a source method with the sources distributed on the exact hydrofoil surface? Is this a consistent formulation?
-
Can their method predict the correct effect of thickness on the hydrofoil loading? (See for example JSR paper on “A General Theory for the Coupling Between Thickness and Loading,” S.Kinnas, 1992). In other words, is their method predicting the correct value of the derivative of the lift L with respect to the τmax (dL/dτmax) while the camber and angle of attack remains the same?
Author's Reply
-
We can select an arbitrary form and location of distributing vortices around the foil. Then we use those of the QCM formally and satisfy the Kutta's condition. Though there is no assumption of a thin wing, we think this is consistent.
-
In Figure A1 we show the SQCM results of the lift variation due to thickness comparing with our panel method and the QCM for the 2-D NACA symmetric wing sections. We can see the thickness increases lift as well as the panel method and the discusser's method.
DISCUSSION
by Kazu-hiro Mori, Hiroshima University
Can we not expect to have the same results even if the expressions of the basic solution are not the same? This can be supported by the results of Cw shown in Fig. 7. The differences in wave elevation shown in Fig. 4 are suspected to have appeared from numerical reasons; the elevation is obtained by the finite difference of the velocity potential with respect to x.
Author's Reply
Thank you for your discussion.
We agree with the discusser in thinking that both results should agree with each other on an ideal numerical calculation. However, we have tried to use finer mesh on still water surface using 2-D circular cylinder problem and have also checked them using double precision (REAL$*8) and four times precision (REAL$*16) options, but it is confirmed that the depression becomes smaller but never agree with the HSA solution. We may say that both results never agree at high speed.
In order to understand this phenomenon we show calculated results in Figure A2. The condition is corresponding to Figure 4(b) of the text, that is, one of the 2-D circular cylinder problem with a point doublet. We inversely obtained the source distribution on the still water surface from the wave profile which is obtained by the HSA. This source distribution differs only near the steep peaks from results of the LSA. This difference causes the peculiar depression above the doublet.
We also show other two results by the ordinary LSA; one is the usual case in which calculated region on the still water surface(−15.0<x <15.0) is divided into about 150 pieces and the other is the 25 times finer mesh case. Even if we use very fine mesh, we can not follow the steep peaks obtained above.
Then, we think the HSA is very effective in order to avoid this numerical difficulty in the high speed range.
DISCUSSION
by Dr. H.Raven, MARIN
Your paper suggests that you have tested two different linearizatons: LSA, with the basic flow being a double body flow, and HSA, with the basic flow being an ‘inverse image flow.' You then conclude that HSA is better because it more closely agrees with analytic solutions. But these analytic solutions are linearized with respect to uniform flow, and will never tell you which linearization is better. To get the best
agreement with these analytic solutions you should impose a Kelvin condition.
On the other hand, (6) is not a useful double-body linearization but is equivalent to a Kelvin condition, could you clarify this?
Author's Reply
Thank you for your discussion.
The Eq. (6) ![]()
![]() is exactly the Kelvin condition which is derived substituting
is exactly the Kelvin condition which is derived substituting ![]() to the linearized free surface condition
to the linearized free surface condition ![]() , but is not double-body linearization, i.e.,
, but is not double-body linearization, i.e.,
in case of normal image.
However, the difference between the LSA and the HSA is not one of linearization but one of the equation expressed in the text. That is, in the case of the LSA, Eq. (6) becomes from ![]() and it becomes also
and it becomes also ![]() from
from ![]() in the case of the HSA.
in the case of the HSA.
DISCUSSION
by Dr. Henry T.Wang, Naval Research Laboratory
The authors are to be commended for bringing out the High Speed Approximation (HSA) as an alternative to the Low Speed Approximation (LSA), which is usually used in ship hydrodynamics. The authors' figures indicate that the wave profile and force coefficient results for LSA and HSA are similar at low Fn and diverge at high Fn. Have the authors considered other criteria, which may indicate a priori the approximate point of divergence of the two theories? For example, could one such criterion be related to the vertical velocity at the free surface (which is identically zero for LSA) reaching a certain fraction of the hydrofoil velocity? Also, can the authors comment on the conditions in which HSA, rather than the presently used LSA, would be more appropriate as the basic flow for surface ship problems?
Author's Reply
Thank you for your discussion.
It seems to be very useful to use such an index. In fact we have tried to search for a criteria, but we have found nothing indicating those matters generally. As the LSA is effective at a somewhat high speed and the HSA is also useful in a low speed problem to a degree, it is relative to use the LSA or the HSA. The point is that the speed range should be respected in which both results agree, and when they begin to diverge numerically, we should choose the HSA or the LSA.
We wish to consider the surface ship problem in the near future.