Numerical Simulation of the Effect of Fillet Forms on Appendage-Body Junction Flow
D.Li and L.-D.Zhou
(China Ship Scientific Research Center, PRC)
ABSTRACT
The possibility of using a fillet form to control the horseshoe vortex flow caused by the turbulent shear flow around wing-body junction has been investigated numerically. A numerical method for the solution of three dimensional incompressible, Reynolds-averaged Navier-Stokes equations with the two-equation (k, ![]() ) turbulence model has been developed to evaluate the effect of fillet forms on appendage-body junction vortex flow. The wing investigated is NACA0020. The Reynolds number based on a chordlength is 1.0×105. Three configurations including a baseline, a triangle fillet form, and a constant radius convex arc fillet form along the entire wing/flat-plate junction are presented. It is shown that a suitable convex filet form can significantly improve the stability of junction horseshoe vortex and reduce the strength of vortex and the non-uniformity in the wake velocity profile. It is also demonstrated the capability of the numerical approach in the design of vortex flow control devices.
) turbulence model has been developed to evaluate the effect of fillet forms on appendage-body junction vortex flow. The wing investigated is NACA0020. The Reynolds number based on a chordlength is 1.0×105. Three configurations including a baseline, a triangle fillet form, and a constant radius convex arc fillet form along the entire wing/flat-plate junction are presented. It is shown that a suitable convex filet form can significantly improve the stability of junction horseshoe vortex and reduce the strength of vortex and the non-uniformity in the wake velocity profile. It is also demonstrated the capability of the numerical approach in the design of vortex flow control devices.
1.INTRODUCTION
When an laminar or turbulent boundary layer on a surface encounters a wing or other protuberances projecting from that surface, a complex and highly three-dimensional flow results. The most significant feature of this flow is the generation of a horseshoe vortex or a set of horseshoe vortices. This horseshoe vortex forms around the nose of the wing and its legs trail downstream into the wake and forms streamwise vortices in the wake. This phenomena occurs at many places including wing/fuselage intersections in aerodynamics, appendage/hull junctions in hydrodynamics, and blade/hub junctions in propellers and turbomachinery, etc.. As a consequence of the generation of the horseshoe vortices, the drag is in general increased and the wake velocity profile becomes significantly non-uniform. This can be a great nuisance in marine applications where a propeller operating in a non-uniform wake results in significant unsteady forces.
As well known, when a boundary layer encounters a protruded bluff body, the streamwise vortex in the form of the horseshoe vortex cannot be prevented from being generated. However, it is possible to minimize the strength of the horseshoe vortex by some flow control devices such that the resulting wake will be less non-uniform and the unsteady forces will be reduced. Experimental and numerical investigations on the use of fillet forms to reduce the interference effects have been reported before [1–5]. In these papers, the type of fillet forms are all concave. According to observation and analysis of our experimental research on the effect of fillet form[6], the strength and the unsteadiness of the horseshoe vortex and non-uniform of wake may be effectively reduced by designing a suitable convex fillet form. Here, a numerical investigation was carried to evaluate the effectiveness of the convex forms and to demonstrate the capability of the numerical approach in the design of vortex flow control devices.
A general purpose computer code for the solution of the complete three-dimensional Reynolds-averaged Navier-Stokes equation has been developed [7]. In this numerical procedure, the 3D Navier-Stokes equation is solved by finite-volume scheme in a nearly-orthogonal body-fitted coordinate system. The pressure-velocity coupling is treated with SIMPLEC algorithm [8] using a non-staggered grid. The Rhie-Chow algorithm [9] is chosen to avoid the well known problems due to chequerboard oscillations in the pressure and velocity fields which are traditionally associated with the naive use of non-staggered grids. The system of algebraic equations formed by the assembly of the convection-diffusion and pressure equations are solved by the strongly implicit procedure (SIP) algorithm and the preconditioned conjugate gradients (PCG) algorithm [7]. The two
equation k-![]() model with wall functions is used for the turbulent flow involving separation and vortices.
model with wall functions is used for the turbulent flow involving separation and vortices.
This numerical procedure is used in the present investigation. Three configurations including a baseline configuration consisting of a wing mounted on a flat-plate junction, a triangle fillet form, and a constant radius convex arc fillet form along the entire wing/flat-plate junction are presented here. The numerical solutions were used to evaluate the relative effectiveness of the three configurations. Particular emphasis is placed on the discussion of effectiveness of convex fillet forms on the stability of the horseshoe vortex.
2.
NUMERICAL METHOD
2.1 Governing Equations
We consider the governing equations in Cartesian coordinates (xi,t)=(x,y,z,t) for unsteady, three-dimensional, incompressible flow. The complete three-dimensional Reynolds-averaged equations of continuity and momentum of the mean flow are
(1)
(2)
where Ui=(U,V,W) and ui=(u,v,w) are, respectively, the Cartesian components of the mean and fluctuating velocities, t is time, p is pressure, ρ is mass density, and μ is dynamic viscosity.
If the Reynolds stresses ![]() are related to the corresponding mean rate of strain through an isotropic eddy viscosity vt,
are related to the corresponding mean rate of strain through an isotropic eddy viscosity vt,
(3)
where ![]() is the turbulent kinetic energy. Here, vt is related to the turbulent kinetic energy k, and its rate of dissipation
is the turbulent kinetic energy. Here, vt is related to the turbulent kinetic energy k, and its rate of dissipation ![]() , by the two-equation k-
, by the two-equation k-![]() model
model
![]() μt=ρνt (4)
μt=ρνt (4)
and k and ![]() are obtained from the transport equations
are obtained from the transport equations
(5)
(6)
where G the rate of production of k is defined by
(7)
and (Cμ,C1,C2,σk,σε) are constants whose values are (0.09, 1.44, 1.90, 1.0, 1.3).
It is convenient to rewrite the equation of continuity and the transport equations(1),(2),(5),(6) for momentum(U,V,W) and turbulence quantities(k, ![]() ) in the following general form:
) in the following general form:
(8)
where ![]() again represents any one of the convective transport quantities (U,V,W,k,
again represents any one of the convective transport quantities (U,V,W,k,![]() ). The scalar diffusivity
). The scalar diffusivity ![]() and source functions
and source functions ![]() for Ui, k and
for Ui, k and ![]() are, respectively,
are, respectively,
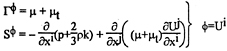
(9a)
(9b)
(9c)
2.2 Body-Fitted Coordinate Systems
In order to extend the capabilities of the difference methods to deal with complex geometries, a curvilinear coordinate transformation is used to map the complex flow domain in physical space to a simple (i.e. rectangular) flow domain in computational space. In other words, the Cartesian coordinate system (xi)=(x,y,z) in the physical domain is replaced by a curvilinear coordinate system (ξi)=(ξ,η,ζ) such that boundaries of the flow domain correspond to surfaces ξi=constant.
For the present application to wing-body junction flow with fillet forms, the body-fitted numerical grids were generated by a system of elliptic partial differential (Possion) equations of the form of
(10)
Here, ▽2 is the Laplacian operator in Cartesian coordinates xi. The nonhomogeneous source functions fi may be assigned appropriate values to yield desirable grid distributions. In practical applications, the inverse transformation of equation(10) is used to obtain the coordinate transformation relations xi=xi(ξi), i.e.,
▽2xi=0 (i=1,2,3) (11)
where ▽2 is the Laplacian operator in the transformed plane. (ξi). Using the transformation relations, the equation(11) can be rewritten as,
(12)
where gjk is the inverse metric tensor[7]. The grid-control functions fi were determined by the specified boundary-node distribution in this paper.
The body-fitted numerical grids generated by above method is a general non-orthogonal coordinate system. In order to simple the calculation and ensure the accuracy of solution, it is important to ensure that the grid is nearly orthogonal at boundaries. In present study, a corrective method[7] is used to generate nearly orthogonal grids.
2.3 Transformation of the Equations
The price that has to be paid for the simplicity of implementing boundary conditions using body-fitted coordinate systems is the increase in complexity of the governing equations when the Cardesian coordinates is transformed to the non-orthogonal coordinate system(ξi). The vector operation in the transformed plane is
(13)
where ![]() are the normal flux components of V, as defined in [7]. It is convenient to write equation(8), in the steady state, in the equivalent form:
are the normal flux components of V, as defined in [7]. It is convenient to write equation(8), in the steady state, in the equivalent form:
(14)
where Ii is called the total(i.e. convective+ diffusive) flux, and is given by:
(15)
Using the expression (13) for the covariant divergence, we obtain immediately:
(16)
i.e. exactly the same form as equation(14), with the effective total flux given in contravariant and normal components by:
(17)
Summarizing, the governing equations in computational space are:
(18)
(19)
where ![]() the normal flux components are the scalar products of velocity vector U with the area vectors
the normal flux components are the scalar products of velocity vector U with the area vectors
(20)
and
(21)
Note that the effective diffusion tensor Гij is a symmetric tensor, by virtue of the fact that gij is symmetric. Also, it is diagonal if and only if gij is diagonal, so the effective diffusion tensor is orthotropic if and only if the coordinate transformation is orthogonal, and it is fully anisotropic if and only if the coordinate transformation is strictly non-orthogonal. Due to its importance in the subsequent discretization process, we give the tensor multiplier in (21) a special symbol:
(22)
and we call Gij the geometric diffusion coefficients.
2.4 Discretization of Equations
The discretisation of the advection-diffusion equation is now straightforward. Integrating (18) over a control volume in computational space, we obtain, since computational space control volumes are unit cubes:
(23)
where nn(nearest neighboring face)=u,d,n,s,e, or w as shown in Figure 1. Using (19), we have:
(24)
or
(25)
where ![]() are the convection and anisotropic diffusion coefficients defined by:
are the convection and anisotropic diffusion coefficients defined by:
(26)
(27)
The standard convection and diffusion coefficients are given by:
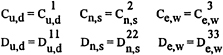
The Rhie-Chow algorithm[9] is used for the interpolation of velocity components to control volume faces required for the computation of convection coefficients. We employ hybrid differences, i.e. central differences when mesh Peclet number is less than 2 and upwind differences when mesh Peclet number is greater than 2, for the values of ![]()
![]() Figure 2). For example, we have:
Figure 2). For example, we have:
![]() etc.
etc.
Explicitly, we obtain, substituting (25) into the discretisation equation (23):
(28)
where ![]() NN are the values of
NN are the values of ![]() nn are the standard matrix coefficients obtained using hybrid differencing normal to control volume faces, and sm is a mass source term, i.e.
nn are the standard matrix coefficients obtained using hybrid differencing normal to control volume faces, and sm is a mass source term, i.e.
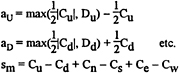
(29)
S' is the extra term arising from the cross-derivatives due to the non-orthogonality of the grid:
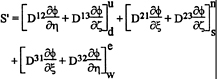
(30)
In full, we have:
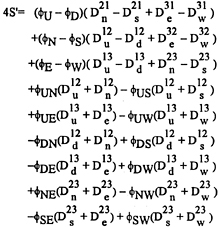
(31)
and inserting (31) into (28) gives the requires linear equations for ![]()
we obtain the linear equations:
(32)
where
Therefore, the 19-point molecule is reduced to a 7-point molecule, and the use of hybrid differencing to compute the matrix coefficients of this 7-point molecule guarantees diagonal dominance of the resulting matrix if the linearisation of the source term is chosen so that sp≤0.
2.5 Velocity-Pressure Coupling Algorithm
If the pressure is known, equation (32) can be employed to solve equation (18) for U,V,W,k,ε. In practice, however, the pressure is not known a priori and must be determined by requiring the velocity field to satisfy the equation of continuity (1). Here, we derive the pressure-correction equation obtained by applying the SIMPLEC algorithm [8] to the momentum equations (32) for Cartesian velocity components on the non-staggered grid.
Let Ui*, P* denote the most recently updated velocity and pressure fields after the linearised momentum equations have been solved. From the equations (32), we may write the momentum equations in the form:
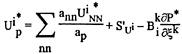
(33)
where S'Ui are the remaining source terms after the pressure gradient source terms have been removed ( i.e. the non-pressure gradient and the non-orthogonality source terms) divided by the matrix diagonal a p,, and is ![]() the matrix multiplier of the computational space pressure gradients:
the matrix multiplier of the computational space pressure gradients:
(34)
Now a solution Ui* of (33) does not in general satisfy the continuity equation; it has a residual mass source:
(35)
The term in (35) involve the values of the normal velocity components on mass control volume faces, and these must be approximated somehow from the velocity components ![]() at mass control volume centers. The prescription for doing this is the whole crux of the Rhie-Chow algorithm.
at mass control volume centers. The prescription for doing this is the whole crux of the Rhie-Chow algorithm.
The main idea of the SIMPLEC algorithm is to find update velocity and pressure fields Ui*, P** obeying the discrete momentum equations and the discrete continuity equation:
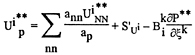
(36)
(37)
We use the term ![]() to minus the bath hand of (36) and (37):
to minus the bath hand of (36) and (37):
(38)
(39)
Assuming:
p'=p**−p*, Ui'=Ui**−Ui*
and
we obtain the following formulae for the velocity-and pressure-corrections by (39)–(38):
(40)
where
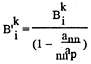
(41)
Thus we obtain update velocity and pressure fields satisfying exact mass continuity and approximately satisfying the discrete momentum equations.
It follows that the corrected values of the normal velocity flux components ![]() are given by:
are given by:
(42)
where
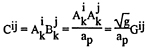
(43)
The pressure-correction equation is obtained by substituting (42) into the continuity equation (37). We obtain:
(44)
where
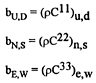
(45)
and S' are the additional terms due to non-orthogonality. It can be obtained by (30) for ![]() =P and
=P and
(46)
2.6 Solution Procedure
The system of algebraic equations is formed by the assembly of the convection-diffusion and velocity-pressure correction equations (28) and (44). This approach ignores the non-linearity of the underlying differential equations. Therefore iteration is used at two levels; an inner iteration to solve for the spatial coupling for each variable and an outer iteration to solve for the coupling between variables. Thus each variables is taken in sequence, regarding all other variables as fixed. By always reforming coefficients using the most recently calculated values of the variables.
In present paper, the U, V, W equations are solved by the SIP algorithm with 5 internal iterations; the P pressure equation is solved by the PCG algorithm with 30 internal iterations; the k, ε equations are solved by the ADI (Alternating-Direction-Implicit) algorithm with 4 internal iterations, different iteration methods. The mass source residual, the error in continuity, is chosen as stopping criteria for the outer iteration.
3. CFD VISUALIZATION
One of the great problems with three-dimensional flow calculations is that of interpreting the sheer amount of outputs of the numerical method. Thus an integrated CFD visualization system VISPLOT [10] is developed to process and analysis the numerical results of this paper. The VISPLOT has a friend user-interface which converts the results into a database and allows the user to dialogue with computer and database. Three forms of data processing are carried out: on one-dimensional grid lines, two-dimensional grid planes, or full three-dimensional graphics. The facilities of VISPLOT include:
-
Color contours of scalar quantities in grid slices and planes.
-
Profiles of the variables on arbitrary lines through the computational domain.
-
Velocity vector plots.
-
Particle tracks.
-
Full exploitation of color to bring out the features of the flow, for example, to overlay velocity vector plots with contours of the pressure.
-
3D plot of grid distribution, geometry of problems, or velocity fields etc..
4. RESULTS AND DISCUSSION
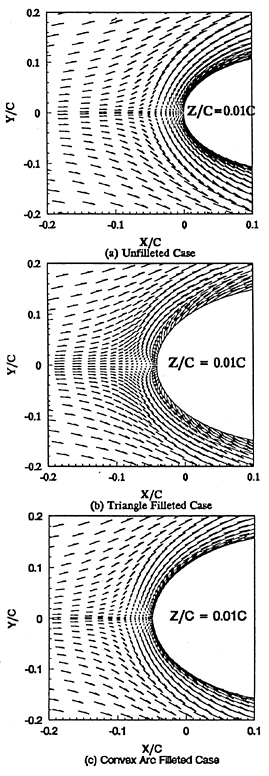
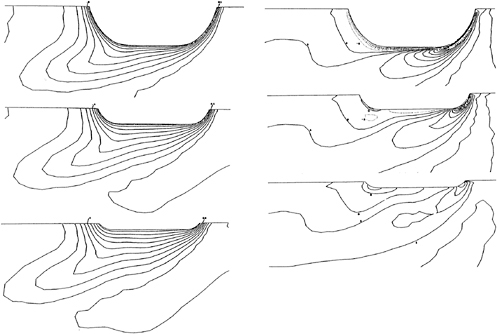
We have selected the same configuration used in our experiments[6]. The wing is 25.9 cm chord length, consisting of a 3:2 semielliptic leading edge and a NACA 0020 aft section. The baseline configuration consists of the wing mounted on the flat-plate(See Fig. 3(a)). The triangle fillet form is a triangle form of side length 0.1C along entire wing/flat-plate junction(See Fig. 3(b)). The Convex arc fillet form is a circular arc form of radius 0.1C along entire wing/flat-plate junction(See Fig. 3(c)). Here, C is chord length of the wing. All computations of turbulent junction flows with and without fillet forms were made on the 50 ×30×30 nearly-orthogonal grids(See Fig. 3). The solution
domain consisted of a semicircular cylinder of radius R/C=1.5 attached to a rectangular region 0 <X/C<2.5, 0<Y/C<1.5, 0<Z/C<1.5. The first spacing normal to the flat-plate and wing is on the order of 0.001C. The mass source residual less than 10−4 was chosen to judge whether convergence has been achieved. In generally the solution became convergence at about 180 cycle outer iterations using about 8 CPU hours on a PC-486/50.
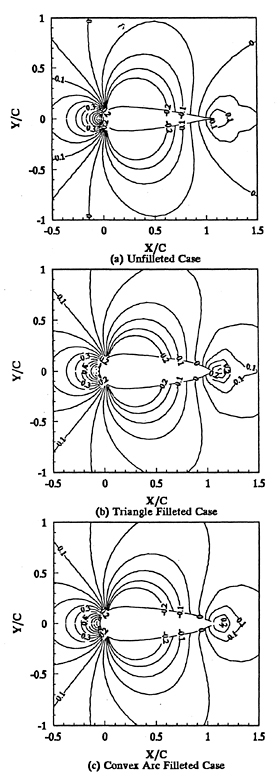
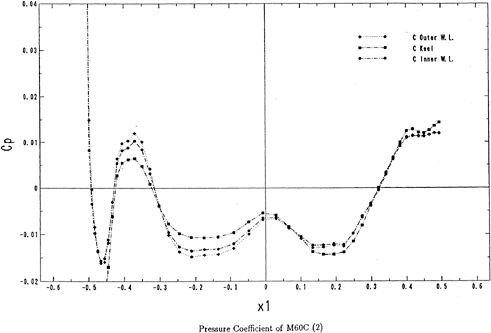
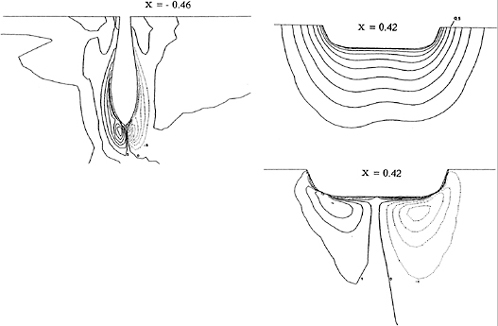
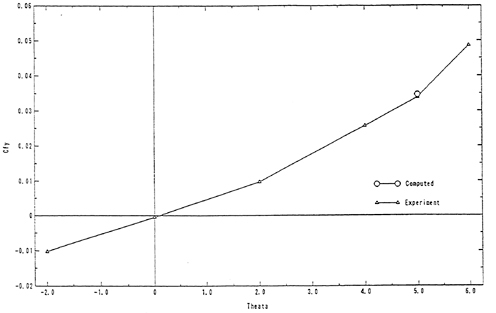
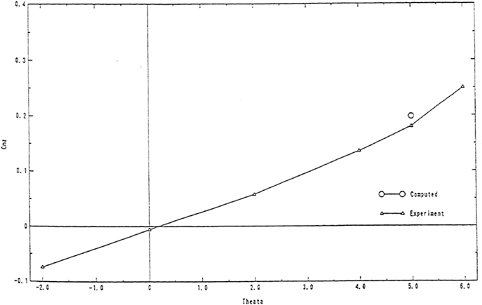
As mentioned earlier, the main objective of using a fillet form is to weaken the horseshoe vortex generated. A simple method can be used to judge these fillet forms with minimum ambiguity on whether the vortex generated in one form is stronger or weaker than the vortex generated by another form. It is by comparing the sharpness of the kinks in the Cp profiles near the leading edge. Sharper kinks in the Cp profiles imply that a stronger vortex has been generated. Applying this criterion to the Cp profiles of the baseline, the triangle fillet form and the convex arc fillet form shown in Figures 4(a), 4(b), and 4(c), it can be seen that the strong kinks exist in the Cp profile of the baseline. But the kinks also exist in the Cp profiles of the fillet forms. This implies that the strength of vortex generated will not be effectively reduced by unsuited fillet forms.
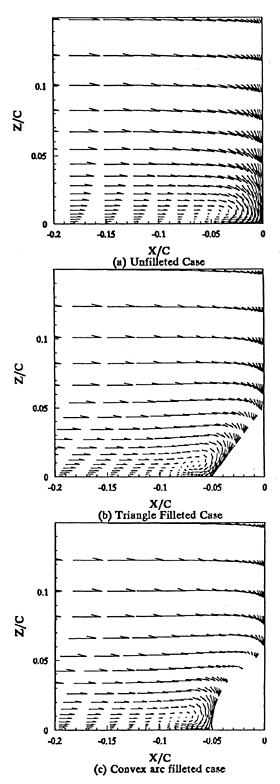
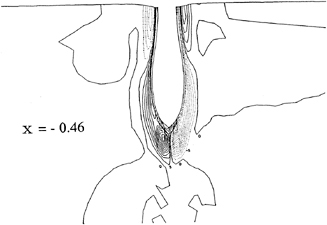
The velocity vector fields in the symmetry plane in front of the leading edge of the baseline, the triangle fillet form and the convex arc fillet form are shown in Figures 5(a), 5(b), and 5(c). It can be seen that the vortex generated by the baseline is an elliptic form but the vortices generated by the fillet forms are circular forms. It means that the vortex generated by the baseline is unstable and will become low-frequently oscillating vortex but the vortex generated by the fillet forms, specially by the convex fillet form, may be stable and adhere the junctions. It is very similar with the observation of our experiments [6]. It implies that the convex fillet form can control the unstable vortex generated by the junction configuration.
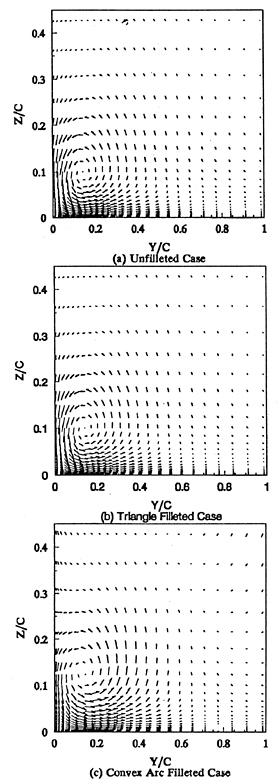
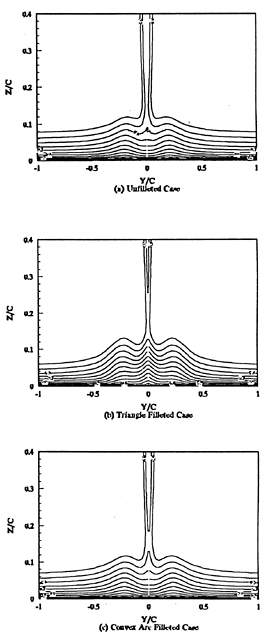
Figures 6(a), 6(b), and 6(c) of velocity vectors in transverse section x/C=2.14 clearly show the streamwise vortices in the wake formed by ahead horseshoe vortices. These vortices cause the wake velocity profiles becoming significantly nonuniform (See Figure 7(a), 7(b), and 7(c)). The velocity fields around the leading edge of wing at z/C=0.01 horizontal plane are shown in Figures 8(a), 8(b), and 8(c). They show the flow reversal in fornt of the wing associated with the ahead vortex.
5. CONCLUSIONS
An improved numerical method for the solution of the complete three-dimensional incompressible, Reynolds-averaged Navier-Stokes equation based on finite-volume scheme in a non-staggered grid has been applied to evaluate the effect of fillet forms on wing-body junction flow. Three configurations including a baseline, a triangle fillet form, and a convex arc fillet form were considered. The computed pressures on the entire flat-plate are first used to discuss the effectiveness of the fillet forms in terms of the ability of each to reduce the strength of the horseshoe vortex. The velocity vector fileds in the symmetry plane ahead leading edge of the wing are used to analysis the ability of each to improve the stability of the horseshoe vortex. It has been demonstrated that the numerical approach is a valuable tool for evaluation of the effectiveness of the fillet forms and the design of vortex flow control devices. It is the main purpose of this paper.
REFERENCES
1. Sung, C.H., Michael, J.G., and Roderick, M.C., “Numerical Evaluation of Vortex Flow Control Devices,” AIAA paper 91–1825, AIAA 22nd Fluid Dynamics, Plasma Dynamics & Lasers Conference, June 24–26, 1991, Hawaii.
2. Kubendran, L.R., Bar-sever, A. and Harvey, W.D., “Juncture Flow Control Using Leading-Edge Fillets,” AIAA Paper 85–4097, 1985.
3. Kubendran, L.R., Bar-sever, A. and Harvey, W.D., “Flow Control in a Wing/Fuselage-type Juncture,” AIAA Paper 88–0614, 1988.
4. Pierce, F.J., Frangistas, G.A. and Nelson, D.J., “Geometry Modification Effects on Junction Vortex Flow,” Symposium on Hydrodynamic Performance Enhancement for Marine Application, Newport, RI, November, 1988.
5. Sung, C.H., and Yang, C.I., “Control of Horseshoe Vortex Juncture Flow Using A Fillet,” Symposium on Hydrodynamic Performance Enhancement for Marine Application, Newport, RI, November, 1988.
6. Li, D., and Zhou, L.D., “The Effect of Juncture Form on Appendage-Body juncture Flow,” Osaka Colloquium '91, Japan.
7. Li, D., “Viscous Flow Around Body-Wing Junctures,” Ph.D. Thesis, China Ship Scientific Research Center, 1992.
8. Von Doormal, J.P. and Raithby, G.D., “ Enhancements of the SIMPLE Method for Predicting Incompressible Fluid Flows,” Numerical Heat Transfer, Vol 7, pp147–163, 1984.
9. Rhie, C.M. and Chow, W.L., “Numerical Study of Turbulent Flow Past an Airfoil with
Trailing Edge Separation,” AIAA Journal, Vol 21, No. 11, pp 1525–1532, 1983.
10. Li, D. and Zhou, L.D., “Computational Fluid Dynamics Visualization System,” To be Published in Journal of Hydrodynamics, 1993
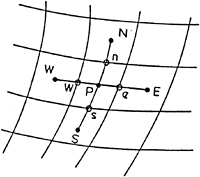
•=Mass control volume centers
○=Mass control volume face centers
Figure 1. Grid Structure and Numerical Molecule
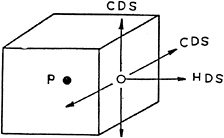
CDS=Central Difference Scheme.
HDS=Hybrid Difference Scheme.
Figure 2. Difference Schemes for Normal and Cross-Derivatives.
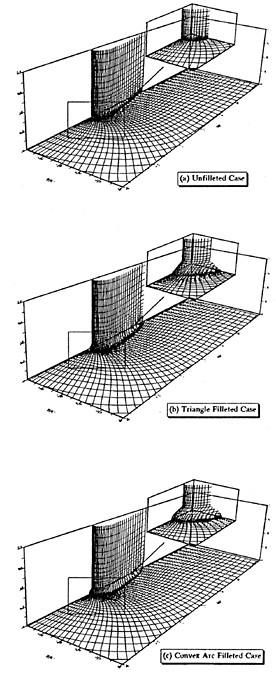
Figure 3. Geometric Configuration of Junction and Computational Grids
Verification of the Viscous Flow-Field Simulation for Practical Hull Forms by a Finite-Volume Method
M.Zhu, O.Yoshida, and H.Miyata (University of Tokyo, Japan) K.Aoki (Isuzu Motors Ltd., Japan)
ABSTRACT
A hybrid turbulence model based on the sub-grid scale (SGS) turbulence model combined with the Baldwin-Lomax turbulence model is introduced into the Navier-Stokes simulation of the viscous flow about the ship model with practical hull configuration. The aim is to develop a numerical method able to cope with the low-Reynolds-stress flow structure near the ship stern. The agreement between the computed results and the measurement indicate the feasibility of this approach to clarify some of the important features of ship stern flow. The stern flow structures of three-dimensional flow separation, the generation of the longitudinal vortex, and the resulting distorted wake pattern are studied and discussed.
INTRODUCTION
The accurate prediction of viscous ship stern flow is important in the evaluation of the ship powering performance. One of the most difficult requirements is to predict the distorted wake pattern in the propeller disk for full ship form. This wake pattern is the result of evolution of the longitudinal vortex which is generated by the flow separation, in the thick turbulent boundary layer about the ship stern. Due to its complex nature, it is not surprising that this wake pattern can not be predicted well in the numerical calculations based on the Reynolds-Averaged Navier-Stokes equations (RANS). The three-dimensional flow separation and the evolution of the longitudinal vortex are presently not modeled very well as shown in the proceedings of the Second SSPA-CTH-IIHR Workshop [1]. In the most successful RANS simulation, the turbulence model is the k-ε two equation model with the wall function or Baldwin-Lomax zero equation model. However, since both models are substantially tuned for the ordinary turbulent boundary layer, the eddy viscosity is too large to properly model the Reynolds stress distributions about the ship stern, which is inconsistent to the observed flow structure there. The measured turbulent shear stresses are found to become smaller in magnitude gradually towards the stern and to fluctuate inside the boundary layer in contrast with the classical boundary layer theory [2] [3] [4] [5]. Some of the flows exhibit quite complicated features, indicating the failure of explanation by the ordinary turbulence structure theory [6]. This is a problem in the flow structure model which may not able to be overcome by the refinement of the numerical solver [7] [8].
It is encouraging to note that turbulence modeling can be improved by CFD (Computational Fluid Dynamics) research combined with the experimental research for the investigation of turbulence structure about the ship stern. However, this approach has not been fully utilized. There is a limited number of research based on CFD databases in the area of ship hydrodynamics. This is the uncertainty of the measurement due to the complexity of the ship stern flow, and then it is quite difficult to make a reasonable model for the numerical simulation. Therefore it is quite difficult to validate the numerical results.
The purpose of this paper is to clarify the flow structure which makes the ship stern flow so complicated to experimentally measure and so difficult to predict in numerical calculations. It is supposed that it is due to the three-dimensional flow separation and the evolution of the induced longitudinal vortex. It is contrary to the viscous flow about a fine ship almost exhibiting minimum or no flow separation which can be predicted quite accurately, such as the hull form of Series 60 model (CB=0.6) [7]. However, very few RANS
simulations have successfully predicted flow separation for full ship form.
The flow separation phenomenon has been investigated in the experiment for simple flow geometry. Simpson [9] described the flow structure in a turbulent separating boundary layer. He showed the large scale vortical motions induced by the flow separation do not significantly contribute to the turbulent shear stresses but distort the mean flow and produce the low-frequency pressure fluctuation. He concluded that this flow behavior makes this type of flow difficult to calculate accurately. Since the influence of thick turbulent boundary layer over the ship hull near the stern is strong, the frequency of the field fluctuations (mainly the pressure fluctuations on the body surface) may not be as low as described by Simpson. It is really possible that the flow structure is changed by the flow separation over the hull as the bifurcation of flow geometry by shifting the frequency of the flow motions of most significant energy to the smaller frequency region in the Fourier space.
This frequency shift is very important to clarify the phenomenon because it opens the possibility how we can capture the stern flow separation phenomenon in the numerical simulation with the present computer capacity. If the boundary layer flow was not so dominant, the field fluctuations from flow separation would not be in the high-frequency region as shown numerically by Zhu et al. [10] for a car-like body. This point should be clarified for the ship stern flow.
For the full ship stern, the low-intensity Reynolds shear stress and the distorted wake pattern are both present. Moreover, the low-intensity Reynolds shear stress can be found not only in the flow separation phenomenon but also in the thick boundary layer almost without flow separation in the case of a modified spheroid of revolution as shown by Patel et al. [11]. Therefore, the low-intensity turbulent shear stress may be related to the flow structure which is mostly responsible for the flow separation phenomenon. This correlation gives us the guidance to tune turbulence model in the present study.
Therefore, the validation of CFD requests the calculation to be capable of capturing the following important features of the ship stern flow.
-
The three-dimensional flow separation from the hull surface;
-
The evolution of the induced longitudinal vortex and its interaction with the turbulent boundary layer;
-
The vortex structure near the propeller plane and the resultant distorted wake pattern inside the propeller disk; and
-
The difference of flow structure due to the change of stern hull configuration.
The above four points may serve as the checking point to verify the degree of resolution and the appropriateness of the numerical method. The flow separation phenomenon is firstly and mostly necessary to be accurately simulated. However, unfortunately, very few measurements of the turbulence on a ship model stern are available for this validation. In this study, we will consider the macroscopic feature of the flow phenomenon about the ship stern and show some detailed turbulent structure by use of the eddy viscosity distribution of the tuned turbulence model in connection with the change of flow structures.
In the present study, the adopted numerical method is an advanced version of a finite-volume solution method developed for the ship viscous flow called WISDAM-V by Zhu, Miyata and Kajitani [12] and Miyata, Zhu and Watanabe [13]. The calculated results [12] [13] demonstrated the suitability of using the sub-grid scale turbulence model to cope with some important features of ship stern flow in their LES-like numerical simulations. In this paper, a combined turbulence model based on the Baldwin-Lomax turbulence model and the sub-grid scale turbulence model is tuned in order to carry out simulations for the purpose of ship design.
This paper presents four topics. The advanced version of WISDAM-V method for viscous flow about the ship hull is first introduced. Secondly, the influence of the boundary condition for the sub-grid scale turbulence model is verified for the case of the viscous flow past a modified spheroid [11]. Thirdly, we tune a hybrid turbulence model based on the Baldwin-Lomax turbulence model and the sub-grid scale turbulence model in the application to the viscous flow about actual ship models. Fourthly, with the aid of computer graphics (CG) technique, we study and discuss the structure of the three-dimensional flow separation from the hull surface due to the ship stern configuration and the generation of the longitudinal vortex, and the resultant distortional wake pattern in the case of an actual ship hull with different stern hull configurations (SR 196 series tanker model).
WISDAM-V FINITE-VOLUME METHOD
Numerical formulation
The WISDAM-V finite-volume solution method is similar to the previous study [12] [13] in some aspects. However some modifications are made. As shown in Fig. 1, the pressure is defined at the center of the cell and the velocity components are defined at the center of respective cell surface. Therefore the staggered arrangement is shifted half diagonally in comparison with the previous studies [12]. The Cartesian coordinates are chosen as the basic coordinate system in the physical region, and the governing equations are formulated in an approach so-called “partial transformation”. The respective area vector is defined as follows as shown in Fig. 1, for example,
S1=Sabcd=rac×rbd (1)
and the volume of the cell is calculated from the surface area and the diagonal length of the cell.
(2)
The Jacobian J and the area vector Sm defined in this way satisfy the geometry conservation law, i.e., the sum of the cell volumes equals the total volume of the flow region [14].
For the incompressible viscous flow, the Navier-Stokes equation can be written into the following conservative form,
(3)
here, F is the external force, u is the velocity, and the stress tensor T is defined as
(4)
where all of the variable is nondimensionalized by the streamwise velocity V and the ship length L. I is the unit tensor, v is the kinematic molecular viscosity of the fluid, p is the pressure divided by the fluid density, R is the Reynolds number and the fluid deformation is defined as,
def u=grad u+(grad u)T. (5)
Therefore the stress tensor T in Eq.(4) is composed of the normal stress of pressure, nonlinear stress, viscous stress.
Separating the pressure term from the others, Eq.(3) becomes,
(6)
and
(7)
Then the stresses in Eq.(7) are
(8)
By use of the area vector of Eq.(1) and the Jacobian of Eq.(2), Eqs. (6) and (7) have their vector forms as follows.
(9)
and
(10)
where the stress tensor of Eq.(8) becomes,
(11)
and the strain tensor is
(12)
Therefore, Eqs.(9) to (11) can be rewritten as follows,
(13)
In order to perform a time dependent calculation, explicit time-marching is employed for the convection term and partial implicit time-marching for the diffusion term. The partial implicit finite-difference scheme for the diffusion term is used same as the previous studies [12] [13] and is abbreviated here. The finite-difference scheme is quite different from the previous studies [12] [13] and is described here in detail. A third-order accurate upwind finite-difference scheme is introduced within
the non-uniform flux-difference splitting framework [15] [7]. The inviscid flux can be considered in following form.
(14)
where q is the arbitrary velocity component, Uj is the volume flux (mass flux) in j sweep, and Fj is the inviscid flux for q in j sweep. Since q is defined on the each cell surface, as shown in Fig. 2, the first order flux for the upwind scheme is written in the following form.
(15)
Following the non-uniform flux-difference splitting method for the third order scheme by Sawada et al.[15], Eq.(15) becomes
(16)
where qi+ and qi− are defined as follows.
(17a)
(17b)
where
(18)
and
(19a)
(19b)
![]() , (19c)
, (19c)
(19d)
Here hi is the conjugate length of the coordinate system and is defined as follows.
(20)
The continuity equation for the incompressible flow is as follows.
div (u)=0, (21)
and its vector form is written as
(22)
Solution Procedure
It is well known that the MAC-type algorithm is one of the best solution procedure for the time-dependent, incompressible viscous flow at a high Reynolds number. Suppose the flow field is determined in the (n)-th time step, the velocity of (n+1)-th time step can be written in the fractional step manner.
a−u(n)=Δt f , (23a)
u(n+1)−a=−Δt ![]() (n+1)p(n+1), (23b)
(n+1)p(n+1), (23b)
where ![]() is the Laplacian operator. If the pressure increase is defined as δp,
is the Laplacian operator. If the pressure increase is defined as δp,
p(n+1)=p(n)+δp. (24)
The artificial compressibility method is introduced for the coupling of the pressure increase and the continuity condition as follows.
(25)
By introducing Eq.(23), Eq.(22b) becomes,
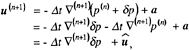
(26)
where ![]() is the velocity predictor using the pressure of (n)-th time step as follows,
is the velocity predictor using the pressure of (n)-th time step as follows,
(27)
Introducing Eq.(25) into Eq.(26), the following matrix equation for δp can be obtained.
(28)
where δω=Δt in the present study. Eq.(28) is solved by means of the approximation factorization method. Therefore, the pressure and the velocity are solved by the simultaneous iterative method by employing
Eqs.(27), (28) and (24). The pressure is assumed to be converged at every time step when the pressure residual satisfies the following criterion at the (m)-th iteration step.
(29)
Boundary and initial condition
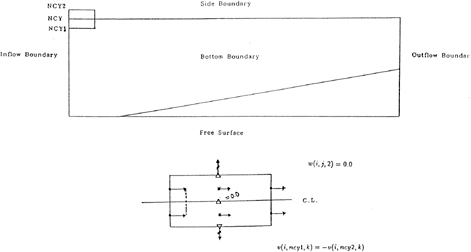
No-slip condition is imposed on the hull body surface and no wall function is used [12] [13]. Since in the present paper, only the viscous problem is dealt with, the symmetric condition is imposed on the still water plane boundary. The velocity is given uniformly on the inflow boundary, and the zero-normal-gradient condition on the downstream boundary. The side boundary is set sufficiently far from the hull so that the velocity is set by the zero-normal-gradient and the pressure is set at zero. As for the initial condition of the computation, the water is still and then gradually accelerated to the steady streamwise speed in 0.5 dimensionless time.
TURBULENCE MODEL
Ship Flow and SGS Turbulence Model
The sub-grid scale turbulence model was applied to the ship viscous problem by Miyata, Sato and Baba [16] for the case of Wigley model at the Reynolds number 104. Zhu, Miyata and Kajitani [12] and Miyata, Zhu and Watanabe [13] introduced a finite-volume method (WISDAM-V) as well as the sub-grid scale turbulence model to achieve the numerical prediction of turbulent ship flow at a model-test Reynolds number. They employed the sub-grid scale model in a RANS-like manner rather than the well known large-eddy simulation (LES).
By use of the sub-grid scale model, the flow simulated in the region of thin turbulent boundary layer results a unrealistic velocity profile. On the other hand, for full ship form such as the HSVA tanker, the use of the sub-grid scale turbulence model [17] [13] leads to a better prediction of the flow separation and the distorted wake pattern in the propeller disk than the other RANS simulations with the conventional models [1].
Therefore, the sub-grid scale model in the expression of the Smagorinsky formula [18] fails in the simulation of thin boundary layer but has some relevance to the flow structure about the ship stern of full form. One of the practical possibility is that the length scale employed in the sub-grid scale model is small than the thin boundary layer so as to be relevant to the low-Reynolds-stress structure as observed in the experiments [2] [3] [4] [5]. On the other hand, for the pure large-eddy simulation, as discussed by Moin [19], there are several problems associated with the sub-grid scale model as,
-
The optimal choice of the coefficient in the expression for the eddy viscosity depends on the type of flow;
-
The limiting behavior of the SGS model is not correct near walls or free surface;
-
The model is too dissipative in laminar regions; and
-
The model does not allow transfer of energy from small scales to large scale.
It is not so difficult to find that, for the viscous ship flow, there are common problems as discussed by Moin. Some of inappropriateness of sub-grid scale model for the application to the ship case, such as the coefficients of the model, have been adjusted in the WISDAM-V method[17]. With respect to the grid resolution, their correlations with the artificial dissipation term in the numerical scheme have also been discussed.
Following Smagorinsky et al. [18] and the other extensive expression, the eddy viscosity of the sub-grid scale model is defined as follows.
[30]
where eij is the fluid strain defined in Eq.(12) and ω is the vorticity vector. Ls is the length scale which should be adjusted in the case of interest. Since in the present study the turbulence model is incorporated in a RANS manner, the following expression is used instead of 1/R in the calculation.
[31]
SGS model for a modified spheroid
In order to validate the body boundary condition of turbulence model, the numerical tests for the viscous flow past a modified spheroid is carried out. The prolate spheroid of six to one proportion is used. A conical tail piece is used to preserve the flow over the tail without flow separation. The mean flow measurements as well as turbulence measurements have been carried out by Patel et al.[ 11] and are available for the validation of the turbulence model [20].
Following the measurement, the Reynolds number based on the spheroid length and streamwise velocity is set at 2.75×106 in the calculation. Fig.3 showed the O-H grid system around the modified
spheroid. The total grid points is 135,642 (141×26×37). The minimum mesh spacing of the innermost velocity point from the body surface is 5×10−5, and time increment is set at 1×10−4. The simulation is carried out until the dimensionless time T reaches 2.5.
We tested two cases for the length scale of turbulence model. In the case A, the length scale is set as follows.
[32]
In the case B, the Van Driest wall damping function is introduced into the length scale.
[33]
where
Df=1−exp(−y+/A+) [34]
and y+ is the normal viscous unit from the body surface and A+ is set at 26.
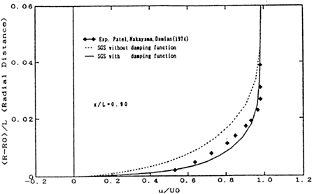
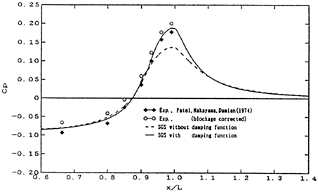
The comparison of the radial distribution of the axial velocity between the two cases of calculation and the experiment is shown in Fig. 4. The comparison of the afterbody pressure distribution along the longitudinal axis is shown in Fig. 5. It is noted that the numerical results are improved by introducing the Van Driest wall damping function. Especially for the pressure distribution, the numerical results of case B showed an excellent agreement with the experiment. However, the velocity distribution needs to be improved near the body surface.
Hybrid turbulence model for ship flow
For the flow about a full ship hull with long parallel middle body a hybrid turbulence model is designed [21]. Assume that the eddy viscosity of SGS model is vs, and that of Bladwin-Lomax model [22] is vb, the hybrid turbulence model is defined in the following way.
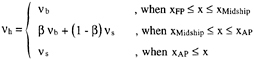
[35]
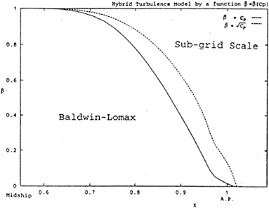
where β is defined as a function of prismatic coefficients of the hull in the present study as follows.
β=(Cp)α [36]
Fig. 6 shows the distributions of prismatic curve of SR196A (see next section) along the streamwise axis and its rooted curve as an example. Yoshida tested this model in detail and recommended α=0.5 [21].
CONDITION OF SIMULATION
A series of full tanker hull named SR196 after the same name of project [23], are employed for the verification of the present method. The displacement of the full-scale ship is 230,000 ton, the length is 320 m and the service speed is 14 kt (7.202 m/s). The principal particulars of the original full-scale ship and 4 m testing model are listed in Table 1. The stern configuration is designed as mariner type for its employment of low-frequency, large-diameter propeller.
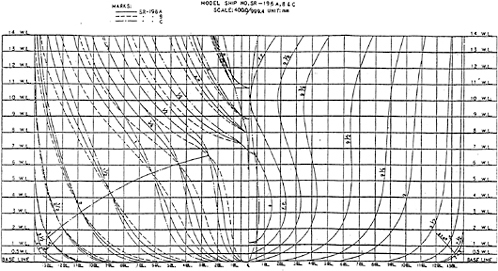
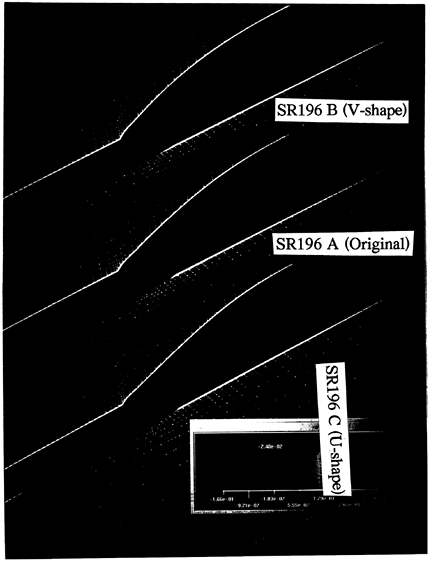
There were 9 types of model hull derived from the original hull proposed for testing [23]. In the present study, three types of hull are adopted. They have common fore part and common prismatic curve but different framelines of after part as shown in Fig. 7. The original hull is called SR196A, the modification with V-shaped stern is SR196B and the U-shaped is SR196C.
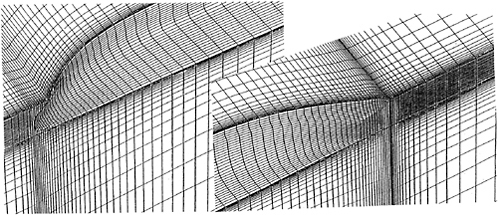
The computational conditions are listed in Table 2. About 65,000 grid points are allotted in the computational domain. Fig. 8 is the grid about the bulbous bow and stern of SR196A hull.
The Reynolds number in the calculation is 106. The time increment is set at 5×10−4. The minimum grid spacing is set at 10−4. This grid spacing ensures the first grid point is set inside the sublayer in the ordinary turbulent boundary layer.
The computation spends almost two days for one case on a engineering workstation (130MIPS).
ANALYSIS OF NUMERICAL RESULTS
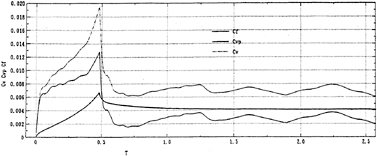
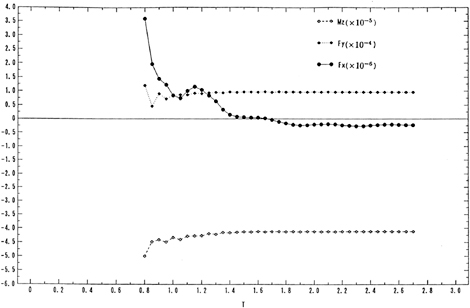
The time sequence of simulated viscous resistance coefficients of SR196A is shown in Fig. 9. The resistance coefficients are defined as follows.
Cv=Cvp+Cf, (37a)
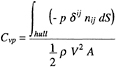 , (37b)
, (37b)
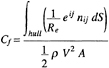 , (37c)
, (37c)
where A is the wetted surface area of the hull, Cv is the total viscous resistance coefficient, Cvp is the viscous pressure resistance coefficient and Cf is the frictional resistance coefficient. One can find the increase of resistance during the acceleration and the convergence of solution within a few dimensionless time unit. The friction resistance coefficients are predicted fairly well for all of the cases. However, the viscous pressure resistance coefficients are overpredicted and fluctuate in time.
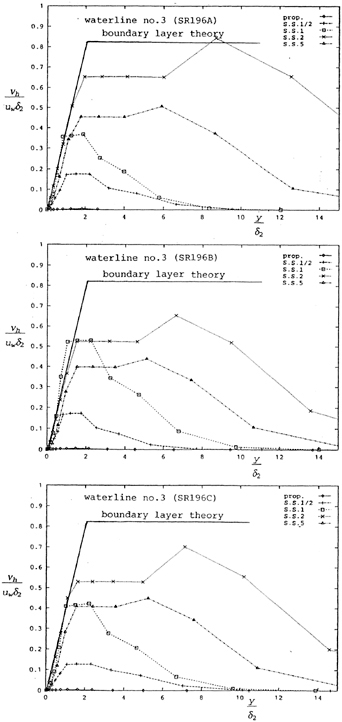
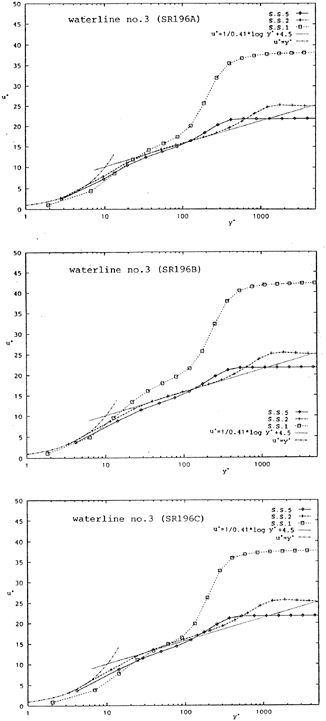
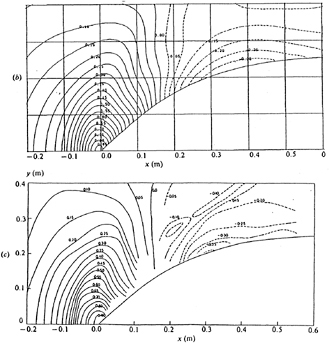
The simulated eddy viscosities of several transverse sections along the waterline No.3 are shown compared with the boundary layer theory [24] in Fig. 10. The eddy viscosity is nondimensionalized by the wall frictional velocity uw and the momentum thickness δ2 of the boundary layer. The distance y from the hull surface is also nondimensionalized by δ2. The lateral velocity profiles at the same position are shown in Fig. 11 fitted to the empirical wall law. It is because that, along waterline no.3, both the change of the hull form and the difference between three hulls are also most significant as shown in Fig.7.
Figs. 10 and 11, for both the eddy viscosity and the velocity profile, indicate that the flow structures along this waterline are still those of a developing turbulent boundary layer at S.S.2. The agreements between the calculation and the theory for both eddy viscosity and velocity profile are fairly good. However, at S.S.1, the eddy viscosity becomes smaller and the velocity profile exhibits its departure from the wall law, indicating that the flow changes its structure during the part of hull between S.S.2 to S.S.1.
The velocity profile at S.S.1 shows a skewness during the viscous unit y+=100∼400. SR196C (U-shape) shows the largest change while SR196B (V-shape) shows the smallest, indicating the correlation of the velocity profile with the hull form.
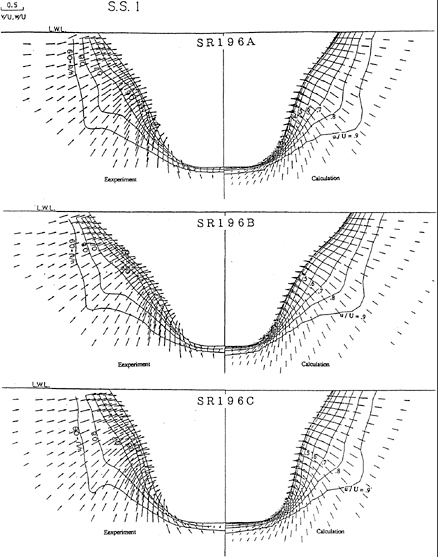
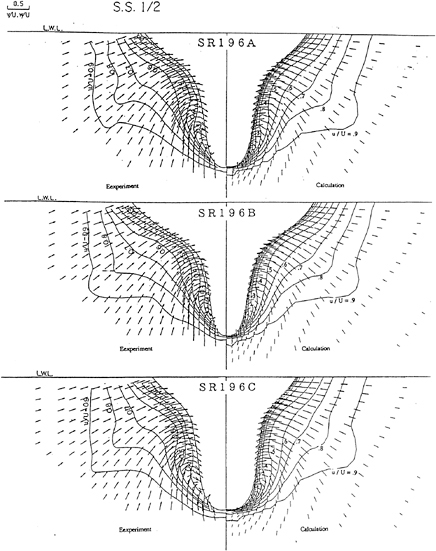
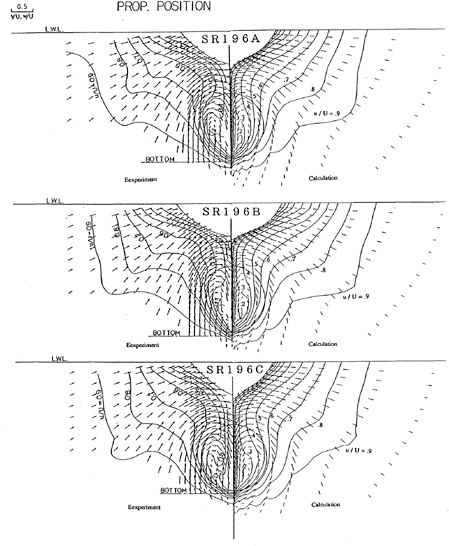
The comparisons of longitudinal velocity distribution between the calculation and the experiment [23] in the transverse sections S.S.1, S.S.1/2 and propeller plane are shown in Figs.12a, 12b and 12c. Although the Reynolds number of the experiment (4×106) is different from the present calculation (106), the evolution of the thick boundary layer as well as the distorted wake pattern are revealed in the calculation. However, the changes of the wake pattern inside the propeller disk due to the difference of hull form are not predicted so distinctly by comparison with the experiment.
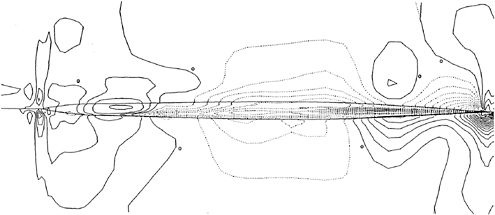
The 3D contour map of iso-longitudinal vortex around the after part of SR196C hull is shown in Fig.13. It is interesting to note that the flow structure may not be described so clearly by the the drawing of the value of longitudinal vortex component. This is because the flow near the stern always diverge from the keel toward the free surface. It creates a circulation which has a main component in the same direction with the longitudinal axis as those of bilge vortex or separated vortex.
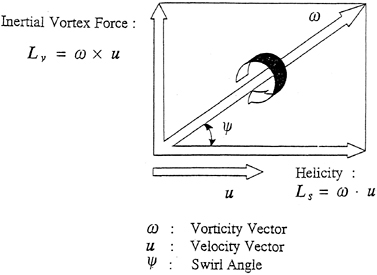
In order to elucidate the vortex structure related to the flow separation, in the present paper, the vorticity is decomposed into the following two parts as shown in Fig.14.
the helicity or Lamb scalar:
Ls=ω·u (38a)
the inertial vortex force or Lamb vector:
Lv=ω×u (38b)
where ω is the vorticity vector and u is the velocity vector. Yamada and Miyata [25] showed that the separated vortices are clarified by use of these values. In a flow separation associated wind noise problem, Zhu-et al.[10] showed that the helical vortex can be employed to distinctly clarify the flow separation phenomenon.
The 3D contour maps of iso-helicity around the after part of SR196B, SR196A and SR196C hulls (from upper side) are showed in Fig.15. It is not surprising that the three-dimensional flow separation phenomenon is described definitely by using the helical vortex. It is worth to be mentioned that there is a strong correlation between the separated vortex structure and the low-pressure part on the hull surface.
It may be safe to say that the present numerical method is capable of elucidating some flow features caused by the difference of hull form. The vortex structures seem to be more three-
dimensional when the hull form changes from V-shape to U-shape. The separated vortex forms a “hook” shape during its interaction with the hull. This is why the velocity profile at S.S.1 was more skewed for SR196C. This “hook” shaped vortex structure may be directly responsible for the distorted wake pattern inside the propeller disk. However, as shown in Fig.15, the vortex seems to be dissipated when it passes the propeller position so that the simulated wake pattern is not so distorted as shown in Fig.12. Considering the grid spacing employed in the present work, both the resolution and the turbulence modeling should be further improved by the collaboration with the experimental investigation in the near future.
CONCLUSIONS
A numerical solution method (WISDAM-V method) has been developed for the viscous flow about a full ship model with practical hull configuration. A hybrid turbulence model is tuned and incorporated into the numerical method in order to cope with the low-Reynolds stress flow structure near the ship stern. Numerical tests have been carried out for a series of SR196 tanker model. It seems that this method is capable of predicting the distorted wake pattern and clarifying the difference of ship stern configuration.
In the present study, the possible correlation between the separated vortex structure and the wake pattern in the propeller plane has been discussed. For the accurate prediction of wake pattern, it is quite important for the numerical simulation to reveal the flow separation as well as the evolution of separated vortex. This work showed the possibility and importance of turbulence modeling for thick boundary layer.
This work is supported by the Project SR222, the Shipbuilding Research Association of Japan. The authors are grateful to Mr. H. Mitsutake, a master student in the authors' laboratory at the University of Tokyo, for his help of making graphics drawing for the present paper, and to Professor H.Kajitani for his deep understanding and continuous interest in their research work.
REFERENCES
[1] Larsson, L., Patel, V.C. and Dyne, G. (editors), Proc. of the 1990 SSPA-CTH-IIHR Workshop on Ship Viscous Flow, Gothenburg, 1991.
[2] Knaack, T., Kux, J. and Wieghardt, K., “On the Structure of the Flow Field on Ship Hulls”, Proc. Osaka Int. Colloq. Ship Visc. Flow, Osaka, 1985, pp.192–208.
[3] Fukuda, K. and Fujii, A., “Turbulence Measurement in Three Dimensional Boundary Layer and Wake around a Ship Model”, J. Soc. Naval Architects of Japan, Vol. 150, Dec. 1981, pp.85–98; “Turbulence Measurement in Three Dimensional Boundary Layer and Wake around a Ship Model (Second Report), J. Soc. Naval Architects of Japan, Vol. 153, June, 1983, pp.29–41. (in Japanese)
[4] Löfdahl, L. and Larrson, L., “Turbulence Measurements Near the Stern of a Ship Model”, J. Ship Research, Vol.28, No.3, 1984, pp.186–201.
[5] Knaack, T., “Laser-Doppler Velocity Measurement on a Double Model of a Ship in a Wind Tunnel”, Inst. Schiffbau, Univ. Hamburg, Report 439, 1984; “LDV Measurement of the Reynolds Stresses in the Wake of a Ship in a Wind Tunnel”, Inst. Schiffbau, Univ. Hamburg, Report 499, 1990. (in German)
[6] Townsend, A.A., The Structure of Turbulent Shear Flow, Cambridge University Press, 2nd Ed., 1976.
[7] Kodama, Y., “Computation of Ship's Resistance Using an NS Solver with Global Conservation—Flat Plate and Series 60 (CB=0.6) Hull -”, J. Soc. of Naval Archit. of Japan, Vol. 172, Dec. 1992, pp.147–156.
[8] Deng, G.B., Piquet J. and Visonneau M., “Viscous Flow Computation Using a Fully Coupled Technique”, Proc. of the Second Osaka Int. Colloq. on Visc. Fluid Dyns in Ship and Ocean Tech., Osaka, 1991, pp.186– 202
[9] Simpson, R.L., “Turbulent Boundary-Layer Separation”, Ann. Rev. Fluid Mech. 21, 1989, pp.205–234.
[10] Zhu, M., Hanaoka, Y. and Miyata, H., “Numerical Study on the Mechanism of Wind Noise Generation About the Front Pillar of a Car-Like Body”, submitted to ASME J. Fluid Engrg., 1993.
[11] Patel, V.C., Nakayama, A. and Damian, R., “Measurements in the Thick Axisymmetric
Turbulent Boundary Layer near the Tail of a Body of Revolution” , J. Fluid Mech., Vol.63, Part 2, 1974, pp.345–367.
[12] Zhu, M., Miyata, H. and Kajitani, H., “A Finite-Volume Method for the Unsteady Flow About a Ship in Generalized Coordinate System”, J. Soc. Naval Archit. of Japan, vol.167, 9, 1990, pp.9–15.
[13] Miyata, H., Zhu, M. and Watanabe, O., “Numerical Study on a Viscous Flow with Free-Surface Waves About a Ship in Steady Straight Course by a Finite-Volume Method”, J. Ship Research. Vol.36, No.4, Dec. 1992, pp.332–345.
[14] Vinokur, M., “Review Article: An Analysis of Finite-Difference and Finite-Volume Formulations of Conservation Laws”, J. Comput. Phys., Vol.81, 1989, pp.1–52.
[15] Sawada, K. and Takanashi, S., “A Numerical Investigation and Wing/Nacelle Interferences of USB configuration ”, AIAA Paper 87–0455, 1987.
[16] Miyata. H., Sato, T. and Baba, N., “Difference Solution of a Viscous Flow with Free-Surface Wave About an Advancing Ship”, J. Comput. Phys., Vol. 72, No.2, 1987, pp.393–421.
[17] Zhu, M., “A Finite-Volume Solution Method for Unsteady, Three-Dimensional Turbulent Flows About A Full Ship Model”, PhD. Thesis, Dept. Naval Architecture and Ocean Engineering, The University of Tokyo, 1991.
[18] Smagorinsky, J., Manabe, S., and Holloway, J., L., “Numerical Results from a Nine-Level General Circulation Model of the Atomsphere”, Monthly Weather Review, 93, Dec. 1965, pp.727–768.
[19] Moin, P., I. The subgrid scale modeling group. In Studying Turbulence Using Numerical Simulation Databases—III, Proceedings of the 1990 Summer Program. Center for Turbulence Research, NASA-Ames Research Center and Stanford University, 1990.
[20] Aoki, K., Zhu, M. and Miyata, H., “Finite-Volume Simulation of 3-D Vortical Flow-Fields about Road Vehicles with Various After-Body Configuration”, 7th Int. Pacific Conf. on Auto. Engrg., Pheonix, Nov., 1993.
[21] Yoshida, O., “Verification of Turbulence Model in the Numerical Simulation of Viscous Ship Stern Flow”, Master Thesis, Dept. Naval Architecture and Ocean Engineering, The University of Tokyo, 1993. (in Japanese)
[22] Baldwin, B.S. and Lomax, H., “Thin Layer Approximation and Algebraic Model for Separated Turbulent Flows”, AIAA paper 75– 257, 1978.
[23] Research on the Design of Ship Stern Hull Configuration—Viscous Flow: Project SR 196, the Shipbuilding Research Association of Japan, 1985.
[24] Cebeci, T. and Bradshaw, P., Momentum Transfer in Boundary Layer, Hemisphere Publishing, 1977.
[25] Yamada Y. and Miyata H., “Computational Study of Large Eddy Structure of Flows past Bluff Body and Oceanic Topography”, J. Soc. Naval Archit. Japan. Vol.173, 1993.
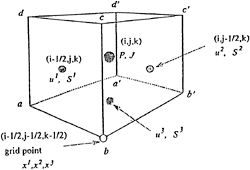
Fig. 1 Variable arrangement
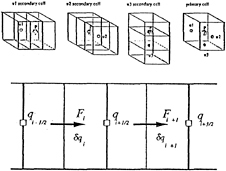
Fig. 2 Definition of the invisid flux
Table 1 Principal particulars of SR 196 hull models
|
Particulars |
Model |
Ship |
|
Lpp(m) |
4.0000 |
320.00 |
|
B (m) |
0.6663 |
53.30 |
|
d (m) |
0.2413 |
19.30 |
|
CB |
0.8017∼0.8027 |
0.802 |
|
Fn |
0.17 (Experiment) |
0.129 (Service Speed) |
|
Re |
4.007×106 |
2.305×109 |
Table 2 Condition of simulation
|
Condition |
SR196 A, B, C |
|
grid points (total amount) |
91×23×31 (64,883) |
|
computational domain length |
2.5 |
|
computational domain width |
1.0 |
|
computational domain depth |
1.0 |
|
minimum grid spacing |
1.0×10−4 |
|
time increment |
5.0×10−4 |
|
time steps for acceleration |
1000 |
|
time of simulation |
2.5∼3.0 |
|
Reynolds number |
106 |
|
turbulence model |
hybrid model |
Fig. 3 Grid system about the modified spheroid
Hydrodynamical Design of Super-Slender-Twin-Hull Ferries by CFD Techniques
H.Miyata, T.Ohmori (University of Tokyo, Japan)
E.M.Kamal (Ishikawajima-Harima Heavy Industries Co. Ltd., Japan)
Abstract
Two CFD techniques are applied in the course of developing a new-type fast ferries named Super-Slender-Twin-Hull. Since this ship is of displacement type and the design Froude number is from 0.4 to 0.8, minimization of wave resistance is of major importance. After pursuing the optimal particulars, the TUMMAC-IV method for ship waves is employed to have the hull-form of minimum wave resistance. By imposing appropriate boundary conditions on the centerline and the bottom the wave systems of a catamaran in both deep and shallow waters are simulated. For the design of the after body the WISDAM-V method, which employs boundary-fitted coordinate system and finite-volume discretization, is used. The difference of the buttock flow due to shortening the length of the after body, the effect of waves on the viscous flow, the effect of the asymmetric hull geometry on the wake are studied. The oblique tow simulation is performed with this method by giving proper inflow boundary conditions. It is demonstrated that the present method can predict lateral force and yaw moment quite correctly.
1. Introduction
Computational Fluid Dynamics (CFD) is now on the new stage of putting the stress on the application to scientific and engineering purposes in a variety of fields. We still have important problems of CFD technique to which continuous efforts should be exerted for improvement. The turbulence models now available are not suitable for separating flow and the resolution of the turbulent flow at high Reynolds number is insufficient. Treatments of moving interface is not yet at the satisfactory level. The grid system must be more conveniently generated with the interface is not yet at the satisfactory level. The grid system must be more conveniently generated with the smallest degree of topological singularity. However, the research works made in the last decade show that the accuracy is on quite a satisfactory level, for the free-surface waves without involving wave breaking, and that the turbulent motions of relatively larger scale including the secondary or longitudinal vortices are resolved by the finite-volume simulation techniques in the curvilinear, boundary-fitted coordinate system. Although we are not sufficiently sure to what extent the degree of resolution ability should be raised for respective problems, some examples of applicational approach seem to provide us promising results. The turbulent flow simulations are also going to be on the applicational stage.
The TUMMAC-IV code and WISDAM-V code with modification are used in the course of the development of a new-type fast ferry “Super-Slender-Twin-Hull ” ( SSTH ). The SSTH is composed of two extremely slender demihulls, which provide sufficiently small degree of wave resistance and relatively lower magnitude of motion transfer functions due to the long ship length, double-stair-bow (DSB) and properly designed hull-form. The development was commenced in 1987 by IHI with the collaboration of the authors' laboratory, and a trials ship was constructed in 1991 and served for the experiments at sea. The principal particulars and the overall configuration are shown in Figs. 1,3 and in Table 1. The development and the full-scale experiments are reported in Ref. [ 1 ] [ 2 ].
Because the SSTH is a displacement-type ship, the optimization of the hull configuration, from all of the fluid-dynamical aspects, is of essential importance. A tremendous amount of water basin experiments were performed at the experimental tanks of both IHI and the University of Tokyo. Linear potential theories were used for the determination of the preliminary prismatic curve and for the estimation of motions in waves. The CFD techniques were used for the improvement of the details of the hull-forms.
Since the hull-form was of the extremely slender type, the classical linear theories were also very useful. The hybrid use of physical experiments, computational simulations and linear analyses seemed to be most effective for the development of a new ship system with completely new configuration.
In this paper, the TUMMAC-IV code for ship waves is used for the design of the fore-body configuration of minimum wave resistance. Demihulls with both symmetric and asymmetric waterlines are served for numerical simulation and not only the optimal prismatic curve but also the optimal degree of asymmetry are derived by modifying the original code so that it may cope with catamarans. The waves in shallow water are also studied. The WISDAM-V code, which is a finite-volume simulation method for the viscous flow about a ship, is used for the detailed understanding of the viscous flow fields, such as the viscous interaction with waves. It is also used for the estimation of the side-force and yaw-moment on the oblique tow condition.
PART-I FORE-BODY DESIGN BY WAVE MAKING SIMULATION
2. FSSW and TUMMAC-IV Method
The nonlinear characteristics of bow waves were experimentally clarified and the newly recognized waves were called free-surface shock waves (FSSW) due to the analogical features with the supersonic shock waves. [3] [4]. They indicated that linear theories cannot cope with this nonlinear wave making. Linear theories including the double-model linear theory called modified Rankine source method are based on the assumption that the order of magnitude of perturbation velocities is sufficiently lower than that of the advance speed. However, perturbation velocity is usually of the same order of magnitude in the vicinity of a bow where the most significant waves are generated. This situation is exaggerated in the case of a ship with a blunt bow for which the region of high perturbation velocities occupies a large area. The effect of a bow bulb is most obvious on the FSSW formation as seen in Fig. 3. Furthermore, the steep wave slope and discontinuous velocity field of FSSW do not permit us to employ any kind of linear theory.
The TUMMAC-IV method [5] [6] was initially developed in 1979 when the important part of the characteristics of FSSW were elucidated. It is a finite-difference solution method for the Navier-Stokes or Euler equation. It is solved in the time marching procedure in the rectangular coordinate system. The free-surface condition is fulfilled on the exact location of the free-surface and ingenious techniques are devised so that the free-slip body boundary condition is implemented with sufficient degree of accuracy in the body boundary cells of which shape varies depending on the curvature of the hull-form. The degree of agreement in bow waves is excellent as shown in Fig. 4.
In order to assure whether this method can be used in the practical design procedure, the accuracy in the relative magnitude of wave energy and integrated pressure distribution on hull surfaces is most important. Better full-form of smaller wave resistance can be obtained by such degree of accuracy. We can recall a large number of theoretical works which conjecture the accurate estimation of the absolute value of wave resistance for a simple hull-form. This does not always guarantee the ability of practical application as the history of wave making resistance suggests. It is well known that the wave resistance is sensitively changed due to a delicate difference of lines rather than many other forces. The usefulness of wave making simulation is verified only when this sensitive change of wave formation is realized in the simulation. The practical use of the TUMMAC-IV method which started in 1985 is based on thorough examination from this standpoint. One of the typical examples is described in Ref. [7]. Although the satisfactory accuracy is not achieved, the systematical variation of the FSSW formation is also exemplified in Ref. [8].
3. Monohull Design
3.1 Optimization procedure
The optimum hull-form of catamaran is based on the optimum hull-form of monohull. Therefore, the development of hull-form was started with the optimization of monohull. The length-beam ratio of conventional ships, including warships, had been less than 12, with which the value of wave resistance coefficient on the last hump is extremely large and the required horsepower exceeds economical limit. This is avoided very easily by increasing the length-beam ratio.
The design point of minimum resistance is determined by compromising the decreasing wave resistance and the increasing frictional resistance due to the elongation of the monohull at the constant volume for buoyancy.
When the first approximation of the optimal particulars of monohull is derived. The slender body theory is employed for the improvement of the prismatic curve of the monohull. For this slender hull, at high Froude numbers, the nonlinearity of the waves is not very dominant. Therefore, this second stage is very economically performed.
In the third stage, the lines (especially near the bow) is improved by the numerical simulation of the waves on the fore-part of the hull. The hull-form is systematically modified and the modified offsets are put into the computation. Since the rectangular coordinate system is employed in the TUMMAC-IV method, the grid generation (cell division) is automatically made and the grid spacing is absolutely common to all modifications.
3.2 Towing test results
The optimal monohull configuration is not derived only from the viewpoint of resistance. The motion properties must be carefully studied since the slamming phenomenon can take place at relatively low angle of pitching for the long, shallow-drafted ship. Therefore, in the above-mentioned procedure of monohull optimization, motion tests are successively made at the towing tank.
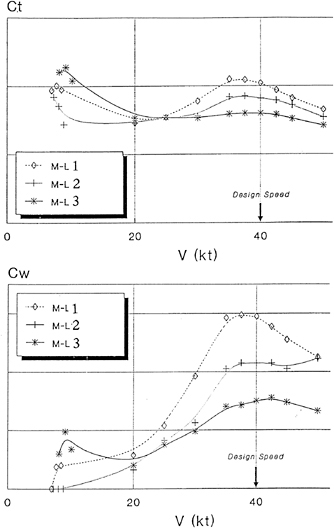
After preliminary optimization of the prismatic curve, the frame-lines and the profile of the monohull in the above-mentioned procedure , the optimal length-beam ratio is experimentally determined. The results of towing test with three ship models with various length-beam ratio are shown in Fig. 5. By the dimensions of M-L3, the total resistance reached almost minimal level for a monohull.
4. Catamaran Design
4.1 Optimization procedure
Design is made of a SSTH catamaran of which displacement is greater than 500ton and the service speed is 40kt.
When the distance between the two demihulls are sufficiently large, the combination of two optimal demihulls makes the optimal catamaran, because the interaction of two demihulls can be ignored. However, since the length-beam ratio of SSTH configuration is around 5, the flow between two demihulls is remarkably influenced by the interaction of the waves from two demihulls. Therefore, the optimization of each demihull must be made by considering the wave interactions on the second stage. The optimal configuration may not be a symmetric one, since the wave resistance is usually increased by the amplification of waves due to the interaction of the two wave systems from two demihulls.
The optimal monohull configuration obtained in the procedure described in the previous section is used as a component of a catamaran and its configuration is improved by the simulation of the TUMMAC-IV method which is modified so that it may cope with the catamaran case.
4.2 Modification of TUMMAC-IV
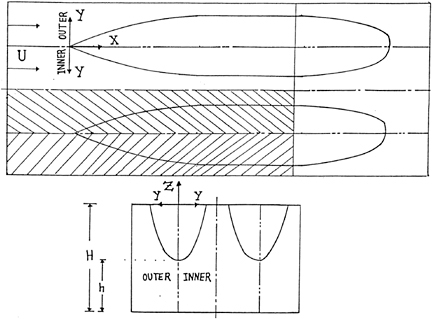
The computational domain for wave simulation is schematically shown in Fig. 6. Only the fore part is considered and the region of computation is devided into inner and outer parts. The flows of both parts are separately computed, which means that the flow is assumed not to go across the centerline of each demihull.
For the flow simulation in the inner region, the centerline condition is imposed on the side boundary as shown in Fig. 7. This is very easily implemented simply by giving zero normal velocity on this surface instead of the zero-normal-gradient condition.
4.3 Computation and results
About 40,000 grid points were allocated in each part of the computational domain and the grid spacing is variable in the vertical direction, which is especially important for SSTH, because the wave height is very small in comparison with the ship length. The flow is accelerated from the still condition to the steadily advancing condition by 400 time steps and the steady state of the waves was researched at the 700-th time step.
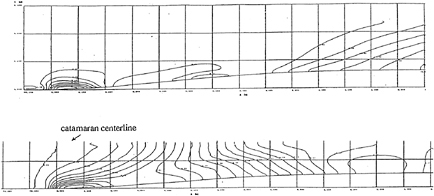
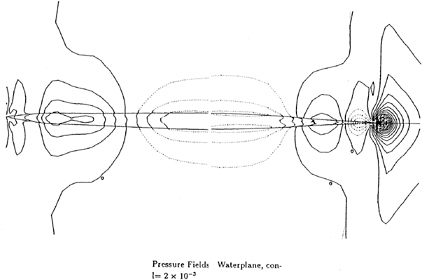
The results of a series simulation are summarized in the wave contour maps in Figs. 8 and 9 for the outer and inner part, respectively. The wave hight is normalized with respect to the head of the uniform stream. Keeping the symmetric configuration the demihull's prismatic curve is modified from M-P1 to M-P2, which unexpectedly resulted in higher waves outside and lower wave depression near the midship although the maximum wave height on the centerline of the catamaran is slightly reduced.
The demihull configuration is further modified and a bow-bulb like configuration is given to M-P3 and M-P4. With the same prismatic curve, these two models have different degree of asymmetry about the centerline of a demihull. When the beam-length of the inner hull is set at 66.67 percent of the outer hull, the displacement volume of the inner hull is 40 percent of the total displacement volume. In this way 40 percent of the displacement is alloted on the inner part of M-P3 and 45 percent on that of M-P4. As shown in Fig. 9, the maximum wave height on the centerline of the catamaran is about 30 percent reduced by the 40 to 60 percent distribution of M-P3. However, the waves outside are significantly accentuated and the integrated wave energy of M-P3 is much larger than M-P4. In this process, the optimal catamaran configuration is derived and its quantitative properties of resistance coefficient are obtained through towing tests.
5. Wave Making in Shallow Water
5.1 Bottom condition
For the TUMMAC-IV method the flow simulation in a restricted water region can be very conveniently performed as is anticipated in the treatment of centerline condition of a catamaran. By simply imposing zero vertical velocity on the point where the vertical velocity is defined in the staggered grid system as shown in Fig. 11 the free-slip bottom boundary condition is implemented. The pressure on the lowest pressure point below the bottom by half of the vertical spacing is extrapolated from the pressure above, through the relation of the Navier-Stokes equation in the vertical direction.
5.2 Simulation results
The condition of the computation is shown in Fig. 10 and only the fore-part of a catamaran M-P4 is served for the computation. The other conditions of
computation are the same with the cases described in the previous section.
The obtained wave contour maps are shown in Fig. 12. It can be seen that the bow waves are reduced on both sides of a demihull and that the free-surface is remarkably suppressed in between the two demihulls. The wave field is quite different from the case in deep water.
PART-II AFTBODY DESIGN BY VISCOUS FLOW SIMULATION
6. WISDAM-V Method
For the viscous flow, simulation for a ship with smooth surface of gentle curvature a boundary-fitted curvilinear coordinate system must be employed. Since the viscous flow is intrinsically unsteady, the time-marching solution procedure, preferably explicit time-accurate one, is most suitable. Due to the limited number of grid points, the longitudinal or girthwise spacing may be 1000 times larger than the grid spacing normal to the hull surface. In such a grid system, the conservation laws of mass and momentum are difficult to fulfill in the finite-difference scheme. Therefore, the finite-volume scheme is often employed in the simulation techniques for flows about bodies of complex geometry.
Since the two-equation turbulence model is not suitable for the separated flow, and many experiences indicate insufficient evolution of the flow with intense vorticity, the subgrid-scale (SGS) turbulence model is employed in the WISDAM-V method. Because an outer flow about a body of complex geometry is treated here and then the periodic condition cannot be imposed at the inflow and outflow boundaries, the SGS turbulence model is used in a very averaged manner. However, the long experience with this turbulence model both in the TUMMAC and WISDAM methods suggests that the complicated 3D structure of vortices in the thick boundary layer and separated flow is more realistically resolved with this model than others. In order to meet the use of the SGS turbulence model, no wall-function is imposed on the body surface. Therefore, the damping function and the length-scale of the turbulence model must be carefully tuned depending on the Reynolds number and the grid spacing. All the computations by the WISDAM-V method in this paper are performed at the Reynolds number 1×106, which is of the same order with the experiments with a small ship model.
The WISDAM-V method is developed with the above-mentioned considerations. The detailed description of the method and numerical tests are already reported in Ref. [7] [8] [9] and they are not repeated in this paper.
7. Effect of Asymmetric Hull on Viscous Flow
7.1 Condition of computation
Since a hull-form of asymmetric configuration turned out to be useful from the resistance point of view, the viscous flow field about the asymmetric after-body must be studied for the proper design of the hull and propeller (SSTH is propelled either propeller or water-jet installed on both of the demihulls.)
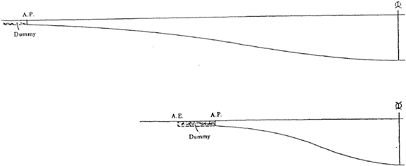
The so-called O-H type grid system is employed for a demihull and both starboard and port side flow-fields are considered so that it may cope with the asymmetrical hull as well as the oblique tow condition. The catamaran configuration is not taken into account because the interaction of viscous flow between two demihulls is supposed to be negligibly small. The transverse view of the grid system is shown in Fig. 13. The length of a ship is devided into 80 grid poinds and the smallest spacing on the hull surface in the direction normal to the hull is less than y+=5, where y+ is the viscous unit. The total number of grid points is around 10 5 in all cases in this paper. Since a stern configuration of transom type is employed for SSTH, a dummy hull is attached in order to avoid topological singularity at the after end.
The computation is started from the still condition and the flow is accelerated to the condition of 40kt by 2000 time steps with the time increment of 2×10−4, where time is made dimensionless with respect to the ship length and the steady advance speed of a ship. Almost steady viscous flow field is attained when the dimensionless time T exceeds 2.0. The drawings of the flow-field in this paper are all for the steady state.
The WISDAM-V method has an advanced version which can simulate the free-surface flow with the free-surface-fitted moving grid system. The grid generation is performed in each time step and the free-surface conditions are implemented on the exact location of the free-surface. The viscous free-surface condition is introduced in a very approximate manner, i.e. , the normal stress is ignored assuming the small curvature of the free-surface and the tangential stress is set to be vanished on the free-surface by giving zero-normal-gradient of horizontal velocity in the thin free-surface layer of which thickness is around 5×10−4. Therefore, the grid system is also attracted to the free-surface.
7.2 Computation and results
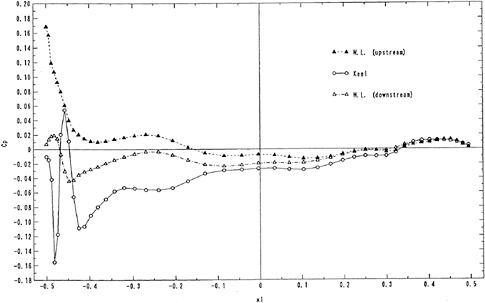
The results of viscous flow simulation for the demihull M-P4 with asymmetric configuration are shown in Figs. 14 to 16. It is noted that the difference of the pressure distribution between two sides of the hull is rather small and the asymmetrical distribution of wake and vorticity does not seem to be influential to the propeller design. It is obviously shown that one pair of longitudinal vortex is present at the stern. This
is much simpler and weaker than the case of a tanker, for which the magnitude of vorticity is 10 times larger and more than two pairs of longitudinal vortices are generated [8].
7.3 Simulation with free-surface
The simulation by another WISDAM-V version with free-surface is performed on the model M-P4 slightly modified by cutting off the stern end.
The results are shown in Figs.17 and 18. The waves are very gentle due to the extreme slenderness of the hull. However, the comparison between Fig. 18 and Fig. 16 very clearly indicates that the vorticity field is remarkably influenced by the presence of free-surface . The vortical motions around the bow look intensified and another pair of longitudinal vortices appear near the keel owing to the action of the free-surface waves.
8. Comparison of Buttock Flow
8.1 Condition of computation
In case a propeller is installed at the stern, its diameter is of the same magnitude with the draft due to the high horsepower for the high service speed. Therefore, the stern configuration is inevitably of the buttock flow type but for such a long ship the suitable configuration is not well known.
The M-P1 hull form is used and the buttock flow configuration is modified as shown in Fig. 19. The length of the after-body of the shortened one is one half of the longer one.
The WISDAM-V method without free-surface is employed and the computation is continued for 10,000 time steps with the time increment of 1× 10−4.
8.2 Simulation results
The results of simulation are shown in Figs. 20 to 22. Relatively high pressure region is caused by the relatively steeper upward slope. These results in the pressure drag coefficient of the shorter version 2.14×10−4, while that of the longer version −0.6×10−7. Although the absolute value is not reliable, the difference between two hulls seems to be well explained. As shown in Fig. 22, the intensity of longitudinal vortex is doubly magnified for the shorter stern. This pair of longitudinal vortex seems to be inevitably generated by the upward variation of the stern configuration.
9. Oblique Tow Simulation
9.1 Condition of computation
For high-speed ships, the directional stability is more important than low-speed ships, while the catamaran configuration and the use of water-jet units often deteriorate this property. In this section, an oblique tow test is achieved in the numerical simulation as a first step to the directional stability simulation. Only a demihull is used for the computation current.
The oblique flow condition is implemented by giving Ucos β and Usin β for the streamwise and lateral velocity components at the inflow boundary, where β is the oblique tow angle. In the stage of flow acceleration to the steady advance speed, the lateral velocity component in the x2 direction is also accelerated in a way similar to that in the x1 direction. The computational domain is stretched laterally so that a complete oblique tow condition is implemented.
The angle of oblique tow is set at 5 degrees and the double-model flow version of the WISDAM-V method is used. The time increment is set at 2.0×10−4 and the computation is continued to the dimensionless time T=2.7.
9.2 Simulation results
The time-history variations of resistance, lateral force and yawing moment are shown in Fig. 23, in which almost steady state is attained after T=2.0. These forces and moment are normalized with respect to the velocity head 1/2ρU2 and 2/3 power of volume or volume itself for forces and moment, respectively.
The flow-field and pressure distribution at the steady state are shown in Figs.24 to 26. Wakes are seriously distorted and the structure of vortices are deformed and the strength of vortices is amplified. It is noted that the contour interval in Fig.24 (right) is five-times magnified than those in Figs 16 and 18.
In Fig.26, the pressure difference between face and back sides of the hull is most obvious at the bow and it is gradually reduced on the after-part of the hull. This pressure distribution on the waterlines is supposed to be caused partly by the usual nature of pressure distribution of a wing section and partly by the buttock flow configuration of the after-part. The detailed pressure distribution on the oblique tow condition seems to be very useful for the understanding of the generation of asymmetric force and moment.
The computed lateral force and yawing moment are compared with the measured results in Figs. 27 and 28. The experiments were conducted at the University Tokyo Tank with a 2.8m long model. The model was steadily fixed to the carriage and obliquely towed at the Froude number 0.2. The forces and moment were measured by a load-cell unit. The towing speed was varied up to Fn=0.30 and the effect of the free-surface motions were studied, and the variation was from 0.032 to 0.041 for the lateral force and from 0.17 to 0.19 for the yawing moment. The agreement seems to be very satisfactory.
A number of research works are known for the theoretical explanation of the forces in the oblique tow condition, quite recently by Tahara [10]. The pressure distribution in Fig. 26 indicates that a simpler
method with some postulations may give satisfactory agreement. However in the hull-form with more complicated stern configuration, the resolution of the 3D vortical flow-field may be of substantial importance.
10. Conclusions
Two numerical simulation techniques are applied in the process of developing a new-type, high-speed ship. Since hydrodynamical properties determine the most important part of a high-speed ship, the assistance of such numerical tools are very useful.
In this paper, two quite different numerical methods are used. Since the grid spacing is too coarse in the region little away from the hull where wave making is still important, the WISDAM-V method is not yet applied to the process of searching a hull-form of minimum wave resistance with sufficient reliability. However, when sufficient number of grid points can be allotted on the free-surface, all the computations will be performed by the WISDAM-V method and all features and values related with resistance will be simultaneously simulated. If the movement of a ship can be treated by use of a moving grid technique, a considerable part of “numerical tank ” will be completed.
The hull-form development of SSTH was conducted by the collaboration with the Technology Development Division and the Research Institute of IHI. This paper describes a part of this work mostly parformed at the University of Tokyo. The authors are grateful to Mr. R.Ono, Mr. H.Nogami, Mr. S. Mizoguchi, Mr. Y.Shirose and all other members of the SSTH project at IHI.
References
1. H.Miyata et al., Fast ferry by super-slender twin hull, Proc. IMAS'91 (The Institute of Marine Engineers International Conference) Sydney, 1991.
2. A.Abe et al., Full-scale experiment and advanced design of SSTH ferries, Proc. Intersociety High Performance Marine Vehicle Conference and Exhibit (American Society of Naval Engineers), Arlington, USA, 1992.
3. T.Inui et al., Experimental investigations on the wave making in the near-field of ships, J.Kansai Soc. Naval Archit. Vol. 173 ( 1979).
4. H.Miyata. et al., Nonlinear ship waves, Adv. Appl. Mech. Vol. 24, ( 1984).
5. H.Miyata et al., Finite-difference simulation of nonlinear waves generated by ships of arbitrary three-dimensional configuration, J. Comput. Phys. Vol. 60–3, 1985.
6. H.Miyata et al., Finite-difference simulation of nonlinear ship waves, J. Fluid Mech. vol. 157, ( 1985).
7. Y.Maekawa et al., A method of optimizing hull-forms by use of the finite-difference technique TUMMAC-IV, Intern. Symposium on Ship Resistance and Powering Performance, Shanghai, China ( 1989).
8. K.Aoki et al., A numerical analysis of nonlinear waves generated by ships of arbitrary waterline (First report) (Second report) , J. Soc. Naval Archit. Japan Vol. 154, 155, ( 1983) ( 1984).
9. O.Watanabe et al., Numerical simulation of a . O.Watanabe et al., Numerical simulation of a viscous flow with free-surface wave about a ship by a finite-volume method, J. Soc. Naval Archit. Japan Vol. 171 ( 1992) (in Japanese).
10. H.Miyata et al., Numerical study on a viscous flow with free-surface waves about a ship in steady straight course by a finite-volume method, J. Ship Research (to appear).
11. O.Yoshida et al., Verification of the viscous flow-field simulation for practical hull-forms by the finite-volume method WISDAM-V, J. Soc. Naval Archit. Japan (to appear) (in Japanese).
12. Y.Tahara, A boundary-element method for calculating free-surface around a yawed ship, J. Kansai Soc. Naval Archit. (to appear).

Fig. 1 Artist impression of SSTH ferry (75m craft)
Table 1 Principal particulars of SSTH ferry design
|
IHI Super Slender Twin Hull (SSTH) ferry design Approximate dimensions and performance when fitted with propellers |
||
|
90m craft |
Trials craft |
|
|
Length bp |
75.0m |
24.0m |
|
Breadth moulded |
19.4m |
5.6m |
|
Depth moulded |
4.9m |
1.9m |
|
Draught |
2.3m |
0.7m |
|
Gross tonnage |
3600tonnes |
52tonnes |
|
Capacity |
||
|
-passengers |
400 |
68 |
|
-cars |
80 |
- |
|
Maximum speed |
40knots |
28.5knots |
|
Main engines |
4×high speed diesels 4×7000ps |
2×high speed diesels 2×605ps |
|
Propulsion system |
waterjet |
propeller |
|
Range |
200n miles |
100n miles |

Fig. 2 SSTH30 trials craft off Yokohama
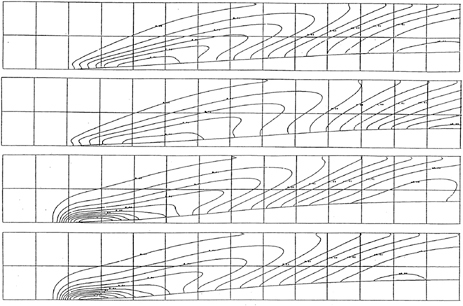
Fig. 8 Comparison of simulated wave contours in the outer region of a catamaran at 40kt, contour interval is 0.01 nondimensional wave height, M-P1, M-P2, M-P3 and M-P4 from above, the contour interval is 0.05.

Fig. 9 Same as Fig. 8, in the inner region of a catamaran, top-side of each figure coincides with the catamaran centerline.
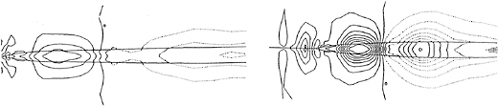
Fig. 20 Comparison of pressure contours on hull surface and waterplene, M-P1 (left) and shortened model (right), the contour interval is 2×10−3
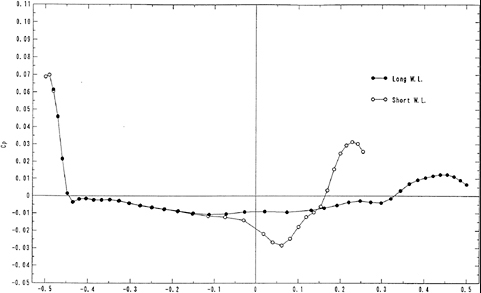
Fig. 21 Comparison of pressure coefficient along waterlines of M-P1 and shortened model.
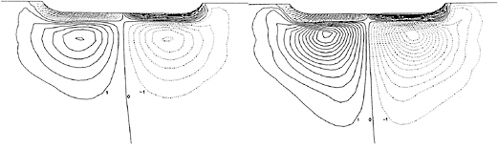
Fig. 22 Comparison of longitudinal vorticity contours at the stern end of M-P1 and the shortened model.
DISCUSSION
by Dr. J.Ando and Dr. K.Nakatake
Kyushu Univ., Japan.
We would like to congratulate the authors for developing SSTH by concerted applications of several numerical techniques. We are interested in the flow field in the stern region where the propeller is operating. According to our experience, the free surface effect on the stern flow becomes large at high speeds. A comparison between Fig. 18 with Fig. 16 in your paper indicates the strong effect of the free surface on the vorticity field. You showed the calculated flow field near the stern region without free surface. If the free surface is considered, however, we believe that the flow field will be fairly different. Would you comment on this point?
Author's Reply
As the discussors suggest, the interaction of the free-surface with the viscous motion is most important at the stern. This is especially true for high-speed vessels and has been one of the major objectives of the researches at the author's laboratory. However, we have not yet reached the satisfactory results due partly to the nonlinearity of the free-surface motion and partly to the inadequacy of the turbulence modelling.
DISCUSSION
by Dr. Raven
MARIN
According to your presentation, you used two (2) criteria to select the best hull form from the wave-resistance point of view:
-
the peak wave heights in between the demi-hulls;
-
the integrated wave energy in the entire domain.
The former is not necessarily related to the wave resistance. Could you clarify the second criterion?
Is this a wave pattern analysis approach, or anything else representative of radiated wave energy?
Author's Reply
One of the shortcomings of such CFD simulation of waves in a restricted region is that the dispersive spread of wave system is not well realized. Therefore, the estimation of the relative magnitude of wave resistance must be made by either integration of wave energy in the computational domain or integration of the surface pressure distribution. For local modification of the hull form the use of the former is useful and the letter for other cases if pressure integration is carefully performed.
DISCUSSION
by Dr. Marshall P.Tulin
Ocean Engineering Laboratory, UCSB
The authors do not provide section plans for the hulls, which are the subject of the paper. It is therefore difficult to analyze their results. Could they provide a sketch showing section plans?
Author's Reply
The purpose of our paper is to demonstrate the extent the CFD techniques can be applied to very practical problems. Unfortunately we cannot show details of the lines, because it is really practical.