The Nonlinear Numerical Prediction of Unsteady Sheet Cavitation for Propellers of Extreme Geometry
N.E.Fine (Engineering Technology Center, USA)
S.A.Kinnas (Massachusetts Institute of Technology, USA)
Abstract
The unsteady flow around cavitating marine propellers is treated in nonlinear theory by employing a low-order potential based boundary element method. The solution is found in the time domain. The kinematic and dynamic boundary conditions, which are fully three dimensional, nonlinear and time-dependent, are satisfied on an approximate surface consisting of the propeller surface beneath the cavity and the portion of the blade wake surface overlapped by the cavity. An efficient and robust algorithm is developed to predict arbitrary cavity shapes, including so-called “mixed” cavity planforms in which the blade is partially cavitating at inner radii and supercavitating near the tip. In previous works, it has been shown that the present solution represents the first iteration of a completely nonlinear solution in which the exact boundary conditions are satisfied on the exact flow boundary. The main emphasis of the present work is to investigate the performance of the method for extreme propeller geometries, such as those with large amounts of skew, rake or pitch. The effect of the hub on the solution is investigated and shown to have more effect on heavily pitched propellers than on moderately pitched ones. The importance of including the crossflow terms in the dynamic boundary condition is also ivestigated for extreme propeller geometries.
1 Introduction
With recent increases in the demand for heavily loaded efficient marine propellers, the occurrence of cavitation has become less and less avoidable. As a result, it has become the task of the hydrodynamicist to predict the cavitation characteristics of a propeller at the design stage, with the expectation that analytical methods can be used to avoid excessive cavitation within an appropriate range of ship speed. Computational tools for the reliable prediction of propeller cavitation are therefore in high demand. Moreover, these tools must be applicable to propellers of extreme geometry (high skew, rake or twist) which have become very common in recent years.
The approach taken in this work is to treat propeller cavitation strictly as sheet cavitation. The travelling bubbles and bubble clouds which often are entrained in the wake of the sheet cavity, or precede the occurrence of sheet cavitation in the incipient stage, are not included in the present analysis. Viscosity will also be neglected in this work, and the inflow will be assumed to be free of vorticity. The advantage of this approach lies in its relative mathematical simplicity. The governing equation is Laplace's equation for the perturbation potential. The use of surface singularities and the now classic application of Green's 3rd identity are well suited for such a problem.
Despite the relative simplicity, however, the problem is far from trivial. The main difficulty arises from the need to determine the cavity free-surface on which the pressure is prescribed. The fact that a portion of the flow boundary is unknown makes the problem nonlinear. In addition, the inherent complexity of solving three dimensional flows around extreme geometries adds to the difficulty of the analysis. Furthermore, the cavity extent and volume variation in time resulting from nonaxisymmetries in the inflow is strongly nonlinear, making it impossible to solve in the frequency domain.
The main disadvantages of treating only sheet cavitation in potential flow result from the combined neglect of viscosity, tip and hub vortex cavitation, bubble cavitation, and cloud cavitation.
However, there are two additional rationales for taking the potential flow avenue. First, it is believed that the first-order contributor to dynamically varying blade loads and radiated pressures is the transient sheet cavity [28]. Second, many or all of the neglected phenomena may be included as refinements to the potential flow solution. For example, a viscous-inviscid boundary layer interaction could be used to model the effects of viscosity. As another example, a local tip solution, including a cavitating tip vortex, could be matched to the outer sheet cavity solution. The potential of such a model to capture most of the physics at reasonable computational expense is the motivation for obtaining an accurate and efficient potential flow solution which is able to treat a wide class of geometries including highly skewed, raked or pitched propellers. At this stage of development, it is also important to investigate the effects of the parameters which are included in the model. For example, the effect of the hub may be investigated to determine its importance to the solution for various geometries and operating conditions. Also, the importance of the crossflow terms in the dynamic boundary condition may be investigated. Finally, the method should be interrogated to determine if it predicts multiple solutions. These are the goals of the present work.
2 Formulation
The mathematical formulation first appeared in [15]. The formulation will be repeated here, but with more detail on the dynamic boundary condition in the wake (section 2.2.2). Details of the numerical implementation are provided in the next section.
Consider a cavitating propeller subject to a nonuniform inflow UW(xs,rs,θs), with the subscript 5 denoting the ship-fixed coordinate system in which the wake is defined. Uw is assumed to be the effective wake. Some details of the geometry are shown in Figure 1. The solution is found in the (x,y,z) coordinate system, which rotates with the propeller. The propeller is assumed (without loss of generality) to be right-handed and to rotate at a constant angular velocity ω. The inflow relative to the propeller is
(1)
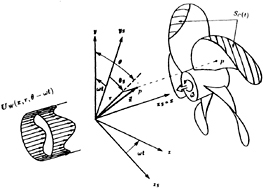
Figure 1: The propeller and cavity geometry, coordinate systems, and nonuniform inflow. xs,ys,zs represent the ship-fixed coordinate system; x,y,z represent the propeller-fixed coordinate system. The point p is a point on the propeller surface, defined by the vector ![]() from the origin of the propeller-fixed system.
from the origin of the propeller-fixed system.
For the moment, assume that the propeller has a developed sheet cavity whose time-dependent surface is denoted by SC(t), as shown in Figure 1. The fluid is assumed to be inviscid and the resulting flow to be incompressible and irrotational. In this case, the time-dependent total flow velocity q(x,y,z,t), can be written in terms of the perturbation potential, ![]() (x, y,z,t), as follows:
(x, y,z,t), as follows:
q(x,y,z,t)=Uin(x,y,z,t)+![]()
![]() (x,y,z,t). (2)
(x,y,z,t). (2)
The goal is to determine the potential field ![]() (x,y,z,t), as well as the cavity surface SC(t)1. Once
(x,y,z,t), as well as the cavity surface SC(t)1. Once ![]() is known, the pressure distribution may be computed by numerically differentiating the potentials and applying Bernoulli's equation. The unsteady blade load distribution may then be determined by integrating the pressure. Knowing SC(t), the cavity volume history may be computed. In the following sections, the equations and boundary conditions necessary for the solution will be derived.
is known, the pressure distribution may be computed by numerically differentiating the potentials and applying Bernoulli's equation. The unsteady blade load distribution may then be determined by integrating the pressure. Knowing SC(t), the cavity volume history may be computed. In the following sections, the equations and boundary conditions necessary for the solution will be derived.
2.1 Green's Formula
The perturbation potential ![]() p(x,y,z ,t) at any point p which lies either on the wetted blade (or
p(x,y,z ,t) at any point p which lies either on the wetted blade (or
|
1 |
The leading edge of the cavity will be assumed to be known, the rest of the surface Sc(t) is to be determined. See section 6 for related discussion. |
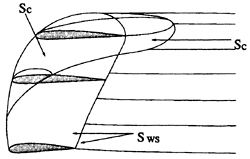
Figure 2: Definition of the flow boundaries on which the boundary conditions should be satisfied.
hub) surface2, SW S(t), or on the cavity surface, SC(t), (both surfaces are shown in Figure 2) must satisfy Green's third identity:

(3)
The subscript q corresponds to the variable point in the integrations. ![]() is the unit vector normal to the surface of the propeller, the cavity, or the wake. The unit normal points into the fluid (on the wake surface,
is the unit vector normal to the surface of the propeller, the cavity, or the wake. The unit normal points into the fluid (on the wake surface, ![]() is oriented such that it points towards the same horizon as the normal on the suction side of the blade). Δ
is oriented such that it points towards the same horizon as the normal on the suction side of the blade). Δ![]() w(r,θ,t) is the potential jump across the wake sheet, SW(t), and G(p; q)=1/R(p; q) is Green's function, where R(p; q) is the distance from the field point p to the variable point q.
w(r,θ,t) is the potential jump across the wake sheet, SW(t), and G(p; q)=1/R(p; q) is Green's function, where R(p; q) is the distance from the field point p to the variable point q.
Equation (3) expresses the perturbation potential on the surface formed by the union of the cavity and blade surfaces, SW S(t) ∪ SC(t), as a superposition of the potentials induced by a continuous source distribution, G, and a continuous dipole distribution, ![]() , on SWS(t)∪SC(t), and a continuous dipole distribution on the trailing wake surface, SW(t). The application of Green's 3rd identity to problems in potential flow is classic [18, 22, 26], while applications to propeller and rotor flows are more recent [21, 23, 7, 8, 10, 16].
, on SWS(t)∪SC(t), and a continuous dipole distribution on the trailing wake surface, SW(t). The application of Green's 3rd identity to problems in potential flow is classic [18, 22, 26], while applications to propeller and rotor flows are more recent [21, 23, 7, 8, 10, 16].
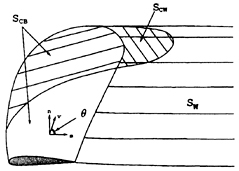
Figure 3: The approximate cavity surface on which the boundary conditions are applied.
Ultimately, the exact nonlinear potential flow solution will be found when the kinematic and dynamic boundary conditions (which may be applied simultaneously with Green's formula (3)) are satisfied on the exact flow boundary. However, we face the usual problem that the position of the cavity surface is unknown. As a first iteration towards the fully nonlinear solution, we apply the boundary conditions on an approximate flow boundary. If the blade is experiencing only partial cavitation, then the approximate boundary coincides with the blade surface (including the part of the blade beneath the cavity). This surface will be referred to as SCB. On the other hand, if the blade is super-cavitating, the upper and lower sides of the super-cavity downstream of the blade trailing edge are collapsed to a single surface and the two sides of the collapsed cavity surface are taken to coincide with the two sides of the zero-thickness trailing wake sheet (see discussion below). This surface will be referred to as SCW(t). Thus the approximate flow boundary consists of the blade surface, SCB, and the portion of the trailing wake sheet which is overlapped by the cavity, SCW(t).
A sketch of the approximate boundary is shown in Figure 3. The geometry of the wake, SW(t) will from here on be assumed to be invariant in time and identical to the steady-flow relaxed wake
|
2 |
The wetted blade surface is that part of the blade which is not cavitating. |
corresponding to the circumferentially averaged inflow [6]. The approximate flow boundary therefore coincides with that of the fully wetted solution, as described by Hsin [8].
A justification for making this approximation as well as a measure of its effect on the cavity solution is given in [3] and [15].
As a result of the linearization of the part of the supercavity downstream of the blade trailing edge, the surface SCW(t) may be considered to be a force-free surface. The pressure across the collapsed cavity surface must therefore be continuous and equal to the cavity pressure pc. The pressure across the blade wake surface must also be continuous. Therefore, it is possible to consider these two surfaces to coincide, with the condition of pressure continuity being
p+=p−=pc on SCW(t)
p+=p−=p on SW. (4)
Satisfying the boundary conditions on the approximate boundary described above may be viewed as the first iteration towards a fully nonlinear solution. In the fully nonlinear solution, subsequent iterations are found by satisfying the dynamic boundary condition on an updated cavity surface, where the kinematic boundary condition is used to update the surface, as described in section 2.3. The solution is then considered to be converged when the cavity surface does not change (to within a tolerance) between two consecutive iterations. However, it was discovered that, using the present potential based panel method, the first iteration solution (where Green's formula is satisfied on the approximate boundary) is extremely close to the converged nonlinear solution for a wide range of operating conditions [13,14,3]. As a result, it is deemed unnecessary to go beyond the first iteration towards the fully nonlinear solution. In view of the high computational cost involved in regridding and re-computing influence coefficients, the importance of this conclusion cannot be overstated.
Considering the approximate boundary, the first integral on the right-hand-side of equation (3) may be decomposed into integrals over the blade surface and the portion of the wake which is overlapped by the cavity (denoted SCB and SCW, respectively, in Figure 3). The exact form of Green's formula depends on the location of the field point, which will either be on SCB or on SCW. Each case will be considered separately in the following.
2.1.1 Field Point on SCB
If the field point is on the blade surface SCB, the local contribution is extracted from the first integral in equation (3) and Green's formula becomes

(5)
where the superscripts + and − correspond to the upper and lower sides of the wake surface, respectively. Note that the wake surface has been divided into SCW and SW, as shown in Figure 3.
The velocity normal to SCW is discontinuous across the surface. The jump in ![]() defines a source distribution, of density qw(t), which represents the cavity thickness:
defines a source distribution, of density qw(t), which represents the cavity thickness:
(6)
The potential is also discontinuous across SW, where the jump Δ![]() w(r,θ,t) is related to the local circulation history.
w(r,θ,t) is related to the local circulation history.
Inserting (6) into (5) yields:
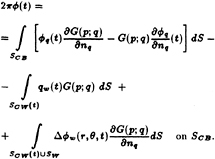
(7)
2.1.2 Field Point on SCW
Now consider the case where the field point is on the upper side of the collapsed cavity surface in the wake, SCW(t). Extracting the local contribution from the integral over SW on the right hand side of (3) and using the expression ![]() +(t)+
+(t)+![]() −(t)=
−(t)=
2![]() +(t)−Δ
+(t)−Δ![]() w(r,θ,t) yields an expression for the potential on the upper wake surface
w(r,θ,t) yields an expression for the potential on the upper wake surface ![]() +:
+:
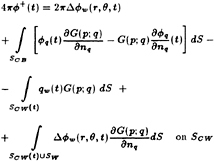
(8)
A detailed derivation of (8) may be found in [3]. Equations (7) and (8) define the potential ![]() (t) on the blade surface beneath the cavity, SCB, and the potential
(t) on the blade surface beneath the cavity, SCB, and the potential ![]() +(t) on the wake sheet, SCW(t), in terms of the following distributions of singularities:
+(t) on the wake sheet, SCW(t), in terms of the following distributions of singularities:
-
continuous source and normal dipole distributions on SCB of strength
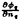 (t) and
(t) and 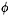 (t), respectively
(t), respectively -
a source distribution on SCW(t) of strength qw(t)
-
a normal dipole distribution on the entire wake sheet SCW(t) ∪ SW of strength Δ
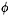 w(r,θ,t).
w(r,θ,t).
On the wake sheet SCW(t) ∪ SW the dipole strength Δ![]() w(r,θ,t) is convected along the assumed wake surface with angular speed ω, in order to ensure that the pressure jump in the wake is equal to zero:
w(r,θ,t) is convected along the assumed wake surface with angular speed ω, in order to ensure that the pressure jump in the wake is equal to zero:
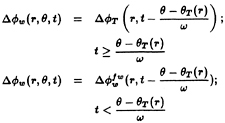
(9)
where r,θ are the cylindrical coordinates of the wake surface and θT(r) is the θ coordinate of the blade trailing edge at radius r. ![]() is the unsteady fully wetted flow potential jump in the wake.
is the unsteady fully wetted flow potential jump in the wake. ![]() is known since the unsteady fully wetted flow solution is found before the unsteady cavity solution.
is known since the unsteady fully wetted flow solution is found before the unsteady cavity solution.
Note that the wake convection given by (9) is identical to the fully wetted convection [17]. This is allowed by the linearization of the supercavity in the wake, where the two force-free surfaces are considered as one.
Everywhere on SCB and SCW(t), either the source distribution is known (a Neumann boundary condition) or the dipole distribution is known (a Dirichlet boundary condition). Green's formulae (7) and (8) may then be discretized and rewritten as a linear system of equations by employing the boundary conditions and shifting all of the known quantities to the right-hand-side.
2.2 Dynamic Boundary Condition
The dynamic boundary condition (DBC) requires that the pressure everywhere inside and on the cavity be constant and equal to the known cavity pressure, pc. Bernoulli's equation with respect to the propeller fixed system is
(10)
where ρ is the fluid density and r is the distance from the axis of rotation. Here qt is the total velocity on the cavity surface. po is the pressure far upstream on the shaft axis; g is the gravitational constant and ys is the vertical distance from the horizontal plane through the axis of rotation, as shown in Figure 1. ys is defined as negative in the direction of gravity.
After some manipulation, and using the definition of the cavitation number:
(11)
where ![]() and D are the propeller revolutions per unit time and diameter, respectively, we find that the magnitude of the total cavity velocity satisfies
and D are the propeller revolutions per unit time and diameter, respectively, we find that the magnitude of the total cavity velocity satisfies
(12)
The function f(s) corresponds to a pressure recovery law at the trailing edge of the cavity along the arc s on the surface of each span wise blade section. The pressure recovery is given by an algebraic expression over a specified portion of the cavity near its trailing edge. This termination model is described in detail in [3].
Since the cavity boundary consists of two parts —one coinciding with the cavitating portion of the blade surface and the other with the cavitating portion of the wake surface—further derivation of the dynamic boundary condition will be considered on each surface separately.
2.2.1 DBC on the Blade Cavity
In addition to the expression (12), the cavity velocity qt may also be expressed in terms of the directional derivatives of the perturbation potential and the components of the inflow along the same curvilinear coordinates [10]. The coordinate system3 on the cavity surface consists of s (chordwise) and ν (spanwise), as shown in Figure 3:
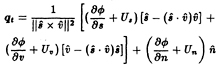
(13)
with ![]() and
and ![]() being the unit vectors corresponding to the coordinates s and ν, respectively, and with
being the unit vectors corresponding to the coordinates s and ν, respectively, and with ![]() being the unit normal vector to the assumed cavity. Us, Uν, and Un are the s, ν and n components of the relative inflow, Uin.
being the unit normal vector to the assumed cavity. Us, Uν, and Un are the s, ν and n components of the relative inflow, Uin.
If s, ν and n were located on the correct cavity surface, then the normal velocity, ![]() , would vanish. However, this is not the case since the cavity curvilinear coordinates are approximated with those on the propeller surface. Nevertheless, in applying the dynamic boundary condition, the normal velocity is assumed to be vanishingly small. In the fully nonlinear scheme, the normal velocity vanishes as the solution converges. As shown in [3] it was found that leaving the normal velocity term out of the dynamic boundary condition has only a small effect on the solution.
, would vanish. However, this is not the case since the cavity curvilinear coordinates are approximated with those on the propeller surface. Nevertheless, in applying the dynamic boundary condition, the normal velocity is assumed to be vanishingly small. In the fully nonlinear scheme, the normal velocity vanishes as the solution converges. As shown in [3] it was found that leaving the normal velocity term out of the dynamic boundary condition has only a small effect on the solution.
Equations (12) and (13) may then be combined to form an equation which is quadratic in the unknown chordwise perturbation velocity, ![]() . The two solutions to the quadratic equation represent potential gradients which are positive and negative in the direction of increasing s. The positive root is chosen to ensure that the cavity velocity points in the direction of increasing s. We can now express
. The two solutions to the quadratic equation represent potential gradients which are positive and negative in the direction of increasing s. The positive root is chosen to ensure that the cavity velocity points in the direction of increasing s. We can now express ![]() in terms of the cavitation number, the inflow velocity, and the unknown derivatives
in terms of the cavitation number, the inflow velocity, and the unknown derivatives ![]() and
and ![]() :
:

(14)
with θ being the angle between s and ν, as shown in Figure 3. Here |qt|2 is defined as in equation (12). Equation (14) is integrated once to form a Dirichlet boundary condition on ![]() :
:
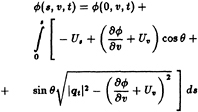
(15)
The integral on the right-hand-side of (15) is determined by trapezoidal quadrature. Since (15) defines the strength of the dipole distribution on the cavity, it may be directly substituted into Green's formula 7.
According to the dynamic boundary condition (15), ![]() depends on both its span wise and time derivatives. These terms will be treated as knowns and will be updated in a time-stepping scheme which will be discussed later. The influence of the crossflow term
depends on both its span wise and time derivatives. These terms will be treated as knowns and will be updated in a time-stepping scheme which will be discussed later. The influence of the crossflow term ![]() was studied first for the case of partially cavitating 3-D hydrofoils and it was found that the global dependence of the solution on the crossflow term was small. This result will be shown in section 4.2, where it will also be demonstrated for the propeller solution. For a discussion of the convergence of the time-derivative with iterations and its effect on the solution, see [3] or [15].
was studied first for the case of partially cavitating 3-D hydrofoils and it was found that the global dependence of the solution on the crossflow term was small. This result will be shown in section 4.2, where it will also be demonstrated for the propeller solution. For a discussion of the convergence of the time-derivative with iterations and its effect on the solution, see [3] or [15].
2.2.2 DBC on the Wake Cavity
The dynamic boundary condition on the cavitat— ing portion of the wake, SCW, may also be written as a Dirichlet condition on ![]() +. In this case, consider the orthogonal system (s,u,n), shown in Figure 4. Assuming that s is the direction of the mean velocity, the total velocity on the upper side of the wake sheet may be written
+. In this case, consider the orthogonal system (s,u,n), shown in Figure 4. Assuming that s is the direction of the mean velocity, the total velocity on the upper side of the wake sheet may be written
|
3 |
In general non-orthogonal. |
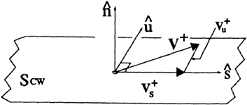
Figure 4: Velocity diagram on the wake surface.
The normal velocity ![]() will be omitted from the dynamic boundary condition, as it was from (13), with the same justification.
will be omitted from the dynamic boundary condition, as it was from (13), with the same justification.
Applying Bernoulli's equation, which is used to define the total velocity on the cavity qt, we have
(16)
The dynamic boundary condition on SCW may thus be written
![]() . (17)
. (17)
Equation (17) may be integrated once to form a Dirichlet boundary condition on the potential on the upper wake surface, ![]() +:
+:

(18)
The integral in (18) is computed by trapezoidal quadrature. Equation (18) defines the potential ![]() + on the upper side of the wake and may be directly substituted into Green's formula (8).
+ on the upper side of the wake and may be directly substituted into Green's formula (8).
2.3 Kinematic Boundary Condition
Since the dynamic boundary condition is applied on the portion of the boundary which is encompassed by the cavity, the other boundary condition, namely the kinematic condition, may be used to determine the position of the actual cavity surface once the singularity strengths have been determined. In this section, the most useful form of the kinematic boundary condition (KBC) will
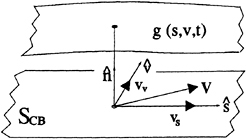
Figure 5: Definition of the cavity surface defined with respect to the blade surface.
be derived. As in the previous section, the cavity boundary will be divided into two zones which will be considered separately.
2.3.1 KBC on the Blade Cavity
The kinematic boundary condition on the cavity is the requirement that the substantial derivative of the cavity surface vanishes:
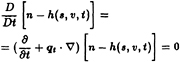
(19)
where n is the coordinate normal to the blade surface (with unit vector ![]() ) and h(s,ν,t) is the thickness of the cavity normal to the blade at the point (s,ν) at time t. Expressing the gradient in terms of the local directional derivatives
) and h(s,ν,t) is the thickness of the cavity normal to the blade at the point (s,ν) at time t. Expressing the gradient in terms of the local directional derivatives
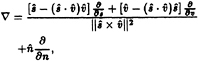
(20)
performing the dot product with qt (as defined in (13)) and substituting the result in (19) yields the following partial differential equation for the cavity thickness:
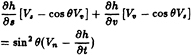
(21)
where
![]() .
.
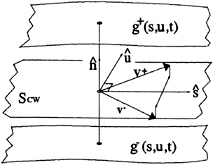
Figure 6: Definition of the cavity surface defined with respect to the wake surface.
2.3.2 KBC on the Wake Cavity
The kinematic boundary condition on the cavity surface in the wake may be derived in a similar fashion, except that now both surfaces of the supercavity must be considered

(22)
where g±(s,u,t) defines the upper and lower cavity surfaces, as shown in Figure 6. Note that (s,u,n) is an orthogonal system. V+ and V− are the total velocities on the upper and lower sides of the wake (also shown in Figure 6), respectively, and may be written
(23)
The upper and lower cavity surfaces, g(s,u,t)±, may be written
where C is the cavity camber in the wake and hw is the cavity thickness. The quantities g, C and hw are all taken along the normal to the wake surface. These quantities are also shown in Figure 7.
Expanding equations (22) we find that
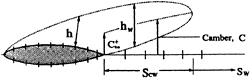
Figure 7: Definition of the cavity camber and height for a supercavitating section of the propeller blade.
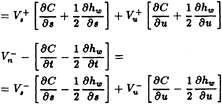
(24)
Taking the difference between the two equations in (24) and assuming that ŝ coincides with the direction of the mean velocity so that
(25)
yields
(26)
Here we have used the definition of the wake source strength (6) and the following equalities:
(27)
which readily follow from the assumption (25) and the fact that the free vorticity must follow the mean velocity vector.
To be consistent with the dynamic boundary condition, we assume that the span wise crossflow velocity is small. Thus, applying equation (16), and the assumption of small span wise slope of the camber C(s,u,t), the kinematic boundary condition (26) reduces to
(28)
Note that the cavity height on the blade and in the wake, both shown in Figure 7, are defined differently and so are given separate symbols.
The position of the cavity surface over the blade surface is determined by adding the cavity thickness h normal to the blade surface at the midspan
of the panel boundaries. In the wake, the cavity camber C(s,u,t) must first be determined. An expression for C(s,u,t) may be found by adding the two equations (24) and dividing through by two:
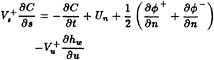
(29)
where Un is the inflow velocity normal to the wake sheet. Equation (29) is numerically integrated to determine the camber surface in the wake. At the trailing edge of the blade, the continuity of camber and thickness is imposed:
(30)
Here, the superscripts + and − denote just upstream and just downstream of the trailing edge, respectively. ![]() is the value of the camber just upstream of the trailing edge. It is determined by adding
is the value of the camber just upstream of the trailing edge. It is determined by adding ![]() to the trailing edge along the blade normal (see Figure 7). The quantity
to the trailing edge along the blade normal (see Figure 7). The quantity ![]() is determined by interpolating the upper cavity surface over the blade at the trailing edge and computing its normal offset from the wake sheet. The upper and lower surfaces of the cavity in the wake are then determined by adding and subtracting half of the cavity thickness hw from the camber surface. This defines the cavity surface at the midspans of all the spanwise strips. The surface of the cavity at the strip boundaries are determined by interpolation and extrapolation.
is determined by interpolating the upper cavity surface over the blade at the trailing edge and computing its normal offset from the wake sheet. The upper and lower surfaces of the cavity in the wake are then determined by adding and subtracting half of the cavity thickness hw from the camber surface. This defines the cavity surface at the midspans of all the spanwise strips. The surface of the cavity at the strip boundaries are determined by interpolation and extrapolation.
2.3.3 KBC on the Wetted Blade
The kinematic boundary condition on the wetted portion of the blade, SWS, defines the source strength there in terms of the known inflow velocity:
(31)
where xq,yq,zq are the coordinates of the point q with respect to the propeller fixed system. As in the case of fully-wetted flow, this boundary condition may be directly substituted in Green 's formula.
2.4 The Kutta Condition
The Kutta condition requires that the fluid velocity be finite at the blade trailing edge. It was found necessary, in the fully wetted steady flow propeller solution, to satisfy a nonlinear Kutta condition which ensures pressure equality between the suction and pressure sides at the trailing edge [20]. The so-called pressure Kutta condition was later refined by Kinnas and Hsin [16], who developed an efficient iterative solution. In the present work, an extension of Morino's steady Kutta condition is applied. Development of a pressure Kutta condition for the cavitating propeller is left for the future.
The value of the dipole strength, Δ![]() T(r,t), at the blade trailing edge at time t is
T(r,t), at the blade trailing edge at time t is
(32)
where ![]() and
and ![]() are the values of the potential at the blade trailing edge at radius r on the suction side and the pressure side, respectively. The potential jump there is also equal to the circulation Г at time t around the blade section at radius r. This condition is equivalent to requiring the shed vorticity from the blade trailing edge to be proportional to the time rate of change of the circulation around the blade (Kelvin's law). An extension of Morino's Kutta condition for steady flow [24], in which the potential jump at the trailing edge of the blade is simply replaced by the potential jump at the nearest control points, is applied.
are the values of the potential at the blade trailing edge at radius r on the suction side and the pressure side, respectively. The potential jump there is also equal to the circulation Г at time t around the blade section at radius r. This condition is equivalent to requiring the shed vorticity from the blade trailing edge to be proportional to the time rate of change of the circulation around the blade (Kelvin's law). An extension of Morino's Kutta condition for steady flow [24], in which the potential jump at the trailing edge of the blade is simply replaced by the potential jump at the nearest control points, is applied.
3 Implementation
The objective of the numerical analysis is to invert equations (7) and (8) subject to the kinematic boundary condition (31), the dynamic boundary conditions (15) and (17), and the Kutta condition. These equations, however, assume that the cavity extent is known. Since it is not, an iterative solution will be employed. This will be described in detail later in this section. First, we will describe how Green's formulae and the boundary conditions are satisfied for a given guess of the cavity extent. To accomplish this, we first tag one blade with the label “key blade”. The solution at a given time step will be obtained only for the key blade, with the influence of the other blades corresponding to an earlier solution of the key blade. The key blade surface is discretized into N chordwise and M spanwise quadrilateral panels with the corners lying on the blade surface SCB and with the control points located at the panel centroids. An example of a discretized blade is shown in Figure 8. The source and normal dipole distributions on each panel are approximated with constant strength distributions.

Figure 8: Discretization of the propeller blade, the cavity, and their trailing wakes; N=16, M=9.
The trailing wake is discretized into panels at constant angular intervals ΔθW=ωΔt with Δt being the time step. The blade and trailing wake discretization is identical to that in the case of fully wetted unsteady flow [8, 17, 16]. If we call
NWS=Number of wetted blade panels
NCB=Number of cavitating blade panels
NCW=Number of cavitating wake panels,
then, among the discrete sources and dipoles, we have NWS known source strengths, via (31), NCB known dipole strengths, via (15) and NCW known dipole strengths, via (18). The following are then unknown and must be solved for: NWS dipole strengths on the wetted blade, NCB source strengths on the cavitating blade and NCW source strengths in the supercavitating wake.
3.1 Discrete Green's Formulae
Prior to substituting the expressions for the known singularity strengths, the discrete Green's formulae (7) and (8) appear as follows:
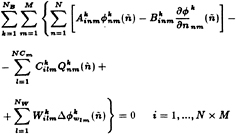
(33)
and
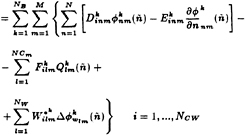
(34)
where ñ is the discrete time step, NB is the number of blades, NW is the number of panels on each strip of the wake, and NCm is the number of cavitating panels on each strip of the wake.
In equations (33) and (34), the indices i and j map quantities to panels. For example, ![]() i(ñ) is the potential at the control point on the ith panel at the ñth time step. However, each panel may also be identified as the nth panel on the mth strip, so
i(ñ) is the potential at the control point on the ith panel at the ñth time step. However, each panel may also be identified as the nth panel on the mth strip, so ![]() i may also be written
i may also be written ![]() nm. In what follows, these indexing alternatives will be used interchangeably to maximize compactness.
nm. In what follows, these indexing alternatives will be used interchangeably to maximize compactness.
![]() and
and ![]() are defined as the potentials induced at the ith control point on the key blade by a unit strength dipole and a unit strength source at the nth panel on the mth strip of the kth blade (k=1 refers to the key blade). When the ith control point lies on the nth panel of the mth strip of the key blade, then
are defined as the potentials induced at the ith control point on the key blade by a unit strength dipole and a unit strength source at the nth panel on the mth strip of the kth blade (k=1 refers to the key blade). When the ith control point lies on the nth panel of the mth strip of the key blade, then
![]() is the potential induced at the ith panel on the key blade due to a unit strength source at the nth panel on the mth strip of the wake of the kth blade.
is the potential induced at the ith panel on the key blade due to a unit strength source at the nth panel on the mth strip of the wake of the kth blade. ![]() is the potential induced at the ith control point on the key blade by a unit strength dipole at the lth panel of the mth strip of the wake of the kth blade.
is the potential induced at the ith control point on the key blade by a unit strength dipole at the lth panel of the mth strip of the wake of the kth blade. ![]() ,
, ![]() ,
, ![]() and
and ![]() are defined similarly, noting that
are defined similarly, noting that
The shape of the surface bounded by the edges of each quadrilateral panel is approximated by a hyperboloidal surface, and the corresponding influence coefficients are determined analytically. The need for hyperboloidal panels was found to be necessary for the convergence and consistency of the steady flow propeller solution, especially when applied to extreme geometries [16, 25, 7]. Discussion of the computation of these influence coefficients may be found in [27] and [8].
Equations (33) and (34) may be regrouped to reflect the fact that at any given time step only the potentials on the key blade are unknown, while the rest are assumed to be known. Equation (33) becomes
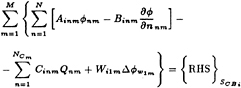
i=1, …, N×M (35)
and (34) becomes
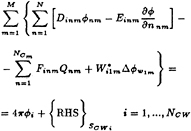
i=1, …, NCW (36)
where

(37)
and
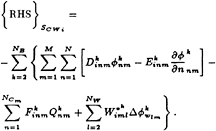
(38)
In (35) and (36) the superscript k=1 is implied. In (37) and (38) the potential ![]() is equal to
is equal to

Figure 9: Index system for discrete equations.
![]() taken from the key blade solution at a previous time step, corresponding to the current location of blade k. The same equivalence is true for the source strengths
taken from the key blade solution at a previous time step, corresponding to the current location of blade k. The same equivalence is true for the source strengths ![]() and
and ![]() and the wake dipole strengths
and the wake dipole strengths ![]() .
.
3.2
Discrete Boundary Conditions
The boundary conditions may now be discretized and incorporated in Green's formulae (35) and (36).
The discrete version of the kinematic boundary condition on the blade (31) is
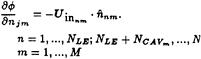
(39)
where ![]() is the inflow velocity at the current time step, defined at the nth control point on the mth spanwise strip of the blade. The system of indexing is shown in Figure 9.
is the inflow velocity at the current time step, defined at the nth control point on the mth spanwise strip of the blade. The system of indexing is shown in Figure 9.
A single discrete equation may be written to replace the dynamic boundary conditions on the blade (15) and in the wake (18)
(40)

Figure 10: Definition of the arclength on a spanwise strip, used in the trapezoidal integration of ![]() .
.
where
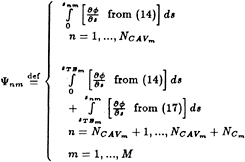
(41)
and sTEM is the value of s at the trailing edge of the blade on the mth spanwise strip, as shown in Figure 10. The integrals in equation (41) are computed by trapezoidal quadrature. The values of the integrands are computed at the control points and at the leading edge of cavity, where s=0. The arclength between two consecutive control points is approximated by the sum of the linear distances between the control points and the panel edges (see Figure 10)
The quantity ![]() 0 in (40) is the perturbation potential at the detachment point of the cavity. It is also an unknown. This term is expressed as a cubic extrapolation in terms of the unknown potentials on the wetted panels on the same strip adjacent to the cavity detachment. The implementation of this term is discussed in detail in [3].
0 in (40) is the perturbation potential at the detachment point of the cavity. It is also an unknown. This term is expressed as a cubic extrapolation in terms of the unknown potentials on the wetted panels on the same strip adjacent to the cavity detachment. The implementation of this term is discussed in detail in [3].
3.3
Cavity Height Computation
Once the problem has been solved for a guessed cavity planform, and ![]() on the cavity panels is
on the cavity panels is
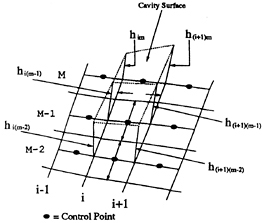
Figure 11: Schematic of h(s,ν,t) computation.
known, the cavity height (h(s,ν,t) on the blade and hw(s,ν,t) in the wake) can be determined by integrating the partial differential equations (21) and (28). This is accomplished by replacing the partial derivatives of h and hw with two-point backwards difference formulae and solving for h and hw recursively. Note that the derivatives are defined at the control points. The finite difference models of the derivatives are as follows (hw may be substituted for h):
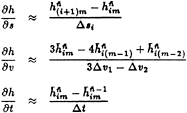
where
Refer to Figure 11 for clarification. Substitution of the finite differences in (21) and (28) yields recursive formulae for ![]() and
and ![]() in terms of previously computed quantities. The height of the cavity at its trailing edge, δ(r,t), will in general be non-zero, unless we have guessed the correct cavity planform. The means by which we arrive at the correct planform will be discussed next.
in terms of previously computed quantities. The height of the cavity at its trailing edge, δ(r,t), will in general be non-zero, unless we have guessed the correct cavity planform. The means by which we arrive at the correct planform will be discussed next.
3.4
The Cavity Planform
As mentioned earlier, the extent (planform) of the unsteady cavity is unknown and must be determined as a part of the solution. The local cavity length (defined as the arclength of the projection of the cavity on the nose-tail helix) is given at each radius r by the function l(r,t). For a given cavitation number, σn, the cavity planform l(r,t) will be determined from the requirement:
(42)
Equation (42) requires that the cavity close at its trailing edge; this requirement will be used as the basis of an iterative solution to find the cavity planform. In discrete form, equation (42) becomes:
δm(l1(t), l2(t), …, lM(t); σn) =0; m=1, …, M (43)
where δm is the openness of the cavity trailing edge at the mth spanwise strip and lm is the value of l(r,t) at the midspan of the same strip. At each time t the vector L=[l1, l2, …, lM]T must be determined by solving the M equations (43). The algorithm to do that is described in detail in [3]. In summary, the planform is determined by solving the system of equations (35) and (36) using an initial guess of L4. For that initial guess, the openness of the cavity at its trailing edge, δm, is determined for all m by integrating equations (21) and (28). If δm≠0, the cavity planform L is updated by applying a Newton-Raphson (secant) scheme on equations (43) and the process is repeated until the δm vanishes for all m, to within a prescribed tolerance.
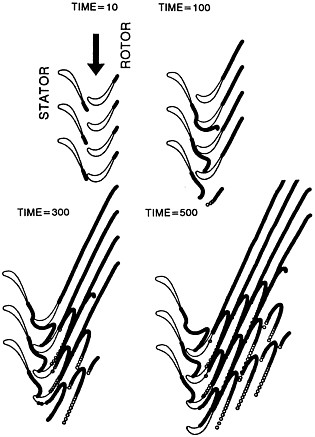
The algorithm is depicted in Figure 12 for the case of a highly pitched propeller (geometry provided in [3]). In this figure, the computed trailing edge cavity heights, δm, are shown for a series of guesses of the cavity planform. The cavity closes at all spanwise strips for only one solution, and this is the correct cavity planform for the given cavitation number and operating conditions.
For arbitrary cavity planforms, one must address the possibility that the cavity trailing edge does not coincide with a panel boundary. Since the singularity distributions span integral panel lengths, a provision must be made for “splitting”

Figure 12: Cavity openness (bottom) corresponding to several cavity planforms (top). Notice that δm=0 for all m for only one of the planforms. The propeller is a heavily pitched (tip unloaded) test propeller whose geometry is given in [3].
a panel into a cavitating part and wetted part5. The so-called “split-panel” method (introduced in [13]) allows cavity planforms to be smooth and independent of the discretization. The price paid for that luxury is the introduction of a small amount of error in the solution. The details of the split-panel method, as well as a discussion of the error it introduces, is provided in [3].
3.5
Time-Marching Scheme
The time marching scheme is identical to that used in the fully wetted solution, and is described in detail in [8]. The main features of the scheme will be outlined here for the sake of completeness.
Time is discretized into equal increments, Δt. During one time step, each propeller blade rotates through an incremental angle Δθ=ωΔt. At each time step, the solution is found for the key blade only, while the singularities on the other blades are assumed to be known. Before proceeding to the next time step, vorticity is shed downstream
|
4 |
A good guess is the final planform L from the previous time step. |
|
5 |
The other option of repanelling the surface to ensure that the cavity ends at a panel boundary is considered too computationally expensive. |
along the assumed wake surface through an angular distance equal to the incremental rotation Δθ. This enforces the equality of the strength of the shed vorticity and the time rate of change of the circulation on the blade. The strength of the circulation is given in terms of the potential jump at the trailing edge of the blade
and the potential jump at the first wake panel is given by
(44)
Thus, the vorticity convection is used to define the wake dipole strengths. Although this an extension of Morino's Kutta condition in steady flow, it is not equivalent to the Kutta condition he applied in unsteady flow [24].
The solution is initiated by the fully wetted steady solution. Next, the fully wetted unsteady solution is obtained, which then serves as the “initial guess” for the unsteady cavity solution. The unsteady cavity solution is turned on when the key blade is at the 6 O'clock position, so that it is likely to start out fully wetted. This was found to be an important time-saving measure in the linear solution by Lee [19]. The singularity strengths on the other blades and their wakes are taken from earlier key blade solutions. During the first revolution of the key blade, the singularities on another blade are taken either from the fully wetted solution or from the cavity solution when the key blade was in the same angular position. For subsequent revolutions, the other blade singularities are taken from previous cavity solutions when the key blade was in the same angular position.
4
Some Results
4.1
Uniqueness of the Solution
For some values of cavitation number, equations (43) may accept more than one solution. For example, it is a well known fact that, in two dimensions, for some cavitation numbers there exist three solutions (corresponding to two partial cavities and one supercavity). Our method has also predicted multiple solutions for three dimensional hydrofoils. For a complete discussion of that result, see [3] or [4]. On the other hand, no multiple solutions have been found for propellers. Figure 13

Figure 13: Investigation of multiple solutions for propellers. No multiple solutions were found for any of the cavitation numbers tried here for this geometry and operating condition. The propeller is an AO-177 operating in steady flow at J=0.6.
shows a series of cavity planforms corresponding to different cavitation numbers. Note that there is a smooth one-to-one correlation between cavitation number and cavity planform for this geometry. Moreover, each predicted planform shown in Figure 13 has been determined using two different initial guesses, one a spanwise uniform short cavity l(r)=0.5 and the other a spanwise uniform long cavity l(r)=1.5. Each resulting planform was the same for the two initial guesses. While this does not necessarily preclude the existence of multiple solutions, it does show that, if they exist, they are difficult to find using this method.
4.2
The Crossflow Terms
It was mentioned in section 2.2 that the crossflow terms ![]() and
and ![]() in the dynamic boundary conditions (15) and (18), respectively, were found to have only a small effect on the solution. This will be shown for three geometries in this section. First, Figure 14 shows the cavity planforms on an elliptic hydrofoil from two consecutive iterations where, in between iterations for the cavity planform, the velocities
in the dynamic boundary conditions (15) and (18), respectively, were found to have only a small effect on the solution. This will be shown for three geometries in this section. First, Figure 14 shows the cavity planforms on an elliptic hydrofoil from two consecutive iterations where, in between iterations for the cavity planform, the velocities ![]() and
and ![]() are updated. The first term is computed by numerically differentiating the potentials using second-order accurate central differences (except for m=1 and m=M, where forward and backward differences are used, respectively). The second term is computed with central differences far downstream in the wake. Since the wake is assumed to be force-free, the crossflow velocity is constant in the stream wise direction for steady flow. Note that the cavity planforms do not change significantly between the two
are updated. The first term is computed by numerically differentiating the potentials using second-order accurate central differences (except for m=1 and m=M, where forward and backward differences are used, respectively). The second term is computed with central differences far downstream in the wake. Since the wake is assumed to be force-free, the crossflow velocity is constant in the stream wise direction for steady flow. Note that the cavity planforms do not change significantly between the two
Table 1: The AO-177 propeller geometry.
iterations. No change was found when an additional iteration was tried. This example shows that the crossflow terms have little effect for supercavitating hydrofoils.
To gauge the importance of the crossflow terms for partially cavitating hydrofoils, a rectangular foil at α=3º is tested for σ=0.5 with and without inclusion of the crossflow terms. The results, shown in Figure 15, indicate that ![]() has a negligible effect on the solution, since the two cavity planforms are nearly indistinguishable.
has a negligible effect on the solution, since the two cavity planforms are nearly indistinguishable.
The third geometry is an AO-177 propeller whose geometry is given in Table 1. Shown in Figure 16 are cavity planforms on the test propeller geometry for consecutive crossflow iterations. From this it is clear that, for the propeller solution, the crossflow term also has a negligible effect on the cavity planform.
4.3
The Hub Effect
The hub geometry may be included in the solution. Hyperboloidal panels are placed on the surface of the hub and Green's formula is satisfied, subject to the kinematic boundary condition. The modelling of the hub has been described by J.T.Lee [20] for the case of fully wetted flows. Figure 17 shows a typical blade and hub discretization. For the cavity solution, the hub is assumed to be fully wetted and the following kinematic boundary condition is applied:
(45)
where SH is the surface of the hub. The discretized Green's formulae (35) and (36) are essentially unchanged, because the hub may be viewed as an extension of the wetted blade surface. The additional equations applied on the hub surface are also
Figure 14: Convergence of the cavity planform with updating of the crossflow terms. Elliptic hydrofoil with maximum thickness-to-chord ratio of 6% at the midspan, tapering elliptically to zero thickness at the tip. α=3° and σ=0.2.
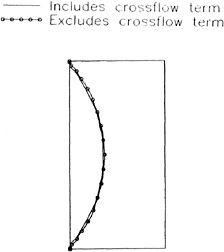
Figure 15: Convergence of the cavity planform with updating of the crossflow terms. Rectangular hydrofoil at α=3º, σ=0.5, ![]()

Figure 16: Convergence of the cavity planform with updating of the crossflow terms for the AO-177 propeller.

Figure 17: Typical blade and hub discretization.

Figure 18: Cavity planform with and without inclusion of the hub for the AO-177 propeller at Js=0.6 and σ=3.5 in steady flow.
similar to (35) and (36) and need not be included here.
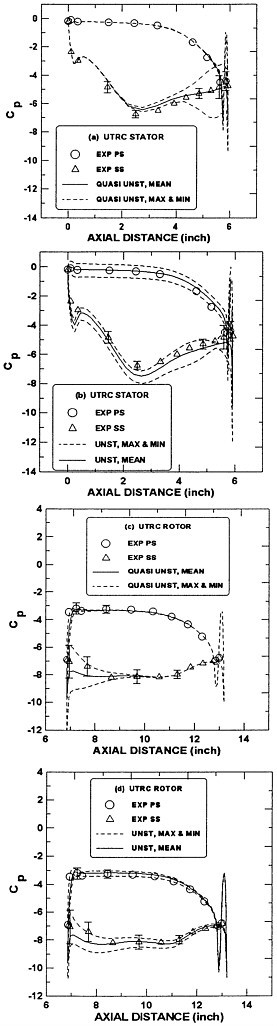
The effect of the hub on the cavity solution is shown in Figure 18 for the AO-177 propeller at Js=0.6 and σn=3.5 in steady flow. Note that the presence of the hub makes the cavity slightly larger at the inner radii because the local increase in circulation.
In the case of a highly twisted propeller, which is lightly loaded at the tip, the hub effects are noticeably larger. Figure 19 shows the cavity solution for a modified N4381 propeller (see [3] for a description of the geometry) in steady flow with and without the hub. Notice that the presence of the hub causes a marked increase in the cavity length at inner radii.
4.4
Comparison to Linear Theory
Figure 20 shows a comparison between the cavity planform computed by the present method (labeled PROPCAV, which is the name of the program) and those computed by linear theory and linear theory with leading edge corrections (labeled PUF-3A [11, 12]). The computations are done for steady flow conditions on the one-bladed AO-177 propeller. Linear theory is seen to overpredict the cavity extent, as it does in 2-D. We see here that the cavity extent is overpredicted by linear theory in both spanwise and chordwise directions. The linear theory with leading edge corrections also overpredicts the extent. A comparison is then made for the same propeller in nonuniform axial wake inflow. In this case, the hydrostatic terms are
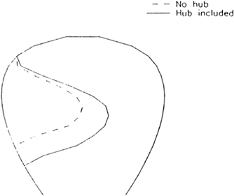
Figure 19: Cavity planform with and without inclusion of the hub for a highly pitched propeller (taken from [3]).
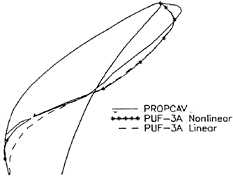
Figure 20: Cavity planforms predicted by PUF-3A (with and without the leading edge correction) and the present method (implemented in the code PROPCAV) on the AO-177 propeller at Js=0.6 and σ=2.7 in uniform flow.
turned on (Fr=n2D/g=4.981). The advance coefficient and the cavitation number are kept the same as in the steady flow case. The cavity volume histories predicted by the three methods are shown in Figure 21.

Figure 21: Cavity volume histories predicted by PUF-3A (with and without the leading edge correction) and the present method on the AO-177 propeller at Js=0.95, Fr=4.981 and σ=2.6 in nonuniform flow (bottom plot). The inflow wake field (top plot) is an axial flow with a 30% wake dent symmetric in θ about θ=0.
5
Conclusions
A potential based boundary element method has been developed for the analysis of unsteady sheet cavitation for propellers of extreme geometry. The method is able to predict, in an efficient and robust manner, arbitrary unsteady cavity planforms on a blade discretization which is fixed in time. An extensive investigation of the solution for varying cavitation number revealed no multiple solutions, such as were found for three dimensional hydrofoils in an earlier work [14]. The method was used to validate the predictions of linear theory (with and without leading edge corrections). It was found that linear theory, with and without the leading edge correction, overpredicts the cavity extent and volume for propellers of extreme geometry. Contrary to this, it was reported in an earlier work that the linear theory with leading edge correc-
tions came reasonably close to the nonlinear result for a more conventional propeller geometry [15].
6
Future Research
As mentioned in section 1, the fundamental assumptions made in order to admit a potential flow solution render the model incomplete. The effects of viscosity, tip and hub vortex cavitation, bubble and cloud cavition, and the cavity trailing edge flow are all unaccounted for in the present model. However, the present model is amenable to inclusion of many of these effects. For instance, the effects of viscosity may be included via an interactive viscous/inviscid boundary layer solution, similar to the one developed by Hufford for fully wetted flows [9]. The boundary layer solution could be used to determine the thickness of the cavity wake so that the openness of the cavity correctly correlates to the sectional drag coefficient. A model for determining the correct detachment point, by correlating the point of laminar separation or turbulent transition to the point of cavity detachment (as suggested by several previous researchers [1, 5]), may also be implemented. A preliminary two-dimensional numerical study of the effects of viscosity on hydrofoil cavitation is underway and shows promising results [29].
A model of the cavitating tip vortex may be added to improve the solution at the tip. This could be accomplished by treating the tip vortex as an inner problem, the solution of which should be matched to the outer solution from the present method. The inner problem could be treated by a boundary element method with a grid which is chosen to fit a vortex with an assumed core radius (possibly determined semi-empirically). In determining the flow at the tip, as well as the trajectory of the tip vortex, methods for the modelling of fully wetted tip flows may be applied. As shown experimentally by Arndt et al [2] the trajectory of the tip vortex does not seem to be sensitive to the value of the cavitation number.
A firm foundation, in the form of an accurate inviscid solution, is required to build our more physical models. The vortex/source lattice method, as implemented in the code PUF-3A, is not a very strong foundation due to the neglect of blade thickness and the crude treatment of the propeller tip geometry. The present method, however, is an accurate inviscid solution and will serve as a good base for implementing the additional models.
7
Acknowledgements
This work was supported by the Applied Hydromechanics Research Program administered by the Office of Naval Research (Contract No. N00014 –90-J-1086).
References
[1] H.Arakeri. Viscous effects on the position of cavitation separation from smooth bodies. Journal of Fluid Mechanics, vol 68(No. 4):pp 779–799, 1975.
[2] R.E.A.Arndt, V.H.Arakeri, and H.Higuchi. Some observations of tip vortex cavitation. Journal of Fluid Mechanics, 229:pp 269–289, 1991.
[3] N.E.Fine. Non-linear Analysis of Cavitating Propellers in Nonuniform Flow. PhD thesis, Department of Ocean Engineering, MIT, 1992.
[4] N.E.Fine and S.A.Kinnas. A Boundary Element Method for the Analysis of the Flow Around 3-D Cavitating Hydrofoils, March 1992. Recommended for publication in Journal of Ship Research.
[5] J.P.Franc and J.M.Michel. Attached cavitation and the boundary layer: Experimental investigation and numerical treatment. Journal of Fluid Mechanics, vol. 154:pp 63–90, 1985.
[6] D.S.Greeley and J.E.Kerwin. Numerical methods for propeller design and analysis in steady flow . Trans. SNAME, vol 90, 1982.
[7] T.Hoshino. Hydrodynamic analysis of propellers in steady flow using a surface panel method. In Proceedings of the Spring Meeting, number 1–6. The Society of Naval Architects of Japan, May 1989.
[8] Ching-Yeh Hsin. Development and Analysis of Panel Method for Propellers in Unsteady Flow. PhD thesis, Department of Ocean Engineering, MIT, September 1990.
[9] G.Hufford. Viscous flow around marine propellers using boundary layer strip theory. Master's thesis, Massachusetts Institute of Technology, May 1992.
[10] J.E.Kerwin, S.A.Kinnas, J-T Lee, and W-Z Shih. A surface panel method for the hydrodynamic analysis of ducted propellers . Trans. SNAME, 95, 1987.
[11] J.E.Kerwin, S.A.Kinnas, M.B.Wilson, and McHugh J. Experimental and analytical techniques for the study of unsteady propeller sheet cavitation. In Proceedings of the Sixteenth Symposium on Naval Hydrodynamics, Berkeley, California, July 1986.
[12] S.A.Kinnas. Leading edge correction to the linear theory of cavitating hydrofoils and propellers. In Int. Symp. on Propeller and Cavitation, Hangzhou, China, September 1992.
[13] S.A.Kinnas and N.E.Fine. A Numerical Nonlinear Analysis of the Flow Around 2-D and 3-D Partially Cavitating Hydrofoils. Journal of Fluid Mechanics. To appear.
[14] S.A.Kinnas and N.E.Fine. Analysis of the flow around supercavitating hydrofoils with midchord and face cavity detachment. Journal of Ship Research, 35(3):pp. 198–209, September 1991.
[15] S.A.Kinnas and N.E.Fine. A nonlinear boundary element method for the analysis of unsteady propeller sheet cavitation. In Proceedings of the Nineteenth Symposium on Naval Hydrodynamics, Seoul, Korea, August 1992.
[16] S.A.Kinnas and C-Y.Hsin. A boundary element method for the analysis of the unsteady flow around extreme propeller geometries. AIAA Journal, March 1992.
[17] S.A.Kinnas, C-Y.Hsin, and D.P.Keenan. A potential based panel method for the unsteady flow around open and ducted propellers. In Proceedings of the Eighteenth Symposium on Naval Hydrodynamics, pages 667– 685, Ann Arbor, Michigan, August 1990.
[18] Sir Horace Lamb. Hydrodynamics. Cambridge University Press, sixth edition, 1932.
[19] Chung-Sup Lee. Prediction of Steady and Unsteady Performance of Marine Propellers with or without Cavitation by Numerical Lifting Surface Theory. PhD thesis, M.I.T., Department of Ocean Engineering, May 1979.
[20] Jin-Tae Lee. A Potential Based Panel Method for the Analysis of Marine Propellers in Steady Flow. PhD thesis, MIT, Department of Ocean Engineering, 1987.
[21] B.Maskew. Prediction of subsonic aerodynamic characteristics: A case for low-order panel methods. Journal of Aircraft, vol 19(no 2):pp 157–163, February 1982.
[22] Jack Moran. An Introduction to Theoretical and Computational Aerodynamics. John Wiley and Sons, 1984.
[23] L.Morino and B.K.Bharadvaj. A unified approach for potential and viscous free-wake analysis of helicopter rotors. Vertica, vol 12(no 1/2), 1988.
[24] L.Morino, Jr. Kaprielian, Z., and S.R.Sipcic. Free wake aerodynamic analysis of helicopter rotors. Technical Report CCAD-TR-83–01, Boston University, MAY 1983.
[25] Luigi Morino and Ching-Chiang Kuo. Subsonic potential aerodynamic for complex configurations : A general theory. AIAA Journal, vol 12(no 2):pp 191–197, February 1974.
[26] J.N.Newman. Marine Hydrodynamics. The MIT Press, Cambridge, Massachusetts, 1977.
[27] J.N.Newman. Distributions of sources and normal dipoles over a quadrilateral panel. Journal of Engineering Mathematics, vol 20:pp 113–126, 1986.
[28] M.P.Tulin. An analysis of unsteady sheet cavitation. In Proceedings of the 19th ATTC Conference, pages 1049–1079, 1980.
[29] R.Villeneuve. The effects of viscosity on hydrofoil cavitation, June 1993.
Numerical Modelling of Propeller Tip Flows
S.A.Kinnas, S.Pyo, C.Y.Hsin, and J.E.Kerwin (Massachusetts Institute of Technology, USA)
Abstract
An improved panel arrangement is introduced for the analysis of flows at the tips of three-dimensional hydrofoils. Only round tip planforms are considered. The proposed grid is normal to the leading edge outline and adapted to the force-free wake geometry at the trailing edge. The location of the tip vortex detachment point is also determined in the process. It is shown that, when an existing boundary element method is applied on the proposed grid, the accuracy of the results improves substantially, not only at the tip but elsewhere on the hydrofoil. In addition, previous differences between results from the boundary element method and a vortex-lattice method (modified to include the thickness/loading coupling) are reconciled when the proposed grid is utilized.
1
INTRODUCTION
Accurate prediction of the flow at the tips of 3-D hydrofoils or propeller blades is essential in determining the characteristics of the tip vortex and its susceptibility to cavitation, as well as in assessing the overall hydrodynamic performance of these devices at off-design and/or cavitating flow conditions.
A Boundary Element Method (BEM) for the analysis of propeller flows (including the presence of the hub and duct) has been developed [ 8],[14]. The method is a low-order BEM based on Green's formula with respect to the perturbation potential. The method was recently extended to include unsteady flow effects [11],[5]. To ensure zero pressure jump across the blade trailing edge an iterative Kutta condition was applied. Recent improvements include: (a) the development of a computationally efficient Newton-Raphson scheme for the application of the iterative pressure Kutta condition, which improved the overall convergence of the method [5], [10], (b) the treatment of highly twisted panels with hyperboloidal rather than planar geometry panels, which improved the convergence of the method for highly skewed propeller blades [5], [6] and, (c) the development of a Blade Orthogonal Grid (BOG), which improved the accuracy of the predicted pressure distributions at the blade tips [6].
A systematic effort to assess the accuracy of this BEM in predicting the flow around lifting surfaces has been carried out. In several applications (such as 3-D rectangular hydrofoils or high aspect ratio propeller blades) the BEM has been found to predict spanwise circulation distributions which are consistent with those predicted from lifting surface theory [5]. This means that the circulation distributions predicted by BEM for lifting surfaces with thickness smoothly (often linearly with thickness) extrapolate to the circulation distribution for the same lifting surface with zero thickness. The zero thickness circulation distribution is predicted by a lifting surface Vortex Lattice Method (VLM), since the BEM formulation becomes degenerate in this case.
For other cases however, especially for lifting surfaces with wide circular tips (similar to those of propeller blades), the circulation distributions predicted by the BEM have been found not to be consistent to those predicted by the VLM [5]. In order to solve this problem our efforts have been concentrated into investigating the results from applying the BEM and the VLM on a circular planform hydrofoil. In this case, it has been found that the BEM predicts a circulation distribution, which is quite different (not only at the tip but elsewhere) before and after the application of the iterative pressure Kutta condition.
In the present work, the primary cause of the problems associated with the application of the BEM on round planform hydrofoils is identified, and a new grid arrangement is proposed which is shown to improve the performance of the BEM appreciably.
2
BOUNDARY ELEMENT METHOD (BEM)
The fundamentals of the BEM are described in [8], [14] and [6]. In brief, the method is based on the classical Green's third identity (applied on the body surface SB):
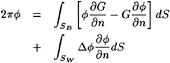
(1)
where the Green's function G is the unit strength source in three dimensions; ![]() is the perturbation potential; SW is the trailing wake surface.
is the perturbation potential; SW is the trailing wake surface.
The BEM implementation involves:
-
Constant strength dipole and source panels.
-
Hyperboloidal panel geometry (critical for highly twisted body geometries).
-
An Iterative Pressure Kutta (IPK) condition which determines the appropriate strength Δ
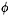 in the wake, in order for the pressure jump across the trailing edge to be equal to zero at all spanwise locations.
in the wake, in order for the pressure jump across the trailing edge to be equal to zero at all spanwise locations.
Two grid arrangements have been used. They are described in the next two sections:
2.1
The conventional grid
The conventional grid has been used traditionally for vortex-lattice applications on 3-D hydrofoils or propeller blades [13], [3]. It has also been called the “constant radii” grid. The panel edges are located along the intersections of the blade with cylinders concentric with the axis of propeller rotation. In the case of three dimensional hydrofoils the panels are arranged along the intersections of the hydrofoil with planes normal to the planform. The conventional grids for a propeller blade and a circular planform hydrofoil are shown in Figures 1 and 2, respectively.
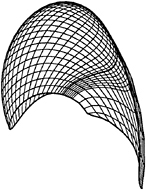
Figure 1: The conventional grid on a propeller blade and its trailing wake.

Figure 2: The conventional grid on a circular planform hydrofoil and its trailing wake.
As stated earlier, the BEM has been validated extensively for several hydrofoil and propeller blade geometries. From these studies it has been found that that the results from applying the BEM for “wide” round tip geometries either do not converge when applying the IPK condition, or do not seem to be consistent with the lifting surface zero thickness results. In order to investigate this peculiar behavior of the BEM we decided to test the simplest round tip propeller at the simplest possible inflow. That is the Circular Planform Hydrofoil (CPH) with zero camber, subject to a uniform inflow, Uo, at an angle of attack α. The maximum thickness to local chord ratio is kept constant along the span. A modified NACA66 thickness form [2] is used at each spanwise location. In order to avoid any ambiguity concerning the shape of the wake it was decided to force the wake to lie on the xy plane1 as shown in Figure 2. At first, it was also decided not to contract the wake. In other words, we assumed that the vorticity vector in the wake was parallel to the x axis2.
The spanwise circulation distribution (symmetric with respect to midspan and thus shown only over half of the span) predicted by the BEM applied for the CPH and for two thickness to chord ratios are shown in Figures 3 and 4. The circulation distribution “before” the IPK condition corresponds to the Morino Kutta condition in which the dipole strength in the wake is taken equal to the difference of the potentials at the panels at the two sides of the trailing edge [15]. This condition has been found to produce pressure distributions which do not match at the trailing edge, especially in the vicinity of the tip, as for example is shown in Figure 5. The circulation distribution “after” the IPK condition, corresponds to the modified wake dipole strength (thus circulation) which ensures pressure equality at the trailing edge. Notice the large difference over the span between the circulation distributions before and after the IPK condition, especially for the 20% thickness to chord ratio CPH, shown in Figure 4. This large difference in circulation has been caused by the relatively small adjustment of the trailing edge pressures in the vicinity of the tip, as shown in Figure 5. Also notice the “peculiar” behavior (sharp change in the slope) of the circulation distribution after the IPK condition, at the tip.

Figure 3: Circulation distribution on a circular planform hydrofoil; ![]() , α=5.73º. Predicted by applying the BEM on the conventional grid; before and after applying the Iterative Pressure Kutta (IPK) condition.
, α=5.73º. Predicted by applying the BEM on the conventional grid; before and after applying the Iterative Pressure Kutta (IPK) condition.
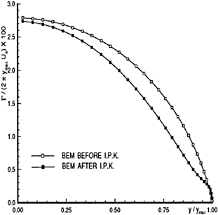
Figure 4: Circulation distribution on a circular planform hydrofoil; ![]() , α=5.73º. Predicted by applying the BEM on the conventional grid; before and after applying the Iterative Pressure Kutta (IPK) condition.
, α=5.73º. Predicted by applying the BEM on the conventional grid; before and after applying the Iterative Pressure Kutta (IPK) condition.
|
1 |
Which, in the case of uncambered hydrofoils, is the same as the bisector plane of the trailing edge angle. |
|
2 |
The validity of this assumption will be examined later in this paper. |
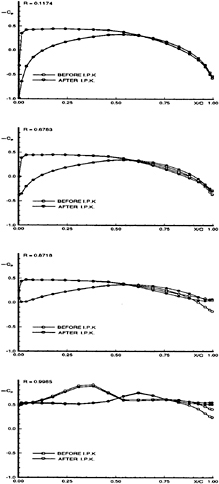
Figure 5: Pressure coefficients predicted from BEM applied on the conventional grid (before and after the IPK condition); circular planform hydrofoil, ![]() , α=5.73º. Cp=
, α=5.73º. Cp= ![]() .
.
Figure 6: The blade orthogonal grid on a circular planform hydrofoil and its trailing wake.
2.2
The blade orthogonal grid
The blade orthogonal grid was introduced in [6]. The grid lines are normal to the blade outline [6], as shown for the CPH in Figure 6. When the BEM was applied on this grid, it was found that the surface pressures at the tips of non-lifting bodies were computed more accurately than when the BEM was applied on the conventional grid [6]. This is the consequence of concentrating more panels at the tip as well as of producing much less distorted panels (of which the sides are of comparable size and almost orthogonal to each other) than the conventional grid. The blade orthogonal grid was also found to improve the convergence of the IPK condition in the case of lifting hydrofoils or propeller blades. This is a direct consequence of the fact that the trailing edge pressures (which drive the IPK condition) at the tips were computed more accurately now than in the case of the conventional grid. The circulation distributions for the CPH are shown in Figure 7. Notice that the difference between the circulation distributions before and after the IPK condition is now larger than that for the conventional grid. An explanation for this will be given in Section 2.3. Also notice that the circulation distribution after the IPK condition is very similar (also “peculiar”) to that in the case of the conventional grid. The results shown in this and the previous section indicate that there must be something fundamentally wrong either with the implementation of the IPK condition and/or with the utilized grids.
2.3
Flow at the trailing edge
In order to understand the behavior of the flow at the trailing edge, the total velocity vectors on both sides of the CPH are shown in Figure 8. The
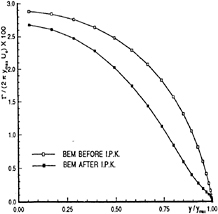
Figure 7: Circulation distribution on a circular planform hydrofoil; ![]() , α=5.73º. Predicted by applying the BEM on the blade orthogonal grid; before and after applying the IPK condition.
, α=5.73º. Predicted by applying the BEM on the blade orthogonal grid; before and after applying the IPK condition.
direction of the vorticity vector in the wake is also shown. Notice that the velocity vectors, V+ and V− at the suction and pressure sides of the trailing edge, respectively, have equal magnitudes as a result of the IPK condition3:
|V+|=|V−| (2)
On the other hand, the direction of the mean velocity vector, Vm=[V+ +V−]/2, is very different from that of the wake vorticity vector γ. This will result in a pressure jump in the wake given by:
Δpw=ρ|Vm×γ| (3)
where ρ is the flow density.
In other words, even though the IPK condition has ensured the equality of pressures at the trailing edge on the blade, it has no way to force the zero pressure jump condition in the wake. Instead, we must align the vorticity vector, i.e. wake geometry, with the mean velocity vector at the trailing edge. Therefore, our earlier assumption of no contraction in the wake must be withdrawn. It would also seem natural for the grid on the blade to be aligned with the mean velocity vector at the trailing edge. A justification for this is given next.
The total potentials Φ+ and Φ− at the suction and pressure sides at the trailing edge, respectively, may be expressed as follows:
(4)
where Φ1 and ΦN are the total potentials at the control points of the trailing edge panels at the suction and pressure sides, respectively; Δs is the distance of the control points from the trailing edge measured along the “chordwise” grid direction on the planform 4, s, as shown in Figure 9; ![]() and
and ![]() are the projections of the total trailing edge velocities V+ and V−, respectively, along s.
are the projections of the total trailing edge velocities V+ and V−, respectively, along s.
The Morino Kutta condition [15] at the trailing edge is:
ΔΦ=Φ+−Φ− (5)
On the other hand, the numerical implementation of equation (5) requires:
ΔΦM=Φ1−ΦN (6)
Thus, the discretization error, E, in implementing the Morino condition (i.e. before the IPK condition), may be expressed, by making use of equations (4), (5) and (6), as follows:
(7)
According to equation (7), in order to minimize the difference between the circulations before and after applying the IPK condition, we should have:
(8)
In light of equation (2), equation (8) is equivalent to requiring that the mean velocity vector Vm is aligned with the grid direction s on the planform. This explains the larger difference between the circulation distributions before and after the IPK condition, in the case of the blade orthogonal grid than in the case of the conventional grid, stated earlier. In the case of the blade orthogonal grid the angle between Vm and the s direction is larger than in the case of the conventional grid.
2.4
The flow adapted grid
Based on the preceeding investigation the grid should have the following characteristics:
-
Be adapted to the resulting flow in the wake.
|
3 |
The IPK condition was found to affect the magnitude of the trailing edge velocities more than their directions |
|
4 |
In gegenal different from the grid direction in the wake. |

Figure 8: Velocity vectors on the suction and pressure sides at the trailing edge of the circular planform; [r/c]max = 0.2, α = 5.73·. Predicted by applying the BEM on the blade onthogonal grid; after the IPK condition. The trailing vorticity vector, γ, is also shown.
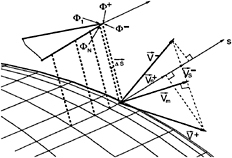
Figure 9: Schematic of the paneling on a 3-D hydrofoil and its wake in the vicinity of the trailing edge.

Figure 10: The effect of thickness sources (or sinks) on the flow field in the wake of a circular planform hydrofoil. The effect of sinks on the wake is stronger than that of sources.
-
Be continuous at the trailing edge (thus also adapted with the wake flow).
-
Be orthogonal at the leading edge (this will result in more accurate pressure predictions at the leading edge).
The proposed grid is called the flow adapted grid. It is defined as follows.
IN THE WAKE:
The total velocity, Vt, in the wake may be decomposed as:
(9)
where ![]() are the induced velocities due to the sources on the hydrofoil surface, the vorticity (or dipoles) on the hydrofoil and, the vorticity in the wake, respectively; Uo is the inflow velocity.
are the induced velocities due to the sources on the hydrofoil surface, the vorticity (or dipoles) on the hydrofoil and, the vorticity in the wake, respectively; Uo is the inflow velocity.
Given that the wake geometry is assumed to lie on the x,y plane, the induced velocity due to the thickness sources will be the predominant contribution in the total wake velocity5. Thus, the total velocity vector in the wake may be approximated as:
(10)
where Uox is the x component of the inflow velocity. ![]() may be expressed as:
may be expressed as:
|
5 |
The vorticity distribution on the hydrofoil and its trailing wake will primarely induce velocities normal to the xy plane. |

Figure 11: Velocity flow field and streamlines around a circular planform hydrofoil; ![]() = 0.2. Only the effect of thickness sources is included. The upper right quadrant of the CPH is only shown.
= 0.2. Only the effect of thickness sources is included. The upper right quadrant of the CPH is only shown.
(11)
![]() is the thickness source distribution, which for planar 3-D hydrofoils is given as follows:
is the thickness source distribution, which for planar 3-D hydrofoils is given as follows:
(12)
where ![]() is the thickness distribution and R is the vector connecting the point in the wake and the source point on the hydrofoil surface.
is the thickness distribution and R is the vector connecting the point in the wake and the source point on the hydrofoil surface.
The integral in equation (11) is determined by discretizing the source distribution into line sources, arranged with a constant spacing in the spanwise direction and a full cosine spacing in the chordwise direction, as described in [3]. In particular, since the thickness sinks at the aft part of the hydrofoil are closer to the wake than the thickness sources at the forward part, it is expected that the combined effect will contract the wake, as shown schematically in Figure 10. The resulting total velocity flow field and the corresponding streamlines 6 for the circular planform hydrofoil with 20% thickness to chord ratio, are shown in Figure 11, where the expected contraction in the wake shape can be clearly seen. The shape of each of the streamlines may be determined by integrating the velocity flow field shown in Figure 11. Instead, we determine the following parameters for each streamline, shown in Figure 12:
-
Its starting point yte, xte at the trailing edge.
-
Its contraction angle, θ, at the trailing edge.
-
Its distance, yult, from the x axis far downstream.
Figure 12: The geometry of wake streamlines.
and then approximate its shape y(x) by the expression:
y(x)=yte−(yte−yult) tanh X (13)
with X defined as
(14)
AT THE TIP:
The outer wake streamline in the case of the conventional and the blade orthogonal grid is parallel to the x axis, starting from the tip of the hydrofoil (defined as the point of maximum y). In the present case the starting point (we also call it the “computational” tip) and the shape of the outer wake streamline are deterined by searching among the streamlines for the one which starts at the largest y location and does not intersect the planform. Due to the contraction of the wake, the computational tip (it may also be seen as the tip vortex detachment point) will be downstream from the actual tip.
ON THE PLANFORM:
Having determined the location of the tip vortex detachment point, Atip, the grid on the planform is determined, by modifying the algorithm on which the blade orthogonal grid was based [6], as follows:
|
6 |
Produced by the graphics program TECPLOT |
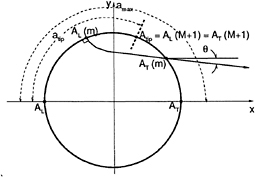
Figure 13: The geometry of grid lines. The location of the “computational” tip, Atip, is taken downstream of the actual tip due to the contraction of the wake.
First, the arcs ALAtip and ATAtip, shown in Figure 13, are divided into M half-cosine intervals, with M being the number of “spanwise” panels. The correspoding arclenghts are given as
ale(m)=atip cosβm
ate(m)=amax−(amax−atip) cosβm
for m=1, 2, …, M
where ale(m), ate(m) are the lengths of the arcs ALAL(m) and ATAT(m), respectively, with βm defined as
(15)
In the case of the blade orthogonal grid, each AL(m) is connected with AT(m) via B-spline curves which are normal to the blade outline. In the present case, the grid lines are still normal to the blade outline at the leading edge, but now they form an angle with the x axis at the trailing edge, which is equal to the corresponding wake contraction angle θ, defined earlier. The arcs of these grid lines are then divided into N/2 full-cosine spaced intervals, with N being the number of “chordwise” panels. The grid on both sides of the 3-D hydrofoil is then determined by moving the grid of the planform normal to the planform and by an amount equal to ![]() .
.
The proposed flow adapted grid for the circular planform hydrofoil with 20% thickness to chord ratio, is shown in Figure 14. The grids for various thickness to chord ratios are shown in Figure 15. Notice that as the thickness reduces, the wake contraction and the distance between the computational and the actual tip also reduce.
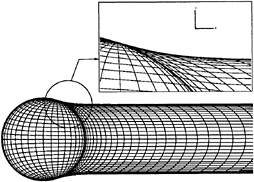
Figure 14: Flow adapted grid on circular planform hydrofoil; ![]() , α=5.73º. The trailing wake is aligned with the inflow, adjusted for the influence of the sources (and sinks) representing the hydrofoil thickness.
, α=5.73º. The trailing wake is aligned with the inflow, adjusted for the influence of the sources (and sinks) representing the hydrofoil thickness.
The circulation distribution predicted from applying the BEM on the flow adapted grid for the CPH are shown in Figure 16. Notice that the circulation distributions before and after applying the IPK condition are closer to each other than they were in the case of the conventional and the blade orthogonal grid. Also notice that the circulation distribution now extends only up to the location of the computational tip and that its values after the IPK condition does not show the previously observed “peculiar” behavior at the tip. The predicted flow at the trailing edge is also shown in Figure 17, where it can be seen that the mean velocity vector is now practically aligned to the trailing wake vorticity vector. Small differences in the directions of the Vm and γ vectors at the trailing edge may be attributed to our restricting the wake on the xy plane. It is anticipated that relaxing the wake and aligning the grid on the planform at the same time, it would further reduce the difference between the circulation distributions before and after the IPK condition. Performing the complete wake relaxation and the corresponding planform grid alignment was outside the scope of the present work.
Figure 15: Flow adapted grids for circular planform hydrofoils with different thickness/chord ratios.
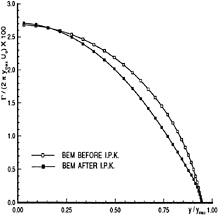
Figure 16: Circulation distribution on a circular planform ![]() = 0.2, α=5.73º hydrofoil; . Predicted by applying the BEM on the flow adapted grid; before and after applying the IPK condition.
= 0.2, α=5.73º hydrofoil; . Predicted by applying the BEM on the flow adapted grid; before and after applying the IPK condition.
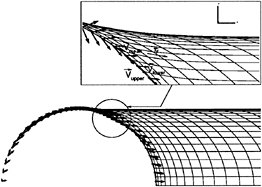
Figure 17: Velocity vectors on the suction and pressure sides at the trailing edge of the circular planform; ![]() = 0.2, α=5.73º. Predicted by applying the BEM on the flow adapted grid; after the IPK condition. The trailing vorticity vector is also shown.
= 0.2, α=5.73º. Predicted by applying the BEM on the flow adapted grid; after the IPK condition. The trailing vorticity vector is also shown.
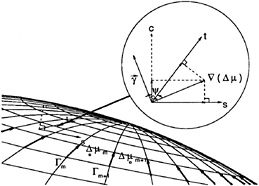
Figure 18: Grid lines in the vortex-lattice method.
3
VORTEX-LATTICE METHOD (VLM)
The fundamentals of the Vortex Lattice Method are described in [13] and [3]. The method models the lifting surface (3-D hydrofoil or propeller blade) with a lattice of line vortices and sources, distributed on the mean camber surface and the trailing wake. This method has recently been modified to account for the coupling between thickness and loading [9]. The modified VLM has been applied on 3-D hydrofoils and propeller blades (by using conventional grids) and has produced results which for most applications are strikingly close to those from applying the BEM method [9], even in the case of highly skewed propeller blades [6]. In the present work we have extended the implementation of the thickness/ loading coupling in the case of general grids, as shown in Figure 18. The method is summarized in the following steps:
-
Solve the zero thickness VLM problem and determine the strengths, Г′s, of the line vortices, by satisfying the kinematic boundary condition at appropriately selected control points on the planform:
Vг · n=−Uon (16)
where Vг is the velocity vector induced by all discrete vortex horseshoes on the planform and its wake; Uon is the component of the inflow normal to the planform, i.e. Uon=Uo · n, with n being the unit normal vector to the planform, pointing towards the positive z axis shown in Figure 2.
-
Evaluate the potential jumps, Δμ's, across the planform, by using the following algorithm:
Δμm=Δμm−1+Гm; m=1, …, M (17)
with Δμ0≡0. Equation (17) is applied along each s grid line. The resulting Δμ's are asigned at the control points of the VLM.
-
Determine the vorticity vector γ on the planform by using the formulas:
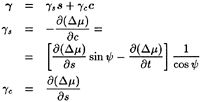
(18)
where s, t are the arclenghts along the two grid directions (in general non-orthogonal); c is the arclength on the planform in directions normal to s; s and c are the unit vectors along s and c respectively; ψ is the angle between the c and t directions; γs and γc are the components of γ along the s and c directions, respectively. Equations (18) are the result of the following equations or definitions:
γ=n×ΔV (19)
ΔV=V+−V− (20)
V+−V−=Δ(▽sμ) (21)
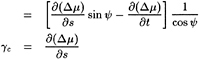
(22)
Δ(▽sμ)=▽s(Δμ) (23)
γ=n×▽s(Δμ) (24)
-
Evaluate the additional normal velocity Vc due to the thickness/loading coupling by using the expression:
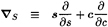
(25)
where
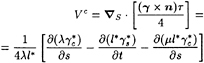
(26)
with xp being the vector expressing the mean camber surface (the xy plane in the case of a planar 3-D hydrofoil) and
 being the hydrofoil thickness distribution. The second part
being the hydrofoil thickness distribution. The second part
-
of equation (25) gives ▽S in terms of functions of the non-orthogonal coordinates s and t, shown in Figure 18. This expression has been derived by applying a similar procedure to that described in Appendix 1 of [9].
-
Modify the kinematic boundary condition of the zero thickness problem by replacing Uon with
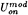 at the RHS of equation (16):
at the RHS of equation (16):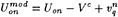
(27)
where
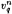 is the induced normal velocity due to the thickness source distribution. For planar 3-D hydrofoils,
is the induced normal velocity due to the thickness source distribution. For planar 3-D hydrofoils, 
-
Solve the VLM problem with the modified kinematic boundary condition to find the new γmod distribution.
The derivatives involved in equations (18) and (25) are evaluated by splining the corresponding functions and then by taking the derivatives of the spline interpolations.
The VLM method has been applied on the circular hydrofoil planform and the results are described in the next section.
4
BEM VS. VLM
Due to the lack of analytic solutions for lifting 3-D hydrofoils with thickness, there is no direct way to validate the accuracy of different numerical methods (VLM's or BEM's) for such applications. To our knowledge, the only analytic solution for 3-D hydrofoils is the one by Jordan [7] for a circular planform hydrofoil with zero thickness. The predicted circulation distribution from applying the VLM on this hydrofoil has been found to agree very well to the analytic solution, even with a 5 by 5 grid [4]. The BEM formulation, however, becomes degenerate for zero thickness, and thus it cannot be applied to this problem. The consistency test, already mentioned in the introduction, is not a direct test, since it requires extrapolations of the results from applying the BEM at a progression of gradually thinning sections.
Instead, in this work, we compare the results from applying the BEM to those from applying the VLM, including the thickness/loading coupling. Such comparisons are shown in Figure 19. Notice the large difference between the circulation distributions in the case of the conventional and the blade orthogonal grid. This is a consequence of the fact that the effect of velocities due to thickness on the Kutta condition, is ignored in the VLM. If this effect is superimposed to the trailing velocity vectors predicted by the VLM, the magnitudes of the velocity vectors and thus pressures at the two sides of the trailing edge will not be equal. Thus, in this case the pressure jump at the trailing edge is non-zero, in addition to being non-zero in the wake (as explained in Section 2.3). However, when applying the VLM on the flow adapted grid, the velocity due to thickness changes the magnitudes of the velocities at the two sides of the trailing edge by the same amount, thus preserving the zero pressure jump across the trailing edge. The good agreement of the circulation distributions predicted from applying the BEM and the VLM on the flow adapted grid, shown at the bottom of Figure 19, is attributed to the fact that both methods satisfy the zero pressure jump condition at the trailing edge on the planform, as well as in the wake.
5
RESULTS
The BEM is applied on three hydrofoils with the following characteristics:
-
Elliptic chord distribution in the spanwise direction.
-
Aspect Ratio AR=3.
-
Modified NACA66 thickness distribution
with 20% maximum thickness to chord ratio (constant in the spanwise direction)
-
Sweep angle varying from −45º (forward sweep) to 0º and 45º.
The circulation distributions predicted from applying the BEM on the conventional and the flow adapted grid are shown in Figure 20. Notice that as the sweep angle decreases the difference between the two circulation distributions increases. This is due to the drastic contraction of the wake geometry, also shown in Figure 20, as the planform is swept forward. The wake contraction is increasing as the planform is swept forward, because the source sinks at the aft part of the planform, shown in Figure 10, have a stronger effect on the wake streamlines at the tip.
Finally, the elliptic planform hydrofoil used in the experiment by Arndt et al. [1] is analyzed by the present method. In particular, the trajectory of the tip vortex is determined, by considering only the effect due to hydrofoil thickness, as descibed in Section 2.4. The spanwise

Figure 19: Circulation distributions predicted from BEM (after the IPK condition) and VLM (including the thickness/ loading coupling) for different grid arrangements. The analytical solution dor zero thickness (Jordan, 73) is also shown. Circular planform hydrofoil, =0.2, α=5.73º. Original grid (top). Orthogonal grid (middle). Proposed grid (bottom).
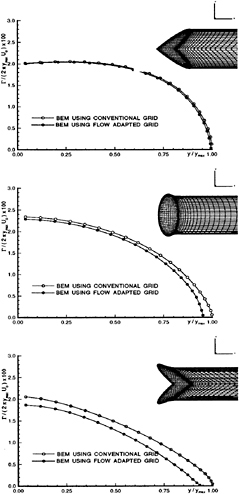
Figure 20: Effect of wake geometry on circulation predicted by BEM for three hydrofoils with elliptic chord distribution along the span;[r/c]max= 0.2, α=5.73º, aspect ratio AR=3. 45º backward sweep (top) no sweep (middle) 45º forward sweep (bottom). The corresponding flow adapted grids are also shown.
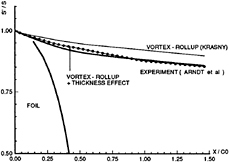
Figure 21: Tip vortex trajectories predicted from analysis and measured in experiment. Elliptic planform hydrofoil; α=15.5º, [r/c]max=0.15, aspect ratio AR=3.
coordinates of this trajectory are then superimposed to those of the tip vortex trajectory predicted by Krasny [12], who only included the effects of the wake sheet rollup. The results are shown, together with the experimental results, in Figure 21. Notice that, under the examined condition, the effects of the wake sheet rollup and that of the hydrofoil thickness on the predicted tip vortex trajectory are equally important, and that when both are included, the trajectory of the tip vortex matches the observed very well. However, in order to validate the prediction methods completely, more comparisons with experiments at several conditions are required. In addition, further computations, which also include the effects of viscosity on the hydrofoil loading, thus on the strength of the wake vortex sheet, must be carried out.
6
CONCLUSIONS
The performance of a boundary element method, when applied for the prediction of flows around lifting surfaces with round tips, has been addressed. Previous grid arrangements have been found to be incompatible with the application of a pressure Kutta condition at the trailing edge. It has been concluded that an improved grid arrangement should have the following characteristics:
-
Be adapted to the mean velocity vector at the trailing edge.
-
Converge to a point at the tip which coincides with the tip vortex detachment point.
When a flow adapted grid was applied on a circular planform hydrofoil, the performance of the boundary element method was found to improve substantially. In addition, the results from applying a vortex-lattice method on the same grid, were found to be in very good agreement to those from the boundary element method. Thus, previous differences between the results from the boundary element and the vortex- lattice method, have been reconciled.
ACKNOWLEDGEMENTS
This research was performed under the MIT Sea Grant Program with support provided by the David Taylor Model Basin.
References
[1] R.E.A.Arndt, V.H.Arakeri, and H.Higuchi. Some observations of tip-vortex cavitation. Journal of Fluid Mechanics, 229:pp. 269– 289, 1991.
[2] T.Brockett. Minimum Pressure Envelopes for Modified NACA-66 Sections with NACA α=0.8 Camber and Buships Type I and Type II Sections. Report 1780, DTNSRDC, Teddington, England, Feb 1966.
[3] D.S.Greeley and J.E.Kerwin. Numerical methods for propeller design and analysis in steady flow . Trans. SNAME, vol 90, 1982.
[4] J.L.Guermond. About collocation methods for marine propeller design. In Proceedings of the Propellers'88 Symposium, pages 1–9 (paper No. 8), Soc. Naval Arch. & Marine Engnrs., Virginia Beach, VA, September 1988.
[5] Ching-Yeh Hsin. Development and Analysis of Panel Method for Propellers in Unsteady Flow. PhD thesis, Department of Ocean Engineering, MIT, September 1990.
[6] C-Y.Hsin, J.E.Kerwin, and S.A.Kinnas. A panel method for the analysis of the flow around highly skewed propellers. In Proceedings of the Propellers/Shafting '91 Symposium, pages 1–13 (paper No. 11), Soc. Naval Arch. & Marine Engnrs., Virginia Beach, VA, September 1991.
[7] Peter F.Jordan. Exact solutions for lifting surfaces. AIAA Journal, 11(8), August 1973.
[8] J.E.Kerwin, S.A.Kinnas, J-T Lee, and W-Z Shih. A surface panel method for the hydrodynamic analysis of ducted propellers . Trans. SNAME, 95, 1987.
[9] S.A.Kinnas. A general theory for the coupling between thickness and loading for wings and propellers. Journal of Ship Research, 36(1):pp. 59–68, March 1992.
[10] S.A.Kinnas and C-Y.Hsin. A boundary element method for the analysis of the unsteady flow around extreme propeller geometries. AIAA Journal, 30(3):688–696, March 1992.
[11] S.A.Kinnas, C-Y.Hsin, and D.P.Keenan. A potential based panel method for the unsteady flow around open and ducted propellers. In Proceedings of the Eighteenth Symposium on Naval Hydrodynamics, pages 667–685, Ann Arbor, Michigan, August 1990.
[12] R.Krasny. Computation of vortex sheet roll-up in the Trefftz plane. Journal of Fluid Mechanics, 184:pp. 123–155, 1987.
[13] C.E.Lan. A quasi vortex-lattice method in thin wing theory. Journal of Aircraft, vol. 11(no. 9), 1974.
[14] Jin-Tae Lee. A Potential Based Panel Method for The Analysis of Marine Propellers in Steady Flow. PhD thesis, M.I.T., Department of Ocean Engineering, August 1987.
[15] Luigi Morino and Ching-Chiang Kuo. Subsonic potential aerodynamic for complex configurations : a general theory. AIAA Journal, vol 12(no 2):pp 191–197, February 1974.
Time-Dependent Inviscid Flow Analysis of Rotor-Stator Systems
Y.T.Lee (David Taylor Model Basin, USA)
J.Feng and C.L.Merkle (The Pennsylvania State University, USA)
ABSTRACT
A time-accurate hybrid panel/Euler computational method for unsteady 2-D/3-D inviscid incompressible flows through a rotor-stator system is presented. The method represents the boundary surfaces by distributing constant-doublet (for 3-D) or piecewise linear-vortex (for 2-D) and constant-source singularities on discrete panels. A local coordinate is assigned to each independently moving object. Blade shed vorticity is convected using the Euler equation. A nonlinear unsteady pressure-type Kutta condition is applied that enforces zero blade trailing-edge loading at each time step. Example problems of the near-encounter between a vortex and an airfoil, as well as unsteady loading on a foil by upstream flapper foils demonstrate the validity of the techniques. Results of rotor-stator calculations indicate that unsteady interactions play an important role in the rotor-stator system. Time-accurate unsteady results are much closer to experimental measurements than are quasi-unsteady approximations that are commonly used.
NOMENCLATURE
|
Cp |
pressure coefficient |
|
c |
chord of the foil |
|
CD |
velocity potential due to doublet |
|
CDL |
velocity potential due to linearly distributed vortex |
|
CDU |
velocity potential due to uniformly distributed vortex |
|
CD1 |
coefficient defined in Eq. (7) |
|
CD2 |
coefficient defined in Eq. (7) |
|
CS |
velocity potential due to uniformly distributed source |
|
D |
scalar matrix defined in Eq. (20) |
|
ds |
differential surface element |
|
dv |
differential volume element |
|
E |
vector matrix defined in Eq. (20) |
|
f |
reduced frequency based on half chord length |
|
G |
Green's function |
|
H |
cascade spacing or pitch |
|
ITS |
total time steps |
|
N |
total number of panels |
|
NS |
total number of surface patches |
|
n |
surface normal |
|
p |
local static pressure |
|
r |
distance vector |
|
S |
panel length |
|
s |
surface tangent |
|
t |
time |
|
T |
period |
|
U |
reference velocity |
|
u |
total velocity |
|
uβ |
surface moving velocity |
|
un |
mean velocity, defined in Eq. (16) |
|
uo |
flow onset velocity |
|
vt |
velocity defined in Eq. (13) |
|
x,y,z |
global ground-fixed coordinate |
|
α |
angle of attack |
|
Г |
circulation around a foil or an isolated vortex |
|
γ |
vortex or doublet strengths |
|
δΩ |
boundary surfaces |
|
κ |
ratio of panel lengths |
|
ξ |
vorticity vector |
|
ρ |
fluid density |
|
σ |
source strength |
|
|
unit vector potential |
|
|
disturbance velocity potential |
|
|
inflow velocity potential |
|
Ω |
flow domain |
|
b |
body or airfoil |
|
e |
exact solution |
|
k |
iteration number |
|
s |
tangent to the surface |
|
u |
upper surface |
|
v |
vortex |
|
W |
wake |
|
ℓ |
lower surface |
INTRODUCTION
Many unconventional marine propulsors, such as counterrotating propellers or propellers with preswirl stators, consist of multiple-blade-row configurations. The flow structure in such geometries is very complex. The wakes shed by upstream blades are nonuniform and time dependent due to the relative motion between the upstream and downstream blade rows. Further, these wakes interact with the downstream blades, generating wake wrapping and wake cutting. Previous studies (1,2) have suggested that such a complex flow is still primarily inviscid and that time-dependent interactions can be properly addressed in an inviscid flow fashion, provided that the vortex shedding and its evolution are handled correctly.
Unsteady potential-flow calculation methods (3,4,5,6) have been developed for propellers and turbomachinery for many years. These methods have demonstrated their capability in many practical design problems. Most of these methods include effects of vortex shedding but do not trace the vorticity field. Instead the shed vorticity is placed on a prescribed path. These approaches are effective in cases where wake vortex effects are small. For large amplitude unsteady motions like marine propeller flows, however, the effect of the blade shed wake becomes important both for the force prediction and also for the other flow induced phenomena. For example, the authors' recent results (7) in predicting blade/vortex interaction noise indicate that correct modelling and tracing of blade shed vorticity is necessary for the accurate prediction of noise generated by acceleration or deceleration of vorticity during blade/vortex and wake/vortex interactions.
In the present paper, a time-accurate hybrid panel/Euler method is developed for inviscid flow through rotor-stator configurations. The unsteady Kutta condition is enforced at the blade trailing edge to account for the neglected viscosity effect. In order to effectively simulate the blade shed vorticity, the vortical wake is modelled using Kelvin's conservation law of vorticity and the appropriate Euler's equation. For developing an efficient calculation scheme and also generating smooth wake vorticity, a vortex splitting and merging procedure is used to reduce vorticity tracing instability due to vortex interactions.
To demonstrate the features of the method, Chow's analytic solution (8) is first presented and compared for a “strong” incoming vortex interacting with a foil. Secondly, MIT's flappers and foil flow simulations (9) are shown by using the multiple-blade-row cascade calculation method. Lastly, a turbine stator-rotor interaction result (10) based on unsteady calculations and quasi-unsteady calculations are presented and compared with measurements.
GOVERNING EQUATIONS
For inviscid incompressible flows past a rotor-stator system, the velocity u at a field point p and time t is given by the integral relation (11),
(1)
The surface integrals are performed on the boundary surface δΩ for surface normal velocity un and surface vorticity ξb. The volume integral is an integration in the flow domain Ω for the shed vorticity ξ, whose motion is governed by the Euler equation,
(2)
The quantity G is the Green function, which is given by −1/4πr for three-dimensional flows and by 1/2π ln (1/r) for two-dimensional flows.
The system given in Eqs. (1) and (2) must satisfy the following boundary condition and auxiliary conditions. On the blade surface, the flow tangency condition beomes
(3)
where ![]() boundary condition is augmented by the Kutta condition, which requires zero pressure loading and permits a tangential slip velocity at the trailing edge.
boundary condition is augmented by the Kutta condition, which requires zero pressure loading and permits a tangential slip velocity at the trailing edge.
pu=pℓat the trailing edge. (4a)
where u and ℓ represent upper and lower surfaces of the blade. For 3-D problems, the two components of the surface vortex ξ are not independent, but their spanwise and tangential derivatives are related by
(4b)
More conveniently, the surface vortex sheet can be replaced by an equivalent doublet sheet which satisfies Eq. (4b) automatically.
For 2-D flows, Eq. (4b) is reduced to a simple restraint of total circulation conservation on the blade surface δΩ and in the wake Ω,
(4c)
The solution of Eqs. (1) and (2) along with the conditions of Eqs. (3) and (4) is accomplished by means of a hybrid panel/Euler solution procedure. This procedure discretizes the blade surfaces into panels. The governing equations then are transformed into a velocity potential form and are enforced at panel control points located at the center of each panel. The boundary condition is implemented by directly substituting un from Eq. (3) into Eq. (1). The calculation of the unsteady force and moment on each moving foil is reduced to an integration using the unsteady Bernoulli equation in a body-fixed coordinate system,
(5)
Here ![]() is the disturbance velocity potential and uo is the onset flow velocity. The panel method then solves for the surface doublet or vortex strengths. The vorticity shed from the trailing edge of the foil is determined by satisfying the Kutta condition to account for the viscosity effect. The induced velocity at each wake vortex location is computed and used to enforce Eq. (2) for vortex convection.
is the disturbance velocity potential and uo is the onset flow velocity. The panel method then solves for the surface doublet or vortex strengths. The vorticity shed from the trailing edge of the foil is determined by satisfying the Kutta condition to account for the viscosity effect. The induced velocity at each wake vortex location is computed and used to enforce Eq. (2) for vortex convection.
NUMERICAL IMPLEMENTATIONS
Surface Singularities
The surface δΩ is discretized into small discrete flat elements (surface panels for 3-D and line segments for 2-D) with the control point located at the centroid. The normal to the surface is approximated by the perpendicular to the flat element. The constant source strength on each element is given by Eq. (3). The strengths of the constant 3-D doublet or the linear 2-D vortex are obtained from solving Eq. (1).
The 2-D velocity potential at an ith element due to a jth element which contains linearly distributed vortices of strength γ(ξ)=(γj+γj+1)/2 +(γj+1−γj)ξ/2Sj, and a constant source σj is given by
(6)
where
(7)
and CDUij and CDLij, given in Ref. (2), represent the velocity potentials due to the uniformly and the linearly distributed vortices. The quantity CSij, which is due to the uniformly distributed source, is given in Ref. (2). The corresponding 3-D velocity potential at an ith element due to a jth constant doublet γj is
(8)
where CDij is the influence coefficient of the doublet.
Equation for Vortex/Doublet Strengths
For a unique solution outside of the surface δΩ described by Eq. (1), the flow inside the surface δΩ can be assumed at rest. If each body/foil surface δΩ is divided into N segments, the quiescent interior flow condition requires
(9)
The no-penetration boundary condition, Eq. (3), is imposed at the control point of each element.
For the two-dimensional case, a set of linear algebraic equations for the bound vortex γi is formed by expanding Eq. (9) as
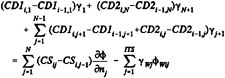
(10)
where ITS represents the total number of time steps. This gives N −1 equations for the N+1 unknown values of γ. Hence two extra equations are required for obtaining a unique solution for 2-D problems. These
conditions are given later.
For 3-D flows the disturbance potential at infinity approaches zero. Consequently Eq. (9) is simplified to ![]() i=0.
i=0.
In this case, the 3-D doublet strengths are obtained from the equations
(11)
Because we use uniform doublets in the 3-D case, Eq. (11) represents a unique system of N equations and N unknowns.
In both the 2-D (Eq. (10)) and the 3-D (Eq. (11)) cases, the vorticity shed at the trailing edge is given by the Kutta condition. This discussion follows.
Kutta Condition
The Kutta-Joukowski condition implicitly accounts for viscous effects otherwise neglected in potential-flow theory. In the present numerical method this is enforced by means of a pressure condition at the trailing edge. Accordingly, the pressures on the upper and the lower surfaces are required to be equal. For 3-D panels, upper and lower surfaces are referred to each specific strip of panels in the chordwise direction. This condition does not restrain the trailing edge from having a variation of pressure in the time domain or spanwise along the trailing edge.
Using the unsteady form of the Bernoulli equation (Eq. (5)), one obtains
(12)
Since the impermeability boundary condition is applied on δΩ, the flow on the upper and lower surfaces is tangent (superscript s) to both surfaces.
For two-dimensional problems, the scalar relations,
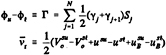
(13)
allow Eq. (12) to be recast into the form,
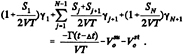
(14)
where ![]() and Г is the circulation of the airfoil defined as positive in a clockwise direction. The total blade circulation Г is linearly dependent on the shedding vortex strength γw as explained in the next section. Equation (14) is nonlinear in γ because VT is not a constant. In the present study, Eq. (14) is solved iteratively to account for this nonlinearity. Both Yao et al. (12) and Kim and Mook (13) ignored this nonlinearity and applied a more restricted Kutta condition at the trailing edge by requiring γ1=γN+1=0 and placing a wake vortex of unknown strength there. As shown later, the nonlinear approach gives improved solutions.
and Г is the circulation of the airfoil defined as positive in a clockwise direction. The total blade circulation Г is linearly dependent on the shedding vortex strength γw as explained in the next section. Equation (14) is nonlinear in γ because VT is not a constant. In the present study, Eq. (14) is solved iteratively to account for this nonlinearity. Both Yao et al. (12) and Kim and Mook (13) ignored this nonlinearity and applied a more restricted Kutta condition at the trailing edge by requiring γ1=γN+1=0 and placing a wake vortex of unknown strength there. As shown later, the nonlinear approach gives improved solutions.
For the present 2-D system, Eq. (14) provides one of the two additional equations needed for solving Eq. (10). A second additional equation is needed to obtain a unique γ-distribution for a lifting body. This condition is provided by requiring the tangential velocity gradients along the trailing edge on both the upper and lower surfaces to be identical,
(15)
Requiring the equality of velocity gradients on both surfaces further ensures the smooth merger of the two flows. When second-order backward differencing is used, Eq. (15) is transformed to
(16)
where κu=SN−1/SN, κℓ=S2/S1 and κ=SN−1(1+κu)/S2(1+κℓ). Hence Eqs. (10), (14) and (16) form a determinate system of nonlinear equations for determining γ for a 2-D lifting configuration. They are solved using an iterative scheme.
For 3-D flows Eq. (12) has to be enforced at every panel along the blade trailing edge in the spanwise direction. Consequently, the analog of Eq. (14) for 2-D flow becomes a set of nonlinear matrix equations in 3-D flows. This system again requires iterative numerical procedures. For the 3-D case, Eq. (12) becomes
(17)
The perturbed form of Eq. (17) can be cast as
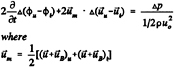
(18)
is the mean velocity at the blade trailing edge, and Δp =pu−pℓ, is the pressure difference between the upper and lower surfaces. In order to drive Δp to zero we adjust the shed vortex strength. This provides a mechanism for vortex shedding in 3-D calculations.
Calculation of Shed Vorticity
Kelvin's theorem states that the total circulation of the fluid at any instant is conserved. This condition provides a mechanism for shedding vorticity into the wake. For 2-D calculations a uniformly distributed vortex segment with strength γw is generated at each time step in the wake adjacent to the foil trailing edge. The length Sw of the vortex segment is set equal to the distance the trailing edge moves between t-Δt and t. At a subsequent time step this uniform line vortex is replaced by a discrete concentrated vortex of equivalent strength located at the center of the segment. The generated trailing-edge vortex segment is related to the total foil circulation, Г, as
(19)
The model depicted in Eq. (19) yields numerically stable solutions that are insensitive to the time-step used. When the nonlinear pressure condition is selected for solving Eq. (14), representative calculations based upon the concentrated vortex model used by Kim and Mook (13) for modeling the trailing-edge vorticity generation were found to be dependent on the time step used
Following the shedding process at the trailing edge, the wake vortices are convected downstream and develop a vorticity field. In the 2-D form of the present numerical scheme, these vortices are tracked through the flow field using Lagrangian techniques. The convection of these discrete vortices is modeled by a predictor-corrector scheme, given in Ref. (2).
The shed vorticity distribution in 3-D flows is obtained by solving Eq. (18) iteratively by relating the nonzero Δp to Δγw by
(20)
where D and ![]() are both matrices representing the disturbed velocity potential and induced velocity due to ΔγW of unit strength. These matrices are only dependent on the blade geometries and are required to be calculated only once. Thus Eq. (18) becomes
are both matrices representing the disturbed velocity potential and induced velocity due to ΔγW of unit strength. These matrices are only dependent on the blade geometries and are required to be calculated only once. Thus Eq. (18) becomes
(21)
The sub-iteration formula at each time step to update shed vorticity strength is then given by
(22)
Vortex Core Splitting and Merging
As Eq. (19) indicates, a vortex is generated at each time step. This mechanism of generating wake shed vorticity will produce tracing instability when the wake vortices start interacting with one another (14). A remedy for redistributing and splitting the vortex cores was proposed by Mook et. al. (14). In addition to the predictor-corrector tracing method mentioned above, the present vortex convection scheme also adopts Mook's splitting and merging techniques. When any pair of vortices is within 1/4 u o Δt, a merging process takes place to reduce the number of vortices. On the other hand, when the distance between two vortices becomes larger than 1.5 uo Δt, a linear splitting process is used. The total circulation around the entire wake and airfoil is, however, maintained exactly. This vortex core splitting procedure maintains reasonably uniform spacing between vortices.
Cascade Formulation
For a 2-D cascade of blades with pitch H, each blade generates circulation. If the cascade runs along the y-axis, there exists an upwash far upstream of the cascade and a downwash far downstream. In conjunction with a specified inflow onset condition, an extra term is needed to ensure a unique upstream inflow condition, i.e.
(23)
for a multi-blade-row cascade flow, where MJ is the total number of blade rows, Hmj is the mj-th cascade spacing or pitch, and Гmj is the blade circulation from the mj-th cascade.
A complete integration of the velocity potentials for the source and the vortex distributions on each segment was performed numerically for the cascade modification. The detailed formulation as well as the modification in Green function for a cascade can be found in Ref. (2).
Gauss-Seidel Solution Procedure
For a 2-D problem, the governing matrix equations are usually small in size, even for multi-row cascade and therefore a direct solver can be used to solve Eq. (10) efficiently. For a 3-D problem, however, the size of the matrix equations is at least an order of magnitude larger than that of the 2-D ones and often reaches a few thousands or more. Consequently, direct matrix solvers are too expensive to execute for matrix equations of this scope.
In the present paper a two-level multi-block Gauss Seidel procedure is developed for obtaining solutions of 3-D problems, First, the left-hand side of Eq. (11) is partitioned on the basis of the larger surface patches such as those on the blade and hub. Thus Eq. (11) becomes
(24)
where NPS(ℓ) and NPE(ℓ) are the starting and ending panel numbers on surface patch ℓ, RHS is the right-hand-side terms of Eq. (11), NS is the total number of surface patches, and ![]() is the latest value of γj. On the ℓf-th surface patch, γj(k+1) is updated by
is the latest value of γj. On the ℓf-th surface patch, γj(k+1) is updated by
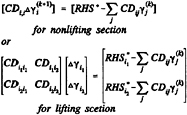
(25)
where RHS*denotes the right-hand-side terms of Eq. (24), and i1 and i2 are indices of the two trailing-edge panels on the same strip of the blade. The advantage of Eq. (25) is that it retains the dominant terms in the left-hand-side matrix of Eqs. (24).
RESULTS AND DISCUSSIONS
The unsteady rotor-stator interaction includes both potential-flow and wake effects. The validation of the current calculation method for a complex rotor-stator system therefore involves two validations of fundamental flow phenomena. The first of these is to demonstrate that the shed vortices from a foil (or cascade) are accurately computed. The second is to demonstrate that the interaction between a vortex and a foil is properly computed. Both of these fundamental phenomena have been demonstrated in Ref. (7).
The capability for accurately modelling shed vorticity was demonstrated by comparing the predicted wake behind an oscillating airfoil with experimental measurements (15). Although the present inviscid approach can not predict the viscous (velocity defect) wake at low blade oscillation frequency, it predicts well the jet-like wake for high frequency oscillation. The vortex and blade interaction process was also demonstrated in Ref. (7) by the computation of the interaction between a free traveling vortex encountering a stationary airfoil (11). The results indicate that the current method is able to accurately predict the interaction forces acting on the foil due to a passing vortex.
A third phenomenon that occurs in rotor-stator interactions is wake vortex cutting. An Example of this was given by Chow and Huang ( 8) who presented an analytical solution based on conformal mapping for a close encounter between a Joukowski airfoil and a moving vortex. The flow phenomenon described by Chow assumes that a “neutral release ” position exists for the incoming vortex which divides the vortex trajectories into those either above or below the airfoil.
Figure 1. Predicted instability of a vortex interacting with a Joukowski foil
Representative calculations for vortices on either side of the neutral release point are presented in Figs. 1 and 2 along with corresponding solutions from Chow and Huang. Figure 1 compares the trajectories of the free vortex at representative time steps for both methods. Because Chow's analytical solution extends only a chord length downstream of the airfoil, the comparison is limited to this region. For perspective we also present a snapshot of the wake vortices at the last time step of our calculation. The curved trajectories wrapping around the airfoil and the large amplitude wake roll-up indicate a very strong interaction between the vortex and the airfoil and thus provide a more critical validation for the present calculation scheme than that in Ref. (7). The corresponding force comparisons for these calculations are given in Fig. 2. When the free vortex travels above the foil, it is first absorbed by the foil as the foil's lift increases. After the vortex passes the trailing edge, the foil repels the vortex and its lift is also dropped. The lift on the foil is eventually leveled off as the vortex travels far downstream. Similarly, when the vortex starts from a location above the foil and travels to the lower side of the foil 's surface, it is again absorbed by the foil. As the vortex gets too close to the foil surface, the surface vorticity of the foil starts repelling the free vortex. At this moment, the lift of the foil drops suddenly and the vortex is repelled backward and starts moving towards lower side of the foil. On the foil's lower side, the trajectory of the vortex is much closer to the foil surface than that on the upper-side motion. During this period, the lift of the foil increases as the vortex moves towards the trailing edge. When the vortex is in the vicinity of the trailing edge, it starts interacting with the shed wake vorticity originating from the foil trailing edge. The spike in the predicted lift distribution near the trailing edge is related to the this strong interaction and depends also upon the Kutta condition used. Nevertheless, the present predicted lift distributions compare favorably with Chow's solutions.
Figure 2. Comparisons of present predicted force on the Joukowski foil with Chow's solutions
An additional demonstration of the effectiveness of the present method, and one that is much more similar to a rotor-stator interaction, is the flapper and foil experiment recently carried out at MIT ( 9,18). In this experiment detailed measurements of the unsteady flowfield around a foil were measured using the setup shown in Fig. 3. In this experiment two small NACA 0025 flapping foils of 3-inch chord were configured
upstream of a larger stationary foil, referred to as the “foil” in the later text, of 18-inch chord. The flappers performed synchronized sinusoidal motions of 6-degree amplitude at a reduced frequency of 3.62. The flappers generate periodic wake fluctuations which impose an unsteady condition on the foil. Velocity and pressure measurements at a Reynolds number of 3.78×106 were taken on the foil and around the foil in a rectangular box downstream of the flappers and enclosing the foil, as shown by the dash line in the Fig. 3. The box measurements were intended to provide upstream and downstream boundary conditions for Navier-Stokes computations. Unsteady flow separation was observed on the suction side near the trailing edge of the foil.
Figure 3. Schematic of MIT Flapping Foil experiment
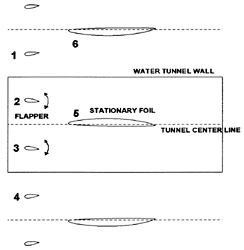
Figure 4. Six-row computational cascade for simulating MIT's flapper and foil experiment
To simulate this flow configuration, a series of image blades were added to the geometry shown in Fig. 3 to incorporate the effects of the tunnel walls. Because of the asymmetry of the foil, the complete system of flappers, foil and image blades is a six-blade-row cascade system as shown in Fig. 4. Since a thick boundary layer exists in the aft region of the foil, a displacement thickness obtained from boundary-layer calculations based on steady solutions to the six row cascade system was added to the foil surface. Computed steady foil surface pressures with and without the displaced thickness correction are shown in Fig. 5. Comparisons of steady pressure distributions for calculations with and without the flappers and its image cascades are nearly the same.
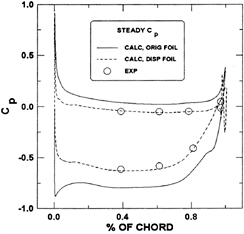
Figure 5. Predicted steady-state pressure distributions on MIT's foil
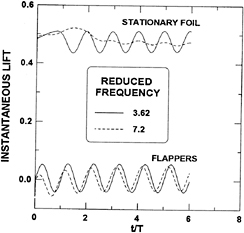
Figure 6. Predicted unsteady lifts on MIT's foil and flappers
The unsteady calculations were started at t=0 from the steady solution. Figure 6 shows the instantaneous lift distributions of the flappers and the foil plotted against nondimensional time at reduced frequencies of 3.62 and 7.2. The foil transient lasts about one period and the calculation extends for six periods with 50 time steps in each period. The corresponding time-averaged mean pressure distributions from the unsteady calculation (reduced frequency of 3.62) are shown in Fig. 7 along with the envelopes of the unsteady solution. These are compared with the measured means and measured local maxima and minima, indicated by I-bars. The calculated mean unsteady pressure agrees well with the measurements. Since the present calculation uses an open trailing-edge for the displaced foil, fluctuations in the predicted pressure distributions exist near the trailing edge, as seen in Fig. 7. Figures 8 and 9 present comparisons of the time history, amplitude and phase angle of Cp at several locations on the stationary foil. Overall, these comparisons in Fig. 8 show the unsteady effects are quantitatively reasonable, but the amplitude are significantly larger than the experimental results. Near the trailing edge the overprediction becomes worse. This is likely due to the aforementioned pressure fluctuation introduced by the open trailing edge (see comparison at x/c=0.972 on Fig. 8).
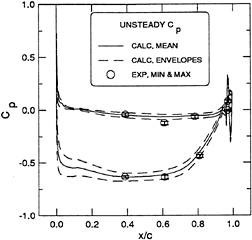
Figure 7. Predicted time-averaged unsteady pressure distributions and unsteady pressure envelopes on MIT's foil
This overprediction is further demonstrated in Fig. 9 by the amplitude of the first harmonic of the pressure distribution around the airfoil. Again the computed amplitude on the suction side (SS) are much larger than the experimental measurements. Close inspection of the measured time history on Fig. 8, however, shows that the experimental variation of the pressure is predominantly a double frequency variation that is twice the reported flapper frequency. For this reason, the calculation was repeated at the double frequency (7.2 reduced frequency) for the flappers. The history of this lift was previously shown in Fig. 6. As this figure shows the amplitude of the fluctuating lift on both flappers is about the same for both high and low frequencies, but that for the stationary foil the amplitude is reduced considerably at the higher frequency. This phenomenon is also evident in the time history and the fundamental harmonic (7.2 reduced frequency) of the pressure distribution (Figs. 8 and 9). Both figures show the predictions of unsteady pressures and its amplitudes. These results show that predictions at high frequency agree surprisingly well with measured values. This suggests a possible discrepancy in the measured frequency of the flapper motion. Corresponding comparisons of the phase distribution of the pressure fluctuation around the foil are also given in Fig. 9 for both reduced frequencies. The predictions show little effect of frequency on the suction side, whereas on the pressure side the predictions show a strong phase lead near the leading edge at the lower frequency. As usual in such comparisons, the phase angle predictions do not compare as well with experiments. This phase comparison thus provides no illumination of the above dilemma.
Figures 10 through 11 show predictions of the rotor-stator interaction for the UTRC single stage, low speed turbine (10). The turbine consists of a 22-blade stator with pitch H=0.854c and a 28-blade rotor with pitch H=0.813c. Both the stator and the rotor have round trailing edges. The gap between the two blade rows is 15% of the stator chord. The rotor operates at a reduced passing frequency of 2.8, based on the turbine diameter.
To reduce the computation effort the 22 stator blades versus 28 rotor blades were simulated at the blade number ratio of 21 stator blades versus 28 rotor blades. This enables us to use three representative stator blades and four rotor blades. Trajectories of the shed vorticity patterns at four different time steps during the start-up period of the stator-rotor interaction, are shown in Fig. 10. As the wakes develop from the rest condition they initially follow a straight line behind the trailing edges of both the stator
and the rotor (t=10). At later times the stator wake begins to roll up as it enters the moving rotor (t=100). This roll-up of the stator wakes continues, and as they are cut by the rotor they begin to approach a periodic state (t=300 and t=500). Throughout, the wakes from the rotor remain essentially straight.
The time-averaged pressure distribution from one period of the later stages of the calculation in Fig. 10 are given in Fig. 11 along with the mean experimental measurements for both the stator (Fig. 11b) and the rotor (Fig. 11d). For reference we also show passage-averaged pressure distributions from quasi-unsteady stator-rotor calculations (Figs. 11a and 11c). These quasi-unsteady calculations were performed as a series of steady state calculations with various relative positions for the rotor-stator blades. Wake vortex shedding was neglected.
The averaged pressure distributions from both the quasi-unsteady calculation and the fully unsteady calculations are in good agreement with experimental measurements. It suggests that for preliminary estimates, especially at an initial stage of design when a large number of comparison studies are needed in a short time period, quasi-unsteady computations should be appropriate for providing reasonable performance predictions. The envelopes of the maxima and minima for both the unsteady and the quasi-unsteady calculations are shown in Fig. 11 along with the corresponding experimental measurements. This comparison clearly shows that the fully unsteady computation which includes vortex shedding and a convection effect has a distinctive advantage over the quasi-unsteady result. First the time-dependent loading is spread evenly over most of the blade. This even spreading of the unsteady loading over the entire blade surfaces is confirmed by the experimental measurements. The quasi-unsteady calculations predict the maxima and minima, variations are restricted to locations near the trailing edge of the stator and the leading edge of the rotor, and the magnitudes of the fluctuations in these regions are very large, far exceeding the experimental measurements. The primary reason for this even spreading of the pressure fluctuations in the true unsteady calculation is the presence of the wake vortex field. The wake vortices are continuously cut by blades as they are convected downstream through the rotor passages. These rolled up vortices have a significant impact on the unsteady pressure distribution on both the rotor and the stator. Clearly, the computational structure of the wake rollup (see Fig. 10) would be impossible to describe in advance.
CONCLUSIONS
A time-accurate hybrid panel/Euler prediction method is presented for unsteady incompressible flows through a rotor-stator system. By tracing wake vorticity, this method is capable of predicting complex flow features such as wake cutting and wake wrapping in rotor-stator systems.
The time-averaged blade pressure distribution predicted by the present approach is in good agreement with experimental measurements. Current results also suggest that for rotor-stator systems quasi-unsteady approaches are appropriate for time-mean performance predictions.
For time-dependent solutions of multiple-blade-row cascade flows, results obtained from the present fully unsteady approach compare well with experimental measurements. Details of the flowfield, such as wake vortex shedding, wake-wrapping and wake-cutting, are simulated for rotor-stator systems from the flow transient to the fully developed periodic stage. For rotor-stator systems quasi-unsteady approaches overpredict the unsteady loading in the strong interacting area of the blade and considerably underpredict in the weak interacting area. By including the complex vortex convection in the flowfield, the present method predicts a much more evenly distributed unsteady pressure as the measurement indicates.
Calculations on the MIT's flapping foil simulation have suggested that the multiple blade row cascade calculation method has correctly modelled the unsteady water-tunnel flow. The unsteady lift on the flappers is independent of its vibrating frequency, but the amplitude (the mean is the same) of the lift on the stationary foil reduces as the flappers move faster. The predictions based on the higher frequency flapper motion, however, agrees better with the measurements in local pressure distributions.
Our results also suggest that the multi-row blade interactions in many rotor-stator systems are inviscid in nature and can be analyzed with more efficient and inexpensive approaches, such as the present method.
The present time-accurate approach can be applied to other unsteady flow problems such as blade passage noise predictions and unsteady cavity flow predictions in rotor-stator systems.
ACKNOWLEDGEMENTS
This work was supported by the Independent Research Program and also by the Submarine Block Program for Hydrodynamics and Hydroacoustics of Internal Flow administrated at the David Taylor Model
Basin. Partial computational results were obtained using the facilities sponsored by the NASA Ames Numerical Aerodynamic Simulation Program.
REFERENCES
1. Giles, M.B., “Calculation of Unsteady Wake/Rotor Interaction,” AIAA J. of Propulsion and Power, Vol. 4, No. 4, 1988, pp. 356–362.
2. Lee, Y.T., Bein, T.W., Feng, J., and Merkle, C.L., “Unsteady Rotor Dynamics in Cascade,” ASME J. of Turbomachinery, Vol. 115, 1993, pp. 85–93.
3. Kerwin, J.E., and Lee, C.S., “Prediction of Steady and Unsteady Marine Propeller Performance by Numerical Lifting-Surface Theory,” SNAME Transactions, Vol. 86, 1978, pp. 218–253.
4. Preuss, R.D., Suciu, E.M., and Morino, L., “Unsteady Potential Aerodynamics of Rotors with Applications to Horizontal-Axis Windmills,” AIAA Journal, Vol. 18, No. 4, 1980, pp. 385–393.
5. Idris, B.M., Maruo, H., and Ikehata, M., “Theoretical Analysis of Unsteady Characteristics of Marine Propeller in Ship's Wake,” J. of the Society of Naval Architects of Japan, Vol. 156, 1984, pp. 60–68.
6. Shoji, H., and Ohashi, H., “Lateral Fluid Forces on Whirling Centrifugal Impeller (1st Report: Theory,” Transactions of the ASME, Vol. 109, 1987, pp. 94–109.
7. Lee, Y.T., Feng, J., and Merkle, C.L., “Prediction of Vortex and Linear Cascade Interaction Noise,” ASME Paper 93-GT-314, 1993.
8. Chow, C.Y., and Huang, M.K., “Unsteady Flows About a Joukowski Airfoil in the Presence of Moving Vortices,” AIAA Paper No. 83–0129, 1983.
9. Kerwin, J., Keenan, D., Mazel, C., Horwich, E., and Knapp, M., “MIT/ONR Flapping Foil Experiment: Unsteady Phase,” MIT/ONR FFX Workshop, David Taylor Model Basin, March 1993.
10. Dring, R.P., Joslyn, H.D., Hardin, L.W., and Wagner, J.H., “Turbine Rotor-Stator Interaction,” ASME J. of Engineering for Power, Vol. 104, 1982, pp. 729–742.
11. Lee, D.J., and Smith, C.A., “Distortion of the Vortex Core During Blade/Vortex Interaction,” AIAA Paper 87–1243, 1987.
12. Yao, Z.X., Garcia-Fogeda, P., Liu, D.D., and Shen, G., “Vortex/Wake Flow Studies For Airfoils in Unsteady Motions,” AIAA Paper 89–2225, 1989.
13. Kim, M.J., and Mook, D.T., “Application of Continuous Vorticity Panels to General Unsteady Incompressible Two-Dimensional Lifting Flows,” J. of Aircraft, Vol.23, No.6, 1986, pp. 464–471.
14. Mook, D.T., Roy, S., Choksi, G., and Dong, B., “Numerical Simulation of the Unsteady Wake Behind an Airfoil,” J. of Aircraft, Vol. 26, No. 6, 1989, pp. 509–514.
15. Koochesfahani, M.M., “Vortical Patterns in the Wake of an Oscillating Airfoil,” AIAA J., Vol. 27, No. 9, 1989, pp. 1200–1205.
16. Fuhs, D., “Comparisons of Calculations and Measurements,” MIT/ONR Flapping Foil Workshop, Washington D.C., March 29–30, 1993.
DISCUSSION
by Dr. S.Kinnas, MIT
The authors presented an interesting application of inviscid flow methods for practical design. It would be very interesting also if they show convergence tests of the involved methods, in particular, with number of panels and time step size for different values of reduced frequency of the incoming gust.
Author's Reply
The numerical convergence for steady flow calculations has been reported in reference (2) of the main text. Numerical errors, defined as the root-mean-square values of the differences between the calculated Cp and the exact Cp distributions, were presented based on different panel numbers for both circular cylinder and NACA 0010 airfoil. It was concluded that the present approach generates results with an accuracy better than the second order methods and the panel number in the order of 100 for airfoil geometries is adequate to drive the error down to 10 −5.
For unsteady flows, the panel size is also governed by two other factors. First, the size of the panels near the foil trailing edge should not be larger than the distance between two successive vortices shed from the trailing edge.
That is
Δs=Δt•Uo (A1)
where Δt=2π/ωnt and nt is the number of time steps in one period. And Eq. (A1), in terms of reduced frequency f=ωc/2uo, becomes
(A2)
Second, when downstream foils cutting through a vortical wake shed from upstream foils, the size of the panels adjacent to the wake vortices is limited to the distance traveled by the vortices in one time step during the close encounter between the vortex and the foil. This condition requires a similar constrain as shown in Eq. (A2) for panels in the front one-third of the foil.
For a typical calculation with a reduced frequency of 10, a normalized unity chord length and freestream velocity, and 25 time steps in one calculation period, c/Δs is about 80. On the average, we use 25 to 50 time steps and 160 to 300 panels to represent periodic foil motion in unsteady flows.