The Simulation of Ship Motions
H.B.Bingham, F.T.Korsmeyer, J.N.Newman, and G.E.Osborne
(Massachusetts Institute of Technology, USA)
Abstract
A three-dimensional panel method is used to solve the linearized ship motions problem for a ship traveling with steady forward speed through quasi-random incident waves. The exact initialboundary-value problem is linearized about a uniform flow, and recast as an integral equation using the transient free-surface Green function. This integral equation is discretized in space by using planar panels, on which the potential is assumed to be constant, and in time by using the trapezoid rule. Collocation is performed at the centroids of each panel.
A technique for approximating the asymptotics of the solution is presented and used to reduce the required length of the computations. Results are shown for a Wigley hull, with and without a steady forward speed. The calculated hydrodynamic coefficients are compared to experiments, as well as to the calculations of two frequency-domain solutions, and a simulation is performed of the ship traveling through a Pierson-Moskowitz sea.
1
Introduction
Since the time when Haskind [6] and Cummins [3] put the superposition principle for transient ship motions on a solid foundation, much work has been focused on calculating the requisite impulseresponse functions, or the analogous frequency-response functions. The linearized theory (elegantly reviewed by Ogilvie [22]), has been implemented for practical ship motions calculations, originally using strip theory methods, and more recently by way of three-dimensional panel methods. For solving problems involving a steady forward speed, the most promising panel methods fall into two categories: solutions using the transient free-surface Green function, where only the ship surface is discretized; and Rankine methods, where singularities are distributed on both the hull and a portion of the free-surface. The present work falls into the first category. Frequency-domain results using Rankine methods have been presented in the last few years, (e.g.: [2]; [20]) and Nakos et al. [19] have recently extended their Rankine, frequency-domain method to the time domain. Solutions using the transient free-surface Green function have been reported by several investigators (e.g.: [9]; [10]; and [14]). More recently the body-exact formulation (where the body boundary condition is applied on the exact instantaneous position of the hull, while the free-surface condition remains linearized) has been used to extend the technique to large amplitude body motions (e.g.: [1]; [16]; [17]).
We have developed a computer code for the transient hydrodynamic analysis of ships and other bodies. The material in this paper is based on our experience in developing and using this code which is called TiMIT (Time domain MIT). We discuss theoretical and practical issues which are germane to the robust and efficient calculation of impulse-response functions, and their subsequent use in performing a simulation of a ship traveling in a seaway. In Sections 2 and 3, we review the linearized formulation of the transient ship motions problem. Section 4 describes the numerical solution, and presents some techniques which can be used to improve the computational efficiency. In particular, we show how a knowledge of the asymptotic behavior of the solution, combined with an appropriate choice of an impulse, may be used to reduce the required length of the computational record. Section 5 presents the results of a simulation of a Wigley hull travel-
ing through a Pierson-Moskowitz spectrum of incident waves. Finally, some concluding remarks appear in Section 6.
2
Equations of Motion
During normal operating conditions the ship's weight, along with the steady, hydrodynamic sinkage force and trim moment acting on it, are all balanced by the hydrostatic pressure acting on the hull, while its steady resistance is overcome by the propulsion. These forces are in balance, and we will focus upon the unsteady perturbations about this equilibrium condition. Through Newton's law, the dynamics of a ship's unsteady oscillations are governed by a balance between the inertia of the ship and the external forces acting upon it. This balance is complicated by the existence of radiated waves, as a consequence both of the ship's own motions and its scattering of the incident waves. This means that waves generated by the ship at any given time will persist indefinitely and, in principle, affect the ship at all subsequent times, a situation which is described mathematically by a convolution integral. Having assumed that the system is linear, the equations of motion may be written in a form which is essentially identical to the model proposed by Cummins [3]:
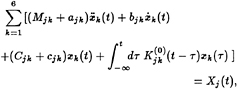 j=1, 2, …, 6, (1)
j=1, 2, …, 6, (1)
where the exciting forces on the right-hand side may be determined from:
(2)
as proposed by King [8].
In equation (1), the ship's displacement from its mean position in each of its six rigid-body modes of motion is given by xk, and the overdots indicate differentiation with respect to time. The excitation of the ship is provided by ζ(t), a time history of the incident wave elevation at some prescribed reference point on the free-surface. The ship's inertia matrix is Mjk, and the linearized hydrostatic restoring force coefficients are given
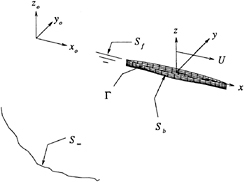
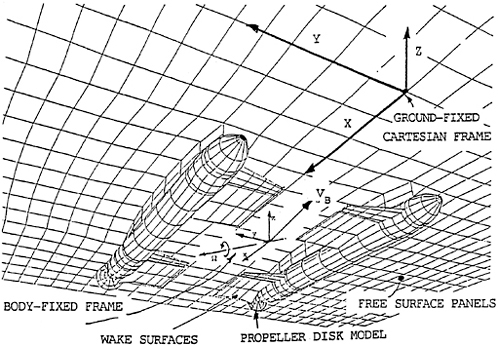
Figure 1: The reference frames and surfaces of the problem.
by Cjk. The hydrodynamic coefficients and the kernel of the convolution on the left-hand side of (1), and the kernel of the convolution on the right-hand side of (2), make up a set of radiation and diffraction impulse-response functions: the combination of ajk, bjk, cjk, and ![]() (t) is the force on the ship in the jth direction due to an impulsive motion in mode k, while the function KjD(t,β) is the force on the ship in the jth direction due to a uni-directional impulsive wave elevation incident from a heading angle of β. Equation (1) differs from the usual form only because the free-surface memory is represented as a convolution with the ship's displacement rather than with its velocity. This choice is convenient in practice because it produces a kernel which vanishes for large time (see Section 4).
(t) is the force on the ship in the jth direction due to an impulsive motion in mode k, while the function KjD(t,β) is the force on the ship in the jth direction due to a uni-directional impulsive wave elevation incident from a heading angle of β. Equation (1) differs from the usual form only because the free-surface memory is represented as a convolution with the ship's displacement rather than with its velocity. This choice is convenient in practice because it produces a kernel which vanishes for large time (see Section 4).
With the hydrodynamic and hydrostatic coefficients in hand, a simulation of the ship translating in an ambient wave field may be carried out by integrating in time the above system of six coupled differential equations.
3
Hydrodynamics
3.1
The Exact Problem
Consider a three-dimensional body in a semiinfinite fluid with a free-surface, as shown in Figure 1. The ship moves through an incident wave field with velocity ![]() , and is allowed to perform small unsteady oscillations about its mean position in any of its six degrees of freedom. The fluid is assumed to be ideal and the flow irrotational, free of separation or lifting effects. Two
, and is allowed to perform small unsteady oscillations about its mean position in any of its six degrees of freedom. The fluid is assumed to be ideal and the flow irrotational, free of separation or lifting effects. Two
coordinate systems will be employed in the ensuing derivations: the ![]() system is fixed in space, and the
system is fixed in space, and the ![]() system is fixed to the mean position of the ship. At t=0, these two coordinate systems coincide.
system is fixed to the mean position of the ship. At t=0, these two coordinate systems coincide.
Subject to the above assumptions, the fluid velocity may be described by the gradient of a scalar velocity potential, ![]() . Conservation of mass requires that this potential satisfy the Laplace equation everywhere in the fluid:
. Conservation of mass requires that this potential satisfy the Laplace equation everywhere in the fluid:
▽2Φ=0. (3)
The pressure in the fluid, ![]() , is given by Bernoulli's equation,
, is given by Bernoulli's equation,
(4)
where g is the acceleration due to gravity, ρ is the fluid density, and pa is the atmospheric pressure, which is assumed to be constant. (Partial differentiation is indicated when the independent variables x,y,z,t appear as subscripts.) If surface tension is neglected and the pressure on the free-surface is set equal to zero, a combined free-surface boundary condition may be written:
![]() on z0=ζ, (5)
on z0=ζ, (5)
where ζ(x0,y0,t) is the unknown free-surface elevation. Since the free-surface condition is second order in time, two initial conditions are required, and it will suffice to let
![]() on z0=0, for t<T0 (6)
on z0=0, for t<T0 (6)
On the submerged portion of the hull the normal components of the fluid velocity and the ship velocity must be equal:
![]() on Sb(t), (7)
on Sb(t), (7)
where Sb(t) is the exact position of the ship surface, ![]() , is the velocity of a point on the ship, and is the unit vector normal to the ship surface. Because of the initial conditions, fluid motions caused by the ship will go to zero at spatial infinity for all finite time,
, is the velocity of a point on the ship, and is the unit vector normal to the ship surface. Because of the initial conditions, fluid motions caused by the ship will go to zero at spatial infinity for all finite time,
3.2
Linearization
In order to make further progress both the free-surface and the body boundary conditions, as well as the Bernoulli equation, will be linearized. Let us now use the coordinate system fixed to the mean position of the ship, which is traveling along the x0-axis with a constant speed U. We will assume that the ship was accelerated to this speed at some time in the past and that all transients due to this acceleration have decayed to zero. The total velocity potential, in the ship fixed reference frame, will be decomposed as follows:
(8)
The combination of ![]() and
and ![]() is the potential due to the steady-state limit of the ship's uniform translation at forward speed U. This will be referred to as the steady problem. The radiation problem ensues when this translating ship is forced with some prescribed motion in a single rigid body mode k. The potential due to this motion is
is the potential due to the steady-state limit of the ship's uniform translation at forward speed U. This will be referred to as the steady problem. The radiation problem ensues when this translating ship is forced with some prescribed motion in a single rigid body mode k. The potential due to this motion is ![]() . If the steadily translating (but otherwise motionless) ship encounters an incident wave system with potential
. If the steadily translating (but otherwise motionless) ship encounters an incident wave system with potential ![]() , the scattering of those waves by the ship will be described by the potential
, the scattering of those waves by the ship will be described by the potential ![]() . This is the diffraction problem. Note that in the moving coordinate system, the fluid velocities in the far field will tend to those of the free stream and the undisturbed incident wave:
. This is the diffraction problem. Note that in the moving coordinate system, the fluid velocities in the far field will tend to those of the free stream and the undisturbed incident wave:
where i is the unit vector in the x-direction. Velocities described by the function ![]() in the above decomposition are assumed to be
in the above decomposition are assumed to be ![]() , while the remaining potentials describe velocities which are small perturbations to this basis flow. Far from the ship the basis flow must tend to the free stream, however the choice of
, while the remaining potentials describe velocities which are small perturbations to this basis flow. Far from the ship the basis flow must tend to the free stream, however the choice of ![]() is not unique.
is not unique.
If the decomposition of equation (8) is used in equations (7) and (5), the free-surface and body boundary conditions may be linearized about the mean positions of the ship and free-surface boundaries. The simplest choice of a basis flow, and the one that will be used here, is the freestream alone:
This choice leads to the familiar Neumann-Kelvin linearization of the pressure, the free-surface condition and the body boundary conditions:
(9)
(10)
(11)
In equations (9) and (10), ![]() is used to represent any of the above mentioned perturbation potentials and the linearized body boundary conditions in equation (11) are to be applied on
is used to represent any of the above mentioned perturbation potentials and the linearized body boundary conditions in equation (11) are to be applied on ![]() , the mean position of the ship surface. The generalized unit normal nk is defined by
, the mean position of the ship surface. The generalized unit normal nk is defined by
(12)
The steady and the unsteady potentials are coupled through the presence of the so-called m-terms in the body boundary condition. For this linearization the m-terms simply reduce to
mk=(0,0,0,0,Un3, −Un2)
Other linearizations can be derived by making a different choice of basis flow, ![]()
3.3
The Integral Equation
The foregoing initial-boundary-value problem can be recast as an integral equation by making use of the transient free-surface Green function. The three perturbation problems described above all satisfy the same boundary-value problem, with the exception of the body boundary condition. Consequently, the same integral equation may be used to solve for any of these potentials. The integral equation is derived by applying Green's theorem to the transient free-surface Green function and the time derivative of the potential. This Green function is derived in Wehausen [24]:
(13)
where
(14)
(15)
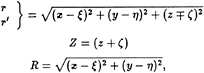
and J0 is the Bessel function of order zero. It is straightforward to verify that this Green function satisfies the complete linearized initial-boundary-value problem, with the exception of the body boundary condition, equation (11). The result of these manipulations is the following integral equation:
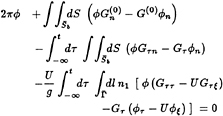
(16)
where the ship waterline ![]() is the intersection of
is the intersection of ![]() and the z=0 plane, and the arguments of the Green function in the convolution integrals are retarded
and the z=0 plane, and the arguments of the Green function in the convolution integrals are retarded ![]() . This equation is identical to that used by King et al. [9], or Lin & Yue [16], for example.
. This equation is identical to that used by King et al. [9], or Lin & Yue [16], for example.
The following sections will discuss in more detail the solution of the perturbation potentials.
3.4
Forced Motion Problems
The steady perturbation potential, when solved as the limit of a transient problem, and the radiation potentials are all solutions to similar (and in some cases identical) forced motion problems. The only difference being that in the steady problem it is the steady-state limit which is of interest, while in the radiation problem we seek a transient response.
3.4.1
The Radiation Problem
For each radiation problem, the steadily translating ship is moved impulsively in mode k, and the force on the ship in mode j (i.e. the corresponding radiation impulse-response function) is calculated. In principle, there are any number of possible forcings for this problem. An impulsive motion of the ship in any derivative (or integral) of its motion will do; or the motion need not even be impulsive, as long as a convenient Fourier transform exists with which to reconstruct the impulse-response from the non-impulse-response [9]. It is clear from the boundary condition that the solution to one impulsive radiation problem is related to that of any other through some number of time derivatives. For example, the body
boundary condition corresponding to an impulsive acceleration of the ship is
(17)
where H(t) is the Heaviside step function and r(t) is the ramp function r(t)=tH(t). The body boundary condition produced by an impulse in the ship's velocity is the time derivative of equation (17)
(18)
where δ(t) is the Dirac delta function. Because this is a linear system, the two solutions are related in the same way, and it can be shown that any canonical radiation potential satisfies
where ![]() is the radiation potential due to an impulse in the nth derivative of the ship's motion. This relationship is not surprising given that the same information can be constructed from any canonical radiation potential. Specifically, the potential due to an arbitrary motion of the ship in mode k, Φk, can be written as a convolution of
is the radiation potential due to an impulse in the nth derivative of the ship's motion. This relationship is not surprising given that the same information can be constructed from any canonical radiation potential. Specifically, the potential due to an arbitrary motion of the ship in mode k, Φk, can be written as a convolution of ![]() with a time history of the nth derivative of the ship's motion in that mode, dnxk/dtn.
with a time history of the nth derivative of the ship's motion in that mode, dnxk/dtn.
(19)
The force on the ship in mode j due to this arbitrary motion in mode k is found by integrating the consequent linearized pressure over the body surface
![]() . (20)
. (20)
This form is computationally inconvenient, since it involves a spatial derivative of the potential, and the calculation may be simplified by using a variant of Stokes' theorem attributed to Tuck [23]:
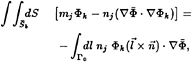
(21)
where ![]() is the unit vector tangent to the mean waterline. For a wall sided ship, the line integral is identically zero and we may write
is the unit vector tangent to the mean waterline. For a wall sided ship, the line integral is identically zero and we may write
![]() . (22)
. (22)
Given the form of the body boundary condition for this problem, it is natural to consider each radiation potential to be the sum of three terms:
(23)
where x(t) and ![]() must be thought of as the generalized functions appropriate to an impulse in the nth derivative of the ship's motion. The two time constants, Nk and
must be thought of as the generalized functions appropriate to an impulse in the nth derivative of the ship's motion. The two time constants, Nk and ![]() , are solutions to pressure release type problems. They satisfy the following pair of boundary value problems:
, are solutions to pressure release type problems. They satisfy the following pair of boundary value problems:
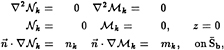
(24)
and may be calculated from the following pair of integral equations
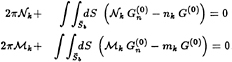
The transient or memory potential, ![]() , will depend upon the type of impulse the ship is forced to undergo.
, will depend upon the type of impulse the ship is forced to undergo.
Generally, this problem is solved by giving the ship an impulse in its velocity, which means setting ![]() and letting n=1 in equation (19). Because the position of the ship is changed by this choice of an impulse, we must expect it to produce a steady-state limit to the memory potential,
and letting n=1 in equation (19). Because the position of the ship is changed by this choice of an impulse, we must expect it to produce a steady-state limit to the memory potential, ![]() . Physically, when the ship is displaced from its original position by the impulse, a change occurs in the steady wave pattern which must be reflected in the large time limit of the radiation potential. This is undesirable from a computational standpoint because it tends to increases the required length of the computations (see Section 4). A simple way to avoid a non-zero steady-state limit is to prescribe a forced motion which will bring the ship back to its original position. An impulse in displacement, i.e. letting x(t)=δ(t), is the obvious choice to satisfy this requirement. The body boundary condition in this case becomes
. Physically, when the ship is displaced from its original position by the impulse, a change occurs in the steady wave pattern which must be reflected in the large time limit of the radiation potential. This is undesirable from a computational standpoint because it tends to increases the required length of the computations (see Section 4). A simple way to avoid a non-zero steady-state limit is to prescribe a forced motion which will bring the ship back to its original position. An impulse in displacement, i.e. letting x(t)=δ(t), is the obvious choice to satisfy this requirement. The body boundary condition in this case becomes
and the solution will be
(25)
In contrast to using an impulsive velocity, this will produce a radiation problem with a memory term that tends to zero at large time.
An integral equation for the impulsive displacement memory potential, ![]() , (where the super- and sub-scripts have been omitted for clarity) may be derived by inserting the decomposition of the potential into equation (16). The result is similar to the equation derived by Liapis [15] for the impulsive velocity memory potential:
, (where the super- and sub-scripts have been omitted for clarity) may be derived by inserting the decomposition of the potential into equation (16). The result is similar to the equation derived by Liapis [15] for the impulsive velocity memory potential:
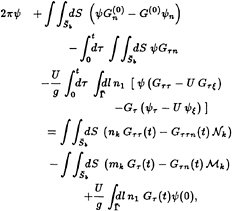
(26)
where ![]() is always non-zero.
is always non-zero.
Using the decomposition of equation (25) through equation (19) and into equation (22), the complete radiation impulse-response function, which consists of the constant coefficients ajk, bjk and cjk combined with the memory function ![]() , may be expressed in terms of the the general canonical radiation potentials as follows:
, may be expressed in terms of the the general canonical radiation potentials as follows:
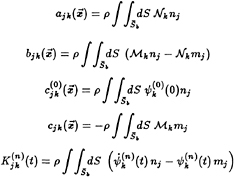
(27)
where the coefficient, ![]() , has appeared because
, has appeared because ![]() , and it must be included with cjk when n=0.
, and it must be included with cjk when n=0.
It has been pointed out in the past that the coefficient ajk is a genuine added-mass coefficient which is independent of both time (or frequency) and forward speed. The coefficients bjk and cjk are, on the other hand, functions of the forward
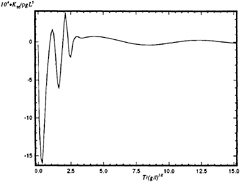
Figure 2: Wigley hull at Fn = 0.3, impulsive pitch displacement memory function.
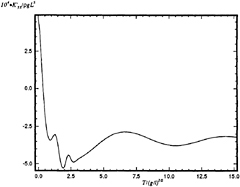
Figure 3: Wigley hull at Fn = 0.3, impulsive pitch velocity memory function.
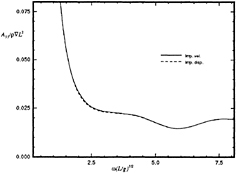
Figure 4: Comparison of the pitch-pitch added-mass coefficient calculated by impulsive displacement and by impulsive velocity of the ship.
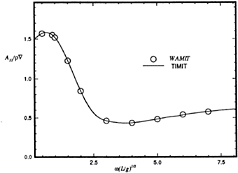
Figure 5: Wigley hull at Fn=0.0, heave-heave added-mass coefficient.
speed. It can be shown by applying Green's theorem to Nk and ![]() , and using the boundary conditions which they satisfy, that the constants bjk satisfy the following relations,
, and using the boundary conditions which they satisfy, that the constants bjk satisfy the following relations,
bjk=0 for j=k (28)
bjk+bkj=0 for j≠k
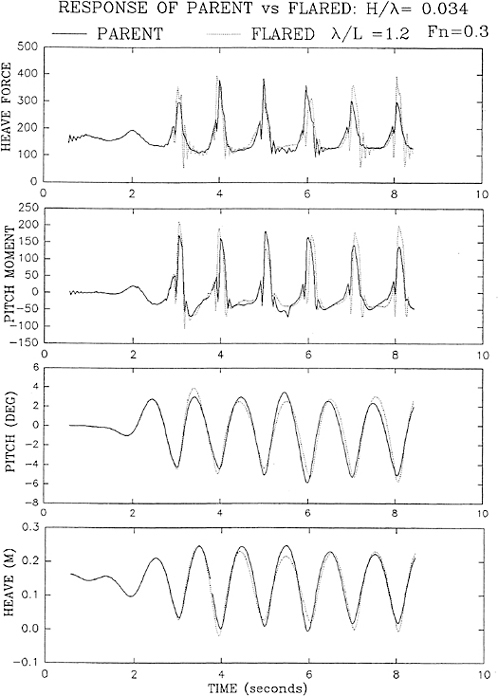
Some sample calculations of the pitch memory functions due to both an impulsive displacement and an impulsive velocity appear in Figures 2 and 3. Both calculations have been made for a Wigley hull at a Froude number 0.3.
It can be shown that the impulsive velocity and the impulsive displacement memory functions are related in the same way as the corresponding radiation potentials. That is,
This means that it is possible to calculate ![]() from
from ![]() , instead of solving the impulsive displacement radiation problem directly, and this may in practice be more convenient.
, instead of solving the impulsive displacement radiation problem directly, and this may in practice be more convenient.
If the motion of the ship is considered to be time harmonic at frequency ω, then the force on the ship may be written in complex form as
Fjk=(ω2Ajk(ω)−iω Bjk(ω)−cjk) xj,
and the impulse-response functions calculated using the canonical radiation potentials at any n, are related to the more familiar frequency-response functions (i.e. the added-mass and
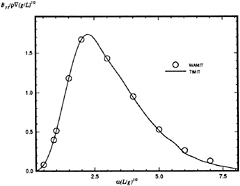
Figure 6: Wigley hull at Fn =0.0, heave-heave damping coefficient
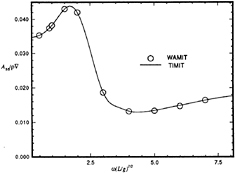
Figure 7: Wigley hull at Fn =0.0, pitch-pitch added-mass coefficient.
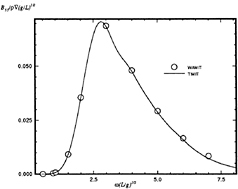
Figure 8: Wigley hull at Fn=0.0, pitch-pitch damping coefficient.
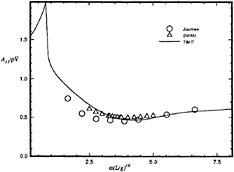
Figure 9: Wigley hull at Fn=0.3, heave-heave added-mass coefficient.
damping coefficients) through a Fourier transform:
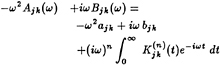
(29)
Figure 4 shows a comparison between the added-mass coefficients calculated using the two memory functions shown in Figures 2 and 3. As expected, the results are practically identical.
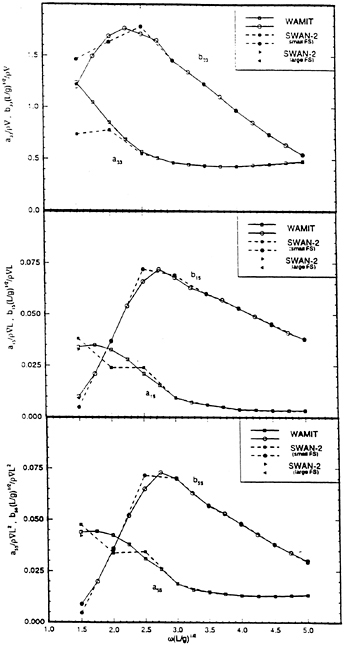
Calculations made using this method are compared to frequency domain calculations using WAMIT at zero forward speed in Figures 5 through 8. The two solutions for a Wigley hull are in excellent agreement. Comparisons between these two computer codes for more complicated bodies, as well as a description of WAMIT, may be found in Korsmeyer, et al. [10]. Figures 9 through 16 show the results of calculations made for the Wigley hull at a Froude number of 0.3. These results are compared both to the experiments of Journée [7], and to calculations made using the Rankine panel method SWAN [ 20]. The difference between these two sets of calculated results may be attributed to the fact that SWAN uses a linearization about the double-body flow rather than the Neumann-Kelvin linearization which is used in TiMIT.
3.4.2
The Steady Problem
The steady perturbation potential, ![]() , can be calculated as the steady-state limit of a particular radiation problem: that of an impulsive accelera
, can be calculated as the steady-state limit of a particular radiation problem: that of an impulsive accelera
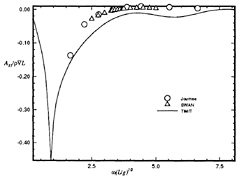
Figure 10: Wigley hull at Fn = 0.3, heave-heave damping coefficient.
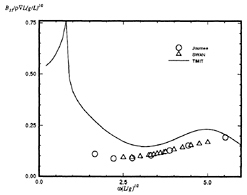
Figure 11: Wigley hull at Fn = 0.3, heave-pitch added-mass coefficient.

Figure 12: Wigley hull at Fn=0.3, heave-pitch damping coefficient.
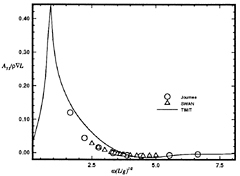
Figure 13: Wigley hull at Fn=0.3, pitch-heave added mass coefficient.
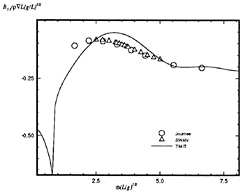
Figure 14: Wigley hull at Fn=0.3, pitch-heave damping coefficient.
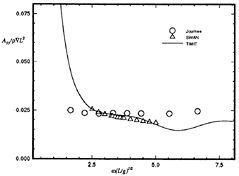
Figure 15: Wigley hull at Fn=0.3, pitch-pitch added-mass coefficient.
tion of the ship to a forward speed U. The boundary conditions for this problem are equations (10) and (17), which in the limit of large time will become the steady-state Neumann-Kelvin conditions
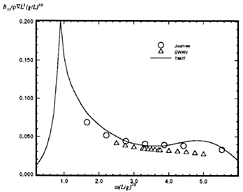
Figure 16: Wigley hull at Fn=0.3, pitch-pitch damping coefficient.
This approach is somewhat indirect, since the Green function for this problem is known (i.e. the Kelvin wave-source potential). The most direct way of calculating the steady potential would be to apply Green's theorem, with the Kelvin wave source potential, and to solve the resulting integral equation for ![]() . However, efforts to calculate the Kelvin wave source potential in a robust and efficient way have not yet been entirely successful. The transient approach, although computationally expensive, is an alternative.
. However, efforts to calculate the Kelvin wave source potential in a robust and efficient way have not yet been entirely successful. The transient approach, although computationally expensive, is an alternative.
3.5
The Diffraction Problem
The diffraction problem, that of finding the velocity potential for the case of the ship fixed to its mean position in the presence of an incident wave, may be solved to find the transient exciting forces. When the diffraction problem is forced by an impulsive wave elevation, the computed transient forces may be related to impulse-response functions. These impulse-response functions are the kernels of convolutions which can be used to compute the exciting forces and moments which appear on the right-hand side of the equations of motion (1) given an arbitrary, known, incident wave elevation.
Equation (16) may be solved for the scattered potential by using the body boundary condition:
(30)
and the force in mode j, KjD(t), is computed as indicated in (22) with Φk=![]() I+
I+![]() s, namely the complete diffraction potential.
s, namely the complete diffraction potential.
Two kinds of impulse-response function are of interest and each may be computed by solving canonical problems for scattered potentials. One of these impulse-response functions relates the exciting force to the wave elevation in the earth-fixed reference frame, and the other relates the exciting force to the wave elevation in the ship-fixed reference frame.
In the following convolution, the exciting forces on the ship due to the wave elevation measured at a fixed point in the earth-fixed reference frame, ζ0(t), may be computed by
![]() . (31)
. (31)
Here the kernel K0jD(t,t') corresponds to the impulse response function of a time-varying linear system. This is due ot the fact that the ship moves in time relative to the reference point where the waves are measured; the ship's response depends on both its position and on the relative time ![]() since the disturbance. From a different viewpoint, the frequency-domain description of ζ0(t) is in terms of the absolute frequency, whereas the description of the ship's exciting force Xj(t) is in terms of the frequency of encounter. Both a phase shift and frequency shift are required to relate these parameters.
since the disturbance. From a different viewpoint, the frequency-domain description of ζ0(t) is in terms of the absolute frequency, whereas the description of the ship's exciting force Xj(t) is in terms of the frequency of encounter. Both a phase shift and frequency shift are required to relate these parameters.
K0jD(t,t') is the force on the ship which is found from solving the canonical diffraction problem forced by the incident potential which is the real part of:
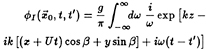 , (32)
, (32)
where the wavenumber k is related to the absolute frequency ω by ![]() and β is the angle of wave propagation measured from the positive sense of the x-axis. This incident velocity potential, is a uni-directional wave system which contains all frequencies with equal weight and describes a wave elevation which is the Dirac function in time, δ(t−t'), when viewed from the origin of the earth-fixed reference frame.
and β is the angle of wave propagation measured from the positive sense of the x-axis. This incident velocity potential, is a uni-directional wave system which contains all frequencies with equal weight and describes a wave elevation which is the Dirac function in time, δ(t−t'), when viewed from the origin of the earth-fixed reference frame.
An alternative approach is the following convolution, developed by King [8], in which the exciting forces due to the wave elevation measured at a fixed point in the ship-fixed reference frame, ζ(t), may be computed by
![]() . (33)
. (33)
Unlike equation (31), the kernel in equation (33) is of the form which corresponds to a time-invariant linear system since the reference point of the waves is fixed with respect to the moving ship.
KjD(t) is the force on the ship which is found from solving the canonical diffraction problem forced by the incident potential which is the real part of:
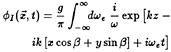
(34)
where ωe=ω−Uk cos β is the encounter frequency. This incident velocity potential, is also a uni-directional wave system which contains all frequencies, but it describes a wave elevation which is the Dirac function in time, δ(t), when viewed from the origin of the ship-fixed reference frame.
In the case of U=0 and t'=0, the de-scriptions (32) and (34) are identical. Note that although these potentials resemble the solution to the two dimensional Cauchy-Poisson problem, that potential describes the evolution of a wave elevation which is initially a Dirac function in space. Here, the spatial concentration of wave elevation is weaker than δ(x), for instance for ![]() :
:
![]() . (35)
. (35)
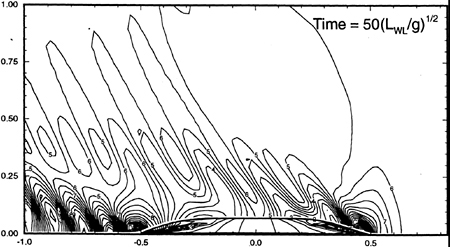
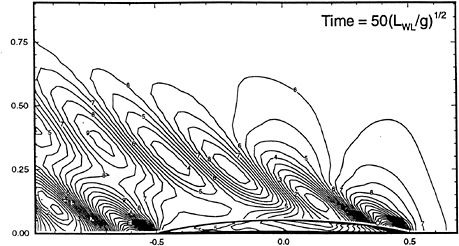
Continuing with the discussion of the case U= 0, β=π, t'=0; at times other than t=0, the waves are dispersed over just one half of the free-surface. For any time t<0, the waves are only in the x0>0 half-space, while for t>0, the waves are only in the x0<0 half-space. In the former, the waves are coalescing to the impulse, and in the latter they are dispersing from the impulse, hence the Fourier components are always ordered such that the wave length increases with |x0| The free-surface profiles are illustrated in Figure 17, and discussed further in Section 4.4.
There is no particular significance in choosing to have this temporal impulse occur along a line
through the origin. Any convenient location is acceptable as long as it is accounted for in the interpretation of the impulse-response function or its Fourier transform. In Korsmeyer [11] it is shown that such a shift in the location is equivalent to a phase shift in the frequency domain.
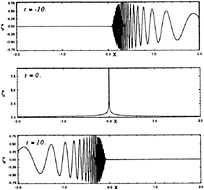
Figure 17: Example free-surface profiles along the x-axis for the case of U=0 and β=π
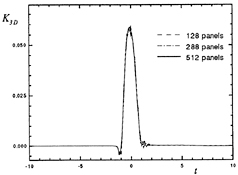
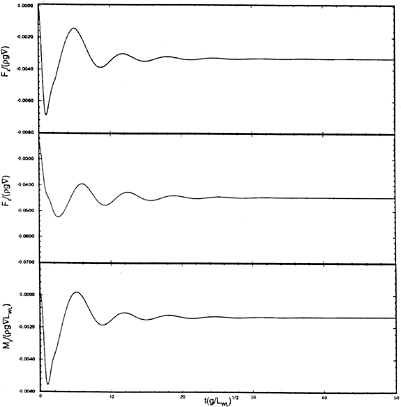
Figure 18: Wigley hull at Fn=0.3, β=π, the heave exciting force impulse-response function.
The frequency domain exciting force coefficients are related to K0jD(t,t') and KjD(t) by
(36)
and
(37)
respectively.
The advantage of K0jD(t, t') over KjD(t) is that the convolution with ζ0(t) (the commonly
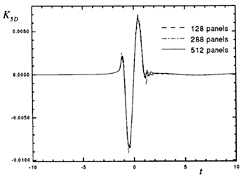
Figure 19: Wigley hull at Fn=0.3, β=π, the pitching exciting moment impulse-response function.
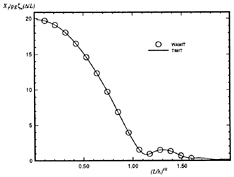
Figure 20: Wigley hull at Fn=0.0, β=π, the heave exciting force amplitude.
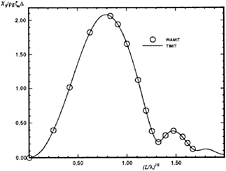
Figure 21: Wigley hull at Fn=0.0, β=π, the pitch exciting moment amplitude.
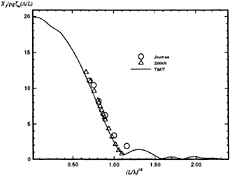
Figure 22: Wigley hull at Fn=0.3, β=π, the heave exciting force amplitude.
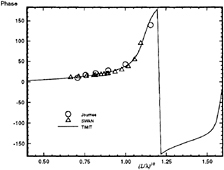
Figure 23: Wigley hull at Fn=0.3, β=π, the heave exciting force phase angle.
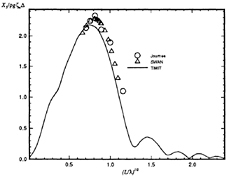
Figure 24: Wigley hull at Fn=0.3, β=π, the pitch exciting moment amplitude.
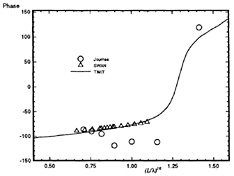
Figure 25: Wigley hull at Fn=0.3, β=π, the pitch exciting moment phase angle.
available input) avoids the difficulty of the non-unique relationship between encounter and absolute frequencies in following seas. If KjD(t) is used in following seas, three hydrodynamic problems must be solved for three impulse-response functions (one for each of three ranges of absolute frequency) in order to uniquely characterize the response in terms of encounter frequency. On the other hand, KjD(t) is computationally more efficient, particularly in head seas, and the wave elevation ζ(t) may be readily computed from ζ0(t) in Fourier space.
Examples of exciting force impulse-response functions K3D(t) and K5D(t) for a Wigley hull, at a Froude number of 0.3 in head seas, are shown in Figures 18 and 19. These functions are computed for three discretizations. The Wigley hull presents no computational difficulties and so a discretization of only 288 panels is adequate for practically useful results. Note that unlike the radiation force impulse-response functions, the diffraction force impulse-response functions are non-zero at times t<0. This is a result of the dispersion of free-surface waves and the fact that the ship is of finite extent. That is, in head seas for instance, at times t<0 the incident impulsive wave has not yet coalesced, but is already being scattered by the forward sections of the ship. This phenomenon must be accounted for in the convolution on the right-hand side of the equations of motion by the choice of an infinite upper limit of integration in equations (31) and (33).
Comparison of the diffraction impulse-response functions with frequency-domain results may be made through the Fourier transform (36) or (37).
Figures 20 and 21 show a comparison of the magnitude of the frequency-domain exciting force coefficients for the heave force and pitch moment on a Wigley hull at a Froude number of 0. The comparison is the Fourier transform of results from TiMIT with calculations conducted in the frequency domain by WAMIT. The results are identical to graphical accuracy, which is expected as these codes are the time-domain and frequencydomain manifestations of the same theory as long as U=0.
Figures 22 through 25 show a comparison of the magnitude and phase angle of the frequency-domain exciting force coefficients for heave force and pitch moment for the Wigley hull at a Froude number of 0.3. The comparison is the Fourier transform of the results from TiMIT shown in Figures 18 and 19 with calculations conducted in the frequency domain by SWAN and experimental results from Journée [7]. As mentioned in Section 3.4.1, the m-terms are treated differently in TiMIT and SWAN and this difference enters into the pitch moment calculation through equation (22). This may account for the fact that the agreement between TiMIT and SWAN is better for the heave exciting force than for the pitch exciting moment. Apparently, using the double-body linearization improves the accuracy of the pitch exciting moment calculation by a small amount.
4
Numerical Issues
There are three major numerical tasks involved in solving the hydrodynamic problems outlined above: calculation of the Green function for pairs of singularity and field points on the representation of the ship hull; calculation of the impulsive incident wave at field points on the ship hull; and solution of the discrete integral equations (16) and (26). The calculation of the Green function is described in detail by Newman [21] and is done to an absolute accuracy of approximately 6 significant digits throughout the computational domain. The computation of the incident potential, along with its temporal and spatial derivatives, is carried out via an extension of algorithms commonly used for the calculation of the complex error function. These algorithms are based on the work of Gautschi [5] and may be found in King [8] and Korsmeyer [13].
4.1
The Discrete Hydrodynamic Problem
The integral equations for the hydrodynamic problems are discretized by subdivision of the hull surface into planar quadrilateral (or triangular) panels upon which the potential is assumed to be constant. A linear system of equations is generated by a collocation scheme where the panel centroids are the collocation points. The convolution terms appear only on the right-hand side, and the convolution is computed by the trapezoid rule (see [12]). If appropriate, the size of the linear system is reduced by exploiting the port and starboard symmetry of the ship. The linear system of equations has a left-hand side matrix which is independent of time, so this matrix may be factored once, with back-substitution used at all subsequent time steps.
The bulk of the computational burden of the solution is in calculating, or fetching from storage, the transient Green function coefficients which appear in the convolution terms. For a zero-speed problem, without exploiting symmetry, the number of coefficients needed at each time step is proportional to ![]() (where Nt is the number of the current time step and NP is the number of panels); however, all but
(where Nt is the number of the current time step and NP is the number of panels); however, all but ![]() have been calculated at previous time steps. If there is sufficient physical memory available, the most efficient strategy is to store the coefficients in memory. If there is not, then they must either all be recalculated at each step, or fetched from storage on disk. On all of the machines that we use (DEC 5000, IRIS Indigo, Cray YMP) storing the coefficients on disk is from three to six times faster than recalculating. The algorithm used to calculate this function requires an average of 1.5 micro seconds on a Cray YMP for one pair of evaluation points at a single time. In the diffraction problem, the incident potential must be calculated at each time step as well, but only NP evaluations are required and this is not a significant contribution to the overall computational effort.
have been calculated at previous time steps. If there is sufficient physical memory available, the most efficient strategy is to store the coefficients in memory. If there is not, then they must either all be recalculated at each step, or fetched from storage on disk. On all of the machines that we use (DEC 5000, IRIS Indigo, Cray YMP) storing the coefficients on disk is from three to six times faster than recalculating. The algorithm used to calculate this function requires an average of 1.5 micro seconds on a Cray YMP for one pair of evaluation points at a single time. In the diffraction problem, the incident potential must be calculated at each time step as well, but only NP evaluations are required and this is not a significant contribution to the overall computational effort.
If the transient coefficients are stored, the space required, whether in RAM or on disk is:
(38)
where NT is the total number of time steps. The total cost of the computation, regardless of whether the coefficients are recalculated or stored is:
(39)
There is an ![]() term in the cost equation, reflecting the factorization of the left-hand side, but
term in the cost equation, reflecting the factorization of the left-hand side, but
that term is dominated by the ![]() term for any typical computation. For the forward-speed problem, additional coefficients are required for the waterline integral.
term for any typical computation. For the forward-speed problem, additional coefficients are required for the waterline integral.
Clearly it is important to use the coarsest spatial and temporal discretizations which will achieve the desired accuracy. Symmetries should always be exploited when possible as this both reduces the size of the linear system and reduces the number of coefficients which must be computed. Reducing the total time range of the calculation is also possible as is discussed in the next section.
4.2
Asymptotic Continuation
The minimum length of an impulse-response function is determined by the decay of transients in the solution. In principle, the force on the ship continues for all time, but in practice we will feel justified in truncating the record when the force has decayed to some small fraction of its peak value (say .5%). The decay of transients in the solution, with steady forward speed, is fundamentally different from the solution of the zero-speed problem because of the resonance at the critical frequency of ![]() . At zero speed, the energy associated with the wave system generated by the impulse propagates away from the ship at the group velocity of the various components. At forward speed however, the impulse excites components whose group velocities are approximately equal to the ship's speed, U, and this energy remains in the vicinity of the ship.
. At zero speed, the energy associated with the wave system generated by the impulse propagates away from the ship at the group velocity of the various components. At forward speed however, the impulse excites components whose group velocities are approximately equal to the ship's speed, U, and this energy remains in the vicinity of the ship.
This concept can be made more quantitative by considering the asymptotics of the Green function. Newman [21] shows that at zero speed the linearized pressure due to the Green function (equation (13)) is to leading order:
When the ship has a steady forward speed, however, the leading order contribution becomes
![]() , (40)
, (40)
where ![]() is the critical frequency of oscillation. This result can be related through a Fourier transform to the results of Dagan & Miloh [4] for the analogous frequency-domain Green function. Asymptotically then, the Green function at forward speed behaves like an oscillation at the critical frequency, which decays at a rate of
is the critical frequency of oscillation. This result can be related through a Fourier transform to the results of Dagan & Miloh [4] for the analogous frequency-domain Green function. Asymptotically then, the Green function at forward speed behaves like an oscillation at the critical frequency, which decays at a rate of ![]() .
.
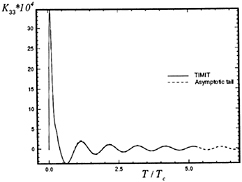
Figure 26: Comparison of the impulse-response function and the proposed asymptotic tail.
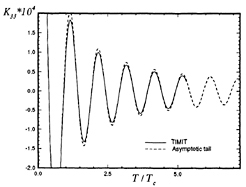
Figure 27: Expanded view of the matching between the asymptotics and the solution.
This behavior in the Green function suggests a similar behavior in the solution to the integral equation, as well as in the impulse-response function. This notion is borne out by numerical experiments, and suggests that a relatively short solution can be extended to any length by matching it to an asymptotic continuation or tail which has a form similar to equation (40). Figures 26 and 27 show a comparison between a very long calculation of an impulse-response function and the proposed asymptotic tail. In these figures the non-dimensional impulse-response function and the asymptotic tail are plotted versus the non-dimensional ratio of time to the critical period, ![]() . The two functions have been matched at a peak near
. The two functions have been matched at a peak near ![]() .
.
Despite the good agreement shown in these
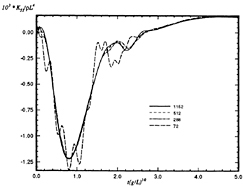
Figure 28: Wigley hull at Fn=0.3, convergence of the pitch-heave response.
figures, this leading-order behavior is based on the potential for a translating source, and is not strictly correct for a collection of singularities such as source and dipole distributions over the panels of a discrete ship geometry. It can be seen in Figure 27, which is an expanded view of the matching shown in Figure 26, that the numerical solution decays slightly faster than ![]() . This is consistent with the recent work of Liu & Yue [18].
. This is consistent with the recent work of Liu & Yue [18].
4.3
Convergence
Convergence of transient problems depends on both spatial and temporal discretization. Figures 28 and 29 show the convergence of two radiation impulse response functions with increasing numbers of panels. All the curves are for a Wigley hull at Froude number of 0.3, and each curve which appears in the figures is itself the converged result of a series of calculations using progressively smaller time steps for the same spatial discretization. Figures 30 and 31 are the Fourier transform of the convergence plots shown in Figure 29 to provide a frequency domain perspective on the convergence of the calculations. As can be seen from these figures, and Figures 18 and 19 from Section 3.5, the radiation and diffraction problems appear to have converged to within graphical accuracy using a discretization of 512 panels over the body (256 unknowns).
4.4
Filtering of Short Wavelengths
As in other hydrodynamic problems where a continuous spectrum of wavelengths is present, very small wavelengths exist which are not considered
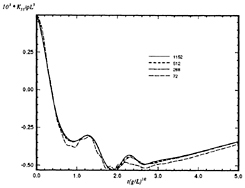
Figure 29: Wigley hull at Fn=0.3, convergence of the pitch-pitch response.
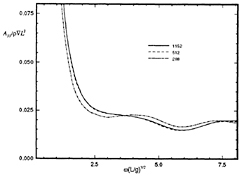
Figure 30: Wigley hull at Fn=0.3, convergence of the pitch-pitch added-mass coefficient.
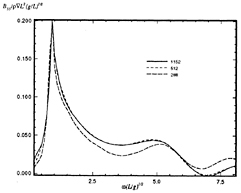
Figure 31: Wigley hull at Fn=0.3, convergence of the pitch-pitch damping coefficient.
to be of physical relevance. These may cause numerical anomalies or errors, since the approximation of the ship's surface by panels upon which the potential is assumed to be constant limits the correct solution to wavelengths substantially longer than the panel dimensions. Since short waves are attenuated exponentially in the vertical direction, this problem is restricted to a relatively thin region adjacent to the free surface.
In the present planar panel method, with the collocation points at the panel centroids, values of the potentials required for the waterline integral in equation (16) are replaced by the corresponding values at the adjacent centroids. This effectively provides an exponential filter to the short wavelengths, scaled in proportion to the panels themselves. This is an ad hoc approach, which is justified by convergence tests and visual examination of the resulting computations, as opposed to a more formal numerical analysis. Difficulties can be anticipated if the centroids approach the free surface faster than the scale of the panels is reduced, as might occur if the aspect ratio of the panels is large (horizontal dimension much greater than vertical) or if there is substantial flare at the waterline (panels approaching the horizontal plane).
For example, the presence of very short wavelengths in the incident-wave profile corresponding to either incident potential (32) or (34) (for U=0 and β=π) is illustrated in Figure 17. The profiles shown in this figure are in fact filtered because we are evaluating
![]() . (41)
. (41)
This is equivalent to the evaluation of the incident potential at the centroids of panels adjacent to the linearized free-surface for a fine discretization of a ship hull.
An alternative filtering scheme for the solution could be based on truncating the integral representation for the Green function, G(f) (15), at some point k=kmax. This is also an ad hoc approach and the truncation point kmax would have to be increased systematically with the refinement of the discretization. Such an approach would be expedient if the integral defining G(f) were evaluated numerically. However for efficient transient hydrodynamic analysis, the rapid evaluation of G(f) is critical and is best achieved by evaluating the Green function by analytical expansions and approximations available only for the complete (semi-infinite) range of the integral.
5
Simulation
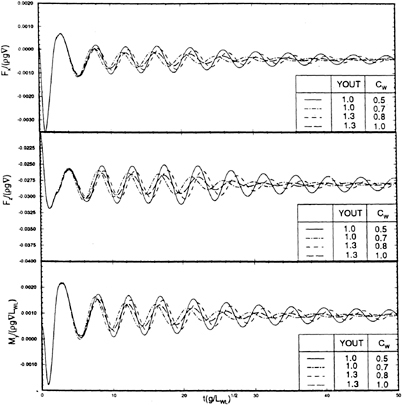
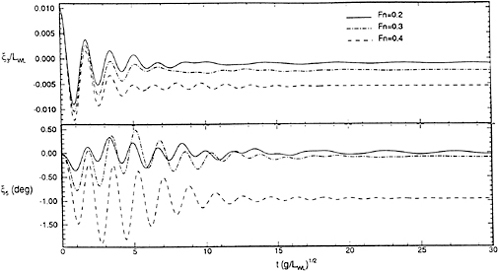
The simulation of a ship traveling in a seaway is carried out by the temporal integration of the equations of motion (1). For the simulation presented here, the exciting forces are calculated by the convolution appearing in equation (33). This simulation is of a Wigley hull at Froude number 0.3, encountering head seas with a Pierson-Moskowitz spectrum corresponding to 5 meters per second wind speed.
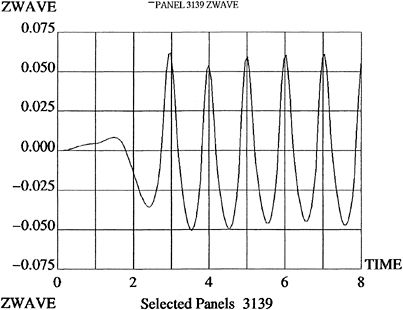
The top of Figure 32 shows a segment of the time history of the incident wave elevation as measured at the origin of the ship-fixed reference frame. The next two time histories in this figure are the heave and pitch responses of the ship respectively.
Validation of these time histories may be made by deducing the frequency-domain response-amplitude operators from the input and output signals:
(42)
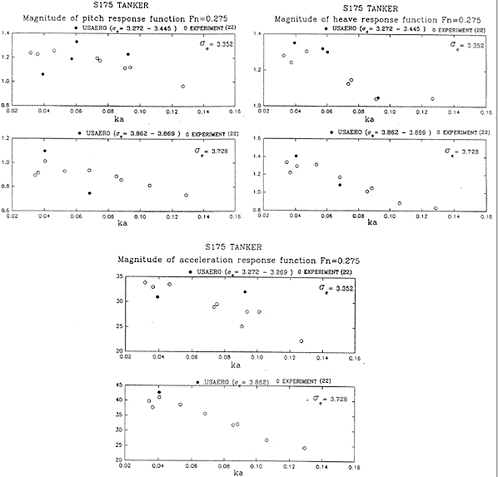
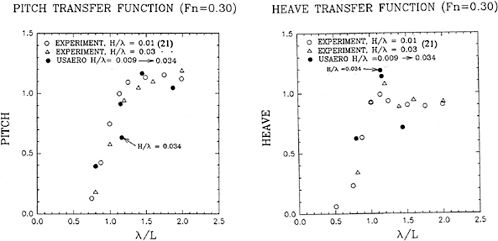
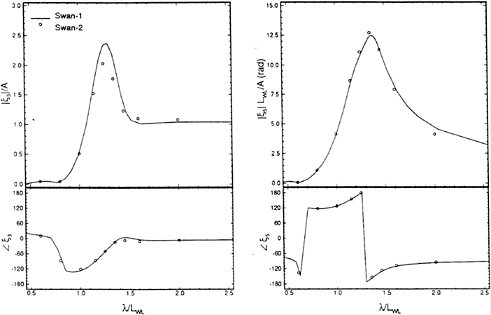
where Xj(ω) and ζ(ω) are obtained by taking the Fourier transforms of the output and input signals respectively. Figures 33 and 34 are plots of the frequency-domain response-amplitude operators compared to experimental results.
We find that the computation of the frequency-domain response-amplitude operators converges more slowly in the vicinity of resonance than at frequencies away from that region, as can be seen in Figures 33 and 34. This is expected since resonance occurs precisely because the determinant of the frequency-domain system of equations of motion becomes small, leading to poor conditioning of this linear system. The convergence of these results is also subject to the reduction of the size of the time-step and the increase of the order of the integration scheme used to solve the time-domain equations-of-motion. A fourth-order Runge-Kutta algorithm is a reasonable choice because it is robust and efficiency is not paramount in this calculation.
To quantify the relatively slow convergence around resonance, we have solved the equations of motion in the frequency domain using the frequency-domain coefficients presented in various figures shown in Section 3, which are the Fourier transforms of time-domain computations. We find that for the Wigley hull in head seas at a Froude number of 0.3, the condition number at the frequency of peak heave and pitch response is approximately twice the value for frequencies
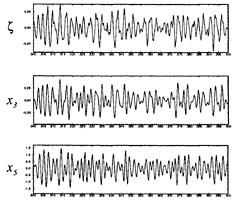
Figure 32: Time histories from a simulation of a Wigley hull at Fn=0.3, β=π. From the top: incident wave elevation in the ship-fixed frame, heave response, pitch response.
away from this peak. It is reasonable to expect that accurate results in the time-domain can only be produced for temporal and spatial discretizations which are sufficiently fine to achieve convergence around resonance.
6
Discussion
A computer code has been developed for the transient hydrodynamic analysis of a ship traveling in a seaway. Results have been presented to demonstrate the convergence of the method for the radiation and diffraction problems, and the calculations are shown to be in satisfactory agreement with both experiments and frequency domain calculations made using other methods. It is also pointed out that the steady problem can be considered to be the large time limit of a particular radiation problem, and the use of an impulse in displacement is suggested as a way of avoiding all steady-state limits in the radiation problem. A technique for extending the impulse response function by asymptotic continuation is also presented and used to reduce the necessary length of the computations.
Topics for the future include improving the calculation of fluid velocities through the use of higher order panels. This is especially important in the steady problem because the forces are determined entirely from gradients of the potential. The calculation of field quantities, such as the free-surface elevation and fluid velocities away from the ship, is also in progress. Real ship forms,
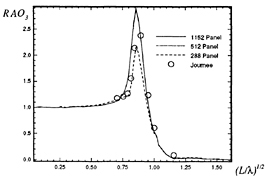
Figure 33: Wigley hull at Fn=0.3, β=π, the heavy response-amplitude operator.
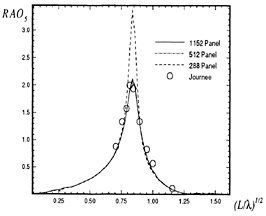
Figure 34: Wigley hull at Fn=0.3, β=π, the pitch response-amplitude operator.
which often have significant flare especially near the stern, present special numerical difficulties for this method of solution and therefore require special care. A ship traveling in following seas is another important topic of further research, and it is not yet clear to us which of the two diffraction formulations discussed in the foregoing will be most useful in this situation.
Acknowledgment
This research was sponsored by the Office of Naval Research, contract number N00014–90-J-1160.
References
[1] R.F.Beck and A.R.Magee. Time domain analysis for predicting ship motions. In Proc. IUTAM Symp. Dynamics of Marine Vehicles & Structures in Waves, London, U.K., 1990.
[2] V.Bertram. A Rankine source approach to forward speed difraction problems. In Proc. 5th Intl. Workshop on Water Waves and Floating Bodies, Manchester, U.K., 1990.
[3] W.E.Cummins. The impulse response function and ship motions. Schiffstecknik, 9:101– 109, 1962.
[4] T.Dagan and G.Miloh. Flow past oscillating bodies at resonant frequency. Proc. 13th Symp. Naval Hydro., pages 355–373, 1980.
[5] W.Gautschi. The complex error function. Collected Algorithms from CACM, 1969.
[6] M.D.Haskind. Two papers on the hydrodynamic theory of heaving and pitching of a ship. Technical Report 1–12, The Society of Naval Architects and Marine Engineers, 601 Pavonia Ave., Jersey City, New Jersey, 1953.
[7] J.M.J.Journée. Experiments and calculations on four Wigley hullforms. Technical Report 909, Delft University of Technology, Ship Hydromechanics Laboratory, Delft, The Netherlands, 1992.
[8] B.W.King. Time-domain analysis of wave exciting forces on ships and bodies. Technical Report 306, The Department of Naval Architecture and Marine Engineering, The University of Michigan, Ann Arbor, Michigan, 1987.
[9] B.W.King, R.F.Beck, and A.R.Magee. Seakeeping calculations with forward speed using time domain analysis . In Proc. 17th Symp. Naval Hydro., The Hague, Netherlands, 1988.
[10] F.T.Korsmeyer. The first- and second-order transient free-surface wave radiation problems. PhD thesis, Massachusetts Institute of Technology, Cambridge, Massachusetts, 1988.
[11] F.T.Korsmeyer. The time domain diffraction problem. In The Sixth International Workshop on Water Waves and Floating Bodies, Woods Hole, Massachusetts, 1991.
[12] F.T.Korsmeyer, C.H.Lee, J.N.Newman, and P.D.Sclavounos. The analysis of wave effects on tension leg platforms. In OMAE Conference, Houston, Texas, 1988.
[13] F.T.Korsmeyer, J.N.Newman, and G.E. Osborne. The linear, transient, free-surface wave diffraction problem. In preparation, 1993.
[14] S.J.Liapis. Time domain analysis of ship motions. PhD thesis, The Department of Naval Architecture and Marine Engineering , The University of Michigan, Ann Arbor, Michigan, 1986.
[15] S.J.Liapis. Time domain analysis of ship motions. Technical Report 302, The Department of Naval Architecture and Marine Engineering, The University of Michigan, Ann Arbor, Michigan, 1986.
[16] W.M.Lin and D.K.P.Yue. Numerical solutions for large-amplitude ship motions in the time domain. In Eighteenth Symp. on Nav. Hydro., Ann Arbor, Michigan, 1990.
[17] W.M.Lin and D.K.P.Yue. Time-domain analysis for floating bodies in mild-slope waves of large amplitude. In 8th Intl. Workshop Water Waves & Floating Bodies, St. John's, Newfoundland, 1993.
[18] Y.Liu and D.K.P.Yue. On the solution near the critical frequency for an oscillating and translating body in or near a free surface. J. Fluid Mechanics, 254:251–266, 1993.
[19] D.E.Nakos, D.E.Kring, and P.D. Sclavounos. Rankine panel methods for time-domain free surface flows. In 6th Intl.
Conf. Num. Ship Hydro., U. Iowa, Iowa City, 1993.
[20] D.E.Nakos and P.D.Sclavounos. Ship motions by a three dimensional Rankine panel method. In Eighteenth Symp. on Nav. Hydro., Ann Arbor, Michigan, 1990.
[21] J.N.Newman. The approximation of free-surface Green functions. In P.A.Martin and G.R.Wickham, editors, Wave Asymptotics, pages 107–135. Cambridge University Press, 1992.
[22] T.F.Ogilvie. Recent progress toward the understanding and prediction of ship motions . In The Fifth Symposium on Naval Hydrodynamics, pages 3–128, Bergen, 1964.
[23] T.F.Ogilvie and E.O.Tuck. A rational strip theory for ship motions, part 1. Technical Report 013, The Department of Naval Architecture and Marine Engineering, The University of Michigan, Ann Arbor, Michigan, 1969.
[24] J.V.Wehausen and E.V.Laitone. Surface waves. In Handbuch der Physik, pages 446– 778. Springer, 1960.
A New Method for the Determination of Resonant States for Fluid-Structure Interaction
O.DeBayser, C.Hazard, and M.Lenoir (CNRS/ENSTA Centre de l'Yvette, France)
D.Martin (Universite de Rennes, France)
Abstract.
In order to compute the resonant states of a ship on the sea, we investigate a variational formulation for the scattering frequencies of this problem, i.e. the poles of the analytic continuation of the solution operator. A practical method, based on the integral representation of the solution is described, the scattering frequencies are shown to be the solutions of a non-linear eigenvalue problem.
The scattering frequencies and the corresponding eigensolutions provide detailed information about the way energy of incident waves can be stored as waves in the vicinity of the ship or motion along one ore more of its degrees of freedom. They can be used for prediction of the frequency and direction of the incoming waves resulting in the maximum response of the ship along one of its degrees of freedom.
Some preliminary results in that direction are shown here, where the body is a model catamaran, fixed in the waves.
1
Introduction.
We study the linearized sea-keeping problem for an elastic body, i.e., the periodic small motions of an elastic structure which floats (without forward speed) at the free surface of the ocean (in the infinite depth case). We are concerned in particular with the dynamic stability of the structure; more precisely, the main question is to find the frequency domains which correspond to the highest risks of instability. Indeed, for some values of the frequency, it may happen that the amplitude of the motions of the structure becomes great compared with the amplitude of the incident swell. This means intuitively that the structure has a tendency to accumulate the energy transmitted by the incident wave. These “resonant frequencies” are not eigenfrequencies of the problem, for the system consisting of the structure coupled with the ocean is not conservative (the energy associated with the scattered wave propagates to infinity). A simple way to determine them is to compute the response curve of the structure, i.e., the total energy of the structure with respect to the frequency of the incident wave (for given amplitude and direction of propagation): the resonant frequencies correspond to the peaks of this curve. However, it is an especially expensive method, since it requires to compute the response of the system for numerous values of the frequency.
The aim of the present paper is to show that the resonant frequencies are nothing but the traces of isolated singularities in the plane of complex frequencies. Indeed, we will see that the sea-keeping problem can be extended analytically to complex values of the frequency, and that this extension has poles in the lower complex half plane: these poles are referred to as “scattering frequencies”. They are intrinsic quantities of the system, since they do not depend on the incident swell (as the eigenvalues of a conservative system do not depend on the external forces exerted on it). The knowlegde of these singularities (more precisely, the ones which are near the real frequencies axis) allows not only to locate the peaks of the response curve, but also to obtain an a priori estimate of the response of the system in the vicinity of such frequencies (see [4], [11]).
We present here a way to construct explicitly the analytic continuation of the sea-keeping problem in the plane of complex frequencies, and to
exhibit the singularities of this extension. The principle of the method is quite simple. We begin by reducing the initial problem to an equivalent one set in a bounded domain, thanks to the so-called coupling method between finite elements and integral representation (introduced by Jami and Lenoir [8]). The reduced problem is then extended to complex frequencies using the analytic continuation of the Green function of the seakeeping problem (Vullierme-Ledard [16]). The scattering frequencies finally appear as the solutions of a nonlinear eigenvalue problem which can be dicretized by finite elements and then solved by a numerical iterative method. In the present paper, the method is described for the general case of the 3-dimensional fluid—structure interation problem. However, the numerical results which are presented here are related to the scattering problem by a fixed rigid body. The case of an elastic floating body is in progress.
In order to focus rather on the numerical aspects of the computation of scattering frequencies, we restrict ourselves to describe the main steps on the method, without going into the mathematical details. For a rigorous mathematical approach, we refer to [11] where the method is applied to the scattering of an acoustic wave by a rigid obstacle. See [16], [4] and soon [6] for the sea-keeping problem. Note that in the finite depth case, an other characterization of the scattering frequencies may be obtained by means of the so-called localized finite element method (see [ 4] in 2-D, and [5] in 3-D). It is based on a series expansion of the solution instead of an integral representation. In the 2-dimensional case, numerical results are given in [5]. Let us finally mention the paper of Wu, Wang and Price [18] who present an intuitive approach of the notion of scattering frequencies: by an asymptotic analysis of a simplified model, they show in particular how the peaks of the response curve are related to the presence of poles in the complex frequency plane.
2
Resonant states and scattering frequencies.
2.1
Linearized equations.
Consider an elastic body which floats at the free surface of the sea, assumed infinite in both horizontal and downward vertical directions. When the system is at rest, the fluid fills an unbounded
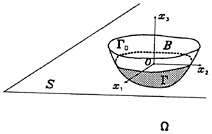
Figure 1: The floating body.
domain Ω whose boundary ∂Ω consists of the free surface S and the immersed surface Г of the body. The body fills a bounded domain B : its boundary ∂B consists of Г and the emerged part Г0 which is assumed free. We denote by n either the outer unitary normal to ∂Ω or the inner normal to ∂B (which coincide on Г). The coordinate system ![]() is defined as shown in Fig. 1:
is defined as shown in Fig. 1: ![]() is an horizontal plane parallel to the free surface S, and
is an horizontal plane parallel to the free surface S, and ![]() is the upward vertical direction.
is the upward vertical direction.
We study the periodic small motions of the coupled system under the action of a given incident monochromatic swell of pulsation ω. Let φ be the velocity potential of the scattered wave and u=(u1,u2,u3), the displacement field of the body. Let eij(u) and σij(u) (for i,j=1, 3) be, respectively, the components of the strain and stress tensors given by
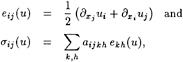
where aijkh are the elastic coefficients which are related, in the case of an isotropic material, to the so-called Lamé coefficients λ and μ by the relations
aijkh=λδijδkh+μ(δihδjk+δikδjh).
The linearized time-harmonic equations of the problem (expressed in a non-dimensional form) consist in the following system, which will be referred to as problem Ρν in the sequel :
Δφ=0 in Ω, (1)
∂nφ−νφ=0 on S, (2)
![]() , (3)
, (3)
σij(u)nj=0 on Г0, (4)
![]() on Г, (5)
on Г, (5)
![]() on Г, (6)
on Г, (6)
![]() , (7)
, (7)
where ν denotes the pulsation squared (ν=ω2), ρ is the (dimensionless) mass density of the body, f and gi (i=1,3) are given functions on Г (which depend on the incident swell), and ΣR is the vertical cylinder ![]() . We refer for example to [9] and [14] for more details concerning the equations of the fluid and the structure. Laplace's equation (1) is nothing but the conservation of mass. The free surface condition (2) results on one hand from the continuity of the pressure across S, on the other hand from the fact that the velocity of the particles located on S is tangent to S. Eqs. (3) are the dynamics equations in a continuous medium, and (4) expresses that the emerged part Г0 of the boundary of B is free. On Г, the two equations (5) and (6) stand, respectively, for the continuity of the normal velocity and the normal stress. Finally, the radiation condition (7) shows that the energy of the scattered wave radiates towards infinity.
. We refer for example to [9] and [14] for more details concerning the equations of the fluid and the structure. Laplace's equation (1) is nothing but the conservation of mass. The free surface condition (2) results on one hand from the continuity of the pressure across S, on the other hand from the fact that the velocity of the particles located on S is tangent to S. Eqs. (3) are the dynamics equations in a continuous medium, and (4) expresses that the emerged part Г0 of the boundary of B is free. On Г, the two equations (5) and (6) stand, respectively, for the continuity of the normal velocity and the normal stress. Finally, the radiation condition (7) shows that the energy of the scattered wave radiates towards infinity.
Note that in the case of a rigid body, the strain tensor vanishes at every point of B. It follows that the linearized displacement field has the form a+b×x (see e.g. [14]): the system (1) to (7) then simplifies to the problem studied by John [9].
Our aim is to show that this problem extends analytically in the complex ν-plane and above all, to describe how to construct explicitely this extension. Let us point out that we cannot exhibit such an extension simply by replacing ν by a complex number in the equations (1) to (7) of Ρν. This follows from the so-called “limiting absorption principle” ([10],[4]) which may be explained as follows. Let Ρν still denote the problem which is obtained by substituting for ν a complex number. It may be easily seen that this problem is well-posed for every v such that Im ν≠0, and that its solution decreases exponentially at infinity (when ![]() →∞). Moreover, if
→∞). Moreover, if
tends to a given ν0 ∈ R+, then the solution of Ρν tends locally to the solution of Ρνo. On the other hand, if
tends to the same point ν0 ∈ R+, this result does not hold : actually, the limit of the solution of Ρν does not satisfy condition (7) any longer. In fact, it verifies
![]() ,
,
which is known as the incoming radiation condition. As a summary, we are able to construct by that way a continuous extension of the initial problem to the upper complex half plane C+. This extension is regular (since Ρν is well-posed for every ν ∈ C+) and no singularity appears in C+.
The extension of the problem to the lower complex half plane C− raises a difficulty which may be understood as follows : noticing that the solution of Ρν is exponentially decreasing at infinity for ν ∈ C+, and oscillating for ν ∈ R+, it will clearly become exponentially increasing when ν ∈ C−. In order to remove this difficulty, the method we present in the sequel consists in reducing the initial problem to an equivalent problem set in a bounded domain: the asymptotic behaviour of φ at infinity is explicitly controled by means of an integral representation formula. The reduced problem will then be extended in the complex ν-plane.
2.2
Reduction to a bounded domain.
In this section, ν denotes a real positive number. We recall here the coupling method between finite elements and integral representation (Jami and Lenoir [8]. We will denote by Gν(x,y) the Green function (or elementary solution) associated with the sea-keeping problem, i.e., the only solution of
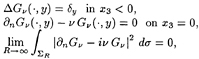
(8)
where δy is the Dirac measure at point y. Several expression of this function have been obtained (see e.g. Wehausen and Laitone [17], Martin [13], Clément [2]).
![]() , (9)
, (9)
where y′ is symmetric to y with respect to the plane x3=0, R and Z are two functions of x and y given by
![]() ,
,
and Hν is defined by
![]() , (10)
, (10)
where the symbol “Pv” denotes the principal value of the integral, and J0 is the Bessel function of the first kind and of order 0 (see [X]).
It is well-known that any solution φ of problem Ρν satisfies the integral representation formula
![]() , (11)
, (11)
where we denote by ![]() and
and ![]() , respectively, the single and double layer surface potentials with density a and b :
, respectively, the single and double layer surface potentials with density a and b :
![]() , (12)
, (12)
![]() . (13)
. (13)
As a consequence, if Σ ⊂ Ω is surface surrounding Г as shown in Fig. 2, we have
![]() , (14)
, (14)
where Qα denotes the boundary operator on Σ
![]() , (15)
, (15)
and α is a complex parameter. Note that the two terms in the right-hand side of (14) simply write
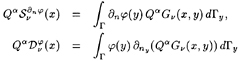
since Г and Σ have no point in common : Gν(x,y) is thus a regular function, which justifies the permutation of the integral sign with Qα.
Consider then the bounded domain ![]() ⊂ Ω located between Г and Σ, and let Ŝ denote the part of S contained in the boundary of
⊂ Ω located between Г and Σ, and let Ŝ denote the part of S contained in the boundary of ![]() (see Fig. 2). Property (14) together with Eqs. (1) to (6) of Ρν clearly show that the pair
(see Fig. 2). Property (14) together with Eqs. (1) to (6) of Ρν clearly show that the pair ![]() (where
(where ![]() denote the restriction of φ to
denote the restriction of φ to ![]() ) is a solution of the following problem, denoted by Ρv in the sequel:
) is a solution of the following problem, denoted by Ρv in the sequel:
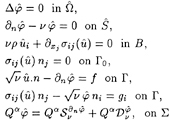 . (16)
. (16)
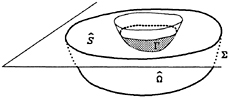
Figure 2: The bounded domain.
Figure 3: The auxiliary problem.
The point is to prove that for a suitable choice of the parameter α, every solution of this latter problem leads to a solution of Ρv by extending ![]() outside
outside ![]() . Using the method described by Jami and Lenoir [8], it may be easily seen that if (
. Using the method described by Jami and Lenoir [8], it may be easily seen that if (![]() ,û) is a solution of
,û) is a solution of ![]() and if the parameter α has a nonzero imaginary part, then the pair
and if the parameter α has a nonzero imaginary part, then the pair
is a solution of the initial problem Ρν. More precisely, this result holds provided that α and ν are chosen such that the following auxiliary problem has no solution but zero :
Δψ=0 in Ω′,
∂nψ−νψ=0 on S′,
Qαψ=0, on Σ, (17)
where Ω′ denotes the domain located inside Σ when the body is removed, and S′ is the part of the free surface contained in its boundary (see Fig. 3). In particular, when α is real, this is a classical eigenvalue problem whose solutions form a sequence of real numbers (νn; n ∈ N) which tends to +∞ : these values of ν are referred to as “irregular frequencies”. If α has a non-zero imaginary part, these frequencies become complex: they are located in the same half plane (C+ or
C−) as α. Indeed, by multiplying Lapace's equation by ![]() , integrating in Ω′ and using Green's formula, we obtain
, integrating in Ω′ and using Green's formula, we obtain
by virtue of the boundary condition in (17). The imaginary part of this expression must be zero. As a consequence, if Im α and Im ν have opposite signs, the only solution is ψ=0 (since ψ=0 on S′ and Σ implies ∂nψ=0 by (17), from which we deduce that ψ vanishes everywhere in Ω′). It follows that there is no irregular frequency in the half plane opposite to α.
In the sequel, we will assume that
Im α>0, (18)
which shows in particular that for every real positive ν, the initial problem Ρν and the reduced one ![]() are equivalent.
are equivalent.
2.3
Analytic continuation.
By virtue of the equivalence between Pν and ![]() , the extension of Ρν to complex frequencies clearly amounts to extending
, the extension of Ρν to complex frequencies clearly amounts to extending ![]() : this is of course far easier, for the question of the asymptotic behaviour of φ at infinity has now disappeared (since
: this is of course far easier, for the question of the asymptotic behaviour of φ at infinity has now disappeared (since ![]() is set in a bounded domain). From Eqs. (16) of
is set in a bounded domain). From Eqs. (16) of ![]() the only difficulty to construct this extension lies in the Green function Gν. Vullierme-Ledard [16] has shown that Gν actually has an analytic continuation in the complex plane where ν=0 is a logarithmic branch point. This means that Gν may be extended to an infinite-sheeted Riemann ν-plane. However, from a practical point of view, it is enough to consider an extension of Gν in a simply connected domain of C \ {0}, as for instance C\R−.
the only difficulty to construct this extension lies in the Green function Gν. Vullierme-Ledard [16] has shown that Gν actually has an analytic continuation in the complex plane where ν=0 is a logarithmic branch point. This means that Gν may be extended to an infinite-sheeted Riemann ν-plane. However, from a practical point of view, it is enough to consider an extension of Gν in a simply connected domain of C \ {0}, as for instance C\R−.
A very simple way to prove this analyticity result (first obtained by Vullierme-Ledard) consists in rewriting the expression (10) of Hν (involved in the definition (9) of Gν) in the form of a Cauchy integral. First note that from the Cauchy 's integral formula, we know that for a positively oriented circle γ of radius ε, whose interior contains ν but not 0, we have
![]() ,
,
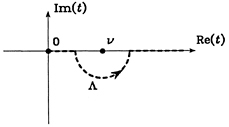
Figure 4: The path Λ for real ν.
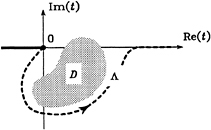
Figure 5: The case of complex ν.
since function etZJ0(tR) is analytic (in C\R−). From the property
![]() ,
,
we deduce
![]() ,
,
and
![]() ,
,
where γ− is the part of γ located in C−. As a consequence, function Hν may be expressed as follows:
![]() , (19)
, (19)
where Λ denotes a curve in the complex plane such as the one shown in Fig. 4. In fact, we can choose for Λ any curve going from 0 to +∞ which lies below the singular point t=ν.
The analytic continuation of this function does not raise any difficulty. If D is a bounded domain
of C\R−, we can always find a path Λ which lies below all the points of D (see Fig. 5). For such a path and for fixed R and Z, the integral in (19) defines an analytic function of ν in D (see e.g. Henrici [7]). This is the unique analytic continuation of Hν in D. The analyticity of the Green function in C\R− follows.
This property allows us to define now problem ![]() for every ν ∈ C \ R−. The main result concerning this extension of
for every ν ∈ C \ R−. The main result concerning this extension of ![]() lies in the fact that the solution of
lies in the fact that the solution of ![]() is a meromorphic function of ν. More precisely, if
is a meromorphic function of ν. More precisely, if ![]() denotes the solution operator associated with
denotes the solution operator associated with ![]() , i.e., the linear operator which maps the datum (f,gi) onto the solution (
, i.e., the linear operator which maps the datum (f,gi) onto the solution (![]() ,û) of ,
,û) of , ![]() we have proved that
we have proved that ![]() depends analytically on ν in C\R− except in the vicinity of isolated points which are poles of
depends analytically on ν in C\R− except in the vicinity of isolated points which are poles of ![]() . This property follows from a theoretical result of Steinberg [15] which concerns the inverse of Fredholm operators (see e.g. [4] for more details). The poles of
. This property follows from a theoretical result of Steinberg [15] which concerns the inverse of Fredholm operators (see e.g. [4] for more details). The poles of ![]() are nothing but the values of ν ∈ C\R− for which problem
are nothing but the values of ν ∈ C\R− for which problem ![]() is ill-posed. In others words, ν is a pole of
is ill-posed. In others words, ν is a pole of ![]() if there exists a nonzero pair (
if there exists a nonzero pair (![]() ,û) solution of the homogeneous problem associated with
,û) solution of the homogeneous problem associated with ![]() :
:
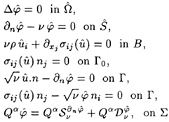 .(20)
.(20)
Before describing how to compute these poles, let us notice that they can be divided into two families : the irregular frequencies and the scattering frequencies.
-
The former family is related to the method which allows us to exhibit the analytic continuation of the initial problem: these are the values of ν for which the reduced problem is
 singular although the initial problem is well-posed. Indeed, it may be easily seen that the solutions of the auxiliary problem (17) are poles of
singular although the initial problem is well-posed. Indeed, it may be easily seen that the solutions of the auxiliary problem (17) are poles of  . By virtue of the assumption (18) on the sign of Im α, these irregular frequencies are located in the upper complex half plane C+. They obviously depend on the choice of the boundary Σ, as well as the parameter a, since these are the solutions of (17).
. By virtue of the assumption (18) on the sign of Im α, these irregular frequencies are located in the upper complex half plane C+. They obviously depend on the choice of the boundary Σ, as well as the parameter a, since these are the solutions of (17). -
On the other hand, the scattering frequencies are intrinsic quantities of the system, for they do not depend on the method which allows us to characterize them. They are located either on the real positive axis R+ or in the lower complex half plane C− (since the extension of Pν is well-posed for every ν ∈ C+, see § 2.1).
Of course, among these two families, the scattering frequencies are the poles we are interested to compute.
2.4
Determination of scattering frequencies.
We show in this section that the determination of scattering frequencies amounts to solving a nonlinear eigenvalue problem. Let us first rewrite the homogeneous problem (20) in variational form.
On one hand, multiplying Laplace's equation by a test function ![]() defined in
defined in ![]() and integrating by parts leads to
and integrating by parts leads to
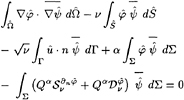 , (21)
, (21)
by virtue of the boundary conditions on ![]() , Г and Σ. On the other hand, multiplying the dynamic equations of the body by a test function
, Г and Σ. On the other hand, multiplying the dynamic equations of the body by a test function ![]() =(
=(![]() 1,
1,![]() 2,
2,![]() 3) defined in B yields
3) defined in B yields
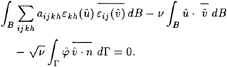
(22)
Let ![]() (respectively) denote
(respectively) denote ![]() the pair (û,
the pair (û,![]() ) (respectively the pair of test functions (
) (respectively the pair of test functions (![]() ,
,![]() )). Consider then the following sesquilinear forms
)). Consider then the following sesquilinear forms
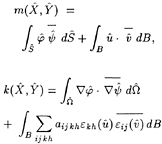 ,
,
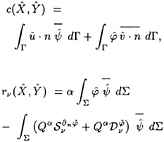 .
.
The form m represents a mass term, k is a stiffness term, c is a coupling term between the fluid and the structure, and rν results from the integral representation formula.
By adding the two variational equations (21) and (22), we finally obtain the variational formulation of the homogeneous problem (20) : a scattering frequencies is a complex value ![]() such that there exists a non-zero
such that there exists a non-zero ![]() pair which satisfies
pair which satisfies
(23)
for every pair of test functions ![]() .
.
This problem may be seen as a nonlinear eigenvalue problem. Indeed, if we denote by λk(ν) any eigenvalue of the following (linear) eigenvalue problem
where ν is considered as a fixed parameter, problem (23) clearly amounts to solving
λk(ν)=v. (24)
This equation is a (nonlinear) fixed point equation (since λk(ν) does not depend linearly on v).
3
Results
3.1
Mélina the finite element code
The numerical results displayed in this paper have been provided by the finite element code Mélina, which has been developped jointly at E.N.S.T.A. and I.R.M.A.R. This fortran code is a library of procedures the most important of which are essentially written to be put together to build straightforwardly a main program to solve P.D.E.'s in either 2 or 3 dimensions. As a matter of fact this set of procedures can be seen as a rather general toolbox for finite element processing and numerical matrix algebra.
This code has been written as to build easily and quickly a great amount of numerical applications for the solution of P.D.E.'s using a finite element scheme without going through tedious programming. For instance and starting from scratch, the main program and two main procedures which involve the nonlinear computation of ‘resonant frequencies' by the secant rule (regula falsi), including the assembly of the matrices of a three-dimensional problem and the computation of eigenvalues using an inverse iteration scheme at each nonlinear iteration, was build in a couple of days by a new user of the code (numerical evaluation of the Green function extended to complex-valued frequency is not included!).
The essential part of the development of such an application of M élina lies in a direct transcription of a (discretized) variational formulation and the choice of a solving algorithm which in most cases reduces to simple CALL's to the so-called high level procedures of the toolbox.
The description of the components of a variational formulation is easily done through the use of a vocabulary of precise keywords. The sentences built upon those keywords can be entered either as a data file or as procedure arguments.
Figure 6: Discretization
Those components or more generally objects handled in the code, which are only referred to with their name, are closely related (or even symbolically identical) to the entities of the mathematical formulation of the problem. Those objects are for instance (meshed) domains defined in the mesh data file by a name, e.g. ‘OMEGA', ‘S', ‘SIGMA' and associated with a list of elements or element boundaries, integrals terms such as the finite element stiffness matrix corresponding to ![]() (‘RIGID') or the f.e. mass matrix
(‘RIGID') or the f.e. mass matrix ![]() (‘MASS') from equ. 2 of (16), data constants or functions.
(‘MASS') from equ. 2 of (16), data constants or functions.
With this symbolic representation of data the typical typing of some steps of a solving process reads (though in French!) closely to
-
compute f.e. term ‘RIGID' on domain ‘OMEGA' (with a list of simple attributes, mainly the type of the integrand and quadrature scheme)
-
compute f.e. term ‘MASS' on domain ‘S'
-
proceed with the assembly of preconditionning matrix P (with the list of the components of the linear combination)
-
proceed with the assembly of the matrix A and if necessary right-hand side b of the linear system
-
solve system Ax=b by conjugate gradient preconditionned by matrix P, or compute generalized eigenvalues for A(ν)x=λ(ν)Bx
As the toolbox is mainly used at E.N.S.T.A. for solving wave propagation problems in unbounded domains, two specific tools for their solution have been developped: the computation of the coupling integral terms of the method of coupling of finite element and integral representation [5] and the boundary terms of the localized finite element method (see e.g. [4] in the 2-D case). Moreover as the formulations of those methods generally lead to non-symmetric linear systems with complex coefficients, efficient iterative gradient methods such as the (preconditionned) biconjugate gradient or conjugate gradient squared are available from the toolbox as high level procedures (the arguments of which are essentially the names of the matrice(s), right-hand side and solution vectors).
The field of applications which have been developped with Mélina encompasses many wave propagation phenomena such as those involving gravity waves (sea-keeping or wave resistance problems in ship hydrodynamics), acoustic waves (Helmholtz' equation and the like), optical wave guides (or integrated optics problems) and more generally electromagnetic wave problems (Maxwell's equation). A complete description of this finite element code and worked out examples of applications can be found in great details in [3].
3.2
Computional aspects of Green function evaluation
Under the form given in (19) Hν is not well suited for computational efficiency, we thus give below the two main expressions we have used for practical implementation of the Green function in the complex domain of frequency ν; similar expressions can be obtained easily for the derivatives of Hν which are required in the computation of the ‘coupling' terms of (21) or discretized sesquilinear form rν in (23) (see other expressions in the real positive domain of ν's in [13]).
Using the following integral definition of Bessel first kind function: ![]() , function Hν (19) can be written as the double integral
, function Hν (19) can be written as the double integral
![]() .
.
After a change of variables of integration and with help of formula ![]() =π(a2+ b2)−1/2, which holds for any complex a and b with a2+b2>0, and with the following relation between Bessel second kind function Y0 and Struve function H0 ([1] chap. 12):
=π(a2+ b2)−1/2, which holds for any complex a and b with a2+b2>0, and with the following relation between Bessel second kind function Y0 and Struve function H0 ([1] chap. 12):
we get the first expression for Hν:
(25)
which is well suited on the computational point of view for non vanishing R (or practically for a not too large −Z to R ratio).
Another formula for Hν is obtained by performing the change of integrals in the double integral formula:
(26)
with q(θ)=Z+iRcosθ and where E1(z)= ![]() is the complex integral exponential function ([1] chap. 5) with a cut in the complex plane along the real positive axis and with a path of integration Гz which is any curve starting from z, with Re z≤0, going to +∞ and lying below the origin. This latter formula is used for non vanishing Z (or a rather large −Z to R ratio).
is the complex integral exponential function ([1] chap. 5) with a cut in the complex plane along the real positive axis and with a path of integration Гz which is any curve starting from z, with Re z≤0, going to +∞ and lying below the origin. This latter formula is used for non vanishing Z (or a rather large −Z to R ratio).
The integrals of expressions (25) and (26) are evaluated using Simpson 's quadrature rule. Bessel functions J0(1) and Y0(1) with complex arguments where computed by ascending series [1], rational approximations or Hankel's asymptotic expansions [1] according to the magnitude of their complex argument. Struve functions H0(1) was computed by ascending series [1] or rational approximations found in [12]. A few numerical tests
show that the criterium for switching from expression (25) to expression (26) of Hν, either for computional accuracy or for time-consuming considerations, is the crossing of the line −Z=10×R of the real (R, Z)-plane.
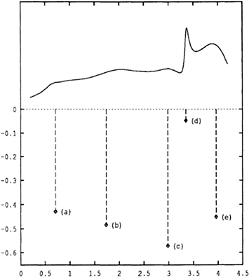
Figure 7: Symmetrical excitation
Figure 8: Vicinity of a scattering frequency : symmetrical case
3.3
Numerical experiments
The numerical results given below correspond to the excitation of a two-hull body (‘catamaran') floating on an infinitely deep ocean by an incident time-harmonic swell. The non-dimensionnal data of the body as shown on Figure 6 are respectively 2.5 for length and 1. for width and depth of each hull; the hull are 1. apart in the transverse direction. Figures 7 and 9 show response curves of the body, i.e. the total energy transmitted to the body with respects to the real frequency squared (ν). The upper part of figure 7 shows the energy
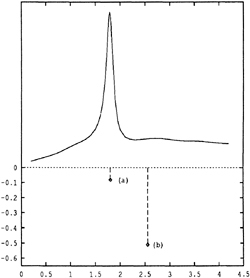
Figure 9: Antisymmetric excitation.
Figure 10: Vicinity of a scattering frequency : antisymmetric case
response curve to an incident swell of the form φw(x,y,z)=eν(z+ix) symmetrized with respect to the vertical planes of coordinates. On the lower part of this figure the scattering frequencies (ν*) are displayed. As one can see their locations in the direction of Re(ν)'s are in good agreement with the peaks and bumps of the re-
sponse curve, with a shift along the direction of Re(ν)'s which is predicted by theory as being of order of (Im(ν*))2 [6]. Moreover as is as well shown by theoretical calculations, when considering the expansion of the solution in the vicinity of a given ν*, the smaller the imaginary part of Im(ν*), the higher and sharper the peak or bump of the response curve. An analogous phenomenon is illustrated on Figure 9, where the energy curve corresponds to an incident swell which is antisymmetric with respect to the transverse direction of the body. Finally on figure 8 (resp. 10), we give the response surface over a complex domain of ν's in the vicinity of the scattering frequency (b) of figure 7 (resp.8). One can easily observe the location of the pole located at (b) of the analytic continuation in C− as a meromorphic function of ν of the approximated resolvent operator.
References
[1] M.ABRAMOWITZ AND I.A.STEGUN. Hand-book of mathematical functions. Dover, New York, 1976.
[2] A.CLÉMENT. Optimisation du calcul de la fonction de Green de la tenue à la mer en profondeur infinie. Rapport de Recherche Nº 165, ENSTA, Palaiseau, France, 1982.
[3] O.DEBAYSER AND D.MARTIN. Mélina, un code d'éléments finis pour les problèmes extérieurs: application à l'hydrodynamique navale. In 91ème session de l'ATMA, Paris, Mars 1991.
[4] C.HAZARD. Etude des résonances pour le problème linéarisé des mouvements d'un navire sur la houle. PhD thesis, Université Pierre et Marie Curie, Paris, 1991.
[5] C.HAZARD AND M.LENOIR. Determination of scattering frequencies for an elastic floating body. SIAM J. Math. Anal., 24, pp. 1458–1514, 1993.
[6] C.HAZARD, M.LENOIR, AND D.MARTIN. Integral representation of resonant states. in preparation.
[7] P.HENRICI. Applied and computational complex analysis (3 vol.). Wiley, New York, 1974.
[8] A.JAMI AND M.LENOIR. A variational formulation for exterior problems in linear hydrodynamics. Comp. Meth. Appl. Mech. Eng., 16, pp. 341–359, 1978.
[9] F.JOHN. On the motion of floating bodies— I. Comm. Pure Appl. Math., 2, pp. 13–57, 1949.
[10] M.LENOIR AND D.MARTIN. An application of the limiting absorption principle to the motion of floating bodies. J. Math. Anal. Appl., 79, pp. 370–383, 1981.
[11] M.LENOIR, M.VULLIERME-LEDARD, AND C.HAZARD. Variational formulations for the determination of resonant states in scattering problems. SIAM J. Math. Anal., 23, pp. 579–608, 1992.
[12] Y.L.LUKE. Mathematical functions and their approximations. Academic Press, New-York, 1975.
[13] D.MARTIN. Etude théorique et numérique du problème linéarisé du mouvement sur la houle tridimensionnel . PhD thesis, Université de Rennes, France, 1980.
[14] J.NECAS AND I.HLAVÁČEK. Mathematical theory of elastic and elasto-plastic bodies. Elsevier, Amsterdam, 1981.
[15] S.STEINBERG. Meromorphic families of compact operators. Arch. Rational Mech. Anal, 31, 1968.
[16] M.VULLIERME-LEDARD. Problèmes a-symptotiques de l'hydrodynamique navale linéarisée et du couplage fluide-structure. PhD thesis, Université Pierre et Marie Curie, Paris, 1987.
[17] J.V.WEHAUSEN AND E.V.LAITONE. Surface waves, in Encyclopedia of Physics. Volume 9, Springer Verlag, 1960.
[18] X.J.Wu, Y.WANG, AND W.G.PRICE. Multiple resonances, responses, and parametric instabilities in offshore structures. Journal of Ship Research, 32, No. 4, pp. 91– 93, 1988.
Prediction of Nonlinear Hydrodynamic Characteristics of Complex Vessels Using a Numerical Time-Domain Approach
B.Maskew, D.M.Tidd, and J.S.Fraser
(Analytical Methods, Inc., USA)
ABSTRACT
A general purpose numerical flow simulation method is being developed for treating complex hydrodynamic problems associated with arbitrary vessels advancing in large amplitude waves. The objective is to treat conditions experienced by modern high performance vessels that are beyond the scope of traditional linearized approaches.
The method uses a non-linear boundary element approach which treats the free surface deformation and finite amplitude vessel motions in a time-stepping procedure. Boundary layer effects and lifting effects are included in the calculations. The code computes total force and moment at each time-step by surface integration of pressure and skin friction loads. Body movement from step to step is computed by direct integration of the equations of motion.
Computed results for pitch and heave transfer functions compare very favorably with measured data for the ITTC S175 standard hull form and for a frigate advancing in head waves. The frigate case includes conditions of green water on the deck.
NOMENCLATURE
|
Cp |
Pressure coefficient |
|
dS |
Element of surface |
|
Fr |
Froude number, |
|
g |
Acceleration due to gravity |
|
L |
Hull length |
|
NH |
Number of active (wetted) panels on the surfaces |
|
NPAN |
Total number of active panels on the free surface and hull(s) |
|
|
Unit normal to the surface pointing into fluid domain |
|
p |
Static pressure |
|
pREF |
Ambient atmospheric pressure |
|
|
Position vector in normalized space |
|
LREF |
Reference length, L/2 |
|
t |
Time |
|
|
Normalized perturbation velocity, |
|
|
Perturbation velocity, |
|
VREF |
Reference speed |
|
x,y,z |
Normalized Cartesian coordinates, x=X/LREF, etc. |
|
X,Y,Z |
Cartesian coordinates, dimensional |
|
s |
Surface distance (normalized) |
|
μ |
Doublet density, |
|
σ |
Source density, −(∂ |
|
τ |
Normalized time, t · VREF/LREF |
|
ρ |
Water density |
|
|
Normalized velocity potential, |
|
Φ |
Velocity potential (units of length2/time) |
|
|
Angular velocity (normalized by VREF/LREF) |
|
λ |
Wave length (dimensional) |
INTRODUCTION
Although methods for analyzing ship hydrodynamic characteristics have progressed significantly in recent years, the theoretical prediction of motions of general, complex vessels proceeding in large amplitude waves is still a challenging problem (1). Strip theory, applied initially by Korvin-Kroukovsky (2) and developed further by Ogilvie and Tuck (3), Salveson et al (4), Kim et al (5), among others, is
|
*Paper presented at 6th International Conference on Numerical Ship Hydrodynamics, Iowa City, Iowa, August 2–5, 1993. |
probably the most accepted, practical tool for predicting motions and sea loads at this time. Even though they are based on linearized assumptions, strip theory methods have been used to analyze nonlinear effects (e.g., Chiu and Fujino (6) and Fang et al (7)); however, such applications are questionable, especially when dealing with large amplitude waves and large amplitude motions of general hull forms with possible conditions for slamming and green water on the deck. Also, the inherent difficulties of accounting for the interaction of steady and unsteady flow components in a consistent manner cannot be readily overcome for conditions at high Froude numbers or on hulls with non-vertical sides at the waterline.
Recent developments based on the three-dimensional Rankine panel method offer a potential improvement relative to the traditional strip theory approach. These developments include both frequency domain methods, e.g., Nakos & Sclavounos (8) and also time-domain approaches, for example, King, Beck and Magee (9), Lin and Yue (10), Nakos, Kring and Sclavounos (11). These methods employ body “exact” boundary conditions on the hull, but retain the linearized free surface boundary condition and therefore might miss important effects at the hull/water intersection line due to body flare, body motion, and the dynamic rise and fall of the water surface. Powlowski and Bass (12) presented a practical method for treating large amplitude ship motions in heavy seas. This uses a method of modal potentials and is based on a weak scatter hypothesis. The time-domain calculations use a set of model amplitudes which must be predetermined for each vessel and load condition.
The present work is part of an ongoing development towards a more general capability for complex vessels in large amplitude motions for which linearizing assumptions are inadequate. The basic method is the USAERO time-dependent code (13) which is a low-order boundary element method employing quadrilateral panels of uniform perturbation doublets and sources. The method includes a powerful geometry module with a number of convenient surface modeling features to help with complex paneling problems. Multiple moving frames of reference (user-defined) allow complicated relative motion problems to be treated, including control deflections, etc. The method includes dynamic vortex wake convection for lifting effects and certain extensive separated flow modeling. Routines developed by Dvorak ( 14) treat unsteady boundary layer characteristics, e.g., displacement effect and skin friction; these are fully coupled within the time-step loop and are driven by the instantaneous surface flow properties. The computed characteristics for boundary layer displacement effect modify the surface boundary condition in the following panel code solution, while the skin friction distribution contributes to the computed force and moment in the next step.
The method was extended for surface piercing vessels with a non-linear treatment of a piece of the free surface in the FSP module (15) (for Free-Surface Program). This applies the kinematic and dynamic boundary conditions on the wavy free surface, using a mixed Eulerian/Lagrangian formulation based on the work of Longuet-Higgens & Cokelet (16). The FSP module addresses the problem of free surface/hull interaction using an automatic repanelling procedure whose purpose is to maintain a “clean” panelling arrangement along the intersection line as the free surface moves relative to the vessel. Although the code can be used to evaluate added mass and damping terms for arbitrary vessels in general forced harmonic motion, the objective behind its development is the step-by-step integration of the equations of motion driven by instantaneous force and moment values.
A wave generator based on a harmonically oscillating velocity potential was added to the upstream “edge” of the free surface (17). This produces a train of incident waves for a moving vessel in a towing tank simulation. Preliminary results for large amplitude motions were presented earlier (18) at the start of a non-linear seakeeping investigation in which the 6 D.O.F., FPI module (19) (for Flight Path Integrator), is coupled with USAERO/FSP. This combined code is also being examined for maneuvering vessels in or near the free surface. Recently, a further extension added the capability for aero-elastic treatment of yacht sails and simultaneous Wind Over Water (WOW) aero/hydrodynamic analysis of complete sailing yachts (20).
The present paper gives further results from the non-linear seakeeping investigation of the coupled USAERO/FSP/FPI code. Calculations are compared with measured data for a frigate model in steep waves ( 21) and for the S175 ITTC standard container ship model (22). The method is covered in broad outline here as it is described more fully in earlier papers (17, 18). Recent developments include coupling with an “order (N)” iterative solver (23) which has significantly reduced computational
time and storage requirements, thereby removing earlier objections of excessive computational requirements for non-linear time-dependent analyses.
NUMERICAL MODEL
The main features of the numerical model are given below for completeness. A more detailed description of the formulation is included in Ref. 18.
The basis of the model is a time-stepping, boundary element formulation with coupled, unsteady, surface boundary layer analysis. The model includes a nonlinear dynamic treatment of the wake convection and free surface deformation. Body movements are treated step-by-step using a 6 degree-of-freedom (DOF) integration of the equations of motion driven by instantaneous computed forces and moments.
The basic problem to be treated consists of an arbitrary vessel undergoing large amplitude motions in or near the free surface. For generality, the vessel may have fixed or moveable lifting hydrofoils, control surfaces and propulsors. The flow region may extend to infinity or it may be bounded locally in towing tank or canal simulations or in shallow water. The vessel is assigned to a movingbody reference frame whose time-dependent location/orientation is described in a ground-fixed inertial Cartesian coordinate system. This has the X and Y axes in the undisturbed free surface and Z positive upwards, Fig. 1. The fluid motion is assumed to be described by a velocity potential, ![]() which satisfies Laplace's equation,
which satisfies Laplace's equation,
▽2Φ=0 (1)
Traditionally, Φ is broken down into a number of component parts to aid in the linearizing of boundary conditions. Here, however, no linearizing assumptions are made, so Φ is left as a whole quantity and therefore encompasses such terms as incident wave potential, diffraction potential, radiation potential, etc. The convention adopted here is that the fluid velocity, ![]() , is the negative gradient of the potential, i.e.,
, is the negative gradient of the potential, i.e.,
(2)
It is convenient to non-dimensionalize the problem with respect to certain reference quantities. A reference length, LREF is used to non-dimensionalize the geometry and a reference speed, VREF, is used to non-dimensionalize velocities. (LREF is usually chosen as half the hull length, L, and VREF is the mean speed of the vessel relative to the water.) In non-dimensional space, therefore, we have the quantities,
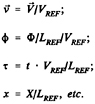
The potential flow is solved using Green's Theorem, which is discretized into a surface panel method based on quadrilaterals of uniform source and doublet singularities. This forms a set of simultaneous equations:
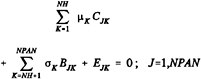
(3)
where
CJJ=−2π,
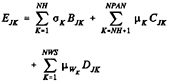
μK,σK are the doublet and source densities, respectively, on panel K.
CJK, BJK are the influence coefficients, respectively, for the uniform doublet and source on panel K acting at the control point of panel J (CJK and BJK are given in Maskew (24).
NH is the number of active (i.e., wet) panels on the hull surfaces.
NPAN is the total number of active panels on all local wetted surfaces, including the free surface. NWS is the total number of free, cross-flow wake segments; this number grows with time. μWK is the
doublet density at the Kth wake segment, and DJK is the influence coefficient for the linearly varying strength distribution over the pair of wake panels just upstream and just downstream of the segment. The influences of the wake segments that are about to be created at the shedding lines are combined with the local upper and lower shedding panel influences in the first term of Eq. (3) since these segment strengths are unknown at the start of each step. Some influence coefficients have to be re- evaluated at each time step—these include all wake panels, moving free-surface panels, and any hull panels which have relative motion with other hull panels or which have been modified by the repanelling procedure.
On the boundaries representing the “solid” surfaces, the source distribution is determined by the external Neumann Boundary Condition specifying the resultant normal velocity of the fluid.
(4)
where νNORM is the required resultant normal velocity, which is zero for a solid boundary and positive or negative, respectively, for outflow/inflow in propulsor modeling. νBL is the boundary layer displacement effect using the transpiration technique,
(5)
where νe is the relative flow speed at the edge of the boundary layer and δ* is the displacement thickness. The derivative is taken with respect to distance in the direction of the local external flow. νBL is zero for stationary boundaries and would be known from the previous step in a time-stepping calculation, ![]() is the body frame velocity and
is the body frame velocity and ![]() is the velocity of rotation about an axis in the body frame. Here,
is the velocity of rotation about an axis in the body frame. Here, ![]() is the position vector of the point in question relative to any point on the rotation axis.
is the position vector of the point in question relative to any point on the rotation axis. ![]() is the unit normal to the surface, and
is the unit normal to the surface, and ![]() is a possible uniform onset flow. The basic unknown on solid boundaries, therefore, is the doublet term which can be obtained from the solution of Eq. (3) at each step.
is a possible uniform onset flow. The basic unknown on solid boundaries, therefore, is the doublet term which can be obtained from the solution of Eq. (3) at each step.
The wake doublet distribution, μw, is essentially known at each step because it is the accumulation of all previous solutions. Basically, at each step a new set of wake elements is created along wake-shedding lines. Each element takes the instantaneous local jump in potential across the shedding line and moves along the local mean velocity vector. This satisfies the unsteady Kutta condition, which is obtained after specifying equal pressure across the separation line,
(6)
vM is the mean convection speed and s is measured in the direction of the local mean flow. μw is the instantaneous jump in doublet strength across the trailing edge, i.e., μw is the newly emerging wake strength.
On the free surface, the initial boundary conditions are that the ![]() and ∂
and ∂![]() /∂n (i.e., μ and σ) are zero, and that the pressure is uniform (Cp=0). The ambient pressure is assumed to be transferred directly to the fluid across the free surface, i.e., the effect of surface tension is neglected at this time. The kinematic condition on the free surface is satisfied by moving the particles with the local flow,
/∂n (i.e., μ and σ) are zero, and that the pressure is uniform (Cp=0). The ambient pressure is assumed to be transferred directly to the fluid across the free surface, i.e., the effect of surface tension is neglected at this time. The kinematic condition on the free surface is satisfied by moving the particles with the local flow,
(7)
Following a particle, the total derivative of ![]() is (from Bernoulli's equation)
is (from Bernoulli's equation)
(8)
Assuming for the moment that the free surface displacement z and perturbation velocity ![]() are known from the previous step, Eq.(8) can be integrated over a small time step to evaluate the current doublet distribution on the free surface. Given this, Eq.(3) can then be solved for the source distribution, (i.e., ∂
are known from the previous step, Eq.(8) can be integrated over a small time step to evaluate the current doublet distribution on the free surface. Given this, Eq.(3) can then be solved for the source distribution, (i.e., ∂![]() /∂n), on the free surface. This, together with the doublet gradient, provides the instantaneous perturbation velocity in Eq.(7). Integrating Eq.(7) then provides the free surface displacement for the next step, and so on.
/∂n), on the free surface. This, together with the doublet gradient, provides the instantaneous perturbation velocity in Eq.(7). Integrating Eq.(7) then provides the free surface displacement for the next step, and so on.
In summary, the simultaneous solution of Eq.(3) on the instantaneous locations of the free surface and hull configuration at each time step provides the complete doublet and source distributions. Basically, on the hull the source is known and the doublet is unknown, while on the free surface the doublet is known and the source is unknown. On
the wake surfaces, the doublet is essentially known and the source is zero.
After solution of the singularity values, the perturbation velocities can be evaluated directly on each panel:
(9)
The normal component, νN, is obtained directly from the panel source value,
νN=4πσ (10)
The tangential component, ![]() , is obtained from the surface gradient of the doublet,
, is obtained from the surface gradient of the doublet,
(11)
The doublet gradient is evaluated in two directions over each panel using a second-order differencing scheme over three panels in each direction. On the “solid” boundaries, the perturbation velocity is combined with the local velocity, ![]() , due to body motion to give the resultant velocity,
, due to body motion to give the resultant velocity,
Bernoulli's equation then provides the pressure distribution. This may be written in the form of a pressure coefficient using the non-dimensional quantities.
(12)
Where p is the local static pressure, PREF is the reference pressure, which is taken here as the ambient atmospheric value, ρ is the water density (constant). z is the height above the undisturbed free surface and Fr represents the Froude number, ![]() where g is the acceleration due to gravity. The z/Fr2 term represents the hydrostatic pressure coefficient.
where g is the acceleration due to gravity. The z/Fr2 term represents the hydrostatic pressure coefficient.
Eq.(12) gives the pressure coefficient at a stationary point in the ground fixed frame; the pressure observed at a point moving with velocity, ![]() , relative to the ground-fixed frame is,
, relative to the ground-fixed frame is,
(13)
where vR is the fluid velocity relative to the moving point and d![]() /dτ is the total derivative of
/dτ is the total derivative of ![]() experienced by the moving point.
experienced by the moving point.
The pressure coefficient, Eq.(13), can be evaluated at each panel center. The ![]() term is evaluated using second-order forward differencing based on the current and two previous solutions.
term is evaluated using second-order forward differencing based on the current and two previous solutions.
The pressure distributions can be integrated over the surface of each part of the configurations to provide the force coefficient,
(14)
and moment coefficient,
(15)
where ![]() is the position vector of a surface element relative to a selected moment reference point, and Cf is the skin friction coefficient from a boundary layer analysis based on the current surface velocity distribution.
is the position vector of a surface element relative to a selected moment reference point, and Cf is the skin friction coefficient from a boundary layer analysis based on the current surface velocity distribution.
The above coefficients are based on an area of LREF2 and a moment arm divided by LREF. They include the effect of hydrostatic pressure (the z/Fr2 term in Eq.(13)), and therefore include the buoyancy force and moment. The 6 DOF response of the vessel to free-surface deformation can therefore be computed by integrating the equations of motion over each time step.
The wetted surfaces of surface-piercing objects, hulls, channel walls, etc. are modified by the deforming free surface and by the movement of the vessel. These effects are accounted for in the numerical treatment of the model.
NUMERICAL PROCEDURE
A brief outline of the numerical procedure is given below; a more detailed account of the basic method is given in Ref. 18. Referring to the numbered steps in the flow chart in Fig. 2.
-
Discretization of the configuration surface into a panel model with uniform source and doublet distributions on quadrilateral panels is fairly standard, except that automatic proce dures distribute the panels over user-defined
-
patches which may be assigned to various moving frames of reference. Motion/orientation schedules versus time may be defined for each frame by the user.
-
At the outset of a time step the current panel geometry is assembled in the ground-fixed frame based on the instantaneous location/orientation of the various reference frames used in the current configuration.
-
An automatic routine then identifies the instantaneous lines of intersection where the free surface meets the hull(s), and repanels both the hull and free surfaces to the intersection line to ensure a smooth matching of panels at the critical junction. During the process, panels are marked as either “wet” or “dry”. Dry panels are temporarily discarded from the current solution process. Another intersection routine monitors vortex wake impingements at solid surfaces and ensures that active wake elements do not arrive inside the body regions; this would violate the basic Dirichlet boundary condition of zero flow perturbation inside the bodies.
-
Influence coefficients are assembled for panels acting on collocation points. Solution of the singularities proceeds as follows: the wet panels are assembled and a solution of Eq.(3) is processed. On the hull panels the doublet values are the unknown, while the source values are evaluated using the expression in Eq.(4). On the free surface panels, the doublet values are known from the previous time step and the source values are unknown. When the solution has been obtained, the free-surface source distribution provides the normal velocity of the free surface, which is used later (in step 8) when satisfying the kinematic boundary condition on the free surface. Whereas in the earlier calculation (17, 18) several hours of computer time were required to run a wave tank simulation, recent advances in fast iterative solvers have given more than an order of magnitude speed up. Most of the cases reported herein were run using the MIT Fastlap (23) solver, which has now been coupled to USAERO.
-
With the complete set of panel singularities known, the analysis proceeds as follows. First, a two-way derivative of the surface doublet distribution provides the perturbation velocities and, hence, pressures on all surfaces—hull, keel, rudder and free surface. The unsteady pressure term in Eq.(13) is evaluated by a second-order finite difference of the doublet values with respect to time. The instantaneous pressure distribution is integrated over each “solid” surface to provide the current force and moment vectors and their spatial distributions. The computed data is stored step-by-step in a plot file for subsequent post processing and graphical display.
-
Instantaneous surface streamlines are traced over the hull, keel, rudder, etc.; unsteady integral boundary layer calculations then provide boundary layer characteristics, such as displacement source term and skin friction coefficient, for the next step. The former modifies the boundary conditions (Eq.(3)), while the latter is included in the force and moment integration, Eqs. (14, 15).
-
Wake elements are convected with the local computed flow for the small time step. The local perturbation velocities are evaluated by summing all panel (surface plus wake) singularity contributions. These are added to the appropriate onset flow. A new set of wake panels is constructed along the wake shedding lines at each step according to the local Kutta condition, Eq.(6).
-
The free surface is treated as follows. First the kinematic boundary condition is satisfied by integrating Eq.(7) over the small time step. This provides the free surface geometry for the next time step. The new doublet distribution is evaluated by integrating Eq.(8) over the small time step. An oscillating potential is applied on the upstream strip of panels which acts as a wave generator.
-
The integrated force and moment values assembled for the body reference frame are transferred to the 6-DOF FPI module. The 6 DOF module solves the equations of motion for a rigid body, assuming that the mass of the body and the mass distribution are constant over time. The 6 DOF module is activated once the force/moment characteristics on the vessel have stabilized, which typically only takes a few time steps to achieve. The starting point is to calculate the hydrodynamic forces and moments acting on the vessel from the coefficients calculated by USAERO/FSP. The external forces such as thrust or gravity are then added to these. Given the force/ moments, the nonlinear equations of motion
-
can be solved for the accelerations, based on computed velocities at the previous timestep. Next, the velocities in the body axes system are updated, based upon known accelerations at the present timestep. This is done using a simple Euler scheme for the calculations described in this paper. Higher order Adams-Bashforth multi-step methods using additional accelerations from previous timesteps have not currently been found to be advantageous. From the velocities, a new orientation of the body in terms of Euler angles can be calculated using a transformation and a further call to the integration scheme. Similarly, the new position of the body relative to the ground-fixed coordinate system can be obtained with a transformation and a final call to the integrator. The new position and orientation of the body is then passed back to USAERO for a revised calculation of the hydrodynamic force/moment data to continue the time-stepping loop of the procedure.
RESULTS
Motions of a Floating Body
As a basic validation exercise of the free motion capability of the method, the decaying motions of a freely floating sphere were computed following an initial displacement of 0.5r where r is the sphere radius. The resulting trace of heave versus time initially follows closely to the measurement of Liapis (25), but with slightly heavier damping (see Fig. 3). The calculated trace is more complicated at a later time when the radiated wave is reflected from the far boundary. The present calculations do not include treatment of the waves arriving at the outer boundaries. Usually, in forward speed cases at least, there has been no need to treat the reflected wave problem. The stationary case, however, needs a wave absorber at the boundary such as the approach described by Nakos et al (11), or Beck and Cao (26).
S175 ITTC Hull Form
A panel model of the S175 hull was constructed using approximately 800 panels. This was placed in a truncated free surface approximately 5L, long by 2.2L wide where L, the length of the hull model, is 3.5 metres in this case. The model was placed 2.5L downstream from the wave-maker.
The hull lines are shown in Fig. 4. A general view of the model and free surface paneling is shown in Fig. 5.
Experimental data reported in Ref. 22 were measured in the U.S. Naval Academy Hydrodynamics Laboratory 116 meter long towing tank. This facility has a dual-flap hydraulically driven wavemaker. Principle characteristics of the S175 hull form —used for comparative studies by the ITTC, are given in the following table.
Table 1. S175 Model Characteristics.
|
Length (Lpp) |
3.5m |
|
Beam |
0.51m |
|
Draft |
0.19m |
|
CB |
0.572 |
|
Ryy/Lpp |
0.24 |
|
Displacement |
193.2kg |
The towing speed case considered here is 1.61m/sec. giving a length Froude number of 0.275.
The calculations start with wave calibration runs in which the period and amplitude of the oscillating velocity potential wave-maker are varied. These cases are run with just the truncated free surface, i.e., the hull model is removed. Precise amplitude and frequency of the generated wave are difficult to obtain at this time, owing to non-linear dependencies. Alternative wave-maker models will be considered in the future. The model will then be extended to include random waves and oblique wave conditions and a Fourier analysis will be applied to the incident wave and the body motion/orientation parameters. In the model used here, the free surface paneling moves with the vessel, thereby eliminating the panel matchup problems encountered in earlier calculations (18) in which the vessel moved through a stationary free surface paneling. In the present model, therefore, the wave-maker strip, being at the upstream “edge” of the free surface, moves with the body frame. It's oscillation is therefore related to the encounter frequency rather than the absolute frequency used earlier. Use of this “moving” free surface allows many more wave encounters to be achieved in a realistic computer time. Also, the earlier restriction which required that the hull step movement be closely related to the x-wise panel size on the free surface has now gone.
The present calculations used a time step increment of .03 seconds. This corresponds to
approximately 70 time steps for a forward movement of 1 hull length. Fig. 6 shows the transfer functions for pitch, heave, and also acceleration. The latter was measured at a point 0.15 Lpp from the bow perpendicular. The values are plotted as a function of wave slope, ka, for two non-dimensional encounter frequency values, σe of 3.352 and 3.728. k is the wave number, 2π/λ, a is the wave amplitude and σe is defined as ![]() . ωe is the wave encounter frequency.
. ωe is the wave encounter frequency.
The heave function is heave amplitude divided by wave amplitude, i.e, z/a; the pitch function is pitch angle divided by wave slope, ka; the acceleration function is ![]() Lpp/(ga). For the experimental data points the amplitudes are the first harmonic term from a Fourier analysis over approximately 10 full cycles. Most of the calculated points are from runs which had less than five wave encounters and so a Fourier analysis was not attempted here: the amplitudes for the calculated points are the average amplitude over the last two wave encounters in each case. This is a temporary measure to get an idea of the general quality of the results, and should be satisfactory at the lower wave slopes where the time traces are fairly regular, but is not very good at the higher wave slopes, especially when the bow takes green water. The latest calculations are covering more cycles thanks to the new matrix solver—and so a Fourier analysis is being added to the routine to process the data.
Lpp/(ga). For the experimental data points the amplitudes are the first harmonic term from a Fourier analysis over approximately 10 full cycles. Most of the calculated points are from runs which had less than five wave encounters and so a Fourier analysis was not attempted here: the amplitudes for the calculated points are the average amplitude over the last two wave encounters in each case. This is a temporary measure to get an idea of the general quality of the results, and should be satisfactory at the lower wave slopes where the time traces are fairly regular, but is not very good at the higher wave slopes, especially when the bow takes green water. The latest calculations are covering more cycles thanks to the new matrix solver—and so a Fourier analysis is being added to the routine to process the data.
The calculations compare favorably with the experimental measurements and display the nonlinear characteristics with respect to wave slope. Note that the σe values in the calculation are not precisely the same as the experimental values. More calculations are being pursued at the higher wave slopes. There have been some difficulties owing to the bow taking green water. The panel model was constructed without a deck and so when the bow becomes submerged, the calculation does not get the download due to water above the deck—consequently, the resulting heave force and pitching moment have an excessive positive value during the part of the cycle when the bow is immersed. Future calculations will include a deck representation in the panel model. However, when pursuing the green-water-on-deck conditions, the question on how detailed a model is required for representing the energy losses in the water jet and spray during slamming encounter has yet to be addressed. The present repanelling procedure in the panel model has to be made more robust before such issues can be addressed with the present approach.
Some general views of the calculated dynamic pressure distribution on the hull at different stages of a wave encounter are shown in Fig. 7. This detailed information can be integrated to provide unsteady shear force and bending moment distribution along the hull.
Frigate Hull
Experimental data are available from a series of tests on a frigate model in steep head waves (21). The results cover fairly extreme conditions, including water on the deck, and cover a range of bow shapes, Fig. 8. The main particulars of the model are given in Table 2 below.
Table 2. Frigate Model Characteristics.
|
Model Length; Lpp |
4.5m |
|
Beam |
0.496m |
|
Draft |
0.163m |
|
CB |
0.454 |
|
Ryy/Lpp |
0.277 |
|
Displacement |
165Kg |
The model was free to pitch and heave, but restrained in surge. The conditions used for comparison here are at a Froude number of 0.3.
Fig. 9 shows views of the panel model for the parent hull and free surface, and Fig. 10 shows the time history of the encountered wave height computed about Lpp/4 ahead of the bow. This shows the regular behavior of the computational wave maker. Fig. 11 shows the heave and pitch response function plotted against λ/L. In general, the calculations compare favorably with the measured data. Cases involving steeper waves—i.e., H/λ greater than .02 (where H is the wave double amplitude), also involve water over the bow and need further investigation as discussed for the S175 hull. In the present case, although the deck was panelled, the automatic repanelling procedure did not behave consistently when the bow became submerged. The complete procedure is being reviewed and a more robust scheme will be installed shortly.
Fig. 12 displays the heave and pitch transfer functions plotted against H/λ for a nominal λ/L= 1.2. The calculated heave transfer tends to be higher than the measured value, but the H/λ value for these points is at 1.14 and so is closer to resonance. The computed pitch transfer functions tend to be on the low side but again, because of a slightly lower λ/L, the conditions are moving down the
steep drop off in the pitch versus λ/L data seen in Fig. 11.
Fig. 13 shows a plot of deck wetness as a function of H/λ. The calculated values for the parent hull are simply the average free surface height over the foredeck during an encounter. This is not very precise at this time, and there are uncertainties over the deck solution as discussed above. However, the trends are certainly encouraging. A similar case has been run with the bow2 variation, but did not show any major change in the wetness measurement, whereas the experimental data does show a tendency for reduced wetness level for this hull. It may be that a greater panel resolution should be used when trying to calculate these more extreme cases, however, bad behavior in the repanelling procedure is certainly affecting these results and is partly responsible for spikes seen in the time response curves of the heave force and pitching moment when the bow becomes submerged (see Fig. 14). Although of short duration, the spikes must have some effect on the integrated pitch and heave responses—certainly the troughs in these traces are much sharper than the peaks. Even so, it is encouraging to see the response amplitudes settle down in the last two encounters. The flared hull (bow2) displays a slight phase lag and higher peak values in the heave force and pitching moment compared with the parent hull. This would be consistent with the expected increased flare slam load (computed earlier under forced motion conditions (18)), however, the current difficulties on repanelling as the water goes over the bow may be influencing the trace here and needs further investigation.
Finally, in Fig. 15, four frames show the frigate at various stages in a wave encounter. The colors depict free surface elevation. The conditions are λ/L=1.2 and H/λ=.021 at Fr=0.3.
Most of the calculations presented here were run on a Silicon Graphics Indigo workstation. Each case involved approximately 2500 panels and 250 time steps, and took approximately four hours to complete, thanks to the new matrix solver (23).
CONCLUSIONS
The present results show a very encouraging progress in the development of a general non-linear numerical method for treating arbitrary ship motions in waves. Computed response functions for a frigate and for the S175 container ship compare favorably with measured data. With the new iterative matrix solver installed, the turnaround time on a workstation is typically four hours.
Future effort will concentrate on improved repanelling procedures before proceeding to the case of oblique waves.
ACKNOWLEDGEMENTS
The present results are from a study supported by the Office of Naval Research under the Applied Hydrodynamics Research Program, Contract N00014–90-C-0047.
REFERENCES
1. Faltinsen, O.M., “On Seakeeping of Conventional and High-Speed Vessels”, Journal of Ship Research, Vol. 37, No. 2, June 1993, pp. 87–101.
2. Korvin-Kroukovsky, B.V., “Investigation of Ship Motions in Regular Waves”, Trans. SHAME, 63, 1955.
3. Ogilvie, T.F. and Tuck, E.O., “A Rational Strip-Theory of Ship Motion”, Part 1, Department of Naval Architecture, The University of Michigan, Ann Arbor, MI, Report No. 013, 1969.
4. Salvesen, N., Tuck, E.O., and Faltinsen, O., “Ship Motions and Sea Loads”, Trans. SHAME, 250–287, 1970.
5. Kim, C.H., Chou, F.S., and Tein, D., “Motions and Hydrodynamic Loads of a Ship Advancing in Oblique Waves ”, Trans. SNAME, 225– 256, 1988.
6. Chiu, F.C. and Fujino, M., “Nonlinear Prediction of Vertical Motions of a Fishing Vessel in Head Sea”, Journal of Ship Research, 35, 1, March, 32–39, 1991.
7. Fang, Ming-Chung, Lee, Ming-Ling, Lee, Chwang-Kuo, “Time Simulation of Water Shipping for a Ship Advancing in Large Longitudinal Waves”, Journal of Ship Research, Vol. 37, No. 2, June 1993, pp. 126–137.
8. Nakos, D.E., and Sclavounos, P.D., “On Steady and Unsteady Ship Wave Patterns,”, Journal of Fluid Mechanics, 1990, Vol. 215, pp. 263–288.
9. King, B.W., Beck, R.F., and Magee, A.R., “Seakeeping Calculations with Forward Speed Using Time-Domain Analysis, ” 17th Symposium on Naval Hydrodynamics, 1988.
10. Lin, W.-M., and Yue, D., “Numerical Solutions of Large-Amplitude Ship Motions in the Time Domain, ” 18th Symposium on Naval Hydrodynamics, 1990.
11. Nakos, D.E., Kring, D.C., Sclavounos, P.D., “Rankine Panel Methods for Time-Domain Free Surface Flows,” to be presented in the Sixth International Conference on Numerical Ship Hydrodynamics, Iowa City, Iowa, August 1993.
12. Pawlowski, J.S., and Bass, D.W., “A Theoretical and Numerical Model of Ship Motions in Heavy Seas”, Presented at SNAME Annual Meeting, 1991.
13. Maskew, B., USAERO, A Time-Stepping Analysis Method for the Flow about Multiple Bodies in General Motions, Users' Manual, Analytical Methods, Inc. , Redmond, WA, 1990.
14. Maskew, B. and Dvorak, F.A., “Prediction of Dynamic Stall Characteristics Using Advanced Nonlinear Panel Methods,” Proc. Workshop Unsteady Separated Flows, USAF Academy, August 1983.
15. Maskew, B., “USAERO/FSP: A Time-Domain Approach to Complex Free-Surface Problems, ” Symp. High-Speed Marine Vehicles, Naples, Italy, 1991.
16. Longuet-Higgins, M.S. and Cokelet, E.D., “The Deformation of Steep Surface Waves on Water: I. A Numerical Method of Computation,” Proc. R. Soc. London, A350, 1976, pp. 1–26.
17. Maskew, B., “A Nonlinear Numerical Method for Transient Wave/Hull Problems on Arbi trary Vessels”, Presented at 1991 Annual SNAME Meeting, New York, N.Y., November 1991.
18. Maskew, B. “Prediction of Nonlinear Wave/Hull Interaction on Complex Vessels”, 19th Symposium on Naval Hydrodynamics, Seoul, Korea, August 1992.
19. Tidd, D.M., “FPI—Flight-Path-Integrator: A Program Module for USAERO for Flight Path Analysis of Arbitrarily Shaped Bodies; Users' Manual”, Analytical Methods, Inc., January 1991.
20. Maskew, B., “Numerical Analysis of a Complete Yacht Using a Time-Domain Boundary Element Method,” presented at the Third International Seminar on Yacht and Small Craft Design, Castelluccio di Pienza, Italy, 19–23 May 1993.
21. O'Dea, J.F., and Walden, D.A., “The Effect of Bow Shape and Nonlinearities on the Prediction of Large Amplitude Motions and Deck Wetness”, Proc. 15th Symp. on Naval Hydro., Hamburg, Germany, 1984.
22. O'Dea, J. (David Taylor Model Basin, USA), Powers, E. (University of Texas at Austin, USA), Zselecsky, J., (U.S. Naval Academy, USA), “Experimental Determination of Nonlinearities in Vertical Plane Ship Motions,” Proc. 19th Symp. on Naval Hydro., Seoul, Korea, August 1992.
23. Nabors, K., Korsmeyer, T., White, J., “Multipole Accelerated Preconditioned Iterative Methods for Solving Three-Dimensional Mixed First and Second Kind Integral Equations ”, Proc. Copper Mountain Conf. on Iterative Methods, Copper Mountain, AK, April 1992.
24. Maskew, B., “Program VSAERO Theory Document,” NASA CR-4023, 1987.
25. Liapis, S.J., “Time-domain Analysis of Ship Motions,” Report No. 302, Dept. Naval Arch. Marine Eng., U. Michigan, Ann Arbor, Michigan, 1986.
26. Beck, R.F., Cao, Y., “Nonlinear Computations of Ship Waves and Wave Resistance,” to be presented at the Sixth International Conf. on Numerical Ship Hydrodynamics, Iowa, August 1993.
DISCUSSION
by Professor E.O.Tuck, University of Adelaide, Australia.
Several times during this talk it has been noted that the agreement between the present computations of heave or pitch motions and experiments is “in the ball park.” In view of the fact that, for about 25 years, linear theory (even with the further approximation of strip theory) has inhabited the same ballpark, it would seem that, although the degree of agreement is reasonable, a smaller ballpark is needed in order to justify the expense of the present approach, relative to strip theory. In particular, some form of differencing would seem to be appropriate. In other words, to what (ballpark?) extent does the present program predict nonlinear effects, as measured by the differences between results from large-amplitude and small-amplitude incident waves?
Author's Reply
The non-linear effects are demonstrated in the pitch and heave response functions plotted against wave steepness in Figure 6 for the S175 tanker and in Figure 12 for the frigate. The agreement with measured data is referred to as “ball park” at this stage because these initial results are not at the precise wave-length values of the experiments. The numerical wave maker is driven by an oscillating velocity potential, and so the precise wave length and wave amplitude are not controlled directly. A number of cases have yet to be run to provide sufficient information for cross-plots to be generated to complete the figures shown in the paper. Bearing in mind all the complex interactions between the various parts of the method, just getting all this running together and getting “ ball park” results was regarded as important progress at this stage.
DISCUSSION
by T.T.Huang, DTMB
Could the authors provide computational uncertainty for the panel number, panel distribution, computation domain and Foude number used for each of computations. A generalized computational uncertainty statement of the USAERO is welcome.
Author's Reply
Detailed sensitivity studies of surface and time discretizations and of free surface truncation as a function of Froude Number have yet to be studied for the seakeeping applications of USAERO. Such studies are planned for the third year of this project and will be reported in a future paper. The discretizations used in the resent paper represent “reasonable” (but not necessarily ideal) conditions, based on earlier experience with this code and with its sister code, VSAERO, which has undergone a number of descretization sensitivity studies. The present objectives have been to examine the general behavior of the various parts of the method in the seakeeping applications—i.e., the free surface deformation, the wave maker, the large amplitude free motion of the vessel, the “on-the-fly” repaneling to the free surfce/hull intersection line, and the calculation of the instantaneous body force and moment. These parts must all work smoothly together before starting a detailed sensitivity study.
DISCUSSION
by Dr. Arthur M.Reed, David Taylor Model Basin
This was an informative presentation on a computational tool which has the ability to analyze a number of useful and relevant Navy problems. Thank-you. I have two questions:
-
You state that your code can include an actuator disk model for a propulsor. What purpose is this intended to serve in the computation?
-
In your non-linear ship motion calculations have you performed any analysis of your results which would indicate which aspects of the non-linear calculations are most important to your results -NL hydrostatics, NL hydrodynamics, etc.?
Author's Reply
-
The actuator disc model in USAERO stems from earlier modeling of aircraft propeller effects on wings, etc. The basic purpose of including it for ship motion calculations is to represent propulsor effects on hull loads; however, current developments, using a blade-element approach, will provide a more complete propulsor modeling capability, including time-
-
dependent thrust effects and non-uniform inflow effects on thrust and side-force.
-
In general, the code works with the complete unsteady pressure distribution which is integrated at each step to provide the instantaneous force and moment acting on the vessel; the separate contribution of the hydrodynamic, and hydrostatic pressures, have not been examined in detail. However, the current analysis now has the option to display the surface distribution of the “1-v2”, the “pzg” and the
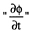 pressure terms separately. It would be straightforward to integrate these terms separately to provide their respective contributions to the straightforward to integrate these terms separately to provide their respective contributions to the force and moment acting on the hull, thereby allowing the relative magnitudes to be examined.
pressure terms separately. It would be straightforward to integrate these terms separately to provide their respective contributions to the straightforward to integrate these terms separately to provide their respective contributions to the force and moment acting on the hull, thereby allowing the relative magnitudes to be examined.
Rankine Panel Methods for Transient Free-Surface Flows
D.E.Nakos (InTec Software, USA)
D.Kring and P.D.Sclavounos
(Massachusetts Institute of Technology, USA)
ABSTRACT
A Rankine Panel Method is developed for the solution of transient wave-body interactions. In the presence of mean forward speed, the free surface and body boundary conditions are linearized about the double-body flow. The choices of space and time discretization are based on a systematic error and stability analysis. An artificial wave-absorbing beach is designed and employed over the outer portion of the free surface computational domain in order to avoid wave sloshing within the computational basin.
The proposed numerical scheme is applied for the solution of flows around realistic ships with or without mean forward speed. The transient wave resistance problem is considered and the rate of convergence of the resultant forces and moments to their steady values is studied. Forced and free motion simulations are also carried out until steady-state is reached and the resulting forces and motions are compared with computations by the well established frequency domain version of the same Rankine Panel Method.
1. INTRODUCTION
Numerical solutions of the transient wave-ship interactions have recently emerged as a popular alternative to their frequency domain counterparts. Studies with and without mean forward speed have been reported by Wehausen (1967), Liapis (1986), Beck and Liapis (1987) Korsmeyer (1988), King, et al, (1988), Lin and Yue (1990), Beck and Magee (1990), and Maskew(1992).
Over the past 15 years Rankine Panel Methods have been successfully employed by s everal research teams for the solution of various free surface problems ranging from the linearized wave resistance and ship motion problems to nonlinear breaking wave simulations. The use of the simple Rankine source as the elementary singularity is mainly motivated by the resulting flexibility in the choice of the free surface conditions to be satisfied. This property does not only render the Rankine Panel Methods as the sole alternative for nonlinear flows, but it also allows the employment of linearized conditions with variable coefficients. The penalty to be paid by such schemes consists of the necessity to discretize a portion of the free surface surrounding the body, which does not only increase the number of unknowns to be determined, but also may potentially distort the resulting wave pattern due to the introduction of numerical dispersion, dissipation and—most importantly—instabilities.
This study presents the design, implementation and application of a Rankine Panel Method for the solution of transient wave-body interactions in three dimensions. At the presence of mean forward speed, the free surface and body boundary conditions are linearized about the double-body flow, as it is outlined in section 2. Previous studies, in the frequency domain, have illustrated the excellent numerical properties of properly designed Rankine Panel Methods in the frequency domain and the performance of such linearization over a wide range of Froude numbers and frequencies for realistic ship flows (see Sclavounos and Nakos(1988) and Nakos and Sclavounos(1990)).
The numerical scheme adopted by the present study is outlined in section 3 and may be shown to posses very desirable global error and stability properties (see Nakos (1993)). The computational domain, consisting of the hull and a portion of the surrounding free surface, is discretized
by a collection of plane quadrilateral panels over which the unknown functions are represented as biquadratic splines. The time dependence of the solution is modeled by allowing the associated spline coefficients to be time dependent and two alternative time-marching schemes are proposed for the integration of the free surface conditions. Discretization errors are found to be large over length scales of the solution which are comparable to the grid size. A low-pass filtering is designed in order to eliminate such wave components which would, otherwise, propagate at erroneous directions and speeds, therefore jeopardizing the overall accuracy of the numerical solution.
Section 4 undertakes the design and implementation of an artificial wave-absorbing beach for the damping of the reflections due to the truncated free surface domain. The wave absorption mechanism is based on Newtonian cooling (see eg. Israeli and Orszag (1981)) which is distributed over the outer portion of the free surface computational domain. Nakos (1993) has demonstrated the effectiveness of the proposed artificial beach by numerical tests, which is found to be satisfactory as long as the width of the beach is comparable to the length of the waves to be absorbed.
The first numerical simulations are carried out for forced harmonic motions of a vessel at zero forward speed. Section 5 compares the force predictions of the present transient solution to results due to the frequency domain computer code WAMIT. The excellent correlation of the two sets of numerical results demonstrates not only the accuracy of the present scheme, but it also serves as a more pragmatic proof of the effectiveness of the adopted artificial beach.
Section 6 presents several simulations of realistic ships advancing steadily at a constant speed. A Series-60 hull and the modified Wigley model are both considered at Froude numbers 0.2 and 0.3. The convergence of the numerical solution with the number of panels is illustrated both with respect to the generated wave patterns and the resultant forces and moments acting on the hull. At low speed the time histories of the forces are shown to contain a slowly-decaying transient oscillation owing to the critical frequency ωU/g= 0.25 which gets excited due to the impulsive start of the vessel.
Forced motion simulations in the presence of constant forward speed are considered in section 7. The resulting steady-state added mass and damping coefficients compare excellently with related predictions by the frequency domain computer code SWAN.
Section 8 presents free motion simulations in the presence of constant forward speed, where the rigid-body equations of motion are solved at each time step. Results are presented for free decay tests and rigid-body response to multichromatic head seas.
2. LINEARIZATION OF BOUNDARY CONDITIONS
The problem requires a formulation for the transient wave flow around at rigid vessel advancing through ambient sea waves. A Cartesian coordinate system Oxyz is utilized with its origin on the calm free surface, its x-axis pointing upstream and its z-axis upwards. The coordinate system will also be fixed to the body. Under the assumptions of inviscid and irrotational flow, the velocity potential Ψ governing the resulting wave flow satisfies Laplace equation in the fluid domain and is subject to the dynamic and kinematic free surface conditions,
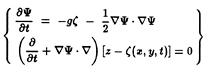
(2.1)
to be imposed at the instantaneous position of the free surface.
Over the wetted portion of the ship hull the normal component of the fluid velocity is equal to the corresponding component of the ship velocity ![]() , or
, or
(2.2)
applied over the instantaneous position of the vessel. In general, the velocity ![]() contains the mean forward speed of the vessel
contains the mean forward speed of the vessel ![]() and an oscillatory component due to the response
and an oscillatory component due to the response ![]() of the ship to ambient waves. The latter may be decomposed in the six rigid-body degrees of freedom,
of the ship to ambient waves. The latter may be decomposed in the six rigid-body degrees of freedom,
(2.3)
where ![]() and
and ![]() denote the motions along the translational and rotational rigid-body modes, respectively.
denote the motions along the translational and rotational rigid-body modes, respectively.
Under the assumption that the total flow Ψ consists of a base-flow Φ, of O(1), and a small amplitude disturbance φ conditions (2.1) and (2.2) may be linearized. This study employs the double-body flow as the basis flow, which satisfies the rigid wall condition over the calm free surface, and offsets the mean forward speed over the mean position of the hull below z=0. The double-body linearization has been employed successfully in the frequency domain by numerous previous studies and its validity has been demonstrated over a wide range of hull shapes, Froude numbers and frequencies (see eg. Nakos and Sclavounos 7(1990)).
Linearization of (2.1) about the double-body flow leads to
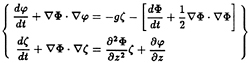 on z=0 (2.4)
on z=0 (2.4)
where ζ=ζ(x,y,t) is the free surface elevation and is assumed to be of the same order as the wave potential φ. The identities ▽Φ·▽Φz=0 and dΦz/dt=0 over z=0 assist the derivation of (2.4). The Cartesian system Oxyz is selected to translate along with vessel, therefore all time derivatives (d/dt) appearing in (2.4) are augmented by the corresponding convective terms. Conditions (2.4) may be combined to eliminate the wave elevation rendering the free surface condition proposed by Nakos and Sclavounos (1990).
The first term in the second member of the linearized kinematic free surface condition (2.4) follows from the transfer of that condition onto the z=0–plane, by means of an appropriate Taylor expansion. The numerical tests presented in this study do not include the effects of the above term, because of the difficulty to properly handle the singular behavior of ∂2Φ/∂z2 at the bow and stern of surface-piercing vessels. That does not imply, necessarily, that the effects of such term are negligible and the related study is proposed for future research.
Under the assumption of small unsteady displacement, the body boundary condition (2.2) may be transferred onto the mean position of the vessel (see Newman (1978)),
(2.5)
where mi are the so-called m-terms, defined in terms of the velocity field ![]() as follows,
as follows,
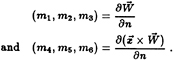
(2.6)
3. THE DISCRETIZATION ALGORITHM
Consider the enforcement of the Laplace equation in the fluid domain by a distribution of Rankine singularities over the free surface and the wetted portion of the hull. Application of Green's second identity to the velocity potential of the wave flow φ and the Rankine source potential ![]() leads to
leads to
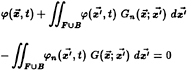
(3.1)
for any finite ![]() on the z=0–plane, F, and the mean position of the hull below z=0, B. The contribution of the closing surface at infinity vanishes owing to the decay of both
on the z=0–plane, F, and the mean position of the hull below z=0, B. The contribution of the closing surface at infinity vanishes owing to the decay of both ![]() and
and ![]() as
as ![]() .
.
The integral equation (3.1) combined with the linearized conditions (2.4) and (2.5) constitute a system of equations for the solution with respect to the velocity potential φ, the wave elevation ζ and the vertical velocity φz over the free surface. The present study elects not to combine (3.1), (2.4) and (2.5) into a single integro-differential equation for φ, for reasons related to the flexibility and modularity of the numerical solution scheme as well as its upgradability with respect to the inclusion of nonlinear effects.
The boundary domain is discretized by a collection of plane quadrilateral panels, over which all three unknowns are approximated, independently, by a linear superposition of biquadratic spline basis functions,
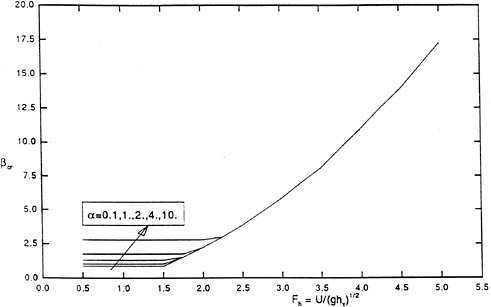
Figure 1. The stability condition for the Emplicit Euler discretization scheme.
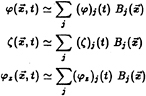
(3.2)
where Bj is the basis function centered at the j'th panel. The above choice of basis functions provides inter-panel continuity of the unknowns and their gradients. The time dependence of the solution is modeled by allowing the spline coefficients to be time dependent. It is worth noting that these spline coefficients are not equal to the value of the respective unknown at the panel centers, although they are linearly related to them.
The discrete formulation follows from collocation at all panel centers, ![]() , and the employment of a discrete time-marching scheme for the integration of the free surface boundary conditions. Recently, Nakos (1993) presented a systematic algorithm for the evaluation of the numerical attributes of alternative discretization schemes, which hinges upon the introduction of the “discrete dispersion relation” governing the wave propagation over discrete free surface and time, extending in the time domain a related study by Nakos and Scalvounos (1990) for the frequency domain problem. Comparison of the continuous and discrete dispersion relations allows the rational definition of the consistency, order and stability properties of the numerical solution scheme. After evaluating numerous solution algorithms, two schemes were selected based on their superior performance.
, and the employment of a discrete time-marching scheme for the integration of the free surface boundary conditions. Recently, Nakos (1993) presented a systematic algorithm for the evaluation of the numerical attributes of alternative discretization schemes, which hinges upon the introduction of the “discrete dispersion relation” governing the wave propagation over discrete free surface and time, extending in the time domain a related study by Nakos and Scalvounos (1990) for the frequency domain problem. Comparison of the continuous and discrete dispersion relations allows the rational definition of the consistency, order and stability properties of the numerical solution scheme. After evaluating numerous solution algorithms, two schemes were selected based on their superior performance.
The lower-order scheme employs the explicit and implicit Euler marching for the kinematic and dynamic free surface conditions, respectively, and it may be summarized as follows,
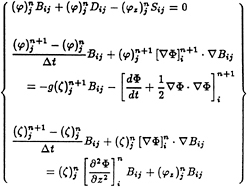
(3.3)
where summation over the multiply occurring j
Figure 2. Continuous vs. discrete dispersion relations.
index is assumed and
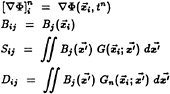 . (3.4)
. (3.4)
It is shown in Nakos (1993) that the above scheme, referred to as “Emplicit Euler (EE)”, is neutrally stable under the stability condition illustrated in figure 1. At low mean forward speeds the critical value of the time step scales with the square root of the typical panel size h, while at higher speeds the stability condition imposes a much more restrictive upper bound of Δt scaling with h3/2.
A remedy to the severe stability criterion of figure 1 may be found in employing a three-step semiimplicit scheme composed of a Leap-frog marching for the kinematic free surface condition and a Trapezoidal approximation of the dynamic condition (see Vada and Nakos (1993)). This scheme, referred to as “TLF”, is also neutrally stable under a stability condition which penalizes high forward speed flows less severly.
Unconditionally neutrally stable time-marching schemes may also be designed, but they have the unfortunate property of being fully implicit. Both the EE and TLF schemes avoid full coupling of the free surface conditions with the integral equation, therefore permitting their successive employment for the evolution of each unknown independently. This is a most welcome attribute, in light of our objective to include nonlinear effects.
The matrix form of (3.3), as well as the corresponding TLF formulation, consists of one full and two banded matrices, associated with the integral equation and the free surface conditions respectively. It is worth noting the the full matrix dependents only on the geometrical configuration of the computational domain and therefore, once it is set and LU-decomposed, may be repeatedly employed for all desired simulations.
Under the assumption of infinitely large free surface computational domain, the discrete formulation may be transferred to the frequency domain where the associated discrete dispersion relation may be identified. This dispersion relation governs the free wave propagation over the discrete medium established by the numerical algorithm. Under neutral stability, the discrete dispersion relation is directly comparable to its continuous counterpart. A sample comparison between the polars of the discrete and continuous dispersion
relations, for the EE scheme, is illustrated in figure 2. The discretization density is quantified in terms of the grid Froude number ![]() , the panel aspect ratio α=hx/hy and the free surface grid number
, the panel aspect ratio α=hx/hy and the free surface grid number ![]() .
.
At small wavenumbers and frequencies the continuous and discrete polars coincide, owing to the consistency of the numerical scheme. However, the corresponding polars divert from each other in the neighborhood of length scales that are barely resolved by the grid. Wave components in that region are miss handled by the discretization scheme and they are seen to propagate at erroneous directions, therefore jeopardizing the overall accuracy of the numerical solution. As a remedy, a low-pass filtering technique is employed for the elimination of the short length scales similar to the “smoothing device” proposed by Longuet-Higgins and Cokelet (1976). The adopted filter shape is based on a 7-point polynomial interpolation designed to have no effect on length scales longer than approximately 4–5 panel sizes. Numerical experience with the adopted filtering has shown that it has an uninvited smoothing effect on the local non-radiating disturbance. Minimization of such side influence may be obtained by a relatively infrequent application of filtering which allows “recovery” of the local disturbance.
The discrete dispersion relation may be also interpreted as the characteristic polynomial of the underlying time-stepping scheme. The degree of the polynomial depends on the order of the time-stepping scheme, which causes the three-step TLF scheme to have three real and distinct roots, under neutral stability. The two principal roots correspond to the roots of the continuous dispersion relation as in the case of the EE time-marching algorithm. The third root gives rise to an undamped spurious wave system composed of all wavelengths, that can be resolved by the mesh, and high frequencies comparable to the Nyquist frequency of the discretization, π/Δt, (see Vada and Nakos (1993)). Such phenomenon is frequently encountered in connection with the use of the Leap-Frog scheme and for its remedy Asselin (1972) has proposed an effective asymmetric time-filtering device, which is employed by the present study. Further details of the stability analysis of the present time-domain Rankine panel method may be found in Nakos (1993).
4. WAVE ABSORBING LAYER
Given a sufficiently long simulation interval, the waves generated by the vessel will propagate outwards and interact with the truncation of the free surface computational domain. The effect of the free surface truncation may be interpreted as reflection by a horizontal rigid lid laid over the free surface, outside the computational domain.
Two clearly distinct strategies are suggested in the literature for dealing with such wave reflections. The first is based on enclosing the computational domain inside a control surface over which appropriate radiation conditions are imposed. The present study elects to deal with the truncation error by adopting the second strategy of wave absorbing layers as they are reviewed by Israeli and Orszag (1981).
Consider the “Fourier pair” of the linear free surface conditions and the corresponding dispersion relation,
(4.1)
A shift of the frequency in the complex plane away from the real axis results in wave damping and may be obtained by introducing Newtonian cooling terms in the kinematic free surface condition, as follows,
(4.2)
where ν>0 is the strength of the Newtonian cooling assumed here to be uniformly distributed. In view of the righthand side of (4.2), ν may also be interpreted as the Rayleigh viscosity used for the enforcement of the proper radiation condition in the frequency domain formulation of the problem. Damped free surface conditions at the presence of forward speed follow from (4.2) by adding the proper convective terms to the ∂/∂t operator.
The design of a wave absorbing layer is based on the employment of the modified free surface conditions (4.2) over the outer portion of the computational domain. This study adopts the recommendations of Israeli and Orszag (1981) for quadratic variation of the cooling strength ν over the damping zone, with zero value and slope along
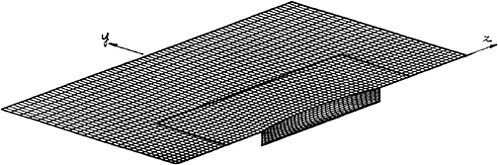
Figure 3. The modified Wigley hull computational domain used for the solution of zero-speed flow. The computational domain outside the square domain drawn on the free surface serves as a numerical beach.
the inside-end of the zone,
(4.3)
where ρ signifies the radial distance from the wavemaking source, with the damping zone starting at ρ=ρ0 and extending over a width Cw. The overall cooling strength of the zone is dictated by the parameter Cs. Similar wave absorbing devices have been successfully implemented in two dimensions by Baker, Meiron and Orszag (1981) and Cointe (1989).
The effectiveness of the proposed artificial beach is extensively tested by Nakos (1993). Its performance depends mainly on the width, Cw, and its successful employment requires minimal tuning. The numerical results of following sections may be considered as a more pragmatic demonstration of the effectiveness of the wave absorption mechanism.
As a general rule, the presence of significant forward speed de-emphasizes the importance of wave absorption. That is because significant waves approach the downstream only portion of the truncation line causing reflections with dispersion characteristics identical to the ones of the main wave field, therefore, propagating downstream and away from the vessel.
5. FORCED HARMONIC MOTIONS AT ZERO FORWARD SPEED
This section discusses the application of the numerical solution algorithm, outlined in the previous sections, for the simulation of wave flows due to forced heave and pitch oscillations of a ship without forward speed. The main purpose of this numerical test is to demonstrate the effectiveness of the adopted artificial beach in realistic situations. The flow around the modified Wigley model is considered. The hull shape and the computational domain are illustrated in figure 3. The free surface grid of figure 3 extends 125% of the waterline length L in the transverse direction and 75% of L upstream and downstream. Due to the transverse symmetry about the centerplane, only the y>0—part of the configuration is discretized. The size and location of the adopted artificial beach is also shown in figure 3. Its width is 75% of L in the transverse direction and 50% of L upstream and downstream. For the following simulations the size of the time step is selected to be ![]() , corresponding to free surface grid number β
, corresponding to free surface grid number β![]() 4. The free surface is assumed to be calm for all time t ≤ 0, and the hull motion starts impulsively at t=0, oscillating thereafter at a number of selected frequencies ωk,
4. The free surface is assumed to be calm for all time t ≤ 0, and the hull motion starts impulsively at t=0, oscillating thereafter at a number of selected frequencies ωk,
![]() , i=1, …6, (5.1)
, i=1, …6, (5.1)
where ![]() is the amplitude of the i'th mode motion at frequency ωk.
is the amplitude of the i'th mode motion at frequency ωk.
The linearized pressure over the hull is given by Bernoulli equation in terms of the wave potential φ,
(5.2)
and it is evaluated at “half-steps”, ![]() , by a two-point centered difference scheme. Numerical experience has shown that employment of the two-point one-sided difference formula for the approximation of (5.2) results in significant discretization errors. An alternative, equally effective, solution is the three-point backward difference scheme for the evaluation of the pressure, which is employed in the freely floating body simulations of section 8.
, by a two-point centered difference scheme. Numerical experience has shown that employment of the two-point one-sided difference formula for the approximation of (5.2) results in significant discretization errors. An alternative, equally effective, solution is the three-point backward difference scheme for the evaluation of the pressure, which is employed in the freely floating body simulations of section 8.
Two instances of the wave field due to forced sinusoidal heaving and pitching motion of the hull at frequency ![]() , were calculated. At zero forward speed, the free wave system contained a single wavelength, which was inversely proportional to the square of the frequency. At all frequencies, the flow was seen to reach rapidly a steady-state. The resulting forces were fitted by a sinusoidal function in order to identify the added mass and damping coefficients shown in figure 4. The results of the present solution algorithm, labeled SWAN-2, obtained by the grid of figure 3 (small FS), are compared with results from the frequency domain computer code WAMIT (see eg. Korsmeyer et al (1988)), whose accuracy has been verified by systematic convergence tests to a level higher than 1%.
, were calculated. At zero forward speed, the free wave system contained a single wavelength, which was inversely proportional to the square of the frequency. At all frequencies, the flow was seen to reach rapidly a steady-state. The resulting forces were fitted by a sinusoidal function in order to identify the added mass and damping coefficients shown in figure 4. The results of the present solution algorithm, labeled SWAN-2, obtained by the grid of figure 3 (small FS), are compared with results from the frequency domain computer code WAMIT (see eg. Korsmeyer et al (1988)), whose accuracy has been verified by systematic convergence tests to a level higher than 1%.
Despite the perfect comparison of the SWAN-2 and WAMIT results at moderate and high frequencies ω, large discrepancies occur in the range ![]() . At these low frequencies, the generated wavelengths are too long to be effectively absorbed by the artificial beach of figure 3. Namely, at
. At these low frequencies, the generated wavelengths are too long to be effectively absorbed by the artificial beach of figure 3. Namely, at ![]() the far-field wavelength is almost four times as long as the width of the wave-absorbing layer. Significant errors due to the free surface truncation are, therefore, expected. In order to verify the latter statement, the flow at
the far-field wavelength is almost four times as long as the width of the wave-absorbing layer. Significant errors due to the free surface truncation are, therefore, expected. In order to verify the latter statement, the flow at ![]() is also solved using a free surface domain of quadruple the size in each direction and 1/3 of the panel density, referred to as (large-FS). Predictions for the time history of the vertical force due to heave, using the two different computational domain, were calculated. Both simulations appear to reach a steady-state, although this becomes significantly more delayed in the results obtained by the (small-FS) domain. The “corrected” added mass and damping coefficients at
is also solved using a free surface domain of quadruple the size in each direction and 1/3 of the panel density, referred to as (large-FS). Predictions for the time history of the vertical force due to heave, using the two different computational domain, were calculated. Both simulations appear to reach a steady-state, although this becomes significantly more delayed in the results obtained by the (small-FS) domain. The “corrected” added mass and damping coefficients at ![]() , resulting from the (large-FS) simulations are superimposed on figure 4 and are seen to compare very well with the corresponding WAMIT predictions, despite the relatively low discretization density of the (large-FS) grid.
, resulting from the (large-FS) simulations are superimposed on figure 4 and are seen to compare very well with the corresponding WAMIT predictions, despite the relatively low discretization density of the (large-FS) grid.
The increased accuracy of the results obtained with the (large-FS) domain solidifies the argument that effective wave absorption can be obtained as long as the size of the numerical beach is comparable or larger than the generated wavelengths.
6. STEADY MOTION AT CONSTANT FORWARD SPEED
This section presents applications of the proposed solution algorithm for the prediction of wave flows due to the steady forward motion of ships. The free surface is assumed to be calm for all time less than t=0, when the vessel starts impulsively moving forward at full speed.
The hydrodynamic pressure over the hull surface is given by Bernoulli equation linearized in a manner consistent with the linearization of the free surface conditions,
(6.1)
where the time derivatives (d/dt) contain the corresponding convective terms. The pressure distribution is evaluated at half-steps, as explained in the preceding section and integrated over the hull surface to render the time history of the wave resistance, sinkage force and trim moment.
The first simulations involve the Series-60, cB= 0.7, hull advancing at Froude number F=0.3. The hull geometry and the surrounding free surface computational domain are shown in figure 5 along with the selected size of the artificial beach. As discussed in section 4, due to the strongly convective nature of the wave flow no absorbing layer is needed downstream. Two different grid densities are used, the one illustrated in figure 5 with 50 panels along the ship length and a coarser one composed by 30 panels along the ship length. Both grids use the same extend of the free surface computational domain and have panels of unit aspect ratio close to the waterline. The transverse panel size increases in the y-direction geometrically at a ratio of 1.05.
Simulations are carried out until time ![]() is reached using time steps Δt=0.03 and 0.04 for the finer and coarser discretizations, respectively. The predicted wave patterns at the final time step of the simulation are compared in figure 6. Good
is reached using time steps Δt=0.03 and 0.04 for the finer and coarser discretizations, respectively. The predicted wave patterns at the final time step of the simulation are compared in figure 6. Good
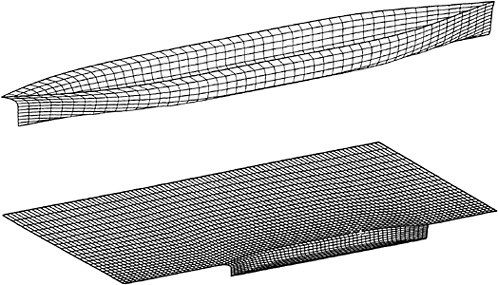
Figure 5. The Series-60, Cb=0.7, hull and computational domain used for solution of the forward speed steady flow.
convergence with the grid density may be observed, especially with respect to the longer length scales of the solution. Shorter diverging wave components are de-emphasized by the coarse discretization mainly due to the application of space-filtering. Figure 6 also shows the pressure distribution over the hull surface which may be seen to be satisfactorily converged.
The time histories of the wave induced forces and moments on the vessel are illustrated in figure 7, as predicted by both the fine and coarse discretizations. All curves show sharp initial transients which settle rapidly to a decaying oscillation at period ![]() , corresponding to the
, corresponding to the ![]() —singularity which is excited due to the impulsive start of the forward motion. The amplitude of these transient oscillations is, however, smaller than related predictions of Lin and Yue (1990).
—singularity which is excited due to the impulsive start of the forward motion. The amplitude of these transient oscillations is, however, smaller than related predictions of Lin and Yue (1990).
The aforementioned “critical” oscillations are much more pronounced in the next simulation which considers the same series-60 hull at Froude number F=0.2. Figure 8 shows the time history of the resultant forces and moments, as predicted by four different computational domains. All grids are of the same density with 50 panels along the waterline length. Two different values of the free surface extent in the transverse direction (YOUT) and of the transverse width of the
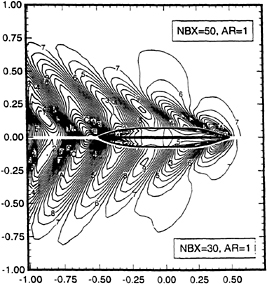
Figure 6. Wave patterns for two discretizations of the Series-60, Cb=0.7, hull in steady motion at a Froude number of 0.3.
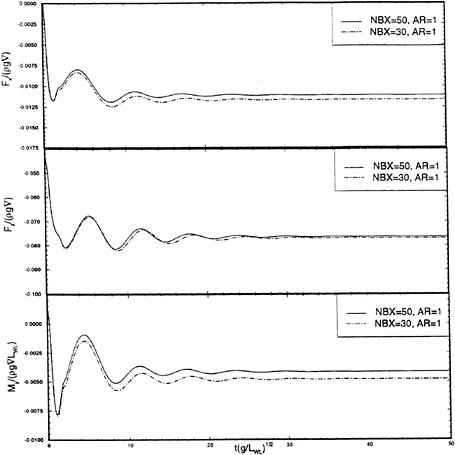
Figure 7. Time history for the Series-60, Cb=0.7, hull in steady motion at a Froude number of 0.3.
artificial beach (CW) are considered. All records oscillate at at approximately the same critical period, Tc, and about the same mean value, but with desperately different amplitudes and phases. Further numerical experimentation has shown that the precise form of the critical transient oscillation depends, almost exclusively, on YOUT and Cw with the general tendency to decrease as the size of the free surface domain and artificial beach increase.
The ![]() —singularity of the forward speed problem which is the underlying cause of the persistent transient oscillations has been been extensively studied over the years. For elementary flows due to translating wave singularities it may be proven that, within linear theory, there exist a wave component with vanishing group velocity whose energy is trapped in the near-field. However, such studies concentrate on the Neumann linearization of the free surface conditions which is not the framework of the present study. Moreover, the presence of the truncated free surface and wave absorbing layer is expected to have a significant effect on the “trapped” wave component whose wavelength is typically much larger than the overall size of the computational domain.
—singularity of the forward speed problem which is the underlying cause of the persistent transient oscillations has been been extensively studied over the years. For elementary flows due to translating wave singularities it may be proven that, within linear theory, there exist a wave component with vanishing group velocity whose energy is trapped in the near-field. However, such studies concentrate on the Neumann linearization of the free surface conditions which is not the framework of the present study. Moreover, the presence of the truncated free surface and wave absorbing layer is expected to have a significant effect on the “trapped” wave component whose wavelength is typically much larger than the overall size of the computational domain.
From the practical standpoint, the transient effect of the critical oscillations causes a significant delay to the onset of the corresponding steady-state and, therefore, increases the computational effort needed for the accurate prediction of the steady-state forces. The idea of filtering any such persisting transients appears very attractive and it is proposed for further study.
The insensitivity of all the above conclusions to the hull shape is illustrated by simulations of the modified Wigley model in steady forward motion at Froude numbers 0.3 and 0.2. Like for the Series-60 hull, the simulations are carried out to time ![]() using a grid density corresponding to 50 panels within the waterline length and a time step of Δt=0.03. Figures 9–13 show the predictions for the wave pattern at the final time step and the time history of the forces and moments acting on the hull. Once again, the critical transient oscillations in the force record are much more pronounced at the low speed.
using a grid density corresponding to 50 panels within the waterline length and a time step of Δt=0.03. Figures 9–13 show the predictions for the wave pattern at the final time step and the time history of the forces and moments acting on the hull. Once again, the critical transient oscillations in the force record are much more pronounced at the low speed.
7. FORCED HARMONIC MOTION AT CONSTANT FORWARD SPEED
The simulation of forced harmonic oscillations of
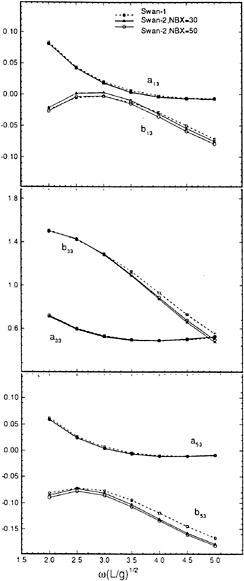
Figure 14. Added mass and damping for the modified Wigley hull at a Froude number of 0.3.
ships advancing at a constant forward speed is the subject of this section. The vessel is considered to be at rest for all time t≤0, when it suddenly starts moving forward at full speed while oscillating with amplitude given by (5.1).
The wave flow due to the forced harmonic heave and pitch motion of the modified Wigley model and the Series-60, cB=0.7, is solved by using both the coarse and fine discretizations of section 6. The time history of the resultant forces and moments is evaluated by integrating the pressure,
(7.1)
over the hull surface. Notice that the last two terms of (6.1) are not included in (7.1) since they do not contribute to the steady-state oscillatory forces.
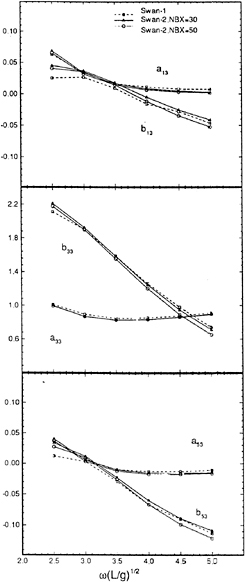
Figure 15. Added mass and damping for the Series-60, Cb=0.7, hull at a Froude number of 0.2.
Simulations are carried out until steady-state is reached and the force records are fitted by appropriate sinusoidal functions in order to identify the “frequency domain” added mass and damping coefficients. Figures 14 and 15 compare the predictions of the present time domain solution algorithm SWAN-2 to computations by the frequency domain solver SWAN-1 (see Nakos and Sclavounos (1990)), using identical linearization of the free surface and body boundary conditions. Very satisfactory agreement is found both for the modified Wigley model at Froude number 0.3 and the Series-60 hull at Froude number 0.2.
8. FREE MOTION AT CONSTANT FORWARD SPEED
This section presents free motion simulations for ships advancing at a constant forward speed. The vessels start impulsively at t=0 and retain freedom of motion in heave and pitch. Incident head seas can be imposed for the simulation of the resulting ship motions. If the ambient sea state is calm, the simulation becomes a free-decay test where the ship transits from the rest, or static equilibrium, position towards her dynamic equilibrium position, defined by the appropriate steady-state sinkage and trim.
The equation of motion of the hull as a rigid body read as follows,
(8.1)
where M is the inertia matrix, C are the hydrostatic restoring coefficients, ![]() are the rigidbody displacements, and
are the rigidbody displacements, and ![]() is the resultant hydrodynamic force or moment. The initial conditions for the ship can vary. It may be started from a calm rest position or given a specified initial heave and/or pitch displacement and/or velocity. Currently, the time-stepping algrorithm for the integration of the equations of motion (8.1) is based on a semi-implicit backwards differentiation scheme which is only first-order accurate. As discussed at the end of this section, a higher-order scheme with more favorable stability properties is necessary and it is currently being designed.
is the resultant hydrodynamic force or moment. The initial conditions for the ship can vary. It may be started from a calm rest position or given a specified initial heave and/or pitch displacement and/or velocity. Currently, the time-stepping algrorithm for the integration of the equations of motion (8.1) is based on a semi-implicit backwards differentiation scheme which is only first-order accurate. As discussed at the end of this section, a higher-order scheme with more favorable stability properties is necessary and it is currently being designed.
Within this study three cases of free motion simulation are examined. The first case, illustrated in Figure 16, shows the heave and pitch response of a modified Wigley hull which starts impulsively at t=0 from its calm-water position with a forward speed corresponding to Froude number F=0.3. For all practical purposes, at time ![]() the initial transients have decayed and the solution has approached the corresponding steady-state sinkage and trim.
the initial transients have decayed and the solution has approached the corresponding steady-state sinkage and trim.
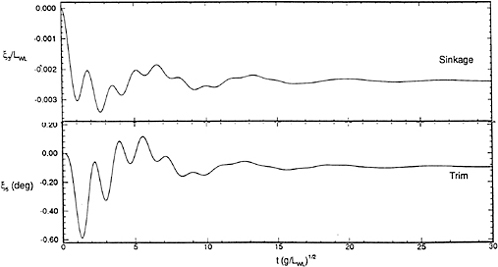
Figure 16. Modified Wigley hull started impulsively from rest and tending towards a forward speed equilibrium position at a Froude number of 0.3.
The behavior of the transients is worthy of note. Two distinct frequencies are evident is the transient response of figure 16. The shorter period is the natural period of oscillation for the ship at this Froude number and corresponds to the peak in the Response Amplitude Operator curve predicted by the frequency domain solver SWAN-1. The longer period corresponds to the critical transient oscillation due to the ![]() —singularity, discussed in preceding sections and it is excited by the impulsive start of the ship.
—singularity, discussed in preceding sections and it is excited by the impulsive start of the ship.
Subsequently simulations of the same modified Wigley model were carried out at Froude numbers 0.2, 0.3, and 0.4, but this time the vessel was given an initial heave displacement equal to 1% of its waterline length. The predicted motion records are illustrated in figure 17. These tests are instructive in examining the decay of the natural modes of oscillation, and indicate how quickly a hull may reach the steady-state limit, given an initial heave and pitch displacement. The natural period of oscillation of the vessel is evident in the transients excited during the latter simulations. However, the scale of the oscillations at the natural frequency is such that nearly overshadows the critical transient oscillations at period T0=8πF. The critical oscillations are most noticeable at the lowest Froude number but also affect the modulation of the motions at the higher speeds. Although there was no initial pitch for these freedecay tests, pitch motion did result due to hydrodynamic cross-coupling, which is amplified at higher speeds. After a sufficiently long interval of time the heave and pitch tend towards the sinkage and trim, respectively, appropriate for these speeds.
The predictions of the steady-state sinkage and trim by the present transient solver are considered superior to related computations made by steady-state solvers like SWAN-1. That is because the present transient approach incorporates, to leading-order, the effect of the sinkage and trim on the resultant force and moment due to the inclusion of the m-terms in the body boundary condition (2.5). Steady-state solvers may also account for the same effect, but only if they are employed iteratively with respect to the dynamic equilibrium position of the hull.
The last simulation test shows the heave and pitch response of the modified Wigley model advancing at Froude number 0.3 through multichromatic head seas. The time records of the resulting heave and pitch motions are illustrated in figure 18. The simulation is carried out for a sufficiently long interval of time so that transients have decayed and the motion records may be safely transformed into the frequency domain. The resultant Response Amplitude Operator is compared to related predictions of the frequency domain solver SWAN-1.
The predictions of both methods compare very favorably except for the peak magnitude of the heave response amplitude. Numerical convergence difficulties are experienced with respect to the time-step size at the peak of heave response, which may be attributed to numerical dissipation errors in the time-stepping algorithm for the integration of the equations of motion. Efforts are currently focused on analyzing this phenomenon and prescribing a higher-order algorithm for the solution of the equations of motion.
9. SUMMARY AND CONCLUSIONS
The design and implementation are presented of a Rankine Panel Method for the solution of transient wave-body interactions in three-dimensions. In the presence of forward speed the free surface and hull boundary condition are linearized about the double-body flow. The space discretization is based on the approximation of all unknowns in terms of the biquadratic B-spline functions and the time evolution is performed by a neutrally stable time-stepping algorithm. An artificial wave-absorbing beach is designed and employed for the damping of reflections due to the finite free surface computational domain.
Wave flows due to forced and free motions of realistic ship hulls are computed with and without mean forward speed. The simulations are continued until steady-state is reached and the resulting steady-state forces are compared to predictions by well-established frequency-domain solvers. The comparison is excellent for all cases, owing to the optimal design of the time-steeping algorithm and the effectiveness of the employed wave absorption device.
In the presence of forward speed, the onset of steady-state conditions is significantly delayed due to the ![]() —singularity of the corresponding frequency domain problem. The time-records of forces and motions are found to be “contaminated” by a slowly-decaying oscillation
—singularity of the corresponding frequency domain problem. The time-records of forces and motions are found to be “contaminated” by a slowly-decaying oscillation
at the critical frequency ωU/g=0.25, which is excited by the impulsive start-up of the vessel's motion. The wavelengths associated with this critical transient oscillation are often too long to be handled by the adopted extend of free surface computational domain and absorbing artificial beach.
Future extensions of the present formulation and solution scheme include relaxation of the body boundary condition linearization, in order to model large-amplitude ship motions, and solution of the wave flow past ships advancing along arbitrary curvilinear paths which addresses the problem of ship maneuvering in the presence of ambient waves.
ACKNOWLEDGEMENTS
This study has been supported by Det Norske Veritas Research AS.
REFERENCES
Asselin, R., 1972, “Frequency filter for time integrations”, Monthly Weather Review, vol. 100, no. 6.
Baker, G.R., Meiron, D.I., and Orszag, S. A., 1981, “Applications of a generalized vortex method to non-linear free surface flows”, Third International Conference on Numerical Ship Hydrodynamics.
Beck, R.F. and Liapis, S.J., 1987, “Transient Motions of Floating Bodies at Zero Forward Speed,” Journal of Ship Research, Vol.31, No.3, pp. 164–176. Beck, R.F. and Magee, A.R., 1990, “Time-Domain Analysis for Predicting Ship Motions,”, Proceedings Symposium on the Dynamics of Marine Vehicles and Structures in Waves , Brunel University, Amsterdam, pp. 49–65.
Cointe, R., 1989, “Nonlinear simulations of transient free surface flows”, Fifth International Conference on Numerical Ship Hydrodynamics.
Israeli M., and Orszag S.A., 1981, “Approximation of radiation boundary conditions”, Journal of Computational Physics, Vol. 41, pp. 115–135.
King, B.W., Beck, R.F., and Magee, A.R., 1988, “Seakeeping calculations with forward speed using time-domain analysis ”, Seventeenth Symposium on Naval Hydrodynamics.
Korsmeyer, F.T., 1988, “The first and second order transient free surface wave radiation problems”, Ph.D. Thesis, Dept of Ocean Eng., MIT.
Korsmeyer, F.T., Lee, C.-H., Newman, J.N., and Sclavounos, P.D., 1988, “The Analysis of Wave Effects on Tension-Leg Platforms”, Offshore Mechanics and Arctic Engineering Conference.
Liapis, S.J., 1986, “Time-domain analysis of ship motions”, Report No. 302, Department of Naval Arch, and Marine Eng., University of Michigan.
Lin, W.-M., and Yue, D., 1990, “Numerical solutions of large-amplitude ship motions in the time domain ”, Eighteenth Symposium on Naval Hydrodynamics.
Longuet-Higgins, M.S., and Cokelet, E.D., 1976, “The deformation of steep surface waves on water. I. A numerical method of computation”, Proc. Roy. Soc. Lond., Vol. 350, pp. 1–26.
Maskew, B., 1992, “Prediction of Nonlinear Wave/Hull Interactions on Complex Vessels ”, Nineteenth Symposium on Naval Hydrodynamics.
Nakos, D.E., 1993, “Stability of transient gravity waves on a discrete free surface”, Submitted for publication.
Nakos, D.E., and Sclavounos, P.D., 1990, “On steady and unsteady ship wave patterns”, Journal of Fluid Mechanics, Vol. 215, pp. 263–288.
Newman, J.N., 1978, “The theory of ship motions”, Advances in Applied Mechanics, Vol 18, pp. 221–283.
Newman, J.N., 1985, “The evaluation of free-surface Green functions”, Forth International Conference on Numerical Ship Hydrodynamics.
Sclavounos, P.D. and Nakos, D.E., 1988, “Stability Analysis of Panel Methods for Free Surface Flows with Forward Speed”, Seventeenth Symposium on Naval Hydrodynamics.
Vada, T., and Nakos, D.E., 1993, “Time-marching schemes for ship motion simulations”, Eighth International Workshop on Water Waves and Floating Bodies.
Wehausen, J.V., 1967, “Initial Value Problem for the Motion in an UNdulating Sea of a Body with Fixed Equilibrium Position,” Journal of Engineering Mathematics, Vol. 1, pp.1–19.