Direct Numerical Simulation of Unsteady Propulsor Blade Section Forces on a Parallel Processor
W.B.Coney,1 S.R.Breit,2 and J.R.Webb1
(1BBN Systems and Technologies, USA, 2Kendall Square Research, USA)
ABSTRACT
This paper describes a numerical method, which has been implemented on a parallel processor, for the direct simulation of inviscid unsteady blade section forces, and its application to several two-dimensional blade-gust interaction problems.
The parallel implementation is discussed in some detail. Timing results obtained on a parallel computer are presented and nearly linear parallel speed-ups are demonstrated.
The application of the present method to three model problems is discussed and results are compared to theoretical, experimental and numerical solutions.
INTRODUCTION
The time-harmonic (blade-rate and its harmonics) and stochastic unsteady forces produced by interaction with non-uniform inflow are the dominant components of the low-frequency acoustic signature of a non-cavitating marine propulsor. Much research has been devoted to analytical and approximate numerical methods for predicting these forces and there has been considerable success with these approaches. However, with the recent dramatic increases in the speed of computers and the advent of parallel computers, direct numerical simulations of unsteady flows through marine propulsors are becoming increasing feasible. The ultimate benefit of such direct simulations will be the ability to deal with arbitrarily complex propulsor geometries and to include possible interaction between the blade-rate and turbulence ingestion mechanisms which are presently treated separately.
The prediction of the response of a two-dimensional blade section to an unsteady gust can be regarded as a preliminary step toward the fully three-dimensional model of the propulsor subject to an unsteady inflow. The force developed in response to harmonic gusts of varying nature has further been the subject of much analysis, leading to both analytical, Sears [1], Naumann and Yeh [2], Atassi [3], etc., and linearized numerical, Atassi and Akai [4], Chiang and Fleeter [5], Hsin [6], etc., approaches. Unsteady blade-gust interaction problems therefore provide a natural test bed for the exploratory development of a numerical simulation of unsteady propulsor forces.
This paper describes a numerical method, which has been implemented on a parallel processor, for the direct simulation of inviscid unsteady blade section forces, and its application to several two-dimensional blade-gust interaction problems. The results selected for presentation highlight circumstances for which “classical” unsteady airfoil theories, such as that of Sears [1], and numerical procedures based on a linearizing assumption of potential flow, for example those of Hsin [6] and of Chiang and Fleeter [5], appear to adequately predict the unsteady force, and circumstances for which they cannot. Three model problems are investigated:
-
transverse gust interacting with a foil
-
pitching foils upstream of a stationery foil
-
distributed vortex interacting with a foil.
The first problem is well modeled by an analytic solution, the second could at least potentially by modeled by an unsteady potential flow simulation, the third, however, requires use of a method which preserves detail of the vortical flow.
NUMERICAL APPROACH
In choosing a numerical method for direct simulations, it should be recognized that the unsteady flow through a typical marine propulsor is characterized by:
-
very low Mach number (below 0.01),
-
high Reynolds number (above 106),
-
complex geometry, and
-
small unsteady pressure (compared to the mean pressure),
or small unsteady thrust (compared to the mean thrust).
With these issues in mind, we chose to implement the time-accurate pseudo-compressibility (TAP) method with upwind-biased spatial differencing, as described by Rogers & Kwak [7] for our simulations. In the limit where the pseudo-time step size is infinite, this method is nearly the same as the Newton iteration scheme of Athavale & Merkle [8]. The TAP method provides an incompressible flow solution which is a very good approximation of a low Mach number flow. In contrast, methods which account for compressible effects break down at very low Mach number. Our initial experience in applying this method to a two-dimensional model problem, with focus upon one aspect of the blade-vortex interaction, is described in Breit, et. al. [9].
The time integration scheme is second-order accurate and fully implicit, including the boundary conditions. Viscous terms are, for the present, neglected. A sparse, block-tridiagonal, linear system must be solved at each pseudo-time iteration. Unlike Rogers & Kwak [7], who use a line relaxation scheme to solve the linear system, we use the approximate LU factorization scheme recommended by Merkle and Athavale [8].
PARALLEL IMPLEMENTATION
Implementing the approximate LU factorization scheme on a massively parallel computer is a programming challenge because the degree of parallelism varies greatly during the course of the factorization procedure. The parallelization was accomplished on a BBN TC2000™ parallel computer. The implementation relied to a large extent on the high complete-exchange bandwidth and high random-access bandwidth of the TC2000 computer.
In theory, the highest parallel efficiency can be achieved if the smallest computational task that can be done in parallel involves the computations for a single grid point. We refer to this as a point parallel approach as opposed to a domain decomposition approach, where the smallest task involves computations for a sub domain of the grid. The domain decomposition approach requires less interprocessor communication than the point parallel approach, but at the cost of reducing the maximum achievable parallel efficiency. The choice of which approach to implement on a particular massively parallel computer depends on the characteristics of its interprocessor communication network. The interprocessor communication is fast enough on the TC2000 to enable a point parallel implementation of the LU algorithm.
The parallelization process was simplified by exploiting the memory management extensions and parallel directives provided by TC2000 FORTRAN. Some data are shared using an interleaving mechanism, with data declarations of the form
common, shared, interleaved /foo/ a(100),..
In this example, the set of 16-byte cache lines that contain array a are dynamically interleaved among the memories of the processors. Thus interprocessor communication is effected through shared memory instead of explicitly passing messages or packets between processors. Automatic load balancing is achieved by dynamically allocating computational tasks to processors. This approach avoids special mapping strategies where tasks and data are preallocated to specific processors. One benefit of this approach is that the number of lines of code that are associated with the parallel implementation is small compared to the total size of the program.
The LU method involves a forward elimination sweep over the grid and then a back substitution sweep in the opposite direction. Consider only the forward elimination sweep and denote a point in a structured 3D grid by the indices (i,j,k). The elimination for a point (i,j,k) can not be done until the points (i-1,j,k), (i,j-1,k) and (i,j,k-1) have been completed. Thus the elimination must start at the point (1,1,1), then proceed to the points (2,1,1), (1,2,1), (1,1,2), and so on. Obviously the degree of parallelism varies widely during the course of the forward elimination sweep and there is a corresponding variation in the degree of parallelism during the back substitution sweep. It is therefore impossible to achieve linear speed-up of this algorithm. The maximum speed-up depends on the problem size and the number of processors.
In order to parallelize the approximate LU factorization we define a set of grid points in some plane n which satisfy
i+j+k=n+2
(1)
For example, on an N×N×N grid, there are 3N-2 such planes and the number of grid points in each plane is given by
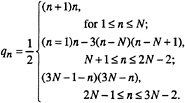
(2)
Such a plane is illustrated in figure 1 for a 16×16×50 grid (used in the investigation [10] of a three dimensional vortex convecting through a converging/diverging channel). In the forward elimination step of the LU algorithm, we loop sequentially over n in ascending order. In our N×N×N example, from 1 to 3N-2, but the operations can be done in parallel on points which lie on the same plane as defined above.
Figure 1. Planes of grid points available for point parallel calculations in the elimination/substitution sweeps of approximate LU factorization algorithm.
The parallelization is effected by means of the TC2000 FORTRAN spread do command, with the do statement acting over the number of grid points, n, on the current plane. The spread do potentially executes each loop iteration on a separate processor.
spread do
do m=1, n
…
end do
end spread
It will be noted from Eq. 2 that for the cubic grid the number of points on the planes range between 1 and 3/4N2, thus the degree of parallelism varies during the course of the forward elimination sweep. The back substitution sweep is similar except that we loop sequentially over n in descending order. Due to the variation in the degree of parallelism during the course of the forward and backward sweeps, the maximum achievable parallel efficiency decreases as the number of processors increases. The present approach is by no means the optimal one, but it does produce good results on a moderate number of processors and was easy to implement
Parallel Timing Results
Figure 2 shows the parallel speed-up obtained with different numbers of processors for an implementation of an approximate LU factorization, similar to that discussed here. These particular results are for the parallelization, performed by a BBN team [11,12], of a parallel benchmark released by NAS. This benchmark is part of a suite of such benchmarks which are intended to, as a whole, “mimic the computation and data movement characteristics of large scale computational fluid dynamic (CFD) applications [13].” The grid size for this calculation was 643.
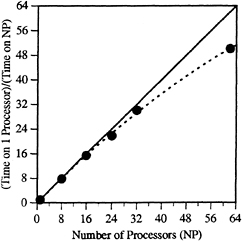
Figure 2. Parallel speed-up achieved for approximate LU factorization on a BBN TC2000 parallel computer.
The solid line in Fig. 2 represents the speed-up for a computation of ideal parallel efficiency, η,
![]() .
.
(2)
Note in Fig. 2 that nearly ideal speed-ups are achieved for as many as P=32 processors, with quite good speed-up (η=91%) obtained for the maximum number of processors, P=55, utilized in this study.
The fall-off in parallel efficiency with number of processors can, in part, be attributed to the previously discussed decrease in the maximum achievable efficiency for the present algorithm due to the varying degree of parallelism throughout the approximate factorization process. An additional drop-off in efficiency is due to the use of the relatively large number of synchronization barriers which are needed to achieve the parallelization as presently implemented. It should be noted that both sources of parallel efficiency loss would play a smaller role as the problem size is increased.
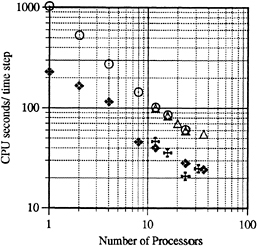
Figure 3. Parallel timing results achieved for present implementation on a time-shared, multiuser system. The various symbols denote runs with differing grids or boundary conditions.
Figure 3 shows some parallel timing results obtained with the present code. Results are for various unsteady simulations performed on the 2-D grids of Fig. 4, Fig. 6 and Fig. 7. Elapsed time per computational time step is plotted against the number of processors used for the computation. The Fig. 3 results are particularly noteworthy in that they are obtained for unsteady calculations using real geometries on a time-shared, multi-user computer, simultaneously in use by other users. This is in contrast with the more usual benchmark timing results, typically obtained under ideal operating conditions, on a “clean” computer. The present results reflect practical speed-ups obtained by performing the computations in parallel. The speed-up is noted to be very nearly linear with the number of processors, up to the largest number of processors utilized in this study.
Even though the BBN TC2000 is no longer in production, we believe that these results illustrate the potential of parallel computing for the practical solution of computational fluid dynamics problems.
RESULTS
Foil in Steady Flow
Figure 4 shows a grid used in the present study. The section shown in Fig. 4 is here denoted “Foil 1”. Foil 1 is a NACA 16 section with a thickness/chord ratio of 11.56% and camber to chord of 3.36%, and an a=0.8 mean camber line. The angle of attack was set to 0.8 degrees. The grid shown in Fig. 4 is a C-grid with 281×71 grid lines.
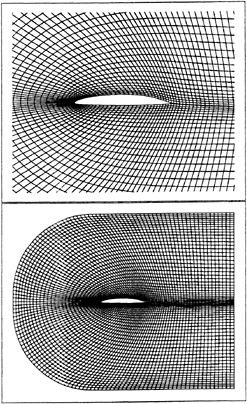
Figure 4. Grid used for Foil 1 transverse gust calculations, a C-grid with 281×71 grid points. For clarity of illustration only every second grid line is shown.
Figure 5 gives the steady-state pressure distribution on the surface of Foil 1 obtained by the present method and with a boundary element method [6]. We note that the differences are small, occurring mostly in the vicinity of the trailing edge. The lift coefficients, CL=L/(1/2ρV2c), obtained with the two methods are nearly identical, CL=0.570 from the present method, vs. CL=0.576 from the boundary element method.
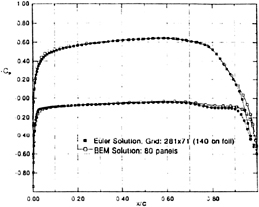
Figure 5. Steady pressure distributions computed for Foil 1 by present method and by a boundary element method [6].
![]() .
.
Transverse Gust
Transverse gusts interacting with three foil geometries were investigated. These geometries were:
-
Foil 1: NACA 16 thickness form, a=0.8 mean camber line, t/c=0.1156, f/c=0.0336, α=0.8 degrees.
-
Foil 2: thickness form identical to that of Foil 1 without camber or angle of attack (see Fig. 6), t/c=0.1156, f/c=0, α=0.
-
Foil 3: one-half the thickness of Foil 2 (see Fig. 7), t/c=0.0578, f/c=0, α=0.
The grids used in the transverse gust computations are shown in Fig. 4, Fig. 6 and Fig. 7. In each case a C-grid with 281×71 grid lines was utilized. The grids were generated with the aid of the INMESH [14] grid generation software.
Transverse sinusoidal gusts were modeled by imposing vertical velocity perturbations on the inflow boundary, the grid line which defines the outermost “C” in the grids of Fig. 4, Fig. 6 and Fig. 7. The imposed vertical perturbation velocity on the boundary was given by:
(3)
Here k is the reduced frequency, k=ωc/2V. A gust amplitude, ![]() , of 4 percent of the steady inflow velocity, V, was employed in the present study. Reduced frequencies of 0.5, 1.0, 2.0 and 5.0 were investigated. A time step size of ΔtV/c=0.025 was used in all of the presented results.
, of 4 percent of the steady inflow velocity, V, was employed in the present study. Reduced frequencies of 0.5, 1.0, 2.0 and 5.0 were investigated. A time step size of ΔtV/c=0.025 was used in all of the presented results.
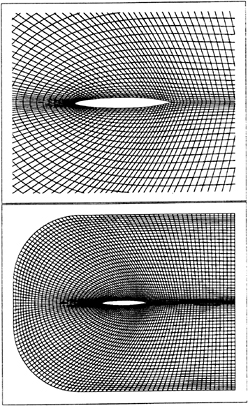
Figure 6. Grid used for Foil 2 transverse gust calculations, a C-grid with 281×71 grid points. For clarity of illustration only every second grid line is shown.
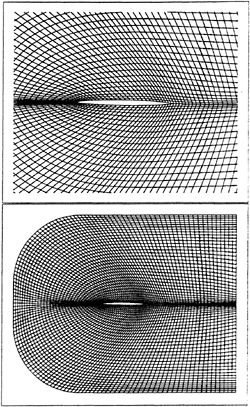
Figure 7. Grid used for Foil 3 transverse gust calculations, a C-grid with 281×71 grid points. For clarity of illustration only every second grid line is shown.
Figure 8 shows the resulting amplitude of the lift response to the transverse gust as a function of the reduced frequency, k. The unsteady lift amplitude in Fig. 8 is normalized by the quantity ![]() , the expected quasi-steady value. Also shown in Fig. 8 is the classical solution due to Sears [1] for an airfoil of zero thickness. We note that agreement between the present method and the Sears solution is relatively good. The value of the phase was also checked against the theoretical value for several of the investigated cases, and was similarly found to be in good agreement
, the expected quasi-steady value. Also shown in Fig. 8 is the classical solution due to Sears [1] for an airfoil of zero thickness. We note that agreement between the present method and the Sears solution is relatively good. The value of the phase was also checked against the theoretical value for several of the investigated cases, and was similarly found to be in good agreement
Flapping Foil
Detailed measurements of the flowfield about a foil experiencing unsteady time harmonic gusts have recently been performed at the Marine Hydrodynamics Laboratory at MIT [15,16,], and have been the subject of an ONR sponsored workshop at which comparisons between the experimental results and numerical simulations were presented [17]. The gusts were created by placing two small “flapping” foils in the water tunnel upstream of a larger stationery foil about which the measurements were made. This arrangement is shown schematically in Fig. 9
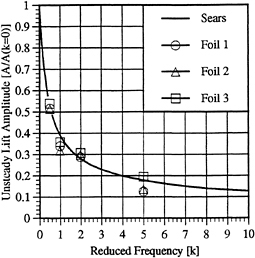
Figure 8. Unsteady lift amplitude due to a transverse gust. Results are shown at several reduced frequencies for the three foil geometries investigated with the present method. The classical solution due to Sears [1] is also shown.
Figure 9. Schematic representation of the flapping foil experiment installed in the MIT water tunnel.
The MIT experiment focused upon measurement of the unsteady velocities in the boundary layer of the stationery foil, with particular emphasis on the trailing edge flows. While the present code is inviscid, and therefore cannot capture the character of such flows, the MIT data still provides a challenging simulation problem for which at least some comparisons with experimental results can be made.

Figure 10. Grid used for flapping foil simulation, a C-grid with 251×51 grid points.
The MIT researchers measured both steady and unsteady velocities at points defining a box surrounding the stationery foil. It was originally our intent to simply extrapolate this data to provide an inflow boundary condition for the numerical simulation. However, there proved to be insufficient data to so proceed. Therefore, a far field boundary condition model was constructed with potential flow singularities to model the effects of the primary elements of the flapping foil experiment. This model is described in the Appendix. Parameters in the model were estimated using a non-linear least squared error approximation to unsteady data and a direct calculation of the steady circulation.
The foil geometry used for the flapping foil simulation is similar to that of the previously described Foil 1, and corresponds to the “unbounded” foil shape which the MIT researchers were attempting to experimentally model in the water tunnel. A somewhat different foil geometry was actually tested by MIT in an attempt to make up for tunnel wall effects. The angle of attack and maximum camber used in the simulation were reduced somewhat so that the predicted lift matched the experimental value. This reduction in lift is attributed to viscous effects which are not modeled by the present method. Fig. 10 shows the grid used for the numerical simulation. We note that the inflow boundary of this grid is quite close to the leading edge of the stationery foil, in order to keep the flapping foils outside of the computational domain.
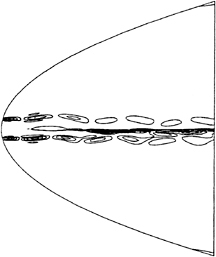
Figure 11. Predicted contours of vorticity induced by the flapping foils.
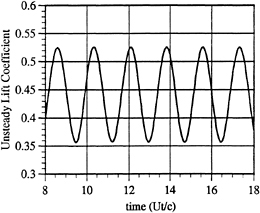
Figure 12. Unsteady lift, ![]() , induced on the stationery foil.
, induced on the stationery foil.
Figure 11 is a contour plot of the predicted levels of vorticity after the simulation had been running for approximately 900 time steps. We note the presence of both the vorticity injected into the grid by the boundary condition representing the flapping foils and the induced vorticity shed by the stationery foil. The reduced frequency of the unsteady disturbance (in terms of the chord of the stationery foil) is 3.6, corresponding to a disturbance wavelength of somewhat less than twice the chord.
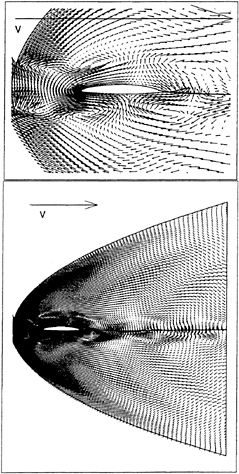
Figure 13. Vector representation of the unsteady velocity field. ![]() induced by the flapping foils. The large arrows represent the unit (freeestream) velocity vectors.
induced by the flapping foils. The large arrows represent the unit (freeestream) velocity vectors.
Figure 12 presents the resulting prediction of the unsteady lift We note that the amplitude of the unsteady lift force is quite large relative to that which one would predict from classical theory, when only the nominal magnitude ![]() of the unsteady vertical velocity component (a purely transverse gust) is considered. We observe, however, that the unsteady velocity field introduced by the flapping foils differs substantially from that of such a transverse gust. This is made apparent in Fig. 13 which shows a vector field describing the unsteady component of velocity at the same time step as the vorticity contours of Fig. 11. The vector field was formed by subtracting the steady solution for the velocity field from the total unsteady solution. Contrast this with Fig. 14 which gives a similar vector field for a transverse gust of k=2.
of the unsteady vertical velocity component (a purely transverse gust) is considered. We observe, however, that the unsteady velocity field introduced by the flapping foils differs substantially from that of such a transverse gust. This is made apparent in Fig. 13 which shows a vector field describing the unsteady component of velocity at the same time step as the vorticity contours of Fig. 11. The vector field was formed by subtracting the steady solution for the velocity field from the total unsteady solution. Contrast this with Fig. 14 which gives a similar vector field for a transverse gust of k=2.
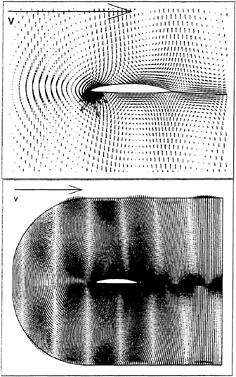
Figure 14. Vector representation of the unsteady velocity field. ![]() of a foil interacting with a transverse gust of k=2.
of a foil interacting with a transverse gust of k=2.
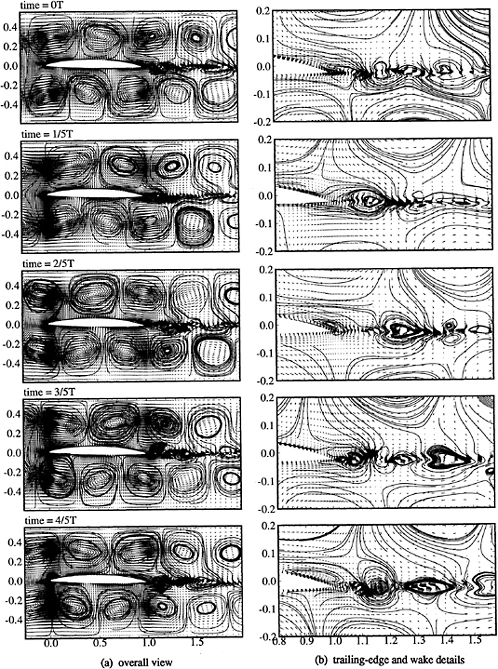
Vortex Chopping
Figure 15 presents a time history of predicted contours of vorticity as a distributed vortex interacts with a foil. Here the foil is a NACA 0012 thickness form without camber and with angle of attack set to zero. A C-grid with 99×33 grid lines was used for this calculation.
The vortex was generated by perturbing the inflow boundary in a manner similar to that employed for the flapping foil study. We specified an initial vorticity distribution of the form:
(3)
where Г is the total circulation, δ is the core radius, and x0=(x0, y0) is the initial position of the vortex center.
The boundary velocities were perturbed consistent with the potential flow about such a vortex in the absence of the foil, and the nominal position of the vortex was convected, at each time step, with the uniform freestream.
For the results presented in Fig. 15, Г=0.4, δ=0.1 and x0=0. The vortex is seen to intersect with and be split by the foil. The distortion of the vortex is associated with the velocity induced by the foil, which is experiencing lift due to the presence of the velocity field of the vortex.
The results obtained with the present method are seen to agree well with numerical results obtained by Lee and Smith [18], who employed a discrete vortex method to investigate this model problem.
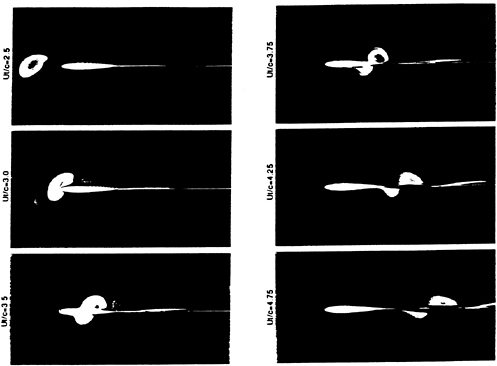
Figure 15. Vorticity contours depicting time history of a distributed vortex interacting with a foil.
CONCLUSIONS
A numerical method for the direct simulation of inviscid unsteady blade section forces has been implemented on a parallel processor. Timing results on the parallel computer showed nearly linear speed-ups with the number of processors employed. The method was applied to three model problems and the results compared favorably with available solutions.
Even though the BBN TC2000 is no longer in production, we believe that these results illustrate the potential of parallel computing for the practical solution of computational fluid dynamics problems.
ACKNOWLEDGMENTS
This work has been supported by the ONR Accelerated Research Initiative on Hydroacoustics of Unsteady Flows through Contract No. N00014– 89-C-0254. Parallel computer resources utilized in this work were made available by the Lawrence Livermore National Laboratory (LLNL) Massively Parallel Computing Initiative (MPCI). We thank Dr. Ching-Yeh Hsin and Professor Justin E.Kerwin of the Massachusetts Institute of Technology for providing the boundary element code described in [6].
REFERENCES
1. W.Sears, “Some Aspects of Non-Stationary Airfoil Theory and its Practical Application, ” Journal of the Aeronautical Sciences. 8(3) 104–108, 1941.
2. H.Naumann & H.Yeh, “Lift and Pressure Fluctuations of a Cambered Airfoil Under Periodic Gusts and Applications in Turbomachinery,” Journal of Engineering for Power, 1–10, January, 1973.
3. H.Atassi, “The Sears Problem for a Lifting Airfoil Revisted—New Results,” Journal of Fluid Mechanics, 141, 109–122, 1984.
4. H.Atassi & T.Akai, “Aerodynamic and Aeroelastic Characteristics of Oscillating Loaded Cascades at Low Mach Number,” Journal of Engineering for Power. 102, 344–351, 1980.
5. H.-W.Chiang & S.Fleeter, “Cascade Aeroacoustics Including Steady Loading Effects,” Noise Control and Engineering Journal, 34(2), 61– 72, 1990.
6. C.-Y.Hsin, “Development and Analysis of Panel Methods for Propellers in Unsteady Flow,” Ph.D. Thesis, MIT Department of Ocean Engineering, 1990.
7. S.Rogers & D.Kwak, “Upwind Differencing Scheme for the Time-Accurate Incompressible Navier-Stokes Equations,” AIAA Journal, 28, 253– 262, 1990.
8. M.Athavale & C.Merkle, “An Upwind Differencing Scheme for Time-Accurate Solutions of Unsteady Incompressible Flow,” AIAA Paper 88–3650, 1988.
9. S.Breit, W.Coney, A.Dickinson & J.Webb, “Computing Boundary Forces Due to Unsteady, Inviscid Incompressible Flow,” AIAA Journal, 30(3), 592–600, 1992.
10. S.Breit, W.Coney, J.Webb, “Vortex Chopping Noise in Turbomachinery: Numerical Simulation on a Parallel Processor,” presented at the ONR/DTRC Workshop on Quiet Turbomachinery Design , Annapolis, MD, November, 1991.
11. S.Breit, W.Celmaster, W.Coney, et. al. “The role of Architectural Balance in the Implementation of the NAS Parallel Benchmarks on the BBN TC2000 Computer,” FED-Vol. 156, CFD Algorithms and Applications for Parallel Processors, ASME, 1993.
12. S.Breit, “Implementing the Incomplete LU Factorization Method on the BBN TC2000 Parallel Computer,” Proceedings of the Conference on “Parallel Computational Fluid Dynamics.” K.G. Reinsch, et al., ed., Stuttgart, Germany, June 1991.
13. D.Bailey, J.Barton, T.Lasinski and H. Simon, The NAS Parallel Benchmarks. NAS White Paper, 1991.
14. R.Coleman, INMESH: An Interactive Program for Numerical Grid Generation. David W. Taylor Naval Ship Research and Development Center Report DTNSRDC-85/054, August 1985.
15. J.Rice, Investigation of a Two-Dimensional Hydrofoil in Steady and Unsteady Flows, SM thesis, Massachusetts Institute of Technology, Department of Ocean Engineering , June 1991.
16. P.Delpero, Investigation of Flows around a Two Dimensional Hydrofoil Subject to a High Reduced Frequency Gust Loading, SM thesis, Massachusetts Institute of Technology, Department of Ocean Engineering , February 1992.
17. “MIT/ONR Flapping Foil Workshop”, Carderock Divison/NSWC, Bethesda, MD, March 29–30, 1993.
18. D.Lee and C.Smith, “Distortion of the Vortex Core During Blade/Vortex Interactions,” AIAA 19th Fluid Dynamics, Plasma Physics and Lasers Conference, AIAA-87 –1243, 1987.
APPENDIX:
Flapping Foil Boundary Condition
A far field boundary condition model is constructed with potential flow singularities to model the primary elements of the flapping foil experiment. Parameters in the model are estimated using a nonlinear, least squared error approximation to unsteady data and a direct calculation of the steady circulation. All elements of the model are assumed to be two dimensional. The principal elements of the model are:
-
A single, steady vortex representing the steady lift component on the fixed foil. The strength of the vortex is computed from the measured steady velocity field.
-
Three unsteady vortices, each representing one of the two moving foils or the unsteady lift component on the fixed foil. Each vortex has a sinusoidally varying circulation distribution in time as in Eq. A-1. The magnitude, frequency and phase of the time variation are estimated from the experimental data.
-
A straight, semi-infinite vortex wake attached to each of the unsteady point vortices. Vorticity is assumed to convect along the length of the wake at a constant rate which is estimated from the experimental data. The local strength of the wake is coupled to the time history of the associated point vortex and the convection velocity and consequantly is sinusoidal in both time and space. Eq. A-3 defines the dependence between the point vortex strength and the wake strength. The induced velocity is given by an integral over the length of the wake as shown in Eq. A-4.
-
In order to ensure the velocity is defined at all locations where a computational boundary is likely to be positioned, the unsteady wakes are assumed to have finite, non-zero thickness. If a boundary point falls inside this region, the velocity due to the wake is computed to be the average of the velocity induced at the top and bottom of the region defined by the wake thickness.
-
Effects due to free vorticity outside of the unsteady wakes and thickness effects of the various airfoils are not included.
The software implementing the boundary condition is provided in two parts. One is a subroutine called by the flow solver. The other is a program used to generate estimates of the parameters in the model from experimental data.
Induced Velocity Formulation
The basic element of the boundary condition model is a point vortex with time varying circulation and an attached wake. The circulation of the point vortex is assumed to be of the form:
Гv(t)=Г0sin(ωt+α) (A-1)
and the associated wake will be:
Гw(x,t)=Г′ sin(kx+β) (A-2)
where we expect β to be time dependent. The strength of the wake will be related to the strength of the point vortex in the following way. Assume a constant convection velocity for the vorticity in the wake, U. For an infinitesimal change in the strength of the point vortex, dГv, there is also, at some position Udt away, a filament of strength -dГν. Since U is constant, we can say:
(A-3)
We will be interested in the induced velocity at a particular point in time so we can treat Гw as a function of the distance along the wake. From these assumptions we can see:
From Eq. A-2 we can see:
Г′=Г0ω
and
The induced velocity from a point vortex is computed from:
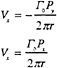
for the coordinate system defined Fig. A-1. The vortex is assumed to be located at the origin of the coordinate system and the velocity is computed at point P.
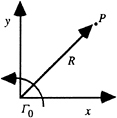
Figure A-1. Point vortex coordinates
For the wake, the situation is considerably more complicated. For a circulation distribution defined by Eq. A-2 and the coordinate system of Fig. A-2, the induced velocity is given by:
where ![]() and
and ![]() are the unit vectors in the x and y coordinate directions. (The above epression is obtained by integrating the velocity due to a planar vortex sheet once in the direction parallel to the vortex filament we are representing with a point vortex.)
are the unit vectors in the x and y coordinate directions. (The above epression is obtained by integrating the velocity due to a planar vortex sheet once in the direction parallel to the vortex filament we are representing with a point vortex.)
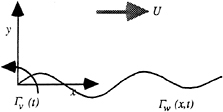
Figure 2. Wake Coordinates
In cases where kx>0 and ky≈0, it is assumed the computation point is inside the viscous region of the wake. For these cases, the velocity is computed at the locations where y=±1/2 (wake thickness) and averaged. The wake thickness is a specified parameter.
Computing the Wake Induced Velocity
Eq. A-4 is evaluated numerically over a finite extent of the wake. In order for this approach to be valid, the influence of a semi-infinite wake must approach zero as the point of interest moves far upstream of the start of the wake. With this assumption, we can rewrite Eq. A-4 as:
(A-5)
where we have assumed kx»ky. We can rewrite this as:
(A-6)
and since we also require x<0, the singularity associ ated with ![]() is not a difficulty.
is not a difficulty.
We can say:
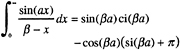
(A-7)
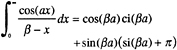
(A-8)
for a>0. The sine and cosine integral functions have been used here where:
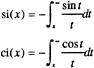
We are interested in the case where x approaches negative infinity. The integral functions evaluate to:
(A-9)
(A-10)
where we will take the real part of Eq. A-10. Substituting these into Eq. A-6 results in:
(A-11)
This argument suggests using a finite portion of the wake will eventually converge as longer extents are integrated. No rigorous assesment of the convergence properties of the sequence generated by this process has been performed. Simple numerical experiments suggest it may be necessary to take 1000 or more periods of the wake to obtain accuracy in the range of 1 part in 104.
Computation of Unsteady Viscous Flow with Application to the MIT Flapping Foil Experiment
E.Paterson and F.Stern
(University of Iowa, USA)
ABSTRACT
A time-accurate unsteady viscous-flow method is validated through calculations and comparisons with the Massachusetts Institute of Technology flapping-foil experiment. Solutions are obtained using a small domain surrounding the foil, a tunnel domain that included the foil and the tunnel walls, and a complete domain that included the foil and both the tunnel walls and the upstream flappers. In the latter case, the CHIMERA overlaid-grid method was used. The solutions give similar overall agreement with the data for both steady and unsteady flow, which demonstrates that such problems can be handled with a variety of formulations, although the boundary data, cpu time, and storage requirements are different. The physics are complex with analogy to Stokes layers and explicated through analysis of the axial pressure gradient, which exhibits upstream and downstream traveling waves over the foil and in the near wake and in the intermediate wake, respectively, due to nonlinearities induced by the convective acceleration and steady/unsteady interactions. The nature of the unsteady displacement thickness suggests viscous-inviscid interaction as a possible mechanism for the axial pressure-gradient response.
NOMENCLATURE
|
c |
=wave speed (=λ/T) |
|
Cp |
=pressure coefficient |
|
L |
=characteristic (foil) length |
|
p |
=pressure |
|
Re |
=Reynolds number (=UoL/v) |
|
t |
=time |
|
Ui |
=ensemble averaged velocity components in Cartesian coordinates (= U,V,W) |
|
|
=Reynolds stress tensor |
|
xi |
=Cartesian coordinates (=x,y,z) |
|
y+ |
=wall coordinate (=Uτy/v) |
|
δ |
=boundary-layer thickness |
|
γ |
=phase angle |
|
ν |
=kinematic viscosity |
|
νt |
=eddy viscosity |
|
ξ |
=frequency parameter (=ωL/U0) |
|
ξi |
=curvilinear coordinates (=ξ,η,ζ) |
|
τw |
=wall-shear stress |
|
|
=transport quantities (U,V,W) |
|
ω |
=circular frequency (=2πf) |
INTRODUCTION
Although most practical engineering flows are inherently unsteady and viscous, the physical understanding is in its infancy in comparison to steady flow, due to the complexity of performing experiments and computations even for simplified configurations, as evidenced by the sparse number of studies documented in the literature for unsteady vs. steady flow (e.g., the proceedings of this conference). Unsteady flows can be conveniently grouped into three categories: (1) natural, (2) forced, and (3) interacting. For all three, the predominant number of studies are experimental vs. computational, as indicated by the example references given.
Naturally unsteady flow refers to conditions under which the unsteadiness arises from flow separation and associated vortex wakes or jet and shear-layer instabilities. Most information is for two-dimensional flows, which includes the Reynolds number (Re) dependence of the separation points, vortex-shedding frequencies [i.e., Strouhal number(St)], and wake-patterns for a variety of bluff bodies both with sharp (e.g., flat plates at incidence) and smooth (e.g., circular cylinders) edges [1,2,3]. The situation is similar for three-dimensional flows, but the number of studies is drastically reduced [4,5].
Forced unsteady flow refers to conditions under which the unsteadiness arises from body motions or moving boundaries (e.g., rotor-type flows and control surfaces) or oscillating streams (e.g., boundary layers with oscillating external flows) such that there is an identifiable predominant forcing frequency. With respect to the former, relatively few studies have been conducted for realistic geometries, due to the complexity of such configurations and the geometric dependence of the resulting data. However, a number of studies have examined the idealized geometry of a pitching foil where the interest has ranged from inviscid flutter analysis [6] to dynamic stall [7–9]. The situation is similar for oscillating external flows where model problems such as flat-plate boundary layers (i.e., Stokes-layer overshoots, phase angles, and streaming) both for laminar and turbulent flow [10] and foils embedded in transverse gusts [11] have been studied.
Interacting unsteady flow refers to conditions under which both natural and forced unsteadiness are present and interact. Obviously, in this case, the least information is available, although this may, in fact, be the most important category with regard to engineering design improvement. The few studies that have been conducted were concerned with wake and separation control [12,13] and blade/vortex [14,15] and rotor/stator [16] interactions. In the former cases, it has been demonstrated that wakes with harmonic disturbances behave like nonlinear oscillators and are characterized by synchronization (i.e., lock-in) vs. non lock-in conditions depending on the ratio of the frequency of the disturbance fe to St (i.e., state-selection diagram or resonant horns of amplitude vs. fe/St), which has been further explicated through stability analysis [ 17], and similarly the ability to control separation through disturbances at certain fe. In the latter cases, the studies are somewhat preliminary in that, thus far, the blade and stator flows, respectively, are usually steady.
The present work is part of a larger project at the Iowa Institute of Hydraulic Research (IIHR) specifically concerning the development of computational fluid dynamics (cfd) methods with application to marine propulsors. Marine propulsors are unique in comparison to related applications (e.g., turbomachinery, turboprops, and rotors) in that they operate in the thick hull boundary layer and/or appendage wakes such that complex naturally (hull flow) and forced (propulsor flow) unsteady interactions occur. Initially, cfd methods were applied to propeller/hull interaction utilizing an interactive approach, i.e., a body-force propeller representation in the viscous-flow method obtained interactively using a vortex-lattice propeller-performance method for specified inflow [18]. Subsequently, cfd methods were applied directly to calculating the propeller-blade and wake flows both for idealized [19] and practical turboprop and marine propulsors [20]. Currently, efforts are being directed towards extending the latter methods for unsteady flow with consideration to issues of efficient large-scale time-accurate computations for fixed- and moving-boundary problems [21, 22].
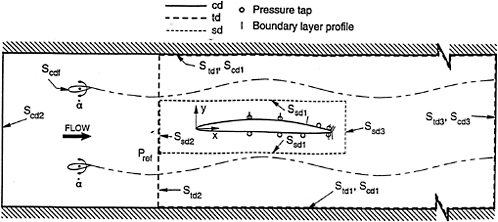
The present paper describes the initial efforts in extensions for unsteady-flow calculations and validation through calculations and comparisons with the Massachusetts Institute of Technology (MIT) Marine Hydrodynamics Laboratory flapping-foil experiment (ffx). ffx represents a two-dimensional simulation of propeller-blade and wake flow, i.e., a blade section (foil) embedded in vertical and horizontal gusts generated by upstream pitching foils (flappers) (figure 1). ffx was conducted such that calculations could be performed either for a small domain with given boundary data (sd), for the tunnel domain with a specified inflow (td), or for the complete domain, including the upstream flappers (cd). Associated with ffx was the 29–30 March 1993 Office of Naval Research (ONR)/MIT Unsteady-Flow Workshop in which various groups of researchers submitted blind computations (i.e., with only the experimental conditions and boundary data) for either sd, td, or cd and met at the workshop for the comparisons with the data and discussion. At the workshop, IIHR submitted blind computations for sd. Herein, these results will be presented along with more recent results for sd, td, and cd. In the latter case, the CHIMERA overlaid-grid method was used, which has also been under investigation for other fixed- and moving-boundary problems [22]. The recent results were presented at the 13 September 1993 post workshop meeting.
In the following, the computational method and ffx are described and the computational conditions, grids, and uncertainty are given. Then, the results are discussed for both steady and unsteady flow, including comparisons with the data, discussion of the ONR/MIT workshop and post workshop meetings, and analysis and analogy to Stokes layers. Lastly, some concluding remarks are made, including future work.
COMPUTATIONAL METHOD
The computational method is based on extensions of [19] for time-accurate unsteady-
flow calculations. Although the basic viscous-flow method [23] utilized in [19,20] was developed with the capability of unsteady-flow calculations, only very limited such calculations had previously been performed. In the following, an overview is given of the equations and coordinate system, turbulence model, discretization and velocity-pressure coupling, solution domains and boundary conditions, and grid generation. The modifications required for time-accurate computations are also discussed. The method is applicable to unsteady three-dimensional flow; however, the current presentation is for unsteady two-dimensional flow in view of ffx. Further details concerning the basic viscous-flow method are provided in [23] and associated references.
Equations and Coordinate System
The continuity and Reynolds-averaged Navier Stokes (RaNS) equations for unsteady incompressible flow are written in the physical domain using Cartesian coordinates and tensor notation with x positive downstream, y normal to x, and the origin at the foil leading edge (figure 1). In nondimensional form the equations are
(1)
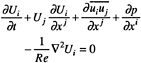
(2)
with ![]() and Ui=(U,V,W) and ui= (u,v,w) are the components of the ensemble-averaged velocity and turbulent fluctuations, respectively, and p is the pressure. All variables are nondimensionalized using Uo, L, and ρ.
and Ui=(U,V,W) and ui= (u,v,w) are the components of the ensemble-averaged velocity and turbulent fluctuations, respectively, and p is the pressure. All variables are nondimensionalized using Uo, L, and ρ.
The Reynolds stress is related to the mean rate of strain by an isotropic eddy viscosity vt
(3)
upon which (2) becomes
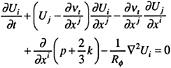
(4)
where ![]() . (5)
. (5)
Transformation of (1–5) into nonorthogonal curvilinear coordinates is such that the computational domain forms a simple rectangular parallelepiped with equal grid spacing. The transformation is a partial one since it involves the coordinates only and not the velocity components. The transformation is accomplished through the use of the expression for the divergence and “chain-rule” definitions of the gradient and Laplacian operators, which relate the orthogonal curvilinear coordinates xi=(x,y,z) to the nonorthogonal curvilinear coordinates ξι= (ξ,η,ζ). In this manner, (1–5) can be rewritten as follows
(6)
(7)
with
(8)
and where ![]() is nonzero only for moving-grid applications.
is nonzero only for moving-grid applications.
Turbulence Model
Closure is attained through a quasi-steady application of the Baldwin-Lomax turbulence model with modifications to account both for the effects of wake asymmetry [24,25] and axial pressure gradients [26]. The former was used to obtain the solutions for all three domains (sd, td, and cd), whereas the latter was only used for td (denoted tddp/dx).
For the standard Baldwin-Lomax model, in the near-wall layer
(9)
where the length scale is based on the mixing length
(10)
and the vorticity ω is used to determine the velocity scale. In the outer-layer
(11)
where
(12)
(13)
(14)
(15)
FKleb is the Klebanoff intermittency function. In Fwk, the first and second expressions are effective in attached and separated boundary layers (and wakes), respectively. The velocity scale Fmax, is determined from (14) and ymax is the corresponding y-coordinate. The empirical constants are: κ=0.4, k=0.0168, Ccp=1.6, CKleb=0.3, Cwk=0.25, and A+=26.
The standard Baldwin-Lomax model is not suitable for asymmetric wakes where two different values for ymax and Fmax result from the merging of the suction- and pressure-side boundary layers. Therefore, the eddy viscosity on the far-wake centerline is rendered single-valued by taking the maximum value from both sides of the wake.
vt,fwk=kCcpFKleb max(Fwk,top,Fwk,bottom) (16)
The eddy-viscosity distribution is asymmetric due to the evaluation of Fkleb on each side of the wake. For both FKleb and Fwk,y is measured from the point of maximum wake deficit. Finally, since (11) is only valid in the far wake, a blending function is used to provide a smooth transition from the boundary layer to the far wake
(17)
where vt,te is the distribution at the trailing edge of the foil.
The effects of axial pressure gradient were investigated through the use of Granville's modified coefficients Ccp and CKleb such that they are functions of a Clauser-type pressure-gradient parameter ![]()
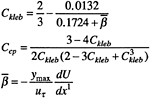
Note that the zero gradient values Ccp=1.2 and Ckleb=0.646 are significantly different from the standard Baldwin-Lomax values.
Discretization and Velocity-Pressure Coupling
The finite-analytic method is used to reduce (7) to algebraic form. Each local rectangular numerical element is linearized by evaluating the coefficients and source functions at the interior node P and transformed again into a normalized form by a simple coordinate stretching. In addition, the temporal derivative is expressed as a second-order backward finite difference. An analytical solution is obtained by separation of variables with specified boundary functions. As a result, a 9-point finite-analytic formula is obtained
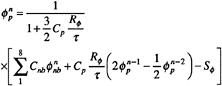
(18)
The resulting computational stencil includes all eight neighboring nodal values and the values at the two previous time-steps. Since (18) is implicit, both in space and time, its assembly for all elements results in a set of simultaneous algebraic equations that is solved using a line-ADI approach with under-relaxation.
The coupling of the velocity and pressure fields in an efficient time-accurate fashion required changing from a SIMPLER algorithm, which requires global iterations for time accuracy, to a split-operator approach based on the PISO algorithm. The first step is to implicitly solve the momentum equations given the pressure field from the previous time step using (18). Next, the implicit pressure equation and the explicit velocity correction are solved iteratively until continuity is satisfied. In both steps, the finite-analytic coefficients Cnb are updated in each iteration, thus retaining the nonlinear nature of the RaNS equations.
Solution Domains and Boundary Conditions
In terms of the notation of figure 1, the boundary conditions are as follows.
For sd: on the top and bottom surfaces Ssd1,
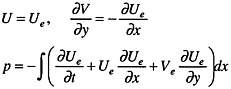
(19)
where irrotationality has been assumed so that the velocity derivatives in the evaluation of the pressure can be prescribed by the data and the upstream lower corner of the sd boundary (see figure 1) is fixed at an instantaneous reference pressure defined as the volume average over the computational domain [27]
(20)
on the inlet Ssd2,
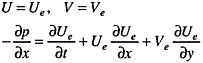
(21)
and on the exit plane Ssd3,
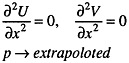
(22)
where Ue and Ve are specified from the data.
For td: on the tunnel walls Std1,
(23)
on the inlet Std2,
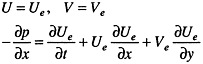
(24)
where Ue and Ve are a combination of the data (figure 3) and an inviscid model of an internal progressive wave (Appendix A), and on the exit plane Std3,
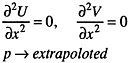
(25)
For cd: on the tunnel walls Scd1and on the exit plane Scd3, (23) and (25) are applied, respectively, on the inlet, Scd2,
(26)
i.e., uniform flow is assumed, and on the flapper surfaces Scdf.
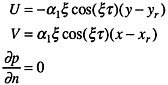
(27)
where α=α1 sin(ξτ) is the flapper angle, (xr,yr) is the center of rotation, τ is the nondimensional time, and ξ (=ωL/Uo) is the frequency parameter (or St), which is twice the reduced frequency k (=1/2ξ).
Grid Generation
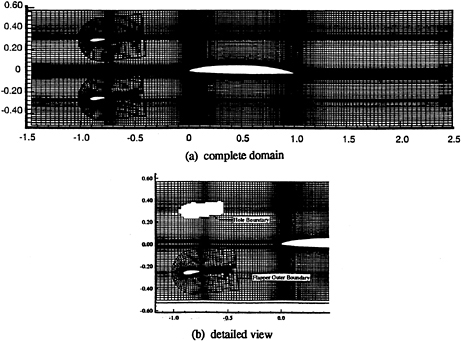
Three grid-generation techniques were used depending on the domain and grid topology. EAGLE [28] was used to generate c-grids for both the foil in sd (figure 2) and the flappers in cd (figure 4). Algebraic h-grids were used for td and cd (figures 3 and 4) with hyperbolic tangent stretching functions and transfinite interpolation such that the grid spacing was controlled along the foil surface, leading and trailing edges, and the flapper wakes. CHIMERA domain decomposition [29,30] was used for cd to resolve the oscillating flappers by decomposing cd into three separate, but coupled domains. Grid-to-grid communication was facilitated through bi-linear interpolation of the flow variables (U,V,p) from the foil grid to the flapper outer boundaries and from the flapper grids to the foil hole boundaries. Holes in the foil grid are created by excluding points that lay within specified boundaries on the flapper grids. Typically, these boundaries are specified such that a three or four point overlap region exists. The interpolation coefficients and holes and hole boundaries were determined a priori for each time step. Figure 4 shows global and detailed views of the overlaid grid system.
The use of oscillating, overlaid grids required modifications of the tridiagonal solver
to incorporate the hole boundary conditions and to solve across hole regions
ai=ai• IBLANKi
bi=bi• IBLANKi+(1−IBLANKi)
ci=ci • IBLANKi
di=di • IBLANKi+(1−IBLANKi)•φi (28)
where IBLANK is 0 for a hole point and 1 for a field point, ai, bi, ci, and di correspond to the lower, center, upper diagonals, and right hand side of the tridiagonal matrix, respectively, and φi corresponds to the flow variable value inside or on the hole boundary.
MIT FLAPPING-FOIL EXPERIMENT
ffx represents a two-dimensional simulation of propeller-blade and wake flow, i.e., a foil embedded in vertical and horizontal gusts. The gust (i.e., traveling-wave) models the flow experienced by a propeller-blade section as it rotates through the nonuniform hull and/or appendage wake. The purpose of the experiment was to provide detailed measurements for validation of unsteady cfd methods and to provide data for the determination of appropriate Kutta conditions for unsteady potential-flow methods. Details of the experimental objectives, apparatus and procedures are documented in [31–33].
Experimental Geometry, Information, and Uncertainty
The experiments were performed in the closed-loop MIT Variable-Pressure Water Tunnel. The test section is 53 inches long and 20 inches square with a freestream turbulence level of about 1%. The foil is a modified NACA 66 with a chord and span length of 18 and 20 inches, respectively, and was fixed at an angle of attack of 1.18–1.34º. Transition was set at x=0.105 on both sides using 0.050 inch diameter epoxy disks 0.008 inch high separated by 0.050 inch. The flappers are NACA 0025 with a chord and span length of 3 and 19.5 inches, respectively, and are driven by a variable-speed motor, which was designed to operate at reduced frequencies of up to 10. The flappers oscillated with an amplitude of 6º and a frequency of 16 Hz. The corresponding Re based on the foil chord length and reference velocity 20.94 ft/sec is 3.78 ×106 and the reduced frequency is k=3.6
Velocity and surface-pressure measurements were made using a two-component laser Doppler velocimeter and miniature pressure transducers, respectively. For the unsteady measurements, the value at each time step is the ensemble, or phase, average over 250 periods and had a temporal discretization of 180 points over the period.
Prior to the workshop, steady and unsteady (U,V) data was provided on sd boundaries (figure 2) and a large portion of td inlet (figure 3) along with steady boundary-layer profiles. After the workshop, unsteady boundary-layer profiles and pressure data was provided at the locations shown in figure 1.
Experimental uncertainty is due to instrument accuracy, geometric uncertainty, and data processing. The velocity data on sd boundaries has a standard deviation of 0.029 in the streamwise direction and 0.016 in the vertical direction. Standard deviations for the boundary-layer profiles vary from about 0.15 close to the foil surface to about 0.025 at the edge of the boundary layer. The unsteady pressure measurements had a standard deviation of 0.02 based upon absolute pressure. There was some uncertainty in the foil angle of attack due to the difficulty of determining the precise location of the foil in the tunnel. The data was normalized by the velocity at the exit of the contraction measured without the flappers and foil, i.e., 20.94 ft/sec. This presents no problems for sd and td comparisons since they use the data for boundary conditions; however, cd was normalized based on a unit reference inlet value such that the presence of the flappers and foil are included, which results in a 3% lower velocity on S td2 in comparison to the data. A similar difference was confirmed by MIT through inviscid-flow predictions.
COMPUTATIONAL GRIDS, CONDITIONS, AND UNCERTAINTY
The grids for sd, td, and cd are shown in figures 2–4, respectively, sd and td grids have 181×80 (14,480) and 180×179 (32,330) points, respectively, cd has 240×179 (42,960) points and 71×40 (2840) points for the foil and flappers, respectively, for a total of 48,640. For each domain, approximately 40 points span the boundary-layer and the near-wall grid spacing was set such that the first grid point was located at y+≈0.1.
The experimental values of Re and ξ were used in the calculations. The calculations were made at an angle of attack of 1.34º. An additional td calculation was made for angle of attack 1.18º, which indicated a 2% change in the steady lift. The unsteady solution was unchanged. The solution submitted for the workshop (denoted sdorig) used the data, which was smoothed using a cubic spline and
interpolated both in time and space along sd boundaries using a bi-quadratic polynomial, to evaluate the pressure from (19). However, the coarseness of the data introduced errors in the evaluation of (19) and lead to erroneous results, especially for pressure. Subsequently, a revised sd (denoted sd) used td to provide finer resolution data for the boundary conditions. For td inlet boundary Std2, smoothed and interpolated data provided approximately 60% of the tunnel inflow area and, as previously mentioned, the remaining 40% was specified using a potential-flow approximation. For cd, the boundary-conditions were well-posed and required no special treatment. However, no turbulence model was used in the flapper domains. Lastly, for each domain, transition was fixed by forcing the eddy viscosity upstream of the boundary-layer trip to zero.
Time-step sensitivity studies were conducted for sd which showed that approximately 50 time steps/period provided a time-step independent solution. For sd and td, the time step was 1/50 of a period (Δt=0.01745) and for cd, the time step was 1/64 of the period (Δt=0.01364). Grid sensitivity studies were conducted for steady flow from which the boundary-layer and near-wall grid spacing described earlier was determined. Resolution of the point distribution in the wake of the flappers for both td and cd was not studied.
The steady-flow solution was used as the starting point for each calculation and typically 2 periods for sd and 4 periods for td and cd were required to attain a periodic solution. Cpu time per period on a CRAY YMP was 15 minutes, 45 minutes, and 2 hours for sd, td, and cd, respectively, and storage requirements ranged from 4 MW for sd to 8 MW for cd. Typically, 25 and 50 iterations were required for the implicit momentum and the pressure-velocity correction steps, respectively, to satisfy the convergence criterion of R<0.0001, where the residual was defined as
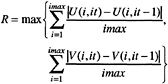
(29)
and i, it, and imax are the grid-point and iteration indices and total number of grid points, respectively.
Uncertainty in the solutions is due to the boundary conditions and truncation errors. For sd and td, the process of using data for boundary conditions introduces errors from smoothing and interpolating, experimental uncertainties, and insufficient spatial resolution. The numerical method is second-order in time and approximately first order in space. Therefore, given Δt≈0.01, the temporal truncation errors are O(10−4).
COMPARISON OF SOLUTIONS AND DATA
sd, sdorig, td, tddp/dx, and cd results are compared with each other and the data. Comments are made concerning the overall results at the ONR/MIT Unsteady-Flow Workshop and post workshop meetings. The velocity, pressure, shear-stress, and force harmonic amplitude and phase are Fourier analyzed
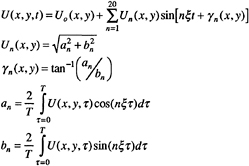
(30)
where γn is with respect to the flapper angle.
Steady Flow (Zeroth Harmonic)
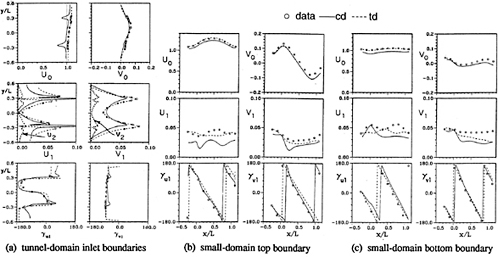
Figure 5 shows td and cd (U0,V0) on Std2 and Ssd1 top and bottom, including data. On Std2, cd U0 shows smaller magnitude and flapper wakes with larger width and deficit than the data and V0 in agreement. On Ssd1, td and data U0 agree, whereas cd agrees in shape, but under predicts the magnitude, td and cd V0 are similar, but show an axial decay in comparison to the data.
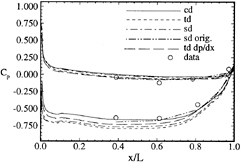
The surface pressure is shown in figure 6. sd and td are close to the data on the pressure side, but over predict on the suction side, cd is similar on the pressure side and closer to the data on the suction side. The latter is consistent with the lower inlet velocity. Over the adverse pressure-gradient region on the suction side, tddp/dx shows improvement (i.e., closer agreement with the data). The corresponding lift for sd, td, cd, sdorig, and tddp/dx are 0.65, 0.65, 0.60, 0.54, and 0.63.
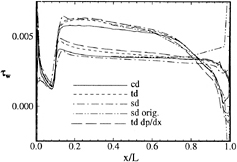
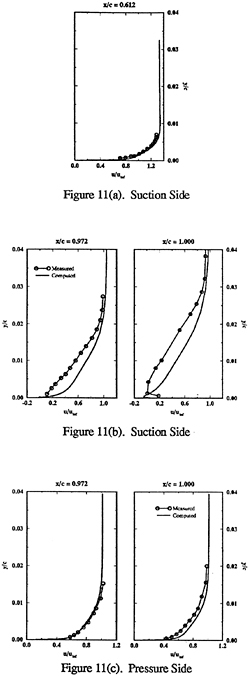
The wall-shear stress is shown in figure 7. The fixed transition along with a small region of separation on the last 5% on the suction side are displayed, sd and td agree, but cd shows lower values.
The steady velocity profiles are shown in figure 8. The solutions agree with the data, except near the trailing edge, where tddp/dx shows improvement, especially on the suction side. The change in the zero-gradient values of Ckleb and Ccp had a larger influence than the ![]() corrections, cd shows a consistent 3% under prediction outside the boundary layer Wall-coordinate profiles of the data [34] indicate extensive regions of transitional flow on both the pressure (x< 0.76) and suction (x<0.61) sides, (i.e., unexpected departures for the data from the logarithmic-overlap law) and boundary effects on the near-wall data, which may partly explain the differences between the solutions and data. However, the level of agreement for the solutions without and with the pressure-gradient modifications appears to be a general assessment of the current capabilities of isotropic turbulence models since it is consistent with the overall results reported in the literature.
corrections, cd shows a consistent 3% under prediction outside the boundary layer Wall-coordinate profiles of the data [34] indicate extensive regions of transitional flow on both the pressure (x< 0.76) and suction (x<0.61) sides, (i.e., unexpected departures for the data from the logarithmic-overlap law) and boundary effects on the near-wall data, which may partly explain the differences between the solutions and data. However, the level of agreement for the solutions without and with the pressure-gradient modifications appears to be a general assessment of the current capabilities of isotropic turbulence models since it is consistent with the overall results reported in the literature.
Unsteady Flow
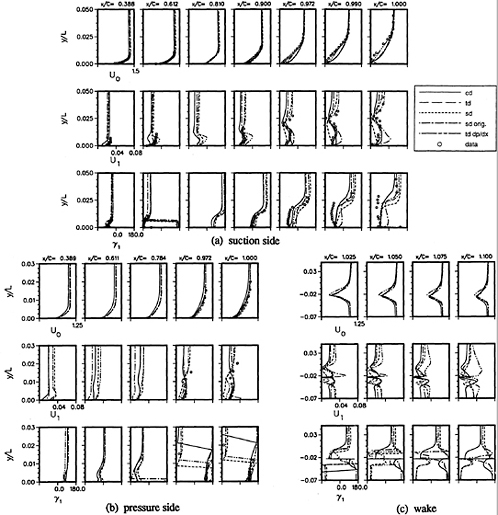
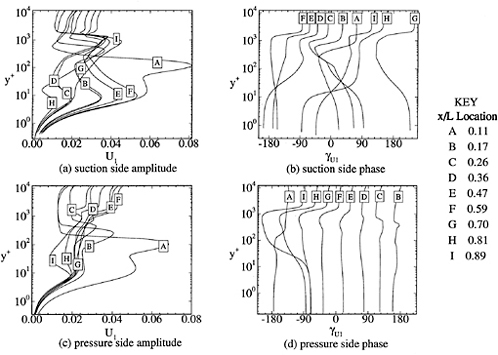
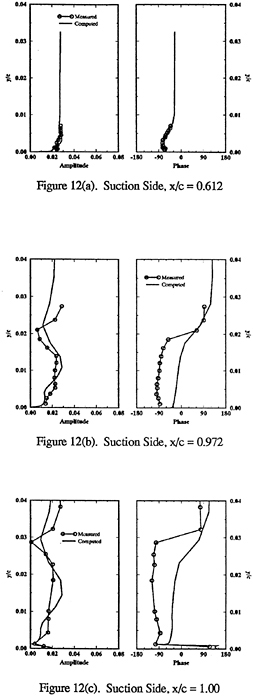
Figure 5 includes td and cd first-harmonic amplitude (U1,V1) and phase (γU1, γV1). On Std2, cd agrees in amplitude shape and phase, but under predicts the former magnitude. Also shown are td second-harmonic amplitudes (U2, V2), which are large, particularly near the flapper wakes. On Ssd1 top, td U1 agrees in magnitude, but lacks the spatial oscillations in the data, cd U1 is under predicted, but displays similar spatial oscillations as the data, td V1 agrees in magnitude and shape and cd V1 in magnitude with the data. On Ssd1 bottom, both td and cd U1 show agreement in magnitude, but under predict the spatial oscillations, td and cd V1 show an axial decay in comparison to the data. The phases are in agreement with the data and show a downstream traveling wave [in the Fourier analysis, the argument of the trigonometric functions (ξt+γ) is equivalent to characteristic lines ξ(t±x/c), which corresponds to downstream(γ=−ξx/c) or upstream(γ= +ξx/c) traveling waves].
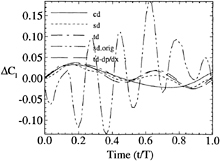
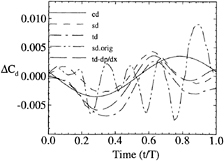
Figures 9 and 10 show the lift and drag time histories. The magnitudes are similar; however, sd, td, and tddp/dx indicate a second harmonic, whereas cd is primarily first harmonic, and sdorig shows large oscillations. There are larger differences for ΔCD than ΔCl,
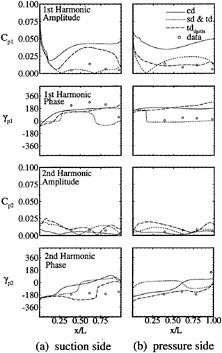
Figure 11 shows the surface-pressure first-and second-harmonic amplitude and phase. In comparison to the data, sd, td, and tddp/dx show amplitudes of similar magnitude. The shapes and zero values at certain x/L are different and unconfirmed by the limited data, tddp/dx shows improvement. The large second harmonic is consistent with the lift and drag and was attributed by MIT to an excited mode of tunnel vibration [33]. Recall the large td second-harmonic amplitudes on Std2. cd first-harmonic amplitude is larger than the others and cd second-harmonic amplitude, the latter of which is similar to the others. This trend is consistent with the lift and drag. On both sides, cd and tddp/dx indicate increasing phase (i.e., upstream traveling wave), whereas sd and td indicate nearly constant values with 180º changes at the zero-value locations. The limited data indicate constant phase with no particular agreement with the solutions.
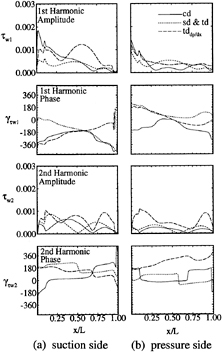
Figure 12 shows the wall-shear stress first-and second-harmonic amplitude and phase. The solutions show amplitudes of similar magnitude for both harmonics. The first-harmonic phases indicate: on the pressure side, decreasing values (i.e., downstream traveling wave) on the forebody and upstream traveling wave on the afterbody for sd, td, and tddp/dx and vice versa for cd; and on the suction side, downstream traveling wave for sd and td, cd similar to the pressure side, and upstream traveling wave for tddp/dx. The second-harmonic phases indicate: on the pressure side, nearly constant values with 180º changes at the zero-value locations for sd, td, and cd and upstream traveling wave for tddp/dx; and on the suction side, nearly constant values with 180º changes at the zero-value locations for sd, td, and tddp/dx and upstream taveling wave for cd.
The velocity first-harmonic amplitude and phase (U1, γU1) profiles are also shown in figure 8. Both the solutions and data indicate, for x≤0.784 (pressure side) and ≤ .9 (suction side), amplitudes with small overshoots and phases with increasing lags with x and smooth transition across the boundary layer, whereas for x greater than these values, amplitudes and phases with a two-layer structure: relatively constant values of different magnitude for the inner and outer flows with a zero amplitude and 180º phase shift at the inner/outer boundary (i.e., boundary-layer thickness). The magnitudes are close to the data and tddp/dx shows improvement, especially near the trailing edge. In the wake, the solutions show large differences, especially near the wake centerline. sd, sdorig, and td have a smaller amplitude near the centerline and a larger amplitude outside the boundary layer in
comparison to cd and and tddp/dx, which show large overshoots. Initially, the phase shows a continuation of the boundary-layer response and then by x=1.1, leads for sd, td, and tddp/dx and lags for cd and sdorig on the pressure side and leads on the suction side.
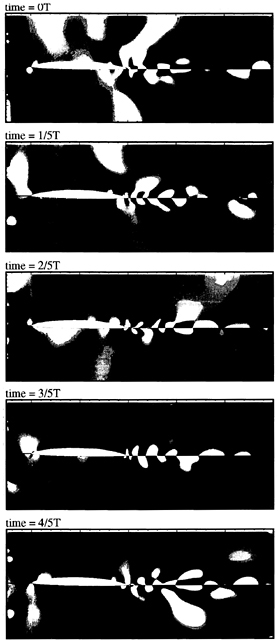
Figure 13 shows axial-velocity contours for sd, td, and cd at t=0. The difference in the domain size, consistency between the solutions, and wavy nature of the flow are evident, cd shows continuity across the overlaid-grid region and flapper wakes that are wider than td, which indicates almost zero width.
The solutions are similar in showing overall good agreement with the data, except for sdorig unsteady lift and drag; however, detailed differences are evident between the solutions and the data. Since tddp/dx showed improvement, it alone will be used for further discussion.
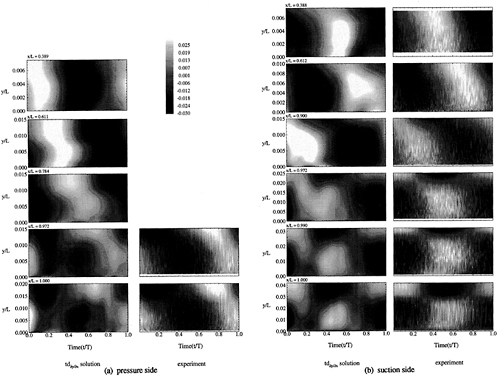
Figure 14 shows the perturbation-velocity (i.e., difference between steady and unsteady) time-history contours, which vividly exhibit the features described with regard to the first-harmonic velocity profiles and data. tddp/dx trends are smoother, due to the coarseness of the data (13 points across the boundary layer).
Figure 15 shows the perturbation velocity vectors and particle traces at various time steps. The interaction between the flapper-induced vortices and foil is complex: distortion and increased speed on the suction (c=1.26) vs. the pressure (c=1.05) side such that 5 vs. 4 vortices are observed; and secondary counter-rotating vortices near the trailing edge and in the wake. The latter directly correlate with and explicate the region where the first-harmonic velocity profiles displayed the two-layer structure.
At the ONR/MIT Unsteady-Flow Workshop [35] and post workshop meetings, ten groups from naval laboratories (DTMB & NRL) and universities (Iowa, Cincinnati, Minnesota, Mississippi State, Penn State, VPI) submitted solutions using a variety of methods (inviscid, boundary-layer, and RaNS) and domains (sd, td, and cd). There were differences/difficulties between/with the solutions for both steady and unsteady flow: the groups using sd had similar problems; the steady lift ranged from 0.54 to 0.70; inability to predict the details of the steady separation; and the unsteady-flow trends varied considerably. However, three groups, Iowa, MSU [36], and PSU [37] had the best results of a similar encouraging level of agreement with the data.
ANALYSIS AND ANALOGY TO STOKES LAYERS
The results are further analyzed through discussion of the relationship between the flow pattern and axial pressure gradient. The analogy between the present flow and Stokes layers for other idealized geometries is discussed.
Figure 16 shows the perturbation axial pressure-gradient contours at the same time steps as figure 15. Comparison of the figures indicates the direct correspondence between the flow pattern and axial pressure gradient, i.e., the flow directions are consistent with the regions of favorable and adverse gradients. The complexity of the wake is evident, including higher harmonics and upstream and downstream traveling waves over the foil and in the near wake and in the intermediate wake, respectively. The upstream traveling waves are consistent with the surface-pressure first-harmonic phase.
The nature of this correspondence can be explicated by solving the axial Euler equation [i.e., (2) without the viscous and Reynolds-stress terms] for the axial pressure gradient and evaluating the relative importance of the various terms using Fourier analysis
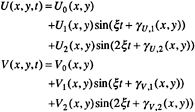
(31)
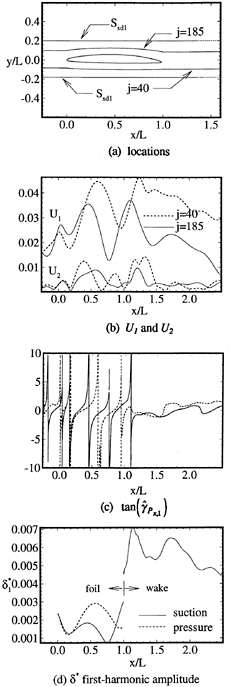
and tddp/dx. Corresponding to orders U0,U1, and U2, 2+11+19=32 terms arise, respectively, which were evaluated along lines j=40 and 185 outside the boundary layer at y+ ≈104 (figure 17a ). In the latter cases, three terms are dominant, one from the temporal and two from the convective acceleration, such that
(32)
where
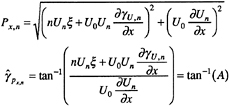
(33)
and ![]() is with respect to
is with respect to ![]() . Three cases are of particular interest: (1) Un≠ Un(x) (i.e., Ux,n=0) such that A=±∞ and
. Three cases are of particular interest: (1) Un≠ Un(x) (i.e., Ux,n=0) such that A=±∞ and ![]() = ±π/2, where+corresponds to a lead (i.e., temporal wave with c → ∞) and−to a lag (i.e., spatial wave with c → 0); and (2) Un≈ax (i.e., Ux,n=a) such that A and
= ±π/2, where+corresponds to a lead (i.e., temporal wave with c → ∞) and−to a lag (i.e., spatial wave with c → 0); and (2) Un≈ax (i.e., Ux,n=a) such that A and ![]() ; and (3) Un≈sin(nξxB/c) (i.e., Ux,n≈cos(nξxB/c)) such that A≈tan(nξxB/c) and
; and (3) Un≈sin(nξxB/c) (i.e., Ux,n≈cos(nξxB/c)) such that A≈tan(nξxB/c) and ![]() where B=1 (i.e., Un primarily first harmonic) corresponds to a temporal wave and B≈2 (i.e., Un primarily second harmonic) an upstream traveling wave.
where B=1 (i.e., Un primarily first harmonic) corresponds to a temporal wave and B≈2 (i.e., Un primarily second harmonic) an upstream traveling wave.
Figure 17b shows the velocity first- and second-harmonic amplitudes along j=40 and 185. The former is primarily second harmonic on the foil (i.e., case 3) and linearly decreasing in the wake (i.e., case 2), which is consistent with figure 5. Figure 17c indicates B=1.2 and 1.8 on the pressure and suction sides, respectively, i.e., upstream traveling waves, which is consistent with figures 11 and 16. The latter is primarily third and second harmonic on the pressure and suction sides, respectively, on the foil and nearly zero in the wake.
Figure 17d shows the displacement-thickness first-harmonic amplitude. Similar spatial oscillations as U1 are observed, but with relatively larger values in the near wake. The maximum value coincides with the location where ![]() changes from upstream vs. zero phase, which suggests viscous-inviscid interaction as the mechanism for the pressure-gradient response.
changes from upstream vs. zero phase, which suggests viscous-inviscid interaction as the mechanism for the pressure-gradient response.
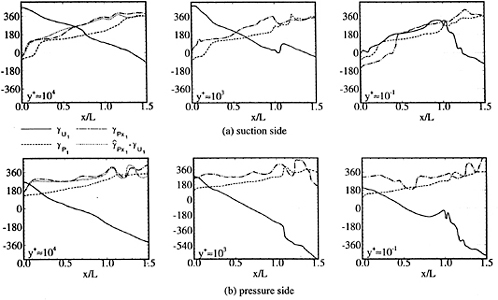
Figure 18 shows the velocity, pressure, and pressure-gradient first-harmonic phase for the outer (y+≈104), overlap (y+≈200), and sub-layer (y+≈0.1) regions. The pressure-gradient phase was obtained by differentiation of the pressure and, additionally, the outer region also includes the Euler-equation solution (33). The pressure and pressure gradient indicate upstream traveling waves. At the outer region, close agreement is shown between the two pressure gradients, which validates the Euler-equation analysis. On the foil in the outer and overlap regions, the velocity shows a downstream traveling wave, whereas in the sub-layer region it follows the pressure gradient, which is consistent with the wall-shear stress. In the wake, the velocity shows a downstream traveling wave.
Figure 19 shows the velocity first harmonic amplitude and phase in wall-coordinates. The largest overshoots occur near y+ ≈1000, where the phase abruptly changes from the outer to inner values. The amplitudes display a double-peak across the boundary layer and the phase is constant in the sub-layer. The large change in phase shown in the overlap region (10<y+< 1000) correspond to the lags shown in the velocity profiles. The role of the turbulence model vs. physics for the sub-layer region is unknown, as no data is available.
In conclusion, ffx physics are complex with analogy to Stokes layers (i.e., overshoots and phase shifts) for temporal, spatial, and traveling horizontal-wave external flows [10,38,39]. The latter study has shown the differences/similarities between these flows and that the response for the latter two is extreme due to nonlinearities induced by the convective acceleration such that further study is required, especially to document the nature of the interaction between the mean and turbulent motions. The present work supports this conclusion and, moreover, displays the additional complexity for combined vertical and horizontal waves.
CONCLUDING REMARKS
A time-accurate unsteady viscous-flow method has been validated through calculations and comparisons with the Massachusetts Institute of Technology flapping-foil experiment. Solutions were obtained using a small domain surrounding the foil, a tunnel domain that included the foil and the tunnel walls, and a complete domain that included the foil and both the tunnel walls and the upstream flappers. The latter case involved the use of the CHIMERA overlaid-grid method. The three solutions gave similar overall agreement for both steady and unsteady flow, which demonstrates that such problems can be handled with a variety of formulations, although the boundary data, CPU time, and storage requirements are quite different. The physics are complex with analogy to Stokes layers and are explicated through analysis of the axial pressure gradient, which exhibits upstream and downstream traveling waves over the foil and in the near wake and in the intermediate wake, respectively, due to nonlinearities induced by the convective acceleration and steady/unsteady interactions. The nature of the unsteady displacement thickness suggests viscous-inviscid interaction as a possible mechanism for the axial pressure-gradient response.
Future work involves a parametric study for the ffx geometry for combined- and vertical-wave inflows (Appendix A) to determine the effects of frequency and extensions for realistic unsteady propeller/hull/appendage flows.
ACKNOWLEDGMENTS
This research was sponsored by ONR under Contracts N00014–92-J-1118 and N00014– 91-J-1203 under the administration of Mr. Jim Fein and Dr. Ed Rood whose support is greatly appreciated. Computer funds were provided by the NASA Numerical Aerodynamic Simulation Program and by ONR NAVOCEANO Primary Oceanographic Prediction System. The first author is grateful for the support provided by the IIHR Hunter Rouse Fellowship.
REFERENCES
1. Fage, A. and Johansen, F.C., “On the Flow of Air Behind an Inclined Flat Plate of Infinite Span, ” Proc. Royal Society A, Vol. 116, 1927, pp. 170–197.
2. Tyler, E., “Vortex Formation Behind Obstacles of Various Sections,” Philosophical Magazine, Vol. 11, No. 7, 1931, pp. 849–891.
3. Bearman, P.W. and Graham, J.M.R., “Vortex Shedding from Bluff Bodies in Oscillatory Flow: a Report on Euromech 119,” J. Fluid Mech., Vol. 99, pp. 225–245.
4. Shirayama, S., “Flow Past a Sphere: Topological Transitions of the Vorticity Field, ” AIAAJ., Vol. 30, No. 2, 1992, pp. 349–366.
5. Perry, A.E. and Watmuff, J.H., “The Phase-Averaged Large-Scale Structures in Three-Dimensional Turbulent Wakes,” J. Fluid Mech., Vol. 103, pp. 38–51.
6. Theodorsen, T, “General Theory of Aerodynamic Instability and the Mechanism of Flutter, ” NACA Report No. 496, 1934.
7. McCroskey, W.J., “Unsteady Airfoils,” Ann. Rev. Fluid Mech., Vol. 14, 1982, pp. 285– 311.
8. Ghia, K.N., Yang, J., Ghia, U. and Osswald, G., “Analysis of Dynamic Stall Phenomenon through Simulation of Forced Oscillatory Flows,” Proc. 5th Symp. on Numerical and Physical Aspects of Aerodynamic Flows, Long Beach, CA, 1992.
9. Ohmi, K., Coutanceau, M., Loc, T.P., and Dulieu, A., “Vortex Formation around an Oscillating and Translating Airfoil at Large Incidences,” J. Fluid Mech., Vol. 211, 1990, pp.37–60.
10. Telionis, D.P., Unsteady Viscous Flow, New York, Springer-Verlag, 1981.
11. Commerford, G.L. and Carta, F.O., “Unsteady Response of a Two-Dimensional Airfoil at High Reduced Frequency, ” AIAA J., Vol. 12, No. 1, 1974, pp. 43–48.
12. Griffin, O.M. and Hall, M.S., “Review-Vortex Shedding Lock-on and Flow Control in Bluff Body Wakes, ” ASME J. Fluids Engineering, vol. 113, no. 4, 1991, pp. 526–537.
13. Katz, Y., Nishri, B., and Wygnanski, I., “The Delay of Turbulent Boundary Layer Separation by Oscillatory Active Control,” AIAA 2nd Shear Flow Conference (AIAA 89–0975), Tempe, AZ, 1989.
14. Favier, D., Maresca, Ch., and Castex, A., “Experimental Study of 2D/3D Interactions Between a Vortical Flow and a Lifting Surface,” Eur. J. Mech., B/Fluids, Vol. 8, No. 5, 1989, pp. 397–430.
15. Srinivasan, G.R., McCroskey, W.J. and Baeder, J.D., “Aerodynamics of Two-Dimensional Blade-Vortex Interaction,” AIAA J., Vol. 24, No. 10, 1986, pp-1569–1576.
16. Rai, M.M., “Three-Dimensional Navier-Stokes Simulations of Turbine Rotor-Stator Interaction; Part II-Results,” J. Propulsion, Vol. 5, No. 3, 1989, pp. 312–319.
17. Huerre, P. and Monkewitz, P.A., “Local and Global Instabilities in Spatially Developing Flows,” Ann. Rev. Fluid Mech., Vol. 22, 1990, pp. 473–537.
18. Stern, F., Kim, H.T., Zhang, D.H., Toda, Y., Kerwin, J., and Jessup, S., “Computation of Viscous Flow around Propeller-Body Configurations: Series 60 CB=.6 Ship Model,” to appear, J. Ship Research.
19. Kim, H.T. and Stern, F., “Viscous Flow around a Propeller-Shaft Configuration with Infinite-Pitch Rectangular Blades,” J. Propulsion Vol. 6, No. 4, 1990, pp. 434–444.
20. Stern, F., Zhang, D.H., Chen, B., Kim, H.T., and S.D.Jessup, “Computation of Viscous Flow around Propeller-Shaft Configurations, ” to appear, Proc. 20th ONR Symposium on Naval Hydrodynamics, Santa Barbara, CA, August 1994.
21. Kim, W.J., Chen, B. and Stern, F., “Efficient Unsteady Three-Dimensional Viscous-Flow Method with Application to Marine Propulsors,” to appear, Proc. 20th ONR Symposium on Naval Hydrodynamics, Santa Barbara, CA, August 1994.
22. Paterson, E.G., “Computation of Natural and Forced Unsteady Viscous Flow,” Ph.D. thesis, The Univerity of Iowa, expected May 1994.
23. Chen, H.C. and Patel, V.C., “Calculation of Trailing-Edge, Stern and Wake Flows by a Time-Marching Solution of the Partially-
Parabolic Equations,” IIHR Report No. 285, Iowa Institute of Hydraulic Research , 1985.
24. Rodi, W. and Srinivas, K., “Computation of Flow and Losses in Transonic Turbine Cascades,” Z.Flugwiss. Weltraumforsch, vol. 13, 1989, pp. 101–119.
25. Cebeci, T., Clark, R.W., Chang, K.C., and Halsey, N.B., “Airfoils with Separation and the Resulting Wakes,” Proc. 3rd Symp. on Numerical and Physical Aspects of Aerodynamic Flows, Long Beach, CA, 1985.
26. Granville, P.S., “Baldwin-Lomax Factors for Turbulent Boundary-Layers in Pressure Gradients, ” AIAA J., Vol. 25, No. 12, 1987, pp. 1624–1627 .
27. Roache, P.J., Computational fluid dynamics, Albuquerque, Hermosa publishers, 1972, pp. 184–185.
28. Thompson, J.F., “A Composite Grid Generation Code for General 3-D Regions,” AIAA 25th Aerospace Sciences Meeting, Reno, NV, 1987.
29. Benek, J.A., “Extended Chimera Grid Embedding Scheme with Applications to Viscous Flows,” AIAA 8th Computational Fluid Dynamics Conference, 1987, Honolulu.
30. Suhs, N.E., and Tramel, R.W., “PEGSUS 4.0 User's Manual,” Arnold Engineering Development Center, AEDC-TR-91–8, 1991.
31. Rice, J.Q., “Investigation of a Two-Dimensional Hydrofoil in Steady and Unsteady Flows,” M.S.Thesis, Massachusetts Institute of Technology, 1991.
32. Delpero, P.M., “Investigation of Flows around a Two-Dimensional Hydrofoil Subject to a High Reduced Frequency Gust Loading,” M.S. Thesis, Massachusetts Institute of Technology, 1992.
33. Horwich Lurie, B. “Unsteady Response of a Two-Dimensional Hydrofoil Subject to High Reduced Rrequency Gust Loading,” M.S.Thesis, Massachusetts Institute of Technology, 1993.
34. Chung, K.N., “Applications of a Zonal Approach and Turbulence Models to Foils and Marine Propellers,” Ph.D Thesis, The University of Iowa, December 1993.
35. Fuhs, D., “Comparisons of Two-Dimensional Unsteady RaNS Calculations and Measurements, ” Carderock Divsison, Naval Surface Warfare Center report (in preparation) .
36. Taylor, L.K., Busby, J.A., Jiang, M.Y., Arabshahi, A., Sreenivas, K., Whitfield, D.L., “Time-Accurate Incompressible Navier-Stokes Simulation of the Flapping Foil Experiment,” Sixth International Conference on Numerical Ship Hydrodynamics, Iowa City, Iowa, Augst 1993.
37. Fan, S., Lakshminarayana, B., Barnett, M., “Low-Reynolds-Number k-Ɛ Model for Unsteady Turbulent Boundary-Layer Flows,” AIAA J., Vol. 31, No. 10, 1993, pp. 1777–1784.
38. Patel, M.H., “On Laminar Boundary Layers in Oscillatory Flow,” Proc. R. Soc. Lon. A. Vol. 347, 1975, pp. 99–123.
39. Choi, J.E., “Role of Free-Surface Boundary Conditions and Nonlinearities in Wave Boundary Layer and Wake Interaction,” Ph.D Thesis, The University of Iowa, December 1993.
Appendix: A:
Tunnel domain inflow, potential flow model
The inflow is divided into three regions: (1) between the bottom tunnel wall and the bottom flapper wake; (2) between the flapper wakes; and (3) between the top flapper wake and the top tunnel wall. For (1) and (3) an analogy can be made between the sinuous wake sheet of the oscillating flappers passing over the tunnel walls and a shallow-water wave. The potential flow describing these regions is:
The region between the flappers (although not used in this paper) is
A study was conducted to compare this model to two other models, one using unsteady, sinusoidal vortex sheets, and one using discrete Oseen vortices convecting at the freestream velocity. The chosen model was easiest to apply and gave the best correlation to the inlet data.
DISCUSSION
by Dr. Ming Zhu, University of Tokyo
First, I would like to congratulate your nice work on the unsteady NS simulation. Please show your Fourier analyses results of field data about the vortex-foil interaction. I would like to know that with your formulation, how much the unsteadiness can be caught.
Authors' Reply
The first twenty harmonics where calculated for the boundary-layer profiles which showed that the frequency content was dominated by the first harmonic. However, the wake of foil showed a much richer frequency content. As far as the temporal resolution of the method is concerned, it is only limited by the time step used in the simulation. Since the method is implicit, fairly large time steps are used, thus making the resolution of higher harmonics difficult. However, if a broadband or higher frequency response was expected, the time step could be reduced such that the frequencies of interest were sufficiently resolved.
DISCUSSION
by Dr. D.H.Choi, Korea Advanced Institute of Science and Technology
The calculations have been performed with three different computational domains. In principle, if the boundary conditions are correct, the small domain solution should be most accurate as it eliminates any uncertainty or inaccuracy associated with outer regions. However, since available experimental data are sparsely distributed, the boundary conditions for the small domain calculation are supplemented by using the tunnel domain calculation. This essentially makes these two calculations identical as the small domain is a sub-domain of the tunnel domain. Therefore, the comparison of the two appears moot.
Authors' Reply
This is exactly the point that we wanted to make. At the ffx workshop, the participants who used the small domain had similarly poor solutions, i.e., erroneous higher harmonics in the pressure field. It was not clear that the small domain could be used for simulation of the ffx. Therefore, to demonstrate the validity of the small-domain boundary-conditions, the tunnel domain solution was used in place of the data with the intention of making this moot comparison the proof that the formulation was correct.
DISCUSSION
by Dr. Charles C.Song, University of Minnesota
Did you compare the calculated unsteady pressure with experimental value? One should expect large differences between numerical results based on incompressible flow theory and the experiment, especially for higher frequency components.
Authors' Reply
Yes. The differences were large, but were most likely due to difficulties in obtaining accurate unsteady pressure data, not compressibility effects.
Time Accurate Incompressible Navier-Stokes Simulation of the Flapping Foil Experiment
L.K.Taylor, J.A.Busby, M.Y.Jiang, A.Arabshahi, K.Sreenivas, and D.L.Whitfield (CFD Laboratory, USA)
ABSTRACT
A numerical simulation of an experiment conducted in the Marine Hydrodynamics Laboratory at Massachusetts Institute of Technology (MIT) has been performed. The experiment was designed to study the flow about a two-dimensional hydrofoil undergoing high reduced frequency gust loading. The gust was created by two NACA 0025 hydrofoils oscillating sinusoidally in phase upstream of the stationary foil. Experimental data was taken in the flowfield near the stationary foil as well as on the foil itself. The numerical computations were performed on the entire experimental domain, including the flapping foils, through the use of a two-dimensional multiblock unsteady incompressible Navier-Stokes algorithm based on artificial compressibility. A comparison of the pressures and velocities on the bounding box and surface of the stationary foil are presented for the steady case, as well as time histories and an harmonic analysis at the same locations for the unsteady case.
NOMENCLATURE
|
A,B, |
Flux Jacobians |
|
|
Roe Matrix |
|
cp |
Pressure coefficient |
|
E,F,K |
Computational space flux vectors |
|
ê, |
Numerical flux vectors |
|
J |
Metric Jacobian |
|
m |
Newton iteration parameter |
|
n |
Time level index |
|
p |
Pressure |
|
Q |
Computational space dependent variable vector |
|
q |
Physical space dependent variable vector |
|
ReL |
Reynolds number based on reference length |
|
T,T−1 |
Eigenmatrices |
|
t |
Time |
|
u,v |
Cartesian velocity components |
|
U,V,θk |
Contravariant velocities |
|
x,y |
Cartesian coordinates |
|
β |
Artificial compressibility parameter |
|
∂ |
Partial differentiation |
|
δ |
Central difference operator |
|
μ |
Viscosity |
|
ϱ |
Density |
|
τ |
Time in computational space; fluid stress vector |
|
ξ,η,k |
Curvilinear coordinates |
INTRODUCTION
Steady and unsteady computations were made of the MIT/ONR Flapping Foil Experiment (1,2) using the Mississippi State University incompressible Navier-Stokes code (3). This code is three-dimensional; however, a two-dimensional version was developed for these computations. The artificial compressibility form of the equations is solved on a time-dependent curvilinear coordinate system. The equations are discretized in finite volume form and the numerical flux formulation at cell faces is based on Roe's approximate Riemann solver (4). The equations are formulated for numerical solution as a formal Newton method where the time derivative of the dependent variable vector, except for the time derivative of pressure in the continuity equation, is included in the residual term. This system is then solved at each time step using what is referred to as discretized Newton-relaxation (5). Relaxation is carried out at each time step using three symmetric Gauss-Seidel passes. The computations are second-order accurate in time,. For steady state solutions, local time stepping is used and the Jacobian matrix is
|
* Research Engineer ** Graduate Student + Professor |
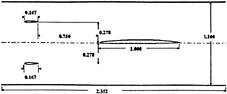
Figure 1. Experimental Setup
updated every 20 cycles. A Baldwin-Lomax turbulence model is used for all the computations.
The Navier-Stokes code is a multiblock dynamic grid code and the computations are performed using the rather complete configuration consisting of the water tunnel walls, flapping foils, and stationary foil (Figs. 1 and 2). No slip boundary conditions are used on the tunnel walls, flapping foils and stationary foil. A steady state solution is first obtained and then motion of the flapping foils is initiated by boundary conforming dynamic grids that move in pitch with the flapping foils at a reduced frequency of 3.62 based on the half-chord of the stationary foil. The grid extends approximately two stationary foil chord lengths upstream of the leading edge of the stationary foil and five stationary chord lengths downstream of the trailing edge of the stationary foil. (Note that the entire grid is not presented in Fig. 2.) Characteristic variable boundary

Figure 2. Computational Grid
conditions are used at both the upstream inflow boundary and downstream outflow boundary. Velocities are specified at the inflow while static pressure is set at the outflow.
For these multiblock computations, four blocks are used. Block one extends from the lower tunnel wall to the centerline of the lower flapping foil. Block two extends from the top of block one to the centerline of the stationary foil. Block three extends from the top of block two to the centerline of the upper flapping foil. Block four extends from the top of block three to the upper tunnel wall. All grids are H-type grids. This blocking arrangement allows the multiblock solutions to correspond exactly to a single block solution, even for unsteady flow. That is, there are no approximations at block boundary interfaces.
A presentation of the equations and numerical discretization will be given first, followed by a discussion of the numerical flux formulation and numerical solution method Then a section containing a description of the stationary and dynamic grids that are used followed by an explanation of the post processing procedures that are necessary to examine the results. Finally, results for both the steady and unsteady cases along with conclusions are presented.
EQUATIONS AND NUMERICAL DISCRETIZATION
Governing Equations
The unsteady two-dimensional incompressible Navier-Stokes equations without body forces are written in Cartesian coordinates and in conservative form. The quantities used to nondimensionalize these equations are, a characteristic length, and freestream values of velocity, density, and viscosity. Pressure is normalized using the following relationship ![]() , where the subscript denotes a freestream or reference value (3). The resulting set of nondimensional equations are then transformed to a general time-dependent body-conforming curvilinear coordinate system given by
, where the subscript denotes a freestream or reference value (3). The resulting set of nondimensional equations are then transformed to a general time-dependent body-conforming curvilinear coordinate system given by
ξ=ξ(x,y,t)
η=η(x,y,t)
τ=t.
(1)
The time-dependent nature of this transformation will allow all computations to be carried out on a fixed uniform computational domain even though components of the physical domain may be in motion.
Artificial compressibility is introduced after the transformation to insure that the continuity equation is satisfied for dynamic grid applications (6). The resulting set of equations may be written as
(2)
where
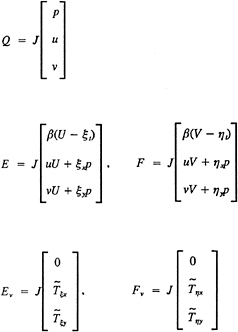
and
U=ξt+ξxu+ξyν
V=ηt+ηxu+ηyν
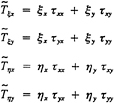
with
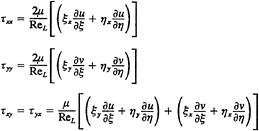
where ReL is the Reynolds number based on the characteristic length. J is the Jacobian of the inverse transformation ![]() , given by
, given by
J=xξyη−yξxη
and the metric quantities are
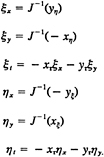
Numerical Discretization
A finite-volume discretization of Eq. (2) in two-dimensional computational space may be written as
(3)
where the indices i, j correspond to a cell center and the central difference operator δ is given by
. (4)
The increments Δξ and Δη are set equal to one for simplicity and Eq. (3) becomes
. (5)
In this expression, the dependent variable vector Q is considered to be constant throughout cell i, j, while the inviscid and viscous fluxes are assumed to be uniform over each of the four surfaces of the cell.
Temporal Discretization
The time derivative appearing in Eq. (5) is approximated with a general difference expression (7), which has been written for computational space, and is given by
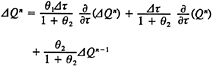
(6)
where
ΔQn=Qn+1−Qn.
The two choices for θ1 and θ2 that were used exclusively in this work are θ1=1, θ2=0 and θ1=1, θ2=0.5, which correspond respectively to the backward Euler implicit scheme (first-order accurate in time) and the three point backward implicit
scheme (second-order accurate in time). Using Eq. (5) in Eq. (6) yields
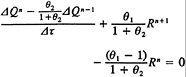
(7)
where
R*=[δi(E−Ev)+δj(F−Fv)]*.
In this particular application, the movement of the flapping foils dictate that a new grid must be generated at each time step. This implies that the Jacobian of the inverse transformation will be a function of the nondimensional time τ. The approach suggested by Janus (8) will be used to account for this dependence. First of all, the following two identities are needed:
ΔQn=Δ(Jq)n≡Jn+1Δqn+qnΔJn
(8)
ΔQn−1=Δ(Jq)n−1≡Jn−1Δqn−1+qnΔJn−1.
Inserting Eq. (8) into Eq. (7) and simplifying leads to
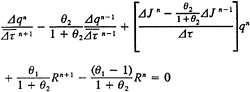
(9)
where
![]() .
.
According to Janus (8). the evaluation of the bracketed term in Eq. (9) must be done with the same numerical scheme that is used to advance the Navier-Stokes equations in time in order to satisfy the geometric conservation law (9). Toward this end, consider the two-dimensional discretized geometric conservation law,
(10)
Using the temporal discretization given by Eq. (6) yields
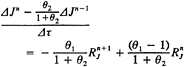
(11a)
where
![]() .
.
(11b)
Now, the left hand side of Eq. (11a) is identically the bracketed term of Eq. (9), thus Eq. (9) can be written as

(12)
The evaluation of both the convective and diffusive flux vectors contained in R will be discussed in the next section.
NUMERICAL FLUX FORMULATION
Convective Flux Evaluation
Flux-Difference Splitting
In this cell-centered finite-volume scheme, the convective numerical flux at cell faces is calculated using the Roe approximate Riemann solver (4). Although originally developed for compressible flow, this approximate Riemann solver can also be implemented in artificial compressibility formulations for incompressible flow (additional details may be found in Reference (10)). An essential ingredient of Roe's solver is the construction of a matrix ![]() , which is representative of the local interface conditions. Roe (4) required this matrix to satisfy certain specific properties, two of which are
, which is representative of the local interface conditions. Roe (4) required this matrix to satisfy certain specific properties, two of which are
![]() .
.
The satisfaction of all these properties in compressible flow is guaranteed by uniquely averaging (11) the dependent variables and then using them in the evaluation of the matrix ![]() These specially averaged variables are commonly referred to as Roe variables. An analogous set of Roe variables can be defined for incompressible flow (6,12,13) and are given by
These specially averaged variables are commonly referred to as Roe variables. An analogous set of Roe variables can be defined for incompressible flow (6,12,13) and are given by
Once these variables have been defined, the mechanics involved in computing the numerical fluxes are the same as those used for compressible flow.
A formulation of the numerical flux at cell face i+1/2 which uses all Roe variables and metrics
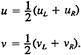
corresponding to cell face i+1/2 can be found in Reference (14). This higher-order numerical flux without limiters is
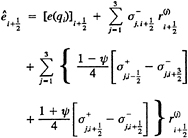
(13)
where
and
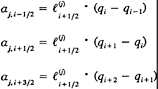
λ±corresponds to the positive and negative eigenvalues of the Roe matrix and r(j) and ℓ(j) are the right and left eigenvectors, respectively. The subscript i+1/2 in the above equations indicate that the metrics used are evaluated at cell face i+1/2. The dependent variables in the eigenvalues and eigenvectors are the aforementioned Roe variables. The flux vector e(qi), however, is evaluated using the dependent variables. All of the results reported herein were obtained using this numerical flux vector with ψ=1/3, which is third-order accurate in space.
Eigensystem of the Transformed Flux Jacobian Matrices
It is apparent from Eq. (13) that the eigenvalues and left and right eigenvectors of the Roe matrix must be known in order to perform the numerical flux calculation. The eigensystem for the Roe matrix can be obtained from the eigensystem of the transformed flux Jacobian by simply using the Roe variables in the latter.
The first step in deriving this eigensystem is the determination of the transformed flux Jacobian matrices. These matrices are defined as
(14)
where E and F are given in Eq. (2) and the vector q is
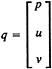
.(15)
The inviscid flux vectors E and F can be written compactly as
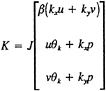
(16)
where
θk=kt+kxu+kyν
and
K=E, θk=U for k=ξ
K=F, θk=V for k=η.
Expressing K in terms of the elements of q and performing the indicated differentiation as defined in Eq. (14) yields the transformed flux Jacobian matrices,
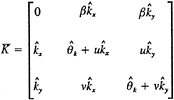
(17)
where
![]() for m=x,y, and t
for m=x,y, and t
and
![]() .
.
To facilitate the determination of the eigenvalues of the matrix ![]() , a similarity transformation will be introduced, which will operate on
, a similarity transformation will be introduced, which will operate on ![]() and produce the matrix x. Since
and produce the matrix x. Since ![]() and x are similar matrices, they will have the same characteristic polynomial (15) and hence the same eigenvalues. However, the matrix x will contain fewer nonzero elements than matrix
and x are similar matrices, they will have the same characteristic polynomial (15) and hence the same eigenvalues. However, the matrix x will contain fewer nonzero elements than matrix ![]() ,
,
and thus the computation of its eigenvalues will be far easier.
Consider the matrices M and M−1
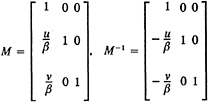
(18) .
Let ![]() , then
, then
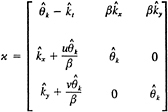
(19)
where
![]() .
.
The eigenvalues of x can be calculated by using the first row to expand the determinant, which yields
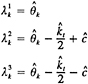
(20)
where
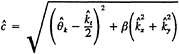
and ![]() , i=1,2,3 are the eigenvalues of A for k= ξ and of B for k=η.
, i=1,2,3 are the eigenvalues of A for k= ξ and of B for k=η.
The right eigenvectors of x are solutions corresponding to the respective eigenvalues of the equation
![]() , s=1,2,3.
, s=1,2,3.
(21)
The matrix Pk, whose columns are the right eigenvectors of x, can be written as
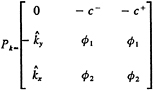
(22)
where
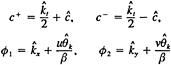 .
.
Having developed a linearly independent set of right eigenvectors, the left eigenvectors will be constructed in such a way that the right and left eigenvectors will be orthonormal. One way to accomplish this task is to simply invert the matrix Pk, which yields
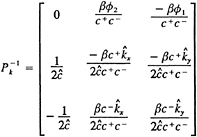
(23) .
The columns of Pk and the rows of ![]() are, respectively, the right and left eigenvectors of x corresponding to the particular eigenvalues. In fact x can be written as
are, respectively, the right and left eigenvectors of x corresponding to the particular eigenvalues. In fact x can be written as
(24)
where Λk is a diagonal matrix whose elements are the eigenvalues λk. Recall that the original intent was to develop the eigensystem of the flux Jacobian matrices A and B. Having generated the eigensystem of x, the eigensystem of the flux Jacobians can be obtained as follows. Using Eq. (19), ![]() can be expressed as
can be expressed as
![]() .
.
(25)
Substituting the expression for x in Eq. (24) into Eq. (25) yields
(26)
or
(27)
where
Performing the indicated multiplication and simplifying, results in the following expressions for Tk and ![]()
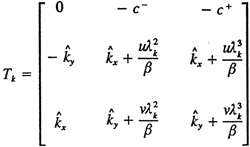
(28)
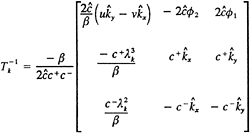
Viscous Flux Evaluation
In this work, all velocity derivatives needed in the evaluation of the viscous flux vectors Ev and Fv are approximated using central differences. Cross derivative terms are calculated by simply averaging the appropriate metric quantities and dependent variables from surrounding cells. Gatlin (16) has given a detailed account of the evaluation of the remaining terms and it will not be repeated here.
NUMERICAL SOLUTION METHOD
The numerical solution of the nonlinear system of equations given by Eq. (12) is obtained by using Newton's method. This formulation is used for both steady state and unsteady solutions. The iterative nature of Newton's method will insure the compatibility of the computed pressure field and the divergence-free velocity field for unsteady calculations. The Jacobian matrix used in this solution procedure is computed by numerically differentiating the first-order Roe flux vector. This discretized Jacobian is then used in a Newton-relaxation scheme where Newton is the primary iteration and relaxation is the secondary iteration. Formally, Ortega and Rheinboldt (5) refer to this particular solution methodology as a discretized Newton-relaxation method, or DNR (17). Reference (18) contains the basic derivation of the aforementioned scheme, while Reference (10) describes the implementation for incompressible flow. The remainder of this section will therefore only touch upon some of the fundamental concepts, while providing the details of its implementation for this particular application.
Newton Formulation and Jacobian Evaluation
Consider a system of nonlinear equations given by
N1 (x1,x2, . . . , xn)=0
N2 (x1,x2, . . . , xn)=0
.
.
.
Nn (x1,x2, . . . , xn)=0 (29)
or more concisely
N(x)=0. (30)
Newton's method for the vector-valued function N(x) can be expressed as
N'(xm)=(xm+1−xm)=−N (xm) (31)
where m=1, 2, 3, … and N′ (xm) is the Jacobian matrix of N(xm) given by
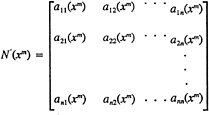
(32)
where ![]() . The approach used to solve Eq. (31) is to replace the analytical Jacobian with a numerically approximated Jacobian. Ortega and Rheinboldt (5) refer to such a method as a discretized Newton iteration. Various finite-difference approximations have been suggested in the numerical analysis literature. A simple and straightforward approximation of the elements of the Jacobian is to replace the analytical Jacobian
. The approach used to solve Eq. (31) is to replace the analytical Jacobian with a numerically approximated Jacobian. Ortega and Rheinboldt (5) refer to such a method as a discretized Newton iteration. Various finite-difference approximations have been suggested in the numerical analysis literature. A simple and straightforward approximation of the elements of the Jacobian is to replace the analytical Jacobian ![]() with
with
where ej is the jth unit vector. Dennis and Schnabel (19) point out that this is the same as approximating the jth column of the Jacobian by
where a constant value of
was used for this work.
Equation (12) is nothing more than Eq. (30), since the only unknown appearing in this equation is qn+1, that is, in Eq. (31) x=qn+1. Thus, Eq. (31) becomes
N′ (qn+1,m)(qn+1,m+1−qn+1,m)=−N(qm) (33)
where now the aij in Eq. (32) are given by
(34)
It should be noted that the only terms in Eq. (12) that are functions of qn+1 are Δqn and Rn+1. Recall that Rn+1 is defined as
Rn+1=[δi(E−Ev)+δj(F−Fv)]n+1 (35)
or
As mentioned previously, the elements of the Jacobian matrix are calculated by using a finite difference approximation for the derivative. The first two terms of Eq. (13) are the first-order contribution to the higher-order Roe flux vector. It can be seen that the numerical flux at a cell face, say i+1/2 , will be a function of the metrics at i+1/2 and the dependent variables on either side of the cell face. The same statement applies to the viscous flux vector if the cross-derivative terms are not included in its evaluation. Mathematically, for cell face i+1/2, j one has
(36)
and similarly for cell face i,j+1/2
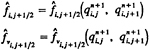
(37)
Now, using the relationships in Eqs. (36) and (37), the left-hand side of Eq. (33) is
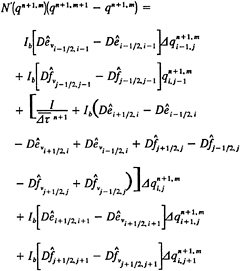
(38)
where
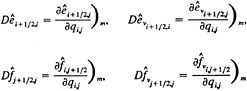
and

Note that the first subscript of the Dg (g=e,ev,f or fv) term corresponds to the location of the cell face, and the second subscript corresponds to the location of the dependent variable vector that the numerical flux vector is differentiated with respect to. Also, the right-hand side of Eq. (33) is
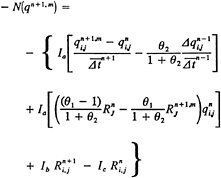
(39)
where
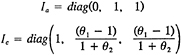
Two items must be addressed pertaining to Eq. (39). First of all, the multiplication of a portion of the equation by the diagonal matrix Ia insures that a divergence free velocity field will be obtained when the iteration in m converges (6). Consequently, the temporal discretization of the continuity equation is taken to be first-order accurate, which leads to the definition of the matrices Ib and Ic in Eqs. (38) and (39). The second item deals with the evaluation of the term ![]() , specifically Eq. (11b) must be evaluated as follows to insure that the conservation property at block interfaces is satisfied for blocks in motion (8).
, specifically Eq. (11b) must be evaluated as follows to insure that the conservation property at block interfaces is satisfied for blocks in motion (8).
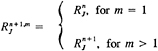
(40)
Solution of Linear Systems
A direct solution of the linear system of equations given by Eqs. (38) and (39) is in general not feasible. One way to circumvent this difficulty is to use a relaxation scheme to solve the linear system at each iteration of Newton's method Using the notation of Reference (18), Eqs. (38) and (39) can be written as
(L+U+B)z=b (41)
where L is a lower block triangular matrix with zeroes on the diagonal, B is a block diagonal matrix, and U is an upper block triangular matrix with zeroes on the diagonal. In Reference (18), the solution of Eq. (41) was computed using the symmetric Gauss-Seidel method A forward pass solution for the change in dependent variable vector z was written as
(L+B)z(1)+Uz(0)=b (42)
where z(0)≡0. Without using z(1) to update b, a backward pass was made using
Lz(1)+(B+U)z(2)=b. (43)
Using Eq. (42), Eq. (43) can be written as
(B+U)z(2)=Bz(1) (44)
or
BΔz =−Uz(2)
where
Δz=z(2)−z(1).
In this work, this procedure has been slightly modified. The forward pass is given by
(L+B)z(1)+Uz(0)=b (45)
where now z(0) ≠0 but is the solution from the previous time step. Once again, z(1) is not used to update b and the backward pass is given by
Lz(1)+(B+U)z(2)=b
or Bz(2)=b−Lz(1)−Uz(2). (46)
All of the solutions contained herein were obtained with three of these symmetric Gauss-Seidel sweeps per Newton iteration.
Turbulence Modeling
The algebraic turbulence model of Baldwin-Lomax (20), which was used in Reference (3) for three-dimensional incompressible flow has been modified for two-dimensional flow. The turbulent wake model used is that of Renze, Buning and Rajagopalan (21). Multiple peaks in the Fmax function are avoided by restricting the search to a specified distance away from vorticity generating surfaces. Also, the method introduced by Chen (22) to calculate wall shear stress and normal distances for nonorthogonal three-dimensional grids has been incorporated into a two-dimensional framework.
Multiblock Approach
An important aspect of computing the flowfield about complex geometries having disparate components with different topologies is grid generation. In this work a domain decomposition technique is used. Once the computation region is decomposed into distinct subregions, each of which
is gridded independently, the grid topology for each subregion is locally consistent with each component of the geometry. The mechanism by which the subregions are connected leads to a variety of approaches, such as the Chimera grid technique (23), the patch grid technique (24), and block-structured grid technique (25). All three approaches have their relative strengths and weaknesses. A common difficulty to Chimera and patched grid technique is constructing a proper scheme for transferring information between interface boundaries. Nevertheless, both Chimera and patched grid have been successful in modeling flows around multiple bodies in relative motion. One approach to overcome this difficulty (i.e. transfer of information between regions) is the use of block-structured grid techniques. The blocked grid idea is not new. It has been applied to three-dimensional problems by Weatherill and Forsey (26), Belk (27), and Arabshahi (28). The basic idea behind blocked grids is that the whole flowfield between the surfaces of the Configuration and some outer farfield boundary consists of a set of blocks. The union of these blocks fills the entire flowfield without either gaps or overlaps; moreover, the grid has complete continuity (including slope continuity if desired) of grid lines across the block-block boundaries. This feature provides a relatively simple means of communication between neighboring blocks with stationary interfaces in computational space even though the blocks may be in motion in physical space. The approach adopted here with regard to block-block interface communication is a direct extraction-injection procedure which was taken by Belk (27). This means the information (such as q,Δq) from within the domain of one block can be extracted and then injected as phantom data in an adjacent block, thereby eliminating any error due to approximations at block boundaries.
STATIONARY AND DYNAMIC GRIDS
The two major requirements for the grids used in this study are: 1) to simulate the entire experimental configuration, and 2) to mimic the dynamic motion of the flapping foils. The stationary grid (i.e., the flapping foils are fixed) is generated using the algebraic capabilities of EagleView (29). The entire physical domain is divided into four blocks. Each block consists of an H-type grid comprised of 326×65 grid points with a normalized (by the foil chord length) spacing of 1.0×10−5 off solid surfaces. Vertical grid lines are aligned with experimental measurement locations upstream and downstream of the stationary foil. Figure 3 is a
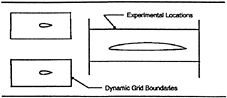
Figure 3. Experimental Locations and Dynamic Grid Boundaries
schematic representation of the experimental measurement locations near the stationary foil.
The efficiency of reconstructing a new grid at each time step to track the movement of the flapping foils is the primary concern for a dynamic grid. To minimize the number of grid points that had to be redistributed, each dynamic portion of the grid is restricted to approximately 101×33 grid points near the corresponding flapping foil. Figure 3 details the extent of this region. The movement of the foils is accomplished by keeping the outer boundary fixed and allowing the foil to oscillate within the confines of these fixed coordinate lines. Weight functions are used to provide a smooth grid distribution between the flapping foils and the outer boundary. These functions, denoted Wi and Wj, are based on an arc length distribution and assumed values from zero to one in each curvilinear direction. The value zero corresponds to no grid motion, while one implies full rotational motion. Thus, the surface of the foil will have a value of one, which decays to zero as the outer boundary is reached. The following combination of weight functions seemed to result in the smoothest grid distribution
(47)
The new position of each point is updated at each time step using the relation
X(new)=(1−Wij) X(fix)+WijLcos(α)
Y(new)=(1−Wij) Y(fix)+WijLsin(α), (48)
where fix denotes the original position at zero degrees angle of attack, L is the distance from the center of rotation, and α is the angle of attack. Since the grid reconstruction is restricted to a small region and an algebraic method is used to generate the new grid in this region, very little additional computational time is required to update the grid at each time step.
POST-PROCESSING
The computed results had to go through an elaborate post-processing procedure in order to be analyzed in an accurate and meaningful manner. In
particular the computed results had to be re-referenced to match MIT's reference conditions, and a harmonic analysis procedure had to be used to reduce the large quantity of data obtained from unsteady flows to a manageable set of data that could be easily understood
The measured and computed data are both referenced to ”freestream conditions”. However, evaluation of the measured total pressure coefficient indicates that the reference velocity ![]() and pressure
and pressure ![]() , used by MIT, are not measured at the same location in the tunnel. As a result,
, used by MIT, are not measured at the same location in the tunnel. As a result, ![]() and
and ![]() are not interchangeable with
are not interchangeable with ![]() and
and ![]() , the reference conditions used in the computations. Thus, to compare “apples with apples”, it is necessary to re-reference the computed data to MIT's reference conditions.
, the reference conditions used in the computations. Thus, to compare “apples with apples”, it is necessary to re-reference the computed data to MIT's reference conditions.
The Fourier transform has proven to be an efficient tool for analyzing unsteady data. It works under the premise that any physical process can be described either in the time domain or the frequency domain. The current implementation uses a modified version of a discrete Fourier transform (30) in order to reduce the computing time required to perform the transform. The transform used can be defined as follows
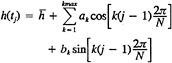
j=1, 2,… N (49)
where
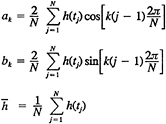
and
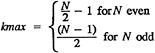
k=1, 2,…, kmax.
N=# of time steps per period.
In terms of amplitude and phase, Eq. (49) can be written as
(50)
where
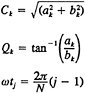
RESULTS
As stated earlier, the computations are being compared with experimental data obtained by MIT (31). Both the steady-state and unsteady computations were carried out using the complete experimental configuration consisting of the water tunnel walls, flapping foils and stationary foil (Fig. 2). The location of the stationary foil coincides with the latest experimental information, specifically, the trailing edge is one centimeter below the centerline of the tunnel and the geometric angle of attack is 1.18 degrees. No slip boundary conditions were used on all solid surfaces, while characteristic variable boundary conditions were used at both the upstream inflow and downstream outflow boundary. Velocities were specified at the inflow while static pressure was set at the outflow. The artificial compressibility factor β was set to 10 for all calculations. All computations were for a Reynolds number of 3.78 million based on the stationary foil chord. The boundary layer on the stationary foil (both the suction and pressure sides) was tripped at a distance of 0.105 chord length from the leading edge, while the boundary layer on the flapping foils and tunnel walls was treated as completely turbulent. A nondimensional grid spacing of 1.0×10−5 off solid surfaces resulted in y+ values of approximately 1.
Steady Results
For the steady-state computations, the flapping foils were held fixed. Since a steady state solution
was sought, local time stepping was used and the Jacobian matrices were updated every 20 cycles. One Newton iteration was used at each time step as well as three Gauss-Seidel sweeps.
Bounding Box Data
Computed velocities and static pressures were compared with measured data obtained for the bounding box shown in Fig. 3. Data for three ”boxes” was available, but since the boxes were so close together, the data were nearly identical for each box. As a result, the computed results were compared with the data from the middle box. The location of each face relative to the trailing edge of the stationary foil and nondimensionalized with the foil chord is as follows: upstream face, 1.259; downstream face, −0.163; top face, 0.219; and bottom face, −0.153. The static pressures were measured at different locations than the velocities. The upstream static pressures were measured at 0.266 chord length in front of the leading edge of the stationary foil, while the downstream static pressures were measured at 0.156 chord length behind the trailing edge of the stationary foil.
Figure 4 compares the u-component of velocity. The agreement with measured data is good for both the upstream and downstream locations. Figure 5 compares the measured and computed static pressure coefficient at the upstream and downstream faces defined above. The largest discrepancy occurs as one moves from the position of the stationary foil to the upper and lower tunnel walls.
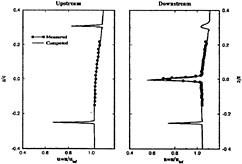
Figure 4. u-Velocity Component
Surface Data
Measured data was available at various locations on the surface of the stationary foil. A comparison of measured and computed surface pressure distributions is shown in Fig. 6. Two representative u-velocity profiles for both the suction and pressure side of the stationary foil are given in Fig. 7. The agreement between experimental and computed profiles on the pressure side, as well as on the suction side upstream of the x/c=0.900 location is good. However, it clearly deteriorates after this station. An argument could be made that this lack of agreement could entirely be attributed to the use of the Baldwin-Lomax turbulence model. However, the inability to match the experimental surface pressure distribution suggests that there may be additional factors. Assuming that the location of the foil in the tunnel and the angle of attack are correct, perhaps there is some slight natural flow angularity in the test section. Another plausible explanation might be that the actual machined geometry differs somewhat from the coordinates given in the experimental reports.
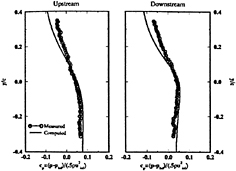
Figure 5. Static Pressure Coefficient
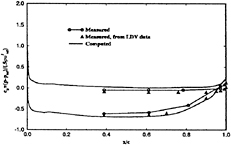
Figure 6. Steady State cp Distribution
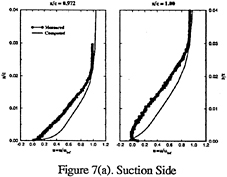
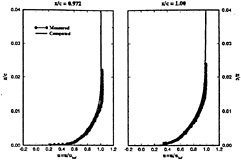
Figure 7. Steady State Velocity Profiles
Unsteady Results
The unsteady solution used the steady state solution as an initial condition and the motion of the flapping foils was initiated by boundary conforming dynamic grids that moved in pitch with the flapping foils at a reduced frequency of 3.62 based on semi-chord of the stationary foil. A minimum nondimensional time step of 8.7.×10−4 was used, which corresponds to 1000 time steps per period of motion for the flapping foils. The Jacobian matrix was updated every cycle and three Newton iterations were performed at each time step.
It should be noted that during the course of this work, several different time steps, both larger and smaller, were tried as well as different numbers of Newton iterations. It was found that nearly identical results were obtained for time steps both larger and smaller than the one reported here. However, different numbers of Newton iterations did affect the solution. Newton iterations of one, three and six were used for each time step. Little or no difference in the bounding box results could be seen for any of the different numbers of Newton iterations used. However, a distinct improvement in the viscous (surface) results could be seen between the three Newton iteration solution and the one Newton iteration solution. No significant improvement could be seen between the six and the three Newton iteration solution for either the bounding box or the viscous results.
Although no results were presented here, a grid with nearly twice the resolution in the direction normal to the flappers and foil was also used. The difference in solutions between those obtained from this grid and those presented here was virtually indistinguishable.
Bounding Box Data
The locations for the bounding box used in the steady state analysis are the same for the unsteady analysis, except for the downstream face. The downstream face is located at −0.108 chord length relative to the trailing edge of the stationary foil. For the unsteady case, the upstream and downstream faces of the box were extended into the wake regions. This provided very valuable experimental wake data for comparison with computations.
A comparison of the measured and computed results for the amplitude and phase of the first harmonic of the u-velocity are shown in Fig. 8 for all the faces of the bounding box. The agreement is good, especially on the upstream and downstream faces. It appears that the disturbances generated by the flapping foils are being convected downstream and are arriving at the upstream face with the correct amplitude and phase. Although the agreement at the downstream face does not appear to be quite as good, one can consider the phase at −180 degrees to be +180 degrees and the agreement is quite good.
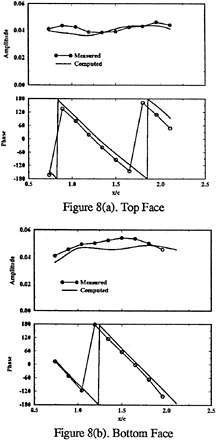
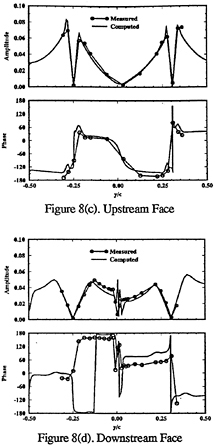
Figure 8. Unsteady Velocity on Bounding Box-First Harmonic
Surface Data
The mean surface pressure distribution is plotted in Fig. 9, while the amplitude and phase of the unsteady surface pressure distribution is shown in Fig. 10. The discrepancy between the measured and computed mean surface pressure distribution is approximately the same magnitude as the steady state case. The amplitudes of the unsteady surface pressure distribution compare favorably for both the suction and pressure side, while the overall trend of the phase is captured.
Figure 11 contains mean velocity profiles from the suction and pressure side. Once again, the difference between the computed and measured values is about the same as in the steady state case. The amplitude and phase of the first harmonic of the unsteady u-velocity profiles appear in Fig. 12. The computed amplitudes compare favorably with the measured data, while the phase for the pressure side agrees better than that of the suction side. Overall, the comparison of the mean unsteady results showed the same type of discrepancies as the steady results. Figure 13 shows a snapshot of the unsteady velocity distribution.
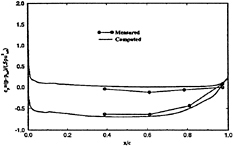
Figure 9. Mean cp Distribution
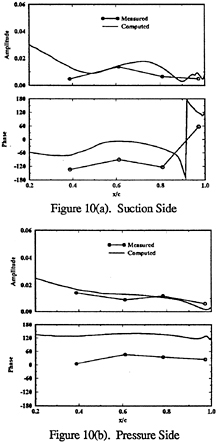
Figure 10. Unsteady cp Distribution— First Harmonic
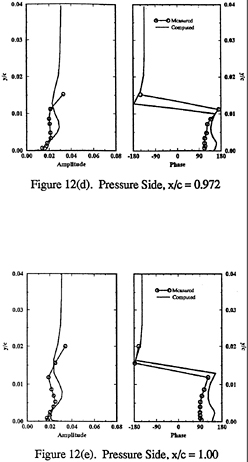
Figure 12. Unsteady Velocity Profiles-First Harmonic
CONCLUSIONS
A two-dimensional multiblock unsteady incompressible Navier-Stokes algorithm based on artificial compressibility has been presented. The unsteady solution was obtained using a dynamic grid that was regenerated at each time step in order to mimic the motion of the flapping foils. For both the steady and unsteady cases, the computed results matched fairly well with the measured bounding box data. However, the computed results for the surface data (in particular, the suction side data) did not match the measured data to the same extent.
Since the solution appears to be grid independent, it seems as though at least two possibilities exist Either the numerical simulation is not being conducted at precisely the same conditions as the experiment or, this is the best that can be expected from the technology in the current algorithm. As to the former, assuming that the angle of attack and location of the foil in the tunnel are accurate, possibilities could include; flow angularity in the test section, alterations in the geometry of the manufactured foil, and the type of flow over the flappers. From a numerical standpoint, the differences could be attributed to the turbulence model used.
Currently, work is being done to adapt the grid to the unsteady wake of the flapping foils in order to minimize the number of grid points required. Future work involves examining alternate turbulence models to see if the discrepancy in the results obtained on the surface can be resolved.
ACKNOWLEDGEMENTS
This work was supported by the Office of Naval Research, grant N00014 –92-J-1060 with James A. Fein as the technical monitor. The authors wish to express their sincere appreciation to the following organizations for providing CRAY-YMP computer resources: U.S. Army Waterway Experiment Station and Cray Research, Incorporated.
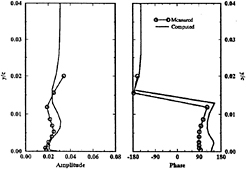
Figure 13. Unsteady Velocity Distribution
BIBLIOGRAPHIC REFERENCES
1. Rice, J.Q., “Investigation of A Two Dimensional Hydrofoil in Steady and Unsteady Flows,” M.S.Thesis, Massachusetts Institute of Technology, June 1991.
2. Delpero, P.M., ”Investigation of Flows around a Two Dimensional Hydrofoil Subject to A High Reduced Frequency Gust Loading,” M.S.Thesis, Massachusetts Institute of Technology, February 1992.
3. Taylor, L.K. and Whitfield, D.L., ”Unsteady Three-Dimensional Incompressible Euler and Navier-Stokes Solver for Stationary and Dynamic Grids,” AIAA-91–1650, June 1991.
4. Roe, P.L., “Approximate Riemann Solvers, Parameter Vectors, and Difference Schemes, ” Journal of Computational Physics. Vol. 43, pp. 357–372, May 1981.
5. Ortega, J.M. and Rheinboldt, W.C., Iterative Solution of Nonlinear Equations in Several Variables. Academic Press, New York, 1970.
6. Pan, D. and Chakravarthy S., “Unified Formulation for Incompressible Flows,” AIAA-89–0122, January 1989.
7. Beam, R.M., and Warming, R.F., “An Implicit Factored Scheme for the Compressible Navier-Stokes Equations, ” AIAA Journal, Vol. 16, No. 4, pp. 393–402, April 1978.
8. Janus, J.M., “Advanced 3-D CFD Algorithm for Turbomachinery,” PhD Dissertation, Mississippi State University, May 1989.
9. Thomas, P.D., and Lombard, C.K., “Geometric Conservation Law and Its Application to How Computations on Moving Grids,” AIAA Journal. Vol. 17, No. 10, 1979.
10. Taylor, L.K., “Unsteady Three-Dimensional Incompressible Algorithm Based on Artificial Compressibility,” PhD Dissertation, Mississippi State University, May 1991.
11. Roe, P.L. and Pike, J., ”Efficient Construction and Utilization of Approximate Riemann Solutions, ” in Computing Methods in Applied Sciences and Engineering, ed. R.Glowinski and J.L.Lions, 6:499–518, Amsterdam: North Holland, 1984.
12. Hsu, C.H., Hartwich, P.M. and Liu, C.H., “Incompressible Navier-Stokes Solutions for a Sharp-Edged Double-Delta Wing,” AIAA -87–0206, January 1987.
13. Rogers, S.E. and Kwak, D., ”Upwind Differencing for the Time-Accurate Incompressible Navier-Stokes Equations,” AIAA Journal, Vol. 28, No. 2, PP.253–262, 1990.
14. Whitfield, D.L., Janus, J.M. and Simpson, L.B., “Implicit Finite Volume High Resolution Wave-Split Scheme for Solving the Unsteady Three-Dimensional Euler and Navier-Stokes Equations on Stationary or Dynamic Grids,” Engineering and Industrial Research Station Report, MSSU-EIRS-ASE-88 –3, Mississippi State University, Mississippi State, February 1988.
15. Sokolnikoff, I.S. and Redheffer, R.M., Mathematics of Physics and Modern Engineering, McGraw-Hill, Inc., New York, NY, 1966.
16. Gatlin, B., “An Implicit, Upwind Method for Obtaining Symbiotic Solutions to the Thin-Layer Navier-Stokes Equations,” PhD Dissertation, Mississippi State University, August 1987.
17. Vanden, K.J., “Direct and Iterative Algorithms for the Three-Dimensional Euler Equations, ” PhD Dissertation, Mississippi State University. December 1992.
18. Whitfield, D.L., and Taylor, L.K., “Discretized Newton-Relaxation Solution of High Resolution Flux-Difference Split Schemes,” AIAA-91–1539, June 1991.
19. Dennis, J.E., Jr. and Schnabel, R.B., Numerical Methods for Unconstrained Optimization and Nonlinear Equations , Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1983.
20. Baldwin, B.S. and Lomax, H., “Thin-Layer Approximation and Algebraic Model for Separated Turbulent Flows,” AIAA-78–257, January 1978.
21. Renze, K.J., Buning, P.G. and Rajagopalan, R.G.,” A Comparative Study of Turbulence Models for Overset Grids,” AIAA-92–0437, January 1992.
22. Chen, J.P., “Unsteady Three-Dimensional Thin-Layer Navier-Stokes Solutions for Turbomachinery In Transonic Flow,” PhD Dissertation, Mississippi State University, December 1991.
23. Benek, J.A., Steger, J.L. and Dougherty, F.C., “A Flexible Grid Embedding Technique with Application to the Euler Equations,” Proceedings of the 6th AIAA Computational Fluid Dynamics Conference, Danvers, MA, 1983.
24. Rai, M.M., “A Conservative Treatment of Zonal Boundaries for Euler Equation Calculation, ” AIAA-84–0164, AIAA 22nd Aerospaces Sciences Meeting, Reno, NV, January 1984.
25. Thompson, J.F., “A Composite Grid Generation Code for General Three-Dimensional Regions, ” AIAA-87–0275, AIAA 25th Aerospace
Sciences Meeting, Reno, NV, January 1987. AIAA Journal, Vol. 26, No. 3, p. 271, March 1988.
26. Weatherill, N.P. and Forsey, C.R., “Grid Generation and Flow Calculations for Complex Aircraft Geometries Using a Multiblock Scheme,” AIAA-84–1665, June 1984.
27. Belk, D.M., “Three-Dimensional Euler Equations Solutions on Dynamic Blocked Grids, ” PhD Dissertation, Mississippi State University, August 1986.
28. Arabshahi, A., “A Dynamic Multiblock Approach to Solving the Unsteady Euler Equations About Complex Configurations,” PhD Dissertation, Mississippi State University, May 1989.
29. Remotique, M.G., Hart, E.T. and Stokes, M.L., ”EAGLEView: A Surface and Grid Generation Program and Its Data Management, ” Software Systems for Surface Modeling and Grid Generation, ed. Robert E.Smith, NASA Conference Publiation 3143, Hampton, VA, April 1992.
30. Singleton, R.C., ”An Algorithm for Computing the Mixed Radix Fast Fourier Transform, ” IEEE Transactions on Audio and Electroacoustics. Vol. AU-17, pp. 93–103, June 1969.
31. Kerwin, J., Keenan, D., Mazel, C., Horwich, and E., Knapp, M., ”MIT/ONR Flapping Foil Experiment, Unsteady Phase,” unpublished data.
DISCUSSION
by Dr. V.C.Patel, The University of Iowa Institute of Hydraulic Research
This question is addressed to this as well as the previous paper. I am very surprised by the rather poor agreement in the velocity profiles with the Baldwin-Lomax model, even in steady flow, especially because this model was optimized for such airfoil flows! Why is that so?
Authors' Reply
Discussions of the tunnel domain with and without Granville's pressure-gradient modifications of the Baldwin-Lomax turbulence model have been included in the paper. It is important to emphasize that Granville's change in the zero-gradient values of Ckleb and Ccp had larger influence in improving the solution than the pressure-gradient corrections to these coefficients.