and their detailed internal structure are predicted by models tobe sensitive to assumptions about properties of the dark matter andthe total amount of matter in the universe. Only the most powerfulparallel supercomputers can adequately represent the gravitationaland gas dynamical processes at sufficient resolution to model clusters.
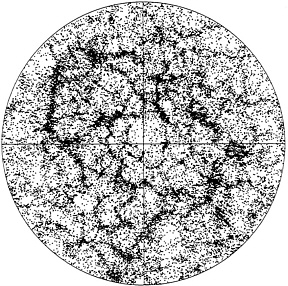
Figure 3. A simulated galaxy redshift survey based on a cosmological modeldominated by cold dark matter and a nonzero cosmological constant.The observer is at the center of the circle, and the outer radiusis at a distance of 600 million light-years. Compare to Figure 2 . (Courtesy of Renyue Cen, Princeton University Observatory.)
An even more challenging problem is the question of how galaxiesformed. For decades these fundamental building blocks of the universewere taken for granted, but now cosmologists realize that galaxyformation represents the smallest scale of the overall process ofstructure formation. Galaxy formation is fearsomely complicated becauseit involves the detailed physics of gas clouds, not just the simplepull of gravity. For example, in order to fall into a forming galaxy,gas has to cool first, which involves the emission of radiation.The cold gas then forms into stars. (Astronomers are not sure justhow or how fast.) Dying stars in turn eject energy and gas back intothe gas reservoir of the galaxy via supernova explosions. All thewhile, gas clouds are colliding and pushing one another around viashock waves and gas pressure. A galaxy is a complex system.
In the past few years computer advances have made possible the firstattempts to calculate galaxy formation starting from expanding universemodels and including the effects of gas. The results are encouraging,but much more computer power is needed to obtain accurate results.Fortunately, with the continuing development of ever-more-powerfulcomputers and sophisticated gas-modeling techniques, one can reasonablyhope that progress in this field will be rapid.
Cosmic Velocity Flows
What are cosmic flows, and why are they important?
Galaxy maps of the universe by themselves are unreliable tracersof the true density of matter because astronomers do not know preciselyhow or where galaxies formed. Perhaps matter did not “light up” equally inall places to make visible galaxies. Matter that did not form intogalaxies may exist today but be invisible. Astronomers sum up thisquestion by asking: Do galaxies fairly trace mass? This cannot betold from redshift maps alone.
Cosmic flows offer a way to answer this question because they aregenerated by the gravity of all matter, whether luminous or not.These flows are the irregularities in the Hubble expansion that arecreated (according to gravitational instability) as galaxies streamout of voids and fall onto clusters and superclusters. A map of cosmicflows can be used to generate a map of the mass density distributionthat caused them, including any dark matter between the galaxies.Such a map is shown in the upper panel of Figure 4, along with a map of the directly observed galaxy distribution ofthe
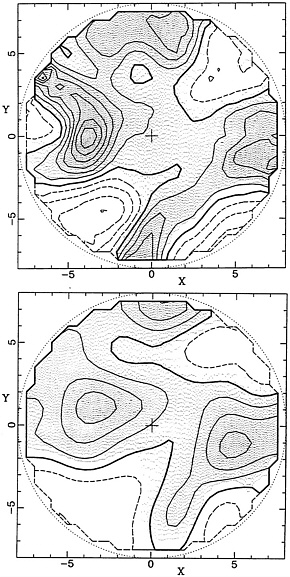
Figure 4. Map of the density distribution of mass inferred from studies oflarge-scale flow (upper panel) compared to the density distributionof galaxies observed in a largeredshift survey (lower panel). (Courtesyof Avishai Dekel et al., Sept. 1993, and Amos Yahil et al., Sept.1993.)
same region in the lower panel. The two roughly agree, suggestingthat galaxies do trace mass, at least approximately. This resultis important evidence that the gravitational instability pictureis basically correct.
Because cosmic flows can measure the clustering of matter on evenvery large scales, they are the best indicator of the absolute levelof density fluctuations in the universe today. This indicator ofdensity fluctuations can be compared to the strength of CMBR fluctuationson larger scales at earlier times. Close to Earth, within 250 millionlight-years where flows are well measured, flow velocities have approximatelythe magnitude predicted if standard dark-matter theories employ theCOBE measurements. This local agreement suggests that our basic modelfor structure formation, spanning many decades of length scale anddepending on details of the nature of dark matter, is approximatelycorrect.
By measuring the size of the flow motions around particular clumpsof galaxies, astronomers can estimate the total amount of matterin each one. If galaxies trace the distribution of matter, or evenif not, as long as their distribution is biased in a consistent andpredictable way, astronomers can generalize from the galaxy massesto estimate the total matter density in the universe. In short, astronomerscan “weigh the universe” and measure the elusive parameter Ω the ratio of the mean mass density to that required to closethe universe and eventually stop its expansion.
Our present knowledge of galaxy formation and biasing is still poor.Nevertheless, cosmologists can draw two conclusions. First, measurementsof cosmic flows on all scales are an important test of competingtheories of structure formation. And second, the high values observedfor cosmic velocity flows are the strongest indicator so far thatΩ might actually be 1, a value favored by theoretical considerations,as explained below in section V.
Measuring cosmic flows
Since cosmic flow is a deviation from the Hubble-law motion of agalaxy, measuring it requires two types of observations: First, theobserved redshift of the galaxy must be measured from its spectrum.Second, an independent estimate of the distance of the galaxy mustbe made, which is much more
difficult. If a galaxy has no motion other than the Hubble flow,its redshift will correlate perfectly with its distance via Hubble's law. Any deviation outside of that due to errors in the estimateddistance represents the cosmic flow.
Unfortunately, distances are hard to estimate, and errors can leadto spurious measurements of cosmic flows. The distance to galaxiesis usually estimated by the Tully-Fisher relation, which states thatbig galaxies rotate faster than small ones. (Rotation speed can bemeasured from features in optical or radio spectra.) Rotation rateis thus a measure of true galaxy brightness, allowing one to deducehow far away a galaxy is based on its apparent brightness. The Tully-Fisherrelation has an accuracy of about 15 percent. This translates toan error in flow motion of 600 km/s at a distance of 200 millionlight-years, and the error grows with distance. Even the largestcosmic motions are no bigger than this. By averaging together severalgalaxies in a group or cluster, the error can be reduced, but measuringflows is still only reliable out to about 400 million light-yearsusing current methods.
Two conclusions follow. First, cosmic flow surveys are limited bydistance errors to volumes that are much smaller than those sampledby redshift surveys. Second, distance measuring techniques with smallererrors are badly needed to increase the viable range of cosmic-flowsurveys. At present, the catalog of flow motions contains about 3,000galaxies out to a radius of 300 million light-years over the wholesky. This volume can be enlarged incrementally with current methods,but a major increase would require better measures of distance. Moreaccurate distance measures would also allow us to study nearby motionsmore precisely, make better density maps, and derive a more precisemeasure of the mean mass density of the universe. An improvementin the accuracy of distance measurements by as little as 30 percentwould be extremely important. Several approaches are under study,including improvements to the Tully-Fisher method as well as someentirely new methods.
Summary and Prospects for Large-Scale Structure
Cosmic flow measurements and redshift maps go hand in hand, sincethe structures they reveal arise from the same cause. Combining thesetwo tools has already had a big impact on our view of structure inthe universe. When combined with the COBE measurement of CMBR fluctuations,flow measurements and maps have quantified the fluctuation amplitudeson virtually all scales of interest. Estimates of mass on the scalesof galaxy clusters and on smaller scales appear to suggest that thedensity of the universe is low, a factor of 10 less than requiredfor closure of the universe (Ω ≈ 0.1). This result has been known fortwo decades and has not changed with recent data. On the other hand,the newer data on large-scale flows, which measure mass on scales30 times larger than the older work, seem to suggest that the universemay contain sufficient density for closure (Ω ≈ 0.5 to 1). This contradictionmust be telling us something about the nature of the dark matterdistribution. It appears as though the dark matter clusters onlyweakly with galaxies and groups of galaxies but clusters more stronglyon the larger scales of superclusters. At present, it is not clearhow these apparently contradictory observations can be reconciled.Whether any of the current models of large-scale structure can describeall the observations is an open question.
The field of large-scale structure is still growing rapidly fromthe infusion of new data, and even more ambitious surveys are nowin the planning stages. Prospects also exist for improvement in theaccuracy of the distance indicators for galaxies. With better dataand theoretical tools, cosmologists have the prospect of solvingseveral key cosmic mysteries: What is the nature of the dark matterand how dense is it? What is the average density of matter in theuniverse? Is it near the closure density, Ω = 1, or is it much lessthan that, as some measurements seem to indicate? Where and how weregalaxies formed?
IV. THE DISTANT UNIVERSE
Measuring the Cosmological Parameters
We have known since the late 1920s that the universe is expanding.Quantifying the expansion is done conventionally in terms of twonumbers. H0, the Hubble constant, measures the current expansion rate of theuniverse, and q0 is the rate at which the expansion is slowing, or decelerating,because of the self-gravitational pull of all the matter in the universe.The standard cosmological solutions of Einstein's equations of generalrelativity are specified by H0 and q0. H0−1, the inverse of the Hubble constant, is a measure of the current ageof the universe, while q0 is a measure of how long the universe will continue to expand.
Two additional quantities that affect the expansion are the cosmologicalconstant, Λ, the vacuum energy density of the universe, and Ω, the ratio of the total mass/energy density in the universeto the critical density, which is required to just bring the expansionto a halt in the infinite future. Consider first the case where Λ = 0. If Ω < 1, the self-gravity of the universe is insufficient ever to stopits expansion (an “open” universe). If Ω > 1, the expansion will eventually stop and theuniverse will collapse (a “closed” universe).
The Λ term represents a strange phenomenon. As noted, it measures theenergy density of a vacuum, which remains constant as the universeexpands, unlike ordinary matter and radiation whose densities decreasewith expansion. A non-zero vacuum energy density would mean thatenergy is present in an empty universe even in the absence of particlesor radiation. Though it seems odd, such a possibility is consistentwith Einstein's theory of gravitation. The key point about Λ is that such energy generates gravity even withoutnormal matter or radiation—hence, gravity from a vacuum. Becauseof this phenomenon, and because Λ remains constant as the universeexpands (a vacuum cannot be diluted), the existence of non-zero Λ radically changes the dynamics of the universe. This is the keyconcept that underlies inflation, which is discussed in section V. If there is currently no vacuum energy density in the universe,then Λ = 0 and q0 = Ω/2; most cosmologists believe that Λ is 0, but understanding why it is so small is a profound questionof fundamental physics.
The Hubble constant, H0
The Hubble constant measures how fast the universe is expanding today.In addition, the age of the universe can be expressed as approximately(2/3)H0−1 (the precise value depends on Ω and Λ). The accurate determination of H0 has occupied astronomers for several decades, and the scientificmotivation for finding an accurate value of this critical constanthas become ever stronger. Another key use of H0 is to estimate the physical distance and size of objects that havemeasurable redshifts. For example, the size of the largest structuresin the universe is related to the distance that light could havetraveled in the time up to the epoch when matter began to dominateover radiation. The corresponding size scale today is an importantrelic of the Big Bang, but its value is proportional to H0−2 and therefore suffers from the current uncertainty. An accurate measurementof H0 is crucial for assessing whether the detailed models of theevolution of structure in the universe can be reconciled with a widerange of observations.
Current estimates of H0 range between 45 km/s per megaparsec (a megaparsec is about 3 millionlight-years) and 90 km/s per megaparsec. A value near 45 to 50 isconsidered low and 80 to 90 is considered high. If Λ = 0 and Ω = 1 (the theoreticallypreferred values for these parameters), then H0 = 50 km/s per megaparsec means an age of 13.3 billion years, andH0 = 90 km/s per megaparsec means 7.4 billion years. A fundamentalreality check comes from requiring the oldest stars in our galaxyto be younger than the age of the universe. This requirement, a logicalnecessity, sets an upper limit to H0. Astronomers' best estimates of the age for such globular cluster stars are near15 billion years, in conflict with
the smaller value of the age of the universe estimated by high valuesof H0.
Ground-based facilities and techniques have improved dramaticallyover the past three decades, yet H0 still remains uncertain to almost a factor of two. The problem isthat different techniques and different research groups get discrepantvalues for H0. This is a sure sign that unknown systematic errors exist. Whichvalue is correct? The successful repair of the Hubble Space Telescope(HST) has enabled that instrument to help resolve this long-standingissue. The HST observations employ a well-established astronomicaltechnique that relies principally on using Cepheid variable starsin other galaxies as “standard candles” of known luminosity. The technique providesestimates of the distance to other galaxies. The distances, togetherwith the recession velocities measured by the redshifts of theirspectra, permit determination of the value of H0. Recent results derived from HST observations yield a value of H0 = 80 ±17 km/s per megaparsec, consistent with low values of the age—below 10 billion years. The resulting conflict with estimates forglobular cluster ages may emerge as one of the most exciting cosmologicalquestions of the next decade. Solving this problem could requiremajor changes to stellar evolution theory, or even non-zero valuesfor Λ.
The planned refurbishment of the HST with a new, advanced camerain 1999 should enable it to make an even more accurate calibrationof the cosmic distance scale and a more definitive measurement ofthe Hubble constant. However, because of the critical conflict betweenthe estimated ages, it is clearly vital to verify the HST value byalternative, independent means. These include methods based on thedetailed study of supernova atmospheres, the attenuation of CMBRradiation as it passes through the hot gas within galaxy clusters(the Sunyaev-Zel'dovich effect), and the difference in arrival timebetween separate components of gravitationally lensed quasars (discussedbelow). All these approaches offer alternative measurements of H0.
The deceleration parameter, q0
Measuring q0 directly requires measuring the change in the universal expansionrate over a large range of cosmic time. This is done using “global” cosmological tests extending over large enough distances that thetravel time of light is an appreciable fraction of the age of theuniverse. The basic idea is that the size and appearance of a distantpatch of the universe, as viewed from our vantage point, dependsboth on how the universe expands (its global geometry) and on thebending of light by the gravity of intervening matter.
Extensive efforts in the 1960s and 1970s to study the apparent luminosityor size of distant objects, such as very luminous galaxies, werebased on the hope that these objects were constant in brightness.These efforts were mostly abandoned after it was learned that theintrinsic luminosity of these standards probably changed significantlywith time because of galaxy evolution. Recent studies of the apparentsize of features in distant radio galaxies might provide a new wayto measure q0. Direct counts of galaxies as a function of measured redshift canalso be a powerful probe of the curvature of space—another name forq0. This test was attempted in the last decade, but again yielded ambiguousconclusions. With improved modeling of the evolution of galaxiesand a major effort to obtain spectra of a large sample of faint galaxies,this test might prove to be an effective way to measure both q0 and Λ. Cosmological models with different values of q0 and Λ predict different volumes of space for a given observed redshift,and the number of galaxies is a measure of the size of that volume.This volume evolution affects not only the number of quasars, supernovae,or galaxies at any redshift, but also the number of potential gravitationallenses (discussed below). Preliminary results from a study of quasarimages with HST suggest that lensed quasars are relatively rare.Models with large Λ overpredict the number of observed gravitationallenses; therefore, Λ is not large.
The density parameter, Ω
Without going to cosmological distances, it is possible to measurethe density parameter Ω, by means of so-called local tests. Manyof the local tests “weigh” local structures by applying the virial theorem,which states that the kinetic energy of a self-gravitating systemshould be approximately equal to its potential energy. Since themotion of luminous galaxies must be observed to estimate the kineticenergy of the system, only the component of the mass density clusteredwith luminous galaxies can be examined in this fashion. As notedearlier, such measurements tend to give low values of around 0.1to 0.2. However, as mentioned in the discussion of cosmic velocityflows in section III, there may be a component of dark matter clumped in sizes largerthan clusters of galaxies but smaller than superclusters. Cosmicvelocity flows may be detecting structures on this scale, givingvalues of Ω near 1. If there exists a perfectly smooth backgroundof mass density unclustered with the galaxy distribution on any scale,it can be detected only by its effects on the curvature of space,in the global measurements of q0.
Deep Imaging of Galaxies
Galaxies have been used as beacons to map the distribution of matterin the universe ever since they were recognized as independent systemsof stars. As described above, the “local” distribution of galaxies showsa complicated network of structures. When averaged over the largestdistances, many billions of light-years, the distribution of matteris expected to be more homogeneous. Current research programs onvery distant galaxies have two distinct goals. The first is to usethe number of visible galaxies as a measure of the surveyed volume.If galaxies were stationary and the geometry of space were determinedby the rules of euclidean geometry, then the number of galaxies seenwould be roughly proportional to the cube of the distance probed(N ∝ r3). When the effects of redshift and non-euclidean geometry are takeninto account, the number of galaxies is expected to increase moreslowly than r3 at larger distances, as is indeed observed. (If these effects werenot present, the night sky would not be dark! This is known as Olbers's paradox.) Questions about the geometry of the universe—is space positively or negatively curved, infinite or finite?—can be related by general relativity to the dynamics of the expansion(will the universe expand forever, or will it stop expanding andcollapse in a Big Crunch?). Thus, measuring the curvature of theuniverse in the past can be used to predict the expansion of theuniverse in the future.
The second use of distant galaxies is to probe for signs of evolutionof galaxies and of the clustering of galaxies in the universe overthe billions of years during which their light has been travelingto us. The notion is that a galaxy seen at an earlier stage in itslife should have more gas available out of which to form new stars,and consequently it should appear brighter and bluer (when adjustedfor redshift) because of the presence of many massive, hot youngstars. A trend to bluer colors in fainter galaxies has been detected,and its detailed interpretation is a subject of active current research.
Normal nearby galaxies emit most of their light at visible wavelengths,but the light received from the most distant galaxies is redshiftedto infrared wavelengths. In the past decade, detectors with highsensitivity have been developed that are ideal for measuring weakinfrared radiation, and the main technical problem that remains isthe strong emission of infrared radiation from the atmosphere andfrom the telescope itself. This problem is analogous to local interferencein the CMBR measurements, and the solution is similar: go where it's cold, to the South Pole or out in space. Plans are well advancedto deploy a telescope at the South Pole to make deep-sky surveysat near-infrared wavelengths. This approach is less expensive thanbuilding space observatories, but it has the disadvantage of beingrestricted by the atmosphere to a relatively narrow spectral range.This effort in Antarctica is complemented by planned space missionssuch as the Space Infrared Telescope






