5
Needs and New Directions in Computing for the Chemical Process Industries
W. David Smith, Jr.
E.I. DuPont
This paper is organized into six sections. The first provides some general background information and highlights the main factors driving the chemical process industries (CPI) today in order to provide a context for all that follows. The second presents my view of the total process simulation requirements of the CPI and defines the scope of the problem. The next section then provides a brief overview of the current tool set that is being used in the CPI. The fourth section introduces the European CAPE OPEN project, funded by Brite-Euram and nearing completion; it also discusses briefly the follow-on project, GLOBAL CAPE OPEN. The fifth section considers the closely related topic of process control, and the final section lists conclusions.
Background and Factors Driving the Chemical Industry
Let's begin with a few general observations about the CPI. Chemical and petroleum plants require huge, long-term capital investments. The lifetime of a plant, once built, will range from 25 to 50 years. Processes and process designs are almost always customized. We (DuPont) have quite a few nylon plants, but no two are alike. Each time a new plant is built, we incorporate improvements that have been learned from the operation of the last plant that was built. This places some constraints on the costs that
AUTHOR'S NOTE: This paper did not go through the approval process that is normally required by DuPont. Therefore, this should not be viewed as an official DuPont perspective on the needs and new directions in computing for the chemical process industries. Rather it is my personal view of the subject that is based on 20 years of university teaching and 20 years of experience with DuPont, the latter being most relevant to the topic at hand. Furthermore, at times it is necessary to refer to commercial software products and make contrasts between their respective features. These references are not meant to be either a recommendation or a condemnation of a particular product but are meant to illustrate different approaches that have been taken to try to satisfy the simulation needs of the chemical process industries. In fact, it is safe to say that the complete simulation tool for all of our needs does not and is never likely to exist because of the enormous diversity within a company like DuPont and the industry as a whole. Also, generalizations will inevitably be used to make a point about the field for which someone will be able to provide an exception or a counterexample, but in a broad-brash overview of any field that is to be expected.
one is willing to accept for a particular plant. For example, if you are designing an airplane and you expect to build a thousand of them, then you can afford to design and build in a super-sophisticated control system because the cost will be spread out over many units. That does not happen in the CPI.
Our plants are large, very complex, and, I am sorry to say, still relatively poorly understood in the sense that we don't know all the details of the chemical reactions and their associated thermodynamics and transport properties needed for the design of these facilities. Because of this lack of knowledge and the inherent safety concerns of handling some very dangerous chemicals, our plants tend to be over-designed to ensure that both safety and production goals will be met. Even for some of our oldest and best-known products we are still improving our fundamental understanding. This is happening largely because of vastly improved analytical instrumentation. In some cases we have benefited significantly from the application of computational chemistry to provide basic data that otherwise would have been too costly and time consuming to measure in the laboratory.
Most of our large plants, particularly those that make polymers, were justified on economies of scale. Initially that made sense because we were only expecting to make one or two products. Over time, because of good chemistry and market demand, the number of products has grown, which has often meant that the plant has had a much broader range of operating conditions. In many cases we have designed and built very good “battleships” but now, because of the proliferation of products, we are forced to try and run them as if they were "PT boats." Another characteristic of those polymer plants that make filament and sheet products is that they typically have a very wide range of time scales. At the front end, the reactor might have a time constant that is measured in hours while at the back end of the process where the filament or sheet is being formed, the time constant may be measured in milliseconds or seconds. The combination of multi-product transitions with wide ranges of operating conditions and time constants leads to some very challenging manufacturing problems.
The essential problem facing the chemical process industries is shown in Figure 5.1. The graph shows the trend of capital productivity with time for both total manufacturing and chemicals. Capital productivity tries to measure how effectively capital is being utilized. Simply stated, for each dollar
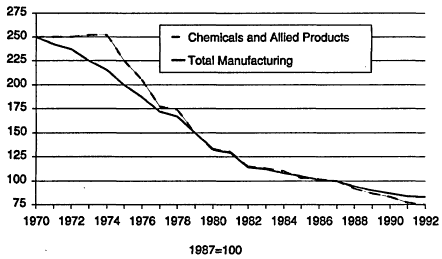
Figure 5.1
Capital productivity for all manufacturing and for chemicals.
invested in manufacturing facilities, how much profit do I make? The break-even point was assigned arbitrarily a value of 100, so it easy to see that since 1987 the chemical industry has not been the best place to invest your money. The major contributors to the decline have been increased energy costs after the oil embargo, overcapacity and tougher global competition, increased costs for environmental programs, and new business ventures outside of core competencies that have been costly and unprofitable.
In this setting, what are chemical companies focusing on? Certainly the answer will vary from company to company but, using DuPont as an example, the top five items are asset productivity, growth, quality, environmental issues, and shorter development cycle. The middle three really don't need any explanation. Asset productivity deals with the problem of squeezing even greater profits from the large investment we already have in the ground. Three of the major factors that govern the productivity of a plant are yield, up-time, and instantaneous production rate. Yield, unfortunately, can be defined in many ways and is often defined to suit the needs of the definer. In an effort to eliminate that ambiguity we use first-pass, first-quality yield, which counts only the amount of the on-aim desired product made in one pass of the fresh feed through the reactor. One wants to eliminate rework and blending of off-specification material as well as product reclassification. In multi-product plants one also tries to minimize transition losses. Up-time focuses on preventive maintenance, as you can't make a product if the plant isn't running. Assuming you can sell what you make, one always wants to run the plant at the maximum instantaneous rate, which is usually based on the best past performance of the plant.
At a recent meeting, a speaker from Dow reported that from the time the chemist comes up with a new idea at the bench to the time that the first pound comes out of a commercial-scale plant, is typically about 12 to 13 years. That process development cycle is just a little longer than the 10- to 11-year average that DuPont likes to claim. Now that is much too long in today's very competitive and rapidly changing marketplace. If it takes you that long to go from idea to finished plant, you will probably have competition from a lower-cost replacement-in-kind product or the market could be dramatically altered by the appearance of another completely new product. Either possibility could invalidate the whole basis for the investment that you have made. In one recent example in DuPont, cycle time was reduced to 5 years. The challenge we face now is to institutionalize what we learned in that very successful project.
Process Simulation Needs of the CPI
What is the process of designing a plant, and what software tools are needed? Figure 5.2 presents a block diagram of the major steps in the process of designing a chemical plant. The impetus to build a plant generally comes from one of three sources: a new discovery from the lab, a response to a customer request, or a needed capacity increase for an existing product. In the third case, the design process should be easier because a lot is already known from the existing plant. Since, in principle, the first two options require more work and essentially the same steps, we will assume that we are dealing with a potential new product that has been discovered in the lab.
Borrowing from Edward Tufte1 in the preparation of Figure 5.2, we intend the thickness of the arrows to convey the bandwidth of the data and information that are transferred between the activities represented by the boxes. The idea for a new product and the process to manufacture it would originate in either Box 1 or 3. Ideally, one would get a process engineer, skilled in process synthesis, working
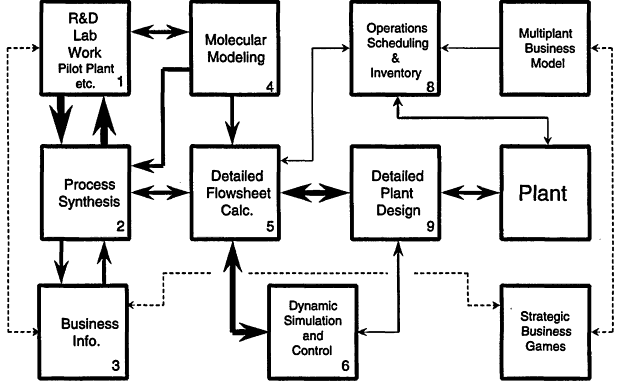
Figure 5.2
Process of plant design.
with the chemist(s) as soon as the potential new product begins to look interesting and preliminary cost estimates for a process to manufacture it are needed. At this stage it is important to examine alternate raw materials and different reaction conditions such as temperature, pressure, choice of solvent, and choice of catalyst. The selectivity, yield, and nature of the by-products of the reaction determine the complexity and cost of the rest of the process. The rapid testing of alternatives at this stage is the key to successful process development and plant design. The heavy arrows connecting Boxes 2 and 3 indicate the intensity of that interaction. Unfortunately, there is no commercially available software to aid in the process synthesis step. One very interesting program, PIP-II, has been developed at the University of Massachusetts by James Douglas and his students to address these activities. The difficulty in using commercial process simulators for process synthesis is that the equipment modules they provide require complete kinetic and thermodynamic data that are never available at this early stage of process design. In some cases one can make effective use of molecular modeling, Box 4, to help develop estimates of the missing data. That played a prominent role in the DuPont example cited above with a development cycle time of only 5 years. This part of the overall design process usually produces a small number of "attractive" process alternatives that have been obtained by using consistent but approximate design and economic calculations to screen many potential processes. During the process synthesis step many calculations were done on the basis of ideal vapor-liquid equilibria data. Since the next step requires
more accurate kinetic and thermodynamic data, every opportunity should be taken during this stage of the development process to extract this information from the available experimental data.
At this time in the process, one needs to develop more rigorous and detailed estimates of process performance and cost so that the final choice can be made between the alternatives developed in the process synthesis step. This is generally accomplished by the use of commercial process simulators from the three major vendors, such as Aspen Plus from Aspen Tech, HYSYS from Hyprotech, and Pro II from Simulation Sciences (see Box 5). A lot of work gets done here, and it is not unusual for about 80 percent of the effort to be spent on getting reasonably accurate kinetic and thermodynamic data. To the extent that this has been done during the process synthesis step it will speed up this part of the process. While the steady-state process design is being evaluated it is also very important to evaluate the controllability and operability of the candidate processes. This is accomplished by developing an appropriate dynamic model of the process (Box 6). Several of the commercial simulation programs now claim to be able to convert the steady-state simulation into a dynamic simulation. For a single piece of equipment, that claim may be correct, but for a process flow sheet that is neither possible nor, in general, desirable. In a steady-state flow sheet the lines connecting the different pieces of equipment do not have to have any diameters or lengths specified since their role is simply to pass information to the next unit. In a dynamic simulation, the size of the lines is essential to track the propagation of disturbances from one vessel to the next. Furthermore, in most process control analyses, approximate or low-fidelity models are perfectly adequate and one would not want to use models of the complexity typically used in a detailed flow sheet calculation.
In the case where the design is for a multi-product plant, we should try to ensure that the equipment is designed such that the product scheduling can be accomplished with minimum cost. At present there are no design methodologies to solve this problem. The design is typically evaluated by doing case studies (Box 8). When controllability and operability with scheduling considerations are satisfied, a basic data package is assembled and transmitted to the organization that will do the detailed equipment design and construction (Box 9).
After the plant is built, we still have to run the plant and worry about what our competitors are doing. If the plant has been built to increase capacity of an existing product, then it is very likely that the other plants will be distributed around the world. We have global operating, scheduling, and inventory decisions that have to be made. These are usually formulated as supply chain optimization problems (Box 9).
Every box in Figure 5.2 requires a different computer program—if one exists at all—and none of them communicate in any reasonable way. This leads to inefficiency in the design process, as some of the output from one program needs to be re-entered into one or more additional programs. The programs come from different vendors, and they invariably use different methods for the evaluation of thermodynamic properties, which adds to our problems. It should also be obvious that this is a significant interdisciplinary process that requires skills that range from wet chemistry to molecular modeling to the optimization of large supply chain problems.
Commercial physical property databases do not cover our needs. We run reactions that range from less than 100 degrees in the liquid phase to solid reactions at 1,200 degrees to plasma reactors at 5,000 degrees. We run polymer reactions that span a pressure range from one to 2,000 atmospheres. Most companies have their own proprietary physical property databases that have to be incorporated into one or more of the simulation programs that are used in Boxes 2, 5, 6, and 9. All of the current commercial simulation products are closed, proprietary programs, which makes the job of incorporating proprietary thermodynamics or equipment modules much more difficult.
Another serious problem that none of the vendors has addressed in a significant way is the visualization of results. Simulation programs generate masses of numbers, and there is no easy way to take the output from these simulation packages and look at it in a way that makes sense. A recent development has been to allow the export of results to an ExcelTM spreadsheet. I suppose that is a small step in the right direction, but I don't consider it to be a general solution to this problem.
An Overview of Current Simulation Programs
To make sense out of some of the comments that follow, it would be helpful to look at Figure 5.3. In my view, there are at least three important views of software. Two views belong to the user community; one group is the casual or infrequent user, while the second is the power user who tries to squeeze as much capability out of the program as he or she can. The final view is that of the person or team designing and writing the software. Issues that the developers need to resolve are experience level of the user for whom the product is intended, choice of computer platform(s), design for easy maintenance, management of versions and updates, provision of help and error diagnostics to the user, etc. For this discussion the first issue is the key one. Is the product intended for the casual user or the power user? If the choice is made to design for the casual user, a lot of care will be taken to prevent the user from inadvertently gaining access to sections of the code that might govern the choice of convergence algorithm or criteria for convergence or other performance parameters to prevent the user from "making mistakes." Once the decision has been made to "bulletproof" the code in this way, the ability of the power user to use the software in sophisticated ways has been significantly curtailed. The power users tend to be frustrated by these imposed limitations. The major concern of the vendors is to be profitable so they need to concentrate on the largest market, which, without question, is the casual user. In DuPont the ratio of casual to power users is about 20/1.
Having decided which category of user to target, there are two choices for the simulation "technology" to implement. They are the sequential modular approach and the equation-based approach. The
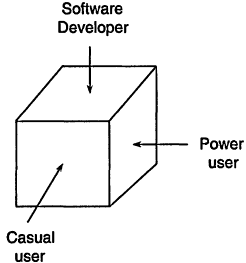
Figure 5.3
Three important perspectives from which to view software.
sequential modular approach is the oldest and most common approach and is used by all the major vendors. In this approach the vendor provides a library of equipment modules that the user can connect in a sequence that best represents the process. The problem is that the vendors have the experience and ability to provide only a limited range of equipment modules to industry. In particular, the ability to model reactors in these systems is very, very limited.
Sequential modular simulators are best suited to do equipment rating instead of equipment design. Equipment rating means that one wants to evaluate the performance of a piece of installed equipment. Taking a distillation column as an example, the user would know the number of trays, location of the feed stream, and the appropriate set of physical properties and would wish to determine the effect of changes in feed rate, reflux ratio, or reboiler heat input on column performance. In contrast, the design problem is usually posed as how big the column has to be to separate a feed stream of known rate and composition to products of specified purity. It is clumsy to do design calculations in sequential modular simulators, but it can be done by trial and error. In my opinion, the sequential simulator has been designed for the casual user. Key word input is giving way to click and drag input on PCs. Convergence is still a problem for large flow sheets, and the diagnostics that are available when convergence fails are not extremely useful.
Equation-based simulators are for the power user. The learning curve is much steeper. One big advantage is that both steady-state and dynamic models are possible. Here the Achilles heel is that it is essential to scale the equations that describe your equipment or you face severe stiffness problems. Until very recently the diagnostics in these systems were abysmal (that is an understatement), and they can still be better.
One of the other advantages of the equation-based approach is that, for a specialized piece of equipment, it is much easier for the engineer to write down the equations that describe it, put them into the equation-based simulator, and let it solve them. Before the solution can proceed, the user has to specify which variables are independent and which ones are fixed. This means that, once the equations have been scaled and entered in the simulator, the user can easily go from the rating problem to the design problem just by specifying what the dependent and the independent variables are in a particular problem. Other advantages of the current generation of equation-based simulators are that partial differential equations can now be handled much more easily and the dynamic models that can be developed in them can easily be linked to a distributed control system to provide operator training systems.
Since they didn't appear in Figure 5.2, some comment should be made about codes for computational fluid mechanics. They involve a very steep learning curve and tend to be used only by specialists. One of the major problems they have is a very serious lack of physical property support. One important application area is multi-phase reactor problems, but those are still very difficult to solve. Accuracy can be a problem because of accumulated round-off errors in these very lengthy calculations. We solve some problems on a Clay computer, running for anywhere from 10 to 24 hours. When a run is complete, the question is, How many significant digits do you believe you really have in the answer? Even with double-precision calculations on the Cray we believe that in some problems we can count on only two significant digits in the answer.
Optimization codes also deserve some comment. These are still largely the domain of specialists and power users. Global optimization methods for general problems are still an active research area. Algorithms often need to be tailored to the structure of the problem to get reasonable solution times.
The European Cape Open Project
CAPE is an acronym for computer-aided process engineering. OPEN refers to having the vendors support non-proprietary open standards for commercial simulators. The funding from Brite-Euram was approximately $3.5 million for 3 years, and this first phase of the project ends in the middle of 1999.
Although this is a European activity, the only major software vendors at the time were all U.S. or Canadian. So by default they were invited to participate. Since that time Hyprotech and Simulation Sciences have been purchased by large British companies, leaving Aspen as the only North American simulation company. QuantiSci, a small consulting company, is also a member. The universities participating are Aachen, Imperial College, and Toulouse. The companies involved are BASF, Bayer, BP, ELF, ICI, IFP, and DuPont Iberica.
Why were people interested in CAPE OPEN? The driving force for this activity was provided by the large German chemical companies under the leadership of Bayer. They had a real concern about the large quantity of old but valuable code that they wanted to keep on using in existing commercial simulators without having to rewrite it. This is often referred to as legacy code.
Every large chemical company that I know probably uses at least two of the three available commercial simulators; some use all three. This is expensive, and when you use two of these simulators to look at the same problem in different parts of the company you waste a lot of time trying to figure out which one of the two is really giving you the right answer, because they will be different. Since the current commercial simulators are closed proprietary systems, it means that if Hyprotech has a good azeotropic distillation model and Aspen has the required thermodynamics, you could not use the two together to solve the problem. It was also recognized that no matter how hard the vendors try, they are not going to be able to provide all the modules that we need to model the wide range of systems that we deal with on a routine basis.
The goal of the CAPE OPEN project is to develop a non-proprietary framework for simulation software that is based on software components. That requires standards for the functional interfaces between classes of software components and the use of a binary standard such as Microsoft's Active X or CORBA. A software component is compiled software, written in any language, that supports the binary standard. A software component can be either a server or a client to any other software that supports the binary standard.
The functional interfaces for which we have developed standards are thermodynamics, unit operations, and numerics. Prototypes exist for these three interfaces. They are in the final stages of testing now and they will be released in the next 6 months. What does this effort buy us? It buys us "plug-and-play" capability. It means that I will be able to take the thermodynamics from Aspen and use them in a Hyprotech simulation and it will run. We have demonstrated that capability, and the vendors are working with us to complete the interface testing. What will a CAPE OPEN-compliant simulator look like? I have tried to indicate this in Figure 5.4.
The part of the simulator that will be proprietary, which enables the vendors to compete, will be the executive. The rest of the simulator is divided into three main sections: the unit operations, which includes reactors and other specialized pieces of processing equipment; thermodynamics and transport properties; and numerical routines of all sorts. Each unit operation will be a software component that will be able to communicate with the other major pieces of the simulator to get any services or information it needs to complete its calculations through the standard interfaces that have been developed. This means that all executives will be able to "use" a unit operations software component that has the standard interfaces regardless of its origin. Clearly similar statements can be made about thermo-
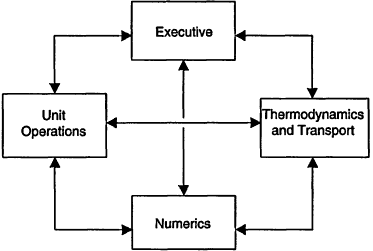
Figure 5.4
A CAPE OPEN-compliant simulator.
dynamics and numerical components. The end result is a plug-and-play simulation environment that will contain a much broader choice of components.
One of the most important aspects of having CAPE OPEN software is that it will facilitate the transfer of technology from universities to industry. DuPont had supported research on azeotropic distillation at the University of Massachusetts and we were interested in extending the contract to work on reactive distillation. Recent research had shown that a change of variables would convert the reactive distillation equations into the same form as the azeotropic equations. Near the end of the first project, the university had negotiated a deal with Hyprotech to commercialize the azeotropic code. Hyprotech was using object-oriented programming (OOP) as was DuPont, so during the planning session for the reactive distillation project the question was raised about using the inheritance features of OOP to build the reactive distillation code from the azeotropic code. Two DuPont staff members, neither accomplished programmers, went to Hyprotech and, with help from Hyprotech programmers to understand the structure of the azeotropic code, they had in 2 weeks a working reactive distillation module that would run in HYSYS. We had budgeted 1 year of time for an experienced postdoc to code the problem in FORTRAN.
One of the questions that this workshop was intended to address was how the advances in computer and communication technology would change the way industry works. You can imagine that a pump vendor, for instance, would have on its Web site a CAPE OPEN-compliant software component for each of its products. If an engineer were doing a simulation and wanted to test a new pump or consider a different pump, he or she could go to the Web site and either download the appropriate software component or run it over the Web on the server, complete the simulation, and evaluate the results. If the results were satisfactory the engineer could check to determine the availability of that model pump and perhaps place an order directly. One can imagine that all equipment suppliers to the CPI would provide similar services.
What is Global CAPE OPEN? The people involved in CAPE OPEN are very conscious of the fact that theirs is a relatively small European activity. They would like the standard interfaces that have been
developed to be accepted as universal or global standards and extended to cover a broader range of applications. Some that have not been addressed for lack of time are solids handling, polymer processing, and pharmaceutical/biological systems. Brite-Euram has granted additional funding for another 2.5 to 3 years. The membership has been extended to 18 partners from Europe, Japan, and North America. There is a problem, however, as the Brite-Euram funding is only for the European partners and, as in the past, most of it is directed to university research. Other participants have to get local funding, and many universities in the United States would like to be a part of this research program but are faced with the problem of finding a U.S. funding agency that is willing to deal with a manufacturing question like this. Industrial participation from North America has not been established as we are still looking for a regional coordinator.
Process Control in the CPI
Most processes in the chemical industry now have distributed control systems (DCSs) and all new plants would almost certainly have one included in the design specification. Furthermore, as a rule of thumb, roughly 80 percent of the control loops can be handled well with simple PID controllers. The other loops usually require some form of advanced control. As the power of the process control computers has increased, more and more advanced process control functionality has been incorporated into the DCS. Now several of the major vendors provide the ability to do moderately sized linear model predictive control applications. On the surface it would appear that most of industry's process control needs have been addressed by current DCS technology.
The process control options that are available are all based on linear control theory because that is what we know best. Unfortunately, almost all chemical processes are nonlinear, and established linear techniques work well only for mild nonlinearities. The business drivers that I described earlier are pushing the operation of our processes into regions where the nonlinearities are emphasized, so the popular linear techniques may no longer be good enough.
In a new application the first question is, Do I need to use nonlinear control? There is no simple answer to this question nor is there a simple calculation that would provide the answer. In practice the question is decided when standard linear techniques do not work, but then another question immediately arises—What nonlinear control strategy should be used? Again experience or trial and error will provide an answer. The final question becomes, How will the nonlinear control algorithm be implemented in the DCS? Currently, this question is always present because the DCS vendors only provide linear control options.
Nonlinear control technology is inherently more complicated and is generally inaccessible to most control practitioners. Nonlinear model development is several orders of magnitude more difficult than that for linear models. Each application is usually unique and a specialized implementation is required. In spite of these difficulties we believe that there is a vast untapped potential economic benefit in cases of moderate nonlinearities where linear methods can be used but where nonlinear methods would yield significant performance improvements.
There is interesting work on nonlinear control being done in the universities that we would like to try, but there is a major barrier to be overcome: the monolithic code that the DCS vendors have implemented in their DCSs. This makes it very difficult for them, let alone industrial control practitioners, to add or try new control algorithms on any commercial DCS. If the DCS vendors adopted the component-based software development strategy of the simulation software vendors, this problem could be solved and we would get a much faster and effective transfer of advanced process control technology from the universities to industry. Everyone would benefit.
Conclusions
|
1. |
Both process simulation and process control will benefit from component-based redesign of their software. |
|
2. |
Technology transfer in both areas will improve dramatically. |
|
3. |
Component-based software operating as clients or servers over the Web will significantly reduce the cycle time for new process development. Component-based software has the potential to alter the way that equipment suppliers market and sell their products to the CPI. |
|
4. |
The potential benefit from the application of nonlinear control is large, and vendors need to provide the capability for easier implementation of these techniques. |
Discussion
Jack Pfeiffer, Air Products and Chemicals, Inc.: Dave, regarding your diagram on the modeling process that you said moved from left to right—one of the things that we have been toying with is a recycle loop that would bring information back from plant operations into the R&D or the process synthesis step. Have you thought about the value of that, and especially have you thought about how the software that we have today, or the directions that you are proposing, may enhance that capability?
David Smith: Well, I do not think there is anything that prevents you from doing that. I think the tools to analyze historical process data do exist but they are not integrated with the tools that I have discussed. That is one area that has not been considered by CAPE OPEN. However, I think the biggest problem you actually have is the cultural problem of what the production or operations people get rewarded for. In DuPont, that is significantly different from what R&D folks get rewarded for, so the problem ultimately becomes the willingness of the plant people to accept change. They get rewarded for continuity of operation, no labor problems, no safety problems, and pounds of product shipped. If you go to the typical operations superintendent with a proposal to improve operations, there will usually be little interest because it means downtime, retraining, and a whole bunch of things that they do not want to deal with. So, it is the cultural problem that is much more difficult than the problem of having that recycle loop of process information.
Jack Pfeiffer: As a further clarification on that, one of the things we are thinking about is that we collect a pot full of data in plants, and these data may be valuable if analyzed using the creative concepts of R&D.
David Smith: That is definitely true. We spend an inordinate amount of money collecting data that we never really analyze. The question is, Why do we do that? One of the major reasons is that we have reduced the number of people at the plants to the minimum, and those people are so busy that they do not have time to go back and look at historical data until the plant is having problems.
Gintaris Reklaitis, Purdue University: If Global CAPE OPEN is such a wonderful thing for the industry, why is the industry not "ponying up" and supporting the activity? It does not appear that there are key technology bottlenecks in terms of how to structure object-oriented codes, how to develop them. Why not "pony up" and do it?
David Smith: The issue was that it was very difficult to convince the vendors to accept the concept of open, nonproprietary simulation systems. Also the business of defining standard interfaces that will support the broad range of modeling activities encountered in the CPI was a very difficult task. One of the reasons for forming Global CAPE OPEN was to have greater participation in testing and extending those standards. Finally, my management says we have “ponied up” for 3 years with three people from DuPont participating in and leading parts of this activity. My current management feels that it is time for another U.S. company to step forward and lead the North American effort in Global CAPE OPEN.
Christos Georgakis, Lehigh University: Dave, what do you perceive as the computational challenges in achieving industrial-scale green chemistry, where green plants produce no pollution, only products? CAPE OPEN is among the challenges, but what other computational challenges exist?
David Smith: CAPE OPEN-compliant simulation software that is integrated as I suggested in Figure 5.2 will help because it will allow the evaluation of more process alternatives and thus increase the chances of finding process designs that will have minimal environmental impact. However, I believe the fundamental challenge is still one of chemistry. Greg McRae and his students have looked at some approaches to this problem. One approach is to start with different raw materials that might make a broader range of salable products but have much less or no waste. I think our businesses would not support this approach, as the yield to products other than the desired product could be significant. I think there is more hope in developing more selective catalysts and bio-catalysts.
Tom Edgar, University of Texas: I had an industrial chemist ask me recently about a problem that he is encountering. He says that his business people are on his case because every time they design a plant they find out they have about 20 percent overcapacity because of the intrinsic conservatism in designing the plant. Do you think one of the bottlenecks is this software problem?
David Smith: No, the problem is not with the existing software, nor will CAPE OPEN-compliant software solve the problem. I think the problem we all have is the fundamental uncertainty about kinetics, thermodynamics, and transport data during the design. It is costly, time-consuming work that is perceived as slowing down the design process. Since you do not know those properties accurately enough you tend to overdesign the plant. Initially that is viewed as a "bad" thing, but then 10 years down the road when you need incremental capacity you look like a hero because you get it cheaply.












