CHAPTER FOUR
What Does TIMSS Say about Instructional Practices?
Science and mathematics teachers around the world face many similar challenges (Robitaille, 1997, p. 32). Most teach classes of about 30 students in lesson blocks that are a little less or a little more than an hour. They generally have a particular curriculum they intend to cover during a course. They want students to acquire certain competencies.
Teachers around the world also have similar concerns. According to data gathered by TIMSS, many teachers believe that high student-to-teacher ratios limit their ability to teach. Many teachers report shortages of equipment for use in demonstrations and other exercises. In the large majority of TIMSS countries, disruptive students, differences in academic abilities, and unmotivated students are cited by many teachers as factors that limit their ability to teach (Martin et al., 1997, pp. 141–143).
How do teachers and educational systems around the world deal with these common
challenges and concerns? The results of TIMSS show that teachers and systems in different countries tend to solve similar problems in different ways. In turn, these solutions often reflect the beliefs and assumptions that teachers—and those who influence teachers—hold about teaching and learning.
This chapter discusses what teachers actually do in the classroom and the reasons behind their actions. It does not address the broader context for teaching and learning, such as teacher preparation and student attitudes (these and other topics are covered in the following chapter). Rather, by examining how teachers in other countries attempt to solve common problems of practice, this chapter presents options for instructional practices in the United States that might not otherwise be considered.
The national standards in both mathematics and science cite the critical importance of teachers' knowledge, understanding, and skills in mathematics and science learning. According to the National Science Education Standards (National Research Council, 1996, p. 28), "Effective teaching is at the heart of science education. . . . The decisions about content and activities that teachers make, their interactions with students, the selection of assessments, the habits of mind that teachers demonstrate and nurture among their students, and the attitudes conveyed wittingly and unwittingly all affect the knowledge, understanding, abilities, and attitudes that students develop."
The Professional Standards for Teaching Mathematics (National Council of Teachers of Mathematics, 1991, p. 22) point out that "teaching is a complex practice and hence not reducible to recipes or prescriptions." Teachers must draw on many kinds of knowledge in the classroom while adapting their teaching to particular students and contexts. They also have to balance multiple goals in deciding what and how to teach. And teachers work within an administrative and cultural context that shapes their actions. Good practice in teaching cannot be prescribed but must emerge from a teacher's knowledge, judgment, and circumstances.
The first section of this chapter discusses some of the variations in instructional practice that emerge from varying circumstances, such as the activities in which students are engaged in mathematics and science classes and how much homework they are assigned. The second part of the chapter probes beneath these specific activities by examining some of the key influences on instructional practices, including the learning goals that teachers hold for students and their beliefs about teaching. The chapter concludes with descriptions and commentary for two sample lessons, one from the United States and one from Japan, demonstrating common teaching practices in each country. As in the previous chapter and the next chapter, questions at the beginning of each major section provide guides for considering educational changes in light of the results from TIMSS.
The information presented in this chapter comes from two main sources: the TIMSS background questionnaires given to administrators, teachers, and students and the video study of eighth-grade mathematics teaching in Germany, Japan, and the United States. It can be difficult to use survey data to illuminate an activity as complex as teaching, but the TIMSS questionnaires probed a wide range of beliefs,
attitudes, and practices. The videotapes, in contrast, provide vivid impressions of what happens in classrooms but are less revealing about the motivations and thinking processes of teachers. (The videotape analysis also looked only at mathematics and only at the eighth grade.) Together, the two sources of data provide complementary insights into teaching practices.
VARIATIONS IN INSTRUCTIONAL PRACTICE
Lesson Structure
Teachers at the fourth-and eighth-grade levels who participated in TIMSS filled out questionnaires asking how much class time they spent on a number of different instructional practices. This analysis revealed that lesson structure has some common features among countries, though interesting differences also appeared.
The two most common activities in U.S. mathematics teachers' classrooms at the fourth-and eighth-grade levels are teachers working with the whole class and students working individually with assistance from the teacher (Beaton et al., 1996a, pp. 151–155; Mullis et al., 1997, pp. 162–166). These two activities are also the most common internationally.
An exception to the predominance of these two activities can be found in fourth-grade science in the United States, where the second most common practice is for the class to work together as a whole with students responding to each other. This also is true in Japan, Korea, and the Netherlands (Martin et al., 1997, pp. 145–147), but it is not the case in eighth-grade science in the United States (Beaton et al., 1996b, pp. 143–147).
The questionnaire on instructional practices also produced information on the amount of review and new material that students received in mathematics and science classes. According to this analysis, more than half of U.S. eighth-grade mathematics students received fewer than 20 minutes of instruction on new material in a typical 50-minute class period. Instruction on
|
QUESTIONS RELATED TO VARIATIONS IN INSTRUCTIONAL PRACTICE
|
new material was somewhat more frequent in science; 43.5 percent of U.S. eighth-grade science teachers provided 20 minutes or more of such material in each class (Schmidt et al., 1999, pp. 65–67). Both internationally and in the United States, review was a more dominant instructional practice for mathematics than for science.
The videotape studies of eighth-grade mathematics in Japan, Germany, and the United States substantiate these findings (Stigler and Hiebert, 1997; Stigler et al., 1999). These data reveal that teachers in all three countries spend more time doing classwork, where the teacher works with the entire class, than seatwork, where students work on their own or in small groups. However, shifts within the lesson from classwork to seatwork and vice versa were considerably more frequent in Japan than in the other two countries. As a result, the duration of segments defined by teaching practices tended to be shorter in Japan than in the other countries, giving the lessons a more punctuated feel.
An important finding from the videotape studies relates to whether teachers or students are doing the bulk of the mathematical work. Most classroom time in all three countries was devoted to setting up tasks, working on tasks, and sharing solutions or correcting tasks either during classwork or seatwork. If a task is done during classwork, teachers are often doing much of the work. If it is done during seatwork, students are more likely to be doing the work. The videotape analysis shows that Japanese classes spent more time working on tasks during seatwork than during classwork, whereas the reverse was true in Germany (Figure 4-1). U.S. classes divided the work equally between classwork and seatwork.
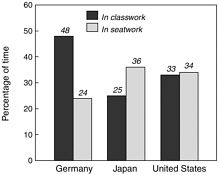
Figure 4-1 Average percentage of lesson time spent working on tasks during classwork and seatwork.
Source: Stigler et al., 1999, p. 87.
The three countries also differed in the complexity of the exercises undertaken by students (Manaster, 1998). In Japan, multistep tasks were most common, occurring in 90 percent of lessons. In the United States and Germany, multistep tasks were found in 62 and 63 percent of lessons, respectively.
The three countries differed starkly in how often the videotapes showed explicit instances of mathematical reasoning (Manaster, 1998). In Japan, 53 percent of lessons had clear instances of reasoning. In Germany, 20 percent of lessons indicated that mathematical reasoning had taken place. In the United States, however, none of the videotaped lessons presented evidence of reasoning in mathematics.
Perhaps the best way to measure student engagement in mathematics is to assess the kind of mathematical activity in which students are engaged during seatwork. Seatwork tasks in the videotaped classes were coded into three categories: practicing routine procedures, applying concepts or procedures in new
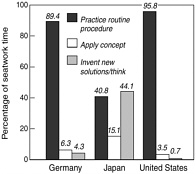
Figure 4-2 Average percentage of seatwork time spent practicing routine procedures, applying concepts, or thinking and inventing new solutions.
Source: Stigler et al., 1999, p. 102.
situations, and inventing something new or analyzing situations in new ways. In this analysis, Japan differed significantly from the United States and Germany (Figure 4-2). Japanese students spent about the same amount of time practicing routine procedures and inventing something new, whereas German and U.S. students spent almost all of their time practicing routine procedures.
Calculators and Computers
U.S. teachers indicated in TIMSS that they use calculators and computers as much as or more than teachers in most other countries. At the population 1 level in mathematics, 39 percent reported using calculators once or twice a week, versus an international average of 18 percent (U.S. Department of Education, 1997b, p. 42). Although calculators are almost universally available in the TIMSS countries, teachers in some countries (including high and low performers) reported never or hardly ever having students use calculators.
At population 2, both teachers and students in a majority of countries reported using calculators pretty often or almost every day in mathematics (Beaton et al., 1996a, pp. 162–168). However, in some countries, including some high-achieving countries (such as Japan and Korea) as well as in some low-achieving countries, mathematics teachers rarely had students use calculators.
Students at the high school level were given the opportunity to use calculators during the assessments of mathematics and science general knowledge in TIMSS. A smaller proportion of U.S. students did so than the international average—71 to 79 percent (U.S. Department of Education, 1998, p. 66).
The United States was one of a quarter of TIMSS countries where 50 to 75 percent of population 1 students had computers at home (Mullis et al., 1997, p. 114). Computers were not used often in U.S. mathematics or science classes by populations 1 or 2, but even this infrequent use surpassed that in most countries.
Among the U.S. physics and advanced mathematics students, 42 percent reported use of computers in some, most, or every lesson (Mullis et al., 1998, pp. 169, 225). This is comparable to the international average, although it is much more frequent than in some countries (e.g., Austria, France, and Germany).
Tests, Quizzes, and External Examinations
U.S. mathematics and science teachers rely heavily on tests and quizzes in the eighth grade, which was the only population at which TIMSS
collected extensive data on assessment practices. For example, 85 percent of U.S. eighth-grade mathematics students report that their teachers ''pretty often'' or "almost always" use tests and quizzes (Beaton et al., 1996a, pp. 172–175). The combined percentage is higher than that reported in any other TIMSS country.
Tests and quizzes in the United States also played a large role in teachers' reports to parents. Among the 38 countries that provided these data at the population 2 level, the United States was one of only five where 80 percent or more of eighth-grade students were taught by teachers who used assessments for this purpose (Beaton et al., 1996a, p. 174).
The effect of external assessments, such as standardized tests and college entrance examinations, on classroom practices was not investigated directly in TIMSS. Nevertheless, these assessments can be assumed to have a substantial impact. In many foreign countries, for example, most major external examinations, and especially those affecting access to different forms of postsecondary education, consist wholly or mostly of items that require extended student responses. Given the enormous impact of these examinations on students' lives, teachers want to be sure their students are prepared for them. It seems reasonable, therefore, that teachers would put a premium on providing instruction that increases students' proficiency in writing extended responses.
Homework
U.S. elementary and middle school teachers seem to assign amounts of homework comparable to teachers in other countries. U.S. fourth-grade teachers typically assign 30 minutes or less of mathematics homework three or more days per week (U.S. Department of Education, 1997b, p. 40). U.S. eighth graders typically spend between a half hour and an hour studying mathematics and science outside school each day (U.S. Department of Education, 1996, p. 63).
At grade 12 the general U.S. student population reports doing considerably less homework overall than students in their final year of secondary school in other countries—1.7 hours per day on all subjects versus 2.6 hours per day for the international average (U.S. Department of Education, 1998, p. 65). U.S. students taking a mathematics or science course reported doing about as much homework in these subjects as students in other countries in their last year of secondary school.
Among students taking advanced mathematics or physics, a much higher percentage of U.S. students report having homework three or more times per week than students in other countries—90 versus 66 percent for advanced mathematics students, and 50 versus 40 percent for physics students (U.S. Department of Education, 1998, p. 74).
Comparisons of homework are complicated by differing meanings for the term. In the United States, homework typically means any educational activity that could be conducted outside school (even if that activity takes place inside school). Homework can mean studying for class tests, doing independent projects, preparing for important external examinations such as college entrance exams, or optional work meant to provide further understanding. In some other countries, teachers, parents, and students tend to make more of a distinction
between homework and studying. In those countries, for example, homework might not include studying for external exams.
The United States is one of very few countries where teachers frequently assign homework that students actually begin during class time. U.S. teachers are almost alone in allocating considerable class time to work on homework—something that foreign researchers found very surprising during the development of TIMSS.
INFLUENCES ON INSTRUCTIONAL PRACTICES
Beneath the observable activities that occur in mathematics and science classes are the external forces and internal motivations that influence instruction in particular ways. Some of these influences are embedded in the curriculum, as described in the previous chapter. Others constitute part of the support systems available to schools, teachers, and students—the subject of the next chapter. The next major section of this chapter describes the information provided by TIMSS on four particularly important factors that affect teaching: decisions about what to teach, lesson objectives, teachers' beliefs about instruction, and the "scripts" that shape teaching. At the end of the chapter, a description of classrooms in two different countries demonstrates how these influences shape teaching.
Deciding What to Teach
When teachers were asked in questionnaires, "What is your main source in deciding which topics to teach?," the most frequent response from U.S. teachers, for both populations 1 and 2 and in both subjects, was the "National Curriculum Guide." This response is somewhat difficult to interpret, since the United States does not have a national curriculum guide. It seems likely, however, that teachers were referring to the national standards and benchmarks in mathematics and science, which would indicate a widespread awareness of those documents. (At the time the questionnaires
|
QUESTIONS RELATED TO INFLUENCES ON INSTRUCTIONAL PRACTICES
|
were distributed, the Benchmarks for Science Literacy produced by Project 2061 of the American Association for the Advancement of Science were available, though the National Science Education Standards from the National Research Council were still in draft form.)
In contrast, teachers in Japan, a country that does have a national curriculum guide, selected the teachers' edition of the text as most influential in deciding what to teach. Part of the explanation for this choice probably is that approved textbook series in Japan follow the national curriculum, and many teachers' manuals in Japan are developed by the teachers themselves and contain rich information for planning lessons. Teachers in Japan may believe that following the teachers' manual both satisfies the national guidelines and provides pedagogical help.
Another item on the teacher questionnaire asked what resources teachers rely on to decide how to present a topic. Perhaps the most interesting result was that many teachers in many countries selected the teachers' edition of the text and the student text. This finding is not surprising in the United States, given previous research showing teachers' reliance on the text. It is interesting that teachers in many other countries responded in similar ways.
Another question, which was asked of the principal of the school, was: "In your school, who has primary responsibility for choosing textbooks?" According to the principals, teachers in the United States have a greater voice in choosing textbooks than in the Asian comparison countries and almost as great a voice as in the European countries. In Japan this is generally not a school responsibility, and in Singapore the principal or department head usually chooses the text. In European countries, choosing a textbook is usually a school affair and often the teachers' responsibility. In some schools, however, the responsibility rests with the principal and in others with the department head.
Another question asked of principals was: "In your school, who has primary responsibility for determining course content?" Again, according to school principals, teachers in the United States have considerable influence in choosing content. The responses to this question, however, should be interpreted with caution. In some countries, determining the course content appears to be less of a school responsibility than choosing the textbook. Perhaps this is because the respondents believed that, once the text is chosen, the content is determined.
One interesting aspect of the responses from both teachers and principals was the rating of the district school board as quite influential in determining course content and curriculum in the United States. In most other countries a comparable entity did not exist.
To greatly simplify the issue of curricular choice and autonomy, it appears that the high achieving countries in TIMSS place the greatest control in the hands of educational experts, either national leaders (e.g., in Japan or Singapore) or classroom teachers (e.g., in the Czech Republic and the Netherlands). The United States introduces a third influence—a middle-level agency, the district school board, composed of individuals who do not work full time in education and generally are not professionally trained in the field.
Objectives of Lessons
Teachers' goals are reflected in the skills and knowledge they seek to impart in lessons. One valuable source of information about these goals are the videotapes made of eighth-grade mathematics classes. Although these videotapes focus on just a single subject at a single grade level, and although statements about patterns inevitably overgeneralize the data, the observed patterns do summarize the interpretations of the researchers who coded the videotapes.
In Germany the teacher is clearly in charge of determining the mathematical content, and the mathematics is quite advanced, at least procedurally. In many lessons the teacher leads the students through a development of procedures for solving general classes of problems. There is a concern for technique, where technique includes both the rationale that underlies the procedures and the precision with which the procedure is executed. A good general description of German mathematics teaching at this level would be "developing advanced procedures."
In Japan the teacher appears to take a less active role, allowing students to invent their own strategies for solving problems. The problems are quite demanding, both procedurally and conceptually. The teacher, however, carefully designs and orchestrates the lesson so that students are likely to use procedures recently developed in class. An appropriate description of Japanese teaching in mathematics would be "structured problem solving."
In the United States the content is less advanced and requires less mathematical reasoning than in the other two countries. Tasks presented to students are less complex, and their solution is less commonly controlled by the student. The teacher presents definitions of terms and demonstrates procedures for solving specific problems, and students are asked to memorize the definitions and practice the procedures. In the United States the general description of eighth-grade mathematics teaching could be "learning terms and practicing procedures."
In Germany and the United States, students engage in mathematics by following the teacher's lead. In Germany this often takes the form of responding to specific questions from the teacher as the whole class develops a relatively advanced procedure. In the United States this often takes the form of following the teacher's directions by practicing relatively simple procedures during seatwork.
Although it may be tempting to say that the reverse is true in Japan—that students control the mathematics—the data indicate that this is not the case. A more accurate picture is that, on average, there is a balance in Japan. The mathematical work is shared by the teacher and the students. Students sometimes, but not always, do creative mathematical work by inventing new methods and presenting them to the class. At other times, teachers control the mathematics—lecturing, demonstrating, asking students to memorize, and so on. The Japanese practice of lesson study, in which groups of teachers come together to study and improve the teaching of particular lessons, helps teachers understand what their students are capable of doing and provides them with knowledge they can use to teach more effectively (Stigler and Hiebert, 1999).
Beliefs about Mathematics Teaching
Based on analysis of the videotapes, teachers in different countries seem to have different beliefs about the nature of mathematics. Although highly inferential, the following observations are consistent with the majority of the videotaped lessons and the responses of videotaped teachers on the questionnaire.
In general, teachers in the United States say that students' success in mathematics is related to their ability to "understand" concepts. However, the typical U.S. lesson is consistent with the belief that school mathematics is a set of skills. In fact, 61 percent of teachers said that the main thing they wanted students to learn from the videotaped lesson was how to perform a particular operation or to acquire a particular skill. Apparently, there is a mismatch between what teachers say is most important for students and the goals they set for individual lessons.
According to the psychology of learning that seems to dominate many U.S. classrooms, skills are learned best by mastering material incrementally, piece by piece. The best learning conditions therefore involve practicing each piece, with high levels of success at each step. Confusion and frustration are taken by teachers as signs that the earlier material was not mastered. This means that the teacher's role is to divide the task into pieces that are manageable, providing all the information needed to complete the task, and providing plenty of practice. Providing information means, to many teachers, demonstrating how to complete a task like those assigned.
In contrast, the typical Japanese lesson seems to be based on a different psychology of learning—one in which students learn best through a variety of activities, including struggling with a problem and then participating in the discussion about how to solve it. Confusion and frustration are seen as a natural part of the process and are used to prepare the student for the information received during the discussion. The teacher's role is to choose a problem that engages students and will reveal the mathematics of interest and to help students understand the problem so they can begin their attempts to solve it. The teacher then manages the discussion such that different methods get heard, and the teacher summarizes the relationships of interest at the conclusion. In addition, the teacher needs to provide information and opportunities for practice when these are needed to construct the intended relationships.
Teaching Scripts
To gain a deeper appreciation for how countries differ in science and mathematics instruction, it is useful to think about instructional differences not just as arbitrary collections of teaching techniques but as unified "scripts" for teaching. These scripts draw on the elements and aspects of instruction described above, including goals for instruction, beliefs about the nature of science and mathematics, beliefs about how those subjects are learned and should be taught, and the characteristics of a normal or typical lesson.
Because TIMSS gathered more information about mathematics instruction than about science instruction, it provides a clearer picture of scripts for the teaching of mathematics than for the teaching of science. These scripts
represent, in some sense, abstractions of the recurring features illustrated in the sample lessons. In brief, the U.S. script for eighth-grade mathematics seems to have four basic components: (1) the teacher reviews previous material (often by checking homework), (2) the teacher demonstrates how to solve that day's problems, (3) students practice (usually individually on assigned seatwork), and (4) the teacher corrects practice problems and assigns homework.
The most instructive contrasts in national teaching scripts can be found in Japan. In Japanese mathematics classes, (1) the teacher reviews previous material (usually by giving a brief lecture or asking students questions), (2) the teacher presents problems for the day, (3) students work on problems (usually for a set number of minutes individually, then sometimes in small groups), (4) the whole class discusses solution methods (often the teacher selects students to share their work based on what he or she has seen while circulating around the class), and (5) the teacher highlights and summarizes major points.
Instructional reform, especially if it involves borrowing from other countries and cultures, needs to appreciate how these scripts are deeply embedded in the culture of their originating country and, in fact, constitute cultures of teaching in their own right. Learning from TIMSS means, in part, appreciating one's individual and collective scripts for teaching science and mathematics and understanding the scripts used by teachers around the world. Focusing on the differences among potential scripts during preservice and ongoing teacher education provides one way in which scripts could be changed or "rewritten." Such rewriting is not necessarily easy, but it becomes possible as insight is gained into how science and mathematics teaching varies among countries and among teachers.
INSTRUCTIONAL PRACTICES AND THE STANDARDS
The national mathematics and science standards call for forms of teaching quite different from what is found in many U.S. classrooms. The teaching described in the standards treats learning as an active process. For example, in the classes described in the science standards, students "describe objects and events, ask questions, construct explanations, test those explanations against current scientific knowledge, and communicate their ideas to others" (National Research Council, 1996, p. 2). In standards-based mathematics classes it is assumed "that students should be exposed to numerous and varied interrelated experiences that encourage them to value the mathematical enterprise, to develop mathematical habits of mind, and to understand and appreciate the role of mathematics in humans affairs; that they should be encouraged to explore, to guess, and even to make and correct errors so that they gain confidence in their ability to solve complex problems; that they should read, write, and discuss mathematics; and that they should conjecture, test, and build arguments about a conjecture's validity" (National Council of Teachers of Mathematics, 1989, p. 5).
This report does not lay out specific recommendations designed to move instructional
practice toward the goals laid out in the national standards documents. However, the descriptions of teaching presented in this chapter do highlight one aspect of reform: changing instructional practices in the United States will require reexamining deep-seated beliefs about teaching and learning. As the National Science Education Standards point out, "All teachers . . . have implicit and explicit beliefs about science, learning, and teaching. Teachers can be effective guides for students learning science only if they have the opportunity to examine their own beliefs" (p. 28). Similarly, the draft Principles and Standards for School Mathematics states that "teachers can provide classrooms that promote thinking, but it takes much more than worthwhile mathematical tasks and a commitment to discourse. It takes deep insight about mathematics, about teaching, and about learners, coupled with a sound and robust mathematics curriculum and thoughtful reflection and planning" (p. 33).
This chapter concludes with descriptions of two classrooms, one in the United States and one in Japan, that demonstrate many of the common features of mathematics teaching in those two countries. These descriptions point to both the potential and the challenges in moving toward standards-based instructional practices.
SAMPLE EIGHTH-GRADE MATHEMATICS LESSONS IN THE UNITED STATES AND JAPAN
The following material describes "typical" U.S. eighth-grade mathematics lessons in the United States and Japan videotaped as part of TIMSS. It is not easy to decide that a specific lesson is typical, given the complexity of the lessons and the variations in each country. Nevertheless, the lessons as a whole reveal certain general patterns, and the following lessons, which focus on geometry, illustrate many of these patterns. These lessons are described in more detail in the book The Teaching Gap by James Stigler and James Hiebert (New York: Free Press, 1999).
A U.S. LESSON
Reviewing Previous Material and Checking Homework
The video begins with Mr. Jones, the teacher, conducting a "warm-up" activity. He points to the top left-hand drawing on the chalkboard.
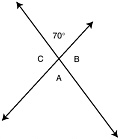
|
Mr. Jones: |
What is the angle vertical to the 70 degree angle? (Pause) John? |
|
John: |
I don't know. |
|
Mr. Jones: |
When I intersect lines I get vertical angles. Right? Look at your definition. I gave them to you. You can look them up. Here we have vertical angles and supplementary angles. Angle A is vertical to which angle? |
|
Students: |
Seventy (in chorus). |
|
Mr. Jones: |
Therefore, angle A must be? |
|
Students: |
Seventy degrees (in chorus). |
|
Mr. Jones: |
Seventy degrees. Go from there. Now you have supplementary angles, don't you? What angle is supplementary to angle B? |
After five minutes of this quick-paced review, Mr. Jones asks the students to "get out the worksheet I gave [you] earlier in the week and make sure we understand complementary, supplementary, and angle measurements." The class goes over the worksheet in a similar way: Mr. Jones asks students for answers and questions them when they are wrong. For example:
|
Mr. Jones: |
What is the complement of an angle of 7 degrees, Jose? |
|
Jose: |
Eighty-three. |
|
Mr. Jones: |
Eighty-three. The complement of an angle of 84, Marsha, would be? |
|
Marsha: |
Sixteen. |
|
Mr. Jones: |
Are you sure about your arithmetic on that one? |
|
Marsha: |
Six? |
|
Mr. Jones: |
Six. Six degrees. Bob, number four. |
The class checks 36 problems on the worksheet during six minutes of similar question/answer interaction. For the last few problems, Mr. Jones draws the picture of two congruent triangles on the chalkboard, positioned as mirror images of each other. The task is to match up the congruent parts of the triangle, and Mr. Jones checks that students completed each of these correctly, emphasizing the notation that is used to label line segments, angles, and congruence.
The patterns for eighth-grade mathematics instruction in the United States are evident—get the terms and definitions straight and learn the procedures for solving specific kinds of problems. The nature and level of the mathematics also are quite simple compared with those found in typical Japanese and German lessons. The opening activities are typical as well—many lessons in the United States begin with warm-up activities, checking homework, or both.
Demonstrating Procedures
Next Mr. Jones distributes a worksheet that contains problems that, he notes, are "just like the warm-up." At the top of the worksheet is a sample problem with the solution and a suggested method shown. Mr. Jones goes over this with the students.
|
Mr. Jones: |
(Referring to the angles in the drawing) One and three are vertical. Two and four are vertical. Two and three are supplementary. So if three is 120, what must two be equal to? |
|
Roxanne: |
Sixty? |
|
Mr. Jones: |
Sixty. If two is 60, what must four be equal to? |
|
Students: |
Sixty (in chorus). |
|
Mr. Jones: |
Okay. All the rest are done the same way. Any questions? I'm curious to see, when you get down to 37 and 38, you're going to have to think a little bit. Curious to see what you can come up with on those. |
Practicing the Procedures
The worksheet contains 40 problems and the students spend the next 11 minutes working on them. The problems, like the homework and the warm-up, emphasize terms and procedures. Mr. Jones circulates around the room, answering questions and giving hints. So far the lesson is unfolding like many lessons in the United States. Procedures are demonstrated, students practice the procedures on similar problems, and the teacher moves around the room to tutor individual students who need help.
Mr. Jones starts receiving questions about numbers 37 and 38 and initiates a class discussion about these problems.
|
Mr. Jones: |
Has anyone come up knowing that the product means multiplication? Has anyone come up with the answer to number 38? (The problem, listed under "Spiral Review" on the worksheet, says, "Write an equation that represents the sentence: The product of 12 and a number k is 192.") |
|
Students: |
(Mixed chorus of no and yes). |
|
Mr. Jones: |
What did you get, Cynthia? |
|
Cynthia: |
(Confused). |
|
Mr. Jones: |
Twelve and k. (Begins to write on the chalkboard 12k and then says slowly) . . . is 192. |
|
Cynthia: |
Equal sign. |
|
Mr. Jones: |
Excellent (fills in "= 192"). |
|
Joshua: |
That's it? |
|
Mr. Jones: |
That's it. Doesn't it say that the product of 12 and the number k is 192? |
It may strike the reader that this task has nothing to do with today's lesson, but some U.S. commercial materials include review of earlier topics in later problem sets. In fact, it is not uncommon to find this kind of topic switch during U.S. lessons.
Demonstrating More Procedures
Mr. Jones gives the students two more minutes to finish the worksheet and then asks them to get out the worksheet they completed last Friday after the quiz. He goes over two problems with them, both involving measuring angles using a protractor. The second problem begins by measuring the interior angles of a hexagon, shown below, and computing the total. Mr. Jones asks if everyone got close to 720 degrees. He then proceeds to the second part of the problem.
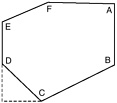
|
Mr. Jones: |
If I took this angle (D) and moved it down here and made it across this way (see dotted lined in drawing). Moved D down here, should that change the sum, the total? |
|
Jason: |
No. (Other students add ''no.'') |
|
Mr. Jones: |
It should not. Why? I still have how many angles? |
|
Obed: |
You still have six. |
|
Mr. Jones: |
I still have six angles. There is a formula, and we are going to go through this after spring break, but I will give you a hint right now. If I take the number of sides and I subtract two, and I multiply that number times 180 degrees, that will tell me how many degrees these add up to. How many sides in this Figure? (Pause) Six. Right? Number of sides subtract two, gives me what? |
|
Students: |
Four. |
|
Mr. Jones: |
Four. What is four times 180 degrees? |
|
Jacquille: |
Seven hundred twenty. |
|
Mr. Jones: |
Should be 720, right? How many degrees should there be in a five-sided figure? (Pause) Take the formula, the number of sides is five . . . subtract two and multiply by 180 degrees. |
|
Mike: |
Five hundred ninety? |
|
Mr. Jones: |
Five hundred forty degrees. All five-sided figures contain 540 degrees. |
What is typical about the preceding segment is that the teacher stated the formula for the sum of the angles in a polygon and asked students to practice using the formula.
Reviewing Procedures and Definitions
After using the formula to calculate the sum of the interior angles in a triangle, Mr. Jones makes several announcements about upcoming activities and future quizzes and tests. He then conducts a quick oral review with the class on the meaning of such terms as complementary, supplementary, obtuse angle, and acute angle. A few minutes remain and Mr. Jones tells the students to use the time "to finish up any of this and ask me questions." The lesson ends with a bell, 48 minutes after it began. It is a bit unusual that no homework is assigned, but the length of the lesson is typical, just short of the U.S. average.
A JAPANESE LESSON
Reviewing the Previous Lesson
The bell rings and a student monitor asks all students to stand and bow. After the customary exchange of bows between the students and the teacher, the students sit down and engage in a bit of joking with Mr. Yoshida. He begins the lesson by reminding the students about the previous lesson. He asks "Do you remember what we did last period?" A student answers "We did mathematics." After more probing, a student replies that they obtained the ''area of triangles which are [between] parallel lines."
"That's right," answers Mr. Yoshida, and he demonstrates the principle derived during the previous class. In a typical fashion the teacher underscores the importance of the principle—the equal areas of triangles with equivalent bases and heights. If the lesson proceeds as expected, this will set the stage for presenting the problem for the day, a problem in which the established principle will play an important role.
Presenting the Problem for the Day
"Prepare just your notebooks. We won't need your textbooks," says the teacher, drawing the following diagram on the board:
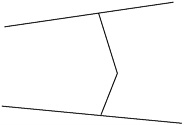
He explains that the land on one side of the bent line is Eda's land, while the land on the other side of the line is Azusa's land. While continuing to banter with the students, he says that the problem for the day is to draw a straight line replacing the bent line so that Eda and Azusa both end up with the same amount of land. After explaining some of the features of the problem, the teacher says, "Please try thinking about . . . methods of changing this shape without changing the area. Okay? Then everybody . . . let's try thinking about it. . . . Please think about it individually for three minutes. Okay, begin."
Working on the Problem Individually
For several minutes the students work individually on constructing a solution to the problem. Mr. Yoshida circulates around the room, answering questions and giving hints. A typical exchange:
|
Mr. Yoshida: |
You made that straight? Is it the same? Definitely? |
|
Student: |
It's approximately. |
|
Mr. Yoshida: |
If it's approximate, wouldn't they fight over it? . . . |
|
Student: |
I can't solve it. |
|
Mr. Yoshida: |
First of all, draw a figure. . . . Is there a method that uses the area of the triangles? |
Working on the Problem in Groups
After working with the individual students for a few minutes, the teacher announces, "Okay, since the three minutes are up, people who have come up with an idea can check it with Teacher Hayakawa [a student teacher in the classroom], and people who want to discuss it with their friends discuss it with your friends. And for now I have placed some hint cards up here so people who want to refer to this can do so."
To this point the lesson has unfolded in typical fashion. The problem for the day has been presented by the teacher but only after students reviewed material that would allow them to begin solving it; students have worked individually for a time as the teacher moved around the room, observing their progress, giving hints, and taking notes. Now students shift to small groups to share what they have found and to continue trying to solve the problem. This is a challenging problem, and some students struggle to work out a solution.
One typical aspect of this lesson is that the students, rather than the teacher, are doing much of the mathematical work. Often, students have just learned procedures they can use to begin solving the new problems, and the teacher selects the problems and designs the lesson so that these new procedures are likely to be used.
Students Demonstrate Solutions
After some time Mr. Yoshida announces, "It's time, huh? Fifteen minutes." He then asks for a student to come to the board and demonstrate a solution. As the student diagrams a possible solution on the board, other students call out questions and suggestions. When the first student cannot arrive at a solution, the teacher asks a second student to come up and try. When that student also has trouble, the
teacher intervenes: "Then I'll draw it for you so, okay?" After considerable help from other students and the teacher, the class together arrives at a solution. "Okay, then applause. Wonderful."
Teacher Summarizes Solution and Presents Another Problem
The teacher then announces that since it is hard to see the solution he will make it clearer. He summarizes the students' method of solving the problems and polls the other students about which method they used.
He then presents another problem. "Without changing the area [of a quadrilateral drawn on the board], please try making it into a triangle. Okay, then, . . . please think three minutes and try doing it your own way."
|
Student: |
Teacher, can we open our textbooks yet? |
|
Mr. Yoshida: |
The textbooks? First try thinking about it by yourselves, okay? You know that it was in the textbook, huh? [You're] sharp. |
The process of working on the problem individually, in small groups, and with the teacher begins again. After about another 20 minutes of work, the teacher summarizes the results for the whole class. He draws the figure on the board and works through a solution. Toward the end of the solution, the bell rings to end class 49 minutes after it has begun. Concluding quickly, the teacher gives as a homework assignment the problem of converting a pentagon into a triangle with the same area.
|
Mr. Yoshida: |
You worked very hard, amazingly hard. Okay? . . . Then let's say the farewell properly. |
At which point the students rise, bow to their teacher, and leave the room.




















