PANEL 1
What features of biology characterize microorganisms at or near nanometer scale?
Is there a theoretical size limit below which free-living organisms cannot be viable?
If we relax the requirement that cells have the biochemical complexity of modern cells, can we model primordial cells well enough to estimate their likely sizes?
Discussion
Summarized by Christian de Duve, Panel Moderator, and Mary Jane Osborn, Steering Group Co-chair
Constraints on Size of a "Minimal Free-living Cell"
Constraints on the lower limits of the size of a free-living prokaryote with conventional biochemistry might be imposed by a variety of factors, including the number of protein and RNA species required for minimal essential functions; the size of the genome required to encode these essential macromolecules; the number of ribosomes necessary for adequate expression of this genome; and physical constraints, such as DNA packing or the minimum radius of curvature required for stability of a lipid bilayer membrane.
The Panel 1 moderator, Dr. de Duve, opened the workshop by commenting on some theoretical calculations of the lower limits of cell size based on the assumptions and calculations shown in Box 1 (see pp. 8-9). The representative results (Tables 1 and 2)—which are based on the unlikely assumptions that only 100 nonribosomal protein species are present in a cell, that each is present in only 10 copies, and that there is only 1 ribosome, 1 tRNA set, and 1 mRNA for each protein species—must be considered unrealistically low. Even under these stringent assumptions, such a cell would have a diameter of 206 nm, including the membrane and wall. With a more realistic assumption of 300 essential non-ribosomal protein species, the diameter would be 262 nm. If each protein were present in 1,000 copies, the diameter would be 231 nm for 100 protein species and 303 nm for 300 species (see Table 2). Thus, the minimum diameter of a spherical cell compatible with a system of genome expression and a biochemistry of contemporary character would appear to lie somewhere between 200 and 300 nm, probably closer to the latter.
Minimal Number of Essential Genes, and Impact of This Number on Minimum Cell Size
The minimal number of genes required by a saprophytic microbe living in a nutrient-rich environment was estimated from minimal requirements for metabolism, genome expression, and other essential cellular functions (Panel 1 presenters Fraenkel, Riley); comparisons of sequenced genomes (Lawrence); and the genetic capacity of the smallest known genome, that of Mycoplasma genitalium (Moore, Lawrence). There was general agreement among panelists and discussants that approximately 250 to 450 genes compose the set of minimal essential genes. This is strikingly consistent with the known composition of the genome of M. genitalium, which contains approximately 470 genes, not all of which are essential. On the other hand M. genitalium is an obligate parasite, lacking functions required for independent, saprophytic life. Thus, the upper limit of 450 genes is likely to be conservative.
In the discussion period, questions were raised about possible ways to reduce the genome size even further. Dr. Riley asked whether a cell wall was essential. The role of some kind of relatively rigid cell wall in preventing osmotic lysis and in maintaining cell shape was cited. Respondents noted that mycoplasmas (and bacterial L-forms) lack a rigid cell wall, but that these cells are pleomorphic and are sensitive to osmotic lysis to a greater or lesser degree. However, a cell wall is clearly not essential for cell division, and "naked" cells should be able to exist in an osmotically protective environment. However, as Dr. Ferris commented, if an organism is not spherical (or pleomorphic), it must have some kind of wall or skeletal structure to confer and maintain a defined shape (e.g., rod, spiral).
Drs. Osborn and Fraenkel wondered whether a reduction in the number of ribosomal proteins might be possible, not only eliminating additional genes, but also yielding a significantly smaller, "minimal" ribosome. However, as discussed further below, this was deemed unlikely by panelists.
Dr. de Duve estimated the contribution of the genome to the dry weight of a cell the size of E. coli to be on the order of 4 to 6%. These modest values, however, are almost certain to be underestimated. They should be almost doubled if only one of the two DNA strands is taken to be coding and must be increased further to the extent that the genome contains non-coding DNA. Thus, values of 10 to 15% of dry weight would seem to be acceptable for the E. coli genome.
Dr. Moore's presentation emphasized that, as cell volume decreases, the fraction of volume occupied by the genome increases greatly, and eventually becomes a major determinant of minimal cell size. Calculated as a fraction of cell volume, the E. coli genome represents a negligible contribution (0.013 g/ ml, ca. 1%). However, that fraction rises to nearly 10% of cell volume (0.10 g/ml) in M. genitalium. Dr. Osborn asked at what density of DNA packing the transcription and replication machinery can no longer function. Dr. Moore responded that T4 phage DNA, which is functionally inert, occupies 65% of the available volume. A question was raised as to whether a single-stranded RNA genome might occupy a relatively smaller volume; however, the sense of the panelists was that the complex three-dimensional structures formed by intramolecular base-pairing would not be likely to offer significant advantage in this regard.
Constraints on Minimal Cell Size Imposed by Number and Size of Ribosomes
Dr. de Duve initially emphasized the importance of the ribosome as a major determinant of minimal cell size, noting that even a single ribosome, if surrounded by membrane and wall, would occupy a sphere of 50 to 60 nm in diameter. Dr. Riley noted that, although E. coli , growing in rich medium, has some 30,000 ribosomes per cell, the number of ribosomes is highly dependent on growth rate. Thus, if one allows the "minimal cell" to have a very long doubling time, the necessary number of ribosomes can
be greatly reduced. As to whether a significantly smaller ribosome, containing a reduced number of protein species, might be feasible, Dr. Moore suggested that the number of proteins might be reduced by a factor of two or three, but that the resulting structure would be appallingly sloppy and inefficient by modem standards. Deletion studies in E. coli some 15 years ago showed that elimination of almost any of the ribosomal proteins resulted in some abnormality in the particles. Most ribosomal proteins optimize or enable the assembly of rRNA into the proper three-dimensional fold.
A Single-Polymer Model of a Minimal Primordial "Cell"
Dr. Lawrence's intriguing model, which allowed for very tiny self-replicating "cells" based on sequential horizontal transfer of single genes "wandering" among a consortium, engendered considerable interest and discussion. Questions centered on issues of evolutionary stability, scaling with an increased number of genes, and "cell" size. Dr. Szostak asked whether the model could operate as an evolutionarily stable strategy. Dr. Lawrence agreed that in any one consortium, only one cell replicates and that the system will collapse if a certain gene is lost or mutated. Dr. Orgel was concerned about how the model scales with the number of genes. Since every gene must visit each compartment ("cell”) at least once, would the system work with, for example, 100 genes? Dr. Lawrence replied that replication would be very slow and would depend on how long-lived the reagents (biosynthetic intermediates) were and on the rate of gene transfer. Dr. Osborn noted that there could be great selective advantage of aggregating more than one gene into a single compartment by cell-cell fusion. Thus, even starting with the minimal mechanically stable vesicle size, the system would tend to move to larger, more efficient compartments. In summary, Dr. Lawrence emphasized that the point of the model was to illustrate that not all cells need have all the essential genetic information at the same time.
Summary and Consensus
Consensus was reached by Panel 1 participants on the following major points, assuming free-living cells with conventional biochemistry:
- A minimum of about 250 to 450 essential genes are required for viability.
- The minimal viable cell diameter is expected to lie in the range of 250 to 300 nm.
- The number of ribosomes required for adequate genome expression is a significant constraint on minimal cell size.
If, however, the requirement for conventional biochemistry and genetics is relaxed, especially with reference to primordial or exobiotic self-replicating systems, the possibility of much smaller "cells" must be considered, such as those envisioned in the single-polymer model.
|
Box 1 Assumptions
Calculations Ribosome 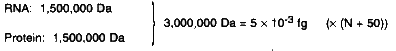 Genome rRNAs and tRNAs: 2,000,000 Da = 3.3 × 10-3 fg Ribosomal proteins: 12,800,000 Da = 21 × 10-3 fg Other proteins: N × 255,000 Da = N × 0.42 × 10-3 fg Total: (24.3 + N × 0.42) × 10-3 fg RNAs Other Than Ribosomal tRNAs: 500,000 Da = 0.8 × 10-3 fg (× (N + 50)) mRNAs: Ribosomal proteins: 13,260,000 Da = 21.9 × 10-3 fg Other proteins: N × 265,000 Da = N × 0.44 × 10-3 fg Total: (61.9 + N × 1.24) × 10-3 fg Other Proteins N × 10 × 30,000 Da = N × 300,000 Da = N × 0.05 × 10-3 fg (DNA + RNA + Protein) = (336.2 + N × 6.71) × 10-3 fg |
Table 1
Cell Size
|
N |
Dry Weight* × 10-3 fg |
Wet Weight × 10-3 fg |
Volume × 10-6 µm3 |
Diameter (nm) |
||
|
|
|
|
|
Naked |
+ Memb. |
+ Wall |
|
100 |
1,007 |
3,022 |
2,747 |
174 |
186 |
206 |
|
200 |
1,678 |
5,035 |
4,577 |
206 |
218 |
238 |
|
300 |
2,349 |
7,048 |
6,407 |
230 |
242 |
262 |
|
450 |
3,356 |
10,067 |
9,152 |
260 |
272 |
292 |
|
950 |
6,711 |
20,132 |
18,302 |
327 |
339 |
359 |
|
* (DNA + RNA + Protein) |
||||||
Table 2
Cell Composition
|
N |
% Dry Weight (DNA + RNA + Protein) |
|
|
Diameter from Table 1 (nm) |
|
|
|
Genome |
Ribosomes |
Other RNAs |
Other Proteins |
|
|
Assuming each protein species present in 10 copies |
|
|
|
||
|
100 |
6.6 |
74.5 |
18.4 |
0.5 |
206 |
|
200 |
6.5 |
74.5 |
18.4 |
0.6 |
238 |
|
300 |
6.4 |
74.5 |
18.5 |
0.6 |
262 |
|
450 |
6.3 |
74.5 |
18.5 |
0.7 |
292 |
|
950 |
6.3 |
74.5 |
18.5 |
0.7 |
359 |
|
Assuming each protein species present in 1,000 copies |
|
|
|||
|
100 |
4.4 |
49.9 |
12.4 |
33.3 |
231 |
|
200 |
4.1 |
46.8 |
11.6 |
37.5 |
272 |
|
300 |
3.9 |
45.7 |
11.3 |
39.1 |
303 |
|
450 |
3.8 |
44.8 |
11.1 |
40.3 |
340 |
|
950 |
3.7 |
43.8 |
10.9 |
41.6 |
422 |
|
As Dr. de Duve commented in opening the workshop, the results given in Tables 1 and 2 above must be regarded as unrealistically low. Referring to the values for cell composition listed In Table 2, he pointed out that In a cell with only 10 copies of each protein species, the ribosomes and the other RNA components of the protein-synthesizing machinery represent more than 90% of the dry weight. Even when 1,000 copies are present, a cell's protein-synthesizing machinery still accounts for more than 50% of its dry weight. Barring the unlikely event that the same ribosome actually serves in the synthesis of several distinct protein species, sizes significantly below the calculated values are possible only if a less bulky machinery makes proteins. Even a single ribosome surrounded by a membrane and a wall would occupy a sphere of 57 nm In diameter. |
|||||
Metabolism and Physiology of Conventional Bacteria
Dan G. Fraenkel
Department of Microbiology and Molecular Genetics Harvard Medical School
The term “nanobacteria" reaches from asteroid fossil to agent of kidney stones, with the common thread of small size. To place the discussion in context, the following items survey the metabolism and physiology of bacteria as we know them, and, other than for item 7, size is not addressed. Bacteria are small, complex objects made of macromolecules, including proteins, which carry out chemical transformations and use simpler components to autonomously form more of themselves in a geometric manner. They have an inside, a membrane, and usually a wall, and their replication depends on coded information. Each term—size, complexity, autonomy, replication, wall, genome, metabolism, etc.—needs qualification, but that is not the present task, nor is discussion, other than implied, of how it all came about or where it is leading.
1. Synthesis of the monomers. Primary carbon assimilation. In nature new cells are ultimately made from inorganic materials, e.g., CO2, NH3, H2S, etc. The ability to derive all carbon from CO2 ("autotrophy") is widespread and perhaps a property of early cells. In that context, metabolism is a network of ca. 20 reactions connecting a few key compounds—sugar-phosphates, acetate, pyruvate, oxalacetate, and a-ketoglutarate (Figure 1), and primary carbon assimilation pathways are ways of contributing these compounds: in methanogens, a linear mute comprising a handful of unique reactions, and more commonly, various cyclic mutes such as the Calvin pathway.
The monomers. A complete chart of intermediary metabolism (see ref. 4) is daunting, but can be thought of as built up from Figure 1, with the key intermediates serving as starting materials for dedicated mutes to the amino acids of the proteins, the constituents of polysaccharides, nucleic acids and lipids, and to cofactors. As seen in Figure 2, certain mutes are short: glutamate is a single step from alpha-ketoglutarate, the reductive amination also introducing -NH2; some are a little longer, serine by three steps and then introduction of—SH giving cysteine, and even the longest is only 10-15 reactions.
This adds up to ca. 120 reactions, including nucleotide interconversions. However, the various pathways share cofactors such as NAD+, TPP, coenzyme-A, etc., which need to be made, too, with likely >150 additional reactions for the purpose.
2. Energy. Energy is needed (i) for provision of reductants for biosynthesis (if H2 is not available) and of inorganic ions at appropriate reduction state (sulfate to H2S, N2 to NH3, etc.), (ii) for kinetic activation of many steps, and (iii) to drive reactions whose equilibria are wrong (e.g., protein synthesis). Many of

Figure 1.
The basic framework of intermediary metabolism.
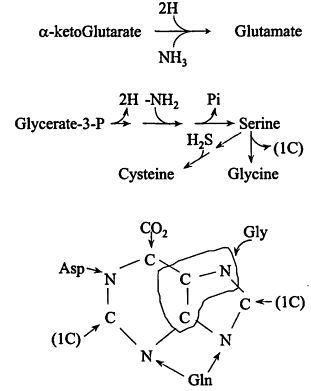
Figure 2
Examples of monomer biosynthesis. The third item shows the source of atoms in purines.
the reactions directly use ATP or pyrophosphate but ultimately depend on ion gradients across the cell membrane formed by primary energy conservation devices. In turn, ion gradients energize an ATP synthase of ca. 10 subunits (Figure 3).
3. Polymers. For RNA, a polymerase (<10 genes). For DNA, a polymerase, plus a packaging and replication machinery (20 genes?). For protein, the tRNA's, amino acid activating enzymes, ribosomes with their associated factors (100 genes?).
4. Membrane. Membrane lipids are derivatives of glycerol (1 reaction from the central network) together with fatty acid esters or long chain ethers from acetate plus various head groups (ca. 20 genes?) Apart from primary energy conservation, the membrane also serves to (i) keep metabolites from dilution by the outside, (ii) exclude toxic materials, and (iii) concentrate materials from outside. The conservation function is partly met by the membrane being easily permeable only to very small uncharged molecules (H2O, NH3, and CO 2). Other materials require transport mechanisms, some being energy linked (Figure 4).
5. Wall. Life of normal sized bacteria in dilute solutions requires a wall to protect cells from lysis by osmotic pressure differences. Peptidoglycan (Figure 5), a cross-linked polymer based on glucosamine chains and amino acid bridges, often contributes this function; the rigid structure also requires a remod-
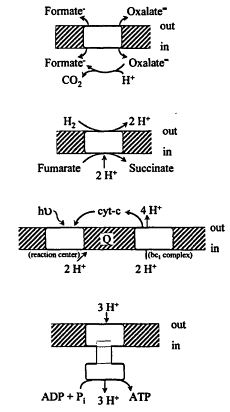
Figure 3.
Examples of generation of protonomotive force (PMF) by (top) antiport; (next) electron transport; (next) photosynthesis; and (bottom) ATP synthesis by the ATPase.
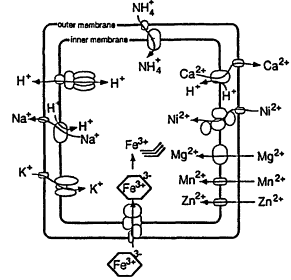
Figure 4.
Cation transport in E. coli. Reprinted, by permission, from Escherichia coli and Salmonella, edited by F.C. Neidhardt et al. (1996), p. 1092. Copyright © 1996 by ASM Press.

Figure 5.
Peptidoglycan (top) and the gram-negative envelope (bottom). Reprinted, by permission, from The Physiology and Biochemistry of Prokaryotes by D. White (1995), pp. 14 and 18. Copyright Ä 1995 by Oxford University Press.
eling mechanism to avoid vulnerability during cell division (20 genes?). Bacterial envelopes are commonly of the complex gram-negative type (Figure 5), and, as a whole, diverse in their components.
6. Heterotrophic metabolism. Catabolic pathways. The best-known bacteria are not autotrophs but heterotrophs, needing an organic carbon source that is transformed by a catabolic pathway into the central network (Figure 6). Then, carbon intermediates and reductants come from the organic substrate. Heterotrophic bacteria of even moderate versatility, such as E. coli, may use dozens of different carbon and nitrogen sources, with hundreds of (nonessential) genes for this purpose.
Preformed monomers. The availability of exogenous monomers allows dispensability of biosynthetic pathways, too. Thus we cannot make and must eat the "essential" amino acids (those with longer
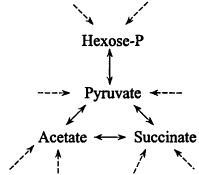
Figure 6.
Catabolism.
pathways) and vitamins, and certain bacteria that live in tissues require even more. This might save ca. 100-200 genes, but transport systems would be needed.
Energy from catabolism. Certain catabolic routes, such as the widespread Embden-Meyerh of glycolytic pathway (Figure 7), which is used by many bacteria with access to carbohydrates, also contribute ATP by cytoplasmic reactions ("substrate level phosphorylation"); when growth depends solely on the latter reactions, the ATPase energizes the membrane rather than vice versa. Catabolism without respiration can involve massive wasting of organic metabolites as fermentation products. How-
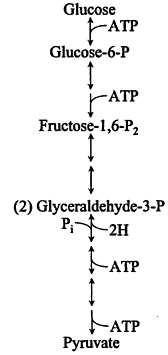
Figure 7.
Embden-Meyerh of glycolytic pathway.
ever, in most heterotrophs, as in autotrophs, ATP derives from anaerobic or aerobic respiration, the latter pathways being similar to those of our mitochondria.
7. How much is needed? The essential set of genes for autonomous growth of modem bacteria in a minimal medium with a single organic carbon source or CO2 is, from the above crude estimates, 400 or 500, and, as mentioned, fewer in an enriched medium. E. coli contains 4,300 genes (4 × 10-15 g DNA) and when growing in minimal medium with glucose has a volume of ca. 1 (µM)3 and a dry mass of 250 × 10-15g. An organism of 1/4 of those linear dimensions and hence ca. 2% of the mass (in line with sizes of "nanobacteria" cited by the organizers) would need to have less DNA than E. coli, and, with the minimal 400 gene complement, DNA would compose ca. 1/4 of its mass—not unreasonable. But an organism 1/10 of E. coli on the side and hence 1/1000 of the mass would already exhaust it with 200 average size genes. The size limitation is far stricter, because at least membrane is obligatory and, as pointed out by de Duve, ribosomes alone are a significant constraint.
Unlike genes, gene products need not be in equal amount: The synthesis of 1 E. coli cell from glucose may use three times its weight in glucose, or 4.2 × 10-9 mmoles; its 5% of dry weight as glycine in protein amounts to 1.7 × 10-10 mmoles and a cofactor at 10 µM in the soluble pool is ca. 3.5 × 10-15 µmoles. The net fluxes in the three enzymic pathways, 1 catabolic and 2 biosynthetic, therefore differ over a 106 range.
Furthermore, the amount of enzymes (their Vmax's) to provide adequate metabolite concentrations depends on growth rate, so if that value were 1/day instead of 1/h the cell might contain proportionately less enzyme. Both considerations—relative use of different pathways, and growth rate—suggest that small and slowly growing cells might have much less than the nominal 0.5 fraction of mass as catalytic protein.
This saving of protein has limitations. Although protein synthesis is related to need (fewer ribosomes in slower growth), the factor of gene expression is not controlled over a range of 106, many enzymes are in large excess, and enzymes vary greatly in their catalytic constants, with values usually higher for catabolic than anabolic reactions. Another constraint is seen from calculation of average number of molecules per cell: a nominal "nanobacterium" with 3 × 10-15g protein, 4 × 10-15ml cytoplasmic volume and 400 different polypeptides of size 40,000 could contain an average of 100 molecules and 30 µM of each one. Although the actual range of values could be large, values of less than one enzyme molecule per cell are possible only for steps whose products are in excess.
It should also be recalled that metabolic fluxes are not always tightly coupled to growth (rapid fermentations can proceed in non-growing cells), so that even "non-viable" bacteria might have significant complements of normally active pathways.
These several points suggest that even apart from physical constraints related to mechanisms of replication, the minimal size of conventional bacteria might be a few percent that of E. coli on glucose. For even smaller size, one could speculate about less-evolved cells with fewer constituents and simpler ribosomes, or about more-evolved ones, with multifunctional polypeptides of higher catalytic constants than presently common, hence little genome and protein but still of conventional design.
References
1. D. White, The Physiology and Biochemistry of Prokaryotes, Oxford University Press, New York, 1995, pp. 14, 18. (This is a useful introduction to bacterial metabolism and physiology from which figures were taken or adapted.)
2. F. Harold, The Vital Force: A Study of Bioenergetics, W.H. Freeman and Co., New York, 1986.
3. F.C. Neidhardt, et al., Escherichia coli and Salmonella, ASM Press, Washington, 1996, p. 1092.
4. Boehringer-Mannheim, Biochemical Pathways, G. Michal, ed., 3rd Ed., 1992. (A chart that shows it all at a glance.)
A Biophysical Chemist's Thoughts on Cell Size
Peter B. Moore
Departments of Chemistry and Molecular Biophysics and Biochemistry Yale University
Abstract
Back-of-the-envelope calculations having to do with genetic complexity and intracellular DNA concentration suggest that actively growing cells significantly smaller than those of Mycoplasma genitalium (diameter ˜ 0.3 µm) are unlikely to exist on Earth today. In addition, the limitations on genome size that accompany small cell size guarantee that cells of that size will have to depend on larger, more complex organisms for supplies of most of the small organic molecules required for their growth. Hence, a biosphere consisting entirely of ultra-small organisms is highly implausible.
Introduction
Cells differ enormously in size. Some of the neurons in the human brain have processes meters in length, and microbiologists routinely study free-living, single-celled organisms that have linear dimensions measured in micrometers. Viruses can be almost two orders of magnitude smaller than that In light of the recent report of McKay et al. (1996) suggesting that objects found in a meteorite of martian origin, which are the size of a large virus (diameter ˜0.1 µm), might derive from ancient organisms, it is interesting to ask how small an object can be and still be a cell. For these purposes, I take a cell to be a membrane-enclosed entity that (1) replicates itself autonomously, and (2) is actively growing.
My perspective on this problem is that of a biophysical chemist, not that of a systematic microbiologist Thus, while I am in no position to testify about the sizes and "lifestyles" of very small terrestrial organisms, I can comment on some of the physical issues that small cells confront
Critical Assessment of the Issues
As it happens, I have spent much of my career working with Escherichia coli, a bacterium whose linear dimensions are of the order of micrometers, and it is useful to start by reviewing its capabilities and chemical composition. E. coli lives primarily in the intestinal tracts of mammals, where the temperature is a comfortable 37° C, and both water and its hosts provide nutrients. Even though this environment is nutritionally rich, E. coli has remarkable metabolic capabilities. It thrives in media consisting of mineral salts and glucose, a diet far too sparse to support human life, for example. E. coli will grow on similar media in which glucose is replaced by many other small organic molecules, including acetate, which is about as simple a substrate as it can manage. Only photosynthetic organisms, which will grow on salts, CO2, and light, can make do with significantly less.
How big is such an E. coli cell, and what does it contain? Answers to both questions may be found in Watson's classic text, Molecular Biology of the Gene (Watson, 1965). Table 1 is a version of a table in Watson's book that I revised using information gleaned from the sequence of the E. coli genome (Blattner et al., 1997). The cell whose contents are outlined in Table 1 is a cylinder 2 µm long and 1 µm in diameter. Its volume is thus about 1.6 µm3 and its mass is about 1.7 × 10-12g. The composition given
Table 1 The Composition of a Typical E. coli Cell
|
Substance |
% of mass |
MW |
# of copies |
# of kinds |
|
Water |
70 |
18 |
4 × 1010 |
1 |
|
Inorganic ions and small molecules of all other kinds |
7 |
˜ 145 |
5 × 108 |
750 |
|
DNA |
1 |
3 × 109 |
4 |
1 |
|
RNA |
6 |
|
|
|
|
16S rRNA |
|
0.5 × 106 |
30,000 |
7 |
|
23S rRNA |
|
1.0 × 106 |
30,000 |
7 |
|
5S rRNA |
|
4.0 × 104 |
30,000 |
7 |
|
tRNA |
|
2.5 × 104 |
300,000 |
86 |
|
mRNA |
|
˜1.0 × 106 |
˜1,000 |
˜1,000 |
|
Proteins |
15 |
˜30,000 |
5 × 106 |
4,288 |
|
SOURCE: Adapted from Watson (1965); data from Blattner et el. (1997). |
||||
is that expected for rapidly growing cells, and that explains why it contains several copies of its genome, not just one.
It is important to realize that the number of ribosomes in bacteria like E. coli is tightly regulated so that if all the ribosomes present in a cell constantly make protein at the maximum possible rate (10-20 amino acids incorporated per ribosome per second), the protein mass in the cell will have just doubled by the time cell division begins. The number of copies of each of the enzymes involved in intermediary metabolism is similarly regulated to balance supply and demand. Hence the macromolecular composition of these cells depends on their overall growth rate, which in turn is coupled to the mix of small organic molecules available in the environment. Finally, it should be noted that the water content of these cells, 70% by weight, is typical of actively metabolizing cytoplasm.
A cell a tenth the volume of E. coli is easy to envision. It might have 2 copies of a genome that is about the same size, which would imply an interior DNA concentration.5 times that of E. coli. This means that there would not quite be room in such a cell for the 3,000 ribosomes and 5 × 105 protein molecules it would require, and still maintain a water content of 70%. However, if the organism's metabolism were adjusted so that its generation time was a bit longer than that of E. coli, all would be well. There is a limit to how far this kind of balancing of generation times and macromolecular compositions will take you. The reason is that while the number of copies of each kind of macro-molecule a cell requires scales approximately with its volume, the amount of genome it takes to encode them does not. The consequences become obvious when we consider cells whose volumes are 1% that of E. coli. A cell that size has a mass of only ˜1010 daltons. If it must do all the things E. coli can, it needs a genome the same size, i.e., one that weighs 3 × 109 daltons. If it also has to be 70% by water weight, there is no room for anything else.
It is instructive to examine Table 2, which compares the DNA concentrations in three DNA-containing objects, the interior volumes of which stand approximately in the ratio of 10,000:100:1: E. coli, Mycoplasma genitalium , a small mammalian parasite, and the head structure of bacteriophage T4, which is a virus. Even though the genome of M. genitalium is significantly smaller than that of E. coli, as one anticipates it must be, it isn't two orders of magnitude smaller, and consequently the DNA concentration in M. genitalium is much higher than in E. coli. The DNA concentration in the T4 head, which is higher still, approaches that of pure, hydrated DNA.
It is important to realize that the DNA in T4 heads is metabolically inert, and is intended to be so.
Table 2 DNA Concentration as a Function of Organism Size
Viruses don't do anything; they are simply genome transport modules. Not only that, it is impossible for the DNA in T4 heads to be replicated or expressed in situ because there isn't room for the macromolecules that catalyze these processes. T4 DNA becomes metabolically active only when injected into bacterial cells where the total DNA concentration is much lower. I take it as axiomatic that DNA packed as densely as it is in bacteriophages will always be inert metabolically. If this is so, unless cellular genomes exist that are even smaller than that of M. genitalium, cells significantly smaller than M. genitalium cells are impossible. On the basis of what has been learned from the sequence of the genome of M. genitalium, this looks unlikely.
As Table 3 indicates, the genome of M. genitalium encodes only a tenth as many proteins as that of E. coli, and it is the absence of these “missing" proteins from its cytoplasm that allows M. genitalium cells to devote as large a fraction of their interior volumes to DNA as they do. However, this reduction in protein inventory has a price. Compared to E. coli, M. genitalium is a physiological cripple. For example, it lacks almost all the proteins required of intermediary metabolism, and hence must find virtually all the small organic molecules it needs in its environment. It is hard to imagine an organism with such limited capabilities surviving, except as a parasite.
Table 3
The Protein Inventories of E. coli and M. genitalium
|
|
Number of Genes |
|
|
Functional Class |
E. coli |
M. genitalium |
|
Regulation |
178 |
7 |
|
Structure |
237 |
17 |
|
Phages and other inserted elements |
87 |
0 |
|
Transport and binding |
427 |
34 |
|
Energy metabolism |
243 |
31 |
|
DNA replication, etc. |
115 |
32 |
|
Transcription |
55 |
12 |
|
Translation |
191 |
101 |
|
Intermediary metabolism |
658 |
37 |
|
Other cell processes |
155 |
21 |
|
Other enzymes and identifiable genes |
277 |
27 |
|
Unknown |
1,632 |
152 |
|
Total |
4,288 |
471 |
|
SOURCE: These data are taken from Blattner et el. (1997) and Fraser et el. (1995). |
||
Marine ultramicrobacteria, which are also unusually small, have "design specifications" consistent with the arguments made above. Sphinogomonas sp., which appears to be typical, has a cell volume 4 times that of M. genitalium, and a genome a quarter the size of E. coli's (Schut et al., 1997). A genome that size is big enough to encode enough enzymes to explain the intermediary metabolism of these organisms, and intracellular DNA concentration is certainly not a problem. The free-living nanobacteria that Kajander and his colleagues have isolated from mammalian cell cultures are harder to understand at this point (Kajander et al., 1997). The volumes of some of the objects seen in such cultures are a tenth that of M. genitalium (!), and it is hard to see how anything could grow autonomously with a genome much smaller than that of M. genitalium. The biochemistry and genomics of these organisms are bound to be very interesting, but one anticipates that when the dust clears, it will be found that they too "fit inside the envelope."
In this connection, it is worthwhile asking whether one can imagine organisms with genomes even smaller than that of M. genitalium? Perhaps. Experiments done in the 1970s suggest that modem proteins might be larger than their functions absolutely require. For the sake of argument, assume that all the genes in our putative nanocell genome are half the size of those found in M. genitalium or E. coli, which, it should be pointed out, are about the same size (˜ 30 kD, on average). Let us also postulate that this genome is single-stranded DNA, not double-stranded, and that it replicates by a process in which only a partial copy of its Watson-Crick complement ever exists. For good measure, let us also arbitrarily dispense with 100 of the genes found in the M. genitalium genome. The molecular weight of the DNA genome that emerges is about 0.7 × 107, and if we allow the intracellular concentration of DNA to rise to 0.2g/ml, which is twice that found in M. genitalium , the estimate for interior cell volume that emerges is ˜10-3 µm3, which is a factor of 10 less than that of M. genitalium. Omitting an allowance for the surrounding bilayer, the radius of the interior of such a nanocell would be 0.06 mm, which is close to the size of the cells Kajander and his colleagues have identified and of the objects that McKay et al. (1996) have suggested might be traces of martian cells.
Several comments are in order. First, in order to arrive at a "design" for this 0.06 mm cell, we have invoked a biochemistry unlike any known in modem cellular life. A cell that is even smaller would require even more radical departures, which I lack the imagination to envision. Second, whatever else this nanocell can do, it is not going to grow on a medium consisting of mineral salts and glucose. Something else, which is far larger and more complicated, will have to do the biochemical "heavy lifting" that makes the survival of such organisms possible. To put it another way, a biosphere consisting entirely of organisms of the size and metabolic complexity of E. coli is easy to envision; it may once have existed on this planet (Schopf, 1983). A biosphere consisting of organisms the size of M. genitalium or smaller looks impossible. Third, these considerations suggest that it is appropriate to scrutinize all reports of cells significantly smaller than M. genitalium with great care. Are these entities really cells, or are they spores, or merely components of cells? Can they grow without a major reorganization of their morphologies and internal composition? Fourth and finally, wise biologists never say “never." Maybe cells significantly smaller than those we have been considering really do exist. If they do, the one thing we can be sure is that their biochemistry will be a lot different from anything we know today.
References
1. Blattner, F.R., G. Plunkett, C.A. Bloch, N.T. Perna, V. Burland, M. Riley, J. Collado-Vides, J.D. Glasner, C.K. Rode, G.F. Mayhew, J. Gregor, N.W. Davis, H.A. Kirkpatrick, M.A. Goeden, D.J. Rose, B. Mau, and Y. Shao. 1997. The complete genome sequence of Escherichia coli K-12. Science 277: 1453-1474.
2. Fraser, C.M., J.D. Gocayne, O. White, M.D. Adams, R.A. Clayton, R.D. Fleischmann, C.J. Bult, A.R. Kerlavage, G. Sutton, J.M. Kelley, J.L. Fritchman, J.F. Weidman, K.V. Small, M. Sandusky, J. Fuhrmann, D. Nguyen, T.R. Utterback, D.M. Saudek, C.A. Phillips, J.M. Merrick, J.-F. Tomb, B.A. Dougherty, K.F. Bott, P.-C. Hu, T.S. Lucier, S.N. Peterson, H.O. Smith, C.A.I. Hutchinson, and J.C. Venter. 1995. The minimal gene complement of Mycoplasma genitalium. Science 270: 397-403.
3. Kajander, E.O., I. Kuronen, K. Akerman*, A. Pelttari, and N. Çiftçioglu. 1997. Nanobacteria from blood, the smallest culturable autonomously replicating agent on Earth. Proceedings of SPIE 3111: 420-428.
4. McKay, D.S., E.K. Gibson, Jr., K.L. Thomas-Keprta, H. Vail, C.S. Romanek, S.J. Clemett, X.D.F. Chillier, C.R. Maechling, and R.N. Zare. 1996. Search for past life on Mars: possible relic biogenic activity in Martian meteorite ALH84001. Science 273: 924-930.
5. Morowitz, H.J. 1992. Beginnings of Cellular Life, New Haven: Yale University Press.
6. Schopf, J.W., ed. 1983. The Earth's Earliest Biosphere, Princeton, N.J.:Princeton University Press.
7. Schut, F., J.C. Gottschal, and R.A. Prins. 1997. Isolation and characterization of the marine ultramicrobacterium Sphingomonas sp. strain RB2256. FEMS Microbiol. Rev. 20: 363-369.
8. Stryer, L. 1981. Biochemistry, 2nd Ed., San Francisco: W.H. Freeman & Co.
9. Watson, J.D. 1965. Molecular Biology of the Gene, 1st Ed., New York: W.A. Benjamin.
Correlates of Smallest Sizes for Microorganisms
Monica Riley
Woods Hole Marine Biological Laboratory
Abstract
The size of Earth-bound bacteria is dictated by a number of factors, the most important of which is the growth rate. If we postulate that ancient cells had very slow growth rates and therefore required few ribosomes, and if they lived in nutritionally rich surroundings, thus requiring few biosynthetic enzymes, they could conceivably be as small as a 200-nanometer-diameter sphere. More drastic scenarios, such as supposing a one-polymer information system or a sharing system for part-time genes, could reduce the size requirement further.
Introduction
We are asking ourselves what, from the point of view of traditional microbiology and biochemistry, are the factors that dictate a lower limit to the size of microorganisms of the kind that are present in our life system? The question has different answers depending on the composition of the environment of the microorganism, but it is possible to consider in turn major factors that influence the estimate.
The Size and Contents of an Average Gram-Negative Organism
Escherichia coli is a typical gram-negative rod bacterium. Its dimensions are those of a cylinder 1.0-2.0 micrometers long, with radius about 0.5 micrometers. Another gram-negative rod, less metabolically independent than E. coli, is Hemophilus influenzae, which has half the length and diameter. Bacteria such as mycoplasma, which have a more modest metabolic capability, are even smaller.
The Effect of Growth Conditions on Cell Constituents
If the environment of the culture of microorganisms is rich, the growth rate will be fast relative to the growth rate in minimal medium. The distribution of contents of E. coli changes with growth rate (1-4) as shown in the Table 1.
The cytoplasm, which contains the soluble proteins and the protein synthesis apparatus, is the dominant space-filling aspect of the microbial cell. Ribosomes dominate the cytoplasm and are major space-occupying cellular elements. Compared to the cytoplasmic proteins and the ribosomes, cellular
Table 1 Cell Contents at Fast and Slow Growth Rates (Percent by Weight)
|
Macromolecule |
Fast Growth (<30 rain doubling time) |
Slow Growth (>150 rain doubling time) |
|
DNA |
3% |
4% |
|
RNA |
35 |
14 |
|
Protein |
60 |
80 |
|
Cell size |
Larger |
Smaller |
ingredients that do not occupy much volume are the DNA, the cell wall, and the membranes with their component transport systems. Nucleoids are composed of compacted DNA neutralized with either positive ions or basic proteins. The DNA is so compacted that within the nucleoid the concentration of DNA reaches 10-20% and constitutes only about 10% of cell volume.
Distribution of Genetic Determinants of E. coli K-12
The genetic determinants of E. coli K-12 distribute as follows:
|
Enzymes |
1,300 |
|
Transporters |
500 |
|
Regulators |
500 |
|
RNAs |
115 |
|
Structure |
200 |
|
Factors |
25 |
|
Unknown |
1,800 |
The numbers and kinds of genes expressed at any one time are determined by the composition of the environment. Enzymes are repressed unless needed, induced when needed. Numbers of ribosomes are determined by environmental conditions (1,3).
Essentials of Conceptually Pared Down Average Cell Like E. Coli
Not So Much DNA
A minimal free-living cell need not have as much DNA as E. coli does because E. coil is able to live in many different circumstances and carries genes for many more than the minimum number of enzymes required at any one time. If one is thinking about organisms living in a biochemically rich soup or organisms like parasitic bacteria that live inside cells and draw on the processes and contents of inhabited cells, the organism could be smaller than if it were a free-living cell that makes all its own substance from scratch. Presently known smallest bacterial genomes are around 600 Kb of DNA.
Ribosomes
A major element determining the size of bacteria is their ribosomes. Under different growing conditions, E. coli has 10,000-60,000 ribosomes. Each ribosome contains two RNA molecules and a very large number, 52, of different proteins: 21 in the 30S subunit, 31 in the 50S subunit. The protein complex called L7/12 is represented 4 times in each ribosome, but probably the rest of the ribosomal proteins are present only once per ribosome (5). Other proteins are involved in directing the correct assembly of the components of the ribosomes.
Thus, ribosomes are a prominent feature determining minimum cell size in any life system using ribosomes as an obligatory element. However, we can imagine circumstances not requiring as many ribosomes as E. coil has. The number of ribosomes is steeply dependent on growth rate; namely, the slower the growth rate, the fewer ribosomes needed (1,2,4). If we postulate that growth rates of very early, very small cells could have been very slow, ribosomal content could have been correspondingly lower than today's organisms. If we postulate extremely slow growth, can we postulate as few as two
ribosomes per cell? This question reaches outside our known world and cannot be answered knowledgeably today.
Proteins
Although some proteins of E. coli are the ribosomal proteins, most are soluble enzymes. Other proteins are integral membrane proteins allowing for cellular localization and carrying out transport functions. Membrane and wall components and also cellular appendages such as flagellae and pili account for a very small part of the weight of a bacterium, so we will leave them aside. Soluble cytoplasmic proteins are chiefly enzymes of metabolism and regulators of all cell processes. The numbers of necessary metabolic enzymes and their regulators required for life depends entirely on the genetic capacities and the metabolic capabilities of the cell.
Metabolism
Quasi-redundancy. E. coli is profligate in its metabolic enzymes. It squanders its information content on multiple enzymes. There are over eighty examples of small-molecule metabolic reactions that are carded out by more than one separately encoded isozyme (6). In addition, there are multiple large-molecule enzymes such as polymerases, helicases, repair enzymes. Whereas E. coil is a versatile organism able to draw on isozymes of slightly different characteristics to guarantee life under different circumstances, our theoretical very small, very early organism may not have been versatile. A minimal organism might have only one enzyme per reaction, and the number of reactions catalyzed may have been small.
"Totipotency." E. coli possesses flexibility and metabolic alternatives as a consequence of containing the enzymes for many metabolic capabilities, only some of which are working under any environmental condition or at any point in time. A minimal organism could make do with minimal metabolic capacity.
Degradation and Energy. All major degradative pathways are in E. coli: glycolysis, pentose shunt, Entner-Douderoff pathway, TCA cycle, and glyoxalate shunt. E. coli has the ability to live anaerobically as well as aerobically, with many other electron acceptors besides oxygen (among them nitrate, sulfate). E. coli can derive energy and make ATP from many oxidizable substances by using either respiration with electron carriers, both aerobic and anaerobic, or fermentation involving only reduced and oxidized organic compounds. E. coli contains the complex formate dehydrogenase system and hydrogenase, enabling it to derive energy from such simple molecules as hydrogen or formate, the simplest organic acid. E. coli can use as carbon and energy sources a wide variety of substrates (although it does not fix CO2). Thus, the degradative and energy metabolism of E. coli is much more complex than it would be for a minimal organism.
Simple ways a minimal organism might use to gain energy are by fermentation, using one organic molecule as electron donor and another molecule as acceptor (as a chemoorganotroph) or by oxidizing inorganic substances such as H2S (as a chemoautotroph).
Anabolism. The synthetic capacities of E. coli are also extensive. It can make all of its small-molecule building blocks such as amino acids, purines, pyrimidines, and cofactors, and for some pathways there are alternative mutes using other enzymes. If the necessary building blocks for life were in the
environment of a minimal cell, the synthetic metabolic capacity would not be needed. However, one would need transport mechanisms to bring the building blocks in and not leak out essential metabolites.
If, on the other hand, primitive environments did not supply preformed metabolites, then the machinery for CO2 fixation, perhaps also for N2 fixation and full anabolic capability would be needed. The complexity and need for more proteins could then rise back up to E. coli levels.
Counting Up
E. coli contains over 1,000 known soluble enzymes, and a high proportion of the 1,800 unknown ORFs [open reading frames (genes likely to code for proteins)] are expected to be enzymes. In a minimal cell with minimal small-molecule metabolism and minimal macromolecule mechanisms, maybe the enzyme count could be reduced to as little as 300.
Reducing the number of proteins also reduces the number of ribosomes needed to synthesize the proteins. Primitive cells with slow growth characteristics could have had far fewer ribosomal RNA molecules and could have used many fewer individual proteins to build primitive ribosomes. Because with slow growth conditions protein (the sum of enzymes and ribosomal protein) is the major component of a cell, reduction in number of unique proteins seems to be a major factor in determining the complexity and size of the cell.
Macromolecule processes such as protein synthesis and DNA replication could have been even simpler in a very small and very ancient cell. What are the minimal needs for these processes in an "RNA world"(7)? Can the machinery be reduced to a much simpler version, eliminating altogether DNA and its replication? Do RNA and protein constitute a two-polymer system? Can we imagine a one-polymer system in which RNA is possessed of adequate catalytic powers to be able to substitute for proteins, or where proteins can replicate themselves without a polynucleotide template?
Envelope
Another factor to think about is the increased surface volume of small cells as compared to large. Although one expects the structures to be much simpler than the envelope of gram-negative bacteria, still a minimal cell would have a higher proportion of its substance in its membrane and wall fractions.
Summary
Can we think, then, about a very early cell with an enclosing membrane that has fewer transporters than at present, only partially controls transport in and out, and contains only a few ribosomes? It would contain only about 300 proteins including enzymes, a small number of generalized regulators, and perhaps no DNA, only RNA performing tasks of coding, processing, and replication. Such a cell would need to have a volume of at least 200 nanometers#03>3. To imagine smaller cells than this requires a higher level of speculation, such as having only part-time genes that come and go, or having a one-polymer system where RNA is possessed of adequate catalytic powers to be able to substitute for proteins (7), or where proteins can replicate themselves without a polynucleotide template.
References
1. Ingraham, J.L., O. Maaloe, and F.C. Neidhardt. 1983. Growth of the Bacterial Cell Sunderland, Mass.: Sinauer Associates, Inc.
2. Bremer, H., and P. Dennis. 1996. Modulation of chemical composition and other parameters of the cell by growth rate. Pp. 1553-1569 in Escherichia coli and Salmonella, 2nd Ed., F. Neidhardt, R. Curtiss III, E.C.C. Lin, J. Ingraham, K.B. Low, B. Magasanik, W. Reznikoff, M. Riley, M. Schaechter, and H.E. Umbarger (eds.), Washington, D.C.: ASM Press.
3. Maaloe, O., and N.O. Kjeldgaard. 1966. Control of Macromolecular Synthesis . New York: W.A. Benjamin Co.
4. Ingraham, J., and A.G. Marr. 1996. Effect of temperature, pressure, pH and osmotic stress on growth. Pp. 1570-1578 in Escherichia coli and Salmonella, 2nd Ed., F. Neidhardt, R. Curtiss III, E.C.C. Lin, J. Ingraham, K.B. Low, B. Magasanik, W. Reznikoff, M. Riley, M. Schaechter, and H.E. Umbarger (eds.), Washington, D.C.:ASM Press.
5. Noller, H.F., and M. Nomura. 1996. Ribosomes. Pp. 167-186 in Escherichia coli and Salmonella, 2nd Ed., F. Neidhardt, R. Curtiss III, E.C.C. Lin, J. Ingraham, K.B. Low, B. Magasanik, W. Reznikoff, M. Riley, M. Schaechter, and H.E. Umbarger (eds.), Washington, D.C.: ASM Press.
6. M. Riley, and B. Labedan. 1996. E. coli gene products: Physiological functions and common ancestries . Pp. 2118-2202 in Escherichia coli and Salmonella, 2nd Ed., F. Neidhardt, R. Curtiss III, E.C.C. Lin, J. Ingraham, K.B. Low, B. Magasanik, W. Reznikoff, M. Riley, M. Schaechter, and H.E. Umbarger (eds.), Washington, D.C.: ASM Press.
7. Gesteland, R.F., T.R. Cech, and J.F. Atkins. 1998. The RNA World , 2nd Ed. Cold Spring Harbor, N.Y.: Cold Spring Harbor Laboratory Press.
Mechanical Characteristics of Very Small Cells
David Boal
Department of Physics Simon Fraser University
Abstract
The smallest terrestrial cells have few structural elements: a fluid membrane to isolate the cell's contents, a very large molecule to carry its genetic information, and, often, a cell wall to offset the osmotic pressure of the cell's interior. There are few theoretical obstacles to constructing cells with radii as small as 50 nm using the same molecular materials as are found in 300 nm mycoplasmas. The energy required to bend a fiat fluid membrane into the shape of a cell is comparatively small, such that closed spherical shapes are energetically favored for radii greater than about 20 nm, depending upon composition. Further, the membrane of a small cell could withstand the osmotic pressures typical of many bacteria without the aid of a cell wall. However, it would be difficult to pack a genetic blueprint with a hundred genes into a small cell using double-stranded DNA, whose rigidity permits only gentle curvature on 50 nm length scales; rather, a small cell would employ most flexible molecules such as RNA or single-stranded DNA.
Introduction
The human body contains about 1013 cells—perhaps a hundred times the number of stars in the Milky Way—although only about 200 different cell types are represented in this collection. A minimal set of mechanical components is present in each cell to perform such tasks as isolating its contents, maintaining its shape or, in some cases, facilitating its movement. The chemical composition of these structural components does not vary strongly from one cell type to another, permitting us to understand, in a somewhat systematic fashion, the architecture that nature has chosen for the cell. Small cells, such as bacteria, have a particularly simple construction:
- a fluid membrane (and possibly a cell wall) forming the cell boundary,
- an interior fluid region likely at higher pressure than the cell's immediate environment,
- at least one large molecule carrying the cell's genetic information.
Some questions that we might ask about the mechanical characteristics of these components are illustrated in Figure 1.
The properties of many of the cell's structural elements are known as a function of their size. For example, the filaments of the cytoskeleton (the molecular scaffolding that helps a cell organize its internal compartments and maintain its shape) display a resistance against bending that grows rapidly with their radius, just as rope is stiffer than string. Thus, we can predict, if crudely, the size of the cytoskeletal components needed for a cell to function under various conditions. In addition, limits or bounds exist on the minimum mechanical strength required of these components: for example, the fluid membrane enclosing the cell must possess a certain minimal resistance against rupture on a time scale appropriate to the cell's lifetime.
Because a given structural element may play several different roles in a cell, a limit based solely on
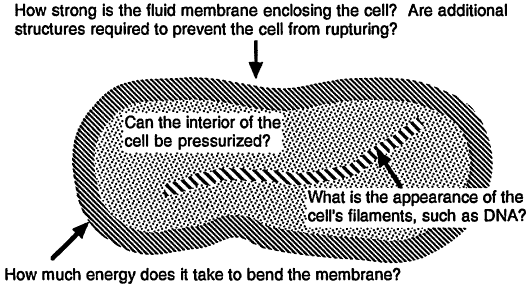
Figure 1.
Some civil engineering issues facing the designer of very small cells.
a single mechanical characteristic may not truly reflect the complete architectural specifications of that element. As an illustration, a membrane with a molecular composition providing good rupture resistance may be so viscous that proteins are unable to diffuse readily within it. Thus, the actual molecular composition of the membrane reflects not only the strict limit on its mechanical strength, but also a softer constraint arising from the functionality of its constituents. Further, the limits are not inviolable and should be regarded more as challenges to Nature. The constraints that we obtain here assume only the most rudimentary architecture and the simplest chemical compositions. We make these assumptions in the belief that the smallest cells arise early in the history of a planet and have not had sufficient time to develop a complex architecture. However, there is nothing to prevent Nature from finding ingenious strategies to circumvent mechanical constraints that strictly apply only to the most structurally simple cells.
Viability of Very Small Cells
In this paper, we focus on just a few of the cell's mechanical properties: the resistance of the boundary membrane to bending and rupture and the elasticity of a cell's filaments. We then discuss the implications of these characteristics to the mechanical functionality of cells much smaller in size than typical terrestrial cells. Our benchmark is a structurally simple cell of radius 50 nm. We demonstrate that:
- In simple models of fluid membranes, the bending energy of a spherical shell is independent of its radius, so that it takes the same amount of energy to bend a fiat membrane into a small spherical shell as
- a large shell. Whether such a cell is stable depends upon its energy compared to other configurations such as a flat disk with a free boundary. The creation of a hole or a free edge in a membrane requires an input of energy that is proportional to the length of the edge boundary. Except for very small membrane segments, it is energetically more favorable for a membrane with a free boundary to close up into a spherical shape, eliminating the boundary. The estimated minimum sphere radius arising from this argument is about 20 nm.
- There is a minimum stress that a membrane can tolerate before it ruptures on conventional time scales. Because the (surface) stress on a spherical shell is proportional to its radius, a small cell can tolerate higher internal pressures than can a large cell for a given membrane composition. Thus, a very small cell would not require a cell wall in order to function at the osmotic pressures typical of many bacteria.
- The bending resistance of a filament rises rapidly with its radius, so that thick filaments are relatively inflexible. Although a very small cell does not have sufficient volume to accommodate a conventional cytoskeleton (whose elements may be 10-25 nm in diameter), even a filament of double-stranded DNA would appear somewhat stiff on the scale of 50 nm. In order to code sufficient genetic information in a linear sequence, small cells would need very flexible molecules with perhaps half the mass per unit length of DNA, a requirement that is consistent with the idea that RNA or some other single-stranded molecule is the evolutionary precursor of DNA as the genetic template.
Detailed Analysis
Membrane Curvature
All cells are bounded by a plasma membrane consisting of a bilayer of dual-chain lipid molecules within which are embedded proteins and other molecules such as cholesterol. Bilayers are serf-assembled structures whose equilibrium configuration is spatially flat if the molecular composition is the same within both layers. Such symmetric bilayers resist bending with an energy cost per unit area e whose simplest parameterization is
where the constants κ (bending rigidity) and κG (Gaussian curvature modulus) have units of energy [for a review of more complete descriptions of bilayer bending, building on the original approach of Helfrich (1973), see Lipowsky (1991)]. The quantities R1 and R2 are the two principal radii of curvature displayed in Figure 2. As an illustration, a sphere of radius R has R1 = R2 = R, while a cylinder has an infinite radius of curvature along the axis of cylindrical symmetry. To find the bending energy of a particular surface, one simply integrates ε over the entire surface: for example, a spherical shell has a bending energy of 8πκ + 4πκG, independent of the shell's radius.
What is the magnitude of the bending energy for typical cells? Lipid bilayers in terrestrial cells are found to have κ= 10-25 kBT, where kB is Boltzmann's constant and T is the temperature [see Evans and Rawicz (1990) and references therein]. The value of κG is much less well known, but is expected to have a similar magnitude as κ. With κ = κG, the energy of a spherical shell is 12πκ. Considering only the contribution from k, the bending energy of a spherical cell would be 250-600 kBT. Although this is not really a large amount of energy (recall that kBT is roughly the kinetic energy of an atom in a gas), why would nature expend this energy to form a closed surface from an open bilayer sheet? To answer this question, we examine how a bilayer might rupture.
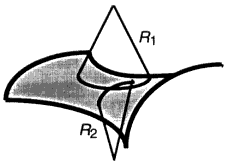
Figure 2.
Principal radii of curvature for a saddle-like surface.
Membrane Rupture
The fluid membrane not only resists bending, but also resists in-plane stretching. Under tensile stress, the membrane first stretches then ruptures once the area has expanded a few percent beyond its unstressed value. The creation of a hole in a membrane likely involves reconfiguring the lipid molecules around the boundary of the hole in order to reduce contact between the aqueous medium surrounding the bilayer and the water-avoiding hydrocarbon chains of the lipid molecules, which are normally buried within the bilayer. In general, the orientation of the lipids at the hole boundary is energetically unfavorable compared to that of an intact bilayer, so that there is an energy penalty if the membrane has a hole or a free edge.
The boundary of the hole can be characterized by an edge tension λ, (energy per unit length along the boundary), which has been measured to be in the 10-11 J/m range (for example, Fromherz, 1983); the measured values are larger than the minimum edge tension for membrane stability estimated from computer simulations of membrane rupture (Boal and Rao, 1992). For example, the edge energy of a fiat disk of radius Rdisk and perimeter 2πRdisk is Edisk = 2πRdiskλ. A membrane having this shape will be energetically favored over the closed sphere considered above (Esphere = 12πκ for κ = κG) if Rdisk < 6κ/λ. If the disk and the sphere have the same surface area then Rsphere = Rdisk/2 (see Figure 3). Thus we expect Rsphere > 3κ/λ (after Fromherz, 1983). Using typical values of κ ˜ 15 kBT and λ = 10-11 J/m leads to Rsphere > 20 nm, a bound whose exact value depends upon the membrane composition. Experimentally, one finds that pure bilayer vesicles (simple artificial cells in some sense) can be produced in the lab with radii as small as 30 nm (Fromherz, 1983; Frisken, 1998, private communication). Once the membrane has adopted a closed shape, the configuration could be further stabilized by the addition of lipids to the outer layer, thus reducing the strain in the bilayer.
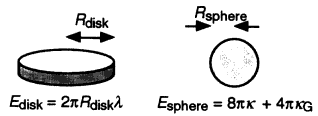
Figure 3.
Energetics of disks and spheres. The two shapes have the same areas if Rsphere = Rdisk/2.
Experiments on membrane failure find that typical bilayers rupture at tensile stresses of 1 × 10-2 J/m2 on laboratory time scales (Needham and Hochmuth, 1989). In cells, a (two-dimensional) surface stress P can result from the osmotic pressure difference P between the cell's interior and its external environment. For a spherical shell of radius R, the stress and pressure are related by (Fung, 1994)
Thus, a spherical shell of radius 1-micron can support a pressure difference of up to 2 × 104 J/m3, if the two-dimensional bursting stress is 1 × 10-2 J/m2 on laboratory timescales. However, many bacteria operate at much higher internal pressures, ranging up to many atmospheres, where 1 atmosphere = 105 J/m3. Most varieties of bacteria accommodate this pressure by the use of a cell wall.
Because the surface stress is proportional to R in Equation (2), a smaller cell would experience a lower stress for a given osmotic pressure P. In fact, a bilayer alone could handle an osmotic pressure of 4 atmospheres for a cell with a radius of just 50 nm, so that very small cells would not need a cell wall to function at moderate osmotic pressures. The absence of a cell wall would reduce the functional tasks of the cell and hence eliminate that part of DNA required to produce the proteins associated with cell wall construction. Alternatively, a small cell could choose to have a cell wall and increase the osmotic pressure at which it operates. Because the osmotic pressure is directly proportional to the concentration of proteins, ions, etc., then small cells could have a higher concentration of chemical reactants. Given that the rate of chemical reactions is proportional to the product of the reactant concentrations, an increase in the concentrations would result in an increase of the chemical reaction rates.
Flexible Filaments
The most evolutionarily advanced cells—eucaryotic cells—contain a filamentous cytoskeleton, which helps maintain the cell's shape, along with its other duties. Components of the cytoskeleton frequently include actin, intermediate filaments, and microtubules, with diameters in the range of 10 to 25 nm. Compared to a typical eucaryotic cell diameter of 10 microns or more, the transverse dimension of a cytoskeletal filament is trivial. Smaller cells such as bacteria, whose evolutionary origin predates eucaryotes, do not contain a cytoskeleton, but may instead possess a strong cell wall surrounding the pressurized bag bounded by a fluid membrane. Even bacteria, with a typical diameter of 1 micron, could accommodate the size of cytoskeletal filaments found in eucaryotes. However, cells with a radius as small as 50 nm would probably not have sufficient interior volume to permit a conventional cytoskeleton.
The absence of a cytoskeleton within a small cell does not imply that there are no filaments present. Cells must have some means of carrying hereditary information; the earliest cells may have used RNA but today's cells use DNA, both of which are linear molecules. Now, the visual appearance of a flexible rope, string, or linear molecule depends on the length scale of observation. For example, a human hair may be curly as seen by the eye on a length scale of centimeters, but a segment of the hair would seem straight if viewed through a microscope on a length scale of less than a millimeter. A quantity called the persistence length can be used to describe the straightness of a linear molecule. Figure 4 illustrates two linear objects; part [a] is convoluted with a short persistence length while [b] is much straighter with a long persistence length. Mathematically, the persistence length is a measure of the length scale over which a curve undergoes a significant change in direction. The arrows in Figure 4b are about a persistence length apart, as measured along the curve.
Now, double-stranded DNA has a persistence length of about 50 run (Bustamante et al., 1994),

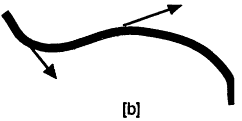
Figure 4.
Schematic representation of strings with short [a] and long [b] persistence lengths. The arrows in [b] are about a persistence length apart, as measured along the contour of the string.
meaning that a 100 nm filament of DNA might look like the configuration in Figure 4b: it would appear to be neither a straight rod, nor a tangled ball of thread. At 0.34 nm per base pair, a 100 nm filament of DNA traversing the cell once would contain just 300 base pairs, not a lot of genetic information. This means that cells probably would have to be larger than 50 nm in radius to accommodate a moderate amount of DNA if it were present as a random chain. It is more likely that small cells would use RNA or another flexible molecule to carry genetic information, consistent with the idea that RNA predated DNA in evolution. Many biopolymers display a persistence length that varies as the square of the mass per unit length along the polymer, a scaling behavior consistent with the theoretical expectation that the persistence length varies as the fourth power of the radius for uniform cylindrical rods (Doi and Edwards, 1986; Landau and Lifshitz, 1986). Thus, a molecule with the same mass density as double-stranded DNA, but only half the mass per unit length, would have a persistence length of one-quarter that of DNA, just 13 nm. With a persistence length closer to 10 nm, a long molecule could be balled up in a cell of 100-nm diameter. Self-interactions along the molecule's length, as might be expected for RNA, would reduce the size of the genetic ball even further.
Acknowledgment
This work is supported in part by the Natural Sciences and Engineering Research Council of Canada.
References
1. Boal, D.H., and M. Rao. 1992. Topology changes in fluid membranes. Phys. Rev. A46: 3037-3045.
2. Bustamante, C., J.F. Marko, E.D. Siggia, and S. Smith. 1994. Entropic elasticity of λ-phage DNA. Science 265: 1599-1600.
3. Doi, M., and S.F. Edwards. 1986. The Theory of Polymer Dynamics . Oxford: Oxford University Press, p. 316.
4. Evans, E., and W. Rawicz. 1990. Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys. Rev. Lett. 64: 2094-2097.
5. Fromherz, P. 1983. Lipid-vesicle structure: size control by edge-active agents. Chem. Phys. Lett. 94: 259-266.
6. Fung, Y.C. 1994. A First Course in Continuum Mechanics. Englewood Cliffs, New Jersey: Prentice-Hall, p. 23.
7. Helfrich, W. 1973. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. 28c: 693-703.
8. Landau, L.D., and E.M. Lifshitz. 1986. Theory of Elasticity (3rd Ed.). Oxford: Pergamon Press, p. 67.
9. Lipowsky, R. 1991. The conformation of membranes. Nature 349: 475-481.
10. Needham, D., and R.M. Hochmuth. 1989. Electromechanical permeabilization of lipid vesicles. Biophys. J. 55: 1001-1009.
Gene Transfer and Minimal Genome Size
Jeffrey G. Lawrence
Department of Biological Sciences University of Pittsburgh
Abstract
Throughout all domains of life, genetic material is exchanged within and among genomes. Horizontal transfer typically denotes rare transfer of genetic material between diverse lineages. This process does not constrain genome size in significant ways. Intraspecific recombination is more common than horizontal exchange, allows for the removal of deleterious mutations, and helps maintenance of species identity. Recombination enables organisms to maintain maximum genome sizes that are larger than those capable without gene exchange (escape of Muller's ratchet), but does not mediate potential reduction of genome size. In these cases, gene exchange allows transfer of non-essential genes among organisms, or reassortment of essential genes within a taxon. Neither process permits a cell to maintain fewer than the minimal complement of genes required for life. A model is presented whereby the frequency of gene exchange is much greater than the frequency of cell division. In this model, cells may be considered way stations for gene replication and transfer; such organisms need not maintain a full complement of genes, and genome sizes may decrease. Simulations predict the propagation of organisms where the average cell contains, on average over time, fewer than 1 gene.
Introduction
Although the influx of DNA sequence data has allowed novel approaches to assessing minimal requirements of life (1), this matter has received attention since genes and genomes were first identified (2,3). Discussion of a minimal size for a “free-living” organism necessarily includes an evaluation of that organism's genetic system. Critical components of genetic architecture include the frequency and nature of genetic exchange, that is, the transfer of genetic information among organisms. Here I will outline the nature of gene exchange mechanisms and their impact on genome size among extant organisms. Moreover, extrapolation of these mechanisms enables the elucidation of viable genetic architectures—and predictions for minimum genome sizes—for cells that are constrained in size. These models highlight potential pitfalls in the identification of organisms based on our expectations of genome content.
Modes of Gene Transfer
Horizontal Gene Transfer
Gene exchange among prokaryotic taxa is not coupled to reproduction, and may occur without direct cell-cell contact through a variety of mechanisms (e.g., transformation or bacteriophage-mediated). Since cell-cell recognition is not required for gene exchange, genetic material may be readily exchanged between distantly related lineages; this process is commonly termed lateral genetic transfer—or horizontal genetic transfer—to denote inheritance of information from outside the vertical inheritance pathway implicit in cell division (4-6). Horizontal transfer serves to shuffle genetic material among
diverse organisms. Because bacterial genes are organized into operons (groups of genes whose products work together to confer a single function), horizontal transfer of DNA can result in the exchange of phenotypic capabilities among organisms, as all genes required for a particular function may be mobilized between organisms. Although this process allows for rapid adaptation of organisms to changing environments, horizontal transfer does not intrinsically limit genome size, nor does it enable substantially smaller genome sizes to be achieved (however, see selfish operons below).
Although horizontal transfer has been observed among virtually all major groups of organisms, the rate of transfer has been assessed only in Escherichia coli (7,8). In that lineage, the rate of introduction of DNA—16 kb/MYr—suggests that horizontal transfer plays a large role in bacterial diversification (9). However, this rate also indicates that gene transfer events occur very rarely relative to the rate of cell division.
The Selfish Operon
The organization of bacterial genes into operons likely reflects selection for mobility (10). If a function is subject to weak selection, and may be lost from an evolutionary lineage, these genes may escape evolutionary loss by horizontal transfer to a naïve host genome. Transfer is successful only if all genes required to confer a selectable phenotype are mobilized together, and all of the genes are expressed in their new host. Because the probability of cotransfer is inversely related to the distance separating the genes, those genes found in clusters will be more mobile—hence more fit—than unclustered genes. As the aggregation of the genes into a cluster does not necessarily affect the fitness of the cell, the cluster may be considered to be a selfish property of the constituent genes. Horizontal transfer serves to disseminate selfish operons among bacterial genomes, where they may confer a beneficial function to their host cells and be maintained by natural selection. This paradigm will be useful when considering models requiring very rapid gene transfer (see below).
Moreover, the process of horizontal transfer facilitates the assembly of genes into operons. As only those genes that contribute to a selectable function will be maintained after horizontal transfer, intervening genes will be removed by deletion. Cotranscription of genes will be selected because a promoter at the site of integration may accomplish expression of all genes following horizontal transfer. In this way, expression of genes in foreign hosts does not require recognition of multiple promoter sites by cells using different sets of transcriptional machinery. In a similar fashion, translational coupling will permit efficient translation of the selfish operon without need for de novo ribosome loading at each protein coding sequence. These factors warrant some small reduction of genome size as a result of horizontal transfer: the elimination of multiple promoter sites and ribosome-binding sites. However, such small sequences are minor factors when considering broad-scale reduction of genome sizes.
Intraspecific Recombination
The same mechanisms that facilitate horizontal gene exchange among distantly related bacteria also mediate intraspecific gene exchange among closely related cells. Among conspecific strains, barriers to effective recombination (e.g., differences in restriction/modification systems, and extensive DNA mispairing) are fewer, and rate of DNA exchange is greater. Intraspecific recombination among Escherichia coli is a common event (11), and its rate has been measured to be on the order of the mutation rate, ˜10-9/bp per generation (12). Estimates of the sizes of DNA fragments mediating gene exchange (0.1 to 1.0 kb) suggest that the frequency of intraspecific recombination events in E. coli is still lower than the rate of cell division (11).
Intraspecific recombination does directly affect genome size. A population of organisms can maintain only a finite number of genes by means of natural selection. As mutation rates (µ is some function of mutation rate) increase, fewer genes (G) can be maintained owing to selection among genes. As population size (N is some function of population size) decreases, fewer numbers of genes are maintained in the face of genetic drift. Lastly, lower rates of recombination (r is some function of recombination rate) concede the accumulation of mutations (Muller's ratchet) and enable the maintenance of fewer numbers of genes. In sum, the maximum number of genes a population can maintain can be denoted by the following relationship:
Therefore, low rates of intraspecific recombination constrain the maximum number of genes a population can maintain by natural selection at any one time. Among higher eucaryotes, recombination is obligately fled to reproduction in the cycle of meiosis and syngamy. Here, the frequency of gene exchange amounts to one-half genome per generation. Although this rate is substantially higher than the rate of intraspecific recombination among prokaryotes, it serves the same purpose in affecting genome size. A population of freely recombining organisms can maintain a larger genome size, as deleterious mutations can be removed by recombination.
Empirical Approaches to Small Genomes
Equation (1) describes the influence of gene exchange on the maintenance of genes by natural selection. Notably, recombination facilitates the removal of deleterious alleles (13) and allows for the simultaneous maintenance of larger numbers of genes by natural selection. Implicit in this discussion—and in the concept of selfish operons—is the idea that many genes found in bacterial cells are not essential for survival. Indeed, the genomes of every organism tested include genes that are not essential for life. Although the E. coli genome bears over 4,500 genes (14), surveys of conditional mutations reveal that fewer than 10% of these loci are essential. Even the Mycoplasma genitalium genome—at 580073 bp and ˜470 genes, which represents the smallest bacterial genome to date (15)—is not composed completely of essential genes (16,17). Comparisons among sequenced genomes suggest that only 256 genes may be required to support a recognizable bacterial cell (1).
These approaches can help describe a minimal gene set enabling the growth of a prokaryotic bacterium, but they are constrained to encoding a sophisticated, highly evolved set of inter-dependent biochemical reactions. These exercises preclude, for example, the definition of a minimal set of genes based on serf-replicating ribozymes. From an exploratory perspective, these approaches do not encompass the definition of potential sets of minimal genes that exploit alternative biochemistries. Therefore, we must divorce discussion of the role of genetic transfer on minimal genome size from the preconceptions of cellular biology. Below, I will develop a context-independent model describing how rapid gene transfer predicts the maintenance of very small genome sizes when cells are constrained to small sizes.
Model of Minimal Genome Size
Minimum Genome Composition and the Cellular Environment
What is represented by the smallest collection of 256 essential genes described by Mushegian and Koonin (1), even for a biochemically complex organism like Mycoplasma? It is the group of genes that
define and describe the cellular environment, in which all genes are replicated. This collection of genes comprises a mutually reliant group; without the function of any one of the genes, the cell cannot survive. More specifically, without the functions of any one of these genes, none of the constituent genes can replicate. In this way, one may consider the cell to be an environment in which genes can replicate. The minimum subset of genes whose products define the cell describes a group with an emergent property: the ability to control their own environment. Regardless of what functions one requires a minimal cell to perform, some subset of replicating genes must be working together to maintain this environment; outside of this environment, genes replicate very poorly. The products of this minimal subset of genes modify the environment so that the group may replicate more efficiently, thereby increasing their fitness. We will call this group of genes the cellular consortium.
Horizontal transfer describes the transfer of genes that do not belong to the cellular consortium; rather, these genes may increase the fitness of the consortium in certain environments (like the lac operon aids E. coli growth), but these selfish operons are not required for cell growth. Intraspecific recombination describes mechanisms of reassorting members of the cellular consortium, but does not allow reduction of this group below the minimal number of genes required to perform cellular function. For gene exchange to affect this minimal number of genes, whose number and nature depend entirely on the properties of the minimal cell, we must speculate how constraints on cell size permit fewer than this minimal number of genes to be present in a cell at any one time. To do this, we must model the assembly of the cellular consortium, and devise a mechanism whereby constraint on cell size permits cells to replicate with fewer than the minimal number of genes required to form the cellular consortium.
Single Replicon Dynamics and the Cellular Consortium
To begin this model, we will consider the self-replicating gene—outside the context of the cell—to be the smallest living creature. A molecule that can self-replicate will increase in numbers as it consumes available resources. Consider the distribution of resources to be non-uniform, where the preferred environments are micelles (to use a familiar term). A successful self-replicating gene would travel from micelle to micelle, consuming the resources contained therein and replicating its genome. At this point, the cellular consortium does not exist, and the self-replicating gene leads a nomadic existence, traveling from resource patch to resource patch to replicate.
Mutants may arise among the self-replicating genes that enable greater replication in the micelle environments; such mutants could, for example, perform some simple biochemical functions that replenish some portion of the available nutrient pool. Different mutants may arise, each performing some different biochemical feat that enables it to replicate to a greater degree in some environment. We may consider these different classes of replicons as protospecies, each of which can replicate successfully in a different set of micelle environments; a hypothetical collection of genes, each with an elementary function, is listed in Table 1. At this stage, the replicons exploit the micelles as resource patches, traveling from micelle to micelle to replicate.
Such a system is shown in Figure 1. Here, each of the four genes listed in Table 1 is rapidly transferred between micelles. If a gene enters a micelle bearing all nutrients required for replication except one, and the replicon encodes a function allowing the synthesis of that compound, the gene and the micelle can replicate (replication-competent micelles). Following division, each daughter micelle would bear high concentrations only of the compound synthesized by the resident gene. For micelle and gene division to occur again, the micelle must be visited by each of the other three replicons.
If the replicons encoding the different functions assemble into a consortium, the most fit consortia would be that which combines a set of functions that would allow exploitation of the largest number of
Table 1 Participants in Micelle Simulation
|
Participant |
Functiona |
|
Gene 1 |
Synthesizes compound A; replicates when provided with compounds B, C, and D |
|
Gene 2 |
Synthesizes compound B; replicates when provided with compounds A, C, and D |
|
Gene 3 |
Synthesizes compound C; replicates when provided with compounds A, B, and D |
|
Gene 4 |
Synthesizes compound D; replicates when provided with compounds A, B, and C |
|
Compound A |
Required for gene replication; synthesized from precursors by Gene 1 |
|
Compound B |
Required for gene replication; synthesized from precursors by Gene 2 |
|
Compound C |
Required for gene replication; synthesized from precursors by Gene 3 |
|
Compound D |
Required for gene replication; synthesized from precursors by Gene 4 |
|
Micelle |
Enclosed environment maintaining compounds A, B, C, and D |
|
a Function in computer simulation (Figure 1). |
|
Figure 1.
Model for micelle propagation of a meta cell. Enclosed boxes represent micelles, which require four compounds to enable gene and micelle division (Table 1). The [X] symbols represent sufficiently high concentrations of compound X to allow replication; the [x] symbols represent post-replication levels.
environments (genes 1, 2, 3, and 4 on a single segment). If cell growth, i.e., propagation of the micelle, provides for better replication of the cellular consortium than does the nomadic lifestyle, a critical transition would occur. The genes comprising the cellular consortium will abandon their nomadic lifestyle and take up agriculture, using their battery of biochemical functions to maintain their preferred micelle environment. This cellular consortium bears the emergent property of cell growth, that is, the propagation of the preferred environment.
Rapid Gene Transfer of the Cellular Consortium and the Meta-Cell
Computer simulations of this model show rapid coalescence of replicons to form a cellular consortium that outcompetes non-cellular, nomadic replicons for available nutrients. However, a tacit assumption of the model is that all necessary pieces—all the individual genes—can coexist in the same cell. If individual micelles cannot support the entire subset of genes required to form the cellular consortium, a "cell" containing the entire cellular consortium cannot evolve. That is, the collection of cooperating genes cannot abandon their nomadic lifestyle in favor of metabolic agriculture. Rather, mini-consortia of replicons maintain their nomadic existence, traveling from micelle to micelle to replicate. At each stop, they may replicate using some subset of the available nutrients it requires, while replenishing others. This collection of mini-consortia replicates among these way stations of micelles. Here, the cell never forms by assembly of the cellular consortia because of constraints on cell size. Rather, the meta-cell develops as subsets of the cellular consortia perform their functions in a temporally and spatially diffuse manner. If propagation of the micelle environment is more favorable than a nomadic lifestyle, as suggested above for the evolution of the cell, the cellular consortium will evolve to propagate micelle. As each micelle cannot house all members of the cellular consortium at the same time, each member of the mini-consortia must travel through any one micelle to allow for micelle division. Therefore, in this model, the rate of transfer of genes among micelles is much more frequent than is micelle division. Rapid gene exchange allows for propagation of the recta-cell organism.
The Specter of Group Selection
Group selection is a framework for understanding cooperativity among competing organisms; each member makes a contribution to the group, and all members benefit. Group selection models are unstable in that members of the group can "cheat" by extracting the benefits of the group without making a contribution. The cellular consortium model does not require group selection for maintenance. Each mini-consortium of genes must perform some function to maintain the meta-cell. Cheaters that perform no biochemical function cannot replicate, as there is no member of the meta-cell that contains a complete complement of nutrients; only the mini-consortia that perform the required function can replicate there. Cheaters could arise as mutants of a mini-consortium that consume the nutrients and fail to synthesize enough of its product to feed other members (who will visit the micelle at a later time) that lack this function. Meta-cells are susceptible to this mutant, but they are less fit, because the micelles lacking this key nutrient accumulate and the meta-cell dies. Simulations show that natural selection maintains meta-cells with a minimal complement of non-contributing members.
Perspective on the Minimum Genome Size
The meta-cell model is a stable means of propagating replicons using high rates of gene transfer among micelles that cannot support the entirety of the cellular consortium. In this case, the rate of
transfer of genes among micelles is far more rapid than the rate of micelle division. Such systems are stable if size constraints prevent the assembly of the cellular consortium in a single micelle to form a cell. In this model, information-bearing micelles—those containing a mini-consortium at any one time—may contain as few as 1 gene. Since all micelles in the meta-cell do not contain genes at all times (each mini-consortium must exit a micelle to allow entry of another mini-consortium), the average genome size may be less than one gene. One may consider the meta-cell to be a single-celled organism whose genome is distributed through a network of micelles. If rapid transfer of genetic material defines a genetic architecture, a cell is not limited to containing all of the genes required for growth.
Acknowledgments
I thank Drs. Anthony Bledsoe, Susan Kalisz, and Roger Hendrix for helpful discussions. This work was supported by grants from the Alfred P. Sloan Foundation and the David and Lucile Packard Foundation.
References
1. Mushegian, A.R., Koonin, E.V. (1996). Proc. Natl. Acad. Sci., USA 93, 10268-10273.
2. Pirie, N.W. (1973). Ann. Rev. Microbiol. 27, 119-132.
3. Haldane, J.B.S. (1928). Possible Worlds and Other Papers (Harper and Brothers, New York).
4. Syvanen, M., Kado, C.I. (1998). Horizontal Gene Transfer (Chapman and Hall, London).
5. Syvanen, M. (1994). Ann. Rev. Genet. 28, 237-261.
6. Kidwell, M. (1993). Ann. Rev. Genet. 27, 235-256.
7. Lawrence, J.G., Ochman, H. (1998). Proc. Natl. Acad. Sci., USA 95, 9413-9417.
8. Lawrence, J.G., Ochman, H. (1997). J. Mol. Evol. 44, 383-397.
9. Lawrence, J.G. (1997). Trends Microbiol. 5, 355-359.
10. Lawrence, J.G., Roth, J.R. (1996). Genetics 143, 1843-1860.
11. Milkman, R. (1997). Genetics 146, 745-750.
12. Guttman, D.S., Dykhuizen, D.E. (1994). Science 266, 1380-1383.
13. Muller, H. (1932). Am. Nat. 66, 118-138.
14. Blattner, F.R., Plunkett, G.R., Bloch, C.A., Perna, N.T., Burland, V., et al. (1997). Science 277, 1453-1474.
15. Fraser, C.M., Gocayne, J.D., White, O., Adams, M.D., Clayton, R.A., et al. (1995). Science 270, 397-403.
16. Arigoni, F., Talabot, F., Peitsch, M., Edgerton, M.D., Meldrum, E., et al. (1998). Nat. Biotechnol. 16, 851-856.
17. Razin, S. (1997). Indian J. Biochem. Biophys. 34, 124-130.


































