Appendix D
Theoretical Modeling of Adsorption
Mitretek used a theoretical analysis to predict the adsorption on carbon of many materials present at very low concentrations in the incinerator flue gas of the baseline system (Mitretek Systems, 1997). The theoretical treatment of adsorption based on work by Polanyi and Dubinin and coworkers is described briefly below. A fuller explanation can be found in Ruthven (1984). The problem encountered at very low gas concentrations is also explained.
Adsorption potential (ε) is defined in terms of the equilibrium pressure of adsorbate in the gas phase (p) and its saturation vapor pressure (Psat):
For a given adsorbate and solid adsorbent, the relation between the volume of adsorbed contaminant and the adsorption potential can be determined experimentally for a particular adsorbent/adsorbate combination at a specified temperature. The characteristic curve defined by this relation can then be used to predict the behavior of other adsorbates on the same adsorbent at the same or other temperatures.
The form of the characteristic curve observed with activated carbon as the adsorbent can usually be expressed in a Gaussian form:
where W= volume adsorbed and Wo = volume absorbed at saturation (taken to be the total micropore volume of the solid adsorbent). If this relationship holds, then it becomes possible to predict the characteristic curve for a second adsorbent, based on a single data point. Dubinin and coworkers rewrote this relationship with an added factor (β) characteristic of the adsorbed materials:
The constant k is a characteristic of the solid adsorbent. From the two relations:
Mitretek measured adsorption equilibrium data for several compounds and found a useful correlation with the following substitutions: β was set equal to the critical temperature, Tc; T/β = reduced temperature, Tr; and W = Vmq, where Vm = liquid molar volume and q = adsorbed phase, mols/kg of carbon. The final empirical relation used by Mitretek was:
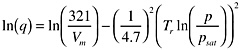
Unfortunately, some of the data of most interest for the baseline incineration system pollution abatement system filter system are in a low concentration range where the Dubinin-Radushkevich (D-R) relation cannot be applied because it will overpredict the adsorbed amount, as indicated in Figure D-1.
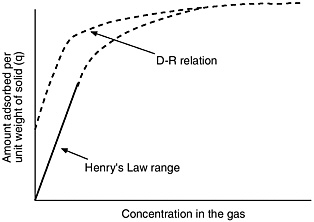
FIGURE D-1 Sketch of adsorption equilibrium.
Once this problem was recognized, suggestions were made for handling it. The D-R relation should hold for ''relative pressure'' values above 10-6. That is, for
(This criterion is given by Mitretek, attributed to Dubinin.)
Therefore, the D-R relation should be applied for values above this criterion. For values below 10-6 to zero, a linear relationship (i.e., Henry's Law) could be applied. The correct equilibrium adsorption (q) will fall between the two relations at values below 10-6. This appears to be a reasonably conservative approach to solving the problem. A more direct approach would be to use data obtained at the very low concentration of interest to define a Henry's Law relation.
The materials of most interest for adsorption in this case are unburned agent (although none was observed in trial bums at JACADS or the TOCDF) and chlorinated dioxins and furans. The latter are responsible for a substantial amount of the health risk in the HRA (health risk assessment) analyses for the baseline incineration system. For the most part, the concentrations of both unburned agent and dioxins and furans are below the criterion suggested by Dubinin, (P/Psat is less than 10-6) for most of these materials. The alternative analysis suggested above could be applied for these materials.
TABLE D-1 Vapor Pressures for Various Chlorinated Dioxins
|
Dioxin |
Vapor Pressure 71ºC (Pa) |
|
Dibenzo dioxin (DD) |
10 |
|
2-chloro DD |
1.8 |
|
2, 3-dichloro DD |
0.1 |
|
1, 2, 3, 4-tetrachloro DD |
0.012 |
|
1, 2, 3, 4, 5-pentachloro DD |
0.001 (est.) |
|
Perchloro DD |
~ 10-7 |
|
Source: Adapted from Rordorf, 1985. |
|
Vapor pressures for various chlorinated dioxins are shown in Table D-1. Trial-bum data showed individual dioxins to be present at concentrations of less than 1 ng/m3. Assuming a concentration of 1 ng/m3, partial pressures can be calculated and compared with the vapor pressures in Table D-1. Results are shown in Table D-2.
Only the most highly chlorinated dioxins have p/psat > 10-6, the Dubinin criterion. A similar estimate suggests that the criterion will not apply to chemical agents. Although no agent was detected in the trial-burn flue gas, they are assumed to be present at the detection limits suggested by Mitretek (see Table D-3).
TABLE D-2 Calculated Partial Pressures for Chlorinated Dioxins Based on 1 ng/m3
|
Dioxin |
Molecular Weight |
p (Pa) |
p/psat (71ºC) |
|
Dibenzo dioxin (DD) |
184 |
1.6 × 10-8 |
1.6 × 10-9 |
|
2-chloro DD |
218.5 |
1.33 × 10-8 |
7.4 × 10-9 |
|
2, 3-dichloro DD |
253 |
1.15 × 10-8 |
1.15 × 10-7 |
|
1, 2, 3, 4-tetrachloro DD |
322 |
0.90 × 10-8 |
7.5 × 10-7 |
|
1, 2, 3, 4, 5-pentachloro DD |
356.5 |
0.81 × 10-8 |
8.1 × 10-6 |
|
Perchloro DD |
460 |
0.63 × 10-8 |
0.063 |
TABLE D-3 Agent Detection Limits
|
Agent |
Detection Limit |
|
GB |
6 × 10-2 (g/m3) |
|
VX |
6 × 10-2 (g/m3) |
|
HD |
8.7 (μg/m3) |
|
Source: U.S. Army, 1998. |
|
Assuming that agents are present at these values and using estimated vapor pressure values, the p/psat values would be those given in Table D-4. All are less than the Dubinin criterion of 10-6.
It should be clear that modeling adsorption for the levels of principal organic hazardous constituents (POHCs) and substances of potential concern (SOPCs) concentrations in baseline-system flue gas is very difficult and is subject to considerable uncertainty. The carbon bed will initially adsorb most organic SOPCs leaving extremely low levels in the flue gas. The uncertainty arises in the duration of the bed life (i.e., how long the bed will remain on stream before materials saturate the carbon and start to appear in the outlet gas). For dioxins and furans, the predicted bed life is based on a theoretical analysis as well as commercial operating experience. The bed life is sufficiently long that, with proper monitoring, adequate notice will be provided for replacement of the bed, which should be infrequent.
The theoretical analysis was not extended to possible agent breakthroughs because agent is routinely monitored in the stack gas, and the facility would automatically shut down if any were detected. Trial bums have shown that agent in the flue gas is below the detection limit (see Appendix B).
ADSORPTION FROM A FLOWING GAS STREAM TO A PACKED BED
The adsorption process in a packed bed has been described in the literature at many different levels of sophistication (e.g., simple to complex equilibrium relations, simultaneous mass and heat transfers, combinations of mass transfer resistance in series, etc). The Mitretek approach is explained in the following excerpt from the Mitretek report (Mitretek Systems, 1997).
TABLE D-4 Agent Vapor Pressures and p/psat Ratios Based on Agent Detection Limits
|
Agent |
Vapor Pressure 71ºC est. (Pa) |
p/psat |
|
GB |
3,750 |
3.3 × 10-10 |
|
VX |
4.17 |
1.6 × 10-7 |
|
HD |
206.6 |
7.7 × 10-7 |
Carbon Filter Simulation Model Development
The computer simulation model is a mathematical representation of the carbon adsorption process. It is based on current theories about the adsorption process. Existing engineering relationships and data were used to the maximum extent possible in developing the model. Where necessary, new relationships were developed and laboratory scale experiments were run to obtain needed data. A major challenge to the modeling effort is the widely different adsorption characteristics of the chemical substances present in the PAS exhaust gases, which are present at very low concentration levels.
The model consists of differential energy and material balance equations which are solved to calculate the changes in the temperature and contaminant concentration in the carbon and in the flowing gas stream with time. The set of equations consists of one material balance equation for each contaminant, and an energy balance equation for the system.
The material balance equation is developed by considering that, at any position in the carbon bed, contaminants are either adsorbed by the carbon or are transported by dispersion and the bulk fluid flow. The governing material balance equation for the fixed-bed adsorption process, excluding fluid phase accumulation, addresses adsorption equilibrium, rate processes for mass transfer and fixed bed dynamics is:
(E1) ![]()
where
ρb = density of the bulk carbon, g/m3
q = moles of contaminant on carbon per unit mass of carbon, moles/kg
t = time, seconds
Dl = dispersion coefficient, cm2/sec
z = axial position in carbon filter, cm
ξ = fractional void space of the carbon bed, unitless
v = interstitial fluid velocity, cm/sec
kjα = rate constant for mass transfer to the adsorbent surface, sec-1
ci = bulk vapor phase concentration of the ith contaminant, moles/cm3
![]() = vapor-phase concentration of the ith contaminant in equilibrium with the adsorbed phase concentration of that contaminant, moles/cm3
= vapor-phase concentration of the ith contaminant in equilibrium with the adsorbed phase concentration of that contaminant, moles/cm3
The energy balance is solved considering only the effects of water adsorption/desorption and temperature changes in the inlet stream. It accounts for the thermal mass of the adsorbent, the thermal mass of the bulk fluid and the enthalpy transfer due to adsorption and desorption of water vapor. The energy balance is as follows:
(E2)![]()
where
cs = heat capacity of the adsorbent (J/kg K), (assumed to be constant in model)
qw = adsorbed-phase concentration of water, moles/kg
cw = adsorbed-phase heat capacity of water (assumed to be constant in model)
T = adsorption temperature (K)
λw = enthalpy of adsorption of water (assumed to be constant in model), J/mole K
ξv = superficial velocity, cm/sec
c = total molar density of the fluid phase, moles/cm3
cp = constant pressure heat capacity of the fluid-phase air-water mixture, J/mole K
z = axial distance, cm
The fluid-phase accumulation and the effective thermal dispersion are neglected. Also, the rate of heat transfer to the adsorbent is assumed to be instantaneous and heat losses to or through the column wall are assumed to be negligible. This simplification of the energy balance was made to permit the simulation of a feed temperature upset and to predict the change in filter temperature due to a change in relative humidity without unduly increasing computation time. It requires the use of accurate estimates of physical and adsorption properties.
The rate at which contaminant mass moves from the bulk gas onto the particle is affected by the resistance to mass transfer both inside and outside of the adsorbent particle. On the basis of empirical data for dimethyl methyl phosphonate (DMMP) (Croft and Friday et al., 1995), the model considers only the resistance external to the particle as defined by the rate constant for adsorption which is equal to the product of the external film mass transfer coefficient, kf, and the area per unit volume of carbon, "a." Intraparticle (solid phase) mass transfer resistance is assumed to be negligible.
The model uses the correlation of Wakao and Funazkri (1978), which is recommended by Yang (1987) for use in modeling fixed bed adsorbers when axial dispersion is included, to calculate values of the external mass transfer film coefficient:
(E3)![]()
where
dp= particle diameter assuming spherical particles, cm
DAB = diffusion coefficient of the chemical in the mixture, cm2/sec
ρ = density of the vapor-phase, gm/cm3
μ = viscosity of the vapor-phase, gram seconds/cm
ξv= superficial velocity, cm/sec
For non-spherical particles the particle diameter may be multiplied by a shape factor, øs to obtain an equivalent diameter. The area per unit volume was defined as
(E4)![]()
Axial dispersion of adsorbate within the carbon bed is another factor that influences the bulk gas concentration gradient within the carbon bed. On the basis of empirical data for DMMP (Croft and Friday et al. 1995) the following modified version of the Langer et al. (1978) correlation was determined to be the appropriate equation to use in the model to calculate the effective dispersion coefficient:
(E5) 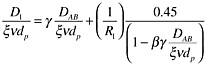
where
γ = tortuosity factor and is set equal to 0.73
β = constant set equal to 10
[This equation does not apply at c = csat]
The first term on the right accounts for molecular diffusion in the axial direction. The second term on the right accounts for dispersion due to non-uniform flow
and the decreased dispersion due to radial diffusion and mixing. The modification involves the addition of the (1/R1) factor where R1 represents the separation factor defined as the ratio of the concentration of contaminants in the bulk gas phase to the concentration of contaminants in the solid phase.
The equilibrium relation for the organic species chosen by Mitretek (and required in this analysis) is the D-R relation described previously. Other equilibrium relations were considered for other species, (described by Mitretek below).
Mercury Isotherm. The available experimental data for mercury adsorption equilibrium does not fit the potential theory-based correlation presented in Figure E-1. An alternative set of parameters for the potential theory based D-R correlation for mercury was obtained by a least squares fit of equilibrium data reported in the open literature for mercury adsorption on non-impregnated activated carbons that are similar to the coconut shell carbon.
The isotherm equation used for mercury in the model is:
(E14)![]()
Acid Gas Isotherm. Hydrogen chloride is another substance in the chemical demilitarization incinerator stack gases that is expected to have a different equilibrium isotherm than the organic compounds. Experimental data for HCl adsorption suggests that, under humid conditions, nearly twice as much HCl is adsorbed as would be expected from water solubility considerations. Thus, an assumption that HCl loading on the carbon is limited by its solubility in the water adsorbed onto the carbon provides a conservative estimate of the capacity of the carbon for HCl. Additional studies are under way to verify the findings of these experiments.
The solubility of HCl in water as a function of its partial pressure in the gas stream can be represented by the following potential type equation:
(E15)![]()
where q is the solubility of HCl in water when the partial pressure of HCl in the gas stream is p and Psat is the saturation vapor pressure of HCl. If the amount of water adsorbed on the carbon is known, then the above equation can be used to calculate the amount of HCl that would dissolve in the adsorbed water.
Water Isotherm. Water does not interact with activated carbon based adsorbents in the same way as most other compounds. The amount of water adsorbed on activated carbon depends markedly on operating conditions prior to the introduction of the water vapor into the gas stream. Therefore for water, alternative isotherm correlations were evaluated from the literature. The best correlation of water isotherm data on coconut shell carbon was obtained from the following equation:
(E16) ![]()
where
θ = q/qsat for water
q = carbon capacity for water at the relative humidity of the bulk gas, moles of water per unit mass of carbon at the partial pressure, p, of water vapor in the bulk gas phase, moles/kg
qsat = carbon capacity for water at 100 percent humidity, moles of water per unit mass of carbon at the saturation vapor pressure Psat of water (100 percent humidity), moles/kg
Tref= 298 K
γ2 =–4.01
γ1/2= 0.35
γ3= 2.91
Multi-component adsorption. When more than one adsorbate is present in the bulk gas phase, each adsorbate fills only a fraction of the pore space that it would have filled as a pure adsorbate. For carbon adsorption, an extension of the potential theory to multi-component adsorption and the ideal adsorbed solution theory (IAST) approaches are commonly used to predict multi-component equilibrium. The IAST assumes that fundamental thermodynamic equations used for liquid-phase equilibrium calculations apply to the adsorbed phase.
The potential theory for multi-component adsorption assumes that the adsorption potential of each component is equal to the adsorption potential of the mixture. If Raoult's law is valid for the relationship between the partial pressure of each adsorbate and its mole fraction in the adsorbed mixture and the adsorbates form an ideal solution (the adsorbate volumes are additive), the amount and composition of adsorbed
mixture corresponding to a given gas phase composition can be calculated from the known single-gas isotherms. This is represented by the following equations:
(E17)![]()
where
xi = mole fraction of the ith component in the absorbed phase
![]() = single component bulk gas phase equilibrium partial pressure, in Pascals, that would be exerted if the loading of the ith component was the same as the total loading of the mixture, i.e., θ0.
= single component bulk gas phase equilibrium partial pressure, in Pascals, that would be exerted if the loading of the ith component was the same as the total loading of the mixture, i.e., θ0.
θ0 = Σθi, the effective fractional loading of the mixture
θi = fractional loading of the ith component in the mixture, i.e., θi = qi/qsat. It is equal to 1 at the saturation vapor pressure of the liquid.
The assumption is made that the partial pressure of each adsorbate in the vapor phase is equal to the product of its mole fraction in the adsorbed phase mixture times the vapor pressure it would exert if it were a pure adsorbate and filled the carbon pores to the same extent as the mixture (like Roault's law).
For the model developed in this study, the extension of the potential theory, suggested by Grant and Manes (1966) was used. This method is explicit and requires no iterative root finding. Therefore it is ideal for use in a numerical model. The evaluation by the model starts with known qi's and T. The mole fractions are determined by:
(E18) ![]()
where qj represents all the adsorbates including qi. The fractional loading for the ith adsorbate, θi, is then determined by dividing the loading of the ith adsorbate, qi, by its pure component loading, qsat, at the saturation vapor pressure. This is the value at which the pore is considered filled. The fractional loadings are summed to determine the total or effective fractional loading. This result is then used in equation (E10) with the value of the parameters of the D-R equation for coconut shell carbon, the bulk gas phase temperature, and the critical temperature of the adsorbate to determine the adsorbate partial pressure.
Effects of Water. Extension of the multi-component model to include water requires the assumption that water forms an ideal mixture with the organics and Raoult's law for adsorption holds. A water isotherm in the form of equation (E16) can then be used to calculate the water partial pressure. It is recognized, however, that Raoult's law may not be appropriate for non-ideal mixtures such as water and non-water-soluble substances. Because the mechanism of adsorption of water is different than it is for organics and the effect of water varies for different adsorbates, e.g., water soluble, volatile adsorbates are affected by water vapor to a greater extent than others, and with different humidity levels, methods to adequately model the effect of water on adsorption are limited. The current model, using a Raoult's law approach for the prediction of water/organic equilibrium, was shown to provide conservative predictions in that it tends to predict earlier breakthrough of the organic adsorbates than is observed experimentally. In an experiment with hexane, this approach was found to over-predict the effect that water has on the adsorption of hexane. Although agreement between experimental data and the predictions was good at low relative humidity (< 50 percent), it aü ôme increasingly poorer as the relative humidity increased. This indicates that water coadsorption with organics represents an extreme case of adsorbed phase non-idealities.
Recently reported experimental results of adsorption experiments with several non-ideal two-component mixtures of various compounds with water on activated carbon suggest that the carbon loading can be dramatically reduced, especially above 70 percent relative humidity for the less strongly adsorbed (light), water-insoluble, organic species vapors. Conversely, for a water-soluble chemical, such as acetone, the presence of adsorbed water actually results in an increase in the carbon loading above the loading observed in the absence of adsorbed water. (Rudisill, Hacskaylo et al., 1992; Eissmann and LeVan, 1993). Further refinement of the model to better account for the effect of humidity could involve a major research effort that may not be warranted at this time.
Effect of inert gases on adsorption. The effect of the presence of inert gases, such as carbon dioxide (CO2), on the capacity of the carbon for the contaminants of concern was also considered. CO2 is of particular interest because it is present in the stack gases at higher concentrations than in air, being on the order of 6 percent by volume. Based on adsorption data for CO2 on BPL carbon, carbon filter loading under the stack conditions is estimated to be 5.8 × 10-5 mole/kg. The CO2 adsorption capacity is orders of magnitude lower than that of all compounds of potential concern with regard to risk to public health except vinyl chloride. Based on this, it is expected that CO2 would only affect break-
through of vinyl chloride, i.e., it may cause vinyl chloride to breakthrough earlier than it might have in the absence of CO2.
Solution of model equations. The differential material balances for each component and the energy balance constitute a set of non-linear partial differential equations. The computer simulation model calculates the temperature and contaminant concentrations in the bulk fluid and in the carbon over the length of the carbon bed after specified increments of time. It does this by solving material balances for each contaminant in the feed stream to the carbon bed. The energy balance is solved considering only the effects of water adsorption/desorption and temperature changes in the inlet stream.
Among the significant assumptions made in order to solve the equations of the model are:
-
The potential theory explains adsorption onto activated carbon.
-
The adsorption potential of each pure adsorbed component in a mixture is determined by the total adsorbate volume of the mixture.
-
Raoult's law is valid as the relationship between the partial pressure of each component and its mole fraction in the mixture.
-
The adsorbate mixture forms an ideal solution.
-
Multi-component equilibrium can be predicted from single component equilibrium relationships.
-
The equilibrium relationship between the bulk gas phase concentration of the organic components and the amount of those components that are adsorbed on the carbon can be represented by a "universal" D-R type equilibrium equation applicable to all organic compounds.
-
Water and other inorganic compounds, such as mercury, form an ideal mixture with the organic compounds, and Raoult's law for adsorption holds.
-
Water soluble compounds, such as HCl, will be adsorbed to the extent of their solubility in adsorbed water.
The computer model works by solving the partial differential equations to calculate the temperatures, bulk gas phase contaminant concentrations, and carbon bed loading along the length of the bed at a discrete time interval by the method of lines. In this method, the carbon column is divided into a series of stages along its length. A series of sets of ordinary differential equations results (one set of equations for each stage) that can be solved using a standard initial value ordinary differential equation solver.
The model is capable of running on a PentiumTM processor equipped PC with a minimum of 8 megabytes of memory. Computer requirements vary depending on the number of contaminants in the feed stream to the carbon bed.
The model requires initial input data from two input files created in a specified format. The first input data file contains information on the filter characteristics, and feed stream characteristics. It also allows specification of whether 25 or 50 stages should be used and whether an energy balance should be performed. Filter characteristics that need to be specified include the cross sectional area, the filter length, the adsorbent shape factor, carbon particle diameter in millimeters, and bulk density of the carbon in kilograms per cubic meter. Feed stream characteristics that need to be specified include the feed temperature in degrees Fahrenheit, the system pressure in Pascals, the relative humidity, the flow rate in standard cubic feet per minute at 80ºF, and the filter operating time in days. The number of adsorbates that are in the stream need to be specified. Each adsorbate needs to be named and physical properties provided (e.g., molecular weight, vapor pressure, and concentration).
The second input file specifies the initial filter loading, q, for each adsorbate in each stage of the filter. If this file does not exist, the model creates it with a loading of zero. As the model runs, the loading data is updated at each time increment during the run.
The model creates three output files. One output file contains data on the concentration of each contaminant in the outlet stream from the filter at each time increment during the run. Software can be used to plot the data. A second output file contains the adsorbed phase loading and the bulk gas phase concentration in each stage of the filter at the end of the run. A third file contains information to assist in verifying that the model performed properly, e.g., a material balance.
The Mitretek model was tested against laboratory breakthrough data with modestly successful results. The reader is referred to the Mitretek report for details. Finally, Mitretek made the following assessment of the approach.
Observations and Conclusions
The prediction of adsorptive filter performance is a complex and difficult task. It is necessary to include all substances in the feed stream to model filter performance because even though some substances may be innocuous from a risk standpoint, they may affect the
adsorption capacity of the filter for the substances that are of concern.
Overall, the current form of the model appears to be appropriate for an order of magnitude prediction of carbon performance which is adequate to support the PFS risk assessment. Comparison of the model with multi-component experimental data indicated that breakthrough time predictions were accurate to within a factor of 3 with the model tending to give conservative results with regard to breakthrough times. Additionally, there was no apparent effect on model predictions due to an increase in the number of compounds in the feed to the filter.
Most of this error is attributable to the use of a universal isotherm (in lieu of measured data for all components) due to the limited availability of isotherm data for many of the contaminants in the CDF incinerator stack gases. This universal correlation appears to provide a satisfactory estimate of adsorption equilibrium for the organic compounds against which it was tested. For adsorbates where no isotherm data are available, the estimated adsorption isotherms provided by this correlation may be in error by two orders of magnitude, especially at low concentrations where information is sparse.
Overall, however, the demonstrated model accuracy is adequate for assessing the fundamental performance issues of dioxin and furan breakthrough times and emission levels relative to detection limits. For a test case based on preliminary ANCDF information, the model has been used to make predictions regarding the capability of the PFS to capture and retain the major chronic risk drivers, i.e., dioxins and furans, for a reasonable time period and also to determine whether the presence of the PFS could contribute to acute health effects during operational upsets in which the filter would be exposed to high temperatures and/or humidity. Results indicated that further improvements in model accuracy would not change the fundamental assessment conclusions.
Improvements in the accuracy of the model would require further research. Confidence in and accuracy of the single-component isotherm estimations could be increased, for example, by obtaining isotherm data for additional adsorbates on coconut shell carbon. Also, alternative multi-component isotherm models could be evaluated. Some models proposed in the literature (Okazaki et al., 1970) for predicting the effects of water on adsorption also appear to provide improved accuracy. Additional resources and time are required to provide a more accurate multi-component carbon filter simulation model that includes the effects of humidity. Given the capability of the current model to support the requirements of the PFS risk assessments, this additional effort is not warranted.
The committee concurs with Mitretek's conclusion. Mitretek performed an excellent study of a very difficult problem, and the results were accurate enough to show very long breakthrough times. The results also appear to be consistent with operating experience from commercial incinerators.
Some factors may not have been adequately considered, however, and surprises are always possible. Operability problems could arise (e.g., dust formation, uneven flow, etc.). Because these are all "first of a kind" plants, these problems will warrant close attention during start-up and early operation.
REFERENCES
Mitretek Systems. 1997. Pollution Abatement System Carbon Filter Simulation Model Development. January 1997. Aberdeen Proving Ground, Md.: U.S. Army Program Manager for Chemical Demilitarization.
Rordorf, B.F. 1985. Thermodynamic and thermal properties of polychlorinated compounds: the vapor pressures and flow tube kinetics of ten dibenzo-para-dioxins. Chemosphere 14(6/7): 885-892.
Ruthven, D.M. 1984. Principles of Adsorption and Adsorption Processes. New York: John Wiley and Sons.
U.S. Army. 1998. Risk Assessment of the Pollution Abatement Filter System for the Anniston Chemical Agent Disposal Facility (ANCDF). Prepared by Mitretek Systems, August 1998. Aberdeen Proving Ground, Md.: U.S. Army Program Manager for Chemical Demilitarization.








