2
Environment for Embedding: Technical Issues
This chapter describes a number of issues that arise when embedding is used to provide national scores for individual students. In keeping with Congress's charge, we focus our attention primarily on embedding as a means of obtaining individual scores on national measures of 4th-grade reading and 8th-grade mathematics. The issues discussed here would arise regardless of the grade level or subject area, although the particulars would vary.
SAMPLING TO CONSTRUCT A TEST1
To understand the likely effects of embedding, it is necessary to consider how tests are constructed to represent subject areas. For present purposes, a key element of this process is sampling. A national test represents a sample of possible tasks or questions drawn from a subject area, and the material to be embedded represents a sample of the national test.
Tests are constructed to assess performance in a defined area of knowledge or skill, typically called a domain. In rare cases, a domain may be
small enough that a test can cover it exhaustively. For example, proficiency in one-digit multiplication could be assessed exhaustively in the space of a fairly short test. As the domain gets larger, however, this becomes less feasible. Even final examinations, administered by teachers at the end of a year-long course, cannot cover every possible content or skill area covered by the curriculum. Many achievement tests—including those that are especially germane to the committee's charge—assess even larger, more complex domains. For example, the NAEP 8th-grade mathematics assessment is intended to tap a broad range of topics that includes a wide variety of mathematical skills and knowledge that students should (or might) master over the course of their first 8 years in school. The assessment therefore includes items representing a variety of different types of skills and knowledge, including numbers and operations, measurement, geometry, algebra and functions, and data analysis and statistics. Commercial achievement test batteries cover equally broad content, as do state assessments.
Because the time available to assess students is limited, wide-ranging tests can include only small samples of the full range of possibilities. Performance on the test items themselves is not as important as is the inference it supports about mastery of the broader domains the tests are designed to measure. Missing 10 of 20 items on a test of general vocabulary is important not because of the 10 words misunderstood, but because missing one-half of the items justifies an inference about a student's level of mastery of the thousands of words from which the test items were sampled.
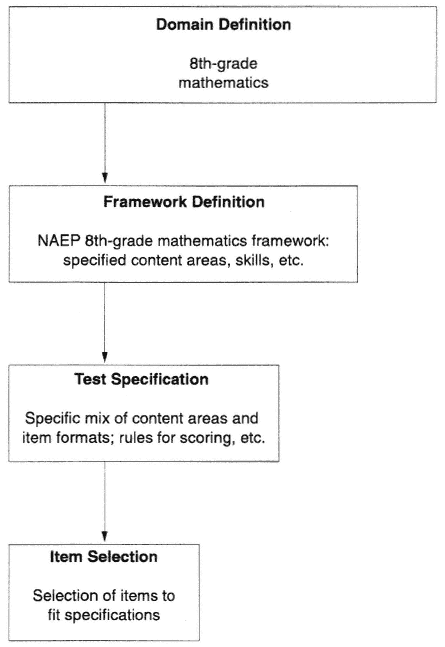
In order to build a test that adequately represents its domain, a number of decisions must be made. It is helpful to think of four stages leading to a final test: domain definition, framework definition, test specification, and item selection (see Figure 2-1). The choices made at each stage reduces the number of content and skills areas that will be directly sampled by the completed test.
First, the developers of an assessment define the scope and extent of the subject area, called the domain, being assessed. For example, the domain of 8th-grade mathematics includes not only material currently taught in (or by) the 8th-grade, but also material that people think ought to be taught. During domain definition, decisions such as whether data analysis and statistics should be tested in the 8th-grade would also be made.
To define the framework, the domain definition must be delineated
in terms of the content to be included, and the processes that students must master in dealing with the content. The NAEP 8th-grade mathematics framework represents choices about how to assess achievement in the content of 8th-grade mathematics. It identifies conceptual understanding, procedural knowledge, and problem solving as facets of proficiency and whether basic knowledge, simple manipulation, and understanding of relationships are to be tested separately or in some context.
Choices made at the next stage, test specification, outline how a test will be constructed to represent the specified content and skills areas defined by the framework. Test specifications, which are aptly called the test blueprint, specify the types and formats of the items to be used, such as the relative number of selected-response items and constructed-response items. Designers must also specify the number of tasks to be included for each part of the framework. Some commercial achievement tests, for example, place a much heavier emphasis on numerical operations than does NAEP. Another choice for a mathematics test is whether items can be included that are best answered with the use of a numerical calculator. NAEP includes such items, but the Third International Mathematics and Science Survey (TIMSS), given in many countries around the globe, does not. The NAEP and TIMSS frameworks are very similar, yet the two assessments have different specifications about calculator use.
Following domain definition, framework definition, and test specification, the final stage of test construction is to obtain a set of items for the test that match the test specification. These can come from a large number of prepared items or they can be written specifically for the test that is being developed. Newly devised items are often tried out in some way, such as including them in an existing test to see how the items fare alongside seasoned items. Responses to the new trial items are not included in the score of the host test. Test constructors evaluate new items with various statistical indices of item performance, including item difficulty, and the relationship of the new items to the accompanying items.
COMMON MEASURES FROM A COMMON TEST
To clarify the distinction between common tests and common measures, and to establish a standard of comparison for embedding, we begin our discussion of methods for obtaining individual scores on a common measure with an approach that entails neither linking nor embedding,
but rather administration of an entire common national test and an entire state test.
Two Free-Standing Tests
In this situation, two free-standing tests are administered without any connection to each other. The national test is administered in its entirety under standardized conditions that are consistent from state to state: students in each state are given the same materials, the same directions, the same amount of time to complete the test, and so on. The combination of a common national test and common, standardized conditions of administration can yield a common measure of individual student performance, but at the cost of a substantial increase in burden (in time, money, and disruption of school routines) relative to the administration of a single state test.
The success of this approach hinges not only on the use of a common test, but also on standardization of administration and similarity in the uses of the scores. If test administration is not consistent from one location to another, for example, across states, even the use of a full common test may not guarantee a common measure. Moreover, when the national measure provides norms based on a standardization sample, the administration of the test must conform to the administration procedures used in the standardization.
However, even standardized administration procedures are not sufficient to guarantee a common measure. For example, suppose that two states administer an identical test and use similar procedures for administering the test, but use the scores in fundamentally different ways: in one state, scores have serious consequences for students as a minimum requirement for graduation; in another state, the scores have no consequences for students and are not even reported to parents, but are used to report school performance to the public. This difference in use could cause large differences in student motivation, and students in the second state may not put much effort into the test. As a result, identical scores in the two states might indicate considerably different levels of mastery of the content the test represents. Regardless of which of the two conditions (high or low motivation) produces more accurate scores, the scores will not be comparable. When scores are different for reasons other than differences in student achievement, comparisons based on scores are problematic.
Reconciling Scores
Two free-standing tests provide two scores for individual students: a state score and a national score. Because the state and national tests differ, the information from these scores would be different. That is, some students would do better on one test than on the other. Some of these differences could be large. Having two scores that are sometimes discrepant could be confusing to parents and policy makers. One can easily imagine, for example, complaints from the parent of a student who scored relatively poorly on a high stakes state test but well on a low-stakes free-standing national test.
Yet, when two tests differ, they may provide different and perhaps complementary information about students' performance. Measurement experts have long warned against reliance on any single measure of student achievement because all measures are limited and prone to errors. The information about a student gathered from the results of two different well-constructed tests of a single domain would in general be more complete and more revealing than that from a single test (National Research Council, 1999b; American Educational Research Association et al., 1985; American Educational Research Association et al., in press).
One key to whether information from two tests would be seen as confusing or helpful is the care with which conclusions are presented and inferences drawn. If users treat scores of an 8th-grade mathematics test, for example, as synonymous with achievement in 8th-grade mathematics, differing results are likely to be confusing. But if users treat scores as different indications of mastery of that domain, the possibility exists for putting discrepancies among measures to productive use. An important caveat, however, is that in some cases, scores on one or the other test could be simply misleading—for example, if the student was ill the day it was administered.
With two free-standing tests another issue is inevitably raised: How fair are comparisons based on this approach? The committee noted that the fairness or reasonableness of a comparison hinges on the particular inferences the test scores are used to support. For example, suppose that two states agree to administer an identical mathematics test in the spring of the 8th-grade. The test emphasizes algebra. In one state, most students study algebra in the 8th-grade. In the second state, however, most students are not presented with this material until the 9th grade, and the corresponding instructional time is allocated instead to basic probability and data analysis, which is given almost no weight in the test. Because
the test is more closely aligned with the curriculum in the first state than in the second, students in the first state will have an advantage on the test, all other things being equal.
Under these circumstances, when would it be fair to conclude that a given student in the second state is doing poorly, relative to students in the first state? If one were simply interested in whether students have mastered algebra and hazarded no speculation about why, it might be reasonable to conclude that the student is doing poorly. The student would in fact know less algebra than many students in the first state, if only because he or she had not been given the opportunity to learn algebra. But, if one wanted to draw inferences about a student's mastery of the broad subject area of mathematics, it might be unreasonable and misleading to infer from the results of this test, that the student in the second state is doing poorly relative to students in the first state.
THREATS TO OBTAINING A COMMON MEASURE
The use of a free-standing common test is in itself insufficient to guarantee comparability. We briefly note here some of the issues that arise when a common test is used to generate common scores. We present this material not to evaluate the two free-standing tests approach, but rather to provide a baseline for comparing the use of embedding. We also discuss these factors in relation to actual state policy and testing programs, with an emphasis on the ways in which differences among these programs can affect the comparability of results.
Standardization of Administration
To make fair and accurate comparisons between test results earned by students in different districts or states, or between students in one district or state and a national sample of students, tests must be administered under standardized conditions, so that the extraneous factors that affect student performance are held constant. For example, instructions to the examinees, the amount of time allowed, the use of manipulatives or testing aids, and the mechanics of marking answers should be the same for all students.
However, because of the expense involved in hiring external test administrators, most state tests are administered by the regular school staff, teachers, counselors, etc. Test administration usually means that
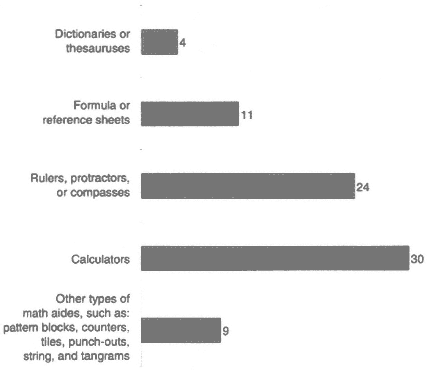
FIGURE 2-2 Manipulatives allowed on 4th-grade reading and 8th-grade mathematics components; number of states. Source: Adapted from Olson et al. (in press).
the staff read the instructions for completing the test to the examinees from a script, which is designed to ensure that all students receive the same instructions and the same amount of time for completing the test. If all of the test administrators adhere to the standardized procedures, there is little cause for concern. There has been some concern expressed, however, by measurement specialists that teachers may vary in how strictly they adhere to standardized testing procedures (see, e.g., Kimmel, 1997; Nolen et al., 1992; Ligon, 1985; Horne and Garty, 1981).
If different states provide different directions for the national test, different opportunities to use calculators or manipulatives (see Figure 2-2), impose different time limits for students, or break the test into a different number of testing sessions, seemingly comparable scores from different states may imply different levels of actual proficiency.
Accommodations
One of the ways in which the standardized procedures for administration are deliberately violated is in the provision of special accommodations for students with special needs, such as students with disabilities or with limited proficiency in English. Accommodations are provided to offset biases caused by disabilities or other factors. For example, one cannot obtain a valid estimate of the mathematics proficiency of a blind student unless the test is offered either orally or in Braille. Other examples include extra time (a common accommodation), shorter testing periods with additional breaks, and use of a scribe for recording answers; see Table 2-1 for a list of accommodations that are used in state testing programs.
Two recent papers prepared by the American Institutes for Research (1998a, 1998b) for the National Assessment Governing Board summarize much of the research on inclusion and accommodation for limited—English-proficient students and for students with disabilities. However, information about the appropriate uses of accommodations for many types of students is unclear, and current guidelines for their use are highly inconsistent from state to state (see, e.g., National Research Council, 1997).
Differences in the use of accommodations could alter the meaning of individual scores across states, and the lack of clear evidence about the effects of accommodations precludes taking them into account in comparing scores (see, e.g., Halla, 1988; Huesman, 1999; Rudman and Raudenbush, 1996; Whitney and Patience, 1981; Dulmage, 1993; Joseph, 1998; Williams, 1981).
Timing of Administration
The time of year at which an assessment is administered will have potentially large effects on the results (see Figure 2-3 for a comparison of state testing schedules). The nature of students' educational growth in different test areas is different and uneven throughout the school year (Beggs and Hieronymus, 1968). In most test areas, all of the growth occurs during the academic school year, and in some areas students actually regress during the summer months (Cooper et al., 1996).
The best source of data documenting student growth comes from the national standardizations of several widely used achievement batteries. These batteries place the performance of students at all grade levels
TABLE 2-1 Accommodations Used by States
|
Type of Accommodation Allowed |
Number of States |
|
Presentation format accommodations |
|
|
Oral reading of questions |
35 |
|
Braille editions |
40 |
|
Use of magnifying equipment |
37 |
|
Large-print editions |
41 |
|
Oral reading of directions |
39 |
|
Signing of directions |
36 |
|
Audiotaped directions |
12 |
|
Repeating of directions |
35 |
|
Interpretation of directions |
24 |
|
Visual field template |
12 |
|
Short segment testing booklet |
5 |
|
Other presentation format accommodations |
14 |
|
Response format accommodations |
|
|
Mark response in booklet |
31 |
|
Use of template for recording answers |
18 |
|
Point to response |
32 |
|
Sign language |
32 |
|
Use of typewriter or computer |
37 |
|
Use of Braille writer |
18 |
|
Use of scribe |
36 |
|
Answers recorded on audiotape |
11 |
|
Other response format accommodations |
8 |
|
Test setting accommodations |
|
|
Alone, in study carrel |
40 |
|
Individual administration |
23 |
|
With small groups |
39 |
|
At home, with appropriate supervision |
17 |
|
In special education class |
35 |
|
Separate room |
23 |
|
Other test setting accommodations |
10 |
|
Timing or scheduling accommodations |
|
|
Extra testing time (same day) |
40 |
|
More breaks |
40 |
|
Extending sessions over multiple days |
29 |
|
Altered time of day |
18 |
|
Other timing-scheduling accommodations |
9 |
|
Other accommodations |
|
|
Out-of-level testing |
9 |
|
Use of word lists or dictionaries |
13 |
|
Use of spell checkers |
7 |
|
Other |
7 |
|
SOURCE: Adapted from Roeber et al. (1998). |
|
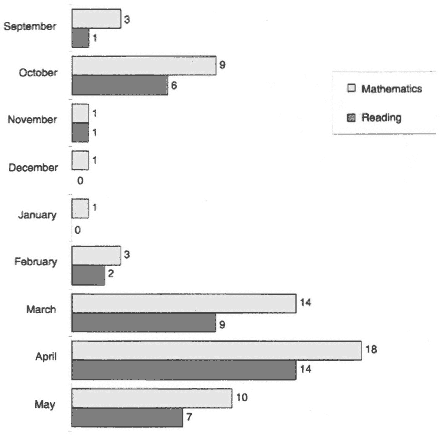
FIGURE 2-3 Time of administration of 4th-grade reading and 8th-grade mathematics components during the 1997-1998 school year; number of states. Notes: States were counted more than once when their assessment programs contained multiple reading or mathematics components that were administered at different times during the year.
Source: Adapted from Olson et al. (in press).
(K-12) on a common scale, making it possible to estimate the amount of growth occurring between successive grade levels.2
The effect that time of year for testing could have on the absolute level of student achievement is illustrated in Table 2-2. This table shows
the average proficiency in reading on the grade 4 1998 NAEP assessment for 39 states, the District of Columbia, and the Virgin Islands. If one were to assume the average within-grade growth for reading, 3 a difference of 3 months—the size of the testing window for NAEP—in the time of year when the test is administered could have up to a 16-point effect on the average proficiency level of a state or district. For illustration, 16 points is the difference in performance between the state ranked 5th (Massachusetts) and the state ranked 31st (Arkansas). A difference in testing time as small as 3 months could lead to changes in state ranking by as many as 26 places.
Some national assessments have norms for only one testing period per grade. NAEP, TIMSS, and the proposed VNT are examples of such tests. If one of these tests is selected to serve as a free-standing test or as the source for the embedded items, the state tests would have to be administered during the same testing period as the national assessment. Other tests, such as most commercially available, large-scale achievement tests, have norms available for various testing periods per grade. With these assessments, testing dates are flexible, and if they are the source for the embedded test, the national test can be administered during a time period that is most suitable for the local situation.
One additional issue that is related to the time of year for testing falls under the umbrella of ''opportunity to learn." For example, if the same test is given at the same time of the year in different states that follow different curricula, or if the same test is given at different times of the year in states that follow the same curricula, students will not have had equal opportunities to learn the material before testing. For example, if reading and analyzing poetry is covered early in the school year in one state and covered after the assessment is given in another, test items that include reading poetry might be easier for students from the first state than for
students from the second state. Similarly, if students who are studying identical content, using the same materials, and following the same sequence of instruction take the same test at different times of the year, students who take the test later in the school term will have an advantage on any test items that measure material covered after students in the first state take the test.
Test Security
The comparability of scores from a test hinges on maintaining comparable levels of test security from one jurisdiction to another. Tight security ensures that students and teachers do not have access to test items before they are administered and that preparation for the test is not focused on specific items. If security is less stringently maintained in one state than in another, scores in the first state may be biased upwards.
Consider what could happen if state A administers a test in October, but state B does not administer it until April. Students and teachers in state B may have the advantage of knowing what is on the test before it is administered and can better prepare for the test.
Additionally, state practices and laws related to test security and the release of test items contained in state tests vary a great deal (see Figure 2-4). Some states release 100 percent of their tests' content every year, others release smaller percentages, and others none at all. But if even one
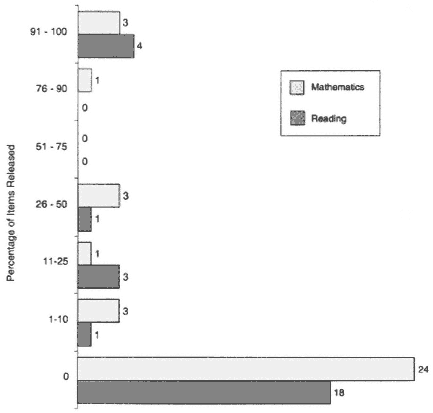
Figure 2-4 Items released from 4th-grade reading and 8th-grade mathematics tests in 1997-1998; number of states. Note: States are listed more than once when they administered multiple reading or mathematics components and released different percentages of each component. Source: Adapted from Olson et al. (in press).
state releases the items contained in a test, then the items must be changed every year so that breaches in test security and differential examinee exposure to the national test items do not differentially affect student performance.
Breaches in item security can arise not only from state practices related to the release of state test materials. Test security can also be compromised during item development and test production, in test delivery, in test return, and in test disposal. In addition, students may remember particular items and discuss them with other students and teachers. School-based test administrators may remember particular items and in-
corporate them, or nearly identical items, in their instruction. This problem of inappropriate coaching, or teaching to the test, is especially apparent if the stakes associated with test performance are high.
To circumvent these problems, most commercial testing programs create several equivalent forms of the same test. The equivalent forms may be used on specified test dates or in different jurisdictions. However, creating equivalent versions of the same test is a complex and costly endeavor, and test publishers do not develop unlimited numbers of equivalent forms of the same test. Consequently, varying dates of test administration pose a security risk.
Stakes
Differences in the consequences or "stakes" attached to scores can also threaten comparability of scores earned on the same free-standing test. The stakes associated with test results will affect student test scores by affecting teacher and student perceptions about the importance of the test, the level of student and teacher preparation for the test, and student motivation during the test (see e.g., Kiplinger and Linn, 1996; O'Neil et al., 1992; Wolf et al., 1995; Frederiksen, 1984).
The specific changes in student and teacher behavior spurred by high stakes will determine whether differences in stakes undermine the ability of a free-standing test to provide a common measure of student performance. For example, suppose that state A imposes serious consequences for scores on a specific national test, while state B does not. This difference in stakes could raise scores in state A, relative to those in state B, in two ways. Students and teachers in state A might simply work harder to learn the material the test is designed to represent—the domain. In that case, higher scores in state A would be appropriate, and the common measure would not be undermined. However, teachers in state A might find ways to take shortcuts, tailoring their instruction closely to the content of the test. In that case, gains in scores would be misleadingly large and would not generalize to other tests designed to measure the same domain. In other words, teachers might teach to the test in inappropriate ways that inflate test scores, thus undermining the common measure (see, e.g., Koretz et al., 1996a; Koretz et al., 1996b).
States administer tests for a variety of purposes: student diagnosis, curriculum planning, program evaluation, instructional improvement, promotion/retention decisions, graduation certification, diploma endorsement, and teacher accountability, to name a few. Some of these purposes,
such as promotion/retention, graduation certification, diploma endorsement, and accountability, are high stakes for individuals or schools. Others, such as student diagnosis, curriculum planning, program evaluation, and instructional improvement are not.
ABRIDGMENT OF TEST CONTENT FOR EMBEDDING
In the previous section we outlined a variety of conditions that must be met to obtain a common measure and outlined how policies and practices of state testing programs make such conditions difficult to achieve, even when embedding is not involved. Embedding, however, often makes it more difficult to meet these conditions and raises a number of additional issues as well.
Reliability
As long as the items in a test are reasonably similar to each other in terms of the constructs they measure, the reliability of scores will generally increase with the number of items in the test. Thus, when items are reasonably similar, the scores from a longer test will be more stable than those from a shorter test. The effect of chance differences among items, as well as the effect of a single item on the total score, is reduced as the total number of items increases. Embedding an abridged national test in a state test or abridging the state test and giving it with the national test would provide efficiency, compared with administration of the entire state and national tests, but it produces that efficiency by using fewer items. Hence, the scores earned on the abridged test would not be as reliable as scores earned on the unabridged national test. The short length of the abridged test will also increase the likelihood of misleading differences among jurisdictions. Test reliability is a necessary condition for valid inferences from scores.
Content Representation
No set of embedded items, nor any complete test, can possibly tap all of the concepts and processes included in subject areas as complex and heterogeneous as 4th-grade reading and 8th-grade mathematics in the limited time that is usually available for testing. Any collection of items will tap only a limited sample of the skills and knowledge that make up
the domain. The items in a national test represent one sample of the domain, and the material selected for embedding represents only a sample of the national test. The smaller the number of items used in embedding, the less likely it is that the embedded material will provide a representative sample of the content and skills that are reflected in the national test in its entirety. How well the national test represents the domain, and how well the embedded material represents the national test, can be affected by both design and chance.
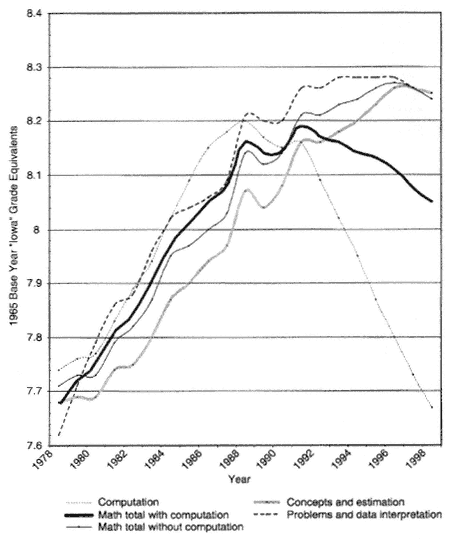
The potentially large effect of differences in sampling from a subject area are illustrated by data from the Iowa Tests of Basic Skills (ITBS) for the state of Iowa (see Figure 2-5). Between 1955 and 1977 the mathematics section of the ITBS consisted of math concepts and math problem-solving tests but did not include a separate math computation test. In 1978 a math computation test was added to the test battery, but the results from this test were not included in the total math score reported in the annual trend data. The trend data from Iowa for 1978-1998 for grade 8 illustrate clearly how quite different inferences might be made about overall trends in math achievement in Iowa depending on whether or not math computation is included in the total math score. Without computation included, it appears that math achievement in Iowa increased steadily from 1978 to the early 1990s and has remained relatively stable since. However, when computation is included in the total math score, overall achievement in 8th-grade mathematics appears to have gone steadily down from its 20-year peak in performance in 1991. Similar differences would be expected in the math performance of individuals, individual school districts, or states depending on whether computation is a major focus of the math curriculum and on how much computation is included in the math test being used to measure performance.
Abridgment of the national test can affect scores even in the absence of systematic decisions to exclude or deemphasize certain content. Even sets of items that are selected at random will differ from each other. Students with similar overall proficiency will often do better on some items than on others. This variation, called "student by task interaction," is the most fundamental source of overall reliability of scores (Gulliksen, 1950; Shavelson et al., 1993; Dunbar et al., 1991; Koretz et al., 1994). Therefore, particularly when the embedded material is short, some students may score considerably differently depending on which sample of items is embedded.
Abridgment could affect not only the scores of individual students, but also the score means of states or districts. As embedded material is
abridged, the remaining sample of material may match the curricula in some states better than in others.
PLACEMENT OF EMBEDDED TEST ITEMS
For embedding to be a useful technique for providing a common measure of individual performance in 4th-grade reading and 8th-grade mathematics, there must be an appropriate state test of those subjects into which the national test can be embedded, and conditions must be such that the embedded items can and will be administered understandardized conditions. The diversity of state testing programs and practices which characterizes the American system of education creates an environment in which either or both of these conditions often cannot be met.
Grades and Subjects Tested
Differing state decisions about the purposes for testing lead to differing decisions about what subjects should be tested, who should be tested, and at what point in a student's education testing should occur. For example, some states test students' reading performance in 3rd grade, others in 4th-grade. Some states treat reading as a distinct content area and measure it with tests designed to tap the content and skills associated only with reading; others treat reading as one component of a larger subject area, such as language arts, or measure it along with a seemingly unrelated subject such as mathematics.
In the 1997-1998 school year, 41 states tested students in 4th-grade reading, 8th-grade mathematics, or both: 27 states assessed students in reading in 4th-grade, and 39 states assessed students in mathematics in 8th grade.4 Only 25 states tested both 4th-grade reading and 8th-grade mathematics, leaving a significant number of states without tests into which items for those subjects could be embedded (see Table 2-3). It could be possible for states that do not administer reading or mathematics tests in grades 4 and 8, respectively, to embed reading or mathematics items in tests of other subjects, but context effects (see below) could be quite large.
TABLE 2-3 Number of States with 4th-Grade Reading, 8th-Grade Mathematics Assessments, or Both
|
Types of Testing Programs |
Number of States |
|
States with one or more separately scored 4th-grade reading components |
27 |
|
States with one or more separately scored 8th-grade mathematics components |
39 |
|
States with both separately scored 4th-grade reading and 8th-grade mathematics components |
25 |
|
SOURCE: Adapted form Olson et al. (in press). |
|
Context Effects
A context effect occurrs when a change in the test or item setting affects student performance. Context effects are gauged in terms of changes in overall test performance (such as the average test score) or item performance (such as item difficulty). These effects are important because they mean that an item or test is being presented in a way that could make it more difficult for one group of students than another, so that differences in student performance are due not to differences in achievement but to differences in testing conditions. With embedding, it is possible that the changes in the context in which the national items are administered will affect student performance. Such context effects can lead to score inaccuracies and misinterpretations.
An extensive body of research examines the effects of changes in context on student performance.5 Context effects vary markedly in size, sometimes in respect to differences in tests, but in other cases for unknown reasons. So the research provides a warning that context effects can be large, but it does not provide a clear basis for estimating them in any particular case.
Following are some of the many characteristics on which tests can differ:
-
wording of instructions for items of the same type;
-
page design with respect to font and font size, spacing of items, use of illustrative art, use of color, graphics, position of passages relative to related questions, and page navigation aids;
-
use of themes (e.g., a carnival as a setting for mathematics items);
-
integration of content areas (e.g., reading and language, mathematics computation and problem solving);
-
display of answer choices in a vertical string versus a horizontal string;
-
convention for ordering numerical answer choices for mathematics items (from smallest to largest or randomly) or ordering of punctuation marks as answer choices for language mechanics items;
-
characteristics of manipulatives used with mathematics items (e.g., rulers, protractors);
-
degree to which multiple-choice and constructed-response items are integrated during test administration;
-
how answer documents are structured for multiple-choice items and constructed-response items;
-
number of answer choices; and
-
use of ''none of the above" as an answer choice.
There are also issues of balance and proportion that occur when items from different tests are integrated, such as: equitable proportions of items that have the keyed (correct) response in each answer choice position and balance in the gender and ethnic characters in items and passages.
In general, as tests become longer, student fatigue becomes more of a factor. An item will tend to be more difficult if it is embedded at the end of a long test than if it is placed at the end of a short test. Similarly, student fatigue tends to be greater at the end of a difficult test—particularly one that involves a lot of reading and constructed-responses—than at the end of an easy test. This "difficulty context" can affect the difficulty of embedded items.
An important part of test standardization can be the amount of time that students are given to respond. When tests are lengthened or shortened, or items are moved from one test context to another, it is common to use rules of thumb related to average time-per-item to attempt to maintain comparable standardization conditions. However, such rules do not take into account the fact that some items can take more time than others. They also do not take into account the effects of the surrounding
context in terms of test length and test difficulty on the time a student may need for an embedded item.
Tests also vary in terms of their representation of different types of content, and this variance can produce a context effect for embedded items. For example, items related to a poetry passage, or to the Civil War, or to the Pythagorean theorem might be easier if they are embedded in another test with more of that same type of item than if they are embedded in a test with no similar items. The content of individual items can also interact. In constructing tests, careful review takes place so that the information in one item does not give away the correct answer to another item. When items from two tests are integrated, that same review would have to occur.
Constructed-response (open-ended) items bear special mention. The instructions and expectations (in terms of length, detail, conformity to writing conventions, etc.) for constructed-responses can vary substantially among tests. Also, many students are more likely to decline to answer a constructed-response item than a multiple-choice item, and the likelihood of responding is affected by the position of the item (Jakwerth et al., 1999). All these factors make constructed-response items particularly susceptible to context effects.
The possibility of context effects can be reduced by prudent, controlled test construction procedures such as: (1) keeping blocks of items intact and maintaining consistent directions and test administration; (2) maintaining the relative position of an item (or block of items) during a testing session; (3) maintaining consistent test length and test difficulty; and (4) making no changes to individual items. Nonetheless, even with careful attempts to follow these suggested test construction procedures, there can be no assurance that context effects have been completely avoided.
SPECIAL ISSUES PERTAINING TO NAEP AND TIMSS
Some embedding plans have the goal of reporting state or district achievement results in terms of the proficiency scales used by the National Assessment of Educational Progress (NAEP), a congressionally mandated achievement survey that first collected data 30 years ago.
Currently, NAEP assesses the achievement of 4th-, 8th-, and 12th-grade students in the nation's schools. Assessments occur every 2 years (in even years), during a 3-month period in the winter. The subject areas
vary from one assessment year to the next. For example, in 1996 students were assessed in mathematics and science; in 1998 they were assessed in reading, writing, and civics.
The choice of the NAEP scale for national comparisons may stem from its recent use in comparing states. Originally, NAEP was prohibited from reporting results at the state, district, school, or individual level (Beaton and Zwick, 1992), but legislation passed in 1988 allowed NAEP to report results for individual states that wished to participate. The first such assessment, considered a "trial," was conducted in 1990. The most recent NAEP state assessment included 43 states and jurisdictions. Whereas the national NAEP is administered by a central contractor, the state NAEP assessments are administered by personnel selected by state officials. (See Hartka and McLaughlin (1994) for a discussion of NAEP administration practices and effects.)
NAEP results for the nation and for groups are reported on a numerical scale of achievement that ranges from 0 to 500. The scale supports such statements as, "The average math proficiency of 8th-graders has increased since the previous assessment," and "35 percent of state A's students are achieving above the national average." To facilitate interpreting the results in terms of standards of proficiency, panels of experts assembled by the National Assessment Governing Board (the governing body for NAEP) established three points along the scale that represent minimum levels that were judged to represent basic, proficient, and advanced achievement in the subject area. The standards support the use of such phrases as "40 percent of 4th-grade students scored at or above the basic level on this assessment." Note that the three standards divide the scale into four segments, which are often called below basic, basic, proficient, and advanced. These descriptions lead quite naturally to the belief that the NAEP results are obtained by first computing scores for individual students and then aggregating these scores, but this is not the case. The goal of NAEP, as presently designed, is not to provide scores for individual students, but to estimate distributions of results for groups, such as students in the western part of the United States, African-American students, or students whose parents attended college. NAEP's survey design, which allows the most efficient estimation of these group results, differs from the design that would have been chosen had the goal been to optimize the quality of individual scores.
Some special properties of the NAEP design have a bearing on the possibility of embedding part of NAEP in another assessment. The important
differences between NAEP and conventional tests are summarized here (see also National Research Council, 1999a; National Research Council, 1999b). Technical details can be found in sets of papers on NAEP that appeared in special issues of the Journal of Educational Statistics (1992) and the Journal of Educational Measurement (1992).
First, NAEP is a survey, not an individual achievement test. Its design does not allow the computation of reliable individual scores; instead, it is designed to optimize the quality of achievement results for groups (e.g., "4th-grade girls whose mothers have at least a college education"). Second, students who participate in NAEP do not receive identical sets of test questions. For example, in the main portion of the 1996 assessment, more than 60 different booklets were administered at each grade. Third, because of NAEP's complex design, the proper statistical analysis of NAEP data requires an understanding of weighting and variance estimation procedures for complex samples and of data imputation methods. Ignoring the special features of the data will, in general, lead to misleading conclusions.
NAEP keeps testing burden to a minimum by testing only a small sample of students, and by testing each student on only a small sample of the items in the assessment. Each tested student receives two or three of the eight or more booklets of items that together constitute the assessment in a given subject area. The booklets are not alternate test forms that would provide similar scores for individual students. The content, difficulty, and number of items vary across the booklets, and no single booklet is representative of the content domain. This approach to the distribution of items to test takers, called matrix sampling, allows coverage of a broad range of content without imposing a heavy testing burden on individual students.
Within the context of NAEP, these features do not present a major obstacle since the proficiency results for students are examined only after they are pooled in estimating group results. As noted above, the data must be aggregated using elaborate statistical methods to obtain group estimates of proficiency for the nation and for specified groups. However, the nonequivalence of the various NAEP booklets within an assessment would be problematic if scores were to be obtained and compared for individual students.
One way to obtain individual student scores on NAEP would be to construct a test of reasonable length in each subject area that covered the same material as NAEP, albeit not as thoroughly. The proposed Volun-
tary National Tests (VNT) is such an effort. The VNT is being planned as a conventional test that will yield individual student scores on a scale as similar as possible to the NAEP scale. The VNT is intended to provide a common metric for reporting achievement results for all test takers. Many of the proponents of embedding hope to achieve this same goal without imposing an additional testing burden on individuals, districts, or states.
In many respects, the design of TIMSS mirrors that of NAEP (see Martin and Kelly (1996) for a detailed description of TIMSS). TIMSS, like NAEP, used matrix sampling of items to increase breadth of content coverage while limiting testing time. The assessment consisted of several different booklets, which were randomly distributed to students. TIMSS, like NAEP, was designed for efficient estimation of the proficiency of groups, rather than individuals; as in NAEP, individual scores are not reported for students.