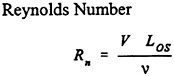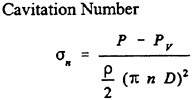Development of an Alternating Color Image Anemometry Method and Its Application in Ship Flow Measurements
S.-Y.Jaw, Y.-Z.Kehr (National Taiwan Ocean University, Taiwan, China)
ABSTRACT
In this study, the alternating color image anemometry (ACIA) method is proposed. Alternating color, multi-exposure particle image was recorded by a three-chip color CCD camera. Knowing that the red, blue, and green CCD chip of a 3-CCD camera has different sensitivity to the color of scattering light, the alternating color, multi-exposure particle image can be separated into sequential images by performing appropriate band processes. With sequential images available, the magnitude and direction of the velocity vectors can be determined from the digital correlation method. The ACIA method thus preserves the merits of both PIV and DPIV methods by analyzing a multi-exposure particle image using the digital correlation method of sequential images. The proposed ACIA method was first calibrated by measuring a constant speed rotating disk and an empty channel flow, and then applied to measure the turbulent wake behind a flat plate and a ship hull. Satisfactory results were obtained.
I. INTRODUCTION
In studying fluid mechanics, flow visualization is a useful technique to observe flow patterns. The classical methods of flow visualization, using dye tracers, hydrogen bubble, or smoke, provide valuable information about the behavior of the whole flow field. However, these methods can only provide qualitative, but not quantitative, velocity distribution. Recent advancement in optics, electronics and imaging techniques allow one to capture the instantaneous Eulerian velocity images for a flow field and thus make quantitative flow visualization possible. The quantitative flow visualization methods have attracted many investigations because of its characteristics that fluid motion was measured frame by frame. This is convenient as compared with traditional point-by-point measurement such as using hot-wire, or Laser Doppler anemometry, especially when the measurement of an unsteady flow field is required. As the velocity distribution is available, one may further take advantage of the digital data processing techniques to derive additional information, such as Reynolds stresses, streamlines, or vorticity distributions, etc..
Overview of quantitative flow visualization methods can be found from several literatures (Hesselink 1988, Adrian 1991, etc.). Recent development of quantitative flow visualization methods is briefly summarized in the following. Their advantages, and also limitations, are clearly explained.
1. Particle Streak Velocimetry (PSV) Method: Among the quantitative flow imaging techniques, the particle streak velocimetry method has been the most popular one since the PSV method is conceptually simple. In the PSV method, the light scattered from the particles that were seeded in the moving fluid was imaged by the recording medium such as film or CCD (Charge Coupled Device). The recorded image was streaks tracing the motion of the particle during the exposure time. By measuring the distance between the end points of the streak and knowing the exposure time, the velocity vectors are obtained at a discrete number of points. The directional ambiguity can be resolved by coding the image of the streaks asymmetrically with a light chopper (Khalighi 1989, Walter and Chen 1989) or using the color coding technique (Wung 1992). The advantage of the PSV method is that it is relatively simple. The drawback of the method is that the flow image is difficult to analyze when particles were densely seeded because the streaks thus obtained may overlap during the exposure time. In addition, the PSV method is inappropriate to measure highly transient or fluctuating flows since the finite streak length required to measure the velocity may not be available in the highly transient flows.
2. Particle Image Velocimetry (PIV) or Laser Speckle Velocimetry (LSV) Method: Unlike the PSV method, the particle image velocimetry method or the laser speckle velocimetry method analyzes the multiple exposure image recorded on a single frame by the Young’s fringe principle. Recently, the PIV method is given a broader definition to include the LSV method. The PIV method, which allows much denser seeding particles, was devised to overcome the limitations of
seeding concentration in the PSV method. In the PIV method, particles moving within the light sheet may be recorded photographically as pairs of particle image. The local fluid velocity was determined statistically from a small interrogating window on the developed photograph by sequentially measuring the displacement of the particle images within each window. The particle displacement within an interrogating window can be found by a variety of methods such as the Young’s fringe method (Meynart 1980 & 1982, Reynolds, et. al. 1985) or the 2-D auto-correlation analysis (He et. al. 1984, Vogel and Lauterborn 1988). One of the difficulties in implementing the PIV method is that there exists no characteristic to distinguish first image from second image on the double-exposure PIV photograph. As a result, measurement of the particle image displacement can not determine the direction of the fluid velocity, and the velocity was ambiguous in direction. To resolve the directional ambiguity, imaging shift (Adrian 1986 & 1988), and thus an introduced velocity, of a certain amount can be applied during the time interval between successive exposures. Subtracting the introduced velocity from the measured fluid velocity, flow direction can be determined from the sign, positive or negative, of the velocity vector. However, this technique tends to complicate the experimental setup and the subsequent analysis. In addition, the multi-exposure particle image should not overlap imposes restrictions on the spatial resolution and the dynamic range of the velocity measurement.
3. Digital Particle Image Velocimetry (DPIV) Method: In order to eliminate the limitations of the PIV method, another technique, called the digital particle image velocimetry method, was proposed in various manners since the late 1980s. Instead of taking multi-exposure images, the DPIV method analyzed a series of time sequential images captured either from a high-speed camera or from a video camera, with each frame containing a single-exposure image. The captured digital images were stored directly to computer memory through A/D converter without conventional picture taking and film development. The major advantage of DPIV method is that both the magnitude and direction of the velocity vector can be determined from the cross-correlation analysis as a series of single-exposure images were available (Willert and Gharib 1991). The cross correlation analysis of two sequential images is also better than the multi-exposure, auto-correlation analysis of the PIV method. The cross-correlation, i.e. the convolution of two sequential images, set restrictions on the particle paring from image one to two, which reduces the opportunity of miscalculating the magnitude and direction of particle displacement. A major disadvantage of the DPIV method is that the time interval between sequential images are limited by the frame speed, usually 30 frames per second, of the recording device. Since velocity is determined from dividing the particle moving displacement with the time interval of sequential images, the dynamic range of the velocity measurement is thus limited to tens of centimeter per second for typical applications. Higher speed recording device is available at the present time, which moderately increases the dynamic range of velocity measurement at the expense of high cost and sacrificing image resolution. Light chopper was also devised (Dabiri and Gharib 1996) to control the time interval between sequential images, which complicates the operation of image capturing, however.
From the descriptions stated above, it is found that each flow visualization method has its advantages and also drawbacks. What’s interesting is that the advantages of one method happen to be the limitations of other methods. For instances, by analyzing multi-exposure particle image, the dynamic range of the velocity measurement of the PIV method is highly increased while the determination of flow direction is ambiguous and requires additional equipment such as the image shifting devices. The DPIV method determines the flow direction easily from a series of sequential images, allows denser seeding particles, but the dynamic range of velocity measurement is limited by the frame speed of the recording device. One way to preserve the advantages of both the PIV and DPIV methods is to analyze the flow field from a multi-exposure particle image using sequential image files. This is accomplished in the proposed alternating color image anemometry (ACIA) method by separating a multi-exposure particle image into sequential images of different color.
II. THE PROPOSED ALTERNATING COLOR IMAGE ANEMOMETRY METHOD
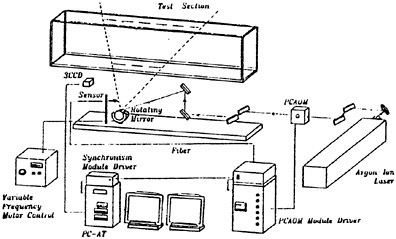
In the proposed ACIA method, the flow image was recorded by a three-chip, color CCD camera. The blue laser and green laser, deflected alternately from a 4 watt, Argon-Ion laser, were adopted as the light source. The laser beam was guided to a multi-facet, rotating mirror to generate alternating color, blue and green laser sheets. The particles seeded in the fluid was then illuminated by the two different, alternating color laser sheets. A single frame, even times exposure, alternating color particle image was then recorded by the red, blue, and green CCD-chip of a 3-CCD camera. Knowing that different color CCD chip has different sensitivity to the color of the incoming
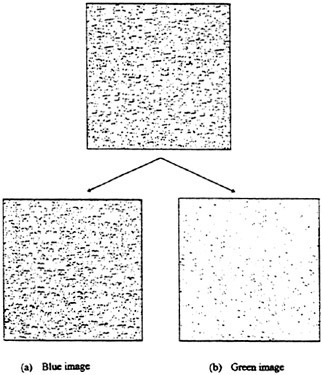
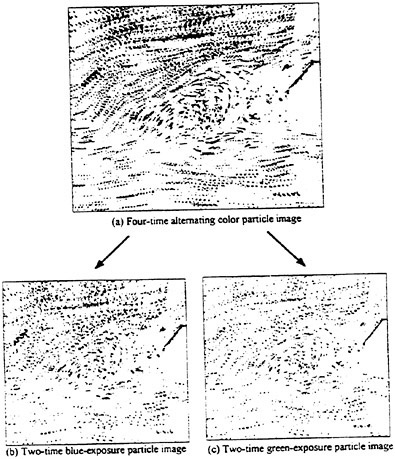
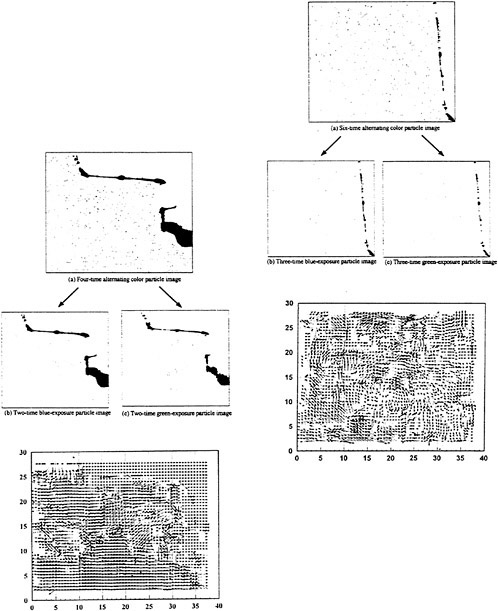
light, the recorded multi-exposure, alternating color particle image can be separated into different color, sequential images by applying appropriate band process. For instance, if the seeding particles were illuminated by the blue laser, the particle image intensity recorded by the blue CCD-chip was much higher than those recorded by the red and green CCD chips, as shown in Fig. 1(a). Similarly, as the seeding particles were illuminated by the green laser, the image intensity recorded by the green CCD chip was much higher than those recorded by the red and blue CCD chips, as shown in Fig. 1(b). To separate the single frame, multi-exposure, alternating color particle image into two sequential images, certain particle image intensity must be specified as the threshold to distinguish signal from noise. If the image intensity is lower than the threshold, it is considered as noise and its value is reset to zero, otherwise it is considered as a signal and its value is reserved. Comparing the image intensity of every pixel in the blue and green images with the threshold respectively, two sequential particle image files, one illuminated by blue laser and the other illuminated by green laser, can be obtained. Figure 2(a) shows a four times exposure, alternating color particle image of a rotating disk. Figures 2 (b), (c) show the separated, blue and green laser exposure sequential images of Fig. 2(a). With two sequential images available, the flow direction and velocity magnitude can be determined by analyzing the flow image using the spatial cross-correlation method, as those adopted in the DPIV method.
It should be emphasized that the time interval between the two separated sequential images is not limited by the frame speed of CCD camera but is determined from the frequency of the generated, alternating color laser sheet. Therefore the dynamic range of the velocity measurement of the ACIA method is much higher than that of the DPIV method. More importantly, each CCD chip of a 3-CCD camera has a resolution of 640*480 pixels, hence the image resolution of each color will not be deteriorated as the alternating color particle image were separated into sequential images of different color. Therefore, the ACIA method does not sacrifice the image resolution to increase the dynamic range of velocity measurement, which is generally the status as using a higher speed CCD camera in the DPIV method.
The experimental setup of the proposed ACIA method is shown in Figure 3. The test section is where the fluid motion was visualized and studied. Guiding an all line Argon Ion laser through a PCAOM (Poly-Chromatic Acousto-Optic Modulator), the monochromatic blue or green laser will be deflected from the PCAOM. Pulsed laser sheet was generated by directing the laser beam to a multi-facets rotating mirror (Rockwell et al. 1993). A fiber optic was placed at the upstream of the laser sheet. If a laser beam is detected by the fiber optic, a voltage signal was sent to the driver of the PCAOM to alter the output wavelength of the monochromatic laser. An alternating color, pulsed laser sheet can thus be generated by such an optical system. The frequency of the generated alternating color laser sheet is equal to the product of the number of mirror facets and the angular velocity of the rotating mirror. For the present setup, a twenty-facet polygon mirror rotates 30 to 500 revolution per second is used. The frequency of the generated alternating color laser sheet thus varies from 30 Hz (one-facet mirror by 30 rev/s) to 10,000 Hz (twenty-facet mirror by 500 rev/s), and the corresponding dynamic range of velocity measurement varies from several centimeters per second to more than three-hundred-fold of it.
III. Flow Image Analysis
Since it is difficult to trace the movement of individual particle between two sequential images, the displacement of a group of particles within a sampled subregion is determined. To find the displacement function s(m,n) in a sampled subregion, one may utilize a statistical technique that applies a spatial correlation method. The method involves the computation of auto-correlation, ![]() of the spatial input signals, f(m,n), and the cross-correlation,
of the spatial input signals, f(m,n), and the cross-correlation, ![]() of the spatial input and output signals, g(m,n). Because the input function f(m,n) correlates with itself in
of the spatial input and output signals, g(m,n). Because the input function f(m,n) correlates with itself in ![]() the maximum of the auto-correlation function is always located at the origin of the correlation domain. The origin thus is the initial position of all particles within the sampled subregion. Cross-correlation
the maximum of the auto-correlation function is always located at the origin of the correlation domain. The origin thus is the initial position of all particles within the sampled subregion. Cross-correlation ![]() is obtained by performing a convolution on the auto-correlation function
is obtained by performing a convolution on the auto-correlation function ![]() with the shift function s(m,n). This operation moves the peak of auto-correlation away from its origin by the average spatial displacement of particles in the sampled region, as shown in Fig. 4. Once the maximum value of
with the shift function s(m,n). This operation moves the peak of auto-correlation away from its origin by the average spatial displacement of particles in the sampled region, as shown in Fig. 4. Once the maximum value of ![]() within the sub-region is determined, one finds the shift function s(m,n) by measuring the distance between the origin and the location of the maximum value of
within the sub-region is determined, one finds the shift function s(m,n) by measuring the distance between the origin and the location of the maximum value of ![]() . Knowing the time interval between two sequential images, the magnitude
. Knowing the time interval between two sequential images, the magnitude
of the velocity vectors at the sampled sub-region can then be determined by dividing the shifted distance with the given time interval. And clearly the flow direction is pointed from the first image to the second.
Physically the cross-correlation function ![]() reveals the degree of matching among particles of initial and shifted images in the sampled subregion with a domain of m by n pixels. The location of the maximum of cross-correlation function represents the most probable displacement of the particles within the sampled area. To obtain the locally averaged displacement of particles, one may divide the digital image into hundreds, or thousands, of small interrogation windows. If the interrogation window is small enough, the averaged displacement of particles may be approximated as the most probable fluid movement at the corresponding area. To determine the full-field velocity distribution, these procedures are repeated on each interrogation window and over the entire flow image.
reveals the degree of matching among particles of initial and shifted images in the sampled subregion with a domain of m by n pixels. The location of the maximum of cross-correlation function represents the most probable displacement of the particles within the sampled area. To obtain the locally averaged displacement of particles, one may divide the digital image into hundreds, or thousands, of small interrogation windows. If the interrogation window is small enough, the averaged displacement of particles may be approximated as the most probable fluid movement at the corresponding area. To determine the full-field velocity distribution, these procedures are repeated on each interrogation window and over the entire flow image.
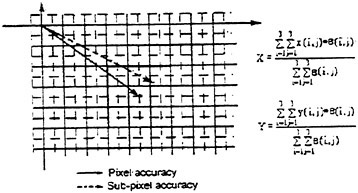
If the highest peak of the cross correlation function is selected to determine the representative velocity of the interrogating window, the accuracy of the velocity vector is limited to the size of pixel. That is, the velocity measurements can have differences only as small as the physical dimension of a pixel. To overcome this limitation, one remedy is to construct the centroid of the cross-correlation function using a weighted interpolation scheme (Chen et al. 1992, Lourenco et al. 1995). The weighted interpolation is performed once the peak location of cross-correlation is found, using the cross-correlation values of its surrounding pixels,
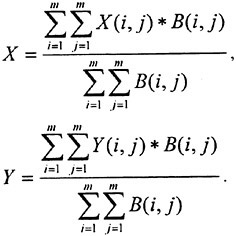
Here i and j is the indices of the correlation peak, X, Y represent the interpolated coordinates on the cross-correlation domain, and B(i,j)’s are the value of cross-correlation determined for the peak and its surrounding pixels. The size of the square region m was varied in proportion to the size of the interrogation spot for the resolution under consideration. Figure 5 illustrates the velocity measured before (pixel accuracy), and after (sub-pixel accuracy), the weighted interpolation. Although Lourenco et. al. (1995) pointed out from an analysis of a multi-exposure particle image using auto-correlation function that for small particle displacements, the determination of centroid will be contaminated by the auto-correlation peak at the origin and hence deteriorates the measurement accuracy. However, such a situation will not happen as analyzing two sequential images using cross-correlation function since there is no cross-correlation peak at the origin. Prasad, et. al. (1992) also pointed out that alternative peak location methods such as parabolic or Gaussian curve fits may yield smaller rms errors than the centroiding technique, nevertheless, that trend is true only for flows wherein the velocity gradient is negligible. When velocity gradients are comparable to those found in real flows the centroid method is actually superior to curve fit techniques. In this study, we found that the interpolation scheme indeed improves the velocity measurement, especially in determining the direction of velocity vectors.
For a steady flow, a series of flow images can be captured at distinct time. Any pair of sequential images can be used to perform the correlation analysis. Theoretically, one needs to process only one pair of two sequential images to measure the velocity. However, in practice different image pairs will often produce different velocities on the same location of the flow field due to the noise of disappearance or addition of particles on the selected image pair. To examine whether a measurement is consistent or not, one needs to define certain criteria to verify the measurements. The magnitude and the angle of the velocity vectors are the indices used for verification of consistency. For two sequential image pairs, if the difference of the velocity magnitude is less than 5% and the difference of the angle is less than 15 degrees (approximately 4% error compared with 360 degrees of allowance), the measured velocity was confirmed as a consistent data. If either one of the above criteria is not satisfied, the process is continued to the next image pairs. Similar processes were repeated for all image pairs until consistent data were found. If no consistent data were found after all image pairs had been examined, the measurement at the sampled area failed to produce meaningful data and no magnitude of the velocity at that location was assigned. The examination then moves to the next sample area. If the velocity data were crucial at a location, one may take new images with different time interval to process and make sure that the velocity is measured at the desired location.
IV Measurement of a rotating disc
The proposed ACIA method was first calibrated by measuring a rotating disk with known angular velocity. Particles were distributed randomly on a disk, with diameter 10 cm and rotating six revolutions per second. For such a case, the tangential velocity at the edge of the disk is about 2 m/s, far beyond the dynamic range can be measured by the DPIV method. The advantages of high dynamic range of velocity measurement of the proposed ACIA method over the DPIV method will thus be clearly manifested.
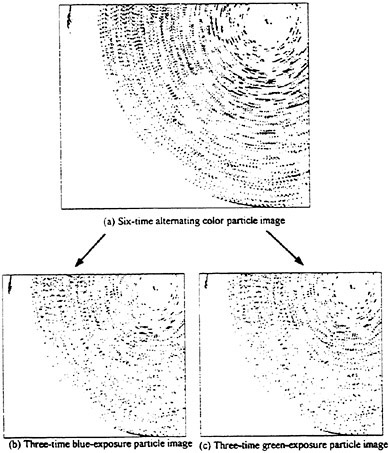
The multi-exposure particle image was recorded by the Sony DXC-9000, three-chip progressive scan color CCD camera. Each CCD chip has a resolution of 640×480 pixels. Hence the separated, blue and green images will have the same image resolution as the alternating color image, i.e. the image resolution will not be deteriorated as the alternating color image was separated into sequential images. The CCD was triggered externally as the blue laser was detected by the fiber optic placed at the upstream of the laser sheet. The total exposure times of the alternating color particle image was determined from the frequency of the pulsed laser sheet and controlled by the shutter speed of the CCD camera. Figures 6 (a), (b), (c) present a six times exposure, alternating color particle image and its separated, blue and green particle images respectively. The shutter speed was set to be 1/250 second and the frequency of the pulsed laser sheet is 1500 Hz. The physical dimension of the image is 88 mm horizontally and 66 mm vertically, covering more than one-quarter of the disk. The pixel size is 137.5 μm. Particles adopted were polymer spheres with diameters around 200 μm such that the particle to pixel ratio is about 2. According to Prasad et al. (1992), such a particle to pixel ration will minimize the total error of the velocity measurements.
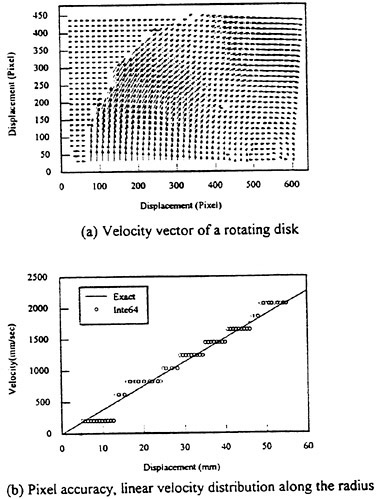
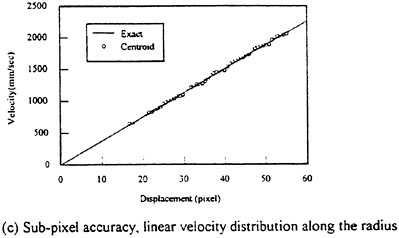
The separated, sequential images were used to calculate the velocity vectors by the digital correlation method with interrogation windows of size 64×64 pixels. For larger particles occupying more than one pixel, the centroid of the particles was found using their image intensity and coordinates on each pixel. Then the larger particles were represented by a pixel located at their centroid with unity intensity. It is found that using the particle centroid to perform the digital correlation analysis really improves the measurement accuracy. The velocity vector, magnitude and direction, of the clockwise rotating disk are clearly determined from the separated sequential images without any difficulty. To obtain a smoother velocity distribution, the interrogation window shifts only 10 pixels as calculating neighboring velocity vectors, allowing most of the interrogating windows overlapped. The particle number within each interrogating window was kept around one hundred to reduce the measurement uncertainty. Figure 7(a) shows the measured velocity vector of the rotating disk. The linear velocity distribution along the radius of the disk is shown in Figs. 7 (b), (c). Figure 7(b) shows the measured tangential velocity without performing sub-pixel accuracy analysis. For a pixel-accuracy calculation, the neighboring velocity can either has no difference or has a whole pixel difference, hence the velocity distribution is like a step-function. Figure 7(c) shows the ensemble averaged velocity distribution of 10 images using the centroiding sub-pixel accuracy analysis. Obviously, the measured velocity distribution is much better than the one shown in Fig. 7(b). For a linear velocity distribution, the centroid method indeed improves the measurement accuracy.
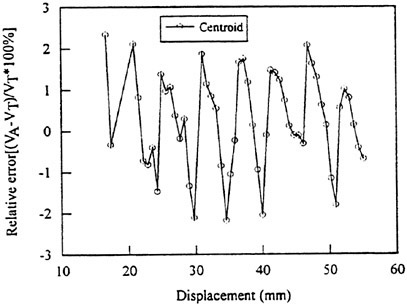
Relative error of each data point was evaluated as follows:
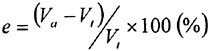
where Va is the velocity measured from ACIA method and Vt is the theoretical velocity of the solid body rotation at the point of measurement. Figure 8 shows the distribution of the relative errors of data points along the radius. The maximum error is less than 3%, which is smaller than the magnitude criterion set in the flow image analysis. It is thus concluded that the proposed ACIA method can successfully, and satisfactorily measure the velocity field of a rotating disk.
V. Measurements of a two-dimensional channel flow
The image of solid-body rotation does not contain some of the defects that occur in a real flow image, such as the pairing loss from one exposure to the next, or the strong velocity gradients near a solid boundary. All these imply that the sequential images may lose some of their correlation with each other. To further verify the applicability of the proposed ACIA method in conducting the quantitative, whole field flow measurement, an empty channel with known uniform velocity is selected as the second test case. Two imaging techniques, namely the proposed ACIA method and the aforementioned DPIV method, were adopted to measure an empty channel and experimental
results were compared with each other. In the DPIV method, a black and white CCD camera with a transfer rate of 30 frames per second is used. In the ACIA method, the alternating color laser sheet is generated by a single facet mirror rotating at a speed of 30 revolutions per second. The shutter speed of the color CCD was set to be 1/15 second. This way, a double exposure, alternating color image can be separated into two sequential images with 1/30-second time difference, comparable to the images taken from 30 frames per second black and white CCD camera. The image resolution is 640*480 pixels for both the black & white and the color CCD cameras.
The experiments were conducted in a circulation water tunnel with a test section 110 cm in length and 25 cm by 25 cm in cross section. The test fluid, water, was seeded with polymer spheres that has a specific weight 1.05, index of reflection 1.59, and 53 μm to 88 μm in diameter, so that the seeded particles will move with the fluid and scatter light as they were exposed to the laser sheet. In general, the adopted polymer spheres meet the primary requirements for the sizing of tracer particles. That is, they must be nearly equal in density to that of the working fluid for neutral buoyancy, the particles must not themselves disturb the flow field, and the particles must be detectable by the recording medium. Figures 9 present the alternating color and its separated flow images of the two-dimensional channel flow acquired from a color CCD camera.
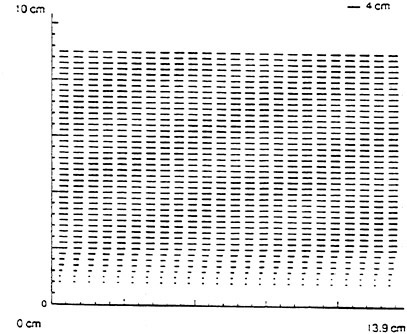
Limited by the frame transfer rate of the black & white CCD camera, the velocity measured using the DPIV method can not be high. Hence a channel flow with uniform velocity 3.28 cm/s was measured. The physical dimension measured is 10 cm in height and 14 cm in length. To increase the image resolution, the domain measured is divided into the near-wall and outer regions. For each domain, the pixel size is kept about 50 μm. To ensure that most of the particles were remained in the interrogating window and a clear cross-correlation peak exists between two sequential images, the maximum particle displacement was kept around 5 pixels only. Since the dimension of the measured physical domain is small, the size of interrogation window is set to be 32*32 pixels. Near the wall, where larger velocity gradients exist, the size of interrogation window is reduced to 32*20 pixels to obtain a better resolution of the near-wall flow. The particle number within each interrogation window was kept more than fifty to reduce the measurement uncertainty.
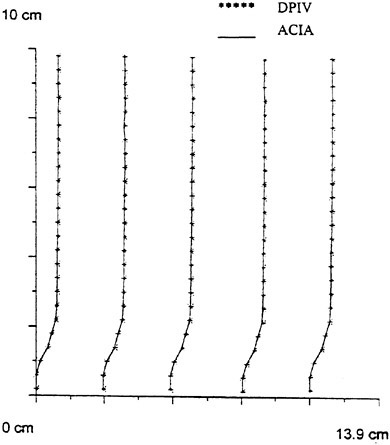
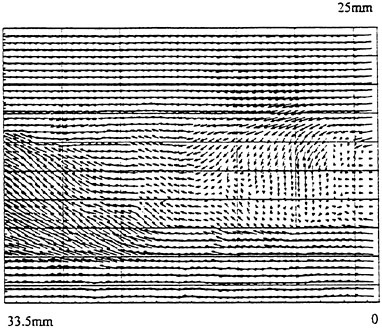
The velocity vectors obtained from the DPIV method is presented in Fig. 10. Velocity distributions obtained from the ACIA and DPIV imaging techniques are compared in Fig. 11 at five different locations. The uniform velocity measured from ACIA method is 3.32 cm/s, and from the DPIV method it is 3.34 cm/s, both are very close to the channel velocity, 3.28 cm/s. Again, the experimental results demonstrate that the proposed ACIA method can successfully measure the flow field.
VI. Turbulent wake flow measurements
As the proposed ACIA method has been successfully calibrated, it is then applied to measure the more complicate turbulent wake flows. A two-dimensional turbulent wake behind a flat plate is measured first. A flat-plate 20 cm long, 25 cm wide, and 0.8 cm thick is placed parallel to the flow in the circulation water tunnel. To reduce the disturbance to the flow, the leading and trailing edges of the plate is sharpen to a wedge shape with a tip angle of 60 degree. The uniform velocity of the incoming flow is 7 cm/s. The corresponding Reynolds number at the trailing edge of the flat plate is 1.4×104, far beyond the critical Reynolds number of a wake flow.
The physical dimension measured is 3.35 cm by 2.5 cm. The image resolution is 640 by 480 pixels, hence the pixel size is about 53 μm. The 500 Hz laser sheet was generated using 10-facet polygon mirror rotating at 50 revolution. The shutter speed of the CCD was set to 1/125 second such that a four-time exposure alternating color particle image can be acquired, as shown in Fig. 12. The measured velocity vector and velocity profiles at different locations are presented in Fig. 13 and 14 respectively.
The final flow field measured is the turbulent wake behind a container ship. A 1:550 scale double model of the “TOYAMA” container ship, 55 cm long, 5.5 cm wide, and 4.5 cm high, as shown in Fig. 15, was placed in the water tunnel. The inflow velocity was set to be 60 cm/s. The corresponding Reynolds number, based on the length of the container ship, is 3.3×105.
The flow around the ship was measured frame by frame from the ship bow to stern. Each frame has a physical dimension of 4.26 cm by 3.2 cm with resolution 640 by 480 pixels. The pixel size is 67 μm. Most of the flow images analyzed were four-time exposure, acquired using a 1000 Hz laser sheet generated from a 20-facet polygon mirror rotating at 50 revolution per second, with the shutter speed 1/250 second. Except in the separation zone right after the ship stern where the flow velocity is low, the flow
image analyzed is six-time exposure, acquired using a 750 Hz laser sheet with shutter speed 1/125 second. Some of the flow images and the measured velocity vectors are presented in Figs. 16. All these experimental results clearly manifest that the proposed ACIA method can successfully measure either a steady or unsteady flow field, from low to high dynamic range and without directional ambiguity.
VII. CONCLUSION
In this study, a new flow visualization technique, the alternating color image anemometry method, is proposed. It is realized from paper review that, to increase the dynamic range of velocity measurement, analyzing a multi-exposure particle image is necessary, while to eliminate the directional ambiguity of a flow, determining its velocity vectors from sequential images is preferred. The proposed ACIA method successfully preserves these advantages by separating a multi-exposure particle image into sequential images and analyzing them using the digital correlation method. Alternating color, blue and green, multi-exposure particle image was acquired from a three-chip color CCD camera. By performing an appropriate band process, the multi-exposure particle image can be separated into two sequential images. Each separated image has the same resolution as the original alternating color image, and the time interval between them is equal to the frequency of the alternating color, pulsed laser sheet. With two sequential images available, the flow direction and velocity distribution can be determined by digital correlation method.
The proposed ACIA method was first calibrated by measuring a constant speed rotating disk and an empty channel flow, and then applied to measure the turbulent wakes behind a flat plate and a container ship. The tangential velocity of the rotating disk, several meters per second, is far beyond the dynamic range that can be measured by the DPIV method, hence only the ACIA measurement was performed. It is demonstrated that high-speed velocity measurement and its direction determination is not a problem for the proposed ACIA method. Limited by the frame transfer rate, generally 30 frames per second, of the CCD camera, the velocity measured using the DPIV method can not be high. An empty channel flow with uniform velocity 3.28 cm/s was measured using both the ACIA and DPIV methods. Experimental results show that the velocity measurements from both methods are almost identical and very close to the velocity setting of the channel. Applications of the proposed ACIA method in turbulent wake flows measurement further manifest that the proposed ACIA method can successfully measure either a steady or unsteady flow field, from low to high dynamic range and without directional ambiguity.
REFERENCES
1. Adrian, R.J., “Image Shifting Technique to Resolve Directional Ambiguity in Double-Pulsed Velocimetry,” Applied Optics, Vol. 25, No. 21, 1986, pp. 3855–3858.
2. Adrian, R.J., “Electrooptical Image Shifting for Particle Image Velocimetry,” Applied Optics, Vol. 27, No. 20, 1988, pp. 4216–4220.
3. Adrian, R.J., “Particle Imaging Techniques for Experimental Fluid Mechanics,” Annual Review of Fluid Mechanics, Vol. 23, 1991, pp. 261–304.
4. Dabiri, D. and Gharib, M., “Generation mechanisms and sources of vorticity within a spilling breaking wave,” Twenty-First Symposium on Naval Hydrodynamics, Trondheim, Norway, June 24–28, 1996, pp. 520–533.
5. He, Z.H., Sutton, Μ.Α., Ranson, W.F., and Peters, W.H., “Two Dimensional Velocity Measurements by Use of Digital-Speckle Correlation Techniques,” Experimental Mechanics, June, 1984, pp. 117–121.
6. Hesselink, L., “Digital Image Processing in Flow Visualization,” Annual Review of Fluid Mechanics, Vol. 20, 1988, pp. 421–485.
7. Khalighi, B., “Quantitative Fluid Velocity Measurements by Automatic Analysis of Flow Visualization Images,” Experiments in Fluids, Vol. 7, No. 2, 1989, pp. 142–144.
8. Chen, C.J., Chen, L.J., and Kim, Y.G., “Quantitative flow visualization of three-dimensional flows,” Proceedings of the Sixth International Symposium on Flow Visualization,” Yokohama, Japan, Oct. 1992, 5–9, pp. 3–11.
9. Lourenco, L. and Krothapalli, A., “On the accuracy of velocity and vorticity measurements with PIV,” Experiments in Fluids, Vol. 18, 1995, pp. 421–428.
10. Meynart, R., “Equal Velocity Fringes in a Rayleigh-Benard Flow by a Speckle Method,” Applied Optics, Vol. 19, No. 9, 1980, pp. 1385–1386.
11. Meynart, R., “Convective Flow Field Measurement by Speckle Velocimetry,” Revue De Physique Appliquee, Vol. 17, 1982, pp. 301–
305.
12. Prasad, A.K., Adrian, R.J., Landreth, C.C., and Offutt, P.W., “Effect of resolution on the speed and accuracy of particle image velocimetry interrogation,” Experiments in Fluids, Vol. 13, 1992, pp. 105–116.
13. Reynolds, G.A., Short, M., and Whiffen, M.C., “Automated Reduction of Instantaneous Flow Field Images,” Optical Engineering, Vol. 24, No. 3, 1985, pp. 475–479.
13. Rockwell, D., Magness, C., Towfighi, J., Akin, O., and Corcoran, T., “High image-density particle image velocimetry using laser scanning techniques,” Experiments in Fluids, Vol. 14, 1993, pp. 181–192.
14. Vogel, A. and Lauterborn, W., “Time Resolved Particle Velocimetry Used in the Investigation of Cavitation Bubble Dynamics,” Applied Optics, Vol. 27, 1988, pp. 1869–1876.
15. Walter, J.A. and Chen, C.J., “Flow Visualization of Particle Streaks in Offset Channel Flow by a Direct CCD Imaging Process,” The Winter Annual Meeting of ASME, San Francisco, CA., FED-85, 1989, 115–120.
16. Willert, C.E. and Gharib, M., “Digital Particle Image Velocimetry,” Experiments in Fluids, Vol. 10, 1991, pp. 181–193.
17. Wung, T.S. and Tseng, F.G., “A Color-Coded Particle Tracking Velocimeter with Application to Natural Convection,” Experiments in Fluids, Vol. 13, 1992, pp. 217–223.
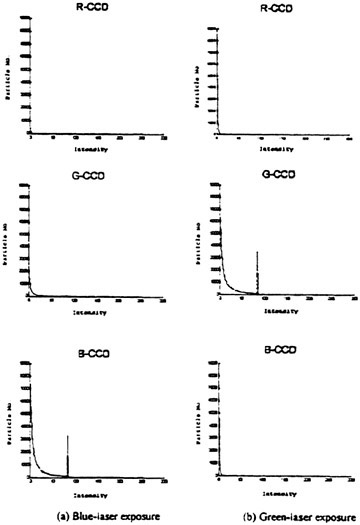
Figure 1 Alternating color image intensity distribution of a 3-CCD camera.
Figure 2 Four-time exposure, alternating color particle image of a rotating disk.
DISCUSSION
T.Huang
Newport News Shipbuilding, USA
Could you provide the results of your measurement uncertainty analysis?
AUTHORS’ REPLY
The main difference between the ACIA and the DPIV methods is in how the sequential images were obtained. Their image, and uncertainty analyses are the same. Figure 8 shows the relative error distribution, compared with the theoretical velocity, along the radius of the rotating disc. By properly controlling the particle size, particle density, and particle displacement, the uncertainty of measurements is within two percent.
DISCUSSION
Y.Himeno
Osaka Prefecture University, Japan
The flow is more or less three-dimensional. How can you treat the particle image which goes out of the sheet of the light?
AUTHORS’ REPLY
The flow is three-dimensional, and certainly some seeding particles will move out of the image plane. However, the velocity vectors are determined from the cross correlation analysis of two sequential images. If the time interval between two sequential images is short and particle density is high such that most of the particles were kept within the interrogating window of the two sequential images, the correlation analysis will result in a clear correlation peak. The distance from the correlation peak to the origin of the correlation map represents the most probable movement of particles within the interrogating window. Determining the velocity vectors this way, the moving out of particles will not cause any trouble for the image analysis.
Investigation of Propeller-Induced Pressure Pulses by Means of High-Speed Video Recording in the Three-Dimensional Wake of a Complete Ship Model
C.Johannsen (Hamburg Ship Model Basin, Germany)
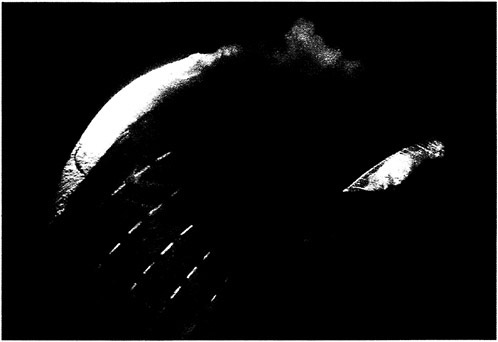
Fig. 1: Bursting Tip Vortex Cavitation in Full Scale
ABSTRACT
The prediction of propeller induced hull pressure pulses is—beside numerical calculations—normally based on model tests carried out in a cavitation tunnel. This prediction represents a vital part of the daily work of ship model basins. To improve the reliability of hull pressure measurements an extensive research project has recently been finished at HSVA.
The paper reports the new testing technique used and the results obtained in this project. The first time worldwide High Speed Video (HSV) records were taken from a cavitating propeller acting in the
realistic three-dimensional wake field of a complete ship model installed in a large cavitation tunnel. The correlation between these videos and simultaneously recorded hull pressure time functions provided valuable insights in the mechanisms and full scale correction requirements of those hull pressure measurements.
The paper shows that different hydrodynamical effects contribute to the peaks of the hull pressure time function, which have to be scaled individually. Especially in case of propellers with pronounced tip vortex cavitation and vortex bursting, this individual handling provides an improved reliability of the full scale prediction. A pragmatic correction method is proposed, based on individual treatment of the time function peaks in dependance of their hydrodynamic origin.
INTRODUCTION
Beside cavitation erosion the propeller induced hull pressure pulses represent the main problem concerning propeller cavitation that ship yards, ship owners and propeller designers are faced with. The increasing reliability of numerical tools, as well as the performance of cavitation tests in the realistic three-dimensional wake field of complete ship models installed in large cavitation tunnels, were suitable to reduce this problem. Nevertheless, the increasing demands upon the propellers of fast passenger vessels and extremely large container ships require the progress to more reliable pressure pulse predictions in the future.
The modern trend to skew propellers with unloaded blade tips was certainly successful in reducing pressure pulses in general, but it is often addressed to be responsible for the rise of pressure pulses of higher order. The physical effects leading to pressure pulses of higher blade rate order are not fully understood. Phenomena as tip vortex cavitation and especially vortex bursting as shown in Fig. 1 in full scale are often mentioned in this context. These effects are very complex since viscosity, compressibility and wake inhomogeneity are of major influence.
Mainly financed by the German Ministry of Research and Technology a large research program started at the Hamburg Ship Model Basin (HSVA) in 1996 to overcome this problem. The influences of
-
unintentional model vibrations
-
the restricted cross section of the cavitation tunnel
-
differences between model and full scale wake
-
oxygen content of the tunnel water
were investigated. Except the first two aspects, which are not addressed in this paper, the findings of this project are described in the following sections.
FUNDAMENTALS
Normally the judgement of propeller induced hull pressure pulses is based on the examination of results obtained from the harmonic analysis of the hull pressure time functions. This procedure is certainly appropriate for the global comparison of different results, especially with respect to hull vibrations induced by those pressure pulses. Nevertheless, for model to full scale correlation studies this procedure is not sufficient.
In general three different physical effects are addressed to contribute to the propeller induced pressure pulses:
-
The displacement effect of the propeller blade itself
-
the influence of the sheet cavitation rapidly growing and shrinking due to the varying static pressure and the inhomogeneity of the wake field
-
the influence of the propeller loading.
A fourth aspect, which has also been addressed in [1], will be introduced in the following sections. It results from the cavitating tip vortex and especially from its bursting.
Being faced to deviations between model and full scale results, and seeking for scaling laws to overcome these deviations, it has to be expected that these physical effects may scale differently. Different occurrences during the propeller revolution (propeller blade entry into the wake peak, vortex bursting etc.) create different peaks in the hull pressure time function. The height of these peaks depends on the special properties of the wake, i.e. the hull form, as well as on the propeller geometry and loading. The correlation of these peak heights between model and full scale certainly suffers from scale effects.
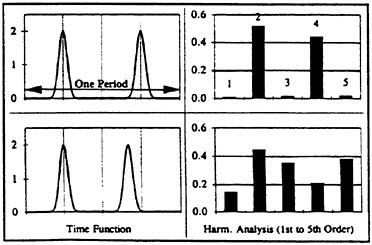
Fig. 2: Artificial Time Functions
Independent of this scaling, the contribution of the peaks to the different components of the harmonic analysis depends on the relative location of the peaks to each other at the time axis. This location depends on geometric parameters such as skew angle or longitudinal distance between propeller plane and rudder. It is therefore an individual characteristic of the whole arrangement, differing from ship to ship.
By means of artificially created time functions Fig. 2 shows that two periodic signals, each comprising of two identical peaks, result in completely different harmonic components, just because the location of the peaks slightly differs. For this reason it must be impossible to establish a universally valid method simply correcting one or the other of these harmonic components. Instead of this the time function peaks have to be treated individually, taking their hydrodynamical origin into account. From a subsequent Fourier Transformation the properly scaled harmonic components will than result automatically.
This individual treatment of course requires the previous identification of the effects leading to the different peaks in the hull pressure time function. Beside the measurement of the hull pressure with highest possible time solution, the simultaneous cavitation observation by means of a HSV system has been found to be a valuable tool for this purpose.
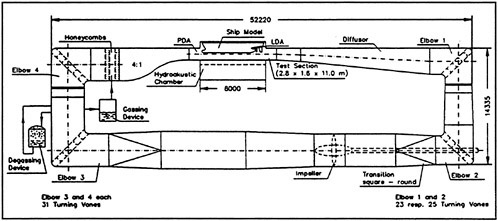
Fig. 3: HYKAT, the Large Hydrodynamics and Cavitation Tunnel of HSVA
THE TEST SETUP
The Hydrodynamics and Cavitation Tunnel
Fig. 3 gives a schematic view of HYKAT, the large Hydrodynamics and Cavitation Tunnel of HSVA. The test section of HYKAT is 2.8 m wide, 1.6 m high, 11 m long and allows the installation of the whole ship model as it is also used for propulsion tests in the towing tank. The ship model is installed in a special trunk, which is located above the test section. The underwater part of the model penetrates into the test section of HYKAT, while its upper part is mounted at a supporting frame inside the trunk. Beside the model wooden plates are mounted in line with the horizontal top of the tunnel to suppress the wave system of the ship. This way, the tunnel water speed can be increased deviating from Froudes scaling law and allowing a considerably higher Reynolds number than in the towing tank. To allow a quick pressure variation, the whole trunk as well as the ship model inside is filled with water. Therefore, the whole instrumentation, comprising of cameras, pressure transducers, dynamometer and motor, have to be water tight.
The tunnel is driven by two electric motors of 1,700 kW total power, acting on an impeller of 3.75 m diameter and allowing a maximum speed of 12.6 m/s in the test section.
A gassing and degassing device is available to vary the oxygen content of the tunnel water. Beside the possibility of difficult void fraction measurements by a Phase-Doppler-Anemometer [2], the normal procedure at HSVA is just to determine the oxygen content of the water by an O2-probe. Based on former investigations [3], a value of about 80% saturation is usual for cavitation tests in HYKAT. A detailed description of HYKAT is given in [4].
Conventional cavitation observations are carried out by stroboscopic light in combination with video cameras installed inside the model. This way, one picture of the cavitation behavior per revolution can be obtained at various angular propeller blade positions. Kulite pressure pick-ups of 3.7 mm diaphragm diameter are installed flush with the model hull above the propeller. The received pressure signals are amplified by self developed amplifiers and
fed into an analog-digital (AD) converter of Data Translation type. A sampling rate of 10,000 values per second can be processed for 32 channels simultaneously. The results are stored in a PC allowing subsequent Harmonic Analysis, Fast Fourier Transformation (FFT) as well as the output of time functions.
The High Speed Video Recording
A HSV system, type EKTAPRO, model 4550, had been lent from KODAK Stuttgart, Germany, for the project. It comprises of a special camera, connected by two multi-pole cables to a signal processor. The camera has a pick-up device of 256× 256 pixels, allowing the differentiation of 256 grey values. At this resolution 4,500 frames per second can be stored by the signal processor over an interval of 0.7 seconds. This is enough to accumulate the pictures of several model propeller revolutions with an angular spacing of about 2°, and to replay them afterwards in slow motion to a conventional video recorder. With reduced number of pixels and by means of extreme illumination the recording rate can be exceeded to more than 40,000 frames per second, which was not appropriate for the present investigations. Beside the received video picture, the signal processor fades the elapsed time as well as an individual frame number into the screen, allowing a subsequent identification of the different frames.

Fig. 4: Model Arrangement
The HSV camera was mounted in a water tight housing consisting of a 900 mm long plastic tube with a perspex front plate. The housing installed inside the ship model was linked with the trunk side wall by a rubber tube of 100 mm diameter to allow a water tight connection between camera and signal processor. For the propeller observation a perspex window was arranged on starboard side in the model hull above the propeller, as illustrated in Fig. 4. Two 2,000 W spotlights were necessary to illuminate the model propeller properly through the side windows of the tunnel.
The AD converter was triggered by the video processor to make sure that the acquisition of video frames and pressure signals is simultaneous. Once per revolution a stroboscopic flash was given, which was visible in the HSV recording. Furthermore, the trigger impulse of this flash was recorded by an additional channel of the AD converter to give an exact coordination between video frames and pressure pulses.
A comparable investigation on cavitation development and noise has been reported in [5], based on a similar HSV technique. Nevertheless, these investigations were carried out behind a dummy model installed in a smaller cavitation tunnel, i.e. the HSV observation was carried out from outside. The HSV system used was limited to 1000 frames per second, which is judged by the authors as being not sufficient.
The Ship
The high speed video recordings were carried out with a model of the C11 class container ship “APL China”, which had been built in 1995 by the Howaldtswerke—Deutsche Werft AG, Kiel, Germany, for the American President Line (APL).
Tab. 1: Main Dimensions of “APL China”
|
Length Between Perpendiculars |
262.0 m |
|
Bredth |
40.0 m |
|
Design Draught |
12.0 m |
|
Displacement |
71,700 m3 |
|
Capacity |
6,100 TEU |
|
Max. Power |
48,840 kW |
|
Propeller Diameter |
8.3 m |
|
No. of Blades |
5 |
|
Blade Area Ratio AE/A0 |
0.815 |
|
Mean Pitch Ration Pm/D |
0.945 |
The ship is driven by a 5-bladed propeller with a diameter of 8.3 m. The main dimensions of ship and propeller are given in Tab. 1. Full scale pressure pulse measurements were carried out by HSVA in May 1995 in the Baltic Sea. During these sea trials the ship was trimmed to design draught by flooding some of the cargo holds. The test procedure for those measurements is described in detail in [6]. Unfortunately, no full scale cavitation observations were carried out aboard of this ship.
A model of the ship existed at HSVA from former investigations. It was built from wood to a scale of 1:32.36. The arrangement of the pressure pick-ups agreed exactly with the full scale situation and is shown in Fig. 4.
Test Conditions
The model tests described here were carried out subsequent to the full scale measurements and under exactly the same conditions as obtained during one of the sea trial test runs. They are summarized in Tab. 2.
For the pressure fluctuation measurements the tunnel pressure was determined assuming σn-identity between ship and model for a horizontal plane through 80% propeller radius in the 12 o’clock blade position.
Tab. 2: Test Conditions
|
Draught |
12.0 m |
|
Estimated Stern Wave |
2.1 m |
|
Propeller Speed |
111.9 RPM |
|
Ship Speed |
26.2 kts |
|
Delivered Power |
47,722 kW |
|
⇒ σn |
0.163 |
|
KQ |
0.0296 |
|
Model Propeller Speed |
27.5 RPS |
NUMERICAL CALCULATIONS
The procedure used in this project for the numerical calculation of propeller induced pressure pulses is based on propeller thrust, shaft speed, the detailed propeller geometry and the wake field obtained from model tests.
In a first step the pressure distribution on both sides of the propeller blades is determined in behind condition. For this purpose a transient Vortex-Lattice method is used [7,8]. In the calculation procedure the advance coefficient based on ship speed is varied until the required mean thrust coefficient KT is met. The unsteady pressure distribution on the blades is subsequently calculated every 6°. These results are valid for a fully wetted propeller blade. In a following step the blades are “allowed” to cavitate and the blade pressures are modified by cavitation accordingly. A pressure condition and an iterative procedure are used to find the length and the thickness of the sheet-cavitation on the blades. To set up the pressure condition it is necessary to relate the vapor pressure of water to the fully wetted pressure coefficient calculated before.
The theoretical calculation method for the hull pressure fluctuations predicts the time dependent pressure field at arbitrary field points, but in an unlimited flow domain. The influence of the ship contour is taken into account by means of a solid boundary factor of 2. This factor can be regarded as an upper limit for any field point on the hull. The fluctuating part of the pressure field around the propeller is mainly excited by the cavitation on the blades. In addition the calculation method takes into account the unsteady blade loading and the effect of blade thickness.
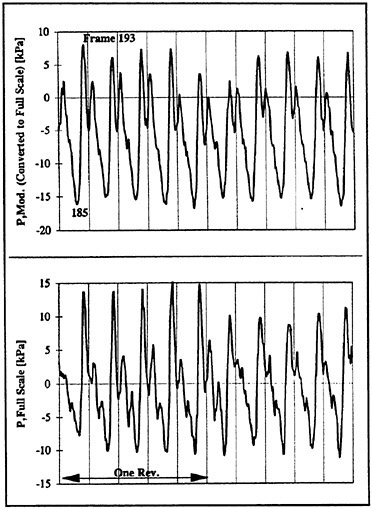
Fig. 5: Time Functions of Hull Pressure
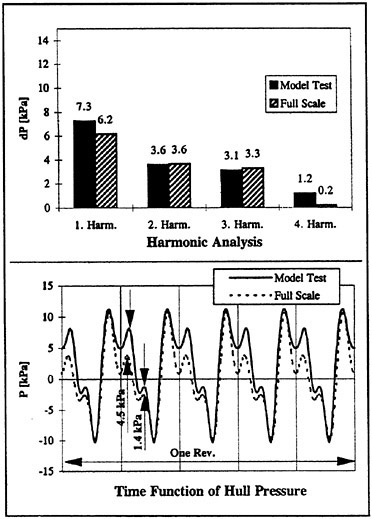
Fig. 6: Averaged Time Functions
RESULTS
In Fig. 5 time functions of the hull pressure are shown, which were obtained under the conditions given in Tab. 2. The upper diagram shows the model values, while in the lower diagram the corresponding result of the full scale sea trial is given. Both functions were received by a pressure pick-up located directly above the propeller plane at ship center line as pin-pointed in Fig 4. Both functions were recorded with an angular solution of about 2° of a propeller revolution. The model values were converted to full scale assuming KP-identity between ship and model, with
The vertical lines in these diagrams, as well as in all following time function diagrams, indicate the 12 o’clock positions of the propeller blades, i.e. the time signals are shown here for two complete propeller revolutions. In theory, for the 5-bladed propeller, 10 equal periods should be expected in the graphs, created by the propeller blades passing the ship or model hull. Nevertheless, model and full scale measurement show a slight variation of the theoretically periodic signals from one blade passing period to the other. In the model test this variation is

Fig. 7: High Speed Video Recording of Tip Vortex Bursting
probably caused by a non-uniform distribution of bubbles in the circulating tunnel water. In full scale a similar inhomogeneity may rather be caused by ship motions. Furthermore it has to be mentioned that the mean value of the functions is accidental since it depends on the actual zero adjustment of the signal amplifiers.
Although the agreement of model and full scale time function seems to be very good at the first glance, the above mentioned variation requires the previous determination of characteristic time signals, i.e. to average the signals of several propeller revolutions. For this purpose a harmonic analysis
was carried out, which resulted in the upper diagram of Fig. 6. A very good agreement for the higher blade rate harmonics can be seen in this figure, while the first harmonic shows a discrepancy of 1.1 kPa. For people experienced in the measurement of hull pressure pulses this deviation may appear as sufficiently small. Nevertheless, the following investigations will show, that the same hydrodynamical effects as described below for “APL China” may lead to much bigger deviations in other cases.
Previous to the detailed analysis of the time functions it has to be mentioned that the full scale pressure amplitudes of 6.2 kPa did not cause any vibration problems aboard of “APL China”.
Neglecting the mean value a0 as well as the non-harmonic orders ![]() from the Fourier Transformation, characteristic averaged time functions could be recalculated for model and full scale, which are compared in the lower diagram of Fig. 6. Both model and full scale function show a similar characteristic, comprising of three positive pressure peaks per blade passing period. In the following the hydrodynamic origin of these peaks will be investigated by means of the HSV recordings as well as conventional cavitation observations under stroboscopic light.
from the Fourier Transformation, characteristic averaged time functions could be recalculated for model and full scale, which are compared in the lower diagram of Fig. 6. Both model and full scale function show a similar characteristic, comprising of three positive pressure peaks per blade passing period. In the following the hydrodynamic origin of these peaks will be investigated by means of the HSV recordings as well as conventional cavitation observations under stroboscopic light.
The Bursting Tip Vortex
As indicated in Fig. 5 (upper diagram), the first and most excited peak refers to the HSV frames No. 185 to 193, which are shown in Fig. 7. Unfortunately, these video prints can only give an idea of the very impressive motion picture shown during the oral presentation of the paper. The motion picture clearly shows (much better than the video prints) that this first pressure peak results from the implosion of the cavitating tip vortex behind the propeller blade. It is known from several full scale cavitation observations that this implosion similarly occurs in full scale. Fig. 1 gives an impressive example, taken from [9] for the container ship “Humbodt Express”.
Comparing the averaged time signals in Fig. 6 at this major peak, it can be seen that the full scale similarity of the model time function is excellent. In this context it has to be mentioned that the model tests were carried out at the “normal” HYKAT oxygen content of 80% saturation. In the following section it will be shown that this O2 level plays a very important role for the similarity especially at this peak. Of course this most excited pressure peak is dominant for the result of the harmonic analysis. Assuming that the ships investigated in [3] also showed pronounced vortex bursting, it is therefore not astonishing that this former study already resulted in an optimum HYKAT gas content of 80% saturation, although no detailed analysis of the pressure time functions had been made.
At this phase of the propeller rotation, i.e. at this first peak, no explanation for the deviations between model and full scale harmonic components can be found. Nevertheless, for future judgement of propeller cavitation behavior it may be helpful to know that vortex bursting is of this dominant effect regarding propeller induced hull pressure pulses.
The Sheet Cavitation
For the hydrodynamic origin of the second peak, reaching its maximum when the propeller blade generator line is located 11° behind the 12 o’clock position (Fig. 6), the HSV recordings give no explanation. Unfortunately, the stern shape of “APL China” did not allow the installation of the observation window right above the propeller. Instead of this the window was arranged on starboard side and slightly in front of the propeller plane (Fig. 4). From this position the vortex bursting could properly be observed. Nevertheless, to explain the second time function peak, conventional video observations under stroboscopic light had to be used, resulting in the sketches shown in Fig. 8. These observations were made by a small conventional camera installed on port side in a water tight housing of 30 mm diameter, and almost flush mounted with the model hull.
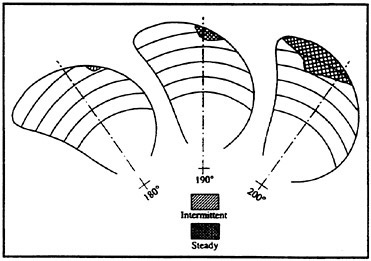
Fig. 8: Sketches from Conventional Cavitation Observation (Back Cavitation)
From the sketches in Fig. 8 the rapid increase of the sheet cavitation to its maximum extent can be seen, occurring between 12 o’clock (180°)
and an angular position of 20° starboard (200°). Since at 200° a thickness of this sheet of about 6 mm (195 mm in full scale!) could be estimated by observations through the tunnel windows, this increase represents an extreme velocity of cavity volume expansion, which is probably responsible for the second peak of the hull pressure function. The static pressure is almost constant in this small angular range, i.e. this increase is exclusively caused by the entry of the propeller blade into the region of maximum wake. This can be confirmed by Fig. 9, were the model wake, obtained in HYKAT in absence of the propeller, is shown in form of lines of constant axial velocity (made non-dimensional with the tunnel water speed). The propeller blade in its 190° position is added in this diagram, showing that in this position the blade center (80% D) is exactly located at the point of minimum velocity. A local wake of more than 40% can be read from Fig. 9 in this location.
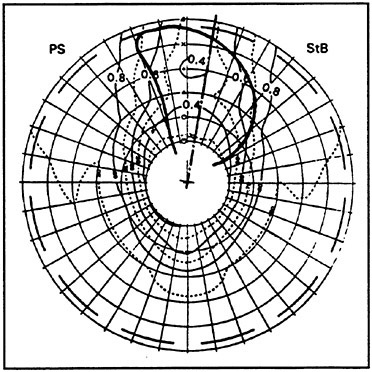
Fig. 9: Model Wake Field of “APL China” (Lines of Constant Axial Velocity VA/VM)
It is known from several publications, that the ship wake is exaggerated in the model test due to the considerably lower Reynolds number. Although the testing technique in HYKAT allows to deviate from Froudes scaling law, i.e. to increase the tunnel water speed and this way the Reynolds number, there was still a factor of Rn,ship/Rn,Model=71 obtained. Several scaling procedures can be found in the literature to correct the model wake for the full scale Reynolds number. Nevertheless, all of them suffer from uncertainties resulting from the small number of available full scale wake measurements. In the present project a quite simple method was used for this purpose [10], just applying a scale dependent factor

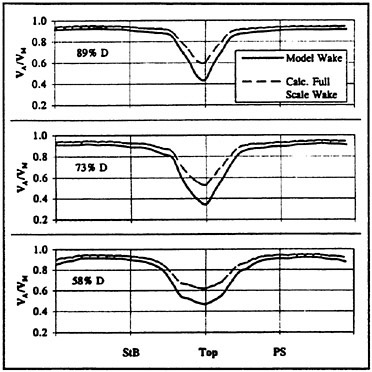
Fig. 10: Comparison of Model Wake and Calculated Full Scale Wake
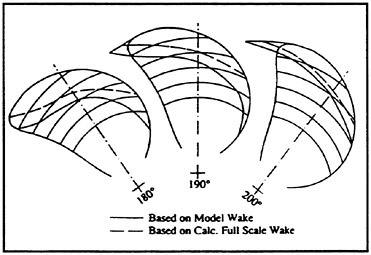
Fig. 11: Influence of Wake on Calculated Back Cavitation Extent
The result can be found in Fig. 10, showing a comparison of measured model wake and calculated full scale wake for three different measuring radii of “APL China”. As expected, the 12 o’clock wake peak, which in case of single screw ships is mainly caused by the boundary layer of the ship hull, is considerably reduced in full scale.
To investigate the influence of this wake reduction on the second peak in the hull pressure time function, comparative numerical calculations were carried out by means of the method described in the foregoing section. The calculated cavitation extent is compared Fig. 11. Using the model wake as input for this calculation, a considerably larger cavitation amount at 200° and especially an increased velocity of cavity volume expansion can be seen. The hull pressure time functions derived from this cavitation behavior are compared in Fig. 12. The result is shown for 2/5 of a propeller revolution, i.e. the vertical line in the center of the diagram again indicates one propeller blade in its 12 o’clock position.
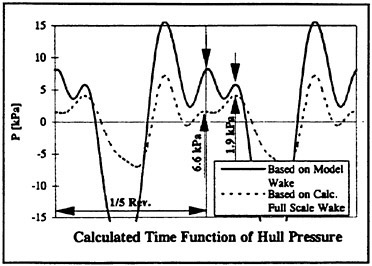
Fig. 12: Influence of Wake on Calculated Time Functions of Hull Pressure
It is interesting, that the character of these functions agrees quite well with both model and full scale measurements. Nevertheless, when using the model wake as input for the calculation, the first peak of the time function is considerably overestimated. This is astonishing, since this peak had been identified above as being caused by tip vortex bursting, which is an effect not considered in the calculation method. This large peak was dominant for the first harmonic pressure amplitude of 12 kPa, which was obtained from this calculation and which is far away from reality. Further investigations for the improved reliability of those calculations, which are no object of this project, should therefore focus on better modeling of this first peak of the hull pressure time function.
Coming back to the second peak of the function, a reduction of 6.6 kPa can be seen in Fig. 12, resulting from the reduced inhomogeneity of the assumed wake. This reduction agrees quite well with the discrepancy obtained between measured model and full scale time function at this peak. As indicated in Fig. 6 a difference of 4.5 kPa was found. This result represents a quite good confirmation of the assumption above: Indeed this peak seems to be caused by the velocity of cavity volume expansion, which is exaggerated in model scale due to the exaggerated 12 o’clock wake peak. For this reason it can be stated here, that a reduction of this peak in the hull pressure time function is recommended, when scaling model measurements to full scale. Comparative calculations should be used to estimate the amount of this reduction. The discrepancy between 4.5 kPa (measured wake influence) and 6.6 kPa (calculated wake influence) indicates that the wake correction assumed as input for the calculation is probably too strong. For this reason a further improvement could probably be achieved from “playing” with this correction method.
Another confirmation for the above findings can be derived from hull pressure measurements carried out for twin screw ships in HYKAT. As recently reported in [11], those measurements generally show a good agreement between model and full scale results. This can be explained by the above findings, since the wake field of these ships mainly suffers from the shaft inclination, resulting in an inhomogeneity of the radial and tangential velocity components. This effect is properly simulated in HYKAT when using complete ship models with realistically inclined shafts. The frictional wake, which is responsible for the above scaling problem, does not play this important role for twin screw ships.
The Displacement Effect of the Blade Itself
From Fig. 6 a third but very small positive pressure peak can be found for a blade position 22° behind 12 o’clock on starboard side. Unfortunately, neither from the conventional nor from the HSV video recordings the hydrodynamic origin of this peak could be identified. The reasonable assumption, that this peak would be caused by the displacement effect of the propeller blade itself, can definitely be excluded by means of model measurements at high tunnel pressure level. These measurements, carried out in absence of any cavitation occurrence, led to a hull pressure time function varying chaotically, but with peaks below 1 kPa (transformed to full scale via KP). Both the hydrodynamic and electronic background disturbance was obviously larger than the peaks created by the non-cavitating propeller blades.
Although this negligible displacement effect is not unusual for container ship propellers, it has to be mentioned that in case of fast twin screw ships a contrary effect has often been seen: For those ships the harmonic analysis of the non-cavitating condition sometimes results in an even larger first harmonic component than this of a condition with fully developed cavitation. Of course, the occurrence of cavitation does not really lower the pressure peak created by the displacement effect of the blade. But the creation of additional peaks resulting from the cavity volume expansion (and/or bursting tip vortex) may sometimes—depending on the location of these peaks on the time axis of the hull pressure time function—cause a decrease of individual components of the harmonic analysis. This is an additional example for the miss-leading conclusions, which can easily be drawn from the exclusive examination of the harmonic components of those time functions. Also this effect can only be understood by examination of the hull pressure time function.
As stated above, no explanation for the third peak of the time functions in Fig. 6 was found. Nevertheless, it can be seen that the discrepancy between model and full scale time function at this peak (1.4 kPa, see Fig. 6) similarly occurs in the comparative calculations given in Fig. 12 (1.9 kPa). Of course, it is unsatisfying to apply this calculated difference for a model to full scale time function correction, as long as no physical understanding has been achieved for this peak. Fortunately, the small height of this third peak allows to leave this question undecided.
THE CORRECTION METHOD
Based on the above findings the proposed method for the full scale correction of hull pressure measurements carried out in model scale is quite obvious. It consists of the following steps:
-
Plotting the model hull pressure time function
-
Averaging the time function by means of harmonic analysis and subsequent recalculation of the time function from the blade rate harmonics only
-
Identification of the pressure peak created by the cavity volume expansion due to the model wake peak
-
Correction of the exaggerated wake influence at this peak in model scale by means of comparative pressure pulse calculations based on both measured model wake and calculated full scale wake
-
Subsequent harmonic analysis of the corrected time function.
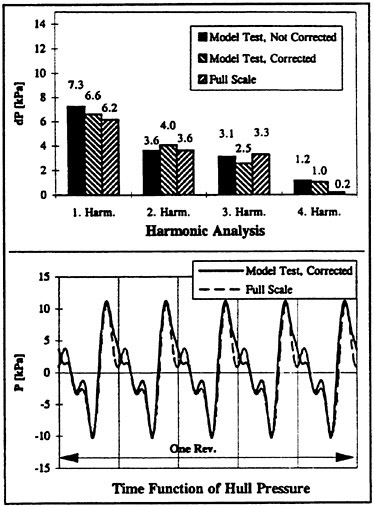
Fig. 13: Result of Time Function Correction
To identify the time function peak to be corrected, the performance of HSV recordings can be a valuable tool. However, HSV recordings are time and money consuming and—at least at HSVA—no standard technique so far. Nevertheless, for propellers with a rather stable cavitation behavior, this pressure peak identification can—as a makeshift—also be achieved from conventional cavitation observations under stroboscopic light.
For the correction of the hull pressure time function a “time function editor” has been developed at HSVA within the research project. This editor is based on the standard PC software “EXCEL” and allows an interactive manipulation of individual peaks of those time functions as well as the immediate evaluation of the resulting harmonic components.
This editor was used to reduce the second peak of the model time function in Fig. 6 by 6.6 kPa as obtained from the comparative calculation (Fig. 12). The result is shown in the lower diagram of Fig. 13 together with the full scale signal. As a result of the calculation accuracy, the reduction of the second peak is exaggerated. The upper diagram in Fig. 13 shows the harmonic analysis derived from this function together with the corresponding graphs taken from Fig. 6. Concerning the first harmonic component a clear improvement was achieved by the time function correction. Unfortunately, this improvement is accompanied by a slight worsening of the agreement for the higher harmonics. Nevertheless, after the correction the discrepancies do not exceed a value of 0.4 kPa for the first three harmonics, which is a very satisfying result.
THE INFLUENCE OF GAS CONTENT
In the foregoing section the perfect full scale similarity of the first pressure peak of the model hull pressure time function was emphasized. This good agreement was achieved by model tests carried out at the “normal” oxygen content of 80% saturation in HYKAT. Additional tests carried out at lower gas contents show, that this high O2-level is very important for this good agreement. Fig. 14 shows a comparison of model time functions obtained at different O2-levels. The upper diagram refers to the “normal” value of 80% saturation, while the lower diagram was obtained after a degassing time of 9 hours, i.e. at about 40% saturation.
It is interesting to see, that the lower gas content does not cause any instability of the cavitation behavior. There is still a very periodic behavior, indicating that the cavitation occurrence still periodically re-appears in the same way for each propeller blade. This is no matter of course since even at 80% saturation the cavitation behavior in HYKAT sometimes suffers from an instability, which is not expected to occur similarly in full scale.
However, averaging the time functions of Fig. 14 as described above, an interesting influence of the gas content can be seen (Fig. 15). The first peak of the time function, which had been identified as a result of the bursting tip vortex cavitation, becomes much more excited at the lower gas content. Comparative HSV recordings carried out at this low oxygen content show, that the tip vortex bursting has
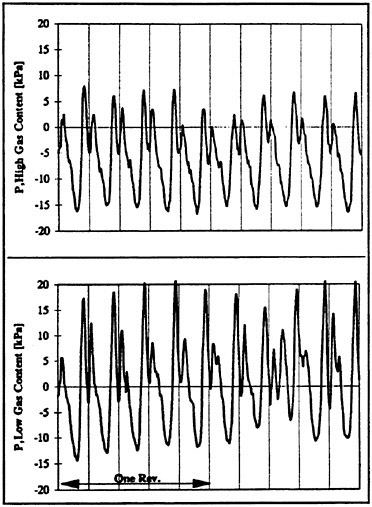
Fig. 14: Time Functions of Model Hull Pressure for Different Gas Contents
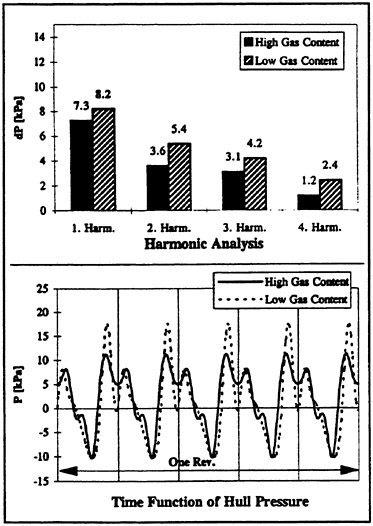
Fig. 15: Averaged Time Functions for Different Gas Contents
an unchanged appearance in comparison to the “normal” water condition. Only the free bubbles, which were plentifully observed at 80% O2, became exceptional in the degassed water. For this reason it has to be expected, that the missing damping effect of these bubbles is responsible for the increased pressure peaks. Since real sea water is almost saturated and additionally mixed with bubbles generated by the surface disturbance of the ship, it is not astonishing that the high saturation level in HYKAT results in a better model to full scale similarity.
From former studies [3] it was already recommended to keep the HYKAT oxygen content high. This recommendation was given with respect to the increased cavitation stability sometimes achieved this way. From the present investigation the same recommendation can be repeated, since it additionally provides a realistic modeling of the damping effect resulting from gas bubbles in the water.
GENERALIZATION
The proposed correction method is approved for only one ship so far. Further successful applications, proved by corresponding full scale results, are necessary before this method will be suitable as a standard tool at HSVA. Unfortunately, no corresponding model and full scale hull pressure time functions are available for other ships at the moment.
From a large research project, which is in progress in cooperation with the certification society “Germanischer Lloyd” (Hamburg), full scale hull pressure measurements will soon be available for three further ships. The sea trials have partially been conducted and the same conditions will be investigated in model scale in HYKAT. The results will form a valuable basis for the verification of the above findings.
Three other container ships formerly investigated in HYKAT resulted in the hull pressure time functions given in Fig. 16. Similar to Fig. 5, all graphs show distinct pressure peaks, probably caused by the same hydrodynamical effects as described above for “APL China”. For this reason it may be expected that the proposed correction method—at least for container ships—will improve the full scale similarity in general. Location and height of the peaks in Fig. 16 varies considerably, since propeller geometries and stern arrangements are different. Following the conclusions from Fig. 2, the proposed correction method would therefore certainly have a completely different influence on the several components of the harmonic analysis. For this reason and as stated above, a correction method must deal with the hull pressure time functions instead of certain components of its harmonic analysis.
When applying the method for other types of ships, especially for fast twin screw ships, additional efforts are necessary for the treatment of the displacement effect. For container ships its contribu-
tion to the hull pressure pulses was found as negligible. Nevertheless, for other ships it has to be investigated, how to scale the time function peak created by this effect.
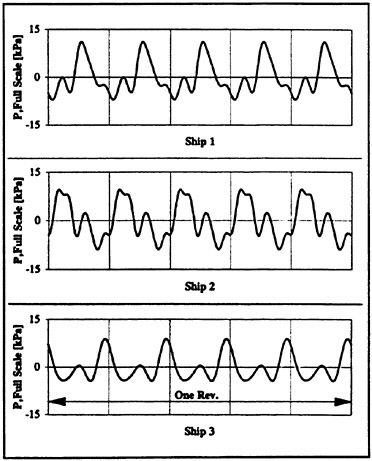
Fig. 16: Model Hull Pressure Time Functions for Different Container Ships
CONCLUSION
Mainly financed by the German Ministry of Research and Technology extensive cavitation tests were carried out in HYKAT, HSVAs large Hydrodynamics and Cavitation Tunnel, to improve the reliability of full scale predictions for propeller induced hull pressure pulses.
By means of High Speed Video records and simultaneous measurements of hull pressure time functions the hydrodynamic origin of the different peaks in these functions could be investigated. From comparison of the model time functions with corresponding full scale results individual scaling requirements for the different peaks could be found in dependence of their hydrodynamic origin.
It was found that for container ships with pronounced tip vortex cavitation this effect is responsible for the dominant peak in the hull pressure time function. To achieve full scale similarity for this peak it is important to ensure a high gas content in the tunnel water, resulting in a proper modeling of the damping effect of the free gas bubbles. Beside that, the high gas content sometimes improves the cavitation stability, which is also of advantage for the full scale similarity. Running the test under this condition no further scaling is required for the pressure pulse contribution from tip vortex cavitation.
An additional peak was found, resulting from the sheet cavity volume expansion in the 12 o’clock wake peak of the ship, which—in opposite to the tip vortex—has to be corrected for the influence of the exaggerated model wake. It was found that numerical pressure pulse calculations in combination with a quite simple assumption for the reduced full scale wake can be used to apply this correction.
For the container ship used in this project the influence of the displacement effect of the propeller blade itself was found to be negligible. Nevertheless, for other ships, this effect certainly contributes to the hull pressure variation, i.e. further research is necessary to investigate the scaling requirements for this effect.
When performing the cavitation test at high gas content in the realistic three-dimensional wake field, i.e. behind the complete ship model, and when applying the above correction for the influence of the exaggerated model wake, a very satisfying agreement between full scale and model hull pressure time function can be achieved. Consequently, the harmonic components, resulting from a subsequent Fourier Transformation of the corrected time function, represent a reliable input for the judgement of the propeller induced vibration excitation.
ACKNOWLEDGMENT
The results presented in this paper were obtained largely within an extensive research project financed by the German Ministry of Research and Technology. This is gratefully acknowledged here. Many members of the staff of HSVA were involved in the tests and evaluations described. Their contributions to this paper are invaluable.
NOMENCLATURE
|
aj, bj |
Fourier Coefficients |
|
D |
Propeller Diameter |
|
KT |
Propeller Thrust Coefficient |
|
LOS |
Overall Submerged Ship Length |
|
n |
Rotational Propeller Speed |
|
P |
Static Pressure |
|
Pv |
Vapor Pressure |
|
ΔΡ |
Amplitude of Hull Pressure |
|
Rn |
|
|
t |
Time |
|
V |
Ship Speed |
|
VA |
Axial Velocity Component |
|
VM |
Model Speed |
|
Z |
Number of Propeller Blades |
|
ρ |
Density of Water |
|
ν |
Cinematic Viscosity of Water |
|
σn |
|
|
ω |
Angular Velocity ω=2 π n |
REFERENCES
1. English, J.W., “Cavitation Induced Hull Surface Pressures—Measurements in a Water Tunnel”, Symp. on Propeller Induced Ship Vibrations, RINA, 1979
2. Tanger, H., Streckwall, H., Weitendorf, E.A., Mills, L., “Recent Investigations of the Free Air Content and its Influence on Cavitation and Propeller-Excited Pressure Fluctuations”, Int. Symp. on Propulsors and Cavitation, Hamburg, 1992
3. Friesch, J., Johannsen, C., Payer, H.G., “Correlation Studies on Propeller Cavitation Making Use of a Large Cavitation Tunnel”, SNAME, New York, 1992
4. Friesch, J., “HΥΚΑΤ, the New Cavitation Test Facility of the Hamburg Ship Model Basin”, HADMAR 91, Varna, 1991
5. Ingelsten, C., Johansson, M., “Cavitation Development and Noise of a Propeller Series”, Report X-97/87 of Chalmers University of Technology, Dep. of Naval Architecture and Ocean Engineering, Göteborg, 1997 (in Swedish)
6. Blake, K., Meyne, K., Kerwin, J.E., Weitendorf, E.A., Friesch, J., “Design of APL C10 Propeller with Full Scale Measurements and Observations under Service Conditioning”, SNAME, San Francisco, 1990
7. Chao, K.Y., Streckwall, H., “Calculation of the Flow Around a Propeller by Means of the Vortex-Lattice-Method”, Jahrbuch der Schiffbautechnischen Gesellschaft (STG), Vol. 83, 1989 (in German)
8. Streckwall, H., “An Instationary Vortex-Lattice-Method for Ship Propellers”, Proceedings of Rostocker Schiffstechnisches Symposium, Rostock, 1991 (in German)
9. Friesch, J., Weitendorf, E.A., “Model-Fullscale Correlation of Cavitation and Propeller-Excited Hull Pressure Fluctuations”, Third Int. Symp. on Practical Design of Ships and Mobile Units (PRADS), Trondheim, 1987
10. Rader, H.P., “The Influence of Wake on the Interaction Between Ship Hull and Propeller”, 11. Fortbildungskurs des Instituts für Schiffbau der Universität Hamburg, 1976 (in German)
11. Friesch, J.: “Correlation Investigations for Higher Order Pressure Fluctuations and Noise for Ship Propellers”, Third Int. Symp. on Cavitation (CAV ’98), Grenoble, 1998
DISCUSSION
Μ.Wilson
Naval Surface Warfare Center, Carderock Division, USA
In this paper, the author has embarked on a laudable and ambitious objective—to try to derive fluid mechanical connections between propeller inflow velocity patterns, cavity dynamics, and explanations of details of propeller-induced unsteady hull pressure time series characteristics. This kind of work could conceivably lead to improved predictions of full scale hull pressures based on a combination of model scale measurements and full scale calculated results.
The particular blade passage unsteady pressure signature discussed in this paper features three prominent local peaks, as illustrated in Figure 5. Vortex bursting is believed to be the cause of the first and highest peak. Rapid cavity volume expansion is suggested as the hydrodynamic origin of the second highest local peak. What is responsible for the third and smallest local feature is not well understood. I have some suggestions presented in the paper for a correction approach that adjusts the magnitude of this second local peak for the improvement of full scale prediction.
Ship wake velocity patterns with narrow V-shaped Vx/V contours, such as seen for radius 0.89R in Figure 10, are often found to be the root cause of large blade cavity volume fluctuations. Usually the strongest unsteady pressure pulse per blade passage comes from the sheet cavity volume collapse, not from the cavity expansion. From my experience with the PUF-3A calculation scheme for computing blade cavity volume variation versus position angle in very similar steep wake velocity patterns to those shown here, I have observed that the slope of cavity volume with position angle is steeper for the cavity collapse phase than for the cavity expansion part. This means that the collapse phase would produce the dominant unsteady pressure peak associated with cavity volume fluctuations. Could the author comment on this point? Have calculations been performed for the position angle (time) history of cavity volumes for this case?
Details about the second peak are important to the suggested Correction Method outlined in the paper. The motivation for making a correction is the difference in the magnitude of the second highest peak between the full scale and model scale values (4.5 kPa for the measured difference, and 6.6 kPa for the calculated difference due to wake influence). Apparently the proposed correction consists of subtracting a delta pressure value from the value of the processed model pressure curve at the exact position of the local peak; then reconstructing the harmonic analysis to obtain improved blade rate harmonics. Could the author comment on how the rest of the corrected pressure curve for the secondary peak is determined? Since the method calls for a recalculated harmonic analysis of the complete corrected time series function, the character of the adjusted curve is important.
DISCUSSION
D.Husson
Bassin d’Essais des Carenes, France
The experience of Bassin d’Essais des Carenes in measurement of pressure fluctuations shows that the similarity between full scale measurements and model scale measurements is widely increased by increasing the Reynolds number to approach as much as possible the real scale Reynolds number. Have you used this possibility in your experiments? At what tunnel speed were your measurements performed?
DISCUSSION
G.Bark
Chalmers University of Technology, Sweden
First of all I would like to congratulate the author on a very interesting paper. Among others the paper contains an original idea for correction of results from model testing as well as data that explains also parts of the physics of the generation of pressure pulses from propellers.
Due to some experience with this type of studies and as the supervisor of ref. 5 in the paper (Ingelsten and Johansson, 1997), I have, however, a few comments.
In application of the suggested correction procedure to the “APL China” I would like to focus on two assumptions that are used. As I interpret the paper these particular assumptions are not a fixed part of the correction procedure
but usually some assumptions of this type have to be used.
Assumption 1:
Supported by the HSV observations it is assumed that the first pressure peak is mainly generated by the implosion of the tip vortex cavity.
Comment:
Provided you are sure that no other violent change of the cavity volume occurs outside the camera view this is a reasonable assumption.
This is also in general agreement with the results from the KAMEWA tunnel, your ref. 5. Although we used a frame rate of only 1000 frames per second there was no doubt that collapses in the tip vortex can generate dominating pressure pulses. In the KAMEWA experiments, however, we also often observed multiple pulsations in the tip vortex cavity that were supposed to generate also multiple pulses. Due to our low frame rate we could not, however, make very precise observations so some doubt remains. From this and other studies of synchronized film and pressure recordings it is however demonstrated how important it is to observe all parts of the cavitating field, a fact also confirmed by your discussion of the sheet cavity in your Fig. 8.
Assumption 2:
In the correction procedure for “APL China” it is assumed without much discussion that it is only, or at least mainly, the sheet cavity that is influenced by a scale effect on the hull boundary layer.
Comment:
Often the sheet cavity partly transforms into a tip vortex cavity (the sheet is more or less fed into the tip vortex) as the blade leaves the wake peak. With this behaviour it may be expected that the tip vortex cavity can be influenced by the volume of the sheet, at least in the early stage.
The strongest part of the tip vortex, generating the part of the vortex cavity that will collapse most violently, may also be highly influenced by the wake produced by the hull boundary layer.
These effects will result in scale effects also on the pressure pulses generated by the tip vortex cavity. The importance of the scale effects will depend on the hull shape but possibly can they be disregarded for “APL China?”
At present there is perhaps no direct and reliable method to correct also the pulse from the tip vortex cavity but in principle it seems fully possible to apply your procedure to all types of cavities.
AUTHOR’S REPLY
First of all, the author would like to thank all discussers for their interest and for their critical comments on the paper.
As expected, the discussion was mainly directed to the proposed method for the correction of the second hull pressure time function peak, which was related by the author to the entrance of the propeller blade into the 12 o’clock wake peak of the ship. The author admits that this correction method must be subject of further investigations. It sensitively depends on the method used for the estimation of the full scale wake. In the paper this estimation was based on a quite simple assumption, which could be replaced by comparative wake calculations based on a RANSE solver for example.
Furthermore, the time function peak correction proved its reliability for only one ship so far. Other stern arrangements, e.g., V-shaped hull forms as mentioned by Mike Wilson, will perhaps create hull pressure time functions of different character, requiring an additional treatment of the pressure peak created by the collapse of the cavity volume. This has not been investigated so far. The width of the subtracted Δp-peak, which was addressed by Mike Wilson, was taken equal to this of the original pressure peak to be corrected (Fig. 1). Nevertheless, the resulting harmonic analysis was found to depend not very sensitively on this width.
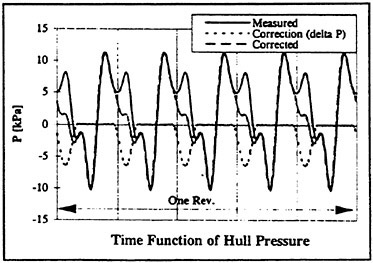
Fig. 1: Correction of Model Hull Pressure Time Function
As mentioned by Göran Bark, no distinct pressure peaks may be recognized in the hull pressure time function, when different kinds of cavitation are mixed or transform into each other. This certainly leads to difficulties in the proposed procedure and requires further investigations. Multiple pulsation of the cavitating tip vortex was not observed for “APL China,” since the cavitating tip vortex did not extend very long before its bursting. Also this may be different for other stern configurations and may lead to additional time function peaks to be investigated [1].
Beside that it has to be clarified, why a positive pressure peak is obtained for “APL China” just when the cavity volume grows. This question was raised by Chris Brennen, and can perhaps be answered by theoretical investigations [2,3], indicating that re-growing single bubbles radiate positive pressure peaks. Nevertheless, even a video frame rate of 4,500 pictures per second is not enough to investigate the behavior of such single bubbles.
As stated in the paper, further ships will be investigated in the ongoing project to verify and/or to modify the proposed procedure with respect to the above comments. Nevertheless, the above uncertainties do not influence the major finding of the project: Different hydrodynamic occurrences contribute to the hull pressure time function—and they scale differently. To get a reliable full scale pressure pulse prediction from model tests, these occurrences, and not the components of the harmonic analysis, must be treated individually. To relate the time function pressure peaks to the different hydrodynamic occurrences, High Speed Video recordings are very valuable. For future tests these recordings should cover the whole cavitation behavior of the model propeller, which requires much effort for the model preparation.
To answer Didier Husson it has to be mentioned that the non-existent free surface is one of the design features of HSVAs Hydrodynamics and Cavitation Tunnel HYKAT. This way the tests can be carried out at the highest possible water speed (deviating from Froudes scaling law), i.e., at highest possible Reynolds number. The tests are normally carried out in HYKAT at model propeller speeds of 25 to 30 revs per second (27.5 RPS in the present tests). Of course this speed does not match the full scale Reynolds number, but the author agrees that it is valuable to improve the full scale similarity of the cavitation behavior in model scale.
References
1. Weitendorf, E.A.: “Experimental Investigations on Pressure Fluctuations Produced by Cavitating Propellers,” Schiff und Hafen, 1973 (in German).
2. Fujikawa, S., Akamatsu, T.: “Effects of the Non-Equilibrium Condensation of Vapor on the Pressure Wave Produced by the Collapse of a Bubble in a Liquid,” Journal of Fluid Mechanics, 1980.
3. Isay, W.H.: “Cavitation,” Schiffahrtsverlag HANSA, 1984 (2nd).
A New Tracer Technique for Turbulent Flow
J.Hoyt (San Diego State University, USA),
R.Sellin (University of Bristol, United Kingdom)
ABSTRACT
A new tracer formulation is described which resists breakup in turbulent and complex separated flows. The capability of the technique is demonstrated using examples of flow around smooth and rough cylinders, as well as in visualizing the large structures in the turbulent boundary layer.
INTRODUCTION
A dye-streak tracer is under development as an inexpensive alternate to laser-based diagnostic tools used in water-flow studies. The tracer is effective in strongly eddying and turbulent-flow situations encountered in water flow around objects and in the turbulent boundary layer.
Flow visualization has provided information useful in all facets of fluid dynamics, since some method of actually seeing the flow events taking place appears to be an optimal way to make progress in understanding the details of fluid motion. One can then arrange more quantitative instrumentation, or simply gather insight regarding the flow.
Visualization of turbulent water flow around objects and in the boundary layer, however, has resisted simple methods, and up to now only very complicated instrumentation has been available to study such flows. A new dye-streak formulation under development offers a return to simplicity in visualizing flows of this kind.
It is interesting that the concept of the tracer evolved from years of effort on additive drag reduction, especially on the idea that coherent “threads” of some kind of additive might reduce the friction by interference with large structures in the flow. This concept eventually proved groundless, but it was noticed that threads formed from certain compounds followed closely the eddies and vortices encountered in turbulent flow. From these observations, shear-thickening and high-extensional viscosity solutions were selected for the tracer.
The tracer is formulated with a colorant of white pigment, which contrasts well with flat-black surfaces in the flow channel. The streamers, dispensed from hypodermic tubing singly or from rakes of tubes, thus show up well against the black background. The tracer resists immediate break-up so as to display streaklines of interest, then dissipates into the overall flow.
Still photos and home-type video with ordinary lighting can be used to record the tracer paths. The videos can then be transferred to a computer and printed frame-by frame to document streaklines. The ease of video recording during tracer experiments and later frame-by-frame capture can provide detailed information helpful in the analysis of fluctuating or non-steady flows.
The technique can be adapted to provide three-dimensional flow information by providing a mirror inclined at 45° over the flow channel. Thus, using the side view through transparent channel walls, and a mirror giving the plan view, 3-D streakline information is readily available on a single film or video clip. There is a slight mismatch in the views due to different optical paths, but no ambiguity.
Flows studied using the new tracer which are of special interest in Naval hydrodynamics include the wakes of smooth and rough cylinders, intersections of cylinders and plates, multiple cylinders, and observation of coherent structures in the turbulent boundary layer. The use of the tracer has lead to new information on all of these flows, and these results will be summarized in this paper.
Offsetting the advantages of the tracer is the inability to provide vorticity information. Hence the tracer is qualitative, not quantitative. Additionally, the components of the tracer are drag-reducing, thus requiring sparing use, a large reservoir for tracer breakdown, or change of water before making resistance measurements. As will be explained, the drag-reducing aspects are unimportant when examining the large-scale eddy and vortex flow
structures, since these are relatively unaffected by the presence of polymers.
We have compared results from a detailed particle-image-velocimetery (PIV) study of flow around shallow-immersion cylinders with a similar experiment using the tracer, and find that the streaklines of the tracer technique offer a virtually identical impression of the principal flow characteristics when compared with the PIV velocity vectors.
TRACER COMPOSITION
The tracer is a mixture of a surfactant, cetyltrimethylammonium salicylate (C16TASal) and a high extensional-viscosity polymer, poly(ethylene oxide) (PEO). Solutions of C16TASal increase in viscosity by factors of 10 or more when subjected to small shear or strain forces. The C16TASal and PEO components are made up in water solutions, and further diluted after mixing. A small amount of white water-based emulsion wall paint is added as a coloring agent. The paint also adds to the stability of the tracer streamers. A more detailed explanation of the method of preparation is given in the Appendix.
A typical formula used in the work described here was:
|
2% C16TASal |
500 ml |
|
1/2% PEO |
250 ml |
|
Tap water |
1000 ml |
|
White paint |
5–10 ml |
The experimenter can select, to some extent, the turbulence scales to be visualized, by varying the dilution and composition of the tracer mix. Weak solutions of the tracer show the smaller turbulence scales, while strongly eddying situations can be visualized with a more concentrated tracer mix. The more dilute the tracer, the greater the detail, until all is swept away as with a traditional dye streak. A more concentrated mix survives extensive turbulent excursions, and is more useful for initial flow explorations.
Since the tracer is composed of a surfactant (i.e. a detergent) and a polymer used in water-treatment, the mixture appears to be environmentally benign, and seems to biodegrade when dispersed in our laboratory water-storage reservoirs. Both components of the tracer are drag-reducing in sufficient concentration, and this aspect of the tracer use must be kept in mind. At Bristol, the large reservoirs in the laboratory system and high-speed recirculating pumps allowed every-day operation without any effects of contamination from the tracer, as judged from frequent checks to assure Newtonian properties of the test water.
Rakes of one or more hypodermic-tubing ejectors can be used to dispense the tracer in front of or in the flow around the object whose wake is to be visualized. A small variable-displacement pump is employed to emit the tracer into the flow at approximately the same velocity as the surrounding stream. Figure 1 shows the tracer being dispensed in front of a circular cylinder. In common with other high-concentration non-Newtonian fluids, the tracer flow first expands as it leaves the ejection tubing (the die-swell effect), then relaxes to form a relatively constant-diameter stream. A surface-tension difference exists between the tracer and the surrounding water; the strands thus become perfectly cylindrical until distorted by turbulence.

Figure 1. Method of ejecting tracer in front of cylinder. The vertical bar is outside the flow channel.
It should be emphasized that this type of tracer is not suitable for low-speed flows; it relies on a small amount of shear or strain to form coherent strands useful in identifying streaklines.
EXPERIMENTAL FACILITY
All the work described here was performed in a small water channel at the University of Bristol. The channel is 102 mm wide and 300 mm deep. A constant-head tank located 24 m above the working section provides gravity feed to a header tank, from which flow enters the channel through a convergent section equipped with honeycomb straighteners and screens. Flow velocities were measured with a calibrated velocity meter, as well as occasional checks with a volume-measuring tank. Most of the tests were made at flow velocities around 0.25 m/sec.
Much of the work was done with experimental cylinders tested in cross-flow. Each cylinder was fitted with a spring-wedge arrangement so that it could be mounted in place at any location spanning the channel. In addition to single and multiple smooth cylinders, configurations consisting of cylinders having “macro” roughness formed from dimples (like a golf ball), gear-type axial grooves,
Figure 2. Sketch showing mirror arrangement for simultaneous three-dimensional viewing.
and circumferential grooves were examined using the tracer. Reynolds numbers of up to 30,000, based on the cylinder diameter, could be obtained while maintaining a smooth free surface on the water channel.
For tests involving the turbulent boundary layer, a 10 mm thick, 2 m long brass plate was mounted with its top surface 50 mm above the channel floor. The channel inflow geometry was modified to provide a horizontal ramp, the height of which was 1 mm below the height of the brass plate. A 2 mm gap between the ramp and the plate (the under surface of which was cut away at an angle) allowed the ramp boundary-layer to be sucked away. Thus the turbulent boundary layer on the plate began at a 1/2 mm wide slot (acting as a trip) just behind its leading edge. The entrance conditions were adjusted very carefully using dye streaks to assure smooth entrance to the plate, and that the turbulent boundary layer began at the trip. The plate was smooth to the touch, before being spray-painted matt black.
Three-dimensional viewing was obtained for several test configurations by mounting a mirror at 45° above the channel. For the boundary-layer visualizations, an auxiliary mirror was provided to give a view aligned with the flow. Hence, as shown in Figure 2, there were three images available for simultaneous viewing.
White stripes on the plate and the adjacent side wall of the channel were used to establish the local Reynolds number and to coordinate the images.
In addition to 35 mm camera records of the flow (taken at 1/250 sec exposure on ISO 1600 film), video on VHS tape using a home-type camera was used to document the visualizations. Ordinary flood-lighting proved satisfactory. Where necessary, frame-by-frame video analysis was used to provide a time base. Video capture was accomplished using a miro DC-20 card with Adobe Premier LE processing on a Pentium-based PC.
EXPERIMENTAL RESULTS
We turn first to visualization of flow around smooth cylinders, one of the oldest problems in fluid mechanics, but one for which as yet there is no adequate understanding for the full range of Reynolds numbers (VD/ν) found in practice. Here V is the free-stream velocity, D the cylinder diameter, and ν the kinematic viscosity. While flow visualization using traditional techniques has been effective up to Reynolds numbers of a few thousand, flow patterns at higher Reynolds numbers are generally not obtainable except with the most sophisticated and expensive equipment.
Smooth Cylinder Studies
The literature on flow around cylinders is enormous, but information on the wake at Reynolds numbers above 2000 is quite limited. Using the tracer, we now have much more detailed knowledge of how the wake is formed, and how the greatly increased wake size as the Reynolds number is raised from, say, 2–3000 to 20,000 or more reflects the 20% increase in drag coefficient in this range (from CD=1.0 to CD=1.2).
Focusing on the question of how the high Reynolds number wake is formed, the literature is rather sparse. Bloor (1) building on earlier work, used hot-wire anemometry to study the transition from laminar to turbulent flow near the surface of the cylinder. She found that as the Reynolds number was increased to 20,000 or so, the separated flow became turbulent in the region “less than one radius downstream of the cylinder center”. She defined a “formation region” as the location between the separation point on the body and the first appearance of the periodic vortex street.
Later, Gerrard (2) studied the high Reynolds number “formation region” in detail. His intuitive sketch (Figure 3) shows the formation region to be the area from the separation point to the location where the upward fluid (in this case) just crosses the horizontal centerline of the cylinder. In the sketch, the arrows representing different fluid paths originate at the end of the formation region. The sketch is remarkable in that only hot-wire data were available as a basis. Using the tracer, we can confirm Gerrard’s ideas as shown in Figure 4.
Figure 3. Gerrarďs sketch of the “formation region”.

Figure 4. The formation region illustrated with the tracer. An 89 mm dia cylinder at Reynolds number of 22,300. (Video frame.)
Figure 4 shows that the formation region of the Kármán vortices extends about 1.5 diameters downstream from the cylinder centerline, as suggested by Gerrard in 1966. The major vortices are seen to form on the horizontal centerline behind the cylinder. The turbulent boundary layer does not seem to trigger the large Kármán vortices, and only occasionally enters into the vortex formation region.
The cylinder wake becomes very large as the Reynolds number is increased from 1800 to much higher values, a possible reason for the drag coefficient to increase by 20% (from approximately 1.0 to 1.2). Figure 5 is a comparison of the cylinder wakes at two different Reynolds numbers.
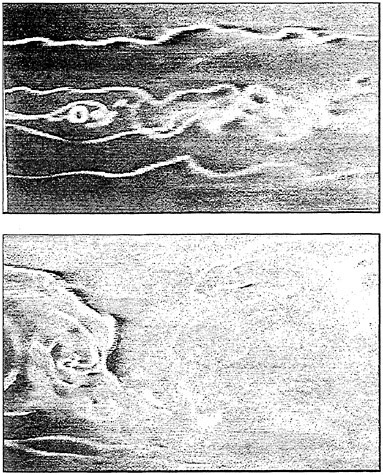
Figure 5. Comparison of cylinder wakes at 1800 and 22,300 Reynolds numbers. 10 mm dia cylinder above, and 89 mm dia below. The drag coefficient is estimated at 1.0 for the upper video frame, and 1.2 for the lower.
Cylinders with Macro Roughness
Cylindrical shapes used in engineering applications often differ significantly from the very smooth cylinders discussed above. Protrusions and depressions on the cylinder surface may result from manufacturing or other considerations. However, the remarkable thing about roughened bluff bodies is that they often show, at higher flow velocities, a distinctly lower drag or resistance than the corresponding perfectly smooth shape. An everyday example is the “dimpled” golf ball, which has a much lower drag than the same size smooth sphere, over a substantial range of high Reynolds numbers. Macro or large-scale roughness on cylinders also leads to lower resistance at relatively low Reynolds numbers.
As early as 1930, Page and Warsap (3) found that by wrapping a smooth cylinder with sandpaper, transition to the lower drag region (sometimes called “critical flow”) could be obtained at Reynolds numbers as low as 30–40,000, or about 1/10 the Reynolds number of a smooth cylinder. Many other workers over the years have confirmed these results for uniform roughness.
More recently, the effect of macro, or large-scale roughness has been the subject of considerable study. Very tiny circumferential grooves, axial grooves resembling a fine-toothed gear, and dimples on the cylinder surface all have been shown to give noticeable drag reduction at Reynolds numbers of 15,000 or less. In spite of the considerable literature on roughened cylinders, analysis has been hindered by lack of any way to view the flow around the cylinder and in the wake. The new flow tracer has been used to visualize some of the low-drag configurations mentioned in the literature.
In general it was found that the cylinders with macro roughness, all having reported low drag at Reynolds numbers of 30,000 or less, show characteristic changes in the wake pattern as that Reynolds number is approached. Apparently, a high-pressure zone is created, preventing the tracer from entering the region behind the cylinder. Thus the drag is lowered.
All the “rough” cylinders studied here had a nominal diameter of 68 mm. Turning first to the gear-type configuration, a cylinder was fabricated having 100 axial grooves with 90° “V” shape, thus resembling a very fine-tooth gear, as shown in Figure 6. The ratio of the groove depth to the outer diameter was 15.6×10−3, geometrically scaled to match earlier drag measurements of Suzuki & Iijima (4) with similar configuration.

Figure 6. Cylinder with gear-type roughness.
The wake from this cylinder changed from a Kármán-vortex trail to a completely separated appearance as the Reynolds number was increased to 27,300, as shown in Figure 7.
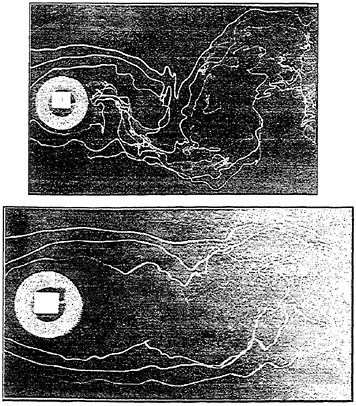
Figure 7. Wake photos from the gear-type cylinder. Above, Reynolds number=8,800; below, Re=27,400.
A hint of vortex formation is seen at least three diameters downstream from the gear-type cylinder. At a slightly lower Reynolds number, 26,100, the Kármán trail begins around two diameters downstream Suzuki & Iijima (4) show that the drag coefficient is decreasing steeply in this Reynolds number region: from 0.9 at Re=26,000 to 0.6 at Re =27,400. The Strouhal number for the 26,100 Re case was estimated from video records to be 0.32, in good agreement with observations of Roshko (5), Bearman (6) and others for smooth cylinders in the critical-flow regime.
Introducing dye into the behind-cylinder region for the high Reynolds number flow shown in Figure 7 indicated that no organized activity exists in the near wake; it seems to be a high-pressure area accounting for the low drag. Similar flow patterns appear for the other low-drag configurations tested.
It is amusing to speculate that this type of roughness has evolved in nature for certain cactus species. The saguaro grows only in the Sonoran desert in the U.S. as a very tall cylinder (some attaining 10 m or more height) with a more coarse vertical gear-type roughness than the cylinder tested here. The cactus grows extremely slowly (5–10 cm/year) and has tiny, shallow roots. Yet they withstand desert storms during their very long lifetime with wind velocities of up to 80 km/hr. Perhaps their drag is greatly reduced, for in addition
to axial grooves, many “needles” or spines exist, growing from the tips of the projections. These may also aid in producing a low aerodynamic resistance.

Figure 8. Cylinder having “dimples” scaled from a golf ball.
The dimples shown on the cylinder in Figure 8 were approximately 6.0 mm dia at the outer surface; the depth of the dimple was 0.635 mm, giving a depth-to-diameter ratio of 9.4×10−3. The dimple density is that of a standard golf ball. Earlier tests with a cylinder having only half the dimple density (similar to the cylinder tested by Bearman & Harvey (7)) led to inconclusive results.
The fully dimpled cylinder gave evidence of a changed wake at the lowest Reynolds number tested, 14,600. Figure 9 shows how the vortices in the wake tend to form two diameters or more downstream from the cylinder centerline, rather than immediately behind as with a smooth cylinder. In this photo, a mirror has been installed above the flow channel to show the three-dimensionality of the wake. As vortices begin to roll up, a noticeable expansion in the direction normal to the flow can be seen in the mirror.
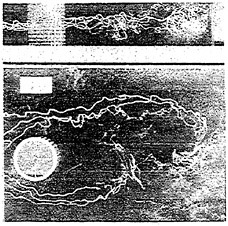
Figure 9. Wake from fully-dimpled cylinder at Reynolds number 14,600. A plan view of the flow is shown in the mirror above.
At a higher Reynolds number, 24,600, the flow appears completely separated, as shown in Figure 10, suggesting that the drag is greatly reduced.

Figure 10. Wake of fully-dimpled cylinder at 24,600 Reynolds number.
By far the most spectacular change in wake appearance was found with a circumferentially grooved cylinder, the grooves extending only around the leading region. Leung, Ko & Tang (8) found that cylinders of this type can show reduced drag coefficients at Reynolds numbers of 20,00 or less. The geometry is quite complex; in the configuration used here, the leading ±75° of the cylinder was prepared by machining tiny sharp-edged circumferential grooves having a 15° included angle. The grooves were 1.22 mm deep, spaced 0.32 mm apart. The remainder of the cylinder surface was machined smooth, at the root diameter of the grooves. Figure 11 depicts a view of the completed cylinder.

Figure 11. Partially circumferentially grooved cylinder.
The flow around this cylinder configuration is amazing. At a Reynolds number of 5,000, the wake shows signs of Kármán vortex formation, but these vortices begin much further behind the cylinder compared with the smooth cylinder wake. At 15,000 Reynolds number, the flow appears completely detached from the cylinder, as shown in Figure 12.

Figure 12. Flow around the partially-grooved cylinder at Reynolds number of 15,000.
The experiments with macro roughened cylinders suggest that flow at speeds beyond the “critical” Reynolds number is much different from the usual textbook explanation. The lack of activity in the separated wake, as suggested by the photos of Figures 7, 10 and 12 was noticed as early as 1961 by Roshko (5), who found that a splitter plate attached to the rear of a smooth cylinder was ineffective in the post “critical” flow. Thus these photos may lead to greater understanding of very high Reynolds number flows.
Intersecting Cylinders
Crossed circular cylinders are common components of engineering structures such as bridges and offshore platform supports. The complicated wake arising from flow around these structures often leads to unforseen vibrations and instabilities. The study of flow through screens and grids (another example of crossed cylinders) is also of technical interest, due to the use of these devices in turbulence management schemes for wind and water tunnels. Progress in understanding these flows has been impeded by lack of a suitable method of flow visualization. Background information on various aspects of crossed-cylinder flows has been summarized by Fox (9).
The tracer has been used to study several configurations of crossed cylinders, of which only a sample can be displayed here. Since these are complex, three-dimensional flows, the mirror arrangement discussed above was utilized to capture details. The cylinders were stainless steel, 18.7 mm diameter (D) and the crossed-cylinder center-to-center spacing (L) was varied to give L/D ratios from 0 to 10. Figure 13 shows the tracer result for L/D=3. It can be seen that the Kármán vortex wake developing from the horizontal cylinder (seen in the side view) is captured by the vertical cylinder, with the resulting vortex wake dominating the flow.

Figure 13. Crossed cylinders with L/D=3. Plan view above; side view below. Note how the vortices from the horizontal cylinder are transformed by the vertical cylinder into a new wake path.
The flow at the intersection of a circular cylinder and a flat plate is of very great interest in connection with the problem of bridge-pier “scour”, in which the material surrounding the base of the pier is removed, possibly to a dangerous degree, by action of flowing water. A portion of this type of flow was modeled by mounting a vertical cylinder on a flat plate. The result, depicted in Figure 14, shows (in three dimensions) strong up-flow movements occurring behind the vertical cylinder. Hence sediment, originally eroded by high shear stress at the front of the pier, may be lifted and carried further downstream by the extremely active vortex wake.

Figure 14. Flow at the intersection of a vertical cylinder and a flat plate. The tracer is embedded in a turbulent boundary layer as it encounters the cylinder. The cylinder is 18.7 mm dia.; the vertical white line at the right of the side view is 50 mm high, and at that point, the undisturbed boundary-layer thickness is 24 mm. The plan view is shown above.
Multiple Cylinders
The tracer has been used to demonstrate flow in multiple cylinder arrangements such as those found in boilers or heat exchangers. The three types of flow oscillations deduced from frequency measurements by Hetz, Dhaubhadel & Telionis (10) can be seen in the tracer photos. The usual nomenclature is adopted with D, the tube diameter (18.7 mm), L the axial distance between centers, and T the transverse spacing of either staggered or in-line rows of tubes.
Figure 15 illustrates the “cavity flow’ regime, where pairs of vortices simply rotate in the cavity between two in-line cylinders.
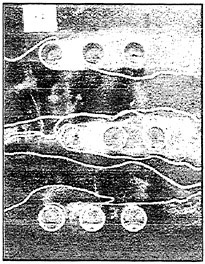
Figure 15. Cavity flow with staggered tube arrangement. L/D=1.61; T/D=3.21; Re=5,800.
With larger axial spacing (L/D=3.21), “gap shedding” occurs, where vortices formed between the cylinders extend out beyond the in-line region, as shown in Figure 16.
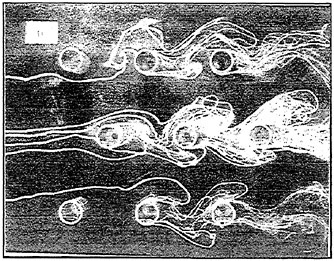
Figure 16. “Gap shedding” at Re=5,600 and L/D=T/D=3.21.
Finally, Figure 17 shows the “bluff-body” regime, where all the cylinders act as a single body, casting a large vortex wake. It is particularly interesting that the many shear layers (often of alternate signs) contributing to the wake in a multiple-body flow can organize into a single oscillating wake, such as that shown in the Figure.
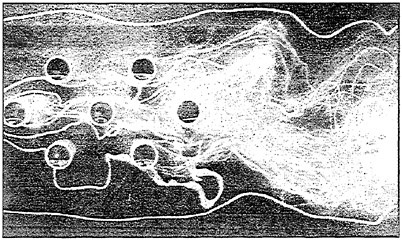
Figure 17. Bluff-body shedding at Re=9,800. L/D=3.21 and T/D=1.61.
Flow visualization thus plays a useful role in revealing the characteristics of complicated flows such as these examples of multiple-cylinder arrangements. The tracer is especially valuable here, since other methods of visualization seem awkward. Laser-sheet illumination, for example, casts shadows from cylinders or other objects; the shadow region thus is opaque, possibly obscuring details necessary for interpretation of the flow.
Comparison with PIV
Recently, an opportunity has arisen to evaluate the usefulness of the tracer information by comparison with a more accepted flow visualization technique. Sheridan, Lin & Rockwell (11) have published results obtained with Particle-Image-Velocimetry for flow past a cylinder close to a free water surface at various immersion depths. We have repeated several of the flow geometries studied by Sheridan, et al. and find that the streaklines of the tracer provide a virtually identical impression of the principal flow characteristics when compared with the PIV velocity vectors. If anything, the tracer provides a clearer guide to interpretation of the flow situation than does the PIV result.
Figure 18 compares the PIV result (from Sheridan, et al.) with video scenes from a similar tracer experiment. Here the top of the cylinder is set at a depth, h, (with reference to an upstream free-surface location) divided by diameter (D)=0.3. This ratio is defined as h* by Sheridan, et al.
Figure 18. Video frames of tracer flow at h*=0.30. At left, flow from the upper surface of the cylinder has induced a vortex rotating clockwise (to observer). Flow from the lower surface induces a counterclockwise vortex, which enters the same space and forms a Coanda-like effect around the base of the cylinder, as shown at the right, 54 frames (2.16 sec) later.
Flow angles at specific locations have been compared, and both the tracer and PIV give comparable results. This favorable comparison suggests that concerns occasionally expressed, based on computer exercises, regarding adequacy of flow visualization in unsteady flow situations (i.e. Gursell, et al. (12)) disappear in real flows. Apparently, the quasi-steady features of the flow are those detected by the flow tracer.
Coherent Structures—Turbulent Boundary Layer
A final area where the tracer has provided results of great interest is in visualizing large structures in the turbulent boundary layer on a flat plate. By dispensing a single filament into the lower region of the boundary layer, coherent larger-scale motions are revealed These structures have been a subject of great interest in fluid mechanics for many years, following the insight provided by the sketches of Theodorsen (13) and others.
When the tracer is dispensed in the boundary-layer flow, horseshoe-type vortices can be readily visualized, as shown in Figure 19. The tracer is picked up by the structures and transported downstream, giving a visual record of the boundary-layer activity.
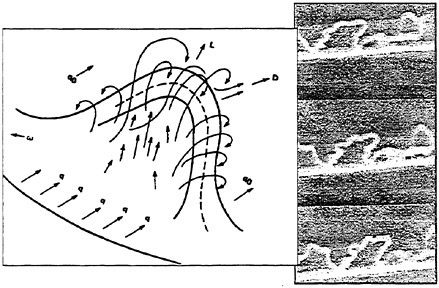
Figure 19. Horseshoe vortices shown by video frames (0.08 sec apart) of the tracer, compared with the famous sketch of Theodorsen (13).

Figure 20. Tracer visualization of horseshoe vortex structure compared with computer simulation of line vortex in a shear layer, from Smith et al. (14).

Figure 21. Three views of boundary-layer activity using mirror arrangement shown in Figure 2. Note the large spanwise excursion of the tracer in the upper right view.
An oblique view of the tracer stream revealing horseshoe-type structures is given in Figure 20. Simultaneous side and plan views of the structures revealed by the tracer can be obtained using mirrors, as shown in Figure 21. The ability of the tracer to show these large structures is certain to increase our knowledge of the role they play in the turbulent boundary layer.
SUMMARY
The development of a new flow tracer technique has made the visualization of both boundary layer and wake flows a simple procedure. We look forward to many new discoveries utilizing this new technique.
ACKNOWLEDGEMENT
The support of the Benjamin Meaker Visiting Professor Fund at the University of Bristol and the U.S. National Science Foundation is very greatly appreciated. We especially wish to acknowledge the confidence in this work expressed by Dr. Michael Roco of the NSF through Grants CTS-9411980, CTS-9508409, and CTS-9713857. We also wish to thank Mr. Philip Leonard (University of Bristol Hydraulics Laboratory) for his skill in fabricating the experimental equipment and assisting with the tests.
REFERENCES
1. Bloor, M.S., “The Transition to Turbulence in the Wake of a Circular Cylinder,”
Journal of Fluid Mechanics, Vol. 19, 1964, pp. 290– 304.2. Gerrard, J.H., “The Mechanics of the Formation Region of Vortices Behind Bluff Bodies,” Journal of Fluid Mechanics, Vol. 25, 1966, pp. 401–413.
3. Page, A. and Warsap, J.H., “The Effects of Turbulence and Surface Roughness on the Drag of a Circular Cylinder,” British ARC Reports and Memoranda No. 1283, 1930.
4. Suzuki, Y. and Iijima, T., “Profile Drag of Circular Cylinders with Surface Roughness of Straight Knurls,” Proceedings FLUCOME ’94, Vol. 2, 1994, pp. 805–810.
5. Roshko, A. “Experiments on the Flow Past a Circular Cylinder at Very High Reynolds Number,” Journal of Fluid Mechanics, Vol. 10, 1961, pp. 345–356.
6. Bearman, P.W., “On Vortex Shedding from a Circular Cylinder in the Critical Reynolds Number Regime,” Journal of Fluid Mechanics, Vol. 37, 1969, pp. 577–585.
7. Bearman, P.W. and Harvey, J.K., “Control of Circular Cylinder Flow by the Use of Dimples,” AIAA Journal, Vol. 31, 1993, pp. 1753–1756.
8. Leung, Y.C., Ko, N.W.M., and Tang, K.M., “Flow Past Circular Cylinder with Different Surface Configurations,” Journal of Fluids Engineering, Vol. 114, 1992, pp. 170–177.
9. Fox, T. A, “Wake Characteristics of Two Circular Cylinders Arranged Perpendicular to Each Other,” Journal of Fluids Engineering, Vol. 113, 1991, pp. 45–50.
10. Hetz, A.A., Dhaubhadel, M.N., and Telionis, D.P., “Vortex Shedding Over Five In-Line Cylinders,” Journal of Fluids and Structures, Vol. 5, 1991, pp. 243–257.
11. Sheridan, J., Lin, J-C., and Rockwell, D., “Flow Past a Cylinder Close to a Free Surface,” Journal of Fluid Mechanics, Vol. 330, 1997, pp. 1–30.
12. Gursul, I., Lusseyran, D., and Rockwell, D., “On Interpretation of Flow Visualization of Unsteady Flows,” Experiments in Fluids, Vol. 9, 1990, pp. 257–266.
DISCUSSION
D.Fruman
Ecole Navale, France
I would like to congratulate the authors for their fine work and the beauty of the visualizations. I have a question concerning the behavior of the visualizing fluid. Because of its properties (visoelastic) the fluid will be reusable to the deformation intensity, that is to say to a time scale proportional to the length scale (L) divided by the velocity scale (V), i.e. L/V. Therefore, the visualization of different length scale models operating at equal Reynolds (v VL) numbers will (or may) be quite different. What is your opinion about this?
AUTHORS’ REPLY
We appreciate the comments and concerns from a very distinguished scholar in the field of viscoelastic flows.
All experiments in which we have had an opportunity to compare our flow visualization results with those of other workers, show very similar visualization patterns. Hence we think the tracer is responding to the length scales in the main body of the flowing liquid (water) rather than scales determined by the tracer itself.
In studies of flow around circular cylinders (Hoyt and Sellin (15)), various size cylinders gave very similar Kármán vortex patterns at the same Reynolds numbers (even though the vortex shedding frequency changed substantially as the cylinder size was changed).
In preparing the reply to discussion of our paper, we discovered that we had omitted references in the text to our previous papers on the topic, and take this opportunity to add a few of the more recent.
References
15. Hoyt, J.W. and Sellin, R.H.J. “A Flow Visualization Study of Separated Flow over Circular, Elliptical and Square Cylinders” in M.V.Otugen, et al., eds. Separated and Complex Flows—1995, ASME FED-Vol. 217, 1995, pp. 115–120.
16. Hoyt, J.W. and Sellin, R.H.J. “Flow Over Tube Banks—A Visualization Study,” Journal of Fluids Engineering, Vol. 119, 1997, pp. 480–483.
17. Hoyt, J.W. and Sellin, R.H.J. “3-D Visualization of Flow Past Intersecting Cylinders,” Proc. ASME Fluids Engineering Division, Summer Meeting 1998 (on disc), Washington, D.C. Paper No. FEDSM-5269, 1998.
18. Hoyt, J.W. and Sellin, R.H.J. “A Mirror and Tracer Method of 3-D Flow Visualization,” Proc. 8th International Symposium on Flow Visualization (1998) (on disc), Sorrento, Italy. Paper No. 2, pp. 2.1–2.6, 1998.