4
THE STRANDS OF MATHEMATICAL PROFICIENCY
During the twentieth century, the meaning of successful mathematics learning underwent several shifts in response to changes in both society and schooling. For roughly the first half of the century, success in learning the mathematics of pre-kindergarten to eighth grade usually meant facility in using the computational procedures of arithmetic, with many educators emphasizing the need for skilled performance and others emphasizing the need for students to learn procedures with understanding.1 In the 1950s and 1960s, the new math movement defined successful mathematics learning primarily in terms of understanding the structure of mathematics together with its unifying ideas, and not just as computational skill. This emphasis was followed by a “back to basics” movement that proposed returning to the view that success in mathematics meant being able to compute accurately and quickly. The reform movement of the 1980s and 1990s pushed the emphasis toward what was called the development of “mathematical power,” which involved reasoning, solving problems, connecting mathematical ideas, and communicating mathematics to others. Reactions to reform proposals stressed such features of mathematics learning as the importance of memorization, of facility in computation, and of being able to prove mathematical assertions. These various emphases have reflected different goals for school mathematics held by different groups of people at different times.
Our analyses of the mathematics to be learned, our reading of the research in cognitive psychology and mathematics education, our experience as learners and teachers of mathematics, and our judgment as to the mathematical knowledge, understanding, and skill people need today have led us to adopt a
composite, comprehensive view of successful mathematics learning. This view, admittedly, represents no more than a single committee’s consensus. Yet our various backgrounds have led us to formulate, in a way that we hope others can and will accept, the goals toward which mathematics learning should be aimed. In this chapter, we describe the kinds of cognitive changes that we want to promote in children so that they can be successful in learning mathematics.
Recognizing that no term captures completely all aspects of expertise, competence, knowledge, and facility in mathematics, we have chosen mathematical proficiency to capture what we believe is necessary for anyone to learn mathematics successfully. Mathematical proficiency, as we see it, has five components, or strands:
-
conceptual understanding—comprehension of mathematical concepts, operations, and relations
-
procedural fluency—skill in carrying out procedures flexibly, accurately, efficiently, and appropriately
-
strategic competence—ability to formulate, represent, and solve mathematical problems
-
adaptive reasoning—capacity for logical thought, reflection, explanation, and justification
-
productive disposition—habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy.
These strands are not independent; they represent different aspects of a complex whole. Each is discussed in more detail below. The most important observation we make here, one stressed throughout this report, is that the five strands are interwoven and interdependent in the development of profi ciency in mathematics (see Box 4–1). Mathematical proficiency is not a one-dimensional trait, and it cannot be achieved by focusing on just one or two of these strands. In later chapters, we argue that helping children acquire mathematical proficiency calls for instructional programs that address all its strands. As they go from pre-kindergarten to eighth grade, all students should become increasingly proficient in mathematics. That proficiency should enable them to cope with the mathematical challenges of daily life and enable them to continue their study of mathematics in high school and beyond.
The five strands are interwoven and interdependent in the development of proficiency in mathematics.
The five strands provide a framework for discussing the knowledge, skills, abilities, and beliefs that constitute mathematical proficiency. This frame-
|
Box 4–1 Intertwined Strands of Proficiency 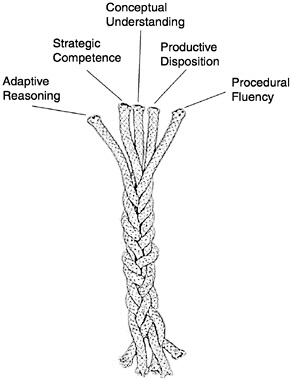 |
work has some similarities with the one used in recent mathematics assessments by the National Assessment of Educational Progress (NAEP), which features three mathematical abilities (conceptual understanding, procedural knowledge, and problem solving) and includes additional specifications for reasoning, connections, and communication.2 The strands also echo components of mathematics learning that have been identified in materials for teachers. At the same time, research and theory in cognitive science provide general support for the ideas contributing to these five strands. Fundamental in that work has been the central role of mental representations. How learners represent and connect pieces of knowledge is a key factor in whether they will understand it deeply and can use it in problem solving. Cognitive
scientists have concluded that competence in an area of inquiry depends upon knowledge that is not merely stored but represented mentally and organized (connected and structured) in ways that facilitate appropriate retrieval and application. Thus, learning with understanding is more powerful than simply memorizing because the organization improves retention, promotes fluency, and facilitates learning related material. The central notion that strands of competence must be interwoven to be useful reflects the finding that having a deep understanding requires that learners connect pieces of knowledge, and that connection in turn is a key factor in whether they can use what they know productively in solving problems. Furthermore, cognitive science studies of problem solving have documented the importance of adaptive expertise and of what is called metacognition: knowledge about one’s own thinking and ability to monitor one’s own understanding and problem-solving activity. These ideas contribute to what we call strategic competence and adaptive reasoning. Finally, learning is also influenced by motivation, a component of productive disposition.3
Although there is not a perfect fit between the strands of mathematical proficiency and the kinds of knowledge and processes identified by cognitive scientists, mathematics educators, and others investigating learning, we see the strands as reflecting a firm, sizable body of scholarly literature both in and outside mathematics education.
Conceptual Understanding
Conceptual understanding refers to an integrated and functional grasp of mathematical ideas. Students with conceptual understanding know more than isolated facts and methods. They understand why a mathematical idea is important and the kinds of contexts in which is it useful. They have organized their knowledge into a coherent whole, which enables them to learn new ideas by connecting those ideas to what they already know.4 Conceptual understanding also supports retention. Because facts and methods learned with understanding are connected, they are easier to remember and use, and they can be reconstructed when forgotten.5 If students understand a method, they are unlikely to remember it incorrectly. They monitor what they remember and try to figure out whether it makes sense. They may attempt to explain the method to themselves and correct it if necessary. Although teachers often look for evidence of conceptual understanding in students’ ability to verbalize connections among concepts and representations, conceptual understanding need not be explicit. Students often understand before they can verbalize that understanding.6
Conceptual understanding refers to an integrated and functional grasp of mathematical ideas.
A significant indicator of conceptual understanding is being able to represent mathematical situations in different ways and knowing how different representations can be useful for different purposes. To find one’s way around the mathematical terrain, it is important to see how the various representations connect with each other, how they are similar, and how they are different. The degree of students’ conceptual understanding is related to the richness and extent of the connections they have made.
For example, suppose students are adding fractional quantities of different sizes, say ![]() They might draw a picture or use concrete materials of various kinds to show the addition. They might also represent the number sentence
They might draw a picture or use concrete materials of various kinds to show the addition. They might also represent the number sentence ![]() as a story. They might turn to the number line, representing each fraction by a segment and adding the fractions by joining the segments. By renaming the fractions so that they have the same denominator, the students might arrive at a common measure for the fractions, determine the sum, and see its magnitude on the number line. By operating on these different representations, students are likely to use different solution methods. This variation allows students to discuss the similarities and differences of the representations, the advantages of each, and how they must be connected if they are to yield the same answer.
as a story. They might turn to the number line, representing each fraction by a segment and adding the fractions by joining the segments. By renaming the fractions so that they have the same denominator, the students might arrive at a common measure for the fractions, determine the sum, and see its magnitude on the number line. By operating on these different representations, students are likely to use different solution methods. This variation allows students to discuss the similarities and differences of the representations, the advantages of each, and how they must be connected if they are to yield the same answer.
Connections are most useful when they link related concepts and methods in appropriate ways. Mnemonic techniques learned by rote may provide connections among ideas that make it easier to perform mathematical operations, but they also may not lead to understanding.7 These are not the kinds of connections that best promote the acquisition of mathematical proficiency.
Knowledge that has been learned with understanding provides the basis for generating new knowledge and for solving new and unfamiliar problems.8 When students have acquired conceptual understanding in an area of mathematics, they see the connections among concepts and procedures and can give arguments to explain why some facts are consequences of others. They gain confidence, which then provides a base from which they can move to another level of understanding.
With respect to the learning of number, when students thoroughly understand concepts and procedures such as place value and operations with single-digit numbers, they can extend these concepts and procedures to new areas. For example, students who understand place value and other multidigit number concepts are more likely than students without such understanding to invent their own procedures for multicolumn addition and to adopt correct procedures for multicolumn subtraction that others have presented to them.9
Thus, learning how to add and subtract multidigit numbers does not have to involve entirely new and unrelated ideas. The same observation can be made for multiplication and division.
Conceptual understanding helps students avoid many critical errors in solving problems, particularly errors of magnitude. For example, if they are multiplying 9.83 and 7.65 and get 7519.95 for the answer, they can immediately decide that it cannot be right. They know that 10×8 is only 80, so multiplying two numbers less than 10 and 8 must give a product less than 80. They might then suspect that the decimal point is incorrectly placed and check that possibility.
Conceptual understanding frequently results in students having less to learn because they can see the deeper similarities between superficially unrelated situations. Their understanding has been encapsulated into compact clusters of interrelated facts and principles. The contents of a given cluster may be summarized by a short sentence or phrase like “properties of multiplication,” which is sufficient for use in many situations. If necessary, however, the cluster can be unpacked if the student needs to explain a principle, wants to reflect on a concept, or is learning new ideas. Often, the structure of students’ understanding is hierarchical, with simpler clusters of ideas packed into larger, more complex ones. A good example of a knowledge cluster for mathematically proficient older students is the number line. In one easily visualized picture, the student can grasp relations between all the number systems described in chapter 3, along with geometric interpretations for the operations of arithmetic. It connects arithmetic to geometry and later in schooling serves as a link to more advanced mathematics.
As an example of how a knowledge cluster can make learning easier, consider the cluster students might develop for adding whole numbers. If students understand that addition is commutative (e.g., 3+5=5+3), their learning of basic addition combinations is reduced by almost half. By exploiting their knowledge of other relationships such as that between the doubles (e.g., 5+5 and 6+6) and other sums, they can reduce still further the number of addition combinations they need to learn. Because young children tend to learn the doubles fairly early, they can use them to produce closely related sums.10 For example, they may see that 6+7 is just one more than 6+6. These relations make it easier for students to learn the new addition combinations because they are generating new knowledge rather than relying on rote memorization. Conceptual understanding, therefore, is a wise investment that pays off for students in many ways.
Procedural Fluency
Procedural fluency refers to knowledge of procedures, knowledge of when and how to use them appropriately, and skill in performing them flexibly, accurately, and efficiently. In the domain of number, procedural fluency is especially needed to support conceptual understanding of place value and the meanings of rational numbers. It also supports the analysis of similarities and differences between methods of calculating. These methods include, in addition to written procedures, mental methods for finding certain sums, differences, products, or quotients, as well as methods that use calculators, computers, or manipulative materials such as blocks, counters, or beads.
Procedural fluency refers to knowledge of procedures, knowledge of when and how to use them appropriately, and skill in performing them flexibly, accurately, and efficiently.
Students need to be efficient and accurate in performing basic computations with whole numbers (6+7, 17–9, 8×4, and so on) without always having to refer to tables or other aids. They also need to know reasonably efficient and accurate ways to add, subtract, multiply, and divide multidigit numbers, both mentally and with pencil and paper. A good conceptual understanding of place value in the base-10 system supports the development of fluency in multidigit computation.11 Such understanding also supports simplified but accurate mental arithmetic and more flexible ways of dealing with numbers than many students ultimately achieve.
Connected with procedural fluency is knowledge of ways to estimate the result of a procedure. It is not as critical as it once was, for example, that students develop speed or efficiency in calculating with large numbers by hand, and there appears to be little value in drilling students to achieve such a goal. But many tasks involving mathematics in everyday life require facility with algorithms for performing computations either mentally or in writing.
In addition to providing tools for computing, some algorithms are important as concepts in their own right, which again illustrates the link between conceptual understanding and procedural fluency. Students need to see that procedures can be developed that will solve entire classes of problems, not just individual problems. By studying algorithms as “general procedures,” students can gain insight into the fact that mathematics is well structured (highly organized, filled with patterns, predictable) and that a carefully developed procedure can be a powerful tool for completing routine tasks.
It is important for computational procedures to be efficient, to be used accurately, and to result in correct answers. Both accuracy and efficiency can be improved with practice, which can also help students maintain fluency. Students also need to be able to apply procedures flexibly. Not all computational situations are alike. For example, applying a standard pencil-and-paper algorithm to find the result of every multiplication problem is neither neces-
sary nor efficient. Students should be able to use a variety of mental strategies to multiply by 10, 20, or 300 (or any power of 10 or multiple of 10). Also, students should be able to perform such operations as finding the sum of 199 and 67 or the product of 4 and 26 by using quick mental strategies rather than relying on paper and pencil. Further, situations vary in their need for exact answers. Sometimes an estimate is good enough, as in calculating a tip on a bill at a restaurant. Sometimes using a calculator or computer is more appropriate than using paper and pencil, as in completing a complicated tax form. Hence, students need facility with a variety of computational tools, and they need to know how to select the appropriate tool for a given situation.
Procedural fluency and conceptual understanding are often seen as competing for attention in school mathematics. But pitting skill against understanding creates a false dichotomy.12 As we noted earlier, the two are interwoven. Understanding makes learning skills easier, less susceptible to common errors, and less prone to forgetting. By the same token, a certain level of skill is required to learn many mathematical concepts with understanding, and using procedures can help strengthen and develop that understanding. For example, it is difficult for students to understand multidigit calculations if they have not attained some reasonable level of skill in single-digit calculations. On the other hand, once students have learned procedures without understanding, it can be difficult to get them to engage in activities to help them understand the reasons underlying the procedure.13 In an experimental study, fifth-grade students who first received instruction on procedures for calculating area and perimeter followed by instruction on understanding those procedures did not perform as well as students who received instruction focused only on understanding.14
Without sufficient procedural fluency, students have trouble deepening their understanding of mathematical ideas or solving mathematics problems. The attention they devote to working out results they should recall or compute easily prevents them from seeing important relationships. Students need well-timed practice of the skills they are learning so that they are not handicapped in developing the other strands of proficiency.
When students practice procedures they do not understand, there is a danger they will practice incorrect procedures, thereby making it more difficult to learn correct ones. For example, on one standardized test, the grade 2 national norms for two-digit subtraction problems requiring borrowing, such as 62–48=?, are 38% correct. Many children subtract the smaller from the larger digit in each column to get 26 as the difference between 62 and 48 (see Box 4–2). If students learn to subtract with understanding, they rarely make
|
Box 4–2 A common error in multidigit subtraction |
this error.15 Further, when students learn a procedure without understanding, they need extensive practice so as not to forget the steps. If students do understand, they are less likely to forget critical steps and are more likely to be able to reconstruct them when they do. Shifting the emphasis to learning with understanding, therefore, can in the long run lead to higher levels of skill than can be attained by practice alone.
If students have been using incorrect procedures for several years, then instruction emphasizing understanding may be less effective.16 When children learn a new, correct procedure, they do not always drop the old one. Rather, they use either the old procedure or the new one depending on the situation. Only with time and practice do they stop using incorrect or inefficient methods.17 Hence initial learning with understanding can make learning more efficient.
When skills are learned without understanding, they are learned as isolated bits of knowledge.18 Learning new topics then becomes harder since there is no network of previously learned concepts and skills to link a new topic to. This practice leads to a compartmentalization of procedures that can become quite extreme, so that students believe that even slightly different problems require different procedures. That belief can arise among children in the early grades when, for example, they learn one procedure for subtraction problems without regrouping and another for subtraction problems with regrouping. Another consequence when children learn without understanding is that they separate what happens in school from what happens outside.19 They have one set of procedures for solving problems outside of school and another they learned and use in school—without seeing the relation between the two. This separation limits children’s ability to apply what they learn in school to solve real problems.
Also, students who learn procedures without understanding can typically do no more than apply the learned procedures, whereas students who learn
with understanding can modify or adapt procedures to make them easier to use. For example, students with limited understanding of addition would ordinarily need paper and pencil to add 598 and 647. Students with more understanding would recognize that 598 is only 2 less than 600, so they might add 600 and 647 and then subtract 2 from that sum.20
Strategic Competence
Strategic competence refers to the ability to formulate mathematical problems, represent them, and solve them. This strand is similar to what has been called problem solving and problem formulation in the literature of mathematics education and cognitive science, and mathematical problem solving, in particular, has been studied extensively.21
Strategic competence refers to the ability to formulate mathematical problems, represent them, and solve them.
Although in school, students are often presented with clearly specified problems to solve, outside of school they encounter situations in which part of the difficulty is to figure out exactly what the problem is. Then they need to formulate the problem so that they can use mathematics to solve it. Consequently, they are likely to need experience and practice in problem formulating as well as in problem solving. They should know a variety of solution strategies as well as which strategies might be useful for solving a specific problem. For example, sixth graders might be asked to pose a problem on the topic of the school cafeteria.22 Some might ask whether the lunches are too expensive or what the most and least favorite lunches are. Others might ask how many trays are used or how many cartons of milk are sold. Still others might ask how the layout of the cafeteria might be improved.
With a formulated problem in hand, the student’s first step in solving it is to represent it mathematically in some fashion, whether numerically, symbolically, verbally, or graphically. Fifth graders solving problems about getting from home to school might describe verbally the route they take or draw a scale map of the neighborhood. Representing a problem situation requires, first, that the student build a mental image of its essential components. Becoming strategically competent involves an avoidance of “number grabbing” methods (in which the student selects numbers and prepares to perform arithmetic operations on them)23 in favor of methods that generate problem models (in which the student constructs a mental model of the variables and relations described in the problem). To represent a problem accurately, students must first understand the situation, including its key features. They then need to generate a mathematical representation of the problem that captures the core mathematical elements and ignores the irrelevant features. This
step may be facilitated by making a drawing, writing an equation, or creating some other tangible representation. Consider the following two-step problem:
At ARCO, gas sells for $1.13 per gallon.
This is 5 cents less per gallon than gas at Chevron.
How much does 5 gallons of gas cost at Chevron?
In a common superficial method for representing this problem, students focus on the numbers in the problem and use so-called keywords to cue appropriate arithmetic operations.24 For example, the quantities $1.83 and 5 cents are followed by the keyword less, suggesting that the student should subtract 5 cents from $1.13 to get $1.08. Then the keywords how much and 5 gallons suggest that 5 should be multiplied by the result, yielding $5.40.
In contrast, a more proficient approach is to construct a problem model— that is, a mental model of the situation described in the problem. A problem model is not a visual picture per se; rather, it is any form of mental representation that maintains the structural relations among the variables in the problem. One way to understand the first two sentences, for example, might be for a student to envision a number line and locate each cost per gallon on it to solve the problem.
In building a problem model, students need to be alert to the quantities in the problem. It is particularly important that students represent the quantities mentally, distinguishing what is known from what is to be found. Analyses of students’ eye fixations reveal that successful solvers of the two-step problem above are likely to focus on terms such as ARCO, Chevron, and this, the principal known and unknown quantities in the problem. Less successful problem solvers tend to focus on specific numbers and keywords such as $1.13, 5 cents, less, and 5 gallons rather than the relationships among the quantities.25
Not only do students need to be able to build representations of individual situations, but they also need to see that some representations share common mathematical structures. Novice problem solvers are inclined to notice similarities in surface features of problems, such as the characters or scenarios described in the problem. More expert problem solvers focus more on the structural relationships within problems, relationships that provide the clues for how problems might be solved.26 For example, one problem might ask students to determine how many different stacks of five blocks can be made using red and green blocks, and another might ask how many different ways hamburgers can be ordered with or without each of the following:
catsup, onions, pickles, lettuce, and tomato. Novices would see these problems as unrelated; experts would see both as involving five choices between two things: red and green, or with and without.27
In becoming proficient problem solvers, students learn how to form mental representations of problems, detect mathematical relationships, and devise novel solution methods when needed. A fundamental characteristic needed throughout the problem-solving process is flexibility. Flexibility develops through the broadening of knowledge required for solving nonroutine problems rather than just routine problems.
Routine problems are problems that the learner knows how to solve based on past experience.28 When confronted with a routine problem, the learner knows a correct solution method and is able to apply it. Routine problems require reproductive thinking; the learner needs only to reproduce and apply a known solution procedure. For example, finding the product of 567 and 46 is a routine problem for most adults because they know what to do and how to do it.
In contrast, nonroutine problems are problems for which the learner does not immediately know a usable solution method. Nonroutine problems require productive thinking because the learner needs to invent a way to understand and solve the problem. For example, for most adults a nonroutine problem of the sort often found in newspaper or magazine puzzle columns is the following:
A cycle shop has a total of 36 bicycles and tricycles in stock.
Collectively there are 80 wheels.
How many bikes and how many tricycles are there?
One solution approach is to reason that all 36 have at least two wheels for a total of 36×2=72 wheels. Since there are 80 wheels in all, the eight additional wheels (80–72) must belong to 8 tricycles. So there are 36–8=28 bikes.
A less sophisticated approach would be to “guess and check”: If there were 20 bikes and 16 tricycles, that would give (20×2)+(16×3)=88 wheels, which is too many. Reducing the number of tricycles, a guess of 24 bikes and 12 tricycles gives (24×2)+(12×3)=84 wheels—still too many. Another reduction of the number of tricycles by 4 gives 28 bikes, 8 tricycles, and the 80 wheels needed.
A more sophisticated, algebraic approach would be to let b be the number of bikes and t the number of tricycles. Then b+t=36 and 2b+3t=80. The solution to this system of equations also yields 28 bikes and 8 tricycles.
A student with strategic competence could not only come up with several approaches to a nonroutine problem such as this one but could also choose flexibly among reasoning, guess-and-check, algebraic, or other methods to suit the demands presented by the problem and the situation in which it was posed.
Flexibility of approach is the major cognitive requirement for solving nonroutine problems. It can be seen when a method is created or adjusted to fit the requirements of a novel situation, such as being able to use general principles about proportions to determine the best buy. For example, when the choice is between a 4-ounce can of peanuts for 45 cents and a 10-ounce can for 90 cents, most people use a ratio strategy: the larger can costs twice as much as the smaller can but contains more than twice as many ounces, so it is a better buy. When the choice is between a 14-ounce jar of sauce for 79 cents and an 18-ounce jar for 81 cents, most people use a difference strategy: the larger jar costs just 2 cents more but gets you 4 more ounces, so it is the better buy. When the choice is between a 3-ounce bag of sunflower seeds for 30 cents and a 4-ounce bag for 44 cents, the most common strategy is unit-cost: The smaller bag costs 10 cents per ounce, whereas the larger costs 11 cents per ounce, so the smaller one is the better buy.
There are mutually supportive relations between strategic competence and both conceptual understanding and procedural fluency, as the various approaches to the cycle shop problem illustrate. The development of strategies for solving nonroutine problems depends on understanding the quantities involved in the problems and their relationships as well as on fluency in solving routine problems. Similarly, developing competence in solving nonroutine problems provides a context and motivation for learning to solve routine problems and for understanding concepts such as given, unknown, condition, and solution.
There are mutually supportive relations between strategic competence and both conceptual understanding and procedural fluency,
Strategic competence comes into play at every step in developing procedural fluency in computation. As students learn how to carry out an operation such as two-digit subtraction (for example, 86–59), they typically progress from conceptually transparent and effortful procedures to compact and more efficient ones (as discussed in detail in chapter 6). For example, an initial procedure for 86–59 might be to use bundles of sticks (see Box 4–3). A compact procedure involves applying a written numerical algorithm that carries out the same steps without the bundles of sticks. Part of developing strategic competence involves learning to replace by more concise and efficient procedures those cumbersome procedures that might at first have been helpful in understanding the operation.
|
Box 4–3 Subtraction Using Sticks: Modeling 86–53=? 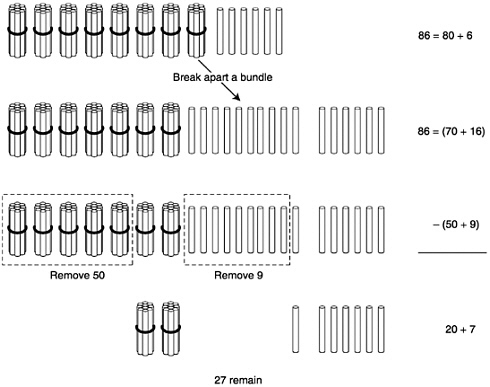 Begin with 8 bundles of 10 sticks along with 6 individual sticks. Because you cannot take away 9 individual sticks, open one bundle, creating 7 bundles of 10 sticks and 16 individual sticks. Take away 5 of the bundles (corresponding to subtracting 50), and take away 9 individual sticks (corresponding to subtracting 9). The number of remaining sticks—2 bundles and 7 individual sticks, or 27—is the answer. |
Students develop procedural fluency as they use their strategic competence to choose among effective procedures. They also learn that solving challenging mathematics problems depends on the ability to carry out procedures readily and, conversely, that problem-solving experience helps them acquire new concepts and skills. Interestingly, very young children use a variety of strategies to solve problems and will tend to select strategies that are well suited to particular problems.29 They thereby show the rudiments of adaptive reasoning, the next strand to be discussed.
Adaptive Reasoning
Adaptive reasoning refers to the capacity to think logically about the relationships among concepts and situations. Such reasoning is correct and valid, stems from careful consideration of alternatives, and includes knowledge of how to justify the conclusions. In mathematics, adaptive reasoning is the glue that holds everything together, the lodestar that guides learning. One uses it to navigate through the many facts, procedures, concepts, and solution methods and to see that they all fit together in some way, that they make sense. In mathematics, deductive reasoning is used to settle disputes and disagreements. Answers are right because they follow from some agreed-upon assumptions through series of logical steps. Students who disagree about a mathematical answer need not rely on checking with the teacher, collecting opinions from their classmates, or gathering data from outside the classroom. In principle, they need only check that their reasoning is valid.
Adaptive reasoning refers to the capacity to think logically about the relationships among concepts and situations.
Many conceptions of mathematical reasoning have been confined to formal proof and other forms of deductive reasoning. Our notion of adaptive reasoning is much broader, including not only informal explanation and justification but also intuitive and inductive reasoning based on pattern, analogy, and metaphor. As one researcher put it, “The human ability to find analogical correspondences is a powerful reasoning mechanism.”30 Analogical reasoning, metaphors, and mental and physical representations are “tools to think with,” often serving as sources of hypotheses, sources of problem-solving operations and techniques, and aids to learning and transfer.31
Some researchers have concluded that children’s reasoning ability is quite limited until they are about 12 years old.32 Yet when asked to talk about how they arrived at their solutions to problems, children as young as 4 and 5 display evidence of encoding and inference and are resistant to counter suggestion.33 With the help of representation-building experiences, children can demonstrate sophisticated reasoning abilities. After working in pairs and
reflecting on their activity, for example, kindergartners can “prove” theorems about sums of even and odd numbers.34 Through a carefully constructed sequence of activities about adding and removing marbles from a bag containing many marbles,35 second graders can reason that 5+(–6)=–1. In the context of cutting short bows from a 12-meter package of ribbon and using physical models to calculate that 12 divided by ![]() is 36, fifth graders can reason that 12 divided by
is 36, fifth graders can reason that 12 divided by ![]() cannot be 72 because that would mean getting more bows from a package when the individual bow is larger, which does not make sense.36 Research suggests that students are able to display reasoning ability when three conditions are met: They have a sufficient knowledge base, the task is understandable and motivating, and the context is familiar and comfortable.37
cannot be 72 because that would mean getting more bows from a package when the individual bow is larger, which does not make sense.36 Research suggests that students are able to display reasoning ability when three conditions are met: They have a sufficient knowledge base, the task is understandable and motivating, and the context is familiar and comfortable.37
One manifestation of adaptive reasoning is the ability to justify one’s work. We use justify in the sense of “provide sufficient reason for.” Proof is a form of justification, but not all justifications are proofs. Proofs (both formal and informal) must be logically complete, but a justification may be more telegraphic, merely suggesting the source of the reasoning. Justification and proof are a hallmark of formal mathematics, often seen as the province of older students. However, as pointed out above, students can start learning to justify their mathematical ideas in the earliest grades in elementary school.38 Kindergarten and first-grade students can be given regular opportunities to talk about the concepts and procedures they are using and to provide good reasons for what they are doing. Classroom norms can be established in which students are expected to justify their mathematical claims and make them clear to others. Students need to be able to justify and explain ideas in order to make their reasoning clear, hone their reasoning skills, and improve their conceptual understanding.39
It is not sufficient to justify a procedure just once. As we discuss below, the development of proficiency occurs over an extended period of time. Students need to use new concepts and procedures for some time and to explain and justify them by relating them to concepts and procedures that they already understand. For example, it is not sufficient for students to do only practice problems on adding fractions after the procedure has been developed. If students are to understand the algorithm, they also need experience in explaining and justifying it themselves with many different problems.
Adaptive reasoning interacts with the other strands of proficiency, particularly during problem solving. Learners draw on their strategic competence to formulate and represent a problem, using heuristic approaches that may provide a solution strategy, but adaptive reasoning must take over when
they are determining the legitimacy of a proposed strategy. Conceptual understanding provides metaphors and representations that can serve as a source of adaptive reasoning, which, taking into account the limitations of the representations, learners use to determine whether a solution is justifiable and then to justify it. Often a solution strategy will require fluent use of procedures for calculation, measurement, or display, but adaptive reasoning should be used to determine whether the procedure is appropriate. And while carrying out a solution plan, learners use their strategic competence to monitor their progress toward a solution and to generate alternative plans if the current plan seems ineffective. This approach both depends upon productive disposition and supports it.
Productive Disposition
Productive disposition refers to the tendency to see sense in mathematics, to perceive it as both useful and worthwhile, to believe that steady effort in learning mathematics pays off, and to see oneself as an effective learner and doer of mathematics.40 If students are to develop conceptual understanding, procedural fluency, strategic competence, and adaptive reasoning abilities, they must believe that mathematics is understandable, not arbitrary; that, with diligent effort, it can be learned and used; and that they are capable of figuring it out. Developing a productive disposition requires frequent opportunities to make sense of mathematics, to recognize the benefits of perseverance, and to experience the rewards of sense making in mathematics.
Productive disposition refers to the tendency to see sense in mathematics, to perceive it as both useful and worthwhile, to believe that steady effort in learning mathematics pays off, and to see oneself as an effective learner and doer of mathematics.
A productive disposition develops when the other strands do and helps each of them develop. For example, as students build strategic competence in solving nonroutine problems, their attitudes and beliefs about themselves as mathematics learners become more positive. The more mathematical concepts they understand, the more sensible mathematics becomes. In contrast, when students are seldom given challenging mathematical problems to solve, they come to expect that memorizing rather than sense making paves the road to learning mathematics,41 and they begin to lose confidence in themselves as learners. Similarly, when students see themselves as capable of learning mathematics and using it to solve problems, they become able to develop further their procedural fluency or their adaptive reasoning abilities. Students’ disposition toward mathematics is a major factor in determining their educational success. Students who view their mathematical ability as fixed and test questions as measuring their ability rather than providing opportunities to learn are likely to avoid challenging problems and be easily dis-
couraged by failure.42 Students who view ability as expandable in response to experience and training are more likely to seek out challenging situations and learn from them. Cross-cultural research studies have found that U.S. children are more likely to attribute success in school to ability rather than effort when compared with students in East Asian countries.43
Most U.S. children enter school eager to learn and with positive attitudes toward mathematics. It is critical that they encounter good mathematics teaching in the early grades. Otherwise, those positive attitudes may turn sour as they come to see themselves as poor learners and mathematics as nonsensical, arbitrary, and impossible to learn except by rote memorization.44 Such views, once adopted, can be extremely difficult to change.45
The teacher of mathematics plays a critical role in encouraging students to maintain positive attitudes toward mathematics. How a teacher views mathematics and its learning affects that teacher’s teaching practice,46 which ultimately affects not only what the students learn but how they view themselves as mathematics learners. Teachers and students inevitably negotiate among themselves the norms of conduct in the class, and when those norms allow students to be comfortable in doing mathematics and sharing their ideas with others, they see themselves as capable of understanding.47 In chapter 9 we discuss some of the ways in which teachers’ expectations and the teaching strategies they use can help students maintain a positive attitude toward mathematics, and in chapter 10 we discuss some programs of teacher development that may help teachers in that endeavor.
An earlier report from the National Research Council identified the cause of much poor performance in school mathematics in the United States:
The unrestricted power of peer pressure often makes good performance in mathematics socially unacceptable. This environment of negative expectation is strongest among minorities and women— those most at risk—during the high school years when students first exercise choice in curricular goals.48
Some of the most important consequences of students’ failure to develop a productive disposition toward mathematics occur in high school, when they have the opportunity to avoid challenging mathematics courses. Avoiding such courses may eliminate the need to face up to peer pressure and other sources of discouragement, but it does so at the expense of precluding careers in science, technology, medicine, and other fields that require a high level of mathematical proficiency.
Research with older students and adults suggests that a phenomenon termed stereotype threat might account for much of the observed differences in mathematics performance between ethnic groups and between male and female students.49 In this phenomenon, good students who care about their performance in mathematics and who belong to groups stereotyped as being poor at mathematics perform poorly on difficult mathematics problems under conditions in which they feel pressure to conform to the stereotype. So-called wise educational environments50 can reduce the harmful effects of stereotype threat. These environments emphasize optimistic teacher-student relationships, give challenging work to all students, and stress the expandability of ability, among other factors.
Students who have developed a productive disposition are confident in their knowledge and ability. They see that mathematics is both reasonable and intelligible and believe that, with appropriate effort and experience, they can learn. It is counterproductive for students to believe that there is some mysterious “math gene” that determines their success in mathematics.
Hence, our view of mathematical proficiency goes beyond being able to understand, compute, solve, and reason. It includes a disposition toward mathematics that is personal. Mathematically proficient people believe that mathematics should make sense, that they can figure it out, that they can solve mathematical problems by working hard on them, and that becoming mathematically proficient is worth the effort.
Properties of Mathematical Proficiency
Now that we have looked at each strand separately, let us consider mathematical proficiency as a whole. As we indicated earlier and as the preceding discussion illustrates, the five strands are interconnected and must work together if students are to learn successfully. Learning is not an all-or-none phenomenon, and as it proceeds, each strand of mathematical proficiency should be developed in synchrony with the others. That development takes time. One of the most challenging tasks faced by teachers in pre-kindergarten to grade 8 is to see that children are making progress along every strand and not just one or two.
Learning is not an all-or-none phenomenon, and as it proceeds, each strand of mathematical proficiency should be developed in synchrony with the others.
The Strands of Proficiency Are interwoven
How the strands of mathematical proficiency interweave and support one another can be seen in the case of conceptual understanding and procedural fluency. Current research indicates that these two strands of proficiency con-
tinually interact.51 As a child gains conceptual understanding, computational procedures are remembered better and used more flexibly to solve new problems. In turn, as a procedure becomes more automatic, the child is enabled to think about other aspects of a problem and to tackle new kinds of problems, which leads to new understanding. When using a procedure, a child may reflect on why the procedure works, which may in turn strengthen existing conceptual understanding.52 Indeed, it is not always necessary, useful, or even possible to distinguish concepts from procedures because understanding and doing are interconnected in such complex ways.
Consider, for instance, the multiplication of multidigit whole numbers. Many algorithms for computing 47×268 use one basic meaning of multiplication as 47 groups of 268, together with place-value knowledge of 47 as 40+7, to break the problem into two simpler ones: 40×268 and 7×268. For example, a common algorithm for computing 47×268 is written the following way, with the two so-called partial products, 10720 and 1876, coming from the two simpler problems:
Familiarity with this algorithm may make it hard for adults to see how much knowledge is needed for it. It requires knowing that 40×268 is 4×10×268; knowing that in the product of 268 and 10, each digit of 268 is one place to the left; having enough fluency with basic multiplication combinations to find 7×8, 7×60, 7×200, and 4×8, 4×60, 4×200; and having enough fluency with multidigit addition to add the partial products. As students learn to execute a multidigit multiplication procedure such as this one, they should develop a deeper understanding of multiplication and its properties. On the other hand, as they deepen their conceptual understanding, they should become more fluent in computation. A beginner who happens to forget the algorithm but who understands the role of the distributive law can reconstruct the process by writing 268×47=268×(40+7)=(268×40)+(268×7) and working from there. A beginner who has simply memorized the algorithm without understanding much about how it works can be lost later when memory fails.
Proficiency is Not All or Nothing
Mathematical proficiency cannot be characterized as simply present or absent. Every important mathematical idea can be understood at many levels and in many ways. For example, even seemingly simple concepts such as even and odd require an integration of several ways of thinking: choosing alternate points on the number line, grouping items by twos, grouping items into two groups, and looking at only the last digit of the number. When children are first learning about even and odd, they may know one or two of these interpretations.53 But at an older age, a deep understanding of even and odd means all four interpretations are connected and can be justified one based on the others.
The research cited in chapter 5 shows that schoolchildren are never complete mathematical novices. They bring important mathematical concepts and skills with them to school as well as misconceptions that must be taken into account in planning instruction. Obviously, a first grader’s understanding of addition is not the same as that of a mathematician or even a lay adult. It is still reasonable, however, to talk about a first grader as being proficient with single-digit addition, as long as the student’s thinking in that realm incorporates all five strands of proficiency. Students should not be thought of as having proficiency when one or more strands are undeveloped.
Proficiency Develops Over Time
Proficiency in mathematics is acquired over time. Each year they are in school, students ought to become increasingly proficient. For example, third graders should be more proficient with the addition of whole numbers than they were in the first grade.
Acquiring proficiency takes time in another sense. Students need enough time to engage in activities around a specific mathematical topic if they are to become proficient with it. When they are provided with only one or two examples to illustrate why a procedure works or what a concept means and then move on to practice in carrying out the procedure or identifying the concept, they may easily fail to learn. To become proficient, they need to spend sustained periods of time doing mathematics—solving problems, reasoning, developing understanding, practicing skills—and building connections between their previous knowledge and new knowledge.
How Mathematically Proficient Are U.S. Students Today?
One question that warrants an immediate answer is whether students in U.S. elementary and middle schools today are becoming mathematically proficient. The answer is important because it influences what might be recommended for the future. If students are failing to develop proficiency, the question of how to improve school mathematics takes on a different cast than if students are already developing high levels of proficiency.
The best source of information about student performance in the United States is, as we noted in chapter 2, the National Assessment of Educational Progress (NAEP), a regular assessment of students’ knowledge and skills in the school subjects. NAEP includes a large and representative sample of U.S. students at about ages 9, 13, and 17, so the results provide a good picture of students’ mathematical performance. We sketched some of that performance in chapter 2, but now we look at it through the frame of mathematical proficiency.
Although the items in the NAEP assessments were not constructed to measure directly the five strands of mathematical proficiency, they provide some useful information about these strands. As in chapter 2, the data reported here are from the 1996 main NAEP assessment except when we refer explicitly to the long-term trend assessment. In general, the performance of 13-year-olds over the past 25 years tells the following story: Given traditional curricula and methods of instruction, students develop proficiency among the five strands in a very uneven way. They are most proficient in aspects of procedural fluency and less proficient in conceptual understanding, strategic competence, adaptive reasoning, and productive disposition. Many students show few connections among these strands. Examples from each strand illustrate the current situation.54
Conceptual Understanding
Students’ conceptual understanding of number can be assessed in part by asking them about properties of the number systems. Although about 90% of U.S. 13-year-olds could add and subtract multidigit numbers, only 60% of them could construct a number given its digits and their place values (e.g., in the number 57, the digit 5 should represent five tens).55 That is a common finding: More students can calculate successfully with numbers than can work with the properties of the same numbers.
The same is true for rational numbers. Only 35% of 13-year-olds correctly ordered three fractions, all in reduced form,56 and only 35%, asked for a number between .03 and .04, chose the correct response.57 These findings suggest that students may be calculating with numbers that they do not really understand.
Procedural Fluency
An overall picture of procedural fluency is provided by the NAEP long-term trend mathematics assessment,58 which indicates that U.S. students’ performance has remained quite steady over the past 25 years (see Box 4–4). A closer look reveals that the picture of procedural fluency is one of high levels of proficiency in the easiest contexts. Questions in which students are asked to add or subtract two- and three-digit whole numbers presented numerically in the standard format are answered correctly by about 90% of 13-year-olds, with almost as good performance among 9-year-olds.59 Performance is slightly lower among 13-year-olds for division.60
|
Box 4–4 NAEP Scale Scores, Long-Term Trend Assessment, 1973–1999 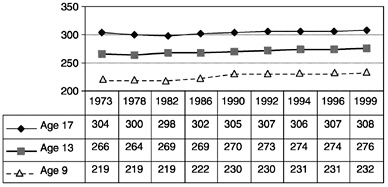 SOURCE: Campbell, Hombo, and Mazzeo, 2000, p. 9. These scale scores include all content areas: number, geometry, algebra, and so on. |
Students are less fluent in operating with rational numbers, both common and decimal fractions. The most recent NAEP in 1996 contained few computation items, but earlier assessments showed that about 50% of 13-year-olds correctly completed problems like ![]() and 4.3–0.53. Again, this level of performance has remained quite steady since the advent of NAEP. One conclusion that can be drawn is that by age 13 many students have not fully developed procedural fluency. Although most can compute well with whole numbers in simple contexts, many still have difficulties computing with rational numbers.
and 4.3–0.53. Again, this level of performance has remained quite steady since the advent of NAEP. One conclusion that can be drawn is that by age 13 many students have not fully developed procedural fluency. Although most can compute well with whole numbers in simple contexts, many still have difficulties computing with rational numbers.
Strategic Competence
Results from NAEP dating back over 25 years have continually documented the fact that one of the greatest deficits in U.S. students’ learning of mathematics is in their ability to solve problems. In the 1996 NAEP, students in the fourth, eighth, and twelfth grades did well on questions about basic whole number operations and concepts in numerical and simple applied contexts. However, students, especially those in the fourth and eighth grades, had difficulty with more complex problem-solving situations. For example, asked to add or subtract two- and three-digit numbers, 73% of fourth graders and 86% of eighth graders gave correct answers. But on a multistep addition and subtraction word problem involving similar numbers, only 33% of fourth graders gave a correct answer (although 76% of eighth graders did). On the 23 problem-solving tasks given as part of the 1996 NAEP in which students had to construct an extended response, the incidence of satisfactory or better responses was less than 10% on about half of the tasks. The incidence of satisfactory responses was greater than 25% on only two tasks.61
Performance on word problems declines dramatically when additional features are included, such as more than one step or extraneous information. Small changes in problem wording, context, or presentation can yield dramatic changes in students’ success,62 perhaps indicating how fragile students’ problem-solving abilities typically are.
Adaptive Reasoning
Several kinds of items measure students’ proficiency in adaptive reasoning, though often in conjunction with other strands. One kind of item asks students to reason about numbers and their properties and also assesses their conceptual understanding. For example,
If 49+83=132 is true, which of the following is true?
49=83+132
49+132=83
132–49=83
83–132=49
Only 61% of 13-year-olds chose the right answer, which again is considerably lower than the percentage of students who can actually compute the result.
Another example is a multiple-choice problem in which students were asked to estimate ![]() The choices were 1, 2, 19, and 21. Fifty-five percent of the 13-year-olds chose either 19 or 21 as the correct response.63 Even modest levels of reasoning should have prevented these errors. Simply observing that
The choices were 1, 2, 19, and 21. Fifty-five percent of the 13-year-olds chose either 19 or 21 as the correct response.63 Even modest levels of reasoning should have prevented these errors. Simply observing that ![]() and
and ![]() are numbers less than one and that the sum of two numbers less than one is less than two would have made it apparent that 19 and 21 were unreasonable answers. This level of performance is especially striking because this kind of reasoning does not require procedural fluency plus additional proficiency. In many ways it is less demanding than the computational task and requires only that basic understanding and reasoning be connected. It is clear that for many students that connection is not being made.
are numbers less than one and that the sum of two numbers less than one is less than two would have made it apparent that 19 and 21 were unreasonable answers. This level of performance is especially striking because this kind of reasoning does not require procedural fluency plus additional proficiency. In many ways it is less demanding than the computational task and requires only that basic understanding and reasoning be connected. It is clear that for many students that connection is not being made.
A second kind of item that measures adaptive reasoning is one that asks students to justify and explain their solutions. One such item (Box 4–5) required that students use subtraction and division to justify claims about the population growth in two towns. Only 1% of eighth graders in 1996 provided a satisfactory response for both claims, and only another 21% provided a partially correct response. The results were only slightly better at grade 12. In this item, Darlene’s claim is stated somewhat cryptically, and students may not have understood that they needed to think about population growth not additively—as in the case of Brian’s claim—but multiplicatively so as to conclude that Town A actually had the larger rate of growth. But given the low levels of performance on the item, we conclude that Darlene’s enigmatic claim was not the only source of difficulty. Students apparently have trouble justifying their answers even in relatively simple cases.
Productive Disposition
Research related to productive disposition has not examined many aspects of the strand as we have defined it. Such research has focused on attitudes
|
Box 4–5 Population Growth in Two Towns In 1980 the populations of Town A and Town B were 5,000 and 6,000, respectively. The 1990 populations of Town A and Town B were 8,000 and 9,000, respectively. Brian claims that from 1980 to 1990 the populations of the two towns grew by the same amount. Use mathematics to explain how Brian might have justified his claim. Darlene claims that from 1980 to 1990 the population of Town A grew more. Use mathematics to explain how Darlene might have justified her claim.
SOURCE: 1996 NAEP assessment. Cited in Wearne and Kouba, 2000, p. 186. Used by permission of National Council of Teachers of Mathematics. |
toward mathematics, beliefs about one’s own ability, and beliefs about the nature of mathematics. In general, U.S. boys have more positive attitudes toward mathematics than U.S. girls do, even though differences in achievement between boys and girls are, in general, not as pronounced today as they were some decades ago.64 Girls’ attitudes toward mathematics also decline more sharply through the grades than those of boys.65 Differences in mathematics achievement remain larger across groups that differ in such factors as race, ethnicity, and social class, but differences in attitudes toward mathematics across these groups are not clearly associated with achievement differences.66
The complex relationship between attitudes and achievement is well illustrated in recent international studies. Although within most countries, positive attitudes toward mathematics are associated with high achievement, eighth graders in some East Asian countries, whose average achievement in mathematics is among the highest in the world, have tended to have, on average, among the most negative attitudes toward mathematics. U.S. eighth
graders, whose achievement is around the international average, have tended to be about average in their attitudes.67 Similarly, within a country, students who perceive themselves as good at mathematics tend to have high levels of achievement, but that relationship does not hold across countries. In Asian countries, perhaps because of cultural traditions encouraging humility or because of the challenging curriculum they face, eighth graders tend to perceive themselves as not very good at mathematics. In the United States, in contrast, eighth graders tend to believe that mathematics is not especially difficult for them and that they are good at it.68
Data from the NAEP student questionnaire show that many U.S. students develop a variety of counterproductive beliefs about mathematics and about themselves as learners of mathematics. For example, 54% of the fourth graders and 40% of the eighth graders in the 1996 NAEP assessment thought that mathematics is mostly a set of rules and that learning mathematics means memorizing the rules. On the other hand, approximately 75% of the fourth graders and 75% of the eighth graders sampled reported that they understand most of what goes on in mathematics class. The data do not indicate, however, whether the students thought they could make sense out of the mathematics themselves or depended on others for explanations.
Despite the finding that many students associate mathematics with memorization, students at all grade levels appear to view mathematics as useful. The 1996 NAEP revealed that 69% of the fourth graders and 70% of the eighth graders agreed that mathematics is useful for solving everyday problems. Although students appear to think mathematics is useful for everyday problems or important to society in general, it is not clear that they think it is important for them as individuals to know a lot of mathematics.69
Proficiency in Other Domains of Mathematics
Although our discussion of mathematical proficiency in this report is focused on the domain of number, the five strands apply equally well to other domains of mathematics such as geometry, measurement, probability, and statistics. Regardless of the domain of mathematics, conceptual understanding refers to an integrated and functional grasp of the mathematical ideas. These may be ideas about shape and space, measure, pattern, function, uncertainty, or change. When applied to other domains of mathematics, procedural fluency refers to skill in performing flexibly, accurately, and efficiently such procedures as constructing shapes, measuring space, computing probabilities, and describing data. It also refers to knowing when and how to use
The five strands apply equally well to other domains of mathematics such as geometry, measurement, probability, and statistics.
those procedures. Strategic competence refers to the ability to formulate mathematical problems, represent them, and solve them whether the problems arise in the context of number, algebra, geometry, measurement, probability, or statistics. Similarly, the capacity to think logically about the relationships among concepts and situations and to reason adaptively applies to every domain of mathematics, not just number, as does the notion of a productive disposition. The tendency to see sense in mathematics, to perceive it as both useful and worthwhile, to believe that steady effort in learning mathematics pays off, and to see oneself as an effective learner and doer of mathematics applies equally to all domains of mathematics. We believe that proficiency in any domain of mathematics means the development of the five strands, that the strands of proficiency are interwoven, and that they develop over time. Further, the strands are interwoven across domains of mathematics in such a way that conceptual understanding in one domain, say geometry, supports conceptual understanding in another, say number.
All Students Should Be Mathematically Proficient
Becoming mathematically proficient is necessary and appropriate for all students. People sometimes assume that only the brightest students who are the most attuned to school can achieve mathematical proficiency. Those students are the ones who have traditionally tended to achieve no matter what kind of instruction they have encountered. But perhaps surprisingly, it is students who have historically been less successful in school who have the most potential to benefit from instruction designed to achieve proficiency.70 All will benefit from a program in which mathematical proficiency is the goal.
Historically, the prevailing ethos in mathematics and mathematics education in the United States has been that mathematics is a discipline for a select group of learners. The continuing failure of some groups to master mathematics—including disproportionate numbers of minorities and poor students—has served to confirm that assumption. More recently, mathematics educators have highlighted the universal aspects of mathematics and have insisted on mathematics for all students, but with little attention to the differential access that some students have to high-quality mathematics teaching.71
One concern has been that too few girls, relative to boys, are developing mathematical proficiency and continuing their study of mathematics. That situation appears to be improving, although perhaps not uniformly across
grades. The 1990 and 1992 NAEP assessments indicated that the few gender differences in mathematics performance that did appear favored male students at grade 12 but not before. These differences were only partly explained by the historical tendency of male students to take more high school mathematics courses than female students do, since that gap had largely closed by 1992. In the 1996 NAEP mathematics assessment, the average scores for male and female students were not significantly different at either grade 8 or grade 12, but the average score for fourth-grade boys was 2% higher than the score for fourth-grade girls.72
With regard to differences among racial and ethnic groups, the situation is rather different. The racial/ethnic diversity of the United States is much greater now than at any previous period in history and promises to become progressively more so for some time to come. The strong connection between economic advantage, school funding, and achievement in the United States has meant that groups of students whose mathematics achievement is low have tended to be disproportionately African American, Hispanic, Native American, students acquiring English, or students located in urban or rural school districts.73 In the NAEP assessments from 1990 to 1996, white students recorded increases in their average mathematics scores at all grades. Over the same period, African American and Hispanic students recorded increases at grades 4 and 12, but not at grade 8.74 Scores for African American, Hispanic, and American Indian students remained below scale scores for white students. The mathematics achievement gaps between average scores for these subgroups did not decrease in 1996.75 The gap appears to be widening for African American students, particularly among students of the best-educated parents, which suggests that the problem is not one solely of poverty and disadvantage.76
Students identified as being of middle and high socioeconomic status (SES) enter school with higher achievement levels in mathematics than low-SES students, and students reporting higher levels of parental education tend to have higher average scores on NAEP assessments. At all three grades, in contrast, students eligible for free or reduced-price lunch programs score lower than those not eligible.77 Such SES-based differences in mathematics achievement are greater among whites than among other racial or ethnic groups.78 Some studies have suggested that the basis for the differences resides in the opportunities available to students, including opportunities to attend effective schools,79 opportunities afforded by social and economic factors of the home and school community,80 and opportunities to get encouragement to continue the study of mathematics.81
Goals for mathematics instruction like those outlined in our discussion of mathematical proficiency need to be set in full recognition of the differential access students have to high-quality mathematics teaching and the differential performance they show. Those goals should never be set low, however, in the mistaken belief that some students do not need or cannot achieve proficiency. In this day of rapidly changing technologies, no one can anticipate all the skills that students will need over their lifetimes or the problems they will encounter. Proficiency in mathematics is therefore an important foundation for further instruction in mathematics as well as for further education in fields that require mathematical competence. Schools need to prepare students to acquire new skills and knowledge and to adapt their knowledge to solve new problems.
The currency of value in the job market today is more than computational competence. It is the ability to apply knowledge to solve problems.82 For students to be able to compete in today’s and tomorrow’s economy, they need to be able to adapt the knowledge they are acquiring. They need to be able to learn new concepts and skills. They need to be able to apply mathematical reasoning to problems. They need to view mathematics as a useful tool that must constantly be sharpened. In short, they need to be mathematically proficient.
Students who have learned only procedural skills and have little understanding of mathematics will have limited access to advanced schooling, better jobs, and other opportunities. If any group of students is deprived of the opportunity to learn with understanding, they are condemned to second-class status in society, or worse.
A Broader, Deeper View
Many people in the United States consider procedural fluency to be the heart of the elementary school mathematics curriculum. They remember school mathematics as being devoted primarily to learning and practicing computational procedures. In this report, we present a much broader view of elementary and middle school mathematics. We also raise the standard for success in learning mathematics and being able to use it. In a significant and fortuitous twist, raising the standard by requiring development across all five strands of mathematical proficiency makes the development of any one strand more feasible. Because the strands interact and boost each other, students who have opportunities to develop all strands of proficiency are more likely to become truly competent with each.
We conclude that during the past 25 years mathematics instruction in U.S. schools has not sufficiently developed mathematical proficiency in the sense we have defined it. It has developed some procedural fluency, but it clearly has not helped students develop the other strands very far, nor has it helped them connect the strands. Consequently, all strands have suffered. In the next four chapters, we look again at students’ learning. We consider not just performance levels but also the nature of the learning process itself. We describe what students are capable of, what the big obstacles are for them, and what knowledge and intuition they have that might be helpful in designing effective learning experiences. This information, we believe, reveals how to improve current efforts to help students become mathematically proficient.
Notes
References
Alexander, P.A., White, C.S., & Daugherty, M. (1997). Analogical reasoning and early mathematics learning. In L.D.English (Ed.), Mathematical reasoning: Analogies, metaphors, and images (pp. 117–147). Mahwah, NJ: Erlbaum.
Alibali, M.W. (1999). How children change their minds: Strategy change can be gradual or abrupt. Developmental Psychology, 35, 127–145.
Ansell, E., & Doerr, H.M. (2000). NAEP findings regarding gender: Achievement, affect, and instructional experiences. In E.A.Silver & P.A.Kenney (Eds.), Results from the seventh mathematics assessment of the National Assessment of Educational Progress (pp. 73– 106). Reston, VA, National Council of Teachers of Mathematics.
Backer, A., & Akin, S. (Eds.). (1993). Every child can succeed: Reading for school improvement. Bloomington, IN: Agency for Instructional Television.
Baddeley, A.D. (1976). The psychology of memory. New York: Basic Books.
Ball, D.L., & Bass, H. (2000). Making believe: The collective construction of public mathematical knowledge in the elementary classroom. In D.Phillips (Ed.), Constructivism in education: Opinions and second opinions on controversial issues (Ninety-ninth Yearbook of the National Society for the Study of Education, Part 1, pp. 193– 224). Chicago: University of Chicago Press.
Beaton, A.E., Mullis, I.V.S., Martin, M.O., Gonzalez, E.J., Kelly, D.L., & Smith, T.A. (1996). Mathematics achievement in the middle school years: IEA’s Third International Mathematics and Science Study. Chestnut Hill, MA: Boston College, Center for the Study of Testing, Evaluation, and Educational Policy. Available: http://www.timss.org/timss1995i/MathB.html.
Bempechat, J. & Drago-Severson, E. (1999). Cross-national differences in academic achievement: Beyond etic conceptions of children’s understanding. Review of Educational Research, 69(3), 287–314.
Bowman, B.T., Donovan, M.S., Burns, M.S. (Eds.). (2001). Eager to learn: Educating our preschoolers. Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/9745.html. [July 10, 2001].
Bransford, J.D., Brown, A.L., & Cocking, R.R. (Eds.). (1999). How people learn: Brain, mind, experience, and school. Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/6160.html. [July 10, 2001].
Brownell, W.A. (1935). Psychological considerations in the learning and the teaching of arithmetic. In W.D.Reeve (Ed.), The teaching of arithmetic (Tenth Yearbook of the National Council of Teachers of Mathematics, pp. 1–31). New York: Columbia University, Teachers College, Bureau of Publications.
Brownell, W.A. (1987). AT classic: Meaning and skill—maintaining the balance. Arithmetic Teacher, 34(8), 18–25. (Original work published 1956).
Bruner, J.S. (1960). The process of education. New York: Vintage Books.
Campbell, J.R., Hombo, C.M., & Mazzeo, J. (2000). NAEP 1999 trends in academic progress: Three decades of student performance, NCES 2000–469. Washington, DC: National Center for Education Statistics. Available: http://nces.ed.gov/spider/webspider/2000469.shtml. [July 10, 2001].
Campbell, J.R., Voelkl, K.E., & Donahue, P.L. (2000). NAEP 1996 trends in academic progress (NCES 97–985r). Washington, DC: National Center for Education Statistics. Available: http://nces.ed.gov/spider/webspider/97985r.shtml. [July 10, 2001].
Carpenter, T.P., Corbitt, M.K., Kepner, H.S., Jr., Lindquist, M.M., & Reys, R.E. (1981). Results from the second mathematics assessment of the National Assessment of Educational Progress. Reston, VA: National Council of Teachers of Mathematics.
Carpenter, T.P., Franke, M.L., Jacobs, V.R., Fennema, E., & Empson, S.B. (1998). A longitudinal study of invention and understanding in children’s multidigit addition and subtraction. Journal for Research in Mathematics Education 29, 3–20.
Carpenter, T.P., & Lehrer, R. (1999). Teaching and learning mathematics with understanding. In E.Fennema & T.A.Romberg (Eds.), Mathematics classrooms that promote understanding (pp. 19–32). Mahway, NJ: Erlbaum.
Carpenter, T.P., & Levi, L. (1999, April). Developing conceptions of algebraic reasoning in the primary grades. Paper presented at the annual meeting of the American Educational Research Association, Montreal.
Cobb, P., & Bauersfeld, H. (Eds.). (1995). The emergence of mathematical meaning: Interaction in classroom cultures. Hillsdale, NJ: Erlbaum.
Cobb, P., Yackel, E., & Wood, T. (1989). Young children’s emotional acts during mathematical problem solving. In D.B.McLeod & V.M.Adams (Eds.), Affect and mathematical problem solving: A new perspective (pp. 117–148). New York: Springer-Verlag.
Cobb, P., Yackel, E., & Wood, T. (1995). The teaching experiment classroom. In P.Cobb & H.Bauersfeld (Eds.), The emergence of mathematical meaning: Interaction in classroom cultures (pp. 17–24). Hillsdale, NJ: Erlbaum.
Committee for Economic Development, Research and Policy Committee. (1995). Connecting students to a changing world: A technology strategy for improving mathematics and science education: A statement. New York: Author.
Davis, R.B., & Maher, C.A. (1997). How students think: The role of representations. In L.D.English (Ed.), Mathematical reasoning: Analogies, metaphors, and images (pp. 93– 115). Mahwah, NJ: Erlbaum.
Donovan, M.S., Bransford, J.D., & Pellegrino, J.W. (Eds.). (1999). How people learn: Bridging research and practice. Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/9457.html. [July 10, 2001].
Druckman, D., & Bjork, R.A. (Eds.). (1991). In the mind’s eye: Enhancing human performance. Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/1580.html. [July 10, 2001].
Dweck, C. (1986). Motivational processes affecting learning. American Psychologist, 41, 1040–1048.
English, L.D. (1997a). Analogies, metaphors, and images: Vehicles for mathematical reasoning. In L.D.English (Ed.), Mathematical reasoning: Analogies, metaphors, and images (pp. 3–18). Mahwah, NJ: Erlbaum.
English, L.D. (Ed.). (1997b). Mathematical reasoning: Analogies, metaphors, and images. Mahwah, NJ: Erlbaum.
Fennema, E. (1995). Mathematics, gender and research. In B.Grevholm & G.Hanna (Eds.), Gender and mathematics education (pp. 21–38). Lund, Sweden: Lund University Press.
Fennema, E., & Romberg, T.A. (Eds.). (1999). Mathematics classroom that promote understanding. Mahwah, NJ: Erlbaum.
Fuson, K.C. (1990). Conceptual structures for multiunit numbers: Implications for learning and teaching multidigit addition, subtraction, and place value. Cognition and Instruction 7, 343–403.
Fuson, K.C. (1992a). Research on learning and teaching addition and subtraction of whole numbers. In G.Leinhardt, R.T.Putnam, & R.A.Hattrup (Eds.), The analysis of arithmetic for mathematics teaching (pp. 53–187). Hillsdale, NJ: Erlbaum.
Fuson, K.C. (1992b). Research on whole number addition and subtraction. In D.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 243–275). New York: Macmillan.
Fuson, K.C., & Briars, D.J. (1990). Using a base-ten blocks learning/teaching approach for first- and second-grade place-value and multidigit addition and subtraction. Journal for Research in Mathematics Education 21, 180–206.
Fuson, K.C., & Burghardt, B.H. (1993). Group case studies of second graders inventing multidigit addition procedures for base-ten blocks and written marks. In J.R.Becker & B.J.Pence (Eds.), Proceedings of the fifteenth annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 240– 246). San Jose, CA: San Jose State University. (ERIC Document Reproduction Service No. ED 372 917).
Fuson, K.C., Carroll, W.M., & Landis, J. (1996). Levels in conceptualization and solving addition and subtraction compare word problems. Cognition and Instruction, 14, 345– 371.
Geary, D.C. (1995). Reflections of evolution and culture in children’s cognition. American Psychologist, 50(1), 24–37.
Greeno, J.G., Pearson, P.D., & Schoenfeld, A.H. (1997). Implications for the NAEP of research on learning and cognition. In R.Linn, R.Glaser, & G.Bohrnstedt (Eds.), Assessment in transition: Monitoring the nation’s educational progress (Background Studies, pp. 151–215). Stanford, CA: National Academy of Education.
Hagarty, M., Mayer, R.E., & Monk, C.A. (1995). Comprehension of arithmetic word problems: A comparison of successful and unsuccessful problem solvers. Journal of Educational Psychology, 87, 18–32.
Hatano, G. (1988, Fall). Social and motivational bases for mathematical understanding. New Directions for Child Development, 41, 55–70.
Hiebert, J. (Ed.). (1986). Conceptual and procedural knowledge: The case of mathematics. Hillsdale, NJ: Erlbaum.
Hiebert, J., & Carpenter, T.P. (1992). Learning and teaching with understanding. In D. A.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 65–97). New York: Macmillan.
Hiebert, J., Carpenter, T.P., Fennema, E., Fuson, K.C., Wearne, D., Murray, H., Olivier, A., & Human, P. (1997). Making sense: Teaching and learning mathematics with understanding. Portsmouth, NH: Heinemann.
Hiebert, J., & Wearne, D. (1986). Procedures over concepts: The acquisition of decimal number knowledge. In J.Hiebert (Ed.), Conceptual and procedural knowledge: The case of mathematics (pp. 199–223). Hillsdale, NJ: Erlbaum.
Hiebert, J., & Wearne, D. (1996). Instruction, understanding, and skill in multidigit addition and subtraction. Cognition and Instruction, 14, 251–283.
Hilgard, E.R. (1957). Introduction to psychology (2nd ed.). New York: Harcourt Brace.
Inhelder, B., & Piaget, J. (1958). The growth of logical thinking from childhood to adolescence. New York: Basic Books.
Katona, G. (1940). Organizing and memorizing. New York: Columbia University Press.
Kilpatrick, J. (1985). Doing mathematics without understanding it: A commentary on Higbee and Kunihira. Educational Psychologist, 20(2), 65–68.
Knapp, M.S., Shields, P.M., & Turnbull, B.J. (1995). Academic challenge in high-poverty classrooms. Phi Delta Kappan, 76, 770–776.
Kouba, V.L., Carpenter, T.P., & Swafford, J.O. (1989). Number and operations. In M. M.Lindquist (Ed.), Results from the fourth mathematics assessment of the National Assessment of Educational Progress (pp. 64–93). Reston, VA: National Council of Teachers of Mathematics.
Kouba, V.L., & Wearne, D. (2000). Whole number properties and operations. In E.A. Silver & P.A.Kenney (Eds.), Results from the seventh mathematics assessment of the National Assessment of Educational Progress (pp. 141–161). Reston, VA: National Council of Teachers of Mathematics.
Krutetskii, V.A. (1976). The psychology of mathematical abilities in schoolchildren (J.Kilpatrick & I.Wirszup, Eds.; J.Teller, Trans.). Chicago: University of Chicago Press. (Original work published 1968).
Ladson-Billings, G. (1999). Mathematics for all? Perspectives on the mathematics achievement gap. Paper prepared for the Mathematics Learning Study Committee, National Research Council, Washington, DC.
Leder, G.C. (1992). Mathematics and gender: Changing perspectives. In D.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 597–622). New York: Macmillan.
Lemaire, P., & Siegler, R.S. (1995). Four aspects of strategic change: Contributions to children’s learning of multiplication. Journal of Experimental Psychology: General, 124, 83–97.
Mack, N.K. (1995). Confounding whole-number and fraction concepts when building on informal knowledge. Journal for Research in Mathematics Education, 26, 422–441.
Maher, C.A., & Martino, A.M. (1996). The development of the idea of mathematical proof: A 5-year case study. Journal for Research in Mathematics Education, 27, 194–214.
Mason, D., Schroeter, D., Combs, R., & Washington, K. (1992). Assigning average achieving eighth graders to advanced mathematics classes in an urban junior high. Elementary School Journal, 92, 587–599.
Mayer, R.E. (1999). The promise of educational psychology. Upper Saddle River, NJ: Prentice Hall .
Mayer, R.E., & Hegarty, M. (1996). The process of understanding mathematical problems. In R.J.Sternberg & T.Ben-Zee (Eds.), The nature of mathematical thinking (Studies in Mathematical Thinking and Learning Series, pp. 29–53). Mahwah, NJ: Erlbaum.
Mayer, R.E., & Wittrock, M.C. (1996). Problem-solving transfer. In D.C.Berliner & R. C.Calfee (Eds.), Handbook of educational psychology (pp. 47–62). New York: Macmillan.
McLeod, D.B. (1992). Research on affect in mathematics education: A reconceptualization. In D.A.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 575–596). New York: Macmillan.
Mullis, I.V.S., Jenkins, F., & Johnson, E.G. (1994). Effective schools in mathematics. Washington, DC: National Center for Education Statistics.
Mullis, I.V.S., Martin, M.O., Gonzalez, E.J., Gregory, K.D., Garden, R.A., O’Connor, K. M., Chrostowski, S.J., & Smith, T.A. (2000). TIMSS 1999 international mathematics report: Findings from IEA’s repeat of the Third International Mathematics and Science Study at the eighth grade . Chestnut Hill, MA: Boston College, Lynch School of Education, International Study Center. Available: http://www.timss.org/timss1999i/math_achievement_report.html. [July 10, 2001].
National Assessment Governing Board. (2000). Mathematics framework for the 1996 and 2000 National Assessment of Educational Progress. Washington, DC: Author. Available: http://www.nagb.org/pubs/96–2000math/toc.html. [July 10, 2001].
National Research Council. (1989). Everybody counts: A report to the nation on the future of mathematics education. Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/1199.html. [July 10, 2001].
National Research Council. (1998). High school mathematics at work: Essays and Examples for the education of all students. Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/5777.html. [July 10, 2001].
Nunes, T. (1992a). Cognitive invariants and cultural variation in mathematical concepts. International Journal of Behavioral Development, 15, 433–453.
Nunes, T. (1992b). Ethnomathematics and everyday cognition. In D.A.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 557–574). New York: Macmillan.
Oakes, J. (1990). Multiplying inequalities: The effects of race, social class, and tracking on opportunities to learn mathematics and science. Santa Monica: CA: RAND Corporation.
Pólya, G. (1945). How to solve it: A new aspect of mathematical method. Princeton, NJ: Princeton University Press.
Pesek, D.D., & Kirshner, D. (2000). Interference of instrumental instruction in subsequent relational learning. Journal for Research in Mathematics Education, 31, 524–540.
Reese, C.M., Miller, K.E., Mazzeo, J., & Dossey, J.A. (1997). NAEP 1996 mathematics report card for the nation and the states. Washington, DC: National Center for Education Statistics. Available: http://nces.ed.gov/spider/webspider/97488.shtml. [July 10, 2001].
Resnick, L.B. (1987). Education and learning to think. Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/1032.html. [July 10, 2001].
Resnick, L.B., & Omanson, S.F. (1987). Learning to understand arithmetic. In R. Glaser (Ed.), Advances in instructional psychology (vol. 3, pp. 41–95). Hillsdale, NJ: Erlbaum.
Rittle-Johnson, B., & Alibali, M.W. (1999). Conceptual and procedural knowledge of mathematics: Does one lead to the other? Journal of Educational Psychology, 91, 175– 189.
Rittle-Johnson, B., & Siegler, R.S. (1998). The relation between conceptual and procedural knowledge in learning mathematics: A review. In C.Donlan (Ed.), The development of mathematical skills (pp. 75–110). East Sussex, UK: Psychology Press.
Saxe, G. (1990). Culture and cognitive development. Hillsdale, NJ: Erlbaum.
Schifter, D. (1999). Reasoning about operations: Early algebraic thinking in grades K-6. In L.V.Stiff (Ed.), Developing mathematical reasoning in grades K-12 (1999 Yearbook of the National Council of Teachers of Mathematics, pp. 62–81). Reston, VA: NCTM.
Schoenfeld, A.H. (1988). Problem solving in context(s). In R.I.Charles & E.A.Silver (Eds.), The teaching and assessing of mathematical problem solving (Research Agenda for Mathematics Education, vol. 3, pp. 82–92). Reston, VA: National Council of Teachers of Mathematics.
Schoenfeld, A.H. (1989). Explorations of students’ mathematical beliefs and behavior. Journal for Research in Mathematics Education, 20, 338–355.
Schoenfeld, A.H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In D.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 334–370). New York: Macmillan.
Secada, W.G. (1992). Race, ethnicity, social class, language, and achievement in mathematics. In D.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 623–660). New York: Macmillan.
Shannon, A. (1999). Keeping score. Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/9635.html. [July 10, 2001].
Siegler, R.S., & Jenkins, E.A. (1989). How children discover new strategies. Hillsdale, NJ: Erlbaum.
Silver, E.A., Alacaci, C., & Stylianou, D.A. (2000). Students’ performance on extended constructed-response tasks. In E.A.Silver & P.A.Kenney (Eds.), Results from the seventh mathematics assessment of the National Assessment of Educational Progress (pp. 301– 341). Reston, VA: National Council of Teachers of Mathematics.
Silver, E.A., & Kenney, P.A. (2000). Results from the seventh mathematics assessment of the National Assessment of Educational Progress. Reston, VA: National Council of Teachers of Mathematics.
Silver, E.A., Strutchens, M.E., & Zawojewski, J.S. (1997). NAEP findings regarding race/ethnicity and gender: Affective issues, mathematics performance, and instructional context. In E.A.Silver & P.A.Kenney (Eds.), Results from the sixth mathematics assessment of the National Assessment of Educational Progress (pp. 33–59). Reston, VA: National Council of Teachers of Mathematics.
Steele, C.M. (1997). A threat in the air: How stereotypes shape intellectual identity and performance. American Psychologist, 52, 613–629.
Steele, C.M., & Aronson, J. (1995). Stereotype threat and the intellectual test performance of African-Americans. Journal of Personality and Social Psychology, 69, 797–811.
Steinberg, R.M. (1985). Instruction on derived facts strategies in addition and subtraction. Journal for Research in Mathematics Education, 16, 337–355.
Sternberg, R.J., & Rifkin, B. (1979). The development of analogical reasoning processes. Journal of Experimental Child Psychology, 27, 195–232.
Stevenson, H.W., & Stigler, J.W. (1992). The learning gap: Why our schools are failing and what we can learn from Japanese and Chinese education. New York: Simon & Schuster.
Strutchens, M.E., & Silver, E.A. (2000). NAEP findings regarding race/ethnicity: Students’ performance, school experiences, and attitudes and beliefs. In E.A.Silver & P.A. Kenney (Eds.), Results from the seventh mathematics assessment of the National Assessment of Educational Progress (pp. 45–72). Reston, VA: National Council of Teachers of Mathematics .
Swafford, J.O., & Brown, C.A. (1989). Attitudes. In M.M.Lindquist (Ed.), Results from the fourth mathematics assessment of the National Assessment of Educational Progress (pp. 106–116). Reston, VA: National Council of Teachers of Mathematics.
Tate, W.F. (1997). Race, ethnicity, SES, gender, and language proficiency trends in mathematics achievement: An update. Journal for Research in Mathematics Education, 28, 652–679.
Thompson, A.G. (1992). Teachers’ beliefs and conceptions: A synthesis of the research. In D.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 127– 146). New York: Macmillan.
Thornton, C.A., & Toohey, M.A. (1985). Basic math facts: Guidelines for teaching and learning. Learning Disabilities Focus, 1(1), 44–57.
U.S. Department of Labor, Secretary’s Commission on Achieving Necessary Skills. (1991). What work requires of schools: A SCANS report for America 2000. Washington, DC: Author. (ERIC Document Reproduction Service No. ED 332 054).
Wearne, D., & Hiebert, J. (1988). A cognitive approach to meaningful mathematics instruction: Testing a local theory using decimal numbers. Journal for Research in Mathematics Education, 19, 371–384.
Wearne, D., & Kouba, V.L. (2000). Rational numbers. In E.A.Silver & P.A.Kenney (Eds.), Results from the seventh mathematics assessment of the National Assessment of Educational Progress (pp. 163–191). Reston, VA: National Council of Teachers of Mathematics.
Wertheimer, M. (1959). Productive thinking. New York: Harper & Row.
Wiest, L.R. (2000). Mathematics that whets the appetite: Student-posed projects problems. Mathematics Teaching in the Middle School, 5, 286–291.
Wu, H. (1999, Fall). Basic skills versus conceptual understanding: A bogus dichotomy in mathematics education. American Educator, 14–19, 50–52.
Yaffee, L. (1999). Highlights of related research. In D.Schifter, V.Bastable, & S.J. Russell with L.Yaffee, J.B.Lester, & S.Cohen, Number and operations: Making meaning for operations. Casebook (pp. 127–149). Parsippany, NJ: Dale Seymour.
Zernike, K. (2000, August 25). Gap widens again on tests given to blacks and whites: Disparity widest among the best educated. The New York Times, p. A14.










































