3
NUMBER: WHAT IS THERE TO KNOW?
Seven. What is seven? Seven children; seven ideas; seven times in a row; seventh grade; a lucky roll in dice; seven yards of cotton; seven stories high; seven miles from here; seven acres of land; seven degrees of incline; seven degrees below zero; seven grams of gold; seven pounds per square inch; seven years old; finishing seventh; seven thousand dollars of debt; seven percent alcohol; Engine No. 7; The Magnificent Seven. How can an idea with one name be used in so many different ways, denoting such various senses of quantity? Consider how different a measure of time (seven years) is from one of temperature (seven degrees), how different a measure of length (seven meters) is from a count (seven children), and how different either of these is from a position (finishing seventh or being in seventh grade). Even within measures, some are represented as ratios (seven pounds per square inch, seven percent alcohol) and others as simple units (seven miles, seven liters). Although normally taken for granted, it is remarkable that seven, or any number, can be used in so many ways. That versatility helps explain why number is so fundamental in describing the world.
Its versatility helps explain why number is so fundamental in describing the world.
This chapter surveys the domain of number. It was developed in part in response to the charge to the committee to describe the context of the study with respect to the areas of mathematics that are important as foundations in grades pre-K to 8 for building continued learning. The intent of this chapter is essentially mathematical; learning and teaching are treated elsewhere. The chapter does not set forth a curriculum for students but instead provides a panoramic view of the territory on which the numerical part of the school curriculum is built. Nor is the chapter intended as a curriculum for teachers. Instead, it identifies some of the crucial ideas about number that we think
teachers should know. Many of these ideas are treated in more detail in textbooks intended for prospective elementary school teachers.
A major theme of the chapter is that numbers are ideas—abstractions that apply to a broad range of real and imagined situations. Operations on numbers, such as addition and multiplication, are also abstractions. Yet in order to communicate about numbers and operations, people need representations—something physical, spoken, or written. And in order to carry out any of these operations, they need algorithms: step-by-step procedures for computation. The chapter closes with a discussion of the relationship between number and other important mathematical domains such as algebra, geometry, and probability.
Number Systems
At first, school arithmetic is mostly concerned with the whole numbers: 0, 1, 2, 3, and so on.1 The child’s focus is on counting and on calculating— adding and subtracting, multiplying and dividing. Later, other numbers are introduced: negative numbers and rational numbers (fractions and mixed numbers, including finite decimals). Children expend considerable effort learning to calculate with these less intuitive kinds of numbers. Another theme in school mathematics is measurement, which forms a bridge between number and geometry.
Mathematicians like to take a bird’s-eye view of the process of developing an understanding of number. Rather than take numbers a pair at a time and worry in detail about the mechanics of adding them or multiplying them, they like to think about whole classes of numbers at once and about the properties of addition (or of multiplication) as a way of combining pairs of numbers in the class. This view leads to the idea of a number system. A number system is a collection of numbers, together with some operations (which, for purposes of this discussion, will always be addition and multiplication), that combine pairs of numbers in the collection to make other numbers in the same collection. The main number systems of arithmetic are (a) the whole numbers, (b) the integers (i.e., the positive whole numbers, their negative counterparts, and zero), and (c) the rational numbers—positive and negative ratios of whole numbers, except for those ratios of a whole number and zero.
Thinking in terms of number systems helps one clarify the basic ideas involved in arithmetic. This approach was an important mathematical discovery in the late nineteenth and early twentieth centuries. Some ideas of arithmetic are fairly subtle and cause problems for students, so it is useful to have a viewpoint from which the connections between ideas can be surveyed.
The Whole Numbers
One of the starting points of arithmetic is counting. Children can find out how many objects are in a collection by counting them: one, two, three, four, five. They also need zero to say that there is not any of some type of thing.2
Addition arises to simplify counting. When children join two collections, instead of recounting all the objects in the combined set, they add the numbers of objects in each of the original sets. (I have five apples, and Dave has three apples. How many apples do we have together?) Multiplication provides a further shortcut when children want to add many copies of the same number. (I have 10 boxes of cookies, with 12 cookies in each box. How many cookies do I have?) The whole numbers, with the two operations of addition and multiplication, form the whole number system, the most basic number system.
It is important to take note that, although the whole numbers with their operations are very familiar, they are already abstract. Although counting is usually done with some particular kind of things (apples or cats or dollars), arithmetic can be independent of the things counted. Five apples plus three apples makes eight apples; five cats plus three cats makes eight cats; five dollars plus three dollars makes eight dollars. (A word of caution: when adding, you must combine units of the same kind: five dollars plus three cats does not make eight of anything in particular.) This independence of the results from whatever is being counted leads to the abstract operation called addition. It is similar with multiplication. Note that the abstract nature of the arithmetic operations is exactly what makes them useful. If addition of apples, of cats, and of dollars each required its own peculiar set of rules, people would probably have no general concept of addition, just ideas about combining each type of object in its own individual way. Mathematics itself might not exist. Certainly, it would require a lot more work.
Although the whole numbers with their operations are very familiar, they are already abstract.
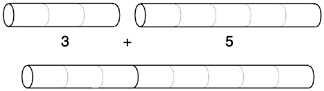
Appropriate to the abstract nature of arithmetic, each operation has several concrete interpretations. We introduced addition by means of its interpretation in terms of combining sets of like objects. Other interpretations are often used. One is the joining of segments of various lengths. If Jane has a rod 3 inches long, and another rod 5 inches long, she can lay them end to end (or perhaps even attach them together) to get a rod 8 inches long.
This interpretation may seem the same, or almost the same, as the combining-sets interpretation. Indeed, it must be somewhat similar, since it is a representation of addition. But it differs in perhaps subtle ways. For example, inches can be subdivided into parts, which are hard to tell from the wholes, except that they are shorter; whereas it is painful to cats to divide
them into parts, and it seriously changes their nature. Thus, joining rods will support an extension of arithmetic into fractional quantities much more easily than counting cats will.
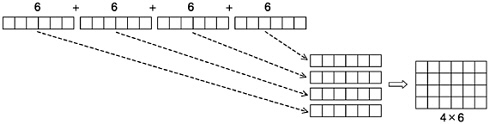
Similarly, multiplication has multiple interpretations. We introduced it as adding the same number many times. The set-combination interpretation of multiplication would be to combine several essentially identical collections, such as the packages of cookies mentioned above. If you think of addition in terms of joining rods, then multiplication would amount to joining several rods of the same length end to end. Thus, 4×6 can be visualized by laying four rods of length six end to end, where you can think of each rod as a little row of boxes. A more compact way to arrange the rods would be to lay them side by side rather than end to end. This arrangement produces an array of four rows of boxes with six boxes in each row, which may be called a rectangular array interpretation of multiplication. When the rods have height one, there is an added benefit: The array looks like a rectangle of boxes, and the area of the rectangle (measured in box areas) is just 4×6. This is the area interpretation of multiplication.
The multiple interpretations of the basic operations is symptomatic of a general feature of mathematics—the tension between abstract and concrete.3 This tension is a fundamental and unavoidable challenge for school mathematics. On the one hand, as we indicated above, the abstractness of math-
ematics is an important reason for its usefulness: A single idea can apply in many circumstances. On the other hand, it is difficult to learn an idea in a purely abstract setting; one or another concrete interpretation must usually be used to make the idea real. But having been introduced to a mathematical concept by means of one interpretation, children then need to pry it away from only that interpretation and take a more expansive view of the abstract idea. That kind of learning often takes time and can be quite difficult. Sometimes the way in which a concept is first learned creates obstacles to learning it in a more abstract way. At other times, overcoming such obstacles seems to be a necessary part of the learning process.
Properties of the Operations
Experience with the operations of addition and multiplication leads to the observation of certain regularities in their behavior. For example, it does not matter in what order two numbers are added. If I dump a basket of three apples into a basket with five apples already in it, there will be eight apples in the basket; and if I dump the basket of five apples into the basket with three, I will also have eight. Thus 5+3=8=3+5. The similar fact is true for any two numbers. Thus, I know that 83,449+173,248,191=173,248,191+83,449 without actually doing either addition. I have used what is known as the commutative law of addition.
When three numbers are to be added, there are several options. To add 1 and 2 and 3, I can add 1 and 2, giving 3, and then add the original 3 to this, to get 6. Or I can add 1 to the result of adding the 2 and the 3. This process again gives 6. These two ways of adding give the same final answer, although the intermediate steps look quite different:
(1+2)+3=3+3=6=1+5=1+(2+3).
This statement of equality uses what is known as the associative law. Again, it holds for any three numbers. I know that
(83,449+173,248,191)+417=83,449+(173,248,191+417)
without doing either sum.
The commutative and associative laws in combination allow tremendous freedom in doing arithmetic. If I want to add three numbers, such as 1, 2, and 3, there are potentially 12 ways to do it:
|
(1+2)+3 |
(2+1)+3 |
(1+3)+2 |
(3+1)+2 |
(2+3)+1 |
(3+2)+1 |
|
1+(2+3) |
2+(1+3) |
1+(3+2) |
3+(1+2) |
2+(3+1) |
3+(2+1) |
Commutativity and associativity guarantee that all 12 ways of doing this sum give the same answer—so it does not matter which one I do. (For adding four numbers, there are 120 (!) conceivable different schemes, all of which again give the same result.) This flexibility is very useful when students do computations. For example, 1+8 can be found by thinking of it as 8+1 and then just recalling the next whole number after 8. The standard procedures for doing multidigit arithmetic also heavily exploit commutativity and associativity. However, the flexibility permitted by these rules also greatly increases the challenges of teaching arithmetic. When there are several ways to do a calculation, it is virtually certain that students will produce the answer more than one way. A teacher must therefore have a sufficiently flexible knowledge of arithmetic to evaluate the various student solutions, to validate the correct ones, and to correct errors productively.
The commutative and associative laws also hold for multiplication (see Box 3–1). The commutativity of multiplication by 2 is also reflected in the equivalence of the two definitions of even number typically offered by children. The “fair share” definition says that a number is even if it can be divided into two equal parts with nothing left over (which may be written as 2×m); the “pairing” definition says that a number is even if it can be divided into pairs with nothing left over (m×2).
In addition to these two laws for each operation, there is a rule, known as the distributive law, connecting the two operations. It can be written symbolically as a×(b+c)=a×b+a×c.
An example would be 2×(3+4)=2×7=14=6+8=2×3+2×4. A good way to visualize the distributive law is in terms of the area interpretation of multiplication. Then it says that if I have two rectangles of the same height, the sum of their areas is equal to the area of the rectangle gotten by joining the two rectangles into a single one of the same height but with a base equal to the sum of the bases of the two rectangles:

The basic properties of addition and multiplication of whole numbers are summarized in Box 3–1.
|
Box 3–1 Properties of the Arithmetic Operations Commutativity of addition. The order of the two numbers does not affect their sum: 3+5=8=5+3. In general, m+n=n+m. Associativity of addition. When adding three (or more) numbers, it does not matter whether the first pair or the last pair is added first: (3+5)+4=8+4=12=3+ 9=3+(5+4). In general, (m+n)+p=m+(n+p). 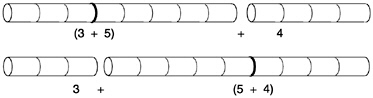 Commutativity of multiplication. The order of the two numbers does not affect their product: 5×8 produces the same answer as 8×5. In general, m×n=m×n. 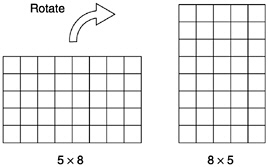 Associativity of multiplication. When multiplying three or more numbers, it does not matter whether the first pair or the last pair is multiplied first: 3×(5×4) is the same as (3×5)×4. In general, (m×n)×p=m×(n×p). 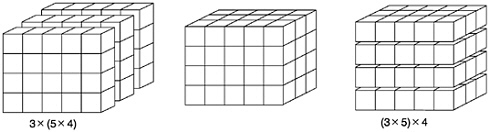 |
|
Distributivity of multiplication over addition. When multiplying a sum of two numbers by a third number, it does not matter whether you find the sum first and then multiply or you first multiply each number to be added and then add the two products: 4×(3+2)=(4×3)+(4×2). In general, m×(n+p)=(m×n)+(m×p). 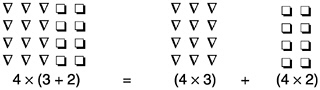 Question: Is subtraction commutative? Answer: No. For example, 6–2=4, but 2–6=–4. Question: Is subtraction associative? Answer: No. For example, (7–4)–2=3–2=1, but 7–(4–2)=7–2=5. |
Subtraction and Division
So far we have talked only about addition and multiplication. It is traditional, however, to list four basic operations: addition and subtraction, multiplication and division. As implied by the usual juxtapositions, subtraction is related to addition, and division is related to multiplication. The relation is in some sense an inverse one. By this, we mean that subtraction undoes addition, and division undoes multiplication. This statement needs more explanation.
Just as people sometimes want to join sets, they sometimes want to break them apart. If Eileen has eight apples and eats three, how many does she have left? The answer can be pictured by thinking of eight apples as composed of two groups, a group of five apples and a group of three apples. When the three are taken away, the five are left. In this solution, you think of eight as 5+3, and then when you subtract the three, you are again left with five. Thus subtracting three undoes the implicit addition of three and leaves you with the original amount. It is the same no matter what amount you start
with: 5+3–3=5; 9+3–3=9; 743+3–3=743. More formally, subtracting 3 is the inverse of adding 3.
It is similar with division and multiplication. Just as people sometimes want to form sets of the same size into one larger set, they sometimes want to break up a large set into equal-sized pieces. If you think of 15 as 5×3, then when you divide 15 by 3, you are again left with 5. Thus division by 3 undoes implicit multiplication by 3 and leaves you with the original amount. It is the same no matter what amount you start with: 5×3÷3=5; 9×3÷3=9; 743×3÷3=743. More formally, dividing by 3 is the inverse of multiplying by 3.
Two interpretations of division deserve particular mention here. If I have 20 cookies, and want to sort them into 5 bags, how many go in each bag? This is the so-called sharing model of division because I know in how many ways the cookies are to be shared. I can find the answer by picturing the 20 cookies arranged in 5 groups of 4 cookies, which will be the contents of 1 bag. If the cookies originally came out of 5 bags of 4 each, when I put them back into those bags, I will again have 4 in each. Thus, division by 5 undoes multiplication by 5, or division by 5 is the inverse of multiplication by 5. The picture below shows the sharing model for this situation.
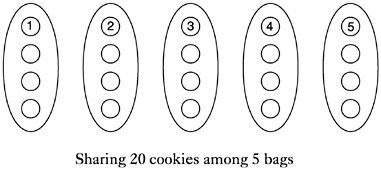
To think about 20÷5, you could also use the measurement model: If I have 20 cookies that are to be packaged in bags of 5 each, how many bags will I get? In the sharing model (also called the partitioning model or partitive division), you know the number of groups and seek the number in a group. In the measurement model (also called quotative division), you know the size of the groups and seek the number of groups. The circled numbers in the figures above and below illustrate a crucial difference between the two models: the order in which the cookies are placed in bags. In the sharing
model, the cookies are dealt into the bags one at a time; in the measurement model, the cookies are counted out by complete bags. When you deal with actual cookies, the processes are quite different, but abstractly they are both 20÷5. Note that because multiplication is commutative, 5 bags of 4 cookies each is the same total number of cookies as 4 bags of 5 cookies each. Eventually students come to see the two kinds of division as interchangeable and use whichever model helps them with a particular division problem.
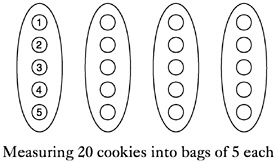
Subtraction and the integers
We might summarize the story so far by saying that there are two pairs of operations—addition and subtraction, and multiplication and division—and these are inversely related in the sense described above. However, this summary would not quite be correct. In fact, subtraction is not actually an operation on whole numbers in the same sense that addition is. You can add any pair of whole numbers together, and the result is again a whole number. Sometimes, however, you cannot subtract one whole number from another. If I have three apples, and Bart asks for five, I can’t give them to him. I just don’t have five apples. If I’m really supposed to give him five apples (maybe he left five apples in my care, I ate two, and then he came back to reclaim his apples), then I am in trouble. This situation can be described by using negative numbers: I have negative-two apples, meaning that after I give Bart all the apples I have, I still owe him two. What is happening mathematically is that I have bumped up against a subtraction problem, 3–5, for which there is no solution (in whole numbers). Mathematicians respond by inventing a solution for it, and they call the solution –2.
Thus, the desire to describe solutions for certain “impossible” subtraction problems leads to the invention of new numbers, the negative integers.4 Thanks to the negative integers, you can solve all whole number subtraction problems. But your problems are not over. You soon find that you cannot be
content simply to admire these new creations. You get into situations in which you want to do arithmetic with them also. If I owe Bart two apples and I owe Teresa four apples, how many apples do I owe all together—that is, what is (–2)+(–4)? If on Monday I get into a situation that leaves me two apples short and this happens again on Tuesday and Wednesday, how many apples short am I then—that is, what is 3×(–2)? Besides enlarging their idea of number, people have had to extend the arithmetic operations to this new larger class of numbers. They have needed to create a new, enlarged number system. The new system, encompassing both positive and negative whole numbers, is called the integers.
How do people decide what arithmetic in this extended system is (or should be)? How do they create recipes for adding and multiplying integers, and what are the properties of these extended operations? They have two guides: (a) intuition and (b) the rules of arithmetic, as described above and in Box 3–1. Fortunately, the guides agree.
Consider first the intuitive approach: Think hard about a lot of different cases and decide what is the right way to add and multiply in each one. To use intuition, you need to think in terms of some concrete interpretation of arithmetic. The yield of financial transactions is a good one for these purposes. Here negative amounts are money you owe, and positive amounts are money that you have or are owed by someone else. If you owe $2 to Joan and $3 to Sammy, then you owe $5 to the two of them together. So (–2)+(–3)=–5. If you owe $2 to three people, then you owe $6, so 3×(–2)=–6. If you have a debt of $2 and someone takes it away, you have gained $2. So –(–2)=2. If someone takes three $2 debts away from you, the amount you owe is then $6 less than before, which means you have $6 more. Therefore (–3)×(–2)=6. Continuing in this way, you can puzzle out what the sum, difference, or product of any two integers should be. The trouble with this approach is that it is somewhat contrived and depends upon making decisions about how to interpret each case in the particular context.5
Another approach6 is to use an exploratory method to reason how the operations should extend from the whole numbers. By extending the patterns in the table below, you find that (–3)×(–2)=6, just as was shown above in context.
|
3+2=5 |
3–2=1 |
3×2=6 |
(–3)×2=–6 |
|
3+1=4 |
3–1=2 |
3×1=3 |
(–3)×1=–3 |
|
3+0=3 |
3–0=3 |
3×0=0 |
(–3)×0=0 |
|
3+(–1)= |
3–(–1)= |
3×(–1)= |
(–3)×(–2)= |
|
3+(–2)= |
3–(–2)= |
3×(–2)= |
(–3)×(–2)= |
By means of somewhat lengthy reasoning, you can find out how to do arithmetic with integers. But are the regularities observed about the whole number system (the rules in Box 3–1) still valid? Going through the cases again will show that they are. So not only has the number system been extended from the whole numbers to all integers, but the arithmetic in the larger system looks very similar to arithmetic in the original one in the sense that these laws are still valid.
Moreover, there are some new notable regularities that describe how the new numbers are related to the original ones. These are summarized in Boxes 3–2 and 3–3.
The extension of whole numbers to integers is an example of the axiomatic method in mathematics: basing a mathematical system on a short list of key properties.
Something much more dramatic is also true. One can show that, if the goal is to extend addition and multiplication from the whole numbers to the integers in such a way that the laws of arithmetic of Boxes 3–1 and 3–2 remain true, then there is only one way to do it. And the rules in Box 3–3 describe how it has to work. Recipes laboriously constructed by means of some sort of concrete interpretation of negative numbers are all completely dictated by this short list of rules of arithmetic. This uniqueness is a striking exhibition of the power of these rules—that they capture in a few general statements a large chunk of people’s intuition about arithmetic. The extension of whole numbers to integers is an example of the axiomatic method in mathematics: basing a mathematical system on a short list of key properties. Its most famous success is the Elements of Euclid for plane geometry. Since Euclid’s time, axiomatic schemes have been constructed to cover most areas of mathematics.
Another rather striking thing has happened during this extension from whole numbers to (all) integers. The reason for making the extension was to
|
Box 3–2 Additional Properties of Addition Additive identity. Adding zero to any number gives that number. For example, 3+0=3 and 0+3=3. In general, m+0=m, and 0+m=m. Additive inverse. Every number has an additive inverse, also called an opposite. The opposite is the unique number that, when added to that number, gives zero. For example, the opposite of 3 is –3 because 3+–3=0; the opposite of –4 is 4 because –4+4=0. In general, –s is the unique solution m for s+m=0. |
|
Box 3–3 Consequences of the Basic Properties: Formulas for the Arithmetic of Negation Subtraction and negation. Subtracting a number is the same as adding its opposite. For example, 5–3=5+(–3) and 5–(–2)=5+2. In general, s–t=s+(–t). Multiplication and negation. Negation is the same as multiplication by –1. For example, –3=(–1)×3 and 2=(–1)×(–2). In general, –s=(–1)×s. Opposite of opposite. The opposite of the opposite of a number is the number itself. For example, –(–3)=3. In general, –(–s)=s. |
be able to solve subtraction problems. Now, in the integers, subtraction is a true operation in the sense that you can subtract any integer from any other. As described in the rule on additive inverses in Box 3–2, for every integer, there is another integer, called its opposite or additive inverse, that counter-balances it: the two sum to zero. Thus 2+(–2)=0, and –84+84=0. The second equation means that –(–84)=84 and leads to the rule on subtraction and negation in Box 3–3, which says that subtracting an integer gives the same result as adding its additive inverse. Thus 2–3=2+(–3), and 24–(–7)=24+(–(–7)), which is equal to 24+7=31. Thus, at least on a conceptual level, subtraction is merged into addition, and you really only need to have the single operation of addition to capture all the arithmetic of addition and subtraction. As soon as subtraction is made into a true operation by extending the whole numbers to the integers, you also get additive inverses, which allows you to subordinate subtraction to addition. This sort of simplification illustrates a kind of mathematical elegance: Two ideas that seemed different can be subsumed under one bigger idea. As we show below, the analogous thing happens to division when you construct rational numbers. That subordination is the best justification for why mathematicians talk about only the two operations of addition and multiplication when discussing number systems, and not all four operations recognized in school arithmetic.
Division and Fractions
Forgetting for a moment the triumph with integers, return to the whole numbers and the problem of division. Here the situation is in some sense
much more complicated than for subtraction. You can subtract in whole numbers about half the time. However, division of one whole number by another rarely comes out even. If I have eight apples and want to share them equally with Carl and Maria (the three of us), I either have to leave two apples out of the division or have to cut them in pieces. The desire to solve this kind of problem leads to new numbers, the positive rational numbers. These are usually written as fractions (here we allow improper fractions, such as ![]() in which the numerator is larger than the denominator), and each one is a solution to a division problem for integers. For example,
in which the numerator is larger than the denominator), and each one is a solution to a division problem for integers. For example, ![]() is the number you get when you divide 2 into 3 equal parts. In other words,
is the number you get when you divide 2 into 3 equal parts. In other words, ![]() is by definition the number such that
is by definition the number such that ![]() Although this definition suffices to specify fractions as mathematical objects, fractions have many concrete interpretations. We refer the reader to the section “Discontinuities in Proficiency” in chapter 7 for a list of such interpretations.
Although this definition suffices to specify fractions as mathematical objects, fractions have many concrete interpretations. We refer the reader to the section “Discontinuities in Proficiency” in chapter 7 for a list of such interpretations.
Again, having introduced these new numbers, you find yourself needing to do arithmetic with them. If I get half an apple from Bart and two thirds of an apple from Teresa, how many apples do I have? If I have ![]() boxes of marbles, and I want to put them in boxes half as large, how many of the small boxes will that make? By figuring out the answers to these questions, you turn the positive rational numbers (along with zero) into a number system, with operations of addition and multiplication extending the old operations on whole numbers. This feat is difficult technically and conceptually. The arithmetic of, and even developing meanings for, fractions is one of the stumbling blocks of the pre-K to grade 8 mathematics curriculum.7
boxes of marbles, and I want to put them in boxes half as large, how many of the small boxes will that make? By figuring out the answers to these questions, you turn the positive rational numbers (along with zero) into a number system, with operations of addition and multiplication extending the old operations on whole numbers. This feat is difficult technically and conceptually. The arithmetic of, and even developing meanings for, fractions is one of the stumbling blocks of the pre-K to grade 8 mathematics curriculum.7
Nevertheless, if you go through the effort of constructing the arithmetic of positive rational numbers by considering various cases and using some sort of concrete model, as with the integers, you find that it can be done. At the end of your labors, being a mathematician, you survey the new system and ask whether the marvelous rules of Box 3–1 still hold. They do! Moreover, there are some further regularities, analogous to the rules of Box 3–2, that relate the new numbers to the old. The new rules for multiplication are listed in Box 3–4.
The analogy with the construction of the integers is remarkable, with multiplication replacing addition, and division replacing subtraction. First, the arithmetic in the laboriously constructed new system is entirely determined by the rules of Boxes 3–1 to 3–4. This means that for the formulas of adding, multiplying, and dividing (positive) rational numbers, as described in Box 3–5, there really was no choice: That is the only way to do it and preserve the rules.8 Furthermore, although the new system was created to allow divi-
|
Box 3–4 Additional Properties of Multiplication Multiplicative identity. Multiplying a number by 1 gives that number: 5×1=5 and 1×5=5. In general, m×1=m and 1×m=m. Multiplicative inverse. Every number other than 0 has a multiplicative inverse, also called a reciprocal. The reciprocal is the unique number that, when multiplied by that number, gives 1. For example, the reciprocal of 3 is |
sion, once you have it, you see that in some sense division is no longer necessary. In enabling division you have created a system in which every (nonzero) number has a multiplicative inverse or reciprocal. In this system, division by a number (other than zero) is accomplished by multiplying by its reciprocal, which is the source of the “invert and multiply” rule for dividing fractions.
The Rational Numbers
You have seen how a desire to solve subtraction problems with no solutions in whole numbers leads to the construction of the integers. In a very similar way, the desire to solve division problems with no solutions in whole numbers leads to the construction of the positive rational numbers (along with zero). But neither of these number systems does it all: There are some integers that will not divide a given integer, and there are some positive rational numbers that cannot be subtracted from a given positive rational number (and still remain within the system). Thus, if you want to be able to always do both operations (except dividing by zero), you have to extend these systems further: You have to annex reciprocals to the integers, and you have to annex negatives to the positive rationals.
That process involves a lot more work. The end result, however, is as elegant as one could wish. It turns out that either procedure produces a system in which all operations are possible, with additive inverses for all numbers and multiplicative inverses for all numbers except zero. In this system, subtraction of a number becomes addition of its additive inverse, and division by a number becomes multiplication by its multiplicative inverse. The
|
Box 3–5 Consequences of the Basic Properties: Formulas for the Arithmetic of Fractions Fraction notation. The fractions 3/2 and Reciprocal of reciprocal. The reciprocal of the reciprocal of a number is the number itself. For example, Equality. For m and s not zero, Addition of fractions. Adding fractions requires that they have a common denominator, which often requires conversion to equivalent fractions. When fractions have a common denominator, their sum is the fraction whose numerator is the sum of their numerators and whose denominator is the common denominator. For example, In general, for m and s not zero, Multiplication of fractions. The product of two fractions is the fraction whose numerator is the product of their numerators and whose denominator is the product of their denominators. For example, In general, for m and s not zero, Division of fractions. Dividing by a fraction is the same as multiplying by its reciprocal. For example, |
rules in Boxes 3–1 to 3–5 all hold. In both systems, all arithmetic is determined by these rules.
Finally, the two procedures actually produce the same system. The end result is essentially the same, whether one first annexes the negatives and then the fractions, or the other way around. The hard part is making sure that you can actually do it—that there really is a system in which you can add, subtract, multiply, and divide, and where all the rules work in harmony to tell you how to do it. Mathematicians call this system the rational numbers.
Arithmetic into Geometry—The Number Line
The rational numbers are harder to visualize than the whole numbers or even the integers, but there is a picture that lets you think about rational numbers geometrically. It lets you interpret whole numbers, negative numbers, and fractions all as part of one overall system. Furthermore, it provides a uniform way to extend the rational number system to include numbers such as p and ![]() that are not rational;9 it provides a link between arithmetic and geometry; and it paves the way for analytic geometry, which connects algebra and geometry. This conceptual tool is called the number line. It can be seen in a rudimentary way in many classrooms, but its potential for organizing thinking about number and making connections with geometry seems not to have been fully exploited. Finding out how to realize this potential might be a profitable line of research in mathematics education.
that are not rational;9 it provides a link between arithmetic and geometry; and it paves the way for analytic geometry, which connects algebra and geometry. This conceptual tool is called the number line. It can be seen in a rudimentary way in many classrooms, but its potential for organizing thinking about number and making connections with geometry seems not to have been fully exploited. Finding out how to realize this potential might be a profitable line of research in mathematics education.
The potential for organizing thinking about number and making connections with geometry seems not to have been fully exploited.
The number line is simply a line, but its points are labeled by numbers. One point on the line is chosen as the origin. It is labeled 0. Then a positive direction (usually to the right) is chosen for the line. This choice amounts to specifying which side of the origin will be the positive half of the line; the other side is then the negative half. Finally, a unit of length is chosen. Any point on the line is labeled by its (directed) distance from the origin measured according to this unit length. The point is labeled positive if it is on the positive half of the line and as negative if it is on the negative half. The integers, then, are the points that are a whole number of units to the left or the right of the origin. Part of the number line is illustrated below, with some points labeled.10
Rational numbers fit into this scheme by dividing up the intervals between the integers. For example, ![]() goes midway between 0 and 1, and
goes midway between 0 and 1, and ![]() goes midway between 1 and 2. The numbers
goes midway between 1 and 2. The numbers ![]() and
and ![]() and divide the interval from 0 to 1 into three parts of equal length, and the numbers
and divide the interval from 0 to 1 into three parts of equal length, and the numbers ![]() and
and ![]() divide the interval between 2 and 3 similarly. If you locate fractions with different denominators on the line, they may appear to be arranged somewhat irregularly.
divide the interval between 2 and 3 similarly. If you locate fractions with different denominators on the line, they may appear to be arranged somewhat irregularly.
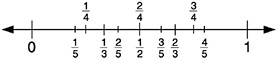
However, if you fix a denominator, and label all points by numbers with that fixed denominator, then you get an evenly spaced set, with each unit interval divided up into the same number of subintervals. Thus all rational numbers, whatever their denominators, have well-defined places on the number line. In particular, decimals with one digit to the right of the decimal point partition each unit interval on the number line into subintervals of length ![]() and decimals with two digits to the right of the decimal point refine this to intervals of length
and decimals with two digits to the right of the decimal point refine this to intervals of length ![]() with 10 of these fitting into each interval of length
with 10 of these fitting into each interval of length ![]() See Box 3–6.
See Box 3–6.
|
Box 3–6 The Number System of Finite Decimals Although they are not usually singled out explicitly, the finite decimals, such as 3, –104, 21.6, 0.333, 0.0125, and 3.14159, form a number system in the sense that you can add them and multiply them and get finite decimals. You can also subtract finite decimals, but you cannot always divide them. For example, The advantage of working with finite decimals rather than all the rational numbers is that the usual arithmetic for integers extends almost without change. The only complication is that one must keep track of the decimal point. (This seemingly small complication is actually a large conceptual leap.) For example, |
|
The finite decimal system does allow division by 10 (and by its divisors, 2 and 5), and it may be characterized as the smallest number system containing the integers and allowing division by 10. Indeed, another way of representing finite decimals is as rational numbers with denominators that are powers of 10. For example, 21.6=216/10 and 0.0125=125/10,000. It may not seem a huge gain to be able to divide by 10. What is the point of enlarging the system of integers to the system of finite decimals? It is that arithmetic can remain procedurally similar to the arithmetic of whole numbers, and yet finite decimals can be arbitrarily small and, as a consequence, can approximate any number as closely as you wish. This process is best illustrated by using the number line. The integers occupy a discrete set of points on the number line, each separated from its neighbors on either side by one unit distance:
The finite decimals with at most one digit to the right of the decimal point label the positions between the integers at the division points:
If you allow two digits to the right of the decimal point, these tenths are further subdivided into hundredths.
As you can see, space between these numbers is already rather small. It would be very difficult to draw a picture of the next division, defined by decimals with three digits to the right of the decimal point. Nonetheless, you can imagine this subdivision process continuing on and on, giving finer and finer partitions of the line. |
|
Geometrically, the digits in a decimal representation can be viewed as being parts of an “address” of the number, with each successive digit locating it more and more accurately. Thus if you have the decimal 1.41421356237, the integer part tells you that the number is between 1 and 2. The first decimal place tells you that the number is between 1.4 and 1.5. The next place says that the number is between 1.41 and 1.42. The first decimal place specifies the number to within an interval of If you think of it in this way, you can imagine applying this “address system” to any number, not just finite decimals. For finite decimals the procedure would effectively stop, with all digits beyond a given point being zero. With a number that is not a finite decimal, the process would go on forever, with each successive digit giving the number 10 times more precision. Thus, the finite decimals give you a systematic method for approximating any number to any desired accuracy. In particular, although the reciprocal of an integer will not usually be a finite decimal, you can approximate it by a finite decimal. Thus, But once you have started allowing approximation, there is no need or reason to restrict yourself to rational numbers. All numbers on the number line— even those that are not rational—can be approximated by finite decimals. For example, the number |
The potential of the number line does not stop at providing a simple way to picture all rational numbers geometrically. It also lets you form geometric models for the operations of arithmetic. These models are at the same time more visual and more sophisticated than most interpretations. Consider addition. We have already mentioned that one way to interpret addition of whole numbers is in terms of joining line segments. Now you can refine that interpretation by taking a standard segment of a given (positive) length to be the segment of that length with its left endpoint at the origin. Then the right
endpoint will lie at the point labeled by the length of the segment. To encompass negative numbers, you must give your segments more structure. You must provide them with an orientation—a beginning and an end, a head and a tail. These oriented segments may be represented as arrows. The positive numbers are then represented by arrows that begin at the origin and end at the positive number that gives their length. Negative numbers are represented by arrows that begin at the origin and end at the negative number. That way, 4 and –4, for example, have the same length but opposite orientation. (Note: For clarity, arrows are shown above rather than on the number line.)
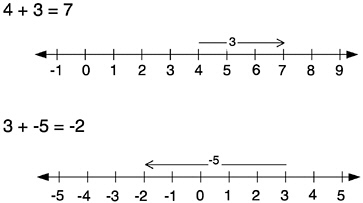
Suppose I want to compute 4+3 on the number line. It is difficult to add the arrows when they both begin at the origin:

But the arrows may be moved left or right, as needed, as long as they maintain the same length and orientation. To add the arrows, I move the second arrow so that it begins at the end of the first arrow.
|
 |
The result of the addition is an arrow that extends from the beginning of the first arrow to the end of the second arrow. |
This geometric approach is quite general: It works for negative integers and rational numbers, although in the latter case it is hard to interpret the answer in simple form without dividing the intervals according to a common denominator.
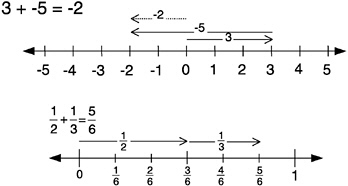
Another method (see below) for illustrating addition on the number line is simpler because it uses only one arrow. The method is more subtle, however, because it requires that some numbers be interpreted as points and others as arrows.
|
 |
Interpret the first number as a point and the second number as an arrow. Position the beginning of the arrow at the point. The result of the addition is given by the point at the end of the arrow. |
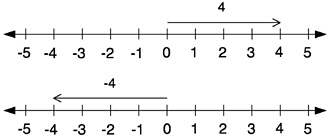
Numbers on the number line have a dual nature: They are simultaneously points and oriented segments (which we represent as arrows). A deep understanding of number and operations on the number line requires flexibility in using each interpretation. A principal advantage to this shorthand method for addition is that it supports the idea that adding 3, for example, amounts to moving the line (translating) three units to the right. By similar reasoning, adding –5 amounts to translating five units to the left. In general, adding any number may be interpreted as a translation of the line. The size of the translation depends on the size of the number, and the direction of the translation depends on its sign (i.e., positive or negative).
Multiplication on the number line is subtler than addition. Multiplication by whole numbers, however, may be interpreted as repeated addition:
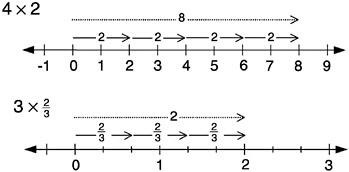
In what way does multiplication transform the line? Multiplication by 4, for example, stretches the line so that all points are four times as far from the origin as they previously were, given a constant unit. Division by 4 (or multiplication by ![]() ) reverses this process, thereby shrinking the line. Then multiplication by
) reverses this process, thereby shrinking the line. Then multiplication by ![]() for example, may be interpreted as stretching by a factor of 3 and then shrinking by a factor of 5. Multiplication by –1 takes positive numbers to their negative counterparts and vice versa, which amounts to flipping the line about the origin.
for example, may be interpreted as stretching by a factor of 3 and then shrinking by a factor of 5. Multiplication by –1 takes positive numbers to their negative counterparts and vice versa, which amounts to flipping the line about the origin.
These geometric interpretations of addition and multiplication as transformations of the line are quite sophisticated despite their pictorial nature. Nonetheless, these interpretations are important because they provide a way to picture the differences between addition and multiplication. Furthermore, the interpretations provide links between number, algebra, geometry, and higher mathematics.
Nested Systems of Numbers
While the number line gives a faithful geometric picture of the real number system, it does not make it easy to see geometrically the expansion of the number systems from whole numbers to integers to rationals, with each system contained in the next. The schematic picture in Box 3–7 illustrates how the number systems are related as sets. In the center is zero, surrounded on the right by the positive whole numbers and on the left by their negative counterparts. Together they form the integers. In the next larger circle are the rationals, which include the integers as a subset. In elementary school, children begin with the right half of the innermost circle (the whole numbers) and then learn about the right half of the next larger circle (nonnegative rationals). In the middle grades, the two circles are completed with the introduction of integers and negative rationals. In the late middle grades or high school, rationals are augmented to form real numbers.
|
Box 3–7 The Real Number System and Its Subsystems 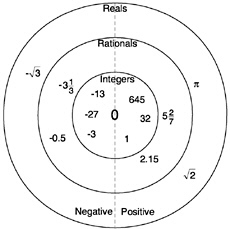 |
The number systems that have emerged over the centuries can be seen as being built on one another, with each new system subsuming an old one. This remarkable consistency helps unify arithmetic. In school, however, each number system is introduced with distinct symbolic notations: negation signs, fractions, decimal points, radical signs, and so on. These multiple representations can obscure the fact that the numbers used in grades pre-K through 8 all reside in a very coherent and unified mathematical structure—the number line.
Representations
In this chapter we are concerned primarily with the physical representations for number, such as symbols, words, pictures, objects, and actions.11 Physical representations serve as tools for mathematical communication, thought, and calculation, allowing personal mathematical ideas to be externalized, shared, and preserved.12 They help clarify ideas in ways that support reasoning and build understanding. These representations also support the development of efficient algorithms for the basic operations.13
Mathematics requires representations. In fact, because of the abstract nature of mathematics, people have access to mathematical ideas only through the representations of those ideas.14 Although on its surface school math-
ematics may seem to be about facts and procedures, much of the real intellectual work in mathematics concerns the interpretation and use of representations of mathematical ideas.15 The discussion of number systems above, for example, would have been impossible without the use of a variety of representations of numbers and operations.
Mathematical ideas are essentially metaphorical.16 The section on number systems made liberal use of metaphors, including the following:
-
number as collection, number as a point on a line, number as an arrow
-
addition as joining, multiplication as area
-
fraction as partitioning, fraction as piece, and fraction as number.
It has been argued that in mathematics “a new concept is the product of a cross-breeding between several metaphors rather than of a single metaphor.”17 This claim suggests that having multiple metaphors is a necessary condition for a concept to be meaningful.
Because many mathematical representations are suggestive of the corresponding metaphors, mathematical ideas are enhanced through multiple representations, which serve not merely as illustrations or pedagogical tricks but form a significant part of the mathematical content and serve as a source of mathematical reasoning. Even the numeral “729” is a representation that embodies a significant amount of mathematical thinking and interpretation.
Mathematical ideas are enhanced through multiple representations.
Numbers may be represented as physical objects, schematic pictures, words, or abstract symbols. For example, the number five may be represented by collections of physical objects, such as five blocks or five beads, by means of schematic (iconic) pictures like ![]() or
or ![]() or by abstract symbols like 5 or V.
or by abstract symbols like 5 or V.
Operations can also be represented. In this chapter, for example, addition is represented by combining plates of cookies, by joining segments, and by symbolic expressions such as 3+5. Similarly, we represent multiplication as repeated addition, as area, and symbolically as 4×6. There is an inherent ambiguity in the symbolic notation for operations that is both useful and difficult to grasp: the expression 3+5, for example, simultaneously represents a process (an addition operation) and the result of that process (the number 8). For division this distinction is sometimes made through different notations (e.g., 164÷17 and 164/17), but in practice, these are often used as synonyms.18
When a child combines a plate of three cookies with a plate of five cookies, he or she could use 3+5 as a representation of the physical situation. Conversely, given the symbolic expression 3+5, the child could represent the
mathematical idea by using plates of cookies. Whether the symbols represent the concrete objects or vice versa depends upon where the child starts. Both symbols and objects, however, represent a mathematical idea that is independent of the particular representation used.
The remainder of this section considers one particular representation system for numbers, the decimal place-value system, which is a significant human achievement. It should be emphasized, however, that representation systems arise out of human activity, and much mathematical insight can be gained by considering the genesis and development of the representation systems of the Egyptians, the Babylonians, the Mayans, or other cultures. Our intent here is more modest: to describe issues of mathematical representation by focusing on the representation system that is the major focus of school mathematics. It should also be emphasized that a representation system discussed previously, the number line, also deserves significant attention. In fact, the main unifying and synthesizing point of the previous section was that the number systems of school mathematics, which remain often fragmented and disjointed in the perceptions conveyed by school curricula, are in fact all subsystems of a single system, which has a geometric model that is the foundation of later analysis and geometry.
Grouping and Place Value
To use numbers effectively, to speak about them, or to manipulate them requires that they have names. Modern societies use decimal place-value notation in daily life and commerce. With just 10 symbols—0, 1, 2,…, 9— any number, no matter how big or small in magnitude, can be represented. For example, there are roughly 300,000,000 people in the United States. Or the diameter of the nucleus of an atom of gold is roughly 0.00000000034 centimeters. The decimal system is versatile and simple, although not necessarily obvious or easily learned. The decimal place-value system is one of the most significant intellectual constructs of humankind, and it has played a decisive role in the development of mathematics and science.
Over the centuries, various notational systems have been invented for naming numbers. To represent numbers symbolically, the ancient Hindus developed a numeration system that is based on the principles of grouping19 and place value, and that forms the basis for our numeration system today. In this system, objects are grouped by tens, then by tens of tens (hundreds), and so on. Hence, this numeration system is a base-10 or decimal system. These are nontrivial ideas that took humankind many centuries to invent and refine.
Early versions of these ideas were present in Roman numerals, for example, where 729 would be represented as DCCXXIX (D=500, C=100, X=10, and I=1). Although Roman numerals use grouping by tens and the interpretation of a numeral depends to some extent on the placement of the symbols,20 they do not at all constitute a place-value system. Also, the system of Roman numerals is ad hoc, in the sense that each new grouping requires a new symbol, so it is strictly limited in extent. A crucial steppingstone in the development of place-value notation was the idea of using a separate symbol to denote zero, which could then be used as a placeholder when necessary. This invention allows the same symbols to be used over and over to describe larger and larger groups.
Since the grouping is by tens, only 10 symbols, the digits 0 through 9, are needed to indicate how many groups there are of a particular size. In a numeral the size of the group depends on the place that the digit appears in the numeral. Thus, in 729 the “7” represents seven hundreds, whereas in 174 the “7” means seven tens.
Some pictorial and physical representations can be helpful in understanding the decimal place-value system. Special blocks, called base-10 blocks, for example, can be used to develop and support an understanding of the importance of tens and hundreds and the meaning of the various digits. The number 729 is pictured with base-10 blocks below.
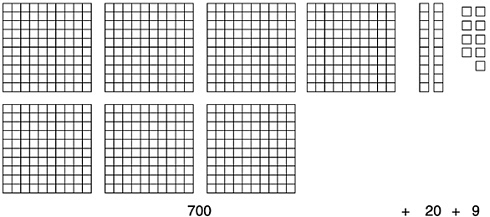
The composition of 729 shown above might be expressed symbolically as follows:
729=700+20+9
=(7×100)+(2×10)+(9×1)
=(7×102)+(2×10)+(9×1)
The symbol 102 means 10×10. In this case, 2 is called the exponent, and 102 is 10 to the second power. Making the meaning of the digits explicit in a larger number requires the use of higher powers of 10. For example,
39,406=(3×10,000)+(9×1,000)+(4×100)+(0×10)+6
=(3×104)+(9×103)+(4×102)+(0×10)+(6×1)
A number in the decimal system is the sum of the products of each digit and an appropriate power of 10, where the power in question corresponds to the position of the digit.
The system is general enough to represent any whole number, no matter how large.21 Furthermore, it is quite concise, requiring only nine digits to represent the population of the United States, and only 10 digits to represent the population of the entire earth. This conciseness, however, presents a challenge to young learners as they try to understand this compact notational system.
Extending the decimal system to the right of the decimal point is accomplished by analogy. As you move to the left, the value of the place is multiplied by 10:1, 10, 100, 1,000, and so on. As you move to the right, this sequence is reversed, so that the value is divided by 10. Continuing past the units (ones) place and over the decimal point, you continue dividing by 10, to reach places for tenths, hundredths, thousandths, and so on. A rational number such as ![]() therefore, is written as 0.375, in perfect analogy with the notation for whole numbers: The number is the sum of the product of each digit to the right of the decimal point with the appropriate reciprocals (see Box 3–4) of powers of 10.
therefore, is written as 0.375, in perfect analogy with the notation for whole numbers: The number is the sum of the product of each digit to the right of the decimal point with the appropriate reciprocals (see Box 3–4) of powers of 10.
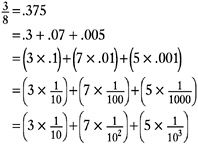
The values of the digits are sometimes shown in a place-value chart, in which 5620.739 might be represented as follows:
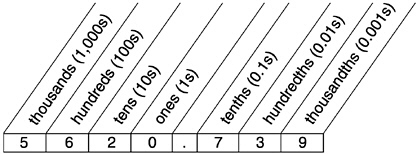
Because the reciprocals of powers of 10 become smaller in magnitude as their exponents get larger in absolute value, such decimal representations can describe quantities that are arbitrarily small. Consequently, any positive number, no matter how small in magnitude, can be represented by a decimal.
Choosing and Translating Among Representations
To represent numbers that are not whole numbers, one could choose a fractional rather than a decimal representation. Representational choices are much broader, however, than whether to use decimals or fractions. In the previous section, for example, we used points and arrows on the number line to indicate fractions, integers, and operations on integers. Fractional values are often represented with pictures, and relationships between quantities are often represented with graphs or tables. Communicating about mathematical ideas, therefore, requires that one choose representations and translate among them. Such choices depend on balancing such characteristics as the following:
-
Transparency. How easily can the idea be seen through the representation? Base-10 blocks, for example, are more transparent than a number line for understanding the decimal notation for whole numbers, whereas the decimal numerals themselves are not at all transparent.
-
Efficiency. Does the representation support efficient communication and use? Is it concise? Symbolic representations are more efficient than base-10 blocks.
-
Generality. Does the representation apply to broad classes of objects? Finger representations are not general. The number line is quite general, allowing the representation of counting numbers, integers, rationals, and reals. If digits on both sides of the decimal point are included, the decimal place-value representation of numbers is completely general in the sense that any number may be so represented.
-
Clarity. Is the representation unambiguous and easy to use? Representations should be clear and unambiguous, but that is often established by convention—how the representation is commonly used. (See Box 3–8.)
|
Box 3–8 Clarity of Representations For simplicity of use, representations should be as clear and unambiguous as possible. Much of that clarity is not inherent in the representation, however, but is established through convention. For example, the expression 3+4×5 is ambiguous on its face because there is no explicit indication of whether to perform the multiplication or the addition first.* One might be tempted to proceed simply from left to right. The conventional order of operations, however, dictates that multiplication and division precede addition and subtraction, so 3+4×5 is evaluated as 23=3+(4×5) and not 35=(3+4)×5. In the middle grades and high school, as algebraic symbolism is introduced, the letter x and the multiplication symbol×can be confused, especially in written (rather than typeset) work. This ambiguity is solved in part by omitting multiplication signs, using parentheses or juxtaposition instead. Thus, xy means x times y, and 5(3) means 5 times 3. But that practice creates another ambiguity. In the notation for mixed numbers, |
-
Precision. How close is the representation to the exact value? Graphs are usually not very precise. With enough digits to the right of the decimal point, decimal representation can be as precise as desired.
Consider the following representations for one-half:
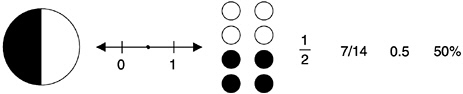
And one-half is the simplest fraction. Much more is involved in understanding and translating among representations of ![]() or rational numbers more generally. (See Box 3–9 for an example.)
or rational numbers more generally. (See Box 3–9 for an example.)
|
Box 3–9 Translating Among Representations: An Example Perhaps the deepest translation problem in pre-K to grade 8 mathematics concerns the translation between fractional and decimal representations of rational numbers. Successful translation requires an understanding of rational numbers as well as decimal and fractional notation—each of which is a significant and multifaceted idea in its own right. In school, children learn a standard way of converting a fraction such as The first written step of the long division is dividing 30 tenths by 8. After three divisions, the process stops because the remainder is zero. The quotient obtained, 0.375, is said to be a finite (or terminating) decimal because the number of digits is finite.  |
Understanding a mathematical idea thoroughly requires that several possible representations be available to allow a choice of those most useful for solving a particular problem. And if children are to be able to use a multiplicity of representations, it is important that they be able to translate among them, such as between fractional and decimal notations or between symbolic representations and the number line or pictorial representations.
Algorithms
Addition is an idea—an abstraction from combining collections of objects or from joining lengths. Carrying out the addition of two numbers requires a strategy that will lead to the result. For single-digit numbers it is reasonable to use or imagine blocks or cookies, but for multidigit numbers you need something more efficient. You need algorithms.
An algorithm is a “precisely-defined sequence of rules telling how to produce specified output information from given input information in a finite number of steps.”22 More simply, an algorithm is a recipe for computation.23 Most people know algorithms for doing addition, subtraction, multiplication, and division with pencil and paper. There are many such algorithms, as well as others that do not use pencil and paper. Years ago many people knew algorithms for computation on fingers, slide rules, and abacuses. Today, calculators and computer algorithms are widely used for arithmetic. (Indeed, a defining characteristic of a computational algorithm is that it be suitable for implementation on a computer.) And in fact, most of algebra, calculus, and even more advanced mathematics may now be done with computer programs that perform calculations with symbols.
An algorithm is a recipe for computation.
When confronted with a need for calculation, one must choose an algorithm that will give the correct result and that can be accomplished with the tools available. Algorithms depend upon representations. (Note, for example, that algorithms for fractions are different from algorithms for decimals.) And as was the case for representations, choosing an algorithm benefits from consideration of certain characteristics: transparency, efficiency, generality, and precision. The more transparent an algorithm, the easier it is to understand, and a child who understands an algorithm can reconstruct it after months or even years of not using it. The need for efficiency depends, of course, on how often an algorithm is used. An additional desired characteristic is simplicity because simple algorithms are easier to remember and easier to perform accurately. Again, the key is finding an appropriate balance among these characteristics because, for example, algorithms that are sufficiently general and efficient are often not very transparent. It is worth noting that pushing buttons on a calculator is the epitome of a nontransparent algorithm, but it can be quite efficient. In Box 3–10, we show some examples of algorithms with various qualities.
Algorithms are important in school mathematics because they can help students understand better the fundamental operations of arithmetic and important concepts such as place value and also because they pave the way for learning more advanced topics. For example, algorithms for the operations on multidigit whole numbers can be generalized (with appropriate modifications) to algorithms for corresponding operations on polynomials in algebra, although the resulting algorithms do not look quite like any typical multiplication algorithms but rather are based upon the idea behind such algorithms: computing and recording partial products and then adding. The polynomial multiplication illustrated below, for example, is somewhat like multiplication
of whole numbers, but the relationship is hard to see, mostly because there is no “carrying,” from the x to the x2 term, for example. The expanded method below shows the relationship a bit more clearly.

|
Box 3–10 Examples of Algorithms The decimal place-value system allows many different algorithms for the four main operations. The following six algorithms for multiplication of two-digit numbers were produced by a class of prospective elementary school teachers. They were asked to show how they were taught to multiply 23 by 15: 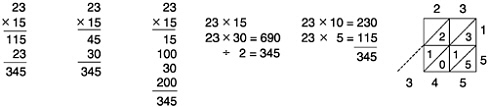 In Method 6, sometimes called lattice multiplication,* the factors are written across the top and on the right, the products of the pairs of digits are put into the cells (for example, 15 is written Note that all of these algorithms produce the correct answer. All except Method 4 are simply methods for organizing the four component multiplications and |
|
adding. The algorithms can be verified by decomposing the factors according to the values of their digits (in this case, 23=20+3 and 15=10+5) and using the distributive law in one of several ways:  A more compelling justification uses the area model of multiplication. If the sides of a 23×15 rectangle are subdivided as 20+3 and 10+5, then the area of the whole rectangle can be computed by summing the areas of the four smaller rectangles.  Note the correspondence between the areas of the four smaller rectangles and the partial products in Method 3. With more careful examination, it is possible to see the same four partial products residing in the four cells in Method 6. (The 2 in the upper left cell, for example, actually represents 200.) Methods 1, |
|
2, and 5 differ from these only in that they record the areas for one pair of these rectangles at a time. Any of the methods—and, in fact, any of the four justifications that followed— could serve as the standard algorithm for the multiplication of whole numbers because they are all general and exact. Mathematically, these methods are essentially the same, differing only in the intermediate products that are calculated and how they are recorded. These methods, however, are quite different in transparency and efficiency. Methods 3 and 5 and the area model justification are the most transparent because the partial products are all displayed clearly and unambiguously. The three justifications using the distributive law also show these partial products unambiguously, but some of the transparency is lost in the maze of symbols. Methods 1 and 2 are the most efficient, but they lack some transparency because the 23 and the 30 actually represent 230 and 300, respectively. Method 4 takes advantage of the fact that doubling the factor 15 gives a factor that is easy to use. It is quite different from the others. For one thing, the intermediate result is larger than the final answer. This method can also be shown to be correct using the properties of whole numbers, since multiplying one factor by 2 and then dividing the product by 2 has no net effect on the final answer. The usefulness of Method 4 depends on the numbers involved. Doubling 15 gives 30, and 23×30 is much easier to calculate mentally than 23×15. Using this method to find a product like 23×17, on the other hand, would require first calculating 23×34, which is no easier than 23×17. Clearly this method, although completely general, is not very practical. For most factors, it is neither simple nor efficient. |
Building Blocks
The preceding sections have described concepts in the domain of number that serve as fundamental building blocks for the entire mathematics curriculum. Other fundamental ideas—such as those about shape, spatial relationships, and chance—are foundational as well. Students do not need to, and should not, master all the number concepts we have described before they study other topics. Rather, number concepts should serve to support mathematics learning in other domains as students are introduced to them, and, conversely, these other domains should support students’ growing understanding of number.
Number is intimately connected with geometry, as illustrated in this chapter by our use of the number line and the area model of multiplication. Those same models of number can, of course, arise when measurement is introduced in geometry. The connection between number and algebra is illustrated in the chapter by our use of algebra to express properties of number systems and other general relationships between numbers. The links from number to geometry and to algebra are forged even more strongly when students are introduced to the coordinate plane, in which perpendicular number lines provide a system of coordinates for each point—an idea first put forward by the French mathematician and philosopher René Descartes (1596–1650), although he did not insist that the number lines were perpendicular. Number is also essential in data analysis, the process of making sense of collections of numbers. Using numbers to investigate processes of variation, such as accumulation and rates of change, can provide students with the numerical underpinnings of calculus.
Some of the manifold connections and dependencies between number and other mathematical domains may be illustrated by the so-called handshake problem:
If eight people are at a party and each person shakes hands exactly once with every other person, how many handshakes are there?
This problem appears often in the literature on problem solving in school mathematics, probably because it can be solved in so many ways. Perhaps the simplest way of getting a solution is just to count the handshakes systematically: The first person shakes hands with seven people; the second person, having shaken the first person’s hand, shakes hands with six people whose hands he or she has not yet shaken; the third person shakes hands with five people; and so on until the seventh person shakes hands with only the eighth person. The number of handshakes, therefore, is 7+6+5+4+3+2+1, which is 28.
This method of solution can be generalized to a situation with any number of people, which is what a mathematician would want to do. For a party with 20 people, for example, there would be 19+18+17+16+15+14+13+12+11+10+9+8+7+6+5+4+3+2+1 handshakes, but the computation would be more time consuming. Because mathematicians are interested not only in generalizations of problems but also in simplifying solutions, it would be nice to find a simple way of adding the numbers. In general, for m+1 people at a party, the number of handshakes would be the sum of the first m counting numbers:24
1+2+…+m.
Numbers that arise in this way are called triangular numbers because they may be arranged in triangular formations, as shown below.

Therefore, 3, 6, 10, 15, 21, and 28 are all triangular numbers. This is a geometric interpretation, but can geometry be used to find a solution to the handshake problem that would simplify the computation?
One way to approach geometrically the problem of adding the numbers from 1 to m is to think about it as a problem of finding the area of the side of a staircase. The sum 1+2+3+4+5+6+7, for example, would then be seen as a staircase of blocks in which each term is represented by one layer, as in the diagram on the left below. The diagram on the right below includes a second copy of the staircase, turned upside down. When the two staircases are put together, the result is a 7×8 rectangle, with area 56. So the area of the staircase is half that, or 28. This reasoning, although specific, supports a general solution for the sum of the whole numbers from 1 to m:m(m+1)/2.
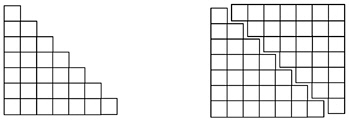
A closely related numerical approach to the problem of counting handshakes comes from a story told of young Carl Friedrich Gauss (1777–1855), whose teacher is said to have asked the class to sum the numbers from 1 to 100, expecting that the task would keep the class busy for some time. The story goes that almost before the teacher could turn around, Gauss handed in his slate with the correct answer. He had quickly noticed that if the numbers to be added are written out and then written again below but in the opposite
order, the combined (double) sum may be computed easily by first adding the pairs of numbers aligned vertically and then adding horizontally. As can be seen below, each vertical sum is 101, and there are exactly 100 of them. So the double sum is 100×101, or 10,100, which means that the desired sum is half that, or 5050.
For the original handshake problem, which involves the sum of the blocks in the staircase above, that means taking the double sum 7×8, or 56, and halving it to get 28.
The handshake problem can be approached by bringing in ideas from other parts of mathematics. If the people are thought of as standing at the vertices of an eight-sided figure (octagon), then the question again becomes geometric but in a different way: How many segments (sides and diagonals) may be drawn between vertices of an octagon? The answer again is 28, as can be verified in the picture below.
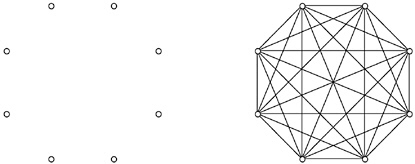
As often happens in mathematics, connections to geometry provide a new way of approaching the problem: Each vertex is an endpoint for exactly 7 segments, and there are 8 vertices, which sounds like there ought to be 7×8=56 segments. But that multiplication counts each segment twice (once for each endpoint), so there are really half as many, or 28, segments.
In still another mathematical domain, combinatorics—the study of counting, grouping, and arranging a finite number of elements in a collection—the
problem becomes how to count the number of ways to choose two items (people shaking hands) from a collection of eight elements. For example, in how many ways can a committee of two be chosen from a group of eight people? This is the same as the handshake problem because each committee of two corresponds to a handshake. It is also the same as the octagon problem because each committee corresponds to a segment (which is identified by its two endpoints).
A critically important mathematical idea in the above discussion lies in noticing that these are all the same problem in different clothing. It also involves solving the problem and finding a representation that captures its key features. For students to develop the mathematical skill and ability they need to understand that seemingly different problems are just variations on the same theme, to solve the problem once and for all, and to develop and use representations that will allow them to move easily from one variation to another, the study of number provides an indispensable launching pad.
Key Ideas About Number
In this chapter, we have surveyed the domain of number with an eye toward the proficiency that students in grades pre-K to 8 need for their future study of mathematics. Several key ideas have been emphasized. First, numbers and operations are abstractions—ideas based on experience but independent of any particular experience. The numbers and operations of school mathematics are organized as number systems, and each system provides ways to consider numbers and operations simultaneously, allowing learners to focus on the regularities and the structure of the system. Despite different notations and their separate treatment in school, these number systems are related through a process of embedding one system in the next one studied. All the number systems of pre-K to grade 8 mathematics lie inside a single system represented by the number line. Second, all mathematical ideas require representations, and their usefulness is enhanced through multiple representations. Because each representation has its advantages and disadvantages, one must be able to choose and translate among representations. The number line and the decimal place-value system are important representational tools in school mathematics, but students should have experience with other useful interpretations and representations, which also are important parts of the content. Third, calculation requires algorithms, and once again there are choices to make because each algorithm has advantages and disadvantages. And finally, the domain of number both supports and is supported by other
branches of mathematics. It is these connections that give mathematics much of its power. If students are to become proficient in mathematics by eighth grade, they need to be proficient with the numbers and operations discussed in this chapter, as well as with beginning algebra, measure, space, data, and chance—all of which are intricately related to number.
Notes
|
1. |
Some authors (see, e.g., Russell, 1919, p. 3; Freudenthal, 1983, pp. 77ff) call these the natural numbers. We are adopting the common usage of the U.S. mathematics education literature, in which the natural numbers begin 1, 2, 3, and so on, and the whole numbers include zero. |
|
2. |
The recognition that zero should be considered a legitimate number—rather than the absence of number—was an important intellectual achievement in the history of mathematics. Zero (as an idea) is present in the earliest schooling, but zero (as a number) is a significant obstacle for some students and teachers. “Zero is nothing,” some people say. “How can we ask whether it is even or odd?” |
|
3. |
“To criticize mathematics for its abstraction is to miss the point entirely. Abstraction is what makes mathematics work. If you concentrate too closely on too limited an application of a mathematical idea, you rob the mathematician of his [or her] most important tools: analogy, generality, and simplicity” (Stewart, 1989, p. 291). |
|
4. |
Although negative numbers are quite familiar today, and part of the standard elementary curriculum, they are quite a recent development in historical terms, having become common only since the Renaissance. Descartes, who invented analytic geometry and after whom the standard Cartesian coordinate system on the plane is named, rejected negative numbers as impossible. (His coordinate axes had only a positive direction.) His reason was that he thought of numbers as quantities and held that there could be no quantity less than nothing. Now, however, people are not limited to thinking of numbers solely in terms of quantity. In dealing with negative numbers, they have learned that if they think of numbers as representing movement along a line, then positive numbers can correspond to movement to the right, and negative numbers can represent movement to the left. This interpretation of numbers as oriented length is subtly different from the old interpretation in terms of quantity, which would here be unoriented length, and gives a sensible and quite concrete way to think about these numbers that Descartes thought impossible. |
|
5. |
Freudenthal, 1983, suggests that “negative numbers did not really become important until they appeared to be indispensable for the permanence of expressions, equations, formulae in the ‘analytic geometry’” (p. 436). “Later on arguments of content character were contrived…although some of them are not quite convincing (positive-negative as capital-debt, gain-loss, and so on)” (p. 435). |
|
6. |
See Freudenthal, 1983, p. 435. |
|
7. |
Although rational numbers seem to present more difficulties for students than negative integers, historically they came well before. The Greeks were comfortable |
|
|
with positive rational numbers over 2000 years before negative numbers became accepted. See also Behr, Harel, Post, and Lesh, 1992. |
|
8. |
The rules are in a sense guided by the fractional notation, a/b. In other notational systems, such as decimal representation, the rules will look somewhat different, although they will be equivalent. |
|
9. |
These numbers (and many others) are not rational because they cannot be expressed as fractions with integers in the numerator and denominator. |
|
10. |
In the number-line illustrations throughout this chapter, the portion displayed and the scale vary to suit the intent of the illustration. That is reasonable not just because one can imagine moving a “lens” left and right and zooming in and out, but also because the ideas are independent of the choice of origin and unit. |
|
11. |
Bruner, 1966 (pp. 10–11), suggests three ways of transforming experience into models of the world: enactive, iconic, and symbolic representations. Enactively, addition might be the action of combining a plate of three cookies with a plate of five cookies; iconically, it might be represented by a picture of two plates of cookies; symbolically, it might be represented as 5 cookies plus 3 cookies, or merely 5+3. |
|
12. |
Greeno and Hall, 1997. |
|
13. |
Pimm, 1995, suggests that people seek representational systems in which they can operate on the symbols as though the symbols were the mathematical objects. |
|
14. |
Duvall, 1999. |
|
15. |
Kaput, 1987, argues that much of elementary school mathematics is not about numbers but about a particular representational system for numbers. See Cuoco, 2001, for detailed discussions of various ways representations come into play in school mathematics. |
|
16. |
See Lakoff and Núñez, 1997, and Sfard, 1997, for detailed discussion of the metaphoric nature of mathematics. |
|
17. |
Sfard, 1997, p. 36, emphasis in original. |
|
18. |
“I remember as a child, in fifth grade, coming to the amazing (to me) realization that the answer to 134 divided by 29 is 134/29 (and so forth). What a tremendous labor-saving device! To me, ‘134 divided by 29’ meant a certain tedious chore, while 134/ 29 was an object with no implicit work. I went excitedly to my father to explain my discovery. He told me that of course this is so, a/b and a divided by b are just synonyms. To him it was just a small variation in notation” (Thurston, 1990, p. 847). |
|
19. |
Grouping is a common approach in measurement activities. For example, in measuring time, there are 60 seconds in a minute, 60 minutes in an hour, 24 hours in a day, approximately 30 days in a month, 12 months in a year, and so on. For distance, the customary U.S. system uses inches, feet, yards, and miles, and the metric system uses centimeters, meters, and kilometers. |
|
20. |
For example, IX means nine (that is, one less than ten), whereas XI means eleven (one more than ten). |
|
21. |
This generality was a significant accomplishment. In the third century B.C. in Greece, with its primitive numeration system, a subject of debate was whether there even existed a number large enough to describe the number of grains of sand in the universe. The issue was serious enough that Archimedes, the greatest mathematician |
|
|
of classical times, wrote a paper in the form of a letter to the king of his city explaining how to write such very large numbers. Archimedes, however, did not go so far as to invent the decimal system, with its potential for extending indefinitely. |
|
22. |
Knuth, 1974, p. 323. |
|
23. |
Steen, 1990. See Morrow and Kenney, 1998, for more perspectives on algorithms. |
|
24. |
The ellipsis points “…” in the expression are a significant piece of abstract mathematical notation, compactly designating the omission of the terms needed (to reach m, in this case). |
References
Behr, M.J., Harel, G., Post, T., & Lesh, R. (1992). Rational number, ratio, and proportion. In D.A.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 296–333). New York: Macmillan.
Bruner, J.S. (1966). Toward a theory of instruction. Cambridge, MA: Belknap Press.
Cuoco, A. (Ed.). (2001). The roles of representation in school mathematics (2001 Yearbook of the National Council of Teachers of Mathematics). Reston, VA: NCTM.
Duvall, R. (1999). Representation, vision, and visualization: Cognitive functions in mathematical thinking. Basic issues for learning. In F.Hitt & M.Santos (Eds.), Proceedings of the twenty-first annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (vol. 1, pp. 3–26). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education. (ERIC Document Reproduction Service No. ED 433 998).
Freudenthal, H. (1983). Didactical phenomenology of mathematical structures. Dordrecht, The Netherlands: Reidel.
Greeno, J.G., & Hall, R. (1997). Practicing representation: Learning with and about representational forms. Phi Delta Kappan, 78, 1–24. Available: http://www.pdkintl.org/kappan/kgreeno.htm. [July 10, 2001].
Kaput,]. (1987). Representation systems and mathematics. In C.Janvier (Ed.), Problems of representation in the teaching and learning of mathematics (pp. 19–26). Hillsdale, NJ: Erlbaum.
Knuth, D.E. (1974). Computer science and its relation to mathematics. American Mathematical Monthly, 81, 323–343.
Lakoff, G., & Núñez, R.E. (1997). The metaphorical structure of mathematics: Sketching out cognitive foundations for a mind-based mathematics. In L.D.English (Ed.), Mathematical reasoning: Analogies, metaphors, and images (pp. 21–89). Mahwah, NJ: Erlbaum.
Morrow, L.J., & Kenney, M.J. (Eds.). (1998). The teaching and learning of algorithms in school mathematics (1998 Yearbook of the National Council of Teachers of Mathematics). Reston, VA: NCTM.
Pimm, D. (1995). Symbols and meanings in school mathematics. London: Routledge.
Russell, B. (1919). Introduction to mathematical philosophy. New York: Macmillan.
Sfard, A. (1997). Commentary: On metaphorical roots of conceptual growth. In L.D. English (Ed.), Mathematical reasoning: Analogies, metaphors, and images (pp. 339–371). Mahwah, NJ: Erlbaum.
Steen, L. (1990). Pattern. In L.Steen (Ed.), On the shoulders of giants: New approaches to numeracy (pp. 1(10). Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/1532.html. [July 10, 2001].
Stevin, S. (1959). On decimal fractions (V.Sanford, Trans). In D.E.Smith (Ed.), A source book in mathematics (pp. 20–34). New York: Dover. (Original work published 1585)
Stewart, I. (1989). Does God play dice? The mathematics of chaos. Oxford, England: Blackwell.
Thurston, W.P. (1990). Mathematical education. Notices of the American Mathematical Society, 37, 844–850.













































