2
How Experts Differ from Novices
People who have developed expertise in particular areas are, by definition, able to think effectively about problems in those areas. Understanding expertise is important because it provides insights into the nature of thinking and problem solving. Research shows that it is not simply general abilities, such as memory or intelligence, nor the use of general strategies that differentiate experts from novices. Instead, experts have acquired extensive knowledge that affects what they notice and how they organize, represent, and interpret information in their environment. This, in turn, affects their abilities to remember, reason, and solve problems.
This chapter illustrates key scientific findings that have come from the study of people who have developed expertise in areas such as chess, physics, mathematics, electronics, and history. We discuss these examples not because all school children are expected to become experts in these or any other areas, but because the study of expertise shows what the results of successful learning look like. In later chapters we explore what is known about processes of learning that can eventually lead to the development of expertise.
We consider several key principles of experts’ knowledge and their potential implications for learning and instruction:
-
Experts notice features and meaningful patterns of information that are not noticed by novices.
-
Experts have acquired a great deal of content knowledge that is organized in ways that reflect a deep understanding of their subject matter.
-
Experts’ knowledge cannot be reduced to sets of isolated facts or propositions but, instead, reflects contexts of applicability: that is, the knowledge is “conditionalized” on a set of circumstances.
-
Experts are able to flexibly retrieve important aspects of their knowledge with little attentional effort.
-
Though experts know their disciplines thoroughly, this does not guarantee that they are able to teach others.
-
Experts have varying levels of flexibility in their approach to new situations.
MEANINGFUL PATTERNS OF INFORMATION
One of the earliest studies of expertise demonstrated that the same stimulus is perceived and understood differently, depending on the knowledge that a person brings to the situation. DeGroot (1965) was interested in understanding how world-class chess masters are consistently able to out-think their opponents. Chess masters and less experienced but still extremely good players were shown examples of chess games and asked to think aloud as they decided on the move they would make if they were one of the players; see Box 2.1. DeGroot’s hypothesis was that the chess masters would be more likely than the nonmasters to (a) think through all the possibilities before making a move (greater breadth of search) and (b) think through all the possible countermoves of the opponent for every move considered (greater depth of search). In this pioneering research, the chess masters did exhibit considerable breadth and depth to their searches, but so did the lesser ranked chess players. And none of them conducted searches that covered all the possibilities. Somehow, the chess masters considered possibilities for moves that were of higher quality than those considered by the lesser experienced players. Something other than differences in general strategies seemed to be responsible for differences in expertise.
DeGroot concluded that the knowledge acquired over tens of thousands of hours of chess playing enabled chess masters to out-play their opponents. Specifically, masters were more likely to recognize meaningful chess configurations and realize the strategic implications of these situations; this recognition allowed them to consider sets of possible moves that were superior to others. The meaningful patterns seemed readily apparent to the masters, leading deGroot (1965:33–34) to note:
We know that increasing experience and knowledge in a specific field (chess, for instance) has the effect that things (properties, etc.) which, at earlier stages, had to be abstracted, or even inferred are apt to be immediately perceived at later stages. To a rather large extent, abstraction is replaced by perception, but we do not know much about how this works, nor where the borderline lies. As an effect of this replacement, a so-called ‘given’ problem situation is not really given since it is seen differently by an expert than it is perceived by an inexperienced person….
DeGroot’s think-aloud method provided for a very careful analysis of the conditions of specialized learning and the kinds of conclusions one can draw from them (see Ericsson and Simon, 1993). Hypotheses generated from think-aloud protocols are usually cross-validated through the use of other methodologies.
The superior recall ability of experts, illustrated in the example in the box, has been explained in terms of how they “chunk” various elements of a configuration that are related by an underlying function or strategy. Since
there are limits on the amount of information that people can hold in short-term memory, short-term memory is enhanced when people are able to chunk information into familiar patterns (Miller, 1956). Chess masters perceive chunks of meaningful information, which affects their memory for what they see. Chess masters are able to chunk together several chess pieces in a configuration that is governed by some strategic component of the game. Lacking a hierarchical, highly organized structure for the domain, novices cannot use this chunking strategy. It is noteworthy that people do not have to be world-class experts to benefit from their abilities to encode meaningful chunks of information: 10- and 11-year-olds who are experienced in chess are able to remember more chess pieces than college students who are not chess players. In contrast, when the college students were presented with other stimuli, such as strings of numbers, they were able to remember more (Chi, 1978; Schneider et al, 1993); see Figure 2.3.
Skills similar to those of master chess players have been demonstrated for experts in other domains, including electronic circuitry (Egan and Schwartz, 1979), radiology (Lesgold, 1988), and computer programming (Ehrlich and Soloway, 1984). In each case, expertise in a domain helps people develop a sensitivity to patterns of meaningful information that are not available to novices. For example, electronics technicians were able to reproduce large portions of complex circuit diagrams after only a few seconds of viewing; novices could not. The expert circuit technicians chunked several individual circuit elements (e.g., resistors and capacitors) that performed the function of an amplifier. By remembering the structure and function of a typical amplifier, experts were able to recall the arrangement of many of the individual circuit elements comprising the “amplifier chunk.”
Mathematics experts are also able to quickly recognize patterns of information, such as particular problem types that involve specific classes of mathematical solutions (Hinsley et al., 1977; Robinson and Hayes, 1978). For example, physicists recognize problems of river currents and problems of headwinds and tailwinds in airplanes as involving similar mathematical principles, such as relative velocities. The expert knowledge that underlies the ability to recognize problem types has been characterized as involving the development of organized conceptual structures, or schemas, that guide how problems are represented and understood (e.g., Glaser and Chi, 1988).
Expert teachers, too, have been shown to have schemas similar to those found in chess and mathematics. Expert and novice teachers were shown a videotaped classroom lesson (Sabers et al., 1991). The experimental set-up involved three screens that showed simultaneous events occurring throughout the classroom (the left, center, and right). During part of the session, the expert and novice teachers were asked to talk aloud about what they were seeing. Later, they were asked questions about classroom events. Overall,
|
In one study, a chess master, a Class A player (good but not a master), and a novice were given 5 seconds to view a chess board position from the middle of a chess game; see Figure 2.1. After 5 seconds the board was covered, and each participant attempted to reconstruct the board position on another board. This procedure was repeated for multiple trials until everyone received a perfect score. On the first trial, the master player correctly placed many more pieces than the Class A player, who in turn placed more than the novice: 16, 8, and 4, respectively. However, these results occurred only when the chess pieces were arranged in configurations that conformed to meaningful games of chess. When chess pieces were randomized and presented for 5 seconds, the recall of the chess master and Class A player were the same as the novice—they placed from 2 to 3 positions correctly. Data over trials for valid and random middle games are shown in Figure 2.2. 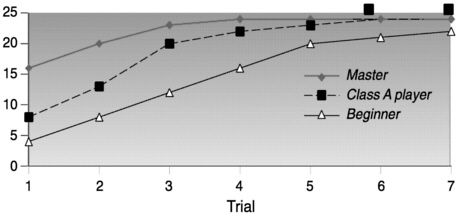 FIGURE 2.2 Recall by chess players by level of expertise. |
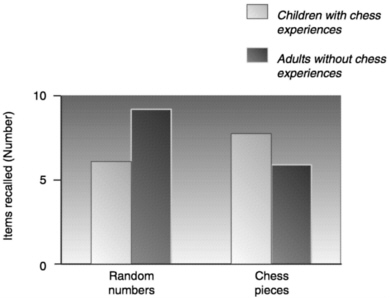
FIGURE 2.3 Recall for numbers and chess pieces. SOURCE: Adapted from Chi (1978).
the expert teachers had very different understandings of the events they were watching than did the novice teachers; see examples in Box 2.2.
The idea that experts recognize features and patterns that are not noticed by novices is potentially important for improving instruction. When viewing instructional texts, slides, and videotapes, for example, the information noticed by novices can be quite different from what is noticed by experts (e.g., Sabers et al., 1991; Bransford et al., 1988). One dimension of acquiring greater competence appears to be the increased ability to segment the perceptual field (learning how to see). Research on expertise suggests the importance of providing students with learning experiences that specifically enhance their abilities to recognize meaningful patterns of information (e.g., Simon, 1980; Bransford et al., 1989).
ORGANIZATION OF KNOWLEDGE
We turn now to the question of how experts’ knowledge is organized and how this affects their abilities to understand and represent problems. Their knowledge is not simply a list of facts and formulas that are relevant to their domain; instead, their knowledge is organized around core concepts or “big ideas” that guide their thinking about their domains.
|
BOX 2.2 What Expert and Novice Teachers Notice Expert and novice teachers notice very different things when viewing a videotape of a classroom lesson. Expert 6: On the left monitor, the students’ note taking indicates that they have seen sheets like this and have had presentations like this before; it’s fairly efficient at this point because they’re used to the format they are using. Expert 7: I don’t understand why the students can’t be finding out this information on their own rather than listening to someone tell them because if you watch the faces of most of them, they start out for about the first 2 or 3 minutes sort of paying attention to what’s going on and then just drift off. Expert 2: …I haven’t heard a bell, but the students are already at their desks and seem to be doing purposeful activity, and this is about the time that I decide they must be an accelerated group because they came into the room and started something rather than just sitting down and socializing. Novice 1: …I can’t tell what they are doing. They’re getting ready for class, but I can’t tell what they’re doing. Novice 3: She’s trying to communicate with them here about something, but I sure couldn’t tell what it was. Another novice: It’s a lot to watch. |
In an example from physics, experts and competent beginners (college students) were asked to describe verbally the approach they would use to solve physics problems. Experts usually mentioned the major principle(s) or law(s) that were applicable to the problem, together with a rationale for why those laws applied to the problem and how one could apply them (Chi et al., 1981). In contrast, competent beginners rarely referred to major principles and laws in physics; instead, they typically described which equations they would use and how those equations would be manipulated (Larkin, 1981, 1983).
Experts’ thinking seems to be organized around big ideas in physics, such as Newton’s second law and how it would apply, while novices tend to
perceive problem solving in physics as memorizing, recalling, and manipulating equations to get answers. When solving problems, experts in physics often pause to draw a simple qualitative diagram—they do not simply attempt to plug numbers into a formula. The diagram is often elaborated as the expert seeks to find a workable solution path (e.g., see Larkin et al., 1980; Larkin and Simon, 1987; Simon and Simon, 1978).
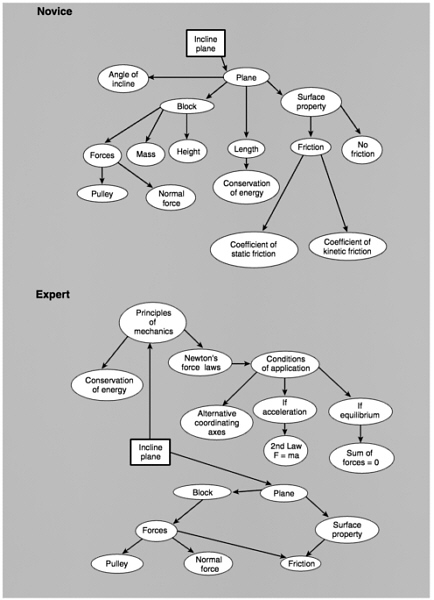
Differences in how physics experts and novices approach problems can also be seen when they are asked to sort problems, written on index cards, according to the approach that could be used to solve them (Chi et al., 1981). Experts’ problem piles are arranged on the basis of the principles that can be applied to solve the problems; novices’ piles are arranged on the basis of the problems’ surface attributes. For example, in the physics subfield of mechanics, an expert’s pile might consist of problems that can be solved by conservation of energy, while a novice’s pile might consist of problems that contain inclined planes; see Figure 2.4. Responding to the surface characteristics of problems is not very useful, since two problems that share the same objects and look very similar may actually be solved by entirely different approaches.
Some studies of experts and novices in physics have explored the organization of the knowledge structures that are available to these different groups of individuals (Chi et al., 1982); see Figure 2.5. In representing a schema for an incline plane, the novice’s schema contains primarily surface features of the incline plane. In contrast, the expert’s schema immediately connects the notion of an incline plane with the laws of physics and the conditions under which laws are applicable.
Pause times have also been used to infer the structure of expert knowledge in domains such as chess and physics. Physics experts appear to evoke sets of related equations, with the recall of one equation activating related equations that are retrieved rapidly (Larkin, 1979). Novices, in contrast, retrieve equations more equally spaced in time, suggesting a sequential search in memory. Experts appear to possess an efficient organization of knowledge with meaningful relations among related elements clustered into related units that are governed by underlying concepts and principles; see Box 2.3. Within this picture of expertise, “knowing more” means having more conceptual chunks in memory, more relations or features defining each chunk, more interrelations among the chunks, and efficient methods for retrieving related chunks and procedures for applying these informational units in problem-solving contexts (Chi et al., 1981).
Differences between how experts and nonexperts organize knowledge has also been demonstrated in such fields as history (Wineburg, 1991). A group of history experts and a group of gifted, high-achieving high school seniors enrolled in an advanced placement course in history were first given a test of facts about the American Revolution. The historians with back-
|
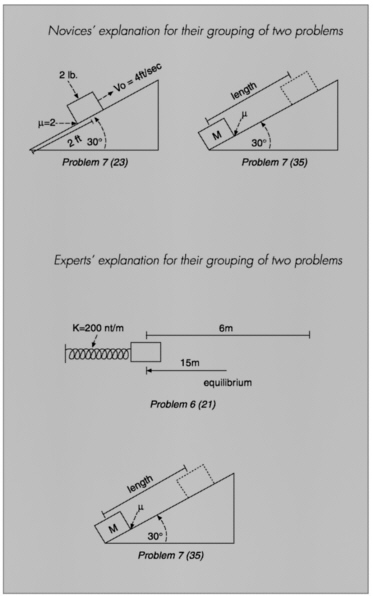 |
Explanations Novice 1: These deal with blocks on on incline plane. Novice 5: Incline plane problems, coefficient of friction. Novice 6: Blocks on inclined planes with angles. Explanations Expert 2: Conservation of energy. Expert 3: Work-theory theorem. They are all straight-forward problems. Expert 4: These can be done from energy considerations. Either you should know the principle of conservation of energy, or work is lost somewhere. |
FIGURE 2.4 An example of sortings of physics problems made by novices and experts. Each picture above represents a diagram that can be drawn from the storyline of a physics problem taken from an introductory physics textbook. The novices and experts in this study were asked to categorize many such problems based on similarity of solution. The two pairs show a marked contrast in the experts’ and novices’ categorization schemes. Novices tend to categorize physics problems as being solved similarly if they “look the same” (that is, share the same surface features), whereas experts categorize according to the major principle that could be applied to solve the problems.
SOURCE: Adapted from Chi et al. (1981).
|
BOX2.3 Understanding and Problem Solving In mathematics, experts are more likely than novices to first try to understand problems, rather than simply attempt to plug numbers into formulas. Experts and students in one study (Paige and Simon, 1966) were asked to solve algebra word problems, such as: A board was sawed into two pieces. One piece was two-thirds as long as the whole board and was exceeded in length by the second piece by four feet. How long was the board before it was cut? The experts quickly realize that the problem as stated is logically impossible. Although some students also come to this realization, others simply apply equations, which results in the answer of a negative length. A similar example comes from a study of adults and children (Reusser, 1993), who were asked: There are 26 sheep and 10 goats on a ship. How old is the captain? Most adults have enough expertise to realize that this problem is unsolvable, but many school children didn’t realize this at all. More than three-quarters of the children in one study attempted to provide a numerical answer to the problems. They asked themselves whether to add, subtract, multiply, or divide, rather than whether the problem made sense. As one fifth-grade child explained, after giving the answer of 36: “Well, you need to add or subtract or multiply in problems like this, and this one seemed to work best if I add” (Bransford and Stein, 1993:196). |
grounds in American history knew most of the items. However, many of the historians had specialties that lay elsewhere and they knew only one-third of the facts on the tests. Several of the students outscored several of the historians on the factual test. The study then compared how the historians and students made sense of historical documents; the result revealed dramatic differences on virtually any criterion. The historians excelled in the elaborateness of understandings they developed in their ability to pose alternative explanations for events and in their use of corroborating evidence. This depth of understanding was as true for the Asian specialists and the medievalists as it was for the Americanists.
When the two groups were asked to select one of three pictures that best reflect their understanding of the battle of Lexington, historians and students displayed the greatest differences. Historians carefully navigated back and forth between the corpus of written documents and the three images of the battlefield. For them, the picture selection task was the quint-
essential epistemological exercise, a task that explored the limits of historical knowledge. They knew that no single document or picture could tell the story of history; hence, they thought very hard about their choices. In contrast, the students generally just looked at the pictures and made a selection without regard or qualification. For students, the process was similar to finding the correct answer on a multiple choice test.
In sum, although the students scored very well on facts about history, they were largely unacquainted with modes of inquiry with real historical thinking. They had no systematic way of making sense of contradictory claims. Thrust into a set of historical documents that demanded that they sort out competing claims and formulate a reasoned interpretation, the students, on the whole, were stymied. They lacked the experts’ deep understanding of how to formulate reasoned interpretations of sets of historical documents. Experts in other social sciences also organize their problem solving around big ideas (see, e.g., Voss et al., 1984).
The fact that experts’ knowledge is organized around important ideas or concepts suggests that curricula should also be organized in ways that lead to conceptual understanding. Many approaches to curriculum design make it difficult for students to organize knowledge meaningfully. Often there is only superficial coverage of facts before moving on to the next topic; there is little time to develop important, organizing ideas. History texts sometimes emphasize facts without providing support for understanding (e.g., Beck et al., 1989, 1991). Many ways of teaching science also overemphasize facts (American Association for the Advancement of Science, 1989; National Research Council, 1996).
The Third International Mathematics and Science Survey (TIMSS) (Schmidt et al., 1997) criticized curricula that were “a mile wide and an inch deep” and argued that this is much more of a problem in America than in most other countries. Research on expertise suggests that a superficial coverage of many topics in the domain may be a poor way to help students develop the competencies that will prepare them for future learning and work. The idea of helping students organize their knowledge also suggests that novices might benefit from models of how experts approach problem solving— especially if they then receive coaching in using similar strategies (e.g., Brown et al., 1989; we discuss this more fully in Chapters 3 and 7).
CONTEXT AND ACCESS TO KNOWLEDGE
Experts have a vast repertoire of knowledge that is relevant to their domain or discipline, but only a subset of that knowledge is relevant to any particular problem. Experts do not have to search through everything they know in order to find what is relevant; such an approach would overwhelm
their working memory (Miller, 1956). For example, the chess masters described above considered only a subset of possible chess moves, but those moves were generally superior to the ones considered by the lesser ranked players. Experts have not only acquired knowledge, but are also good at retrieving the knowledge that is relevant to a particular task. In the language of cognitive scientists, experts’ knowledge is “conditionalized” —it includes a specification of the contexts in which it is useful (Simon, 1980; Glaser, 1992). Knowledge that is not conditionalized is often “inert” because it is not activated, even though it is relevant (Whitehead, 1929).
The concept of conditionalized knowledge has implications for the design of curriculum, instruction, and assessment practices that promote effective learning. Many forms of curricula and instruction do not help students conditionalize their knowledge: “Textbooks are much more explicit in enunciating the laws of mathematics or of nature than in saying anything about when these laws may be useful in solving problems” (Simon, 1980:92). It is left largely to students to generate the condition-action pairs required for solving novel problems.
One way to help students learn about conditions of applicability is to assign word problems that require students to use appropriate concepts and formulas (Lesgold, 1984, 1988; Simon, 1980). If well designed, these problems can help students learn when, where, and why to use the knowledge they are learning. Sometimes, however, students can solve sets of practice problems but fail to conditionalize their knowledge because they know which chapter the problems came from and so automatically use this information to decide which concepts and formulas are relevant. Practice problems that are organized into very structured worksheets can also cause this problem. Sometimes students who have done well on such assignments—and believe that they are learning—are unpleasantly surprised when they take tests in which problems from the entire course are randomly presented so there are no clues about where they appeared in a text (Bransford, 1979).
The concept of conditionalized knowledge also has important implications for assessment practices that provide feedback about learning. Many types of tests fail to help teachers and students assess the degree to which the students’ knowledge is conditionalized. For example, students might be asked whether the formula that quantifies the relationship between mass and energy is E=MC, E=MC2, or E=MC3. A correct answer requires no knowledge of the conditions under which it is appropriate to use the formula. Similarly, students in a literature class might be asked to explain the meaning of familiar proverbs, such as “he who hesitates is lost” or “too many cooks spoil the broth.” The ability to explain the meaning of each proverb provides no guarantee that students will know the conditions under which either proverb is useful. Such knowledge is important because, when viewed solely as propositions, proverbs often contradict one another. To use them
effectively, people need to know when and why it is appropriate to apply the maxim “too many cooks spoil the broth” versus “many hands make light work” or “he who hesitates is lost” versus “haste makes waste” (see Bransford and Stein, 1993).
FLUENT RETRIEVAL
People’s abilities to retrieve relevant knowledge can vary from being “effortful” to “relatively effortless” (fluent) to “automatic” (Schneider and Shiffrin, 1977). Automatic and fluent retrieval are important characteristics of expertise.
Fluent retrieval does not mean that experts always perform a task faster than novices. Because experts attempt to understand problems rather than to jump immediately to solution strategies, they sometimes take more time than novices (e.g., Getzels and Csikszentmihalyi, 1976). But within the overall process of problem solving there are a number of subprocesses that, for experts, vary from fluent to automatic. Fluency is important because effortless processing places fewer demands on conscious attention. Since the amount of information a person can attend to at any one time is limited (Miller, 1956), ease of processing some aspects of a task gives a person more capacity to attend to other aspects of the task (LaBerge and Samuels, 1974; Schneider and Shiffrin, 1985; Anderson, 1981, 1982; Lesgold et al., 1988).
Learning to drive a car provides a good example of fluency and automaticity. When first learning, novices cannot drive and simultaneously carry on a conversation. With experience, it becomes easy to do so. Similarly, novice readers whose ability to decode words is not yet fluent are unable to devote attention to the task of understanding what they are reading (LaBerge and Samuels, 1974). Issues of fluency are very important for understanding learning and instruction. Many instructional environments stop short of helping all students develop the fluency needed to successfully perform cognitive tasks (Beck et al., 1989; Case, 1978; Hasselbring et al., 1987; LaBerge and Samuels, 1974).
An important aspect of learning is to become fluent at recognizing problem types in particular domains—such as problems involving Newton’s second law or concepts of rate and functions—so that appropriate solutions can be easily retrieved from memory. The use of instructional procedures that speed pattern recognition are promising in this regard (e.g., Simon, 1980).
EXPERTS AND TEACHING
Expertise in a particular domain does not guarantee that one is good at helping others learn it. In fact, expertise can sometimes hurt teaching because many experts forget what is easy and what is difficult for students.
Recognizing this fact, some groups who design educational materials pair content area experts with “accomplished novices” whose area of expertise lies elsewhere: their task is to continually challenge the experts until the experts’ ideas for instruction begin to make sense to them (Cognition and Technology Group at Vanderbilt, 1997).
The content knowledge necessary for expertise in a discipline needs to be differentiated from the pedagogical content knowledge that underlies effective teaching (Redish, 1996; Shulman, 1986, 1987). The latter includes information about typical difficulties that students encounter as they attempt to learn about a set of topics; typical paths students must traverse in order to achieve understanding; and sets of potential strategies for helping students overcome the difficulties that they encounter. Shulman (1986, 1987) argues that pedagogical content knowledge is not equivalent to knowledge of a content domain plus a generic set of teaching strategies; instead, teaching strategies differ across disciplines. Expert teachers know the kinds of difficulties that students are likely to face; they know how to tap into students’ existing knowledge in order to make new information meaningful; and they know how to assess their students’ progress. Expert teachers have acquired pedagogical content knowledge as well as content knowledge; see Box 2.4. In the absence of pedagogical content knowledge, teachers often rely on textbook publishers for decisions about how to best organize subjects for students. They are therefore forced to rely on the “prescriptions of absentee curriculum developers” (Brophy, 1983), who know nothing about the particular students in each teacher’s classroom. Pedagogical content knowledge is an extremely important part of what teachers need to learn to be more effective. (This topic is discussed more fully in Chapter 7.)
ADAPTIVE EXPERTISE
An important question for educators is whether some ways of organizing knowledge are better at helping people remain flexible and adaptive to new situations than others. For example, contrast two types of Japanese sushi experts (Hatano and Inagaki, 1986): one excels at following a fixed recipe; the other has “adaptive expertise” and is able to prepare sushi quite creatively. These appear to be examples of two very different types of expertise, one that is relatively routinized and one that is flexible and more adaptable to external demands: experts have been characterized as being “merely skilled” versus “highly competent” or more colorfully as “artisans” versus “virtuosos” (Miller, 1978). These differences apparently exist across a wide range of jobs.
One analysis looked at these differences in terms of information systems design (Miller, 1978). Information systems designers typically work with clients who specify what they want. The goal of the designer is to construct systems that allow people to efficiently store and access relevant informa
|
BOX 2.4 TeachingHamlet Two new English teachers, Jake and Steven, with similar subject-matter backgrounds from elite private universities, set out to teach Hamlet in high school (Grossman, 1990). In his teaching, Jake spent 7 weeks leading his students through a word-by-word explication du texte, focusing on notions of “linguistic reflexivity,” and issues of modernism. His assignments included in-depth analyses of soliloquies, memorization of long passages, and a final paper on the importance of language in Hamlet. Jake’s model for this instruction was his own undergraduate coursework; there was little transformation of his knowledge, except to parcel it out in chunks that fit into the 50-minute containers of the school day. Jake’s image for how students would respond was his own responses as a student who loved Shakespeare and delighted in close textual analysis. Consequently, when students responded in less than enthusiastic ways, Jake was ill-equipped to understand their confusion: “The biggest problem I have with teaching by far is trying to get into the mind-set of a ninth grader…” Steven began his unit on Hamlet without ever mentioning the name of the play. To help his students grasp the initial outline of the themes and issues of the play, he asked them to imagine that their parents had recently divorced and that their mothers had taken up with a new man. This new man had replaced their father at work, and “there’s some talk that he had something to do with the ousting of your dad” (Grossman, 1990:24). Steven then asked students to think about the circumstances that might drive them so mad that they would contemplate murdering another human being. Only then, after students had contemplated these issues and done some writing on them, did Steven introduce the play they would be reading. |
tion (usually through computers). Artisan experts seek to identify the functions that their clients want automated; they tend to accept the problem and its limits as stated by the clients. They approach new problems as opportunities to use their existing expertise to do familiar tasks more efficiently. It is important to emphasize that artisans’ skills are often extensive and should not be underestimated. In contrast, however, the virtuoso experts treat the client’s statement of the problem with respect, but consider it “a point for departure and exploration” (Miller, 1978). They view assignments as opportunities to explore and expand their current levels of expertise. Miller also observes that, in his experience, virtuosos exhibit their positive characteristics despite their training, which is usually restricted solely to technical skills.
The concept of adaptive expertise has also been explored in a study of history experts (Wineburg, 1998). Two history experts and a group of future teachers were asked to read and interpret a set of documents about Abraham Lincoln and his view of slavery. This is a complex issue that, for Lincoln, involved conflicts between enacted law (the Constitution), natural law (as encoded in the Declaration of Independence), and divine law (assumptions about basic rights). One of the historians was an expert on Lincoln; the second historian’s expertise lay elsewhere. The Lincoln expert brought detailed content knowledge to the documents and easily interpreted them; the other historian was familiar with some of the broad themes in the documents but quickly became confused in the details. In fact, at the beginning of the task, the second historian reacted no differently than a group of future high school teachers who were faced with the same task (Wineburg and Fournier, 1994): attempting to harmonize discrepant information about Lincoln’s position, they both appealed to an array of present social forms and institutions—such as speech writers, press conferences, and “spin doctors” —to explain why things seemed discrepant. Unlike the future teachers, however, the second historian did not stop with his initial analysis. He instead adopted a working hypothesis that assumed that the apparent contradictions might be rooted less in Lincoln’s duplicity than in his own ignorance of the nineteenth century. The expert stepped back from his own initial interpretation and searched for a deeper understanding of the issues. As he read texts from this perspective, his understanding deepened, and he learned from the experience. After considerable work, the second historian was able to piece together an interpretive structure that brought him by the task’s end to where his more knowledgeable colleague had begun. The future history teachers, in contrast, never moved beyond their initial interpretations of events.
An important characteristic exhibited by the history expert involves what is known as “metacognition” —the ability to monitor one’s current level of understanding and decide when it is not adequate. The concept of metacognition was originally introduced in the context of studying young children (e.g., Brown, 1980; Flavell, 1985, 1991). For example, young children often erroneously believe that they can remember information and hence fail to use effective strategies, such as rehearsal. The ability to recognize the limits of one’s current knowledge, then take steps to remedy the situation, is extremely important for learners at all ages. The history expert who was not a specialist in Lincoln was metacognitive in the sense that he successfully recognized the insufficiency of his initial attempts to explain Lincoln’s position. As a consequence, he adopted the working hypothesis that he needed to learn more about the context of Lincoln’s times before coming to a reasoned conclusion.
Beliefs about what it means to be an expert can affect the degree to which people explicitly search for what they don’t know and take steps to improve the situation. In a study of researchers and veteran teachers, a common assumption was that “an expert is someone who knows all the answers” (Cognition and Technology Group at Vanderbilt, 1997). This assumption had been implicit rather than explicit and had never been questioned and discussed. But when the researchers and teachers discussed this concept, they discovered that it placed severe constraints on new learning because the tendency was to worry about looking competent rather than publicly acknowledging the need for help in certain areas (see Dweck, 1989, for similar findings with students). The researchers and the teachers found it useful to replace their previous model of “answer-filled experts” with the model of “accomplished novices.” Accomplished novices are skilled in many areas and proud of their accomplishments, but they realize that what they know is minuscule compared to all that is potentially knowable. This model helps free people to continue to learn even though they may have spent 10 to 20 years as an “expert” in their field.
The concept of adaptive expertise (Hatano and Inagaki, 1986) provides an important model of successful learning. Adaptive experts are able to approach new situations flexibly and to learn throughout their lifetimes. They not only use what they have learned, they are metacognitive and continually question their current levels of expertise and attempt to move beyond them. They don’t simply attempt to do the same things more efficiently; they attempt to do things better. A major challenge for theories of learning is to understand how particular kinds of learning experiences develop adaptive expertise or “virtuosos.”
CONCLUSION
Experts’ abilities to reason and solve problems depend on well-organized knowledge that affects what they notice and how they represent problems. Experts are not simply “general problem solvers” who have learned a set of strategies that operate across all domains. The fact that experts are more likely than novices to recognize meaningful patterns of information applies in all domains, whether chess, electronics, mathematics, or classroom teaching. In deGroot’s (1965) words, a “given” problem situation is not really a given. Because of their ability to see patterns of meaningful information, experts begin problem solving at “a higher place” (deGroot, 1965). An emphasis on the patterns perceived by experts suggests that pattern recognition is an important strategy for helping students develop confidence and competence. These patterns provide triggering conditions for accessing knowledge that is relevant to a task.
Studies in areas such as physics, mathematics, and history also demon-
strata that experts first seek to develop an understanding of problems, and this often involves thinking in terms of core concepts or big ideas, such as Newton’s second law in physics. Novices’ knowledge is much less likely to be organized around big ideas; they are more likely to approach problems by searching for correct formulas and pat answers that fit their everyday intuitions.
Curricula that emphasize breadth of knowledge may prevent effective organization of knowledge because there is not enough time to learn anything in depth. Instruction that enables students to see models of how experts organize and solve problems may be helpful. However, as discussed in more detail in later chapters, the level of complexity of the models must be tailored to the learners’ current levels of knowledge and skills.
While experts possess a vast repertoire of knowledge, only a subset of it is relevant to any particular problem. Experts do not conduct an exhaustive search of everything they know; this would overwhelm their working memory (Miller, 1956). Instead, information that is relevant to a task tends to be selectively retrieved (e.g., Ericsson and Staszewski, 1989; deGroot, 1965).
The issue of retrieving relevant information provides clues about the nature of usable knowledge. Knowledge must be “conditionalized” in order to be retrieved when it is needed; otherwise, it remains inert (Whitehead, 1929). Many designs for curriculum instruction and assessment practices fail to emphasize the importance of conditionalized knowledge. For example, texts often present facts and formulas with little attention to helping students learn the conditions under which they are most useful. Many assessments measure only propositional (factual) knowledge and never ask whether students know when, where, and why to use that knowledge.
Another important characteristic of expertise is the ability to retrieve relevant knowledge in a manner that is relatively “effortless.” This fluent retrieval does not mean that experts always accomplish tasks in less time than novices; often they take more time in order to fully understand a problem. But their ability to retrieve information effortlessly is extremely important because fluency places fewer demands on conscious attention, which is limited in capacity (Schneider and Shiffrin, 1977, 1985). Effortful retrieval, by contrast, places many demands on a learner’s attention: attentional effort is being expended on remembering instead of learning. Instruction that focuses solely on accuracy does not necessarily help students develop fluency (e.g., Beck et al., 1989; Hasselbring et al., 1987; LaBerge and Samuels, 1974).
Expertise in an area does not guarantee that one can effectively teach others about that area. Expert teachers know the kinds of difficulties that students are likely to face, and they know how to tap into their students’ existing knowledge in order to make new information meaningful plus assess their students’ progress. In Shulman’s (1986, 1987) terms, expert teach-
ers have acquired pedagogical content knowledge and not just content knowledge. (This concept is explored more fully in Chapter 7.)
The concept of adaptive expertise raises the question of whether some ways of organizing knowledge lead to greater flexibility in problem solving than others (Hatano and Inagaki, 1986; Spiro et al., 1991). Differences between the “merely skilled” (artisans) and the “highly competent” (virtuosos) can be seen in fields as disparate as sushi making and information design. Virtuosos not only apply expertise to a given problem, they also consider whether the problem as presented is the best way to begin.
The ability to monitor one’s approach to problem solving—to be metacognitive—is an important aspect of the expert’s competence. Experts step back from their first, oversimplistic interpretation of a problem or situation and question their own knowledge that is relevant. People’s mental models of what it means to be an expert can affect the degree to which they learn throughout their lifetimes. A model that assumes that experts know all the answers is very different from a model of the accomplished novice, who is proud of his or her achievements and yet also realizes that there is much more to learn.
We close this chapter with two important cautionary notes. First, the six principles of expertise need to be considered simultaneously, as parts of an overall system. We divided our discussion into six points in order to facilitate explanation, but each point interacts with the others; this interrelationship has important educational implications. For example, the idea of promoting fluent access to knowledge (principle 4) must be approached with an eye toward helping students develop an understanding of the subject matter (principle 2), learn when, where and why to use information (principle 3), and learn to recognize meaningful patterns of information (principle 1). Furthermore, all these need to be approached from the perspective of helping students develop adaptive expertise (principle 6), which includes helping them become metacognitive about their learning so that they can assess their own progress and continually identify and pursue new learning goals. An example in mathematics is getting students to recognize when a proof is needed. Metacognition can help students develop personally relevant pedagogical content knowledge, analogous to the pedagogical content knowledge available to effective teachers (principle 5). In short, students need to develop the ability to teach themselves.
The second cautionary note is that although the study of experts provides important information about learning and instruction, it can be misleading if applied inappropriately. For example, it would be a mistake simply to expose novices to expert models and assume that the novices will learn effectively; what they will learn depends on how much they know already. Discussions in the next chapters (3 and 4) show that effective instruction begins with the knowledge and skills that learners bring to the learning task.