3
Learning and Transfer
Processes of learning and the transfer of learning are central to understanding how people develop important competencies. Learning is important because no one is born with the ability to function competently as an adult in society. It is especially important to understand the kinds of learning experiences that lead to transfer, defined as the ability to extend what has been learned in one context to new contexts (e.g., Byrnes, 1996:74). Educators hope that students will transfer learning from one problem to another within a course, from one year in school to another, between school and home, and from school to workplace. Assumptions about transfer accompany the belief that it is better to broadly “educate” people than simply “train” them to perform particular tasks (e.g., Broudy, 1977).
Measures of transfer play an important role in assessing the quality of people’s learning experiences. Different kinds of learning experiences can look equivalent when tests of learning focus solely on remembering (e.g., on the ability to repeat previously taught facts or procedures), but they can look quite different when tests of transfer are used. Some kinds of learning experiences result in effective memory but poor transfer; others produce effective memory plus positive transfer.
Thorndike and his colleagues were among the first to use transfer tests to examine assumptions about learning (e.g., Thorndike and Woodworth, 1901). One of their goals was to test the doctrine of “formal discipline” that was prevalent at the turn of the century. According to this doctrine, practice by learning Latin and other difficult subjects had broad-based effects, such as developing general skills of learning and attention. But these studies raised serious questions about the fruitfulness of designing educational experiences based on the assumption of formal discipline. Rather than developing some kind of “general skill” or “mental muscle” that affected a wide range of performances, people seemed to learn things that were more specific; see Box 3.1.
Early research on the transfer of learning was guided by theories that emphasized the similarity between conditions of learning and conditions of transfer. Thorndike (1913), for example, hypothesized that the degree of transfer between initial and later learning depends upon the match between
|
BOX 3.1 What People Learn Ericsson et al. (1980) worked extensively with a college student for well over a year, increasing his capacity to remember digit strings (e.g., 982761093…). As expected, at the outset he could remember only about seven numbers. After practice, he could remember 70 or more; see Figure 3.1. How? Did he develop a general skill analogous to strengthening a “mental muscle?” No, what happened was that he learned to use his specific background knowledge to “chunk” information into meaningful groups. The student had extensive knowledge about winning times for famous track races, including the times of national and world records. For example 941003591992100 could be chunked into 94100 (9.41 seconds for 100 yards). 3591 (3 minutes, 59.1 seconds for a mile), etc. But it took the student a huge amount of practice before he could perform at his final level, and when he was tested with letter strings, he was back to remembering about seven items. SOURCE: Ericsson et al. (1980:1181–1182). Reprinted by permission. 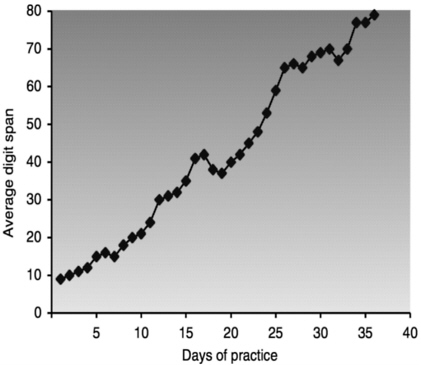 FIGURE 3.1 Change in average digit span remembered. |
elements across the two events. The essential elements were presumed to be specific facts and skills. By such an account, skills of writing letters of the alphabet are useful to writing words (vertical transfer). The theory posited that transfer from one school task and a highly similar task (near transfer), and from school subjects to nonschool settings (far transfer), could be facilitated by teaching knowledge and skills in school subjects that have elements identical to activities encountered in the transfer context (Klausmeier, 1985). Transfer could also be negative in the sense that experience with one set of events could hurt performance on related tasks (Luchins and Luchins, 1970); see Box 3.2.
The emphasis on identical elements of tasks excluded consideration of any learner characteristics, including when attention was directed, whether relevant principles were extrapolated, problem solving, or creativity and motivation. The primary emphasis was on drill and practice. Modern theories of learning and transfer retain the emphasis on practice, but they specify the kinds of practice that are important and take learner characteristics (e.g., existing knowledge and strategies) into account (e.g., Singley and Anderson, 1989).
In the discussion below we explore key characteristics of learning and transfer that have important implications for education:
-
Initial learning is necessary for transfer, and a considerable amount is known about the kinds of learning experiences that support transfer.
-
Knowledge that is overly contextualized can reduce transfer; abstract representations of knowledge can help promote transfer.
-
Transfer is best viewed as an active, dynamic process rather than a passive end-product of a particular set of learning experiences.
-
All new learning involves transfer based on previous learning, and this fact has important implications for the design of instruction that helps students learn.
ELEMENTS THAT PROMOTE INITIAL LEARNING
The first factor that influences successful transfer is degree of mastery of the original subject. Without an adequate level of initial learning, transfer cannot be expected. This point seems obvious, but it is often overlooked.
The importance of initial learning is illustrated by a series of studies designed to assess the effects of learning to program in the computer language LOGO. The hypothesis was that students who learned LOGO would transfer this knowledge to other areas that required thinking and problem solving (Papert, 1980). Yet in many cases, the studies found no differences on transfer tests between students who had been taught LOGO and those who had not (see Cognition and Technology Group at Vanderbilt, 1996;
|
BOX 3.2 An Example of Negative Transfer Luchins and Luchins (1970) studied how prior experience can limit people’s abilities to function efficiently in new settings. They used water jar problems where participants had three jars of varying sizes and an unlimited water supply and were asked to obtain a required amount of water. Everyone received a practice problem. People in the experimental group then received five problems (problems 2–6) prior to critical test problems (7, 8, 10, and 11). People in the control group went straight from the practice problems to problems 7–11. Problems 2–6 were designed to establish a “set” (Einstellung) for solving the problems in a particular manner (using containers b-a-2c as a solution). People in the experimental group were highly likely to use the Einstellung Solution on the critical problems even though more efficient procedures were available. In contrast, people in the control group used solutions that were much more direct.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Possible Answers for Critical Problems (7, 8, 10, 11)
Performance of Typical Subjects on Critical Problems
|
|||||||||||||||||||||||||||||||||||||||
Mayer, 1988). However, many of these studies failed to assess the degree to which LOGO was learned in the first place (see Klahr and Carver, 1988; Littlefield et al., 1988). When initial learning was assessed, it was found that students often had not learned enough about LOGO to provide a basis for transfer. Subsequent studies began to pay more attention to student learning, and they did find transfer to related tasks (Klahr and Carver, 1988; Littlefield et al., 1988). Other research studies have shown that additional qualities of initial learning affect transfer and are reviewed next.
Understanding Versus Memorizing
Transfer is affected by the degree to which people learn with understanding rather than merely memorize sets of facts or follow a fixed set of procedures; see Boxes 3.3 and 3.4.
In Chapter 1, the advantages of learning with understanding were illus-
|
BOX 3.3 Throwing Darts In one of the most famous early studies comparing the effects of “learning a procedure” with “learning with understanding,” two groups of children practiced throwing darts at a target underwater (Scholckow and Judd, described in Judd, 1908; see a conceptual replication by Hendrickson and Schroeder, 1941). One group received an explanation of refraction of light, which causes the apparent location of the target to be deceptive. The other group only practiced dart throwing, without the explanation. Both groups did equally well on the practice task, which involved a target 12 inches under water. But the group that had been instructed about the abstract principle did much better when they had to transfer to a situation in which the target was under only 4 inches of water. Because they understood what they were doing, the group that had received instruction about the refraction of light could adjust their behavior to the new task. |
trated with an example from biology that involved learning about the physical properties of veins and arteries. We noted that the ability to remember properties of veins and arteries (e.g., that arteries are thicker than veins, more elastic, and carry blood from the heart) is not the same as understanding why they have particular properties. The ability to understand becomes important for transfer problems, such as: “Imagine trying to design an artificial artery. Would it have to be elastic? Why or why not?” Students who only memorize facts have little basis for approaching this kind of problem-solving task (Bransford and Stein, 1993; Bransford et al., 1983). The act of organizing facts about veins and arteries around more general principles such as “how structure is related to function” is consistent with the knowledge organization of experts discussed in Chapter 2.
Time to Learn
It is important to be realistic about the amount of time it takes to learn complex subject matter. It has been estimated that world-class chess masters require from 50,000 to 100,000 hours of practice to reach that level of expertise; they rely on a knowledge base containing some 50,000 familiar chess patterns to guide their selection of moves (Chase and Simon, 1973; Simon and Chase, 1973). Much of this time involves the development of pattern recognition skills that support the fluent identification of meaningful patterns of information plus knowledge of their implications for future outcomes (see Chapter 2). In all domains of learning, the development of
|
BOX 3.4 Finding the Area of a Figure Understanding Method The understanding method encouraged students to see the structural relations in the parallelogram, for example, that the parallelogram could be rearranged into a rectangle by moving a triangle from one side to the other. Since the students knew how to find the area of a rectangle, finding the area of a parallelogram was easy once they discovered the appropriate structural relations. 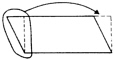 Rote Method In the rote method, students were taught to drop a perpendicular and then apply the memorized solution formula. 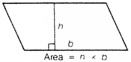 Transfer Both groups performed well on typical problems asking for the area of parallelograms; however, only the understanding group could transfer to novel problems, such as finding the area of the figures below. 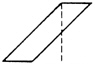 or distinguishing between solvable and unsolvable problems such as  The response of the “rote” group to novel problems was, “We haven’t had that yet.” SOURCE: Based on Wertheimer (1959). |
|
BOX 3.5 Learning Algebra Students taking regular algebra in a major school system received an average of 65 hours of instruction and homework during the year. In contrast, those taking honors algebra received approximately 250 hours of instruction and homework (John Anderson, personal communication). Clearly, it was recognized that significant learning takes major investments of time. |
expertise occurs only with major investments of time, and the amount of time it takes to learn material is roughly proportional to the amount of material being learned (Singley and Anderson, 1989); see Box 3.5. Although many people believe that “talent” plays a role in who becomes an expert in a particular area, even seemingly talented individuals require a great deal of practice in order to develop their expertise (Ericsson et al., 1993).
Learners, especially in school settings, are often faced with tasks that do not have apparent meaning or logic (Klausmeier, 1985). It can be difficult for them to learn with understanding at the start; they may need to take time to explore underlying concepts and to generate connections to other information they possess. Attempts to cover too many topics too quickly may hinder learning and subsequent transfer because students (a) learn only isolated sets of facts that are not organized and connected or (b) are introduced to organizing principles that they cannot grasp because they lack enough specific knowledge to make them meaningful. Providing students with opportunities to first grapple with specific information relevant to a topic has been shown to create a “time for telling” that enables them to learn much more from an organizing lecture (as measured by subsequent abilities to transfer) than students who did not first have these specific opportunities; see Box 3.6.
Providing students with time to learn also includes providing enough time for them to process information. Pezdek and Miceli (1982) found that on one particular task, it took 3rd graders 15 seconds to integrate pictorial and verbal information; when given only 8 seconds, they couldn’t mentally integrate the information, probably due to short-term memory limitations. The implication is that learning cannot be rushed; the complex cognitive activity of information integration requires time.
Beyond “Time on Task”
It is clear that different ways of using one’s time have different effects on learning and transfer. A considerable amount is known about variables that affect learning. For example, learning is most effective when people engage
|
BOX3.6 Preparation for Learning with Understanding Three different groups of college students received different kinds of instruction about schema theory and memory and then completed a transfer task where they were asked to make detailed predictions about the results of a new memory study. Students in Group 1 read and summarized a text on the topic of schema theory and then listened to a lecture designed to help them organize their knowledge and learn with understanding. Group 2 did not read the text but, instead, actively compared simplified data sets from schema experiments on memory and then heard the same lecture as Group 1. Group 3 spent twice as much time as Group 2 working with the data sets but did not receive the organizing lecture. On the transfer test, students in Group 2 performed much better than those in Groups 1 and 3. Their work with the data sets set the stage for them to learn from the lecture. The lecture was necessary, as indicated by the poor performance of Group 3. 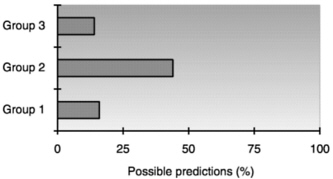 SOURCE: From Schwortz et al. (1999). |
in “deliberate practice” that includes active monitoring of one’s learning experiences (Ericsson et al., 1993). Monitoring involves attempts to seek and use feedback about one’s progress. Feedback has long been identified as important for successful learning (see, e.g., Thorndike, 1913), but it should not be regarded as a unidimensional concept. For example, feedback that signals progress in memorizing facts and formulas is different from feedback that signals the state of the students’ understanding (Chi et al., 1989, 1994). In addition, as noted in Chapter 2, students need feedback about the degree to which they know when, where, and how to use the knowledge they are learning. By inadvertently relying on clues—such as which chapter in a text
the practice problems came from—students can erroneously think they have conditionalized their knowledge when, in fact, they have not (Bransford, 1979).
Understanding when, where, and why to use new knowledge can be enhanced through the use of “contrasting cases,” a concept from the field of perceptual learning (see, e.g., Gagné and Gibson, 1947; Garner, 1974; Gibson and Gibson, 1955). Appropriately arranged contrasts can help people notice new features that previously escaped their attention and learn which features are relevant or irrelevant to a particular concept. The benefits of appropriately arranged contrasting cases apply not only to perceptual learning, but also to conceptual learning (Bransford et al., 1989; Schwartz et al., 1999). For example, the concept of linear function becomes clearer when contrasted with nonlinear functions; the concept of recognition memory becomes clearer when contrasted with measures such as free recall and cued recall.
A number of studies converge on the conclusion that transfer is enhanced by helping students see potential transfer implications of what they are learning (Anderson et al., 1996). In one of the studies on learning LOGO programming (Klahr and Carver, 1988), the goal was to help students learn to generate “bug-free” instructions for others to follow. The researchers first conducted a careful task analysis of the important skills underlying the ability to program in LOGO and focused especially on LOGO debugging skills—the process by which children find and correct errors in their programs. Part of the researchers’ success in teaching LOGO depended on this task analysis. The researchers identified the four key aspects of debugging a program as identifying the buggy behavior, representing the program, locating the bug in the program, and then correcting the bug. They highlighted these key abstract steps and signaled to the students that the steps would be relevant to the transfer task of writing debugging directions. Students who had LOGO training increased from 33 percent correct instructions to 55 percent correct instructions. They could have approached this task by memorizing the procedures for programming LOGO routines to “make a house,” “make a polygon,” and so forth. Simply memorizing the procedures, however, would not be expected to help students accomplish the transfer task of generating clear, bug-free instructions.
Motivation to Learn
Motivation affects the amount of time that people are willing to devote to learning. Humans are motivated to develop competence and to solve problems; they have, as White (1959) put it, “competence motivation.” Although extrinsic rewards and punishments clearly affect behavior (see Chapter 1), people work hard for intrinsic reasons, as well.
Challenges, however, must be at the proper level of difficulty in order to be and to remain motivating: tasks that are too easy become boring; tasks that are too difficult cause frustration. In addition, learners’ tendencies to persist in the face of difficulty are strongly affected by whether they are “performance oriented” or “learning oriented” (Dweck, 1989). Students who are learning oriented like new challenges; those who are performance oriented are more worried about making errors than about learning. Being learning oriented is similar to the concept of adaptive expertise discussed in Chapter 2. It is probable, but needs to be verified experimentally, that being “learning oriented” or “performance oriented” is not a stable trait of an individual but, instead, varies across disciplines (e.g., a person may be performance oriented in mathematics but learning oriented in science and social studies or vice versa).
Social opportunities also affect motivation. Feeling that one is contributing something to others appears to be especially motivating (Schwartz et al., 1999). For example, young learners are highly motivated to write stories and draw pictures that they can share with others. First graders in an inner-city school were so highly motivated to write books to be shared with others that the teachers had to make a rule: “No leaving recess early to go back to class to work on your book” (Cognition and Technology Group at Vanderbilt, 1998).
Learners of all ages are more motivated when they can see the usefulness of what they are learning and when they can use that information to do something that has an impact on others—especially their local community (McCombs, 1996; Pintrich and Schunk, 1996). Sixth graders in an inner-city school were asked to explain the highlights of their previous year in fifth grade to an anonymous interviewer, who asked them to describe anything that made them feel proud, successful, or creative (Barron et al., 1998). Students frequently mentioned projects that had strong social consequences, such as tutoring younger children, learning to make presentations to outside audiences, designing blueprints for playhouses that were to be built by professionals and then donated to preschool programs, and learning to work effectively in groups. Many of the activities mentioned by the students had involved a great deal of hard work on their part: for example, they had had to learn about geometry and architecture in order to get the chance to create blueprints for the playhouses, and they had had to explain their blueprints to a group of outside experts who held them to very high standards. (For other examples and discussions of highly motivating activities, see Pintrich and Schunk, 1996.)
OTHER FACTORS THAT INFLUENCE TRANSFER
Context
Transfer is also affected by the context of original learning; people can learn in one context, yet fail to transfer to other contexts. For example, a group of Orange County homemakers did very well at making supermarket best-buy calculations despite doing poorly on equivalent school-like paper-and-pencil mathematics problems (Lave, 1988). Similarly, some Brazilian street children could perform mathematics when making sales in the street but were unable to answer similar problems presented in a school context (Carraher, 1986; Carraher et al, 1985).
How tightly learning is tied to contexts depends on how the knowledge is acquired (Eich, 1985). Research has indicated that transfer across contexts is especially difficult when a subject is taught only in a single context rather than in multiple contexts (Bjork and Richardson-Klavhen, 1989). One frequently used teaching technique is to get learners to elaborate on the examples used during learning in order to facilitate retrieval at a later time. The practice, however, has the potential of actually making it more difficult to retrieve the lesson material in other contexts, because knowledge tends to be especially context-bound when learners elaborate the new material with details of the context in which the material is learned (Eich, 1985). When a subject is taught in multiple contexts, however, and includes examples that demonstrate wide application of what is being taught, people are more likely to abstract the relevant features of concepts and to develop a flexible representation of knowledge (Gick and Holyoak, 1983).
The problem of overly contextualized knowledge has been studied in instructional programs that use case-based and problem-based learning. In these programs, information is presented in a context of attempting to solve complex, realistic problems (e.g., Barrows, 1985; Cognition and Technology Group at Vanderbilt, 1997; Gragg, 1940; Hmelo, 1995; Williams, 1992). For example, fifth- and sixth-grade students may learn mathematical concepts of distance-rate-time in the context of solving a complex case involving planning for a boat trip. The findings indicate that if students learn only in this context, they often fail to transfer flexibly to new situations (Cognition and Technology Group at Vanderbilt, 1997). The issue is how to promote wide transfer of the learning.
One way to deal with lack of flexibility is to ask learners to solve a specific case and then provide them with an additional, similar case; the goal is to help them abstract general principles that lead to more flexible transfer (Gick and Holyoak, 1983); see Box 3.7. A second way to improve flexibility is to let students learn in a specific context and then help them engage in “what-if” problem solving designed to increase the flexibility of their understanding. They might be asked: “What if this part of the problem
were changed, or this part?” (Cognition and Technology Group at Vanderbilt, 1997). A third way is to generalize the case so that learners are asked to create a solution that applies not simply to a single problem, but to a whole class of related problems. For example, instead of planning a single boat trip, students might run a trip planning company that has to advise people on travel times for different regions of the country. Learners are asked to adopt the goal of learning to “work smart” by creating mathematical models that characterize a variety of travel problems and using these models to create tools, ranging from simple tables and graphs to computer programs. Under these conditions, transfer to novel problems is enhanced (e.g., Bransford et al., 1998).
Problem Representations
Transfer is also enhanced by instruction that helps students represent problems at higher levels of abstraction. For example, students who create a specific business plan for a complex problem may not initially realize that their plan works well for “fixed-cost” situations but not for others. Helping students represent their solution strategies at a more general level can help them increase the probability of positive transfer and decrease the degree to which a previous solution strategy is used inappropriately (negative transfer).
Advantages of abstract problem representations have been studied in the context of algebra word problems involving mixtures. Some students were trained with pictures of the mixtures and other students were trained with abstract tabular representations that highlighted the underlying mathematical relationships (Singley and Anderson, 1989). Students who were trained on specific task components without being provided with the principles underlying the problems could do the specific tasks well, but they could not apply their learning to new problems. By contrast, the students who received abstract training showed transfer to new problems that involved analogous mathematical relations. Research has also shown that developing a suite of representations enables learners to think flexibly about complex domains (Spiro et al., 1991).
Relationships Between Learning and Transfer Conditions
Transfer is always a function of relationships between what is learned and what is tested. Many theorists argue that the amount of transfer will be a function of the overlap between the original domain of learning and the novel one. Measuring overlap requires a theory of how knowledge is represented and conceptually mapped across domains. Examples of research
|
BOX 3.7 Flexible Transfer College students were presented with the following passage about a general and a fortress (Gick and Holyoak, 1980:309). A general wishes to capture a fortress located in the center of a country. There are many roads radiating outward from the fortress. All have been mined so that while small groups of men can pass over the roads safely, a large force will detonate the mines. A full-scale direct attack is therefore impossible. The general’s solution is to divide his army into small groups, send each group to the head of a different road, and have the groups converge simultaneously on the fortress. Students memorized the information in the passage and were then asked to try another task, which was to solve the following problem (Gick and Holyoak, 1980:307– 308). You are a doctor faced with a patient who has a malignant tumor in his stomach. It is impossible to operate on the patient, but unless the tumor is destroyed the patient will die. There is a kind of ray that may be used to destroy the tumor. If the rays reach the tumor all at once and with sufficiently high intensity, the tumor will be destroyed, but surrounding tissue may be damaged as well. At lower intensities the rays are harmless to healthy tissue, but they will not affect the tumor either. What type of procedure might be used to destroy the tumor with the rays, and at the same time avoid destroying the healthy tissue? Few college students were able to solve this problem when left to their own devices. However, over 90 percent were able to solve the tumor problem when they were explicitly told to use information about the general and the fortress to help them. These students perceived the analogy between dividing the troops into small units and using a number of small-dose rays that each converge on the same point—the cancerous tissue. Each ray is too weak to harm tissue except at the point of convergence. Despite the relevance of the fortress problem to the tumor problem, the information was not used spontaneously—the connection between the two sets of information had to be explicitly pointed out. |
studies on conceptual representation include Brown (1986), Bassok and Holyoak (1989a, b), and Singley and Anderson (1989). Whether students will transfer across domains—such as distance formulas from physics to formally equivalent biological growth problems, for example—depends on whether they conceive of the growth as occurring continuously (successful transfer) or in discrete steps (unsuccessful transfer) (Bassok and Olseth, 1995).
Singley and Anderson (1989) argue that transfer between tasks is a function of the degree to which the tasks share cognitive elements. This hypothesis was also put forth very early in the development of research on transfer of identical elements, mentioned previously (Thorndike and Woodworth, 1901; Woodworth, 1938), but it was hard to test experimentally until there was a way to identify task components. In addition, modern theorists include cognitive representations and strategies as “elements” that vary across tasks (Singley and Anderson, 1989).
Singley and Anderson taught students several text editors, one after another, and sought to predict transfer, defined as the savings in time of learning a new editor when it was not taught first. They found that students learned subsequent text editors more rapidly and that the number of procedural elements shared by two text editors predicted the amount of this transfer. In fact, there was large transfer across editors that were very different in surface structures but that had common abstract structures. Singley and Anderson also found that similar principles govern transfer of mathematical competence across multiple domains when they considered transfer of declarative as well as procedural knowledge.
A study by Biederman and Shiffrar (1987) is a striking example of the benefits of abstract instruction. They studied a task that is typically difficult to learn in apprentice-like roles: how to examine day-old chicks to determine their sex. Biederman and Shiffrar found that twenty minutes of instruction on abstract principles helped the novices improve considerably (see also Anderson et al., 1996). Research studies generally provide strong support for the benefits of helping students represent their experiences at levels of abstraction that transcend the specificity of particular contexts and examples (National Research Council, 1994). Examples include algebra (Singley and Anderson, 1989), computer language tasks (Klahr and Carver, 1988), motor skills (e.g., dart throwing, Judd, 1908), analogical reasoning (Gick and Holyoak, 1983), and visual learning (e.g., sexing chicks, Biederman and Shiffrar, 1987).
Studies show that abstracted representations do not remain as isolated instances of events but become components of larger, related events, schemata (Holyoak, 1984; Novick and Holyoak, 1991). Knowledge representations are built up through many opportunities for observing similarities and differences across diverse events. Schemata are posited as particularly im-
portant guides to complex thinking, including analogical reasoning: “Successful analogical transfer leads to the induction of a general schema for the solved problems that can be applied to subsequent problems” (National Research Council, 1994:43). Memory retrieval and transfer are promoted by schemata because they derive from a broader scope of related instances than single learning experiences.
Active Versus Passive Approaches to Transfer
It is important to view transfer as a dynamic process that requires learners to actively choose and evaluate strategies, consider resources, and receive feedback. This active view of transfer is different from more static views, which assume that transfer is adequately reflected by learners’ abilities to solve a set of transfer problems right after they have engaged in an initial learning task. These “one-shot” tests often seriously underestimate the amount of transfer that students display from one domain to another (Bransford and Schwartz, 1999; Brown et al, 1983; Bruer, 1993).
Studies of transfer from learning one text editor to another illustrate the importance of viewing transfer from a dynamic rather than a static perspective. Researchers have found much greater transfer to a second text editor on the second day of transfer than the first (Singley and Anderson, 1989): this finding suggests that transfer should be viewed as increased speed in learning a new domain—not simply initial performance. Similarly, one educational goal for a course in calculus is how it facilitates learning of physics, but not necessarily its benefit on the first day of physics class.
Ideally, an individual spontaneously transfers appropriate knowledge without a need for prompting. Sometimes, however, prompting is necessary. With prompting, transfer can improve quite dramatically (e.g., Gick and Holyoak, 1980; Perfetto et al., 1983). “The amount of transfer depends on where attention is directed during learning or at transfer” (Anderson et al, 1996:8).
An especially sensitive way to assess the degree to which students’ learning has prepared them for transfer is to use methods of dynamic assessment, such as “graduated prompting” (Campione and Brown, 1987; Newman et al, 1989). This method can be used to assess the amount of help needed for transfer by counting the number and types of prompts that are necessary before students are able to transfer. Some learners can transfer after receiving a general prompt such as “Can you think of something you did earlier that might be relevant?” Other learners need prompts that are much more specific. Tests of transfer that use graduated prompting provide more fine-grained analysis of learning and its effects on transfer than simple one-shot assessments of whether or not transfer occurs.
Transfer and Metacognition
Transfer can be improved by helping students become more aware of themselves as learners who actively monitor their learning strategies and resources and assess their readiness for particular tests and performances. We briefly discussed the concept of metacognition in Chapters 1 and 3 (see Brown, 1975; Flavell, 1973). Metacognitive approaches to instruction have been shown to increase the degree to which students will transfer to new situations without the need for explicit prompting. The following examples illustrate research on teaching metacognitive skills across domains of reading, writing, and mathematics.
Reciprocal teaching to increase reading comprehension (Palincsar and Brown, 1984) is designed to help students acquire specific knowledge and also to learn a set of strategies for explicating, elaborating, and monitoring the understanding necessary for independent learning. The three major components of reciprocal teaching are instruction and practice with strategies that enable students to monitor their understanding; provision, initially by a teacher, of an expert model of metacognitive processes; and a social setting that enables joint negotiation for understanding. The knowledge-acquisition strategies the students learn in working on a specific text are not acquired as abstract memorized procedures, but as skills instrumental in achieving subject-area knowledge and understanding. The instructional procedure is reciprocal in the sense that a teacher and a group of students take turns in leading the group to discuss and use strategies for comprehending and remembering text content.
A program of procedural facilitation for teaching written composition (Scardamalia et al., 1984) shares many features with reciprocal teaching. The method prompts learners to adopt the metacognitive activities embedded in sophisticated writing strategies. The prompts help learners think about and reflect on the activities by getting them to identify goals, generate new ideas, improve and elaborate existing ideas, and strive for idea cohesion. Students in the procedural facilitation program take turns presenting their ideas to the group and detailing how they use prompts in planning to write. The teacher also models these procedures. Thus, the program involves modeling, scaffolding, and taking turns which are designed to help students externalize mental events in a collaborative context.
Alan Schoenfeld (1983, 1985, 1991) teaches heuristic methods for mathematical problem solving to college students. The methods are derived, to some extent, from the problem-solving heuristics of Polya (1957). Schoenfeld’s program adopts methods similar to reciprocal teaching and procedural facilitation. He teaches and demonstrates control or managerial strategies and makes explicit such processes as generating alternative courses of action, evaluating which course one will be able to carry out and whether it can be managed in the time available, and assessing one’s progress. Again,
elements of modeling, coaching, and scaffolding, as well as collective problem solving and whole-class and small group discussions, are used. Gradually, students come to ask self-regulatory questions themselves as the teacher fades out. At the end of each of the problem-solving sessions, students and teacher alternate in characterizing major themes by analyzing what they did and why. The recapitulations highlight the generalizable features of the critical decisions and actions and focus on strategic levels rather than on the specific solutions (see also White and Frederickson, 1998).
An emphasis on metacognition can enhance many programs that use new technologies to introduce students to the inquiry methods and other tools that are used by professionals in the workplace (see Chapter 8). The important role of metacognition for learning has been demonstrated in the context of a “thinker tools” program that lets students run simulations of physics experiments (White and Frederickson, 1998), as well as in adding a metacognitive component to a computer program designed to help college students learn biology. The value of using video to model important metacognitive learning procedures has also been shown to help learners analyze and reflect on models (Bielaczyc et al., 1995). All of these strategies engage learners as active participants in their learning by focusing their attention on critical elements, encouraging abstraction of common themes or procedures (principles), and evaluating their own progress toward understanding.
LEARNING AS TRANSFER FROM PREVIOUS EXPERIENCES
When people think about transfer, it is common to think first about learning something and then assessing the learner’s abilities to apply it to something else. But even the initial learning phase involves transfer because it is based on the knowledge that people bring to any learning situation; see Box 3.8. The principle that people learn by using what they know to construct new understandings (see Chapter 1) can be paraphrased as “all learning involves transfer from previous experiences.” This principle has a number of important implications for educational practice. First, students may have knowledge that is relevant to a learning situation that is not activated. By helping activate this knowledge, teachers can build on students’ strengths. Second, students may misinterpret new information because of previous knowledge they use to construct new understandings. Third, students may have difficulty with particular school teaching practices that conflict with practices in their community. This section discusses these three implications.
|
BOX 3.8 Everyday and Formal Math The importance of building on previous experiences is relevant for adults as well as children. A mathematics instructor describes his realization of his mother’s knowledge (Fasheh, 1990:21–22): Math was necessary for my mother in a much more sense than it was for me. Unable to read or write, my mother routinely took rectangles of fabric and, with few measurements and no patterns, cut them and turned them into perfectly fitted clothing for people…I realized that the mathematics she was using was beyond my comprehension. Moreover, although mathematics was a subject matter that I studied and taught, for her it was basic to the operation of her understanding. What she was doing was math in the sense that it embodied order, pattern, relations, and measurement. It was math because she was breaking a whole into smaller parts and constructing a new whole out of most of the pieces, a new whole that had its own style, shape, size, and that had to fit a specific person. Mistakes in her math entailed practical consequences, unlike mistakes in my math. Imagine Fasheh’s mother enrolling in a course on formal mathematics. The structure of many courses would fail to provide the kinds of support that could help her make contact with her rich set of informal knowledge. Would the mother’s learning of formal mathematics be enhanced if it were connected to this knowledge? The literature on learning and transfer suggests that this is an important question to pursue. |
Building on Existing Knowledge
Children’s early mathematics knowledge illustrates the benefits of helping students draw on relevant knowledge that can serve as a source of transfer. By the time children begin school, most have built a considerable knowledge store relevant to arithmetic. They have experiences of adding and subtracting numbers of items in their everyday play, although they lack the symbolic representations of addition and subtraction that are taught in school. If children’s knowledge is tapped and built on as teachers attempt to teach them the formal operations of addition and subtraction, it is likely that children will acquire a more coherent and thorough understanding of these processes than if they taught them as isolated abstractions. Without specific guidance from teachers, students may fail to connect everyday knowledge to subjects taught in school.
Understanding Conceptual Change
Because learning involves transfer from previous experiences, one’s existing knowledge can also make it difficult to learn new information. Sometimes new information will seem incomprehensible to students, but this feeling of confusion can at least let them identify the existence of a problem (see, e.g., Bransford and Johnson, 1972; Dooling and Lachman, 1971). A more problematic situation occurs when people construct a coherent (for them) representation of information while deeply misunderstanding the new information. Under these conditions, the learner doesn’t realize that he or she is failing to understand. Two examples of this phenomenon are in Chapter 1: Fish Is Fish (Lionni, 1970), where the fish listens to the frog’s descriptions of people and constructs its own idiosyncratic images, and attempts to help children learn that the earth is spherical (Vosniadou and Brewer, 1989). Children’s interpretations of the new information are much different than what adults intend.
The Fish Is Fish scenario is relevant to many additional attempts to help students learn new information. For example, when high school or college physics students are asked to identify the forces being exerted on a ball that is thrown vertically up in the air after it leaves the hand, many mention the “force of the hand” (Clement, 1982a, b). This force is exerted only so long as the ball is in contact with the hand, but is not present when the ball is in flight. Students claim that this force diminishes as the ball ascends and is used up by the time the ball reaches the top of its trajectory. As the ball descends, these students claim, it “acquires” increasing amounts of the gravitational force, which results in the ball picking up speed as it falls back down. This “motion requires a force” misconception is quite common among students and is akin to the medieval theory of “impetus” (Hestenes et al., 1992). These explanations fail to take account of the fact that the only forces being exerted on the ball while it is traveling through the air are the gravitational force caused by the earth and the drag force due to air resistance. (For similar examples, see Mestre, 1994.)
In biology, people’s knowledge of human and animal needs for food provides an example of how existing knowledge can make it difficult to understand new information. A study of how plants make food was conducted with students from elementary school through college. It probed understanding of the role of soil and photosynthesis in plant growth and of the primary source of food in green plants (Wandersee, 1983). Although students in the higher grades displayed a better understanding, students from all levels displayed several misconceptions: soil is the plants’ food; plants get their food from the roots and store it in the leaves; and chlorophyll is the plants’ blood. Many of the students in this study, especially those in the higher grades, had already studied photosynthesis. Yet formal instruction had done little to overcome their erroneous prior beliefs. Clearly, presenting a sophisticated explanation in science class, without also probing
for students’ preconceptions on the subject, will leave many students with incorrect understanding (for a review of studies, see Mestre, 1994).
For young children, early concepts in mathematics guide students’ attention and thinking (Gelman, 1967; we discuss this more in Chapter 4). Most children bring to their school mathematics lessons the idea that numbers are grounded in the counting principles (and related rules of addition and subtraction). This knowledge works well during the early years of schooling. However, once students are introduced to rational numbers, their assumptions about mathematics can hurt their abilities to learn.
Consider learning about fractions. The mathematical principles underlying the numberhood of fractions are not consistent with the principles of counting and children’s ideas that numbers are sets of things that are counted and addition involves “putting together” two sets. One cannot count things to generate a fraction. Formally, a fraction is defined as the division of one cardinal number by another: this definition solves the problem that there is a lack of closure of the integers under division. To complicate matters, some number-counting principles do not apply to fractions. Rational numbers do not have unique successors; there is an infinite number of numbers between any two rational numbers. One cannot use counting-based algorithms for sequencing fractions: for example, 1/4 is not more than 1/2. Neither the nonverbal nor the verbal counting principle maps to a tripartite symbolic representations of fractions—two cardinal numbers X and Y separated by a line. Related mapping problems have been noted by others (e.g., Behr et al., 1992; Fishbein et al., 1985; Silver et al., 1993). Overall, early knowledge of numbers has the potential to serve as a barrier to learning about fractions— and for many learners it does.
The fact that learners construct new understandings based on their current knowledge highlights some of the dangers in “teaching by telling.” Lectures and other forms of direct instruction can sometimes be very useful, but only under the right conditions (Schwartz and Bransford, 1998). Often, students construct understandings like those noted above. To counteract these problems, teachers must strive to make students’ thinking visible and find ways to help them reconceptualize faulty conceptions. (Strategies for such teaching are discussed in more detail in Chapters 6 and 7.)
Transfer and Cultural Practices
Prior knowledge is not simply the individual learning that students bring to the classroom, based on their personal and idiosyncratic experiences (e.g., some children will know many things because they have traveled widely or because their parents have particular kinds of jobs; some children may have suffered a traumatic experience). Prior knowledge is also not only a generic set of experiences attributable to developmental stages through which learners may have passed (i.e., believing that heaven is “up” or that milk comes
from refrigerated cartons). Prior knowledge also includes the kind of knowledge that learners acquire because of their social roles, such as those connected with race, class, gender, and their culture and ethnic affiliations (Brice-Heath, 1981, 1983; Lave, 1988; Moll and Whitmore, 1993; Moll et al., 1993–1998; Rogoff, 1990, 1998; Saxe, 1990). This cultural knowledge can sometimes support and sometimes conflict with children’s learning in schools (Greenfield and Suzuki, 1998); see Box 3.9.
School failure may be partly explained by the mismatch between what students have learned in their home cultures and what is required of them in school (see Allen and Boykin, 1992; Au and Jordan, 1981; Boykin and Tom, 1985; Erickson and Mohatt, 1982). Everyday family habits and rituals can either be reinforced or ignored in schools, and they can produce different responses from teachers (Heath, 1983). For example, if young learners are never asked questions at home that seem obvious to some families—such as “What color is the sky?” or “Where is your nose?” —teachers who ask such questions may find students reluctant or resistant to answer. How teachers interpret this reticence or resistance has consequences for how intelligent or academically capable they judge students and their instructional approaches toward them.
|
BOX 3.9 Eating Pie and Learning Fractions Even small differences in cultural knowledge have the potential to affect students’ learning. For example, a primary school teacher is helping students to understand fractional parts by using what she thinks is a commonplace reference. “Today, we’re going to talk about cutting up a Thanksgiving holiday favorite—pumpkin pie.” She continues with an explanation of parts. Well into her discourse, a young African American boy, looking puzzled, asks, “What is pumpkin pie?” (Tate, 1994). Most African Americans are likely to serve sweet potato pie for holiday dinners. In fact, one of the ways that African American parents explain pumpkin pie to their children is to say that it is Something like sweet potato pie. For them, sweet potato pie is the common referent. Even the slight difference of being unfamiliar with pumpkin pie can serve as a source of interference for the student. Rather than be engaged actively in the lesson, he may have been preoccupied with trying to imagine pumpkin pie: What does it taste like? How does it smell? Is its texture chunky like apple or cherry pie? In the mind of a child, all of these questions can become more of the focus than the subject of fractions that the teacher is attempting to teach. |
These differences have their roots in early adult-infant interactions (Blake, 1994). Whereas middle-class Anglo mothers tend to have frequent language interactions that are focused on didactic naming and pointing with their infants around objects (“Look at that red truck!”), African American mothers show comparable frequency levels of language interactions with their infants, but focused on affective dimensions of language (“Isn’t that a pretty toy? Doesn’t it make you feel happy?”). The language that children bring with them to school involves a broad set of skills rooted in the early context of adult-child interactions. What happens when the adults, peers, and contexts change (Suina, 1988; Suina and Smolkin, 1994)? This is an important question that relates to the transfer of learning.
The meanings that are attached to cultural knowledge are important in promoting transfer—that is, in encouraging people to use what they have learned. For example, story-telling is a language skill. Topic-associative oral styles have been observed among African American children (Michaels, 1981a,b; 1986). In contrast, white children use a more linear narrative style that more closely approximates the linear expository style of writing and speaking that schools teach (see Gee, 1989; Taylor and Lee, 1987; Cazden et al., 1985; Lee and Slaughter-Defoe, 1995). Judgments may be made by white and black teachers as they listen to these two language styles: white teachers find the topic-associative stories hard to follow and are much more likely to infer that the narrator is a low-achieving student; black teachers are more likely to positively evaluate the topic-associative style (Cazden, 1988:17). African American children who come to school speaking in a topic-associative style may be seen by many teachers as having less potential for learning. Teachers can be helped to view different cultural backgrounds as strengths to be built on, rather than as signs of “deficits.”
TRANSFER BETWEEN SCHOOL AND EVERYDAY LIFE
We began this chapter by stressing that the ultimate goal of learning is to have access to information for a wide set of purposes—that the learning will in some way transfer to other circumstances. In this sense, then, the ultimate goal of schooling is to help students transfer what they have learned in school to everyday settings of home, community, and workplace. Since transfer between tasks is a function of the similarity by transfer tasks and learning experiences, an important strategy for enhancing transfer from schools to other settings may be to better understand the nonschool environments in which students must function. Since these environments change rapidly, it is also important to explore ways to help students develop the characteristics of adaptive expertise (see Chapter 1).
The question of how people function in a number of practical settings has been examined by many scientists, including cognitive anthropologists,
sociologists, and psychologists (e.g., Lave, 1988; Rogoff, 1990). One major contrast between everyday settings and school environments is that the latter place much more emphasis on individual work than most other environments (Resnick, 1987). A study of navigation on U.S. ships found that no individual can pilot the ship alone; people must work collaboratively and share their expertise. More recent studies of collaboration confirm its importance. For example, many scientific discoveries in several genetics laboratories involve in-depth collaboration (Dunbar, 1996). Similarly, decision making in hospital emergency rooms is distributed among many different members of the medical team (Patel et al., 1996).
A second major contrast between schools and everyday settings is the heavy use of tools to solve problems in everyday settings, compared with “mental work” in school settings (Resnick, 1987). The use of tools in practical environments helps people work almost error free (e.g., Cohen, 1983; Schliemann and Acioly, 1989; Simon, 1972; see also Norman, 1993). New technologies make it possible for students in schools to use tools very much like those used by professionals in workplaces (see Chapter 8). Proficiency with relevant tools may provide a way to enhance transfer across domains.
A third contrast between schools and everyday environments is that abstract reasoning is often emphasized in school, whereas contextualized reasoning is often used in everyday settings (Resnick, 1987). Reasoning can be improved when abstract logical arguments are embodied in concrete contexts (see Wason and Johnson-Laird, 1972). A well-known study of people in a Weight Watchers program provides similar insights into everyday problem solving (see Lave et al., 1984). One example is of a man who needed three-fourths of two-thirds of a cup of cottage cheese to create a dish he was cooking. He did not attempt to multiply the fractions as students would do in a school context. Instead, he measured two-thirds of a cup of cottage cheese, removed that amount from the measuring cup and then patted the cheese into a round shape, divided it into quarters, and used three of the quarters; see Box 3.10. Abstract arithmetic was never used. In similar examples of contextualized reasoning, dairy workers use knowledge, such as the size of milk cases, to make their computational work more efficient (Scribner, 1984); grocery store shoppers use nonschool mathematics under standard supermarket and simulated conditions (Lave, 1988); see Box 3.11.
There are potential problems with contextualized reasoning, which are similar to those associated with overly contextualized knowledge in general. The “pat it out” strategy used for cottage cheese works in only a narrow range of situations; the man would have difficulty if he were trying to measure molasses or other liquids rather than cottage cheese (Wineburg, 1989a, b; see also Bereiter, 1997). Could he generate a new strategy for molasses or other liquids? The answer to this question depends on the degree to which he can relate his procedure to more general sets of solution strategies.
|
BOX 3.10 The Cottage Cheese Problem
School Mathematics Strategy
Invented Strategy
|
|
BOX 3.11 Three Solutions to the Best-Buy Problem
|
|||||||||||||||||||||||||||||||
Analyses of everyday environments have potential implications for education that are intriguing but need to be thought through and researched carefully. There are many appealing strengths to the idea that learning should be organized around authentic problems and projects that are frequently encountered in nonschool settings: in John Dewey’s vision, “School should be less about preparation for life and more like life itself.” The use of problem-based learning in medical schools is an excellent example of the benefits of looking at what people need to do once they graduate and then crafting educational experiences that best prepare them for these competencies (Barrows, 1985). Opportunities to engage in problem-based learning during the first year of medical school lead to a greater ability to diagnose and understand medical problems than do opportunities to learn in typical lecture-based medical courses (Hmelo, 1995). Attempts to make schooling more relevant to the subsequent workplace have also guided the use of case-based learning in business schools, law schools, and schools that teach educational leadership (Hallinger et al, 1993; Williams, 1992).
The transfer literature also highlights some of the potential limitations of learning in particular contexts. Simply learning to perform procedures, and learning in only a single context, does not promote flexible transfer. The transfer literature suggests that the most effective transfer may come from a balance of specific examples and general principles, not from either one alone.
SUMMARY AND CONCLUSION
A major goal of schooling is to prepare students for flexible adaptation to new problems and settings. The ability of students to transfer provides an important index of learning that can help teachers evaluate and improve their instruction. Many approaches to instruction look equivalent when the only measure of learning is memory for information that was specifically presented. Instructional differences become more apparent when evaluated from the perspective of how well the learning transfers to new problems and settings.
Several critical features of learning affect people’s abilities to transfer what they have learned. The amount and kind of initial learning is a key determinant of the development of expertise and the ability to transfer knowledge. Students are motivated to spend the time needed to learn complex subjects and to solve problems that they find interesting. Opportunities to use knowledge to create products and benefits for others are particularly motivating for students.
While time on task is necessary for learning, it is not sufficient for effective learning. Time spent learning for understanding has different consequences for transfer than time spent simply memorizing facts or procedures
from textbooks or lectures. In order for learners to gain insight into their learning and their understanding, frequent feedback is critical: students need to monitor their learning and actively evaluate their strategies and their current levels of understanding.
The context in which one learns is also important for promoting transfer. Knowledge that is taught in only a single context is less likely to support flexible transfer than knowledge that is taught in multiple contexts. With multiple contexts, students are more likely to abstract the relevant features of concepts and develop a more flexible representation of knowledge. The use of well-chosen contrasting cases can help students learn the conditions under which new knowledge is applicable. Abstract representations of problems can also facilitate transfer. Transfer between tasks is related to the degree to which they share common elements, although the concept of elements must be defined cognitively. In assessing learning, the key is increased speed of learning the concepts underlying the new material, rather than early performance attempts in a new subject domain.
All new learning involves transfer. Previous knowledge can help or hinder the understanding of new information. For example, knowledge of everyday counting-based arithmetic can make it difficult to deal with rational numbers; assumptions based on everyday physical experiences (e.g., walking upright on a seemingly flat earth) can make it difficult for learners to understand concepts in astronomy and physics and so forth. Teachers can help students change their original conceptions by helping students make their thinking visible so that misconceptions can be corrected and so that students can be encouraged to think beyond the specific problem or to think about variations on the problem. One aspect of previous knowledge that is extremely important for understanding learning is cultural practices that support learners’ prior knowledge. Effective teaching supports positive transfer by actively identifying the relevant knowledge and strengths that students bring to a learning situation and building on them.
Transfer from school to everyday environments is the ultimate purpose of school-based learning. An analysis of everyday environments provides opportunities to rethink school practices in order to bring them into alignment with the requirements of everyday environments. But it is important to avoid instruction that is overly dependent on context. Helping learners choose, adapt, and invent tools for solving problems is one way to facilitate transfer while also encouraging flexibility.
Finally, a metacognative approach to teaching can increase transfer by helping students learn about themselves as learners in the context of acquiring content knowledge. One characteristic of experts is an ability to monitor and regulate their own understanding in ways that allows them to keep learning adaptive expertise: this is an important model for students to emulate.