CHAPTER 5
PRESENTATION OF UNCERTAINTY AND USE OF FORECASTS WITH EXPLICIT UNCERTAINTY
All models are wrong; some models are useful.
George Box
Any forecasting effort should communicate two things: the usefulness of the model and its limitations. How to present uncertainty is essentially a question of how to present the limitations of a model. A forecast must depend on assumptions about the future values of variables that drive the model. How certain are we about those assumptions? For short-range forecasts, we may be quite certain that the expected values of the variables will materialize. As we peer further into the future, such certainty declines. Thus, short-term and long-term forecasts have very different properties, very different uses, and very different levels of uncertainty. A short-term forecast, a one-or two-year forecast using annual data, can do a good job of forecasting point estimates, such as the expected number of engineering graduates in the year 2000. These future graduates are already sitting in classrooms and rates of attrition are relatively constant over time.
Increasing the span—the level of aggregation over occupations—typically increases forecast accuracy because random errors and movements between the occupations in the aggregate are averaged out. However, this may not be the case if increasing span increases heterogeneity, and the forecasting model is not successful in representing the effects of this heterogeneity.
Nancy Kirkendall of the Office of Management and Budget discussed different approaches to presenting the uncer-
tainty of forecasts that are used in the federal government. Different measures of error are appropriate to forecasts with different time frames. For short-term models, the uncertainty of point estimates can be measured by the mean squared error, in which forecasted values are compared with actual observations. Other measures of uncertainty include the confidence interval and mean absolute percentage error. These simple methods do a good job of representing uncertainty. Some forecast competitions have shown that these are the best methods to measure uncertainty for short-term forecasts.
Longer-term forecasts are more complex than short-term forecasts and are more vulnerable to unanticipated changes in the economic environment. Forecasts made for a longer time span are typically less accurate than those made for a shorter span.1 Although the mean squared error may be computed for long-term forecasts, it may not be a good measure of the model's usefulness. The Bureau of Labor Statistics (BLS) routinely assesses the accuracy of its forecasts. The example below shows the systematic reduction in the forecast's percent error as the time span of the forecast decreases. It is possible to take these errors and attribute them to factors unknown at the time of the forecast, such as immigration rates.
|
1 |
There may be exceptions to the relative accuracy of long- and short-term forecasts due to the volatility in conditioning variables. For example, annual rainfall may be forecasted with better percentage accuracy than rainfall on any particular day because short-run volatility tends to average our over the long run. |
The Energy Information Administration (EIA) publishes a short-term forecasting system that projects energy prices for one to two years. The EIA computes the mean squared errors for these different forecasts and uses the information to fine-tune its models. However, for long-term forecasts they do not publish the error terms. Because the accuracy of the forecasts would not be very good, long-term forecasts should not be used to produce point estimates. Long-term forecasting models are useful for other purposes. The examples that follow demonstrate some of these uses.
Scenario analyses are useful in illustrating the variability and uncertainty of long-term forecasts. An example is the case of natural gas forecasting. Figure 5-1 shows the historical trend in natural gas wellhead prices and forecasts future prices with a reference case and two additional scenarios. The scenarios reflect changes that might happen in the forecast depending on the assumptions made on how rapidly new technology penetrates the
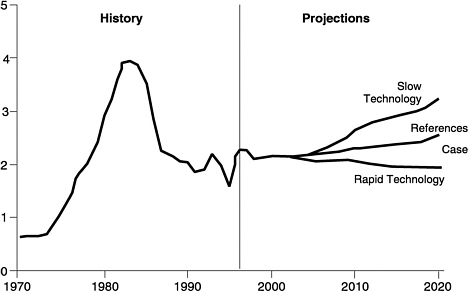
FIGURE 5-1 Natural gas wellhead prices in three cases, 1970–2020 (1996 dollars per thousand cubic feet).
market. The scenarios include high economic growth (2.5 percent annually) and low economic growth (1.3 percent annually). The reference case posits 1.7 percent growth per year. Scenario analysis can be quite instructive if past data are highly variable. Past variability communicates to the user that the assumption of smooth patterns of change is unwarranted but that volatility may not be predictable. Sometimes scenarios are constructed from statistical confidence bounds on model inputs or parameters, such as confidence limits on the future economic growth rate. Users can be misled, however, if they interpret the resulting scenarios as confidence bounds, as neither future paths nor forecasts at particular dates need be contained between “high” and “low” scenarios with any degree of confidence. This is particularly an issue when the
“high” and “low” scenarios are a concatenation of events that are not necessarily independent of one another. Finally, the scenarios can illustrate a range of outcomes under the assumption that there are no large shocks.
Providing a model in which users can adjust inputs is another way to help users understand the effects of uncertainty in forecasts. For example, in 1997 the EIA made a series of assumptions in its forecasts of the price of electricity. The Annual Energy Outlook 1997 addressed electricity restructuring by incorporating the Federal Energy Regulatory Commission actions on open access, lower costs for natural gas-fired generation plants, and early retirements of higher-cost fossil plants. The Annual Energy Outlook 1998 makes additional assumptions about competitive pricing and restructuring, including:
-
Lower operation and maintenance costs.
-
Lower capital costs and improved efficiency for coal-and gas-fired plants.
-
Lower general and administrative costs.
-
Early retirement of high-cost nuclear plants.
-
Capital recovery period will be reduced from 30 to 20 years.
-
California, New York, and New England will begin competitive pricing in 1998 with stranded cost recovery phased out by 2008.
As illustrated in Figure 5-2, because of the additions to and changes in model assumptions and lower projected coal prices, average forecasted electricity prices for 2015 are 13 percent lower than were forecasted in 1997.
There are four fundamental sources of uncertainty in the forecasts made for the availability of scientists and engineers. The first may be identified as exogenous variables, factors that are outside the labor market for scientists and engineers but never-

FIGURE 5-2 Electricity prices, AEO98 vs. AEO97, 1970–2020 (1996 cents per kilowatt-hour).
theless affect it. These include economic growth both in the United States and elsewhere in the world, technology growth, defense needs, wars, and the demographics of scientists and engineers. We are reasonably good at describing the overall demographics of the population, but scientists and engineers are a special group that is affected by things that we are not good at predicting, such as labor force participation and immigration. The demographics of scientists and engineers may also be affected by the changing ethnic and gender composition of the work force. To date, white and Asian American males have been far more likely to go into careers in science and engineering than members of other groups, which make up an increasing share of the student population. Finally, we need to be concerned about the number of people who have sufficient preparation in mathematics to enter the scientific and engineering fields.
A second source of uncertainty stems from factors that are subject to policy control but that do not necessarily accord with the interests of optimizing the labor market for scientists and engineers. For example, to some extent, we know that immigration policy incorporates concerns about the market for scientists and engineers. However, immigration policy is also directed toward a number of other objectives. Moreover, government subsidies may also affect the market for scientists and engineers. In addition to the funding for research and education provided by NSF and NIH, spending on defense contracts, defense-related research, and funding of medical schools through the Medicare program must be considered. While these variables are somewhat subject to policy control, they are directed toward goals other than ensuring that the market for scientists and engineers remains stable or grows at some desired rate.
The third source of uncertainty is behavioral uncertainty, which comes from our inability to predict perfectly how people will respond to the market. These areas of uncertainty include attitudes of college students toward science, plans of the scientists or engineers for shifting from scientific work to other tasks such as administration, and attitudes toward retirement.
The fourth source of uncertainty is the most serious and the hardest to convey to forecast users—what economists call parameter uncertainty (also called systematic errors), or uncertainty in the estimated model itself. This uncertainty relates to both our inability to capture all the nuances of the real world in our models (parameter uncertainty) and limits our ability to calibrate our models perfectly with limited data (model uncertainty). We would like to believe that we could build a structural model that really incorporates all of the behavioral decisions that people make when they choose to enter science or engineering. In fact, we have neither the data nor the behavioral laws to permit the construction of such a model. Our models are not true structural models, and their parameters change as adjustment occurs at neglected margins.
For example, in recent years when the wages for scientists, engineers, or other technically trained people rose, employers divided jobs into components. Some of these components did not require a highly trained analytical person and could be given to people who had lesser or more simpler technical training. Variation in the skill requirements needed to achieve a particular kind of production is not typically incorporated in the models we build. In addition, it is difficult to measure the potential of using technology to make one person able to do a job previously done by two people. These measures of quality and substitution are very difficult to quantify.
Forecasts should be designed for a specific objective. We recognize that the labor market for scientists and engineers is not a classic spot market in which workers offer their labor in response to a wage offer by employers and higher wage offers immediately bring forth a supply of additional workers. Were it so, the demand for labor by government and industry would be quickly met by a supply of scientists and engineers and the market would clear easily. In actuality, the NSF, NIH, and others who really need these forecasts the most are making long-term decisions. They are trying to decide how many graduate fellowships and traineeships to provide in order to create opportunities for people who years later may become scientists and engineers.
Targeting quantity with sufficient lead time for consumers of these forecasts is very difficult. However, it is less difficult to assess whether the wages of scientists and engineers are similar to those of other personnel with comparable aptitude (based on SATs and ACTs) who take jobs where there is some substitution with science and engineering. It is not difficult to know whether the salaries of scientists have stayed constant while the salaries of other groups with similar years of training (for example, lawyers) have risen (see Figure 5-3).
We should also examine possible sources of short-run adjustment. Institutions could make the market for scientists and engineers more like a spot market. These actions include:
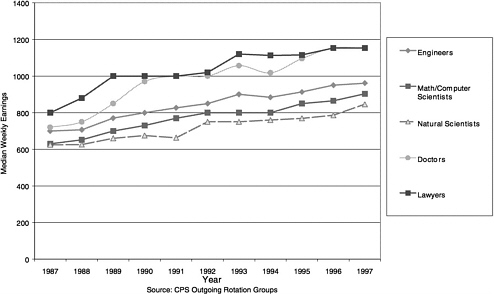
FIGURE 5-3 Median weekly earnings for selected occupations by year.
(1) development of more flexible programs for the use of “temporary” immigrant scientists and engineers; (2) development of more stable and humane versions of the postdoctoral pool that would make these individuals more productive in research and prepare them to move in and out of employment in specific specializations depending on market conditions; and (3) institutional ceilings on enrollments that are responsive to short-term market forecasts. Usually this final measure is destabilizing, since institutions have difficulty expanding or contracting faculty size in the short term.
A distinction should be made between the instruments of policy control (e.g., enrollment quotas) and the targets of policy control, e.g., the number of research personnel. While the former are subject to rapid change, the latter are not likely to be characterized by volatility or disruptions that have extreme private or social
costs. One not only needs to understand how policy affects behavior, but also to project how short-term behavioral adjustments translate into long-term market conditions.
Forecasters need ways to reassure the users of their forecasts that what they are doing is acceptable, correct, and scientific. They need to describe forecasts more clearly and to describe how they should and should not be used. Finally, forecasters should document exactly what they do. Even with very clear documentation, some skeptics will assume that the forecasters have fiddled with the numbers.
A concomitant issue develops from users of forecasts for scientists and engineers. Some users may ignore uncertainty and convert an estimate that is presented as uncertain into a point estimate (Kahneman et al., 1982). Moreover, they may subjectively or unconsciously amplify the probability of rare events. Finally, they may tend to overemphasize losses as opposed to gains. These behaviors may explain why forecasts are often considered by users to be more certain than forecasters intended and why forecasts of a shortage or glut of scientists and engineers receive far more public attention than justified by their estimated probabilities.
The confusion of users about how to use forecasts argues for conducting research to determine the best ways to present forecasts. Several statistical agencies have started cognitive laboratories that evaluate questionnaires. They examine the wording of questions to find out whether people understand what they are being asked and whether they give accurate answers. This helps agencies to fine-tune the questions and tailor the responses to address agency goals. Perhaps the forecasting community could conduct cognitive studies on how best to present a forecast's usefulness and accuracy. Research of this type could provide good scientific information about what does and does not work in terms of presenting forecasts.
In summary, to present uncertainty in ways that will not mystify users, several steps should be taken:
-
First, the user should know if the forecast is conditional or unconditional —whether the forecaster is assuming that the future values of the explanatory variables are known with certainty (unconditional) or whether these values are uncertain, so that the forecast is conditional on whether these values materialize.2
-
Second, the forecaster needs to consider exactly what the model is expected to accomplish. Is the forecast short term or long term? If the model is short-term, supply is constrained by what is already in the pipeline and demand is substantially constrained by commitments to budgets and research programs. Long-term market forecasts are made for time periods where there are substantial problems in forecasting “fundamentals,” such as choice of college major and national research priorities and funding. With long-term forecasts the focus should not be on actual forecast accuracy—although accuracy within some limits is desirable.
-
Third, forecasting needs to be a continuous, dynamic process in which past performance is tracked, and the forecasters learn from their past mistakes.
-
Fourth, the forecaster must decide on the objectives of the forecast. Should the forecaster conduct a scenario analysis? To what factors should the forecast be sensitive?
-
Fifth, the forecaster must ensure that the required data are available.
-
Sixth, once committed to the forecast, the forecaster must quantitatively evaluate the model against the objective function in order to assess the model's accuracy. If the model is inaccurate, it should be respecified.
|
2 |
An example of an almost unconditional forecast is the number of 18-21 year olds six years from now, since we are almost certain about age-specific rates of mortality and we know how many 12-15 year olds there are now. A forecast of college enrollment for 18-21 year olds, however, is likely to be conditional, since it depends on rates of high school completion and college participation that are uncertain and may depend on variables outside the pure demographic model, e.g., job prospects for high school graduates and availability of financial aid. |
-
Seventh, the data and the methodology for the model must be well documented. The documentation needs to be widely available and readable, and all the test results should be made available to all users.
-
Eighth, cognitive studies should be used to provide input on how best to present the forecasts and the information. Employ policymakers and staff to participate in a cognitive study to help refine information and forecast presentation.
-
Finally, forecasters need to conduct research into methods of displaying uncertainty of forecasts. The goal is to discover the most convincing ways to display forecast results so the audience understands that forecasting models are a useful tool in the policy formation process, but have limitations in accuracy that affect how they should be interpreted and used.












