This paper was presented at a colloquium entitled “Vision: From Photon to Perception,” organized by John Dowling, Lubert Stryer (chair), and Torsten Wiesel, held May 20–22, 1995, at the National Academy of Sciences in Irvine, CA.
Computational models of cortical visual processing
(vision/neurons/cerebral cortex)
DAVID J. HEEGER*, EERO P. SIMONCELLI†, AND J. ANTHONY MOVSHON‡§
|
* Department of Psychology, Stanford University, Stanford, CA 94305; |
|
† Department of Computer and Information Science, University of Pennsylvania, Philadelphia, PA 19104; and |
|
‡Howard Hughes Medical Institute and Center for Neural Science, New York University, New York, NY 10003 |
ABSTRACT The visual responses of neurons in the cerebral cortex were first adequately characterized in the 1960s by D. H. Hubel and T. N. Wiesel [(1962) J. Physiol. (London) 160, 106–154; (1968) J. Physiol. (London) 195, 215–243] using qualitative analyses based on simple geometric visual targets. Over the past 30 years, it has become common to consider the properties of these neurons by attempting to make formal descriptions of the transformations they execute on the visual image. Most such models have their roots in linear-systems approaches pioneered in the retina by C. Enroth-Cugell and J. R. Robson [(1966) J. Physiol. (London) 187, 517–552], but it is clear that purely linear models of cortical neurons are inadequate. We present two related models: one designed to account for the responses of simple cells in primary visual cortex (V1) and one designed to account for the responses of pattern direction selective cells in MT (or V5), an extrastriate visual area thought to be involved in the analysis of visual motion. These models share a common structure that operates in the same way on different kinds of input, and instantiate the widely held view that computational strategies are similar throughout the cerebral cortex. Implementations of these models for Macintosh microcomputers are available and can be used to explore the models ' properties.
The ultimate goal of our research is to develop detailed, quantitative models of neuronal function in visual cortex. We consider a model to be successful if it captures the behavior of the target neurons with a tractable number of measurable parameters. With such a model, we can hope to understand the neural basis of perceptual experience and perceptually driven behavior, as far as these depend on the activity of the neurons being modeled.
Simple cells in V1 of cats and monkeys respond in a selective way to variations in stimulus position, orientation, size, and direction of motion (1,2). Based on the early success of linear-systems analysis in retina (3,4), there is an established tradition of modeling simple cells as linear neurons (5–9). The response of a linear visual neuron is a weighted sum, over local space and recently past time, of the distribution of light intensity values in the stimulus. According to the linear model, orientation and other spatial selectivities arise from variations in the degree to which particular stimuli match the shape and location of excitatory (positively weighted) and inhibitory (negatively weighted) subregions of the receptive field. Direction selectivity arises similarly from differences in the time course of responses evoked from different parts of the cell's receptive field. The linear model of simple cells is attractive because, if successful, it allows us to predict the responses of a simple cell to any visual stimulus, based on a limited number of measurements. For example, any visual image can be approximated by summing light intensity in a number of small regions (“pixels”). For a linear neuron, the response would be given by summing the independent responses elicited by each pixel, and thus measuring the neuron' s response to each pixel would enable one to predict the response to any visual image.
There are a number of problems with the linear model of simple cells. One relatively simple issue is that neural responses (firing rates) are positive, whereas idealized linear cells can have positive or negative responses. The typical interpretation of the linear model is that the positive and negative values are encoded by two cells: one responsible for the positive part, and the other one responsible for the negative part. The response of each cell is halfwave-rectified so that only one of the two cells has a non-zero response at any given time. A more complicated set of departures from linearity becomes evident when the model is tested in detail. To explain these, we and others have recently proposed a model of simple cell responses called the “normalization model” (10–15).
Almost all neurons in MT (or V5), an extrastriate area of the monkey 's visual cortex, are selective for the direction of movement. MT receives a strong input from V1, which arises from directionally selective neurons (16). MT contains two types of directionally selective neurons: component directionselective neurons and pattern direction-selective neurons (17,18). Component direction-selective neurons respond like directionally selective neurons in V1, signaling the movement of individual oriented components of complex moving patterns. Pattern direction-selective neurons, on the other hand, combine information across multiple orientations to signal unambiguously the motion of whole patterns. Both types of neuron have nonlinear spatial summation and have response properties that differ in a variety of ways from their inputs in V1 (19). Nonetheless, a model whose architecture is identical to the normalization model for V1 simple cells can explain the transformation of signals from directionally selective V1 cells into those of pattern direction-selective cells in MT.
Models of V1 and MT Neurons
Our current models describe two concatenated stages corresponding broadly to cortical areas V1 and MT. The models attempt to capture the behavior of cells like V1 simple cells and like pattern direction-selective cells in MT but include ideas that can be useful in understanding other cell types. As indicated in Fig. 1, the computation is very similar in each model. A model neuron computes a linear combination of its inputs, followed by rectification and normalization (in which each neuron's response is divided by a quantity proportional to the pooled activity of a group of neurons presumed to be its
The publication costs of this article were defrayed in part by page charge payment. This article must therfore be hereby marked “advertisement” in accordance with 18 U.S.C. §1734 solely to indicate this fact.
|
§ To whom reprint requests should be addressed at: Center for Neural Science, New York University, 4 Washington Place, Room 809, New York, NY 10003. |
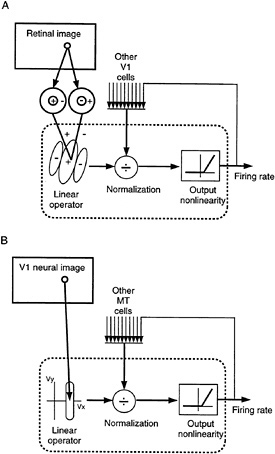
FIG. 1. Illustrations of the two models. In each, a model neuron computes a linear combination of its inputs, followed by rectification and normalization (see text). (A) V1 model. The linear weighting of each V1 neuron is designed so that it responds selectively to intensity patterns of a particular orientation and direction of motion. The linear stage combines complementary inputs from the lateral geniculate nucleus. The central excitatory subregion of the receptive field sums responses of ON-center cells and subtracts responses of OFF-center cells with spatially superimposed receptive fields. The flanking inhibitory subregions are obtained by the opposite arrangement of excitation and inhibition. (B) MT model. The linear weighting function of each MT neuron is designed so that it responds selectively to a particular image velocity (i.e., speed and direction). Each of the V1 afferents is selective for a different direction of component motion, but all of these component motions are consistent with the same overall pattern motion.
near neighbors in the cortex). The behavior of the model neurons at each stage is determined by the properties of the input neurons and the way these are weighted by the initial linear combination.
A model V1 neuron sums image intensities over a local spatial region and recently past time. The linear weighting of these neurons is designed so that they respond selectively to a particular image velocity (i.e., speed and direction).
In this paper we do not attempt to make the models of V1 and MT responses biologically realistic; they are presented as mathematical abstractions, whose goal is to describe informational transformations rather than the details of the neuronal mechanisms that perform those transformations. The models can, however, be implemented with biologically reasonable mechanisms (15). Complete mathematical details are provided elsewhere (refs.12–15; E.P.S. and D.J.H., unpublished data).
Examples of the Behavior of the Model of V1 Responses. Many aspects of simple cell responses are consistent with the linear model. However, there also are important violations of linearity. One major fault with the linear model is the fact that simple cell responses saturate (level off) at high contrasts, as in Fig. 2A (20,21). The responses of a truly linear neuron would increase in proportion to stimulus contrast over the entire range of contrasts.
A second fault with the linear model is revealed by testing linear superposition. A typical simple cell responds vigorously to stimuli at the preferred orientation and direction of motion (e.g., a vertical grating moving rightward), but not at all to the perpendicular orientation/direction (e.g., a horizontal grating moving upward). Superposition is tested by displaying both stimuli at once, the upward moving grating superimposed on the rightward moving grating. According to the linear model, the response to the superimposed pair of stimuli (preferred plus perpendicular) should equal the response to the preferred stimulus presented alone (since there is no response to the upward grating alone). Surprisingly, this prediction is wrong; the response to the superimposed pair of gratings is typically about half the response to the rightward grating alone. This phenomenon is known as cross-orientation inhibition, and is an example of a variety of phenomena that can collectively be described as “nonspecific suppression.” Fig. 2C shows that adding a “masking” grating of a different orientation reduces the response elicited by an optimal grating presented alone (horizontal line) (22). The reduction in response is maximal for near-orthogonal stimuli but is evident for stimuli of other orientations.
It is the normalization stage of the normalization model that allows it to account for these data. Each neuron's linear response to the stimulus is divided by a quantity proportional to the pooled activity of a number of other neurons from the nearby cortical “neighborhood. ” Activity in this large pool of neurons partially suppresses the response of each individual neuron. Normalization is a nonlinear operation: one input (a neuron's underlying linear response) is divided by another input (the pooled activity of a large number of neurons). The effect of this divisive suppression is that the response of each neuron is normalized (rescaled) with respect to stimulus contrast. The normalization model exhibits amplitude saturation (Fig. 2B) because the divisive suppression increases with stimulus contrast. The model exhibits nonspecific suppression (Fig. 2D) because the normalization signal is pooled over many other neurons with a wide variety of tuning properties, including many that respond to orthogonal gratings.
Examples of the Behavior of the Model of MT Responses. Because of the structure of the linear portion of their receptive fields, V1 neurons can only signal the component of motion that is perpendicular to their preferred orientation. When stimulated with a complex stimulus containing multiple orientation components, a V1 neuron responds vigorously when any one of the oriented components is aligned with the neuron's preferred orientation (17,23). Fig. 3A and B show polar plots of direction tuning for V1 neurons using two stimuli: (i) drifting sinusoidal gratings and (ii) drifting plaid patterns composed of two gratings. For both real neurons and model neurons there is a unimodal response, a single preferred direction, for drifting grating stimuli. The direction tuning curves for plaids, however, are very different, with two distinct lobes. Each lobe is due to responses elicited by one of the plaid 's component gratings. The normalization model of V1 cells correctly predicts this behavior (Fig. 3 C and D).
A recombination of motion signals is required to compute and represent stimulus velocity independently of the stimulus' spatial pattern. This second stage appears to exist in area MT. For some MT neurons, the direction tuning curves are uni-
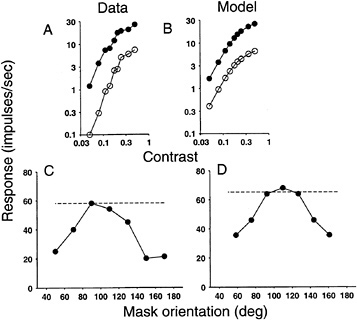
FIG. 2. (A and B) Response saturation in a real V1 neuron: data replotted from Tolhurst and Dean (21) and a model V1 neuron. Response (firing rate) of a simple cell as a function of stimulus contrast for drifting sine-grating (periodic dark and light bar) stimuli. There are three critical results. ( i) The cells are direction selective, meaning that they respond more vigorously to stimuli moving in a preferred direction (closed symbols) but less well to stimuli moving in the opposite direction (open symbols). (ii) The responses saturate for high contrast. (iii) The curves shift downward (on the logarithmic scale) for motion in the opposite direction. In other words, direction selectivity (defined here as the ratio of the responses produced by the two different stimuli) is largely invariant with respect to stimulus contrast, in spite of saturation. This invariance is critical for encoding information about motion independent of contrast. Direction and orientation selectivity in the model are due to the underlying linear summation of stimulus intensities. Response saturation and the downward shift are both due to normalization. (C and D) Cross-orientation suppression in a real V1 neuron: data replotted from Bonds (22) and a model V1 neuron. Dashed horizontal lines are response to single gratings at the preferred orientation. The solid curves are responses to a pair of superimposed gratings, a base grating of optimal orientation superimposed on a second (mask) grating of variable orientation. Responses were suppressed for nonpreferred orientations of the second (mask) grating, due to normalization.
modal for both grating and plaid stimuli (17, 18). An example is shown in Fig. 3E and F. This MT neuron responded to the motion of the entire plaid pattern, not to tahe motions of the component gratings. Fig. 3G and H show that the normalization model of MT cells predicts this behavior. Pattern direction selectivity arises in the model because each MT neuron sums inputs from several V1 afferents. Each of the V1 afferents is selective for a different direction of component motion, but their component motions are all consistent with the same overall pattern motion. The preferred velocity of a model MT neuron depends on which V1 afferents are combined and on the linear weighting function used to sum their responses.
This mechanism for velocity selectivity may be viewed as a neural implementation of the “intersection-of-constraints” scheme proposed by Adelson and Movshon (24) and is related to a number of other proposed models of MT function (17,25–35).
Fig. 4 shows some further comparisons between real and model MT neurons. For the data shown in Fig. 4A, the stimuli were stochastic dot patterns consisting of a coherently moving field of dots superimposed upon a background of randomly moving dots (36). The percentage of randomly versus coherently moving dots was systematically varied to alter the strength of the unidirectional motion signal, in close analogy to varying contrast while recording from V1 neurons (see Fig. 2A). For MT neurons, response rises nearly linearly with stimulus coherence for motion in the preferred direction, and response falls nearly linearly with stimulus coherence for motion in the opposite direction. This behavior is well captured by the normalization model of MT ( Fig. 4B).
The decrease in response for motion stimuli in the “null” direction represents a suppression of MT responses by “inappropriate” motions. Fig. 4C shows this suppression in another way, analogous to the V1 cross-orientation results shown in Fig. 2C The dashed horizontal line is the response to a single dot field moving in the preferred direction. A second dot field was superimposed upon the first and the direction of motion of the added dots was varied. The solid curves show that responses were suppressed by the presence of the added field of dots, especially for nonoptimal directions (37). Fig. 4D shows that the model also accounts for this kind of suppression, which results from the normalization stages in both the V1 and MT components of the model.
Our model differs from earlier MT models in three important ways. (i) These and other simulation results demonstrate that the model accounts for a wide variety of physiological data. (ii) Unlike some of the previous models, the model is sufficiently elaborated that model responses can be computed for any visual stimulus (any spatiotemporal distribution of image intensities). (iii) The model prescribes a precise relationship (derived mathematically) between the response properties of a population of V1 and MT neurons. This theoretical relationship allows for a complete and unbiased representation of velocity while using a minimal number of neurons. The point here is not that the brain literally uses the minimum possible number of neurons; it simply guarantees that a complete/ intact representation of velocity can be computed with a finite
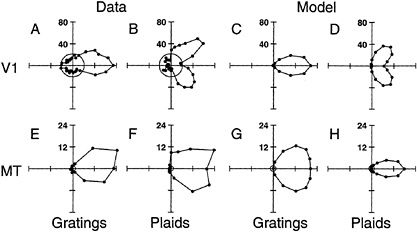
FIG. 3. Component direction selectivity and pattern direction selectivity. (A–D) Direction tuning curves of a real V1 neuron: (A and B) data replotted from Movshon et al. (17); (C and D) a model V1 neuron. Stimuli were drifting gratings and plaid patterns composed of two gratings. Response is plotted radially and the direction of stimulus motion is indicated by the angular coordinate. Circles near the origin indicate the spontaneous firing rate. The direction tuning for plaids is bimodal, indicating that these neurons responded separately to the motions of the two component gratings. (E and H) Direction tuning curves for a real MT neuron: (E and F) data replotted from Movshon et al. (17); (G and H) a model MT neuron. The direction tuning curves for plaids are unimodal, indicating that these neurons responded to the combined motion of entire plaid pattern, not to the motions of the component gratings. Pattern selectivity arises in the model because each model MT neuron sums inputs from several V1 afferents; each V1 afferent is selective for a different component motion, but all of these component motions are consistent with the same pattern motion.
number of neurons. In addition, knowing this theoretical minimal number allows us to perform the model simulations efficiently and accurately.
Role of Models in Visual Neuroscience
Models of the kind described in this paper are of great value for uncovering the organizational principles that determine the responses of visual cortical neurons. By incorporating our knowledge of these neurons' response properties into a formal computational structure, we greatly enhance our ability to test our understanding of the fundamental operations performed by cortical circuits. In this our approach differs sharply from those who seek to understand cortical computation by attempting to simulate the biology of the neurons (e.g., refs.38–41). Rather than trying to sort out a coherent neuronal model from the wealth of anatomical, physiological, and biophysical data available, we attempt to deduce the function of cortical circuits by analysis and simulation of the signals carried, and transformed, by cortical neurons. There is value, of course, in both approaches. Those whose models are founded on accurate models of neurons and circuits are inherently more likely to come close to biological accuracy. On the other hand, we know so little about the detailed function of most elements of the circuitry of neocortex that biologically based models must inevitably be built upon many uncertainties. To model neocortex on the basis of signal transformations is also difficult, since it is presumptuous to assume that all of the data necessary to create a sound model are available and sufficiently accurate. Nonetheless, the richness of our understanding of visual processing is considerable and provides a strong foundation for models of the kind we have described. The usefulness of these models does not depend crucially on the accuracy of a particular proposal (e.g., ref.15) for how they might be implemented biologically. Rather, the identification of several well-defined functional elements in the models encourages physiological experimentation designed to uncover the neuronal mechanisms involved.
An attractive feature of these two models is their commonality of structure. It is often noted that the computational architecture of the cerebral cortex is very much the same from one neocortical area to another: the types, arrangements, and connections of cortical neurons are highly stereotyped. Yet in recent years it has become clear that there is great heteroge-
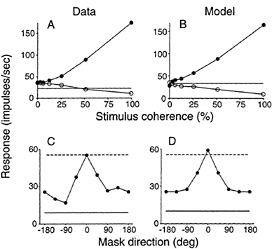
FIG. 4. (A and B) MT response as a function of motion signal strength for a real MT neuron: data replotted from Britten et al. (36) and a model MT neuron. Stimuli were stochastic dot patterns consisting of a coherently moving field of dots superimposed with randomly moving dots. Horizontal lines show the spontaneous firing rate. Responses increase nearly linearly for motion in the preferred direction (closed symbols) as a function of motion signal strength (percentage of coherently moving dots). Responses decrease nearly linearly for motion in the opposite (nonpreferred) direction (open symbols). (C and D) Suppression in MT responses for a real MT neuron: data replotted from Snowden et al. (37) and a model MT neuron. Solid horizontal lines are the spontaneous firing rate in the absence of a dot stimulus. Dashed horizontal lines are responses to a single dot field moving in the preferred direction. The solid curves are responses to a pair of superimposed drifting dot fields, one field drifting in the preferred direction superimposed on a second (mask) field of variable direction. Responses were suppressed when the second (mask) dot field moved in nonpreferred directions, due to normalization.
neity in the functional properties of neurons in different cortical areas. A natural explanation is that each cortical area conducts calculations of the same form but that the inputs to each area are different and distinctive. Certainly there is ample evidence that the neurons carrying output signals from one cortical area to another are quite inhomogeneous in their properties and distribution, and it is unusual to find individual cortical neurons projecting to more than one cortical target area (42). Our models suggest a particular computational architecture that can be applied successfully to at least two cortical areas, based only on differences in their inputs. We hope in the future to show that this architecture can be applied to other cortical areas, differing in each case only in the nature of the input signals that each area receives.
Available Implementation. A simulation program for Macintosh computers that implements these two models (as well as the linear model of simple cell receptive fields) is available on the World Wide Web at the URL http://white.stanford.edu/ or via anonymous ftp from white.stanford.edu, in directory ∼/v1-mt-model/.
We are grateful to Matteo Carandini for helpful discussions. The work described in this paper was supported by grants from the National Institutes of Health (MH50228 and EY02017) and by the Howard Hughes Medical Institute. D.J.H. is an Alfred P. Sloan Research Fellow.
1. Hubel, D. H. & Wiesel, T. N. ( 1962) J. Physiol. (London) 160, 106–154.
2. Hubel, D. H. & Wiesel, T. N. ( 1968) J. Physiol. (London) 195, 215–243.
3. Enroth-Cugell, C. & Robson, J. G. ( 1966) J. Physiol. (London) 187, 517–552.
4. Rodieck, R. W. ( 1965) Vision Res. 5, 583–601.
5. Movshon, J. A., Thompson, I. D. & Tolhurst, D. J. ( 1978) J. Physiol. (London) 283, 53–77.
6. DeValois, R. L., Albrecht, D. G. & Thorell, L. G. ( 1982) Vision Res. 22, 545–559.
7. Adelson, E. H. & Bergen, J. R. ( 1985) J. Opt. Soc. Am. A 2, 284–299.
8. van Santen, J. P. H. & Spelling, G. ( 1985) J. Opt. Soc. Am. A 2, 300–321.
9. Watson, A. B. & Ahumada, A. J. ( 1985) J. Opt. Soc. Am. A 2, 322–342.
10. Robson, J. G., DeAngelis, G. C., Ohzawa, I. & Freeman, R. D. ( 1991) Invest. Ophthalmol. Visual Sci. Suppl. 32, 429.
11. Albrecht, D. G. & Geisler, W. S. ( 1991) Visual Neurosci. 7, 531–546.
12. Heeger, D. J. ( 1991) in Computational Models of Visual Processing, eds. Landy, M. & Movshon, J. A. (MIT Press, Cambridge, MA), pp. 119–133.
13. Heeger, D. J. ( 1992) Visual Neurosci. 9, 181–198.
14. Heeger, D. J. ( 1993) J. Neurophysiol. 70, 1885–1898.
15. Carandini, M. & Heeger, D. J. ( 1994) Science 264, 1333–1336.
16. Movshon, J. A. & Newsome, W. T. ( 1984) Soc. Neurosci. Abstr. 10, 933.
17. Movshon, J. A, Adelson, E. H., Gizzi, M. S. & Newsome, W. T. ( 1985) Pontif. Acad. Sci. Scr. Varia 54, 117–151.
18. Rodman, H. R. & Albright, T. D. ( 1989) Exp. Brain Res. 75, 53–64.
19. Maunsell, J. H. R. & Van Essen, D. C. ( 1983) J. Neurophysiol. 49, 1127–1147.
20. Albrecht, D. G. & Hamilton, D. B. ( 1982) J. Neurophysiol. 48, 217–237.
21. Tolhurst, D. J. & Dean, A. F. ( 1991) Visual Neurosci. 6, 421–428.
22. Bonds, A. B. ( 1989) Visual Neurosci. 2, 41–55.
23. Gizzi, M. S., Katz, E, Schumer, R. A. & Movshon, J. A. ( 1990) J. Neurophysiol. 63, 1529–1543.
24. Adelson, E. H. & Movshon, J. A. ( 1982) Nature (London) 300, 523–525.
25. Albright, T. D. ( 1984) J. Neurophysiol. 52, 1106–1130.
26. Heeger, D. J. ( 1987) J. Opt. Soc. Am. A 4, 1455–1471.
27. Wang, H. T., Mathur, B. & Koch, C. ( 1989) Neural Comp. 1, 92–103.
28. Grzywacz, N. M. & Yuille, A. L. ( 1990) Proc. R. Soc. London A 239, 129–161.
29. Wilson, H. R., Ferrara, V. P. & Yo, C. ( 1992) Visual Neurosci. 9, 79–97.
30. Wilson, H. R. & Kim, J. ( 1994) Vis. Neurosci. 11, 1205–1220.
31. Heeger, D. J. & Simoncelli, E. P. ( 1993) in Spatial Vision in Humans and Robots, eds. Harris, L. & Jenkin. M. (Cambridge Univ. Press, New York) pp. 367–392.
32. Sereno, M. E. ( 1993) Neural Computation of Pattern Motion: Modeling Stages of Motion Analysis in the Primage Visual Cortex (MIT Press, Cambridge, MA).
33. Smith, J. A. & Grzywacz, N. M. ( 1994) in Computation and Neural Systems, eds. Eeckman, F. H. & Bower, J. M. (Kluwer, Hingham, MA), pp. 177–181.
34. Qian, N., Andersen, R. A. & Adelson, E. H. ( 1994) J. Neurosci. 14, 7381–7392.
35. Nowlan, S. J. & Sejnowski, T. J. ( 1995) J. Neurosci. 15, 1195– 1214.
36. Britten, K. H., Shadlen, M. N., Newsome, W. T. & Movshon, J. A. ( 1993) Visual Neurosci. 10, 1157–1169.
37. Snowden, R. J., Treue, S., Erikson, R. G. & Andersen, R. A. ( 1991) J. Neurosci. 11, 2768–2785.
38. Douglas, R. J., Martin, K. A. C. & Whitteridge, D. ( 1991) J. Physiol. (London) 440, 735–769.
39. Bush, P. C. & Douglas, R. J. ( 1991) Neural Comp. 3, 19–30.
40. Bernander, O., Douglas, R. J., Martin, K. A. C. & Koch, C. ( 1991) Proc. Natl. Acad. Sci. USA 88, 11569–11573.
41. Somers, D. C., Nelson, S. B. & Sur, M. ( 1995) J. Neurosci. 15, 5448–5465.
42. Felleman, D. J. & Van Essen, D. C. ( 1991) Cerebral Cortex 1, 1–47.





