This paper was presented at a colloquium entitled “Vision: From Photon to Perception,” organized by John Dowling, Lubert Stryer (chair), and Torsten Wiesel, held May 20–22, 1995, at the National Academy of Sciences, in Irvine, CA.
Binocular visual surface perception
KEN NAKAYAMA
Department of Psychology, Harvard University, 33 Kirkland Street, Cambridge, MA 02138
ABSTRACT Binocular disparity, the differential angular separation between pairs of image points in the two eyes, is the well-recognized basis for binocular distance perception. Without denying disparity 's role in perceiving depth, we describe two perceptual phenomena, which indicate that a wider view of binocular vision is warranted. First, we show that disparity can play a critical role in two-dimensional perception by determining whether separate image fragments should be grouped as part of a single surface or segregated as parts of separate surfaces. Second, we show that stereoscopic vision is not limited to the registration and interpretation of binocular disparity but that it relies on half-occluded points, visible to one eye and not the other, to determine the layout and transparency of surfaces. Because these half-visible points are coded by neurons carrying eye-of-origin information, we suggest that the perception of these surface properties depends on neural activity available at visual cortical area V1.
The concept of a separate and modular encoding of low-level image properties has emerged over the past 20–30 years in studies of the visual cortex. Neurons in the striate and extrastriate cortex respond differentially to particular aspects of the visual image. For example, receptive field mapping studies in cortical area V1 indicate that cells are selectively sensitive to orientation, spatial frequency, direction of motion, color, and eye of stimulation. The anatomical parcellation of function in V1 appears to be maintained in its projections to higher extrastriate cortical areas. Cortical area V2 receives afferents from V1 in a highly organized manner, such that its subdivisions receive inputs from differing classes of cells in cortical V1 (1,2).
Psychophysical investigations in human observers provided parallel evidence for the existence of such orientation and spatial frequency units in the human cortex. For example, prolonged exposure to stimuli of specific orientation and spatial frequency decreases sensitivity to these same attributes in a manner consistent with the notion of adaptable or fatigable cortical neurons in the human visual system. In addition, the exposure to moving stimuli decreased the subsequent sensitivity to moving patterns in the same direction (3,4).
These findings, taken together, suggest that in humans as well as in monkeys, there are specific sets of analyzers or channels, each tuned to particular aspects of the image. Both physiologists (5) and psychologists (6) have conceived of early vision as consisting of retinotopic maps, parceling the image into different dimensions.
One of the most important arguments in favor of a modularity or division of labor in the early processing of the image has been the existence of binocular stereopsis. The invention of the random dot stereogram by Julesz further reinforced the notion that depth perception can occur without familiar structure in the monocular image, that binocular disparity alone is sufficient to mediate perceived depth. Shortly after the invention of the random dot stereogram, Barlow et al. (7) reported that cells in the striate cortex of cat were disparity tuned; each cell has a specific binocular receptive field separation bestowing it with the ability to respond selectively to real-world targets at specific distances. The existence of these cells provided striking and independent confirmation that binocular disparity alone could mediate perceived depth. Assuming that the visual system could monitor the convergence of the eyes with accuracy and precision, the properties of disparity selective neurons could provide for the metrical encoding of perceived distance.
So great has been the force of these important findings on binocular disparity that it has acquired special status in the understanding of depth perception, overshadowing other wellknown cues such as linear perspective, interposition, T-junctions, etc. Overlooked also are other functions for depth encoding, ones that are not obviously related to perceived depth as such.
In this paper, we emphasize two underappreciated aspects about stereoscopic depth perception. First, we suggest that it can play a critical role not only in the perception of depth but also in supplying the needed perceptual organization for the simple identification of two-dimensional (2D) shapes. Second, we suggest a more expanded concept of binocular vision beyond that supplied by binocular disparity, arguing for a role of half-visible points, which are ever-present in ordinary scenes. We report that such half-visible points can be of decisive importance in mediating the perception of transparency.
Role of Stereopsis in 2D Vision
Consider the perception and identification of letters. Letters are 2D forms, and one might reasonably assume that the coding of the third dimension would be irrelevant. Stereopsis might be needed for encoding the third dimension, but why would it be necessary to code 2D forms?
We argue that we cannot meaningfully think of 2D vision apart from its relation to three-dimensional vision. Most obvious is the mapping of the 2D image onto the retina as we view such surfaces from various view points and angles. Images of even the simplest 2D forms become foreshortened and skewed. Second, and the topic under consideration, is the problem posed by occlusion. Because we inhabit a world composed of opaque objects lying at different distances, 2D surfaces in the world are often only partially visible. All visual systems have had to face this fundamental fact of occlusion, even for the case of 2D vision.
For the case of human vision, consider the task of viewing a simple 2D form, say the letter “C” when it is alone (Fig. 1 a) and occluded by a rectangle (Fig. 1 b). If we consider the literally visible bounding contours corresponding to the letters in Fig. 1 c, it is obvious that it no longer is in the shape of a C.
The publication costs of this article were defrayed in part by page charge payment. This article must therfore be hereby marked “advertisement” in accordance with 18 U.S.C. §1734 solely to indicate this fact.
Abbreviations: 2D, two dimensional.
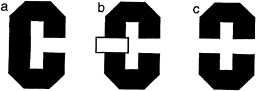
FIG. 1. Illustration of occluded letter, (a) The letter C, unoccluded. (b) The same letter C, occluded by a small rectangle. (c) The same visible letter fragments as in b, but now the fragments remain separated. Instead of seeing the single letter, we see two smaller U-shaped parts, one upside down.
Instead it is broken up into two pieces, each having the shape of the letter U, one right side up, the other inverted. Yet we have very little trouble in recognizing the separated fragments in Fig. 1 b as the letter C, despite the change in the image. Somehow our visual system has ignored the boundary between the letter and the rectangle and considers the C as continuing behind the rectangle. We do not see it as two separate letters (as in Fig. 1 c).
This single example suggests that a three-dimensional interpretation may be needed even before 2D information can be fully evaluated. Two problems seem most apparent. First, it is necessary to distinguish between the true boundaries of 2D surfaces and those arbitrary or spurious boundaries occasioned by occlusion. Second, the visual system needs a method to determine whether separate image patches should be joined together or whether they should be regarded as parts of different surfaces.
First, let us consider the spurious boundary problem in relation to the example. We can see intuitively that from the standpoint of considering the image patches corresponding to the letter C, the boundary between the C and the rectangle is arbitrary. It exists mainly as a consequence of the properties and position of the occluding rectangle. The border between the rectangle and the C does not “ belong” to the C but to the rectangle. The determination of border ownership is a necessary intermediate step in the building of a surface representation. How is border ownership to be determined? We hypothesize that it is dictated by that surface patch which is seen in front. This means that regions corresponding to the U-shaped fragments do not have a border where they meet the rectangle. In terms of representing these image patches as surfaces, these fragments are locally unbounded.
We also need to consider the second problem posed by occlusion. How can the visual system determine which fragments are part of the same surface and which are on separate surfaces? Should the two U-shaped pieces be linked together or should they be considered as separate? We have hypothesized elsewhere that when such unbounded regions face each other, they can be part of a single surface, which is completed behind an occluder. That stereoscopic depth plays a decisive role in dictating both border ownership and surface linkage can be appreciated by fusing the stereoscopic images shown in Fig. 2. [Fusion can be accomplished with or without optical aids. For instructional guidance see Nakayama et al., (8).] Here we see that when the small rectangle is seen as in back, the two U-shaped fragments remain as perceptually separated. They do not link to form a single extended surface. When the rectangle is seen as in back, however, there is a large qualitative difference. Now the two fragments join easily, enabling us to see the letter C.
A similar situation can be seen for more complex perceptual tasks such as the recognition of faces. It is often presumed that there must be an internal template of the face stored in visual memory and that this is compared to the image of the face. Our concern with occlusion forces us to consider an even more elementary problem. What portions of an image should the visual system use for the process of recognition and which parts should be ignored? Note the cartoon face shown in Fig. 3, which appears partially visible, seen through an aperture. If one only considers the outer boundaries of the face region, these might reasonably conform to the contour labeled x, indicating a narrow face. We suggest the recognition system must discount this edge because it belongs to the occluder in front. Thus, before recognition occurs, there needs to be a prior distinction between those edges belonging to that which should be recognized and all else.
This is illustrated in the stereogram presented as Fig. 4, where we present identical information in the right and left eye views. The only difference is a tiny horizontal shift of the face fragments in each monocular image such that when fused, the fragments are seen as either in front of or in back of the interposed strips. When viewing the two possible stereoscopic displays (face-in-front vs. face-in-back), there is a dramatic difference in the clarity of the whole face. When the face strips are seen in front, each strip stands alone and isolated against the background. The face fragments are visible, but they do not cohere. It is very different when the face fragments are seen

FIG. 2. 2D pattern of the letter C, occluded by a small rectangle. As in Fig. 1 b, the letter C is visible even though it is split into two parts, each U-shaped. When viewed as a stereogram, however, the rectangle is seen in back and the two U-shaped fragments are seen as separate. They do not complete to form a larger letter C. [In this and all subsequent stereograms in this paper, the reader is instructed to cross fuse (X) the left and center images or to uncross (U) fuse the center and right images. To view the configuration in the reverse manner, simply do the reverse.]
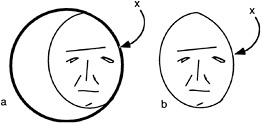
FIG. 3. (a) Face seen through a window. (b) Face truncated by window. Note that the border denoted by x is extrinsic to the face.
in back. Here the individual strips seem almost seamlessly connected.
This obvious difference in clarity is also substantiated in studies of face recognition, where percent correct identifications were significantly higher in the face-in-back condition (9).
Because of differences of depth, our visual system is able to discount the edges of the strips of the face, treating them as contours extrinsic to the image fragments to be matched with stored templates. Thus stereoscopic depth can play an important role in the recognition of objects, even though the recognition process itself may be 2D.
Half-Visible Points and the Perception of Transparent Surfaces
As mentioned earlier, studies in binocular vision have been dominated by the concept of binocular disparity. Yet, it is becoming apparent that the scope of binocular vision needs to be expanded to incorporate the existence of a wider range of binocular phenomena. Relatively little explored is the manner in which the visual system deals with differential binocular occlusion. This binocular difference arises because the eyes must necessarily assume different positions in the world, such that there are image points in one eye having no counterpart in the other. This can be best illustrated in Fig. 5 a and b, where we have outlined a situation where a binocular observer is viewing a square in front of a farther surface. Note from this top view diagram that there are image points on the more distant surface (shown as the hatched bars) that are to the left of the occluding surface that are visible only to the left eye, and correspondingly, there are image points just to the right of the occluding surface that are visible only to the right eye. The visual system is remarkably adaptive in dealing with these unmatched points (10,11). First, they are not treated as rivalrous as are other stimuli that are unmatched in the two eyes. Second, they are perceived at appropriate depths. Finally, they give rise to subjective surfaces and contours, which provide a consistent interpretation of the binocular array in terms of a set of real-world objects. In addition, they have been shown to aid in the matching process required for disparity encoding (12). The role of unmatched points can be demonstrated in Fig. 5 c, a stereogram where each unpaired point leads to the appearance of a subjective surface in front. This surface is framed by the half-occluded (left eye only, right eye only) points depicted in Fig. 5 b.
Occlusion, however, is not the only situation leading to half-visibility. Such unpaired image points can also arise with strong back and weak front illumination. Such conditions give rise to silhouettes, say when an observer is positioned within a dimly lit room, viewing objects nearby against the brighter sky.
Consider the stereogram depicted in Fig. 6 a, which contains fragments of a large red vertical ellipse and a smaller black horizontal ellipse. Viewed ordinarily (not as a stereogram), the two portions of the red ellipse can be perceived either as separate red fragments of a tiled mosaic pattern or, alternatively, as described earlier, a single larger figure completing behind. When viewed as a stereogram, a dramatic change occurs. The red large portion perceptually completes in front and is perceived as a single large red transparent surface partially covering a small black ellipse. This perceptual “illusion” is so strong that the red color spreads into the area where it “covers” the smaller ellipse. Furthermore, it is bounded by subjective contour enclosing this area. Fig. 6 c schematizes the perceptual experience to this stereoscopic display. Compare this to the case where the red ellipse is coded in back (by viewing the stereogram in its reversed configuration). Now one sees a red ellipse completing behind the black one. There is no color spreading or subjective contours, nor is there any perceived transparency (13,14).
The requirements for seeing the transparency require not only the correct depth relations but also the appropriate luminance ordering. The transparent surface must be of intermediate luminance relative to that of the background and the covered surface (15). The role of luminance can be appreciated by examining the stereogram in Fig. 6 b. Although the exact same forms are present with identical disparities, the colors and correspondingly the luminances have been altered. Now the luminance of the transparent surface no longer conforms to the Metelli (15) conditions. Consequently, we do not see a transparent surface. Instead, we see the black ellipse,
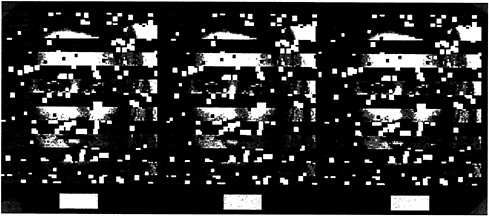
FIG. 4. Stereogram of a face either in front of or behind occluding strips. Note that the face is more easily perceived when it is behind. [Reprinted with permission from ref.9 (copyright Pion Limited, London).]
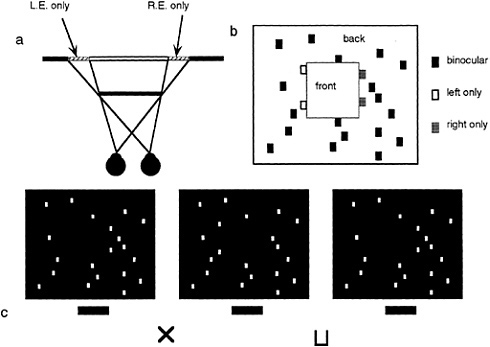
FIG. 5. DaVinci stereopsis. (a) Top view diagram showing regions of a background plane that are visible only to the left eye (L.E.) and right eye (R.E.) (hatched regions). Note that the left-eye-only points are to the immediate left of the occluding surface and that the right-eye-only points are to the immediate right of the occluding surface. (b) Unpaired right eye only (small gray boxes) and left eye only (small open boxes) are again seen in the same relation to occluding surfaces in front (square marked with the word “front”). (c) Stereogram illustrating the power of unpaired points in eliciting the perception of a surface.
broken in two, lying in front of the red ellipse (as schematized by the diagram in Fig. 6 d).
We now describe a new and related phenomenon, the perception of transparency mediated by half-visible points alone. Here no information is supplied by binocular disparity. Examine the Stereogram depicted in Fig. 7 a. Note that in the left and right eye views there are little tabs that are present in one eye and not in the other. The red tabs a and b are visible
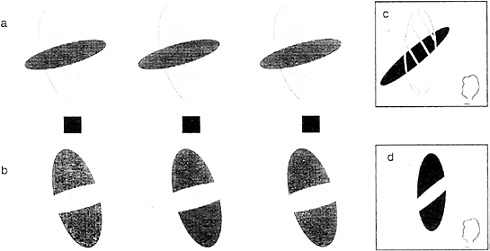
FIG. 6. Conditions for perceived transparency in stereograms. By fusing the Stereogram in a, we see a transparent red ellipse in front of a smaller black ellipse (as illustrated in c). By fusing the stereogram in b, which has exactly the same disparity relations but differing luminance values, we no longer see transparency but fragments of a black ellipse in front of a smaller red ellipse behind (see illustration in d).
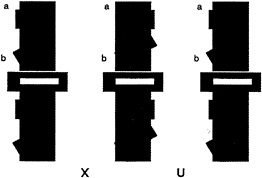
FIG. 7. Conditions for perceiving transparency from half-visible points in stereograms. Spatial arrangement of monocular tabs (labeled a and b in upper portion of the stereogram) are identical to that in the lower. Because of the luminance conditions, one sees them as part of larger red transparent surfaces above but only as isolated black tabs below (depicted in Fig. 8a and b, respectively).
only to the right eye and are placed to the left of the dark vertical bar. Correspondingly, there are two similar tabs on the right side of the bar visible only to the left eye. Fusing the pattern as a stereogram leads to the perception of transparency. Two transparent red bars can be perceived, the upper one adjacent to tab a is horizontal; the lower one adjacent to tab b is oblique (see Fig. 8 a for a pictorial description of the configuration of perceived transparent surfaces).
To appreciate how this pattern of stimulation might arise in a real-world situation, consider Fig. 8 c, which shows a top view drawing of a red horizontal filter placed in front of a black vertical bar. The exact constituents of each eye's image can be understood by referring to Fig. 8 d. Because the scene is back and not front illuminated, no portion of the filter is visible where it covers the black bar. This large area of the transparent surface, which is physically invisible to both eyes, is demarcated by the hatched red area (labeled as invisible in Fig. 8 d). Extending from beyond the confines of the dark background, however, are small portions visible to the right eye and left eye only (labeled R and L, respectively, in Fig. 8 d). It should be clear that this geometrical situation is exactly the configuration as portrayed in the stereogram in Fig. 7 a. What is remarkable is the fact that such an impoverished stimulus is still sufficient to support the perception of transparency. The oblique contour at tab 2 further attests to the strength of this interpretation, given that there is little in the way of colinearity to join the two surfaces.
Eye-of-origin information is critical here. Reversing these eye-of-origin points changes perception dramatically (as can be seen by simply reversing the two stereograms in Fig. 7 a). Here we now see the red tabs in back confirming the earlier work on DaVinci stereopsis (10). One additional factor is also important: the Metelli luminance conditions. Fusing the companion stereogram in Fig. 7 ax is particularly telling. Note that the Metelli conditions are not fulfilled when the vertical bar is red and the tabs are black. Consequently, we do not see a single transparent surface completing across a wide expanse. All we see are some little tabs, slanted in depth (see illustration in Fig. 8 b).
DISCUSSION
We have shown two very different cases where half-visible points in a defined spatial relation to fully visible points can provide critical information for the interpretation of a scene
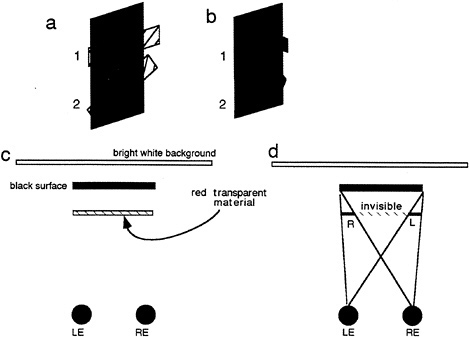
FIG. 8. Explanation of conditions simulated by the stereogram shown in Fig. 7. (a) Perceived surface arrangement seen in Fig. 7 a. (b) Perceived surface arrangement seen in Fig. 7 b. (c) Top view of a transparent surface seen against a black surface, which in turn is seen against a bright white background, thus creating conditions of strong back but weak front illumination. (d) Top view to depict the visibility of the presumed transparent surface in each eye. Each sees a portion of the surface with one eye only as depicted. LE, Left eye; RE, right eye.
layout. First is the case of DaVinci stereopsis (10), where as a consequence of occlusion, left- and right-eye-only points are interpreted to be in back of adjacent surfaces (see also ref.16). Second, and a new observation reported in this paper, are more restricted conditions (requiring more stringent luminance requirements), which indicate that unpaired points can also trigger the perception of surfaces continuing in front [see also von Szily (17) for related a case concerning silhouettes]. All of these demonstrations with half-visible points share an important characteristic. Not only is it important that there be only one eye stimulated but more important is the identity of the eye receiving the visual input. Interestingly, we as human observers are generally unaware as to which of our eyes received a given visual stimulus. It is also true for the majority of neurons in the extrastriate cortical visual pathway. Neurons here, say in V3, V2, and V4 are essentially all binocular (18). Each receives more or less equal amounts of neuronal activation independent of which eye received stimulation. Each of these neurons, therefore, is indifferent as to which eye was stimulated. Required for our phenomenon are neurons that have very different properties. Cells need to respond only to input from one eye and not the other. Where in the nervous system might this information be available?
The only obvious candidates are neurons in the striate cortex (V1). Here, because of the well-known ocular dominance structure of V1 (1), it is clear that there exist neurons that respond differentially to which eye received visual stimulation. Thus, we are drawn to the conclusion that information directly available from cortical area V1 is needed for the higher order interpretation of surface relations. One additional requirement is also pertinent. Cells in this area also need to respond only to one eye but not to both. Tuned inhibitory cells described by Poggio (19), if selectively excited by right or left eye stimulation, might be useful for this purpose, particularly if the suppressive tuning for disparity is fairly broad.
1. Hubel, D. H. ( 1988) Eye, Brain, and Vision (Scientific American Library, New York).
2. Felleman, D. J. & Van Essen, D. C. ( 1991) Cereb. Cortex 1, 1–47.
3. Sekuler, R. & Ganz, L. ( 1963) Science 139, 419–420.
4. Raymond, J. ( 1993) Vision Res. 33, 1865–1870.
5. Zeki, S. ( 1978) Nature (London) 274, 423–428.
6. Treisman, A. ( 1982) J. Exp. Psychol. Hum. Percept. Perform. 8, 194–214.
7. Barlow, H. B., Blakemore, C. & Pettigrew, J. D. ( 1967) J. Physiol. (London) 193, 327–342.
8. Nakayama, K., He, Z. & Shimojo, S. ( 1995) in Invitation to Cognitive Science, eds. Kosslyn, S. M. & Osherson, D. N. (MIT Press, Cambridge, MA), pp. 1–70.
9. Nakayama, K., Shimojo, S. & Silverman, G. H. ( 1989) Perception 18, 55–68.
10. Nakayama, K. & Shimojo, S. ( 1990) Vision Res. 30, 1811–1825.
11. Shimojo, S. & Nakayama, K. ( 1990) Vision Res. 30, 69–80.
12. Anderson, B. L. & Nakayama, K. ( 1994) Psychol. Rev. 101, 414–445.
13. Nakayama, K., Shimojo, S. & Ramachandran, V. S. ( 1990) Perception 19, 497–513.
14. Nakayama, K. & Shimojo, S. ( 1992) Science 257, 1357–1363.
15. Metelli, F. ( 1974) Sci. Am. 230, 90–98.
16. Anderson, B. L. ( 1994) Nature (London) 367, 365–368.
17. von Szily, A. ( 1921) Graefes Arch. Ophthalmol. 105, 964–972.
18. Burkhalter, A. & Van Essen, D. C. ( 1986) J. Neurosci. 6, 2327– 2351.
19. Poggio, G. F., Gonzales, F. & Krause, F. ( 1988) J. Neurosci. 8, 4531–4550.






