C
Solar Reflection Region Measurements
This appendix presents a potentially new data processing and calibration paradigm for solar reflection measurements. Since the paradigm is a departure from the traditional calibration methodology based on radiance, this discussion of it is somewhat tutorial. A calibration of reflectance involves measurement of the incoming and the outgoing radiation and then calculating the ratio (Hsia and Weidner, 1981). For a diffusely reflecting material (radiation scatter), the incident radiation is in units of irradiance (radiant power per area, within a specified spectral band) and the outgoing radiation is in units of radiance (radiant power per area per solid angle, within the same band). Reflectance is a relative, not absolute, calibration since it is the ratio of the radiance to the irradiance. The units of radiant power and area cancel out. The units of bidirectional reflectance are 1/steradians and therefore are not traceable to any of the seven fundamental units of measurement. Calibrations of reflectance are much simpler to perform than calibrations of absolute spectral radiance. Reflectance-based calibrations could provide considerable savings in cost and instrument complexity over present methods. A sensor on orbit does not measure a radiant source but a reflector of the radiant energy from the Sun. This is illustrated in Figure C.1. The reflectance of a diffuser depends upon the directions of the incident and the exiting radiation and is usually called bidirectional reflectance. A complete set of measurements over all directions of incoming and outgoing radiation is called the bidirectional reflectance distribution function. Since, for most remote sensing instruments, reflectance measurements will be made over a limited set of incoming and outgoing angles, a full distribution function calibration is not necessary.
For a remote sensing instrument operating in the solar reflective spectral region, the radiation incident at the aperture is the product of the bidirectional reflectance of Earth (surface plus atmosphere), ρE(λ, θ, ![]() ), times the solar irradiance, ES(λ, θ). The incident angle is θ and the view angle is represented by
), times the solar irradiance, ES(λ, θ). The incident angle is θ and the view angle is represented by ![]() . (Out of plane, bidirectional reflectance is covered by these same arguments.) For the ith channel that has a relative spectral response ri(λ), the sensor output, DNi, is the calibration factor, Ki, times the integration over the wavelength:
. (Out of plane, bidirectional reflectance is covered by these same arguments.) For the ith channel that has a relative spectral response ri(λ), the sensor output, DNi, is the calibration factor, Ki, times the integration over the wavelength:
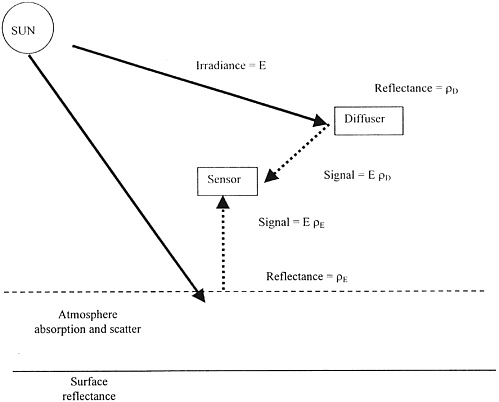
FIGURE C.1 Calibration shown in terms of the reflectance of an on-board diffuser.
For sensors that have an on-board diffuser, such as SeaWiFS and MODIS, the sensor output when viewing the diffuser would be
Taking the ratio of these two equations yields the following equation,
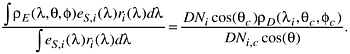
Here we have normalized the solar spectral irradiance function at the wavelength λi,
This shows explicitly the independence of Earth reflectance on the absolute value of the solar spectral irradiance. The bidirectional reflectance of the diffuser is nearly spectrally flat. In almost all cases it can be assumed constant within the bandwidth of the channel and equal to its value at λi. The bidirectional reflectance of Earth is the combined effect of the atmosphere transmission and scattering, and the bidirectional reflectance of the surface. If these functions are constant over the bandwidth of the channel, then the bidirectional reflectance of Earth is
One is still left with the problem of extracting the surface reflectance term from the overall reflectance, that is, separating the surface reflectance from the effects of the atmosphere. Characterization of the atmosphere and the problem of solving for the surface reflectance will remain the objective of much research. However, what has been gained is a result that is independent of the absolute value of the solar irradiance and a calibration accomplished simply in terms of the bidirectional reflectance of an on-board diffuser. Many of the existing models of atmospheric effects and surface reflectance may require as input the value of the radiance at the top of the atmosphere. For these cases one simply needs to multiply the combined absorption, scattering, and reflectance operator, ρE(λi), by the values of solar irradiance to obtain absolute radiance (Gordon, 1981; Kaufmann, 1989).
Recall that bidirectional reflectance is a relative, not an absolute, calibration and as such does not require traceability to an SI unit. Gordon (1981, p. 209) in the case of the Coastal Zone Color Scanner recognized this conclusion. At that time he did not pursue this line of reasoning. Perhaps he did not see a way to guarantee the stability of the diffuser. Recent developments, however, have overcome this difficulty.
The assumption of constancy over the bandwidth of most channels is certainly true for molecular and aerosol scattering. It is usually true as well as for the surface reflectance, since the bandwidth of the channels is normally selected to satisfy this condition. However, absorption of the atmosphere’s molecular constituents results in sharp spectral features and, if occurring within a band, will not satisfy the constant-value assumption; see, for example, band 7 of SeaWiFS (Mueller et al., 1995, Chapter 2). In this case the equation becomes more difficult to solve. However, effective use can be made of the fact that the relative solar irradiance function appears in both the numerator and denominator. Also, the surface reflectance and atmospheric scattering functions can be made to appear as multiplicative operators within the integral. Both considerations should lead to a simplification of the problem. The lesson to be learned here is to select bandwidths that avoid the atmosphere absorption features, if at all possible, for bands used to measure surface or low-cloud features.
Another simplification that accrues from using a reflectance-based calibration is that bandwidth and wavelength stability on orbit become less critical. One of the major problems in this regard is due to the highly structured solar spectrum. If the bandwidth of a channel includes a Fraunhofer line or is very close to one, then shifts in the band wavelength or shape could significantly affect the calibration of that channel (Flittner and Slater, 1991). A portion of the problem arises from the fact that the laboratory calibration uses an artificial light source, an incandescent lamp, whose spectral output is radically different from that of the Sun. Since incandescent sources would not be required in a reflectance calibration, spectral band inaccuracy and instability should be less of a problem.
It should be noted that there is one data product in the solar reflective region that relies on an absolute radiance calibration, the measurement of chlorophyll fluorescence. Chlorophyll is a reflective measurement (the backscatter of sunlight from phytoplankton after absorption by chlorophyll), whereas fluorescence is emitted by phytoplankton (Letelier and Abbott, 1996). In this case once the reflectance of the surface has been determined and multiplication by the atmosphere corrected, absolute solar irradiance will yield the absolute radiance.
Backscattered microwave radiation is also a reflectance measurement; however, the calibration methodology described above does not carry over into the microwave region simply because the radiation source is not the Sun but rather a microwave source aboard the satellite.
The committee believes that NASA should evaluate the merits of this possible new approach.
REFERENCES
Flittner, D.E., and P.N. Slater. 1991. “Stability of narrow-band filter radiometers in the solar-reflective range,” Photogramm. Eng. Remote Sensing 57:165-171.
Gordon, H.R. 1981. “Reduction of error introduced in the processing of coastal zone color scanner-type imagery resulting from sensor calibration and solar irradiance uncertainty,” Appl. Opt. 20:207-210.
Hsia, J.J., and V.R. Weidner. 1981. “NBS 45-degree/normal reflectometer for absolute reflectance factors,” Metrologia 17:97-102.
Kaufman, Y.J. 1989. Theory and Applications of Optical Remote Sensing, Ghassem Asrar, ed. Wiley, New York, pp. 350-378.
Letelier, M., and M.R. Abbott. 1996. “An analysis of chlorophyll fluorescence algorithms for the Moderate Resolution Imaging Spectrometer (MODIS),” Remote Sensing Environ. 58:215-223.
Mueller, J.L., R.S. Fraser, S.F. Biggar, K.J. Thome, P.N. Slater, A.W. Holmes, R.A. Barnes, C.T. Weir, D.A. Siegel, D.W. Menzies, A.F. Michaels, and G. Podesta. 1995. Case Studies for SeaWiFS Calibration and Validation, Part 3. NASA Tech. Memo. 104566, 27, S.B. Hooker, E.R. Firestone, and J.G. Acker, eds. NASA Goddard Space Flight Center, Greenbelt, Md.




