4
Risk Analysis Techniques
Multidisciplinary factors contribute to the risk of flooding in riverine systems. Yet levee safety planning in the United States has traditionally been conducted along disciplinary lines. For instance, in hydrology, levees are evaluated for their ability to withstand the flood of a given magnitude, usually defined by a return period. In geotechnical engineering, levees are assessed for their stability and potential for failure by seepage through the embankment. This disciplinary approach has inhibited the development of quantitative procedures that evaluate the total risk of flooding, reflecting possible contributions of various operational, hydrologic, hydraulic, and geotechnical factors and how they might act individually and jointly.
Among the various sources contributing to flood risk, only the flood – frequency component has traditionally been considered probabilistically. This component is indeed a major factor contributing to the flood risk, often accounting for more than 50 percent of the failure risk. But several other factors are significant and should be accounted for quantitatively. In addition, even for the flood–frequency component, conventional evaluation procedures may be incomplete.
Many factors contribute to flooding of protected areas, depending upon the hydrology and hydraulics of different riverine systems. Before starting a flood damage reduction study, it is important to differentiate between significant and insignificant factors. The following list addresses factors that are often important in determining flood risks.
Hydrologic factors — flood frequency and volume and time distribution of the flood along the stream, which in turn depend on snow melt and/or rainfall characteristics, rainfall–runoff relationships of the water-
shed, and the characteristics of the stream network. Rainfall factors include spatial and temporal distributions of the precipitation, the sample representativeness, accuracy and adequacy of the rainfall data, and the methods of analysis or simulation. Likewise, there are uncertainties in the representativeness, accuracy, and adequacy of the flood data in both space and time, and in the methods used to analyze these uncertainties. Watershed-stream factors include storage in lakes, reservoirs, and wetlands. There are also uncertainties in soil moisture, rain interception, and changing land uses.
Hydraulic factors — the nature of flood propagation in the channel and the equations and methods to simulate the flood propagation, which in turn depend on channel geometry, the roughness and slope of the channel bed, and the nature of the floodplain. Also included are the effects of hydraulic structures in the watershed, such as dams and spillways, levees, locks, weirs, sluices, gates, valves, bridges, intakes, and other diversion structures; also included are effects of sediment in the river, including erosion, scour, and deposition along the channel. Effects of wind and waves should also be considered.
Structural and geotechnical factors — geologic properties of the foundation, seepage through and cutoff beneath levees, internal erosion or piping of levee materials, strength instabilities in embankments or the subsurface, deep seepage failure away from the levee, and other soil mechanics issues.
Seismic factors (on dams and levees) — frequency and magnitude of earthquakes, fault and tectonic characteristics, earthquake-induced ground motion at the dam or levee site and liquefaction of foundation soil, and flooding probability associated with earthquake-induced dam or levee failure.
Materials and construction factors — type and quality of materials used for dams and levees, thermal and moisture variations affecting dam or levee quality during its service period and during its construction, and construction quality control.
Other geophysical factors — ice action in the river and on dams, levees or other structures, flash flooding from failure of dams, levees, or other facilities; thunder/lightning destruction; and tornado and other weather-related impacts.
Operational and maintenance factors — operational procedures on water diversion and release prior to and during flooding; operational procedures when an incident occurs; safety inspections of the river system; regulations on boat traffic and fishing during flooding; repair and main-
tenance rules; grazing and other land uses; and vegetation cover and type.
CORPS FRAMEWORK
The notion of using risk analysis to study the magnitude of floods is not new. Indeed, the relationship between the magnitude of a flood and its likely return period was established years ago by Gumbel (Gumbel, 1941), who drew on statistical theory developed during the 1920s concerning the distributions of extreme events. Standardized procedures for determining flood–frequency curves were defined by the Corps of Engineers during the 1950s (Beard, 1962). In the United States, passage of the National Flood Insurance Act of 1968, which created the National Flood Insurance Program (NFIP), also led to a period of comprehensive study of methods for determining flood frequency curves. This culminated in the publication in 1981 of the widely-used Bulletin 17B (IACWD, 1981). A similar comprehensive study of flood frequency was made in the United Kingdom at about the same time (NERC, 1975; Institute of Hydrology, 1999). Although the methods that evolved in the U.S. and U.K. studies are different, they have become standards adhered to since that time and are widely emulated in other countries.
A formal risk analysis includes seven phases. First, the level of unacceptable flooding performance is defined to allow a probabilistic failure analysis. Second, a method is identified that can be used to combine the different processes or events that lead to unacceptable performance. Third, the parameters involved in each of the processes or events is identified. Fourth, uncertainty analysis is performed for each of the parameters. Fifth, the component parameter uncertainties are combined to yield a system failure probability. Sixth, an economic damage function of flooding is determined along with associated uncertainty. Finally, the failure probability and damage function are combined to yield expected annual damage. This analysis is performed for each protection alternative considered.
The first five phases—finding the system failure probability, without considering the consequences of failure—are referred to as reliability analysis. A prerequisite of a successful reliability analysis is a comprehensive understanding of the problem and of the significant parameters involved. More than seventy years ago, industrial engineers applied some reliability techniques for quality control of manufactured products. In response to high failure rates and damages of military airborne and
electronic equipment during World War II, the U.S. Joint Army–Navy Committees on Parts Standards and on Vacuum Tube Development were established in June 1943 to improve military equipment reliability. Carhart (1953) produced an early state-of-the-art report on reliability engineering. In November 1953 the U.S. Department of Defense set up the Advisory Group on the Reliability of Electronic Equipment to monitor and promote reliability evaluation and analysis. Textbooks on reliability engineering started to appear in the early 1960s (Bazovsky, 1961; Calabro, 1962). Concerns regarding the safety of nuclear power plants and the reliability of space vehicles further accelerated the development of this topic. In civil engineering, structural engineers have made considerable advances in understanding the risks that earthquakes and high winds pose to structures. Progress has also been made in geotechnical and water resources engineering (Yen and Tung, 1993).
NATURAL VARIABILITY AND IMPERFECT KNOWLEDGE
A risk analysis of flood hazards needs to address uncertainties associated with natural variability, engineering or economic models, and statistical relationships. Figure 4.1 provides a conceptual model (also known as an event tree) for describing the transformation of hydrologic risk, to variation in reservoir operations, to river-stage-to-reservoiroutflow relationship, to levee reliability, and finally to estimates of economic damages should a levee fail. This figure essentially represents the current Corps framework.
Some of the relationships in Figure 4.1 relate to natural variability. These relationships might be called random or stochastic because they are treated as random processes over time or space. For example, possible values of annual flood flows are treated as random events in time, and levee failures related to geotechnical weaknesses are treated, in part, as random events over space.
Other relationships in Figure 4.1 relate to engineering calculations or functional rules. These relationships might be called deterministic because a fixed dependent variable is assigned with a fixed value of an independent variable. For example, damages resulting from a given water level in a given structure are treated as deterministic. In this case, however, an estimation error is applied to the result to reflect imprecision in the physical survey of properties in the floodplain.
Finally, other relationships relate to empirical correlations. These relationships might be called statistical because they are treated as statisti-
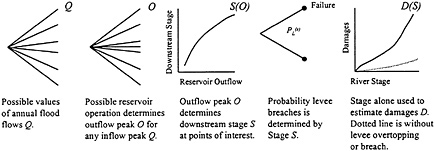
FIGURE 4.1. Event tree describing the transformation of flood discharge into damage. Some of the steps in this process are deterministic; others are stochastic. SOURCE: NRC (1995).
cal regression functions. For example, river stage as a function of floodflow is treated as statistical. The estimation error applied to the damage– stage relationship mentioned previously is also modeled as a statistical error.
For each phase of Figure 4.1 there is thus a mathematical relationship that translates input variables to output variables, and each relationship introduces uncertainties. Some of the uncertainties derive from natural variations, others from engineering calculations, and still others from statistical estimation. For each relationship in the event tree of Figure 4.1 there is a set of parameters that define the corresponding equation or curve. The values of these parameters are uncertain. Consider two phases in the event tree (which shows five phases) as illustrative; the flood–frequency relationship on the left (the first phase), and the stage– discharge relationship in the middle (the third phase).
The possible values of the annual flood flow Q are represented by an exceedance probability distribution. These flood flows are assumed to be naturally variable and are describable with probabilities. This requires a set of parameters to specify the distribution shape and location along the axis of river flows (discharges). The parameters used are usually the mean, variance, and skewness coefficient of the logarithms of the flows. On the other hand, the shape and the location of the probability distribution are themselves uncertain because of imperfect knowledge about which distribution model to fit to historical data and about the best
values of distribution parameters for that model. Thus, the flood flows involve both natural variability and knowledge uncertainty.
The stage–discharge relationship is represented by a regression equation. This requires a set of parameters to describe the shape and location of the relationship on a graph of stage vs. discharge. The parameters used are usually an intercept, slope, and maybe some form of shape factor. To some extent, the stage–discharge relationship reflects natural variability over time or within the river reach (e.g., variability caused by water temperature, by scour and deposition or by stages of tributaries). On the other hand, the regression equation is estimated from limited data. The shape and the location of the regression curve are themselves uncertain because of imperfect knowledge about which equation to fit to historical data and about the best values of regression parameters for that equation. As with the flood–frequency curve, there is imperfect knowledge about which probability distribution model to fit to natural variations of historical stage data, about the regression curve, and about appropriate values of the distribution parameters for that model. Thus, the stage–discharge relationship also involves both natural variability and knowledge uncertainties. The largest knowledge uncertainties are for uncommon, extremely large floods.
The Corps's objective in flood damage reduction studies is to determine the expected annual damage (EAD) along a section of river caused by possible floods, and to compare changes in those damages as a function of project alternatives. The Corps's method for such calculations starts with flood discharge, Q, which is equaled or exceeded—on average—once in T years. T is said to be the return period of the flood discharge Q. Corresponding to this return period T is a probability p that the discharge Q is equaled or exceeded in any given year. This annual exceedance probability is the reciprocal of the return period, T, and is given by
For a flood of annual probability p, a corresponding value of flood damage D(p) can be estimated. This is based on the depth of inundation of the floodplain and on the value of the inundated structures. The EAD is the average value of such damages taken over floods of all different annual exceedance probabilities and over a long period of years. Stated mathematically, the EAD is,
The current Corps method divides the calculation of Equation 4.2 into three steps (Figure 4.2):
-
determining flood frequencies, which describe the probability of floods equal to or greater than some discharge Q (i.e., volume of flow) occurring within a given period of time—shown in the upper-right panel of Figure 4.2,
-
determining stage–discharge relations, which describe how high the flow of water in a reach of river (the stage) might be for a given volume of flow (discharge)—shown in the upper-left panel of Figure 4.2, and
-
determining damage–stage relations, which describe the amount of damage that might occur, given a certain height of flow—shown in the lower left panel of Figure 4.2.
The lower-right panel of Figure 4.2 relates annual damage to exceedance probability, p. The shaded area under the curve is the expected annual damage, given by Equation 4.2. To find the damage for a given probability p, the discharge QT for that probability is first taken from the flood–frequency curve, given in the upper-right panel. Then the stage height (water surface elevation) for that discharge, H, is found from the upper-left panel. From the value of H, the damage D for stage height is found from the lower-left panel. By plotting this damage on the lower-right panel for the given probability, and by repeating this process for a sequence of flood probabilities, the damage–frequency curve is established. This curve is then integrated to give expected annual damage. In the Corps's method, annual exceedance probabilities of p = 0.5, 0.2, 0.1, 0.04, 0.02, 0.01, 0.004, and 0.002 are the values used in the computation.
Uncertainties enter the calculations in each step of the analysis and are propagated from one step to the next, ultimately accumulating in the EAD—the estimate of damages that might occur in a given year. These uncertainties in damage estimates are expressed as a frequency curve of damages—analogous to a frequency curve of flooding—describing the probability of damages of a given magnitude being exceeded in a given period of time (e.g., annually). This frequency curve of damages is
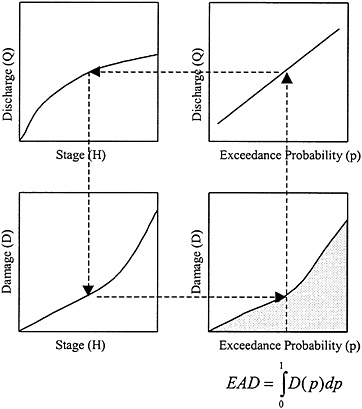
FIGURE 4.2 Basis of the Corps's computation of expected annual damage (EAD). The logic of this figure flows counterclockwise starting from the upper right panel and ending in the lower right panel. SOURCE: Adapted from Moser (1997).
shown in the lower right panel of Figure 4.2. The Corps's conceptual approach to modeling flood hazard and associated damages —using the relationships between flood frequency, stage–discharge, and damage– stage—is consistent with longstanding scientific understanding.
The computational procedure in the Corps's method uses Monte Carlo sampling to perform numerical integration of the damage exceedance probability curve for a damage reach. The damage-exceedance probability function is obtained from the discharge-exceedance probability, stage-discharge, and damage-stage functions. The numerical inte-
gration is necessary because the damage-exceedance probability function in not defined by a continuous analytic function. In this procedure, (pseudo-) random numbers are used to generate a single realization of each of the three relationships: discharge-exceedance probability function, stage-discharge function, and stage-damage function. From these, a single realization of the damage-exceedance probability curve is calculated. The expected annual damage (EAD) is calculated for this realization by integrating the damage-exceedance probability curve. This process is repeated many times and statistically averaged. The numerical results can be made arbitrarily precise, at least from a statistical point of view, by increasing the number of realizations calculated in this way.
The Corps's approach is a reasonable risk analysis procedure that deserves consideration for wider adoption in the flood management community. It provides a mechanism for combining uncertainty in estimating flood discharge and stage with the inherent risk of different flood severities, to give overall risk measures of the system's engineering performance that are more complete than those customarily used.
RISK ANALYSIS
Determination of EAD in Equation 4.2, as historically performed, considered the range of flood magnitudes that could occur, but it did not consider uncertainties in hydrologic, hydraulic, or economic information used in the damage calculation. The curves of Figure 4.2 were treated as known. The traditional approach, as illustrated by Figure 4.2, does not tell us how sure we can be that the calculated expected annual damages will not be exceeded. This is because there are uncertainties in the probability distribution of annual peak flood flows, in the relationship between flood flow and flood stage, and in the relationship between flood stage and economic damage. Just how accurate is the calculated estimate of EAD damage? The Corps's new risk analysis for flood damage assessment attempts to quantify both the natural variability and the knowledge uncertainty in the above procedure.
Risk analysis provides a means of estimating a range of expected annual flood damages, each of which is associated with a level of assurance that it will not be exceeded. Similarly, risk analysis can be employed to calculate the range of expected probabilities of levee failure, each of which is associated with a level of assurance that that probability will not be exceeded. Consider the upper-right quadrant in Figure 4.2. The peak flow expected once in 100 years, on average, is the flow corresponding
to an annual exceedance probability of p = 0.01. How sure can we be that if we protect ourselves from a flow of that particular magnitude, we will actually be protecting ourselves from all flows that occur less frequently, on average, than once in 100 years? Risk analysis addresses such questions.
Assume that the probability distribution capturing the uncertainty about the probability of exceedance of the peak flows at the potential damage site (as shown in the upper-right quadrant of Figure 4.2) was determined as part of a risk analysis. Figure 4.3 shows a portion of that function. To be, say, 90 percent sure that protection is provided for the 100-year return period flow, Q100 depends on the uncertainty in the estimated flow probabilities (see Figure 4.3), stage–discharge relationship, and in the levee system reliability.
Risk, uncertainty, and variability are inherent in flood damage reduction planning. There is uncertainty in any forecast of stream or river flood flows and the resulting damage simply because we cannot know enough about all the factors that contribute to them. Uncertainties in the stage–damage function in the lower-left quadrant of Figure 4.2 include:
-
economic activities and the economic condition or value of the property on the floodplain during a flood,
-
warning time and response of floodplain inhabitants,
-
velocity of the floodwaters and the amount of mud and debris, and
-
time required to repair damaged property.
Uncertainties in the discharge–stage function in the upper-left quadrant of Figure 4.2 include:
-
physical characteristics of channel,
-
winds that may affect flood stages associated with given flows, and
-
vegetation, debris, and other obstructions including ice in the channel.
Uncertainties in the probability of exceedance distribution of annual peak flows in the upper-right quadrant of Figure 4.2 include:
-
limited data from which to statistically estimate hydrographs,
-
when and how severe a rain storm or other event (e.g., upstream dam failure or upstream or downstream levee failure) may be that could
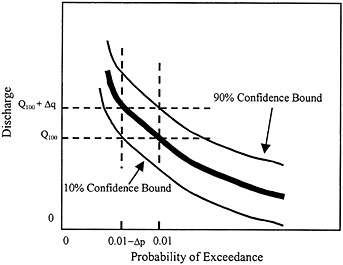
FIGURE 4.3. The darkest of these three curves represents the expected probability of exceedance of peak flow derived from a floodfrequency analysis. The two lighter lines that bound this curve define the 10% and 90% confidence bounds, respectively, around the expected probability of exceedance. Q100 represents discharge that has a 0.01 probability of being exceeded, while Q100+Δq is the discharge level for which there is a 90 percent confidence that the 100-year flow will not exceed this level. In terms of expected probability, this discharge has a 0.01-/Δp probability of being exceeded. This approach corresponds to a safety factor that accounts for the uncertainty in the hydrologic analysis and the assessment of flood frequencies.
-
result in a flood,
-
duration and distribution of rainfall on an area draining a potential flood damage site, and the precise rainfall–runoff and flow routing events (such as watershed topography, land use and cover, soil moisture content) that exist during such a storm,
-
the likelihood of levee or upstream dam (structural) failures or operator (nonstructural) “failures” at upstream dams, and
-
actions (temporary measures) taken upstream during a flood to protect upstream sites.
Peak flow records are commonly used to estimate the chance of a flood of a given or greater magnitude. But such estimates are uncertain for at least two reasons. One is the limited (and perhaps inaccurate) number of observations of past peak flows used to estimate the likelihood of equaling or exceeding a particular peak flow in any year. The other is the changing and varying character of the drainage basin that influences the peak flow resulting from a specific rainfall. In many cases the probability distribution of peak flows is changing, even assuming, perhaps incorrectly at least in the long run, that the probabilistic character of the rainfall is not.
The Corps's search for a better method of quantifying flood risk was prompted by issues related to riverine levee freeboard, described at a workshop held in Monticello, Minnesota (USACE, 1991a). There were concerns that arbitrarily defined safety margins were not explicitly related to the causes of uncertainty in levee performance and that the additional height (freeboard) required to meet these safety margins was not properly accounted for in the evaluation of project benefits. At the Monticello meeting a methodology was presented for quantifying uncertainty in discharge, stage, and damage, (Davis, 1991) from which the current procedure has evolved. At first, the risk analyses for flood damage assessment were computed with a spreadsheet with an add-in, commercial-off-the-shelf program, as described by Davis (1991). In January 1998 the Corps's Hydrologic Engineering Center (HEC) released Version 1.0 of the HEC-Flood Damage Assessment computer program (HECFDA) (HEC, 1998a), which provided an improved Windows program for carrying out the computations.
MONTE CARLO SIMULATION
Figure 4.4 shows a sequence of three graphs describing uncertainties in discharge, stage, and damage. The uncertainty in these quantities is signified by the probability distributions and dashed confidence-limit lines drawn around each curve and also by the dash–dot lines on each graph, which are possible alternative locations of the curves. The first graph shows the uncertainty in discharge Q for a given exceedance probability p, f1(Q|p). This uncertainty, f1(Q|p), can be specified rather precisely using the noncentral t distribution if the flood–frequency curve is described by the log normal distribution, and approximately so if the flood–frequency curve is described by other methods. A flood–frequency curve based on the log normal distribution is completely speci-
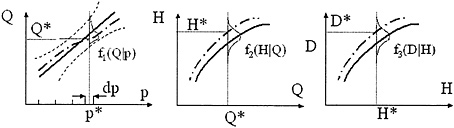
FIGURE 4.4 Uncertainties in the discharge (Q), stage (H), and damage (D) relationships that are part of the risk analysis method. The first figure shows the relationship between discharge vs. exceedance probability (p). The solid curve is the best estimate of this relationship, while the dash-dot curve represents one potential realization that the actual curve might assume. The dotted lines show probability contours of the function f1 (Q|p), which is the probability density function describing uncertainty in discharge for a given exceedance probability. The second figure shows the relationship between discharge and water height (i.e., the rating curve). The solid line is the best estimate and the dash-dot curve is one potential realization that the actual curve might assume. The function f2(H| Q) is the probability density function of height given discharge. The third figure shows the relationship between damage and water height. The solid line is the best estimate of this relationship and the dash-dot curve is one potential realization that the actual curve might assume. The function f3(D|H) is the probability density function of damage given water height.
fied by its mean and standard deviation, so if the mean and standard deviation are varied, then different flood–frequency curves result. The statistical uncertainty in the mean and standard deviation can be quantified based on the number of data values used in calculating them. By using Monte Carlo simulation to generate different means and standard deviations and then plotting the resulting flood–frequency curves, different “realizations” of the flood–frequency curve are defined, one example of which is shown by the dash–dot line in f1(Q|p) in Figure 4.4. It should be noted that several methods could be used for risk value computations, and that the Corps uses the Monte Carlo method.
Similarly, the uncertainty in the rating curve, or relationship between the stage height H and the discharge Q, is symbolized by the probability distribution around the f2(H|Q) curve in Figure 4.4 and by the alternative realization of that curve shown by the dash –dot line in that figure. In this
case, the Monte Carlo analysis uses only a single random variable that serves to vertically displace the average rating curve.
Finally, the uncertainty in the damage–stage function is symbolized by the probability distribution around the f3(D|H) curve in Figure 4.4 and the alternative realization of that curve, given by the dash –dot line. This function combines the effects of several different kinds of uncertainty, including the likelihood of levee failure, uncertainty in elevations of structures in the floodplain, lack of knowledge of the degree of flood damage for a given depth of inundation in a structure, and uncertainty in property and content values within the structures.
Monte Carlo simulation is used to generate new realizations of each of the three curves in Figure 4.4. For each of these sets of realizations, a new value of expected annual damages (EAD) is found by the same process as described in Figure 4.2, as if each realization were the true value of the curve. In other words, for each exceedance probability interval dp, a representative exceedance probability p* is used, from which the flood discharge Q* is found using the flood–frequency curve, the corresponding stage height H* from the discharge–stage curve, and the consequential damage D* from the damage–stage function. By continuing this process across the exceedance probability axis and then integrating the results using Equation 4.2, the EAD is found. The Monte Carlo simulation is continued for a few thousand cycles of generating realizations and computing EAD, until the statistics of the EAD values are sufficiently accurate. This form of Monte Carlo simulation is more sophisticated than the simpler approach of simply generating a flood, finding the stage and damage, generating a new flood, finding the stage and damage, and so on. Thus, the Monte Carlo simulation uses random numbers to perturb the relationships linking the key variables, rather than to generate random floods and examine their consequences.
As the Corps's risk analysis methods evolve, it is possible that a direct Monte Carlo approach will become impractical. The approach requires large numbers of repetitive calculations, and should the analysis models become more involved, alternative calculation approaches may be desirable.
ASSESSMENT OF ENGINEERING PERFORMANCE
The engineering performance of a flood damage reduction project is measured by the probability that the land to be protected by the project will be flooded in any given year. Such probabilities are estimated for
each damage reach in the project and consider hydrologic, hydraulic, and geotechnical uncertainties. Engineering performance is not concerned with estimates of economic damage, which are assessed separately. The performance measures require the definition of a target stage for each damage reach, as shown in Figure 4.5. The target stage is defined as the water surface elevation in a reach at which significant economic damage occurs. To determine the target stage, the damage–frequency curve is obtained for the damage reach by the process shown in Figure 4.2, transforming the flood–frequency curve through the damage–stage curve without consideration of errors in these curves. The 1 percent chance of flooding damage is found from this damage–frequency curve. A fraction of this damage (usually 10 percent) is taken and is used to determine the corresponding stage from the damage–stage curve, which then becomes the target stage for the reach.
As Figure 4.6 shows, engineering performance can be stated in two ways—either as a risk of failure, measured by the exceedance probability of a target stage, or as a reliability, measured by the nonexceedance probability of the target stage. Performance can also be measured by conditional probabilities dependent on the occurrence of a flood of a given severity (e.g., the 100-year flood) or dependent on the annual probabilities integrated over all the floods that could occur within a given year. In the Corps's method, the two main engineering performance measures combine the two sets of distinctions into the following measures:
-
annual exceedance probability—the probability that the target stage will be exceeded in any year considering all potential floods and
-
conditional nonexceedance probability—the probability that the target stage will not be exceeded given a specific flood severity.
FIGURE 4.5 Definition of a target stage used in assessing engineering performance.
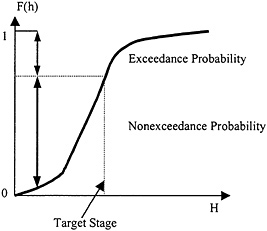
FIGURE 4.6 Exceedance and nonexceedance probabilities.
The assessment of engineering performance to create the annual exceedance and conditional nonexceedance probabilities is carried out as illustrated in Figure 4.7. The first two panels in Figure 4.7 show the flood–frequency curve and the stage–discharge curve. In each cycle of the Monte Carlo procedure, a new realization of the flood–frequency curve f1(Q|p) and the stage- damage curve f2(H|Q) ) is generated, where H represents stage height and Q represents discharge. The flood–frequency curve is defined at discrete intervals of annual flood probability, p (p = 0.5, 0.2, 0.1, 0.04, 0.02, 0.01, 0.004, 0.002). If a particular value of p is chosen, say p*, the corresponding flood discharge Q* can be found from the flood–frequency curve, and the resulting stage height H* can be found from the stage–discharge curve. By combining these pairs of (H*, p*) values, a stage–frequency curve can be constructed, f3(H|p), as shown in the third panel in Figure 4.7.
The annual exceedance probability, pe, is estimated from the stage– frequency curve as that probability corresponding to the target stage for the damage reach. This computation is repeated for N cycles of Monte Carlo simulations, and the expected value of the annual exceedance probability is found as the average over the N sample values from the

FIGURE 4.7 Computation of risk measures using a target stage.
simulations. The median annual exceedance probability is the 50 percent value of this distribution.
Conditional nonexceedance probabilities are also determined from the stage–frequency curve. For each value of p*, there corresponds an H*, determined in the manner just described. After all the Monte Carlo simulations are complete, a set of N values of H* exists, of which a subset, n, have stages not exceeding the target stage. The conditional nonexceedance probability of the target stage is given by n/N. The HEC-FDA program presents such conditional nonexceedance probabilities for each damage reach for annual event probabilities of 0.1, 0.04, 0.02, 0.01, 0.004, and 0.002, shown in the following chapter in Figure 5.10. Figure 5.10 also shows the chance that the target stage will be exceeded at least once in 10, 25, and 50 years, computed as 1 − (1−pe)n, where n = 10, 25, or 50, respectively.
GEOTECHNICAL RELIABILITY
Even if not overtopped by floods, levees may fail for geotechnical reasons. The Corps's risk analysis procedure incorporates the chance of such failures through a geotechnical reliability model. This model leads to a relationship between water height and probability of geotechnical failure, which is then applied individually to each damage reach of river. The logic of this calculation is that damages accrue in one of two ways— either the river becomes high enough that a levee is overtopped, or even though the river does not overtop a levee, it is high enough to cause geotechnical failure.
The Corps's geotechnical reliability model is a sound first step in balancing scientific understanding with the practical needs of planning studies and risk analysis. This is a difficult problem. The geotechnical performance of a levee depends on local soil conditions and construction details, neither of which are known in detail during the planning study. Many of the levees of concern to risk analysis studies were not designed by the Corps and are neither owned nor maintained by federal agencies.
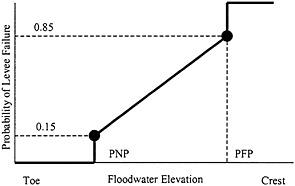
The Corps's original geotechnical reliability model is a simple relationship based on two critical stage heights for the levee: the probable failure point (PFP) and the probable nonfailure point (PNP) (USACE, 1991b). The probable failure point is the stage height associated with a high probability of failure. Numerically, this probability is set at 0.85. The probable nonfailure point is the stage height associated with a negligible probability of failure. Numerically, this probability is set at 0.15. A line is drawn between the PFP and PNP, as shown in Figure 4.8. These points are assessed for local conditions of the project area, and they may change from reach to reach. To avoid complications arising from failures in multiple locations on a long levee, the Corps models the damage such that the reach covers the whole length of the levee under consideration. Thus, the risk function in Figure 4.8 refers to the chance of failure at only the weakest point over this reach. This original model appears to be still widely used in the Corps's district offices.
The original reliability model has been updated (USACE, 1999b) to reflect more sophisticated understanding of geotechnical performance. The updated model considers multiple modes of geotechnical failure, including underseepage, through seepage, and strength instability. This results in a composite curve that varies smoothly between probabilities of 0 and 1, rather than being anchored to a probable failure point and a probable nonfailure point (Figure 4.9).
Although the updated model is based on better scientific understanding of levee performance, the numerical difference in risk analysis results compared to the initial model may not be large. The updated model, however, supports a more complete geotechnical analysis and should to replace the initial model.
The risk measures for engineering performance, including geotechnical reliability, are calculated as shown in Figure 4.10. The first panel of this figure shows the stage–frequency curve, f3(H|p), from Figure 4.7, which is determined from the hydrologic and hydraulic models and their attendant uncertainties. For each frequency value (p* = 0.5, 0.2, 0.1, 0.04, 0.02, 0.01, 0.004, 0.002), a corresponding stage height H* is de-
termined. The middle panel of Figure 4.10 is the risk of levee failure R as a function of stage, f4(R|H), derived from Figure 4.8 or Figure 4.9 using this function. For the given value of H*, the corresponding risk of failure R* is determined. The pairs of values (R*, p*) are combined to form a risk– frequency curve, R(p), as shown in the last panel of Figure 4.10. The annual exceedance probability pe including geotechnical uncertainty is then found in an analogous manner to the expected annual damage using Equation (4.3):
FIGURE 4.8 Two-point model of geotechnical levee reliability. PFP is probable failure point; PNP is the probable nonfailure point.
The conditional nonexceedance probability for any given value of p* is simply 1 − R* in Figure 4.10.
By repeating this computation many times using a Monte Carlo simulation, a set of of pe and 1 − R* values is obtained. The pe values are averaged to find the expected value of the annual exceedance probability, and the 1 − R* values are averaged to find the expected value of the conditional-nonexceedance probability. Consider, for example, the construction of a levee with a specified conditional nonexceedance probability of, for example, 90 percent or 95 percent for a 100-year flood. In
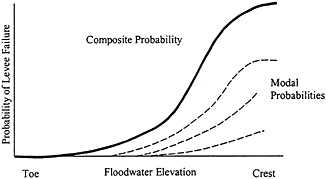
FIGURE 4.9 Continuous model of geotechnical levee reliability.
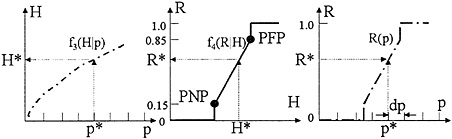
FIGURE 4.10 Computation of risk measures including geotechnical reliability.
this instance, the above procedure is executed with a specified value of p* = 0.01, and the levee height is raised or lowered until the required conditional nonexceedance probability is obtained.
The Corps's analysis combines uncertainty about the parameters and analysis models with the variability inherent in natural systems. Applications are discussed in Chapter 5.




















