Appendix D
How Do Response Problems Affect Survey Measurement of Trends in Drug Use?
John V.Pepper
As discussed in Chapter 2, two databases are widely used to monitor the prevalence of drug use in the United States. Monitoring the Future (MTF) surveys high school students, and the National Household Survey of Drug Abuse (NHSDA) surveys the noninstitutionalized residential population age 12 and over. Each year, respondents from these surveys are drawn from known populations—students and noninstitutionalized people—according to well-specified probabilistic sampling schemes.1 Hence, in principle, these data can be used to draw statistical inferences on the fractions of the surveyed populations who use drugs.
It is inevitable, however, for questions to be raised about the quality of self-reports of drug use. Two well-known response problems hinder one’s ability to monitor levels and trends: nonresponse, which occurs when some members of the surveyed population do not respond, and inaccurate response, which occurs when some surveyed persons give incorrect responses to the questions posed. These response problems occur to some degree in almost all surveys. In surveys of illicit activity, how-
ever, there is more reason to be concerned that decisions to respond truthfully, if at all, are motivated by respondents’ reluctance to report that they engage in illegal and socially unacceptable behavior. To the extent that nonresponse and inaccurate response are systematic, surveys may yield invalid inferences about illicit drug use in the United States.
In fact, it is widely thought that self-reported surveys of drug use provide downward biased measures of the fraction of users in the surveyed subpopulations (Caspar, 1992; Harrison, 1997; Mieczkowski, 1996). Nonrespondents are likely to have higher prevalence rates than those who respond. False negative responses may be extensive in a survey of illicit activity. While it is presumed that self-report surveys fail to accurately measure levels of use, they are often assumed to reveal trends. The principal investigators of MTF summarize this widely held view when they state (Johnston et al., 1998a:47–48):
To the extent that any biases remain because of limits in school and/or student participation, and to the extent that there are distortions (lack of validity) in the responses of some students, it seems very likely that such problems will exist in much the same way from one year to the next. In other words, biases in the survey will tend to be consistent from one year to another, which means that our measurement of trends should be affected very little by any such biases.
These same ideas are expressed in the popular press as well as in the academic literature. Joseph Califano, Jr., the former secretary of health, education and welfare, summarized this widely accepted view about the existing prevalence measures (Molotsky, New York Times, August 19, 1999): “These numbers understate drug use, alcohol and smoking, but statisticians will say that you get the same level of dissembling every year. As a trend, it’s probably valid.” Anglin, Caulkins, and Hser (1993:350) suggest that “making relative estimates is usually simpler than determining absolute estimates…. [I]t is easier to generate trend information…than to determine the absolute level.”
To illustrate the inferential problems that arise from nonresponse and inaccurate response, consider using the MTF and the NHSDA surveys to draw inferences on the annual prevalence of use rates for adolescents. Annual prevalence measures indicate use of marijuana, cocaine, inhalants, hallucinogens, heroin or nonmedical use of psychotherapeutics at least once during the year. Different conclusions about levels and trends might be drawn for other outcome indicators and for other subpopulations.
Figure D.1 and Table D.1 display a time-series of the fraction of adolescent users as reported in the official annual summaries of the MTF (Johnston et al., 1998b) and the NHSDA (Office of Applied Studies, 1997).
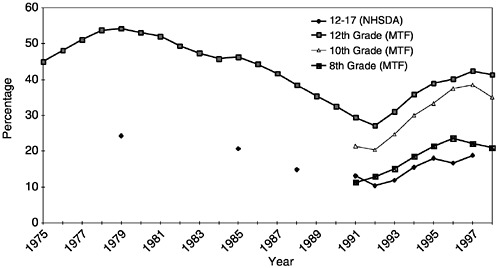
FIGURE D.1 Annual prevalence rate of use of an illegal drug for people ages 12– 17, 1975–1999, National Household Survey of Drug Abuse (NHSDA) and Monitoring the Future (MTF). Note: Annual prevalence measures indicate use of marijuana, cocaine, inhalants, hallucinogens, heroin or nonmedical use of psychotherapeutics at least once during the year.
SOURCES: LD Johnston, PM O’Malley, JG Bachman. (Dec. 1998). Drug use by American young people begins to turn downward. University of Michigan News and Information Services: Ann Arbor, MI. [On_line]. Tables 1b and 3. Available: www.isr.umich.edu/src/mtf; accessed 11/16/99.
Data from the MTF imply that annual prevalence rates for students in 12th grade increased from 29 percent in 1991 to 42 percent in 1997. Data from the NHSDA indicate that the annual prevalence rates for adolescents ages 12–17 increased from 13 percent in 1991 to 19 percent in 1997. The level estimates from the two surveys differ, with those from the MTF being more than twice those from the NHSDA.2 Still, the trends across surveys are generally consistent. Both series suggest that from 1991 to 1997, the fraction of teenagers using drugs increased by nearly 50 percent. Does the congruence in the NHSDA and MTF series for adolescents imply that both surveys identify the trends, if not the levels, or does it merely
TABLE D.1 Estimated Prevalence Rate of Use of Any Illegal Drugs During the Past Year, National Household Survey of Drug Abuse (NHSDA) and Monitoring the Future (MTF)
|
Year |
MTF 12th Graders |
NHSDA, Ages 12–17 |
|
1975 |
45.0 |
|
|
1976 |
48.1 |
|
|
1977 |
51.1 |
|
|
1978 |
53.8 |
|
|
1979 |
54.2 |
24.3 |
|
1980 |
53.1 |
|
|
1981 |
52.1 |
|
|
1982 |
49.4 |
|
|
1983 |
47.4 |
|
|
1984 |
45.8 |
|
|
1985 |
46.3 |
20.7 |
|
1986 |
44.3 |
|
|
1987 |
41.7 |
|
|
1988 |
38.5 |
14.9 |
|
1989 |
35.4 |
|
|
1990 |
32.5 |
|
|
1991 |
29.4 |
13.1 |
|
1992 |
27.1 |
10.4 |
|
1993 |
31.0 |
11.9 |
|
1994 |
35.8 |
15.5 |
|
1995 |
39.0 |
18.0 |
|
1996 |
40.2 |
16.7 |
|
1997 |
42.4 |
18.8 |
|
NOTE: These annual prevalence measures indicate use of marijuana, cocaine, inhalants, hallucinogens, heroin or nonmedical use of psychotherapeutics at least once during the year. SOURCES: L.D.Johnston, P.M.O’Malley, J.G.Bachman. 1998b. Drug use by American young people begins to turn downward. University of Michigan News and Information Services: Ann Arbor, MI. [On_line]. Tables 1b and 3. Available: www.isr.umich.edu/src/mtf; accessed 11/ 16/99. Office of Applied Studies National Household Survey on Drug Abuse: Main Findings 1997, Department of Health and Human Services, Substance Abuse and Mental Health Services Administration. Table 2.6. Available:http://www.samhsa.gov/oas/NHSDA/1997Main/Table%20of%20Contents.htm; accessed 11/16/99 |
||
indicate that both surveys are affected by response problems in the same way?
This appendix evaluates the potential implications of response problems in the MTF and the NHSDA for assessment of trends in adolescent drug use. Assessment depends critically on the maintained assumptions. After all, the data cannot reveal whether a nonrespondent used drugs or whether a respondent revealed the truth.3 The data alone cannot reveal the fraction of drug users. Thus, as with all response problems, a fundamental trade-off exists between credibility and the strength of the conclusions. Under the common assumption of stability of error processes, which is implicit in the quotes above, the data identify trends if not levels. This assumption, however, is not innocuous. To the contrary, the assumption that response errors are fixed over time lacks credibility if, for example, the stigma of drug use changes over time. The preferred starting point might instead be to make no assumptions at all, and so obtain maximal consensus (Manski, 1995). In this case, the data do not reveal the trends, but informative bounds may be obtained.
In the drug use context, however, analysis imposing no assumptions at all seems too conservative because there is good reason to believe that observed rates are lower bounds.4 I take this as a starting point. That is, I assume that in 1991 no less than 29 percent of 12th graders and 13 percent of adolescents ages 12–17 consumed illegal drugs. In 1997 no less than 42 percent of 12th graders and 19 percent of adolescents ages 12–17 consumed illegal drugs.
Under what additional assumptions do these data reveal time trends in the prevalence of drug use, or at least the directions of trends? I find that the necessary conditions depend on the response problem. Given nonresponse alone, the data effectively identify the direction of large changes in prevalence rates and even reveal the direction of smaller year-to-year variations under seemingly modest restrictions on the trends in use among nonrespondents. Drawing inferences given inaccurate response requires stronger assumptions. Given the inaccurate response
problem alone, the data do not reveal the levels, trends, or direction of even the larger changes in the prevalence rates of use. By restricting the variation over time in the accuracy of response and linking inaccurate response to the degree of stigma associated with using drugs, the direction of the trend can be identified.
NONRESPONSE
Nonresponse is an endemic problem in survey sampling. Each year, about 20 to 25 percent of selected individuals do not respond to the NHSDA questionnaire. In the MTF, nearly half of the schools originally surveyed refuse to participate, and nearly 15 percent of the surveyed students fail to respond to the questionnaire.5 The data are uninformative about nonrespondents. If illegal drug use systematically differs between respondents and nonrespondents, then the data may not identify prevalence levels or trends for the surveyed population.
To see this identification problem, let yt indicate whether a respondent used drugs in period t, with yt=1 if the respondent used drugs and 0 otherwise. Let zt indicate whether a respondent completed the survey in period t. We are interested in learning the fraction of users at time t
P[yt=1].
(1)
The problem is highlighted using the law of total probability, which shows that
P[yt=1]=P[yt=1|zt=1]P[zt=1]+P[yt=1|zt=0]P[zt=0].
(2)
The data identify the fraction of respondents, P[zt=1], and the usage rates among respondents, P[yt=1|zt=1]. The data cannot reveal the prevalence rates among those who did not respond, P[yt=1|zt=0].
Likewise, the data alone cannot reveal the magnitude or direction of the trend. For simplicity, assume that the fraction of nonrespondents is fixed over time.6 Then, to see this identification problem note that
P[yt+j=1]–P[yt=1]={P[yt+j=1|zt+j=1]
–P[yt=1|zt=1]}P[z=1]+{P[yt+j=1|zt+j=0]
–P[yt=1|zt=0]}P[z=0].
(3)
While the data reveal the trends in use for respondents, P[yt+j=1|zt+j= 1]–P[yt=1|zt=1], and the fraction of respondents, P[z=1], the data cannot reveal the trends in use for nonrespondents, P[yt+j=1|zt+j=0]– P[yt=1|zt=0].
Data Missing at Random
The most common assumption used to identify the fraction of users is to assume that, conditional on certain covariates, the prevalence rate for nonrespondents equals the rate for respondents.7 That is, nonresponse is random conditional on these covariates. This assumption is implicit when researchers use survey weights to account for nonresponse. In fact, the NHSDA includes sampling weights that apply a procedure common to many federal surveys. Nonresponse weights are derived under the assumption that within observed subgroups (e.g., age, sex, and race groups) the fraction of drug users is identical for respondents and nonrespondents. If this missing-at-random assumption is true, weights may correct for survey nonresponse. If false, the estimates may be biased.
I do not find it plausible to assume that the decision to respond to drug surveys is random. In fact, there is some evidence to support this claim. Reporting on a study in which nonrespondents in the NHSDA were matched to their 1990 census questionnaires, Gfroerer and colleagues (1997a:292) conclude that “The Census Match Study demonstrates that response rates are not constant across various interviewer, respondent, household, and neighborhood characteristics. To the extent that rates of drug use vary by these same characteristics, bias due to nonresponse may be a problem.” If the missing-at-random assumption applies within the subgroups, these observed differences between respondents and nonrespondents might be accounted for using sampling weights. However, since the Census Match Study does not reveal the drug use behavior of nonrespondents, there is no way to evaluate the validity of the missing at random assumption. Even within observed subgroups, nonresponse in surveys of illegal activities may be systematic.
Caspar (1992) provides the only direct evidence on the drug use be-
havior of nonrespondents. With a shortened questionnaire and monetary incentives, Caspar (1992) surveyed nearly 40 percent of the nonrespondents to the 1990 NHSDA in the Washington, D.C., area. In this survey, nonrespondents have higher prevalence rates than respondents. Whether these findings apply to all nonrespondents, not just the fraction who replied to the follow-up survey in the Washington, D.C., area, is unknown.
The Monotone Selection Assumption
Rather than impose the missing-at-random assumption, it might be sensible to assume that the prevalence rate of nonrespondents is no less than the observed rate for respondents. Arguably, given the stigma associated with use, nonrespondents have higher prevalence rates than respondents. Formally, this monotone selection assumption implies
P[yt=1|zt=1]=P[yt=1|zt=0]=1.
(4)
The lower bound results if the prevalence rate for nonrespondents equals the rate for respondents. The upper bound results if all nonrespondents consume illegal drugs. The true rate lies within these bounds.
This restriction on the prevalence rates for nonrespondents implies bounds on the population prevalence rates:
Notice that the lower bound is the fraction of respondents who use illegal drugs in the past year, while the upper bound increases with the fraction of nonrespondents. The width of the bound equals {1–P[yt=1|zt=1] }P[zt=0]. Thus, the uncertainty reflected in the bounds increases with the fraction of nonrespondents, P[zt=0] and decreases with the prevalence rates of respondents. In the extreme, if all respondents are using drugs, then the monotonicity assumption implies that all nonrespondents would be using drugs as well, so that the prevalence rate would be identified.
Given the MTS assumption in Equation (4), we can also bound the trend from time (t) to time (t+j):
{P[yt+j=1|zt+j=1]–P[yt=1|zt=1]}P[z=1]
+{P[yt+j=1|zt+j=1]–1}P[z=0]=P[yt+j=1]–P[yt=1]=
{P[yt+j=1|zt+j=1]–P[yt=1|zt=1]}P[z=1]
+{1–P[yt=1|zt=1]}P[z=0]
(6)
The upper bound for the trend equals the upper bound for the usage rate at time t+j minus the lower bound at time t. Thus, if the lower bound at time t exceeds the upper bound at time t+j, the fraction of users must have fallen over the period. Likewise, if the lower bound at time t+j exceeds the upper bound at time t, then the fraction of users must have risen.
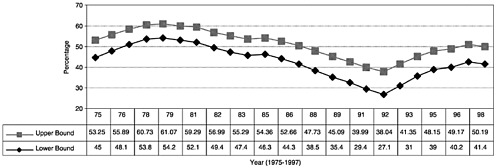
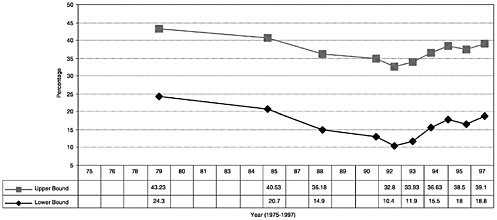
Figures D.2 and D.3 display the estimated bounds from 1975 to 1997 for 12th graders from the MTF survey and for adolescents ages 12–17 from the NHSDA, respectively. For simplicity, I assume the nonresponse rate is fixed at 15 percent in the MTF survey and 25 percent in the NHSDA. I also abstract from concerns about statistical variability and instead focus on the point estimates.
Under the monotone selection assumption, data from the MTF imply that the annual prevalence rate for 12th graders lies between 29 and 40 percent in 1991 and between 42 and 51 percent in 1997.9 Thus, the data bound the level estimates to lie within about a 10-point range. Notice also that these estimates imply that the fraction of users increased in the 1990s, although the magnitude of these changes and the directions of the year-to-year variations are not revealed. In particular, from 1991 to 1997, the prevalence rate increased by at least 2 points (from 40 to 42 percent), and perhaps by as much as 22 points (from 29 to 51 percent).
The bounds displayed in Figure D.2 reveal the uncertainly implied by student nonresponse to the MTF. These bounds, however, do not reflect school nonresponse. The MTF uses a clustered sampling design whereby schools and then individuals within a school are asked to participate in the study. Each year between 30 to 50 percent of the selected schools decline to participate and are replaced by similar schools in terms of observed characteristics such as size, geographic area, urbanicity, and so forth (Johnston et al., 1998a). In 1995, for example, nearly 38 percent of schools and 16 percent of students declined to participate, so that the overall response rate for the 12th grade survey is only 52 percent (Gfroerer et al., 1997b).
To the extent that nonrespondent schools have drug usage rates that systematically differ from respondent schools, inferences drawn using the survey will be biased. With school nonresponse and replacement rates of nearly 50 percent, this is an especially important nonresponse problem. If incorporated into the bounds developed above, the data no longer even reveal the direction of the largest trends.
Data from the NHSDA imply that the annual prevalence rate of use
for adolescents ages 12–17 lies between 13 and 35 percent in 1991 and between 19 and 39 percent in 1997. Thus, the data combined with the monotone selection assumption bound the prevalence rate to lie within about a 20-point range. In this case, the direction of the trend is not revealed. The fraction of users might have fallen by 16 points (from 35 to 19 percent) or increased by 26 points (from 13 to 39 percent). Thus, in the absence of additional information, the NHSDA data are uninformative about the direction of even large changes over this period. The sharp increase in the fraction of surveyed adolescents using illegal drugs during the 1990s does not rule out a sharp decrease in the rates of use for adolescents who failed to respond to the survey.
The Switching Threshold
There may be informative restrictions on the rate of use among nonrespondents over time that would allow one to identify the direction of the trend. Did the fraction of adolescent users increase in the 1990s? Certainly, that would be the case if we knew that the prevalence rates for respondents and nonrespondents moved in the same direction. More generally, the data could imply a positive trend even if one allowed for the possibility that fewer nonrespondents used illegal drugs, as long as the reduction in the prevalence rate for nonrespondents was not too large. If one is unwilling to rule out the possibility of extreme variation in the behavior of nonrespondents, for example, that all nonrespondents used drugs in 1991 but only 19 percent used drugs in 1997, then the data are less likely to reveal the direction of the trend.
The bound in Equation (6), however, does not impose explicit restrictions on the behavior of nonrespondents over time. Only the monotone selection assumption in Equation (4) applies. Consider, for example, the annual variation in the fraction of users in the early 1990s for adolescents ages 12–17, as revealed in Figure D.3. The bounds on trends allow for the possibility that the usage rate for nonrespondents increased from 10 percent in 1992 to 100 percent in 1993, then back to 12 percent in 1994, and so forth.
Some might argue that such extreme variation in the annual prevalence rate is unlikely. After all, in the NHSDA the reported prevalence rates from one year to the next have never increased by more than 4 percent and never decreased by more than 3 percent. Likewise, the observed annual change in the MTF is bounded between [–3.2, 4.8]. These bounds on the variation in prevalence rates for respondents cannot rule out more extreme volatility in the prevalence rates for nonrespondents. Still, it may be plausible to rule out year-to-year variation in the annual
prevalence rates for nonrespondents on the order of the 50 or more points allowed for in Figures D.2 and D.3.
Insight into whether the sign of the trend is identified can be found by evaluating the restrictions on the temporal variation in the prevalence rates of nonrespondents that would be required to identify the direction of change. Suppose that the direction of the trend in prevalence rates for respondents is positive (negative). Then, from Equation (3) we see that the direction of change for the population must also be positive (negative) if the prevalence rate for nonrespondents cannot fall (rise) by more than the switching threshold
(7)
Thus, if it is known that the growth in usage rates for nonrespondents is less (in absolute value) than this switching threshold, the sign of the trend is identified. If, however, the trend in use for nonrespondents might exceed this threshold, the sign of the trend is ambiguous. Notice that to identify the sign of the trend, one need not know the magnitude or direction of the trend for nonrespondents. Rather, one simply needs to rule out the possibility that the trend for nonrespondents exceeds this threshold.
Intuitively, the switching threshold increases with the fraction of respondents and with the prevalence rate of respondents. As the fraction of respondents increases, the behavior of nonrespondents has less impact on the overall prevalence rates; hence the trend in usage rates among nonrespondents must be more exaggerated to switch the sign of the observed trend. Likewise, as the observed prevalence rate of use increases over time, the switching threshold for nonrespondents must also increase.
Table D.2 displays the estimated switching threshold along with the annual trends in usage rates from the MTF. The threshold for the MTF survey is computed by multiplying the observed trend by –5.7(=–85/15). Consider, for instance, the trend from 1992 to 1993. The fraction of respondents using drugs increased 3.9 points, implying a switching threshold of –22.1(=–5.7*3.9). That is, for the annual trend from 1992 to 1993 to fall, the rate of use among nonrespondents must have declined by over 22 points. The monotonicity assumption in Equation (4) does not rule out such large drops among nonrespondents. In fact, the rate of use may have fallen by as much as 69 points, from 100 percent in 1992 to 31 percent in 1993. If, however, it is known that the annual variation in the prevalence rates for nonrespondents cannot exceed 20 points, then the sign of the trend is identified.
Table D.3 displays the estimated switching threshold along with the annual trends in usage rates from the NHSDA. In the NHSDA, there are
TABLE D.2 Observed Annual Trends in Prevalence Rates of Illegal Drug Use Among 12th Graders and the Switching Threshold for Nonrespondents, Monitoring the Future.
|
Year |
Observed Trend |
Switching Threshold 12th Graders |
|
1976 |
3.1 |
–17.6 |
|
1977 |
3.0 |
–17.0 |
|
1978 |
2.7 |
–15.3 |
|
1979 |
0.4 |
–2.3 |
|
1980 |
–1.1 |
6.2 |
|
1981 |
–1.0 |
5.7 |
|
1982 |
–2.7 |
15.3 |
|
1983 |
–2.0 |
11.3 |
|
1984 |
–1.6 |
9.1 |
|
1985 |
0.5 |
–2.8 |
|
1986 |
–2.0 |
11.3 |
|
1987 |
–2.6 |
14.7 |
|
1988 |
–3.2 |
18.1 |
|
1989 |
–3.1 |
17.6 |
|
1990 |
–2.9 |
16.4 |
|
1991 |
–3.1 |
17.6 |
|
1992 |
–2.3 |
13.0 |
|
1993 |
3.9 |
–22.1 |
|
1994 |
4.8 |
–27.2 |
|
1995 |
3.2 |
–18.1 |
|
1996 |
1.2 |
–6.8 |
|
1997 |
2.2 |
–12.5 |
|
1991–1997 |
13.0 |
73.7 |
three respondents for every nonrespondent. Thus, uncertainty about the direction of the trend exists only if one cannot rule out the possibility that the trend for nonrespondents is three times the negative of the observed trend. Since the observed prevalence rate increased by 5.7 points from 1991 to 1997, the trend is positive if the usage rates for nonrespondents did not fall by more than 17.1 points from 1991 to 1997. If one is willing to assume that the trends in usage rates cannot exceed this threshold, then the data identify the sign of the trend. Otherwise, the sign of the trend is indeterminate.
INACCURATE RESPONSE
Self-report surveys on deviant behavior invariably yield some inaccurate reports. Respondents concerned about the legality of their behavior may falsely deny consuming illegal drugs. Desires to fit into a deviant culture may lead some respondents to falsely claim to consume illegal
TABLE D.3 Observed Annual Trends in Prevalence Rates of Illegal Drug Use Adolescents Ages 12–17 and the Switching Threshold for Nonrespondents, National Household Survey of Drug Abuse.
|
Year |
Observed Trend |
Switching Threshold Adolescents Ages 12–17 |
|
1992 |
–2.7 |
8.1 |
|
1993 |
1.5 |
–4.5 |
|
1994 |
3.6 |
–10.8 |
|
1995 |
2.5 |
–7.5 |
|
1996 |
–1.3 |
3.9 |
|
1997 |
2.1 |
–6.3 |
|
1991–1997 |
5.7 |
17.1 |
drugs.10 Thus, despite considerable resources devoted to reducing misreporting in the national drug use surveys, inaccurate response remains an inherent concern. Surely some respondents fail to provide valid information about whether they consume illegal drugs.
Inaccurate reporting in drug use surveys is conceptually different from the nonresponse problem examined above. While the fraction of nonrespondents is known, the data do not reveal the fraction of respondents who give invalid responses to the questionnaire. It might be that all positive reports are invalid, in which case the usage rate may be zero. Alternatively, it might be that all negative reports are invalid, in which case the entire population may have consumed illegal drugs. Thus, to draw inferences about the fraction of users in the United States, one must impose assumptions about self-reporting errors.
To evaluate the impact of invalid response on the ability to infer levels of use, I introduce notation that distinguishes between self-reports and the truth. Let wt be the self-reported measure in period t, where wt= 1 if the respondent reported use and 0 otherwise. Let yt be the truth, where yt=1 if the respondent consumed drugs and 0 otherwise. We are interested in learning probability of use, P[yt=1]. Formally, we can relate this unobserved prevalence rate to the self-reported usage rates as follows:
P[yt=1]=P[wt=1, yt=1]+P[wt=0, yt=1]=P[wt=1]
+P[wt=0, yt=1]–P[wt=1, yt=0].
(8)
The data identify the fraction of the population who self-report use, P[wt =1]. The data cannot identify the fraction who falsely claim to have consumed drugs, P[wt=1, yt=0], or who falsely claim to have abstained, P[wt=0, yt=1]. The data identify prevalence rates if the fraction of false negatives is exactly offset by the fraction of false positive reports, that is, if P[wt=0, zt=0]=P[wt=1, zt=0]. Otherwise, the fraction of users is not identified.
Magnitude of Inaccurate Response
There is a large literature that provides direct evidence on the magnitude of misreporting in some self-reported drug use surveys. Validation studies have been conducted on arrestees (see, for example, Harrison 1992 and 1997; Mieczkowski, 1990), addicts in treatment programs (see, for example, Darke, 1998; Magura et al., 1987, 1992; Morral et al., 2000; Kilpatrick et al., 2000), employees (Cook et al., 1997), people living in high-risk neighborhoods (Fendrich et al., 1999), and other settings. See Harrison and Hughes (1997) for a review of the literature.
The most consistent information is collected as part of the Arrestee Drug Abuse Monitoring/Drug Use Forecasting (ADAM/DUF) survey of arrestees. To enable inferences on the extent of inaccurate reporting among arrestees, this survey elicits information on drug use from self-reports and urinalysis.11 Harrison (1992, 1997), for example, compares self-reports of marijuana and cocaine use during the past three days to urinalysis test results for the same period. In general, between 20 and 30 percent of respondents appear to give inaccurate responses. In the 1988 survey, for example, 27.9 percent of respondents falsely deny using cocaine and 1.4 percent falsely claim to have used cocaine. For marijuana, the false negative rates are lower (18.1 percent) and the false positive rates are higher (6.4 percent), but the same basic picture emerges. About half of those testing positive report use, while a substantially higher fraction testing negative report truthfully.
Despite this literature, very little is known about misreporting in the national probability samples. The existing validation studies have largely been conducted on samples of people who have much higher rates of drug use than the general population. Response rates in the validation studies are often quite low and, moreover, respondents are usually not randomly sampled from some known population.
A few notable studies have attempted to evaluate misreporting in broad-based, representative samples. However, lacking direct evidence on misreporting, these studies have to rely on strong, unverifiable assumptions to infer validity rates. Biemer and Witt (1996), for instance, analyze misreporting in the NHSDA under the assumptions that (1) smoking tobacco is positively related to illegal drug use and (2) the inaccurate reporting rate is the same for both smokers and nonsmokers. Under these assumptions, they find false negative rates (defined here as the fraction of users who claim to have abstained) in the NHSDA that vary between 0 and 9 percent. Fendrich and Vaughn (1994) evaluate denial rates using panel data on illegal drug use from the National Longitudinal Survey of Youth (NLSY), a nationally representative sample of individuals who were ages 14–21 in the base year of 1979. Of the respondents to the 1984 survey who claimed to have ever used cocaine, nearly 20 percent denied use and 40 percent reported less frequent lifetime use in the 1988 follow-up. Likewise, of those claiming to have ever used marijuana in 1984, 12 percent later denied use and just over 30 percent report less lifetime use. These logical inconsistencies in the data are informative about validity if the original 1984 responses are correct.
These papers make important contributions to the literature. In particular, they illustrate the types of models and assumptions that are required to identify the extent of misreporting in the surveys.12 Still, the conclusions are based on unsubstantiated assumptions. Arguably, smokers and nonsmokers may have different reactions to stigma and thus may respond differently to questions about illicit behavior. Arguably, the self-reports in the 1984 NLSY are not all valid.
To evaluate the fraction of users in the population in light of inaccurate response, I begin by imposing the following assumptions on misreporting rates:
IR-1: In any period t, no more than P percent of the self-reports are invalid. That is, P[wt=0, yt=1]+P[wt=1, yt=0]=P.
IR-2: The fraction of false negative reports exceeds the fraction of false positive reports. That is, P[wt=0, yt=1]=P[wt=1, yt=0].
These assumptions imply that the prevalence rate is bounded as follows:
P[wt=1]=P[yt=1]=min{P[wt=1]+P, 1}.
(9)
The upper bound follows from IR-1, whereas the lower bound follows
from IR-2. Under these assumptions, the observed trends provide a lower bound for the prevalence rate of use for illegal drugs. The upper bound depends on both the self-reported prevalence rates as well as the largest possible fraction of false negative reports, P.
The upper bound P on the fraction of false reports is not revealed by the data but instead must be known or assumed by the researcher. Suppose, for purposes of illustration, one knows that less than 30 percent of respondents give invalid self-reports of illegal drug use. In this case, the width of the bound on prevalence rates is 0.30, so that the data provide only modest information about the fraction of users. Consider, for instance, estimating the fraction of 12th graders using drugs in 1997. In total, 42.4 percent of respondents in the MTF reported consuming drugs during the year. If as many as 30 percent of respondents give false negative reports, the true fraction of users must lie between 42.4 and 72.4 percent.
Alternatively, one might consider setting this upper bound figure much lower than 30 percent. Suppose, for example, one is willing to assume that less than 5 percent of respondents provide invalid reports of drug use. In this case, the prevalence bounds from Equation 9 will be more informative. The estimated prevalence rate of use for 12th graders in 1997, for instance, must lie between [42.4, 47.4] percent.
Clearly, our ability to draw inferences on the prevalence rate of drug use in the United States depends directly on the magnitude of inaccurate reporting. Without better information, readers may differ in their opinions of the persuasiveness and plausibility of particular upper bound assumptions. A 30-point upper bound may be consistent with the inaccurate reporting rates found in DUF/ADAM, but whether arrestees are more or less likely to hide illegal activities is unknown.13 A 5-point upper bound may be consistent with the model-based results of Biemer and Witt (1996), but whether the model accurately measures the degree of inaccurate reporting is unknown.
Inaccurate Reporting Rates Over Time
Despite acknowledged uncertainty surrounding the level estimates, many continue to assert that the data do in fact reveal trends. What restrictions would need to be imposed to identify the trend or direction of
the trend? Assume, for convenience, that the fraction of people falsely reporting that they used drugs is fixed over time. In this case, the trend is revealed if the fraction of people falsely denying use is also fixed over time. The direction of the trend is revealed if one can rule out the possibility that the fraction of respondents falsely denying use changes enough to offset the observed trend. For instance, the reported prevalence rates for adolescents ages 12–17 in the NHSDA increased from 13.1 percent in 1991 to 18.8 percent in 1997. As long as the fraction of respondents falsely denying use did not decrease by more than 5.7 points, the actual prevalence rate increased.
Formally, the trend equals
P[yt+j=1]–P[yt=1]=
P[wt+j=1]–P[wt=1]
+{P[wt+j=0, yt+j=1]–P[wt+j=1, yt+j=0]}
–{P[wt=0, yt=1]–P[wt=1, yt=0]}
(10)
The growth in prevalence rates equals the trend in reported use plus the trend in net misreporting, where net misreporting is defined as the difference between the fraction of false negative and false positive reports. Thus, the data identify trends if net misreporting is fixed over time. This assumption does not require the fraction of false negative reports to be fixed over time. Rather, any change in the fraction of false negative reports must be exactly offset by an equal change in the fraction of false positives.
For the drug use surveys, this invariance assumption seems untenable. There is no time-series evidence on inaccurate response that is directly relevant to the national household surveys. Some, however, have argued that the propensity to give valid responses is affected by social pressures that have certainly changed over time. That is, the incentive to give false negative reports may increase as drug use becomes increasingly stigmatized (Harrison, 1997). In this case, inaccurate response is likely to vary over time.
Figure D.4 displays the MTF and NHSDA reported time-series in prevalence rates along with measures of the stigma of drug use elicited from MTF 12th graders and from NHSDA respondents ages 12–17. This stigma index measures the fraction of respondents who either disapprove of illegal drug consumption (MTF) or perceive it to be harmful (NHSDA).14 The striking feature of this figure is that these prevalence rate
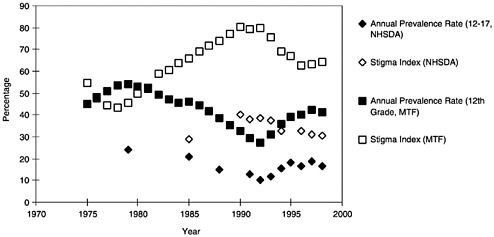
FIGURE D.4 Prevalence of use rates and the stigma index, 1975–1999, National Household Survey of Drug Abuse (NHSDA) and Monitoring the Future (MTF). Note: The specific question from MTF used to create this index is: “Do you disapprove of people (who are 18 or older) smoking marijuana occasionally?” The NHSDA question used to create the index is: “How much do you think people risk harming themselves physically or in other ways when they smoke marijuana occasionally/once a month?” This question is asked of 12–17-year-olds.
SOURCE of Stigma Index: LD Johnston, PM O’Malley, JG Bachman. (Dec. 1998). Drug use by American young people begins to turn downward. University of Michigan News and Information Services: Ann Arbor, MI. [On_line]. Table 9. Available: www.isr.umich.edu/src/mtf; accessed 11/16/99.
and stigma series are almost mirror images of each other. As stigma increases, use decreases. One might interpret these results as evidence that the reported measures are valid. That is, use decreases as perceptions of harm increase. Alternatively, these results are consistent with the idea that changes in stigma are associated with changes in invalid reporting. As stigma increases, false negative reports increase. The consensus view that the data reveal trends seems inconsistent with the view that the fraction of false reports varies with the stigmatization of drugs.
In the absence of an invariance assumption, the data do not identify the trends in illegal drug use. However, the data might reveal the direction of the trend. Consider the level estimates implied by assumption IR-1 and IR-2. Here, if P=0.30, the width of the bound on trends is 60 points—the observed trend plus and minus 0.30. In this case, the sign of the trend is identified if the observed prevalence rates change by more than 30 points over the period.
In practice, this bound implies that the data do not in general reveal the direction of the trend in prevalence rates. Since the observed annual (absolute) change in the prevalence rates never exceeds 5 points, the sign of the annual trend is not identified. Likewise, the observed increase in the fraction of adolescent users during the 1990s is at most estimated to be around 13 points. Thus, if one adopts the restriction that the invalid response rate is less than 30 percent, the observed data would not reveal whether use increased in the 1990s. If one were willing to impose a stronger restriction on misreporting (e.g., P=0.05), the observed data would be able to identify the sign of this trend.
Linking Stigma and Inaccurate Reporting
Imposing explicit restrictions on the behavior of invalid response over time can further narrow the bounds on the trends in prevalence rates. Suppose there is a positive relationship between false negative reporting and the stigmatization of illegal drugs. In particular, assume that
IR-3: the fraction of false positive reports, P[wt=1, yt=0], is fixed over time,
and that
IR-4: the fraction of users who claim to have abstained, P[wt=0|yt= 1], increases with an index, St, of the degree that illicit drugs are stigmatized. That is, if St+j=St, then P[wt+j=0|yt+j=1]=P[wt+j=0|yt= 1].
If stigma increases over time, assumptions IR 1–4 imply that
Min{P[wt+j=1]–P[wt=1], (P[wt+j=1]
–P[wt=1])/{1–Kmax)}
=P[yt+j=1]–P[yt=1]=
P[wt+j=1]–P[wt=1]+P,
(11)
where Kmax=P/(P+max(P[wt+j=1], P[wt=1]).15 A similar formula applies when stigma falls during the period of interest.
Intuitively, if both the observed trends in stigma and in the fraction of drug users are positive, the data reveal that the prevalence rates increased. In particular, the trend in illegal drug consumption will be no less than the observed trend and no greater than the reported trend plus P. Thus, by imposing assumptions IR-3 and IR-4, the width of the bound on the trend is reduced in half, from 0.60 to 0.30 when P=0.30. If the reported trend is negative, the results are less certain. Here, the lower bound will be less than the reported negative trend, while the upper bound will be positive if the reported prevalence rates from period (t) to (t+j) declined by less than P points.
Table D.4 presents the annual trend in the fraction of high school seniors who report using illegal drugs, the direction of change in the stigma index (1=stigma increased, –1=stigma decreased) and the estimated bounds for the annual trend under that assumption that no more than 30 percent of respondents misreport drug use. These bounds on trends are much tighter than those derived without imposing the additional assumptions IR-3 and IR-4. In fact, the uncertainty is reduced nearly in half from 60 points to just over 30 points. Even under these stronger assumptions, however, the data do not generally reveal the sign of the annual trend. In only three cases do the data reveal that the annual trend in prevalence rates increases, while in one case the prevalence rate falls. In all other cases, the estimated sign of the annual trend is uncertain, reflecting the fact that the reported trends are almost a mirror image of the trends in the stigma index (see Figure D.4).
Consider, for instance, the bounds on the trend from 1991 to 1992. During this period, the fraction of self-reported users declined by 2.3 points. Over the same period, the stigma index increased. Thus, from Equation (11), we know that the upper bound on the trend equals –2.3+P and the lower bound on the trend lies slightly below the observed trend. If the maximum possible misreporting rate is greater than 2.3 percent, the data cannot reject the possibility that the trend is positive. In contrast, the fraction of self-reported users from 1990 to 1991 decreased by 3.1 points, while the stigma index also decreased. In this case, the bounds are strictly negative regardless of P.
TABLE D.4 Bounds on Annual Trends in Illegal Drug Consumption for 12th Graders Given Invalid Reporting, Monitoring the Future
|
Reported Year |
Reported Trend |
Stigmaa |
LB(30)b |
UB(30)b |
|
1976 |
3.1 |
–1 |
–26.9 |
5.0 |
|
1977 |
3.0 |
–1 |
–27.0 |
4.8 |
|
1978 |
2.7 |
–1 |
–27.3 |
4.2 |
|
1979 |
0.4 |
1 |
0.4 |
30.4 |
|
1980 |
–1.1 |
1 |
–1.7 |
28.9 |
|
1981 |
–1.0 |
1 |
–1.6 |
29.0 |
|
1982 |
–2.7 |
1 |
–4.3 |
27.3 |
|
1983 |
–2.0 |
1 |
–3.2 |
28.0 |
|
1984 |
–1.6 |
1 |
–2.6 |
28.4 |
|
1985 |
0.5 |
1 |
0.5 |
30.5 |
|
1986 |
–2.0 |
1 |
–3.3 |
28.0 |
|
1987 |
–2.6 |
1 |
–4.4 |
27.4 |
|
1988 |
–3.2 |
1 |
–5.5 |
26.8 |
|
1989 |
–3.1 |
1 |
–5.5 |
26.9 |
|
1990 |
–2.9 |
1 |
–5.4 |
27.1 |
|
1991 |
–3.1 |
–1 |
–33.1 |
–3.1 |
|
1992 |
–2.3 |
1 |
–4.6 |
27.7 |
|
1993 |
3.9 |
–1 |
–26.1 |
7.7 |
|
1994 |
4.8 |
–1 |
–25.2 |
8.8 |
|
1995 |
3.2 |
–1 |
–26.8 |
5.7 |
|
1996 |
1.2 |
–1 |
–28.8 |
2.1 |
|
1997 |
2.2 |
1 |
2.2 |
32.2 |
|
1991–1997 |
13.0 |
–1 |
–17.0 |
22.4 |
|
aReported stigma equals 1 if the stigma index increased and –1 if it decreased. The specific question from MTF used to create this index is: “Do you disapprove of people (who are 18 or older) smoking marijuana occasionally?” The NHSDA question used to create the index is: “How much do you think people risk harming themselves physically or in other ways when they smoke marijuana occasionally/once a month?” bUB(z) and LB(z) are the upper and lower bound respectively, under the assumption that no more than z percent of the respondents would give invalid responses. Source of Stigma Index Data: LD Johnston, PM O’Malley, JG Bachmam, 1998b. Drug use by American young people begins to turn downward. University of Michigan News and Information Services: Ann Arbor, MI. [On_line]. Table 9. Available:www.isr.umich.edu/src/mtf; accessed 11/16/99. |
||||
The bounds in Equation (11) may also be used to examine whether the prevalence rate increased from 1991 to 1997. Over this period, the observed rate increased while stigma appeared to be decreasing. Thus, even under the stronger restrictions implied by IR3–4, the data may not reveal whether the large reported increase in use over the 1990s reflects an underlying increase in the number of adolescent users, or if it instead
indicates changes in the degree of inaccurate reporting. Depending on the maximum inaccurate reporting rate, P, the sign of the trend may be ambiguous. In fact, if P=0.30, the lower bound is negative. For the MTF, the bound restricts the trend to lie between –17.0 and 22.4, while for the NSHDA the bound implies that the trend lies between [–24.3, 35.7]. With P=0.05, however, the lower bound is positive. In this case, the bound for MTF 12th graders is [8.0, 14.6] and for NHSDA adolescents is [0.7, 10.7].
CONCLUSIONS
The Monitoring the Future survey and the National Household Survey of Drug Abuse provide important data for tracking the numbers and characteristics of illegal drug users in the United States. Response problems, however, continue to hinder credible inference. While nonresponse may be problematic, the lack of detailed information on the accuracy of response in the two national drug use surveys is especially troubling. Data are not available on the extent of inaccurate reporting or on how inaccurate response changes over time. In the absence of good information on inaccurate reporting over time, inferences on the levels and trends in the fraction of users over time are largely speculative. It might be, as many have suggested, that misreporting rates are stable over time. It might also be that these rates vary widely from one period to the next.
These problems, however, do not imply that the data are uninformative or that the surveys should be discontinued. Rather, researchers using these data must either tolerate a certain degree of ambiguity or must be willing to impose strong assumptions. The problem, of course, is that ambiguous findings may lead to indeterminate conclusions, whereas strong assumptions may be inaccurate and yield flawed conclusions (Manski, 1995; Manski et al., 2000).
There are practical solutions to this quandary. If stronger assumptions are not imposed, the way to resolve an indeterminate finding is to collect richer data. Data on the nature of the nonresponse problem (e.g., the prevalence rate of nonrespondents) and on the nature and extent of inaccurate response in the national surveys might be used to both supplement the existing data and to impose more credible assumptions. Efforts to increase the valid response rate may reduce the potential effects of these problems.
ACKNOWLEDGMENT
I wish to thank Richard Bonnie, Joel Horowitz, Charles Manski, Dan Melnick, and the members of the Committee on Data and Research for Policy on Illegal Drugs for their many helpful comments on an earlier
draft of this paper. Also, I would like to thank Faith Mitchell at the National Research Council for her participation in this project.
TECHNICAL NOTE: STIGMA MODEL
In this appendix, I derive the Equation (11) bounds on the prevalence rate of use implied by assumptions IR 1–4. Recall that
IR-3: the fraction of false positive reports, P[wt=1, yt=0], is fixed over time,
and
IR-4: the fraction of users who claim to have abstained, P[wt=0|yt= 1], increases with an index, St, of the degree that illicit drugs are stigmatized. That is, if St+j=St, then P[wt+j=0|yt+j=1]=P[wt+j=0|yt= 1].
The restriction imposed in IR-3 serves to simplify the notation and can be easily generalized. Under this assumption, inferences about trends in illicit drug use are not influenced by false positive reports. That is,
P[yt+j=1]–P[yt=1]=P[wt+j=1]–P[wt=1]
+P[wt+j=0, yt+j=1]–P[wt=0, yt=1].
(A1)
Note that this restriction does not contain identifying information. In the absence of additional restrictions, assumptions IR 1–3 imply that in both periods (t) and (t+j) the fraction of false negative reports must lie between [0, P]. Thus, the upper bound on the trend in prevalence rates equals the observed trend plus P, while the lower bound is the observed trend minus P. The width of the bound on trend remains 2P.
By restricting the false negative reports over time, Assumption IR-4 does narrow the bounds. Rewrite Equation (A1) as
P[yt+j=1]–P[yt=1]
=P[wt+j=1]–P[wt=1]
+P[wt+j=0|yt+j=1]P[yt+j=1]–P[wt
=0|yt=1]P[yt=1]
(A2)
and consider the case where the stigma of using drugs increases from period (t) to (t+j).16 Although assumption IR-4 does not affect the upper bound, it does narrow the lower bound: the fraction of users who claim to have abstained cannot decrease over time. Thus, the lower bound is found by setting the two conditional probabilities equal in which case we know that
P[yt+j=1]–P[yt=1]∃{P[wt+j=1]–P[wt=1]}/(1–K),
(A3)
where K is the common misreporting rate.
This lower bound depends on the possible value of K, which must lie between
0≤K≤P/(P+max(P[wt+j=1], P[wt=1])=Kmax.17
(A4)
Equations (A3) and (A4) imply that if the observed trend is positive, the lower bound is found by setting K=0. If the observed trend is negative, the lower bound is found by setting K=Kmax.
Thus, under assumptions IR 1–4
Min{P[wt+j=1]–P[wt=1], (P[wt+j=1]
–P[wt=1])/(1–Kmax)}
≤P[yt+j=1]–P[yt=1]≤
P[wt+j=1]–P[wt=1]+P.
(A5)
REFERENCES
Anglin, M.D., J.P.Caulkins, and Y.-I Hser 1993 Prevalence estimation: Policy needs, current status, and future potential. Journal of Drug Issues 345–361.
Biemer, P., and M.Witt 1996 Estimation of measurement bias in self-reports of drug use with applications to the National Household Survey on Drug Abuse. Journal of Official Statistics 12(3):275–300.
Caspar, R. 1992 Followup of nonrespondents in 1990. In C.F.Turner, J.T.Lessler, and J.C.Gfroerer, eds., Survey Measurement of Drug Use: Methodological Studies. DHHS Pub. No (ADM) 92–1929.
Cook, R.F., A.D.Bernstein, and C.M.Andrews 1997 Assessing drug use in the workplace: A comparison of self-report, urinalysis, and hair analysis. In L.Harrison and A.Hughes, eds., The Validity of Self-Reported Drug Use: Improving the Accuracy of Survey Estimates. NIDA Research Monograph, Number 167.
Darke, S. 1998 Self report among injecting drug users: A review. Drug Alcohol Dependence 51:253– 63.
Fendrich, M., T.P.Johnson, S.Sudman, J.S.Wislar, and V.Spiehler 1999 Validity of drug use reporting in a high risk community sample: A comparison of cocaine and heroin survey reports with hair tests. American Journal of Epidemiology 149(10):955–962.
Fendrich, M., and C.M.Vaughn 1994 Diminished lifetime substance use over time: An inquiry into differential underreporting. Public Opinion Quarterly 58(1):96–123.
Gfroerer, J., J.Lessler, and T.Parsley 1997 Studies of nonresponse and measurement error in the National Household Survey on Drug Abuse. Pp. 273–295 in L.Harrison and A.Hughes, eds., The Validity of Self-Reported Drug Use: Improving the Accuracy of Survey Estimates. NIDA Research Monograph, Number 167.
Gfroerer, J., D.Wright, and A.Kopstein 1997 Prevalence of youth substance use: The impact of methodological differences between two national surveys. Drug and Alcohol Dependence 47:19–30.
Harrison, L.D. 1992 Trends in illicit drug use in the United States: Conflicting results from national surveys. International Journal of the Addictions 27(7):917–947.
1997 The validity of self-reported drug use in survey research: An overview and critique of research methods. Pp. 17–36 in L.Harrison and A.Hughes, eds., The Validity of Self-Reported Drug Use: Improving the Accuracy of Survey Estimates. NIDA Research Monograph, Number 167.
Harrison, L.D., and A.Hughes, eds. 1997 The Validity of Self-Reported Drug Use: Improving the Accuracy of Survey Estimates. NIDA Research Monograph, Number 167.
Horowitz, J., and C.F.Manski 1998 Censoring of outcomes and regressors due to survey nonresponse: Identification and estimation using weights and imputations. Journal of Econometrics 84:37–58.
2000 Nonparametric analysis of randomized experiments with missing covariate and outcome data. Journal of the American Statistical Association 95:77–84.
Johnston, L.D., P.M.O’Malley, and J.G.Bachman 1998a National Survey Results on Drug Use from the Monitoring the Future Study, 1975– 1997, Vol. I.
1998b Drug Use by American Young People Begins to Turn Downward. University of Michigan News and Information Services, Ann Arbor, MI. [On line]. Tables 1b and 3. Available: www.isr.umich.edu/src/mtf [accessed 11/16/99].
Kilpatrick, K., M.Howlett, P.Dedwick, and A.H.Ghodse 2000 Drug use self-report and urinalysis. Drug and Alcohol Dependence 58(1–2):111–116.
Magura, S., D.Goldsmith, C.Casriel, P.J.Goldstein, and D.S.Linton 1987 The validity of methadone clients’ self-reported drug use. International Journal of Addiction 22(8):727–749.
Magura, S., R.C.Freeman, Q.Siddiqi, and D.S.Lipton 1992 The validity of hair analysis for detecting cocaine and heroin use among addicts. International Journal of Addictions 27:54–69.
Manski, C.F. 1995 Identification Problems in the Social Sciences. Cambridge, MA: Harvard University Press.
Manski, C.F., J.Newman, and J.V.Pepper 2000 Using Performance Standards to Evaluate Social Programs with Incomplete Outcome Data: General Issues and Application to a Higher Education Block Grant Program. Thomas Jefferson Center Discussion Paper 312.
Manski, C.F., and J.V.Pepper 2000 Monotone instrumental variables: With an application to the returns to schooling. Econometrica 68(4):997–1010.
Mieczkowski, T.M. 1996 The prevalence of drug use in the United States. Pp. 347–351 in M.Tonry, ed., Crime and Justice: A Review of Research, Vol. 20.
1990 The accuracy of self-reported drug use: An evaluation and analysis of new data. In R Weisheit, ed., Drugs, Crime and the Criminal Justice System.
Molotsky, I. 1999 Agency survey shows decline last year in drug use by young. New York Times, August 19.
Morral, A.R., D.McCaffrey, and M.Y.Iguchi 2000 Hardcore drug users claim to be occasional users: Drug use frequency underreporting. Drug and Alcohol Dependence 57(3):193–202.
Office of Applied Studies 1997 National Household Survey on Drug Abuse: Main Findings 1997. U.S. Department of Health and Human Services, Substance Abuse and Mental Health Services Administration. Table 2.6. Available: http://www.samhsa.gov/oas/NHSDA/1997Main/Table%20of%20Contents.htm; accessed 11/16/99