APPENDIX
A
Models for County and State Poverty Estimates
William R. Bell
Statistical Research Division, Bureau of the Census
This appendix reviews the models investigated by the Census Bureau for the 1993 county poverty estimates for children aged 5-17; the state model is also reviewed briefly. The same model forms can be used for poverty statistics for other age groups, with appropriately defined dependent and regression variables.
NOTATION
The following notation is used in the estimation program:
-
yit = CPS 5-17 poverty estimate for county i in year t;
-
Ceni = previous census estimate for county i (where necessary, a specific census is distinguished by writing Cen90 i or Cen80i);
-
Yit, Zi = “true” quantities estimated by yit and Ceni (i.e., Zi is not assumed to be true poverty, since the census could be biased relative to CPS);
-
eit,
 = sampling errors in yit and Ceni, assumed independent N (0, ve/nit) and N (0, ci), with ci and nit known, and ve a parameter to be estimated;
= sampling errors in yit and Ceni, assumed independent N (0, ve/nit) and N (0, ci), with ci and nit known, and ve a parameter to be estimated; -
nit = CPS sample size (number of households) in county i in year t;
-
xit, xi,89 = vectors of a constant term (i.e., 1) and regression variables from administrative records for county i in income years t and 1989, respectively;
-
β, η = corresponding vectors of regression parameters.
The CPS data that are modeled are for income year (t) 1993 or 1989 (for CPS samples taken in March 1994 and March 1990, respectively). The census data
modeled are from the 1990 census and are for income year 1989. The 1980 census data (for income year 1979) enter SAIPE models as regression variables in the equation for the 1990 census data but are not themselves the dependent variable in any model (because the corresponding regression variables xi,79 are not available.)
Note that yit = Yit + eit and ![]() . The nature of Yit and Zi, and their estimators, yitand Ceni, varies. They can be log(numbers of poor), log(poverty rates), or unlogged poverty rates, depending on the model. Similarly, xit and xi,89 vary over models. These variations are noted below for the specific models.
. The nature of Yit and Zi, and their estimators, yitand Ceni, varies. They can be log(numbers of poor), log(poverty rates), or unlogged poverty rates, depending on the model. Similarly, xit and xi,89 vary over models. These variations are noted below for the specific models.
The CPS estimates yit and sample sizes nit are 3-year “averages” of CPS estimates centered on year t. The specific formulation depends on whether log(numbers of poor children) are being modeled, as opposed to either child poverty rates or their logarithms (see below for details). Given that yit involves a 3-year average, the corresponding “sample size” nit is defined by counting the number of households in sample in county i in each year of the average (t − 1, t, t + 1) and adding the three numbers together. For counties with a CPS sample in only 2 of the 3 years, yit is defined from just a 2-year average, and the corresponding nit is defined by summing the households in sample for the 2 years. For counties with a sample in just one of the years, the estimate and sample size for just that year are used.
MODELS
SAIPE Model for Log Number Poor
Let yit and Ceni denote CPS and census estimates of log(number of poor related children, 5-17). The 1993 SAIPE model (using CPS data for income year 1993) is
![]()
![]()
The model errors wit and ![]() are both assumed i.i.d. N(0,
are both assumed i.i.d. N(0, ![]() ) and independent of each other.1 The basic regression variables xit are defined below. Recall that eit and
) and independent of each other.1 The basic regression variables xit are defined below. Recall that eit and ![]() , the sampling errors in yit and Cen90i, are assumed independent
, the sampling errors in yit and Cen90i, are assumed independent
|
1 |
Assuming wit independent of |
N(0, ve/ nit) and N(0, ci), with ci and nitknown, and ve a parameter to be estimated. The unknown parameters to be estimated in (1) and (2) are thus the regression parameters β, γ, η, and ![]() ; the common model error variance
; the common model error variance ![]() ; and the sampling error variance parameter ve. Decennial census sampling error variances for estimates of number of poor are available from published formulas (generalized variances). If Ri = exp(Cen90i) is the census estimated number of poor, then from a Taylor series linearization, ci, the sampling error variance in Cen90i, is approximately
; and the sampling error variance parameter ve. Decennial census sampling error variances for estimates of number of poor are available from published formulas (generalized variances). If Ri = exp(Cen90i) is the census estimated number of poor, then from a Taylor series linearization, ci, the sampling error variance in Cen90i, is approximately
![]()
Actually, a slight refinement of (3), based on properties of the lognormal distribution was used, as described by Fisher (1997). Practically speaking, the results are not materially different from (3).
The key distinguishing feature of the SAIPE model is the use of the previous census data as a regression variable—the γCen90i term in (1) and the ![]() Cen80i term in (2). This SAIPE model form contrasts with the bivariate model efform, discussed in the next section. In the SAIPE model form the model error variance, denoted here by
Cen80i term in (2). This SAIPE model form contrasts with the bivariate model efform, discussed in the next section. In the SAIPE model form the model error variance, denoted here by ![]() , can be essentially thought of as Var(Yi | xi, Cen90i), which differs from the model error variance for the bivariate model form,
, can be essentially thought of as Var(Yi | xi, Cen90i), which differs from the model error variance for the bivariate model form, ![]() = Var(Yi | xi). The two are not comparable; one would expect
= Var(Yi | xi). The two are not comparable; one would expect ![]() <
< ![]() .
.
The 1989 SAIPE model (using CPS data for income year 1989) is
(![]()
![]()
with t = 1989. Notice that xit = xi,89, and the regression variables in (4) and (5) are the same. The regression parameters, (β, γ) and (η, ![]() ), are still allowed to be different, however. The same assumptions as above are made about the model errors. Assuming that wit and
), are still allowed to be different, however. The same assumptions as above are made about the model errors. Assuming that wit and ![]() are independent makes less sense here, since both equations refer to the same year and Cen90i does not enter (4) as a regression variable. Fortunately, this assumption is unnecessary. Since (4) and (5) contain “identical explanatory variables,” regression fitting of these two equations separately produces the same results as fitting them jointly (Theil, 1971:309-310). Finally, notice that the second (census) equations of both the 1993 and 1989 SAIPE models—(2) and (5)—must be the same. Although it might be more appropriate for the 1989 model to replace (5) by the corresponding equation for Cen80i, this cannot be done because the required regression variables xi,79 are not available.
are independent makes less sense here, since both equations refer to the same year and Cen90i does not enter (4) as a regression variable. Fortunately, this assumption is unnecessary. Since (4) and (5) contain “identical explanatory variables,” regression fitting of these two equations separately produces the same results as fitting them jointly (Theil, 1971:309-310). Finally, notice that the second (census) equations of both the 1993 and 1989 SAIPE models—(2) and (5)—must be the same. Although it might be more appropriate for the 1989 model to replace (5) by the corresponding equation for Cen80i, this cannot be done because the required regression variables xi,79 are not available.
For this and other models of log(number poor), the CPS estimates yit are defined using 3 years of CPS data for each county i as follows:
yit = log([3-yr weighted avg poverty rate] × [3-yr weighted avg poverty universe]). (6)
The weights given to data from years t − 1, t, and t + 1 for the weighted averages in (6) are proportional to the numbers of interviewed housing units in county i that contain at least one child aged 5-17 for the year in question. The CPS poverty rate in (6) for county i in year j (= t − 1, t, t + 1) is

Note that the second term in (6) is the 3-year weighted average of the denominators in (7) for j = t − 1, t, t + 1. The CPS poverty universe, and the number of poor related children aged 5-17, are estimated from CPS data for each year using CPS weights modified to make each county “self-representing.”
For counties with a CPS sample in only 1 or 2 of the 3 years, the values for only that year, or for the 2-year average corresponding to (6), are used. For counties with no poor children observed in the CPS sample, the direct CPS estimate of the number of poor children is 0. Since logarithms cannot be taken when the direct estimate is 0, yit is not defined, and these counties must be dropped from the model fitting. The same problem arises with the census data, though only for a few counties.
The basic regression variables, xit = (x0it, ..., x4it)′, are defined as follows, all but x0it derived from tabulating certain data for each county i:
x0it = 1 (constant term)
x1it = log (number of IRS dependent child tax exemptions on tax returns with income below poverty);
x2it = log (number of food stamp program participants) (from USDA);
x3it = log (resident population aged 0-21);
x4it = log (number of IRS total dependent child tax exemptions). (8)
More recently, Census Bureau analysts have experimented with changing the age limits defining x3it to 0-17. This removed some bias found in evaluations and regression diagnostics for counties with high group quarters populations (usually because of college dorms and military barracks).
Bivariate Model for Log Number Poor
Let yit and Ceni denote estimates of log(number of poor), as above. The bivariate model form is
![]()
![]()
The model errors uit and zi are both i.i.d. N(0, ![]() ), with
), with ![]()
![]() constant over i. This is the “constrained” bivariate model. The “unconstrained” bivariate model, allowing
constant over i. This is the “constrained” bivariate model. The “unconstrained” bivariate model, allowing ![]() , was investigated and found to produce unreasonable results, and it is not considered further here. As above, the sampling errors eit and
, was investigated and found to produce unreasonable results, and it is not considered further here. As above, the sampling errors eit and ![]() are assumed independent N(0, ve / nit) and N(0, ci), with ci and nit known, and ve a parameter to be estimated. Parameters in (9) and (10) to be estimated are thus the regression parameter vectors β and η; the common model error variance
are assumed independent N(0, ve / nit) and N(0, ci), with ci and nit known, and ve a parameter to be estimated. Parameters in (9) and (10) to be estimated are thus the regression parameter vectors β and η; the common model error variance ![]() ; the model error correlation ρ; and the sampling error variance parameter ve.
; the model error correlation ρ; and the sampling error variance parameter ve.
Note that the bivariate model form differs from the SAIPE model form in that it does not include the previous census data as a regression variable, and it also allows the model errors to be correlated. These two differences in model form are related. In fact, by making a linear transformation, one could replace (9) by
![]()
where
![]()
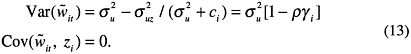
Replacing (9) by (11) makes the bivariate model form look more like the SAIPE model form, in that both now have the census data on the right-hand side of the CPS equation, and the model errors of the two equations are now uncorrelated. The two differences between (11) and (1) are that (11) uses the regression residuals Ceni − ![]() η instead of just Ceni, and that γi and
η instead of just Ceni, and that γi and ![]() for (11) vary over counties i. The latter feature makes (11) inconvenient for model estimation
for (11) vary over counties i. The latter feature makes (11) inconvenient for model estimation
|
2 |
More details related to this transformation of the bivariate model are given in Bell (1997a). To interpret (11), it may help to note that |
relative to (9). However, having fitted a bivariate model using (9) and (10), one can compute estimates of γi and ![]() and compare them to the corresponding quantities γ and
and compare them to the corresponding quantities γ and ![]() from the SAIPE model (which assumes they are constant over counties). (Histograms of γi and
from the SAIPE model (which assumes they are constant over counties). (Histograms of γi and ![]() are provided as part of the regression diagnostics for the fitted bivariate models.)2
are provided as part of the regression diagnostics for the fitted bivariate models.)2
Because the bivariate model uses previous census data Ceni by jointly modeling it with the CPS data yit, it could not be applied for t = 1989 because the regression variables xi,79 needed for modeling the 1980 census data are not available. Consequently, the bivariate model was applied only for t = 1993, and Ceni in (10) always denotes Cen90i, (The bivariate model approach can be applied to jointly model 1990 CPS and 1990 census data, but this is a different exercise, since the resulting smoothed estimates of Yit would use current year census data, rather than previous census data.)
Adding Fixed State Effects to Models
Any of the basic models discussed here can be augmented to include fixed state effects by replacing x0it = 1 by a set of 51 state indicator variables, constructed alphabetically: I1t = 1 for all counties in Alabama and 0 otherwise, I2i = 1 for all counties in Alaska and 0 otherwise, etc., through I51,i = 1 for all counties in Wyoming and 0 otherwise. The resulting regression effect can be written as ![]() , where the αj are state intercept parameters. Alternatively, the regression can be reparameterized as follows to maintain the overall constant term β0x0it, but with 50 state contrast variables added to the regression variables for each equation:
, where the αj are state intercept parameters. Alternatively, the regression can be reparameterized as follows to maintain the overall constant term β0x0it, but with 50 state contrast variables added to the regression variables for each equation:
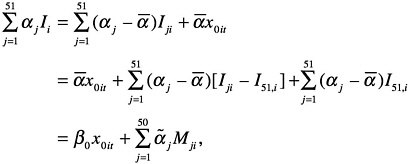
where ![]() is the mean of the 51 state intercepts;
is the mean of the 51 state intercepts; ![]() are the differential state effects; and Mji = Iji − I51,i are 50 contrast variables that are 1 when county i is in state j, −1 when county i is in Wyoming, and 0 otherwise. The differential state effect for Wyoming is
are the differential state effects; and Mji = Iji − I51,i are 50 contrast variables that are 1 when county i is in state j, −1 when county i is in Wyoming, and 0 otherwise. The differential state effect for Wyoming is ![]() , which is obtained from the constraint
, which is obtained from the constraint ![]()
Two sets of state indicator variables (or state contrast variables) are used—one one set for the CPS equation and one set for the census equation. These can be
denoted Ijit (Mjit) and Iji,89 (Mji,89), which lets the state intercepts ![]() be distinct for the CPS and census equations. (The two sets of intercepts could be denoted αjt and αj,cen, or the two sets of contrasts could be denoted
be distinct for the CPS and census equations. (The two sets of intercepts could be denoted αjt and αj,cen, or the two sets of contrasts could be denoted ![]() and
and ![]() .) Thus, adding state effects to a model adds 100 additional parameters, 50 in each of the two equations: this holds even when modeling CPS data for t = 1989, the same income year as for the census. This approach avoids assuming that state effects are the same for the CPS and census data (though I and my colleagues did do some experimentation with common state effects in the bivariate model).
.) Thus, adding state effects to a model adds 100 additional parameters, 50 in each of the two equations: this holds even when modeling CPS data for t = 1989, the same income year as for the census. This approach avoids assuming that state effects are the same for the CPS and census data (though I and my colleagues did do some experimentation with common state effects in the bivariate model).
SAIPE and Bivariate Models for Poverty Rates
All the models that have been investigated are of either the SAIPE or bivariate form, with or without fixed state effects; they are simply applied to different data than discussed above. For modeling poverty rates, Ceni denotes the census estimated poverty rate for county i (for related children, 5-17). The CPS data yit are defined as an aggregate 3-year “poverty rate,” using CPS data for years t − 1, t, and t + 1:
where ∑t indicates the 3-year sum over t − 1, t, and t + 1. The estimated numbers for the numerator and denominator of (14) are produced by using CPS weights modified to make each county “ self-representing.” CPS sample sizes nit are defined as before.
Notice that the denominator of (14) is not the CPS poverty universe (poor related children 5-17 in families), as it was for the single-year poverty rates defined in (7); rather, it is the CPS total number of children 5-17. This choice of denominator for the “poverty rate ” in (14) is necessary because county population estimates are available for all children 5-17, but not for the 5-17 CPS poverty universe (restricted to related children in families). Population estimates corresponding to the denominator of (14) are needed to convert smoothed poverty rate estimates to estimates of the number of poor children.
For some counties with very small CPS sample sizes there may be no related children aged 5-17 observed in the sample. For these counties, the poverty rates are not defined, and they cannot be used in the model fitting. However, it is not necessary to drop counties just because no poor 5-17 children are found in the sample, as it is with the models for log number poor and log poverty rate; the poverty rate models use the most CPS observations for model fitting; 304 counties had CPS sample but no poor age 5-17 in the sample in 1993.
The basic regression variables xit = (x0it, . . ., x3it)′ used in poverty rate models are three other rate variables and an intercept, defined as follows:
x0it = 1 (constant term); (15)
x1it = (number of IRS dependent child tax exemptions on returns with income below poverty )/(total IRS dependent child tax exemptions);
x2it = (number of food stamp participants) / (resident population, all ages);
x3it = (total IRS dependent child tax exemptions) / (resident pop. age 0-21).
Except for the constant term, the numerators and denominators of these variables derive from tabulations of administrative records data or population estimates for county i. It should be noted that for a significant number of counties (292 in 1993 and 82 in 1989) the IRS dependent child exemption “rate,” x3it, exceeds 1: this is partly due to errors in geocoding the IRS tax return data, and partly due to differences between IRS and census residence definitions.
Having thus defined the data and regression variables, either the SAIPE model form given by (1) and (2) or the bivariate model form given by (9) and (10) can be used for the estimates. In doing so, the same assumptions about the error structure are used. Thus, for SAIPE poverty rate models, the model errors wit and ![]() in (1) and (2) are both assumed i.i.d. N(0,
in (1) and (2) are both assumed i.i.d. N(0, ![]() ) and independent of each other. For bivariate poverty rate models, both model errors uit and zi in (9) and (10) are assumed i.i.d. N(0,
) and independent of each other. For bivariate poverty rate models, both model errors uit and zi in (9) and (10) are assumed i.i.d. N(0, ![]() ), with Cov(uit,zi) = σuz = ρ
), with Cov(uit,zi) = σuz = ρ ![]() constant over i. And for both SAIPE and bivariate models the CPS sampling errors eit are assumed i.i.d. N(0, ve / nit), and the census sampling errors
constant over i. And for both SAIPE and bivariate models the CPS sampling errors eit are assumed i.i.d. N(0, ve / nit), and the census sampling errors ![]() are assumed i.i.d. N(0, ci). Obviously, the values of the variance parameters will be different from those in the log number poor models: in particular, the census sampling error variances ci are obtained from published census generalized variances for rate estimates.
are assumed i.i.d. N(0, ci). Obviously, the values of the variance parameters will be different from those in the log number poor models: in particular, the census sampling error variances ci are obtained from published census generalized variances for rate estimates.
To assume that the CPS sampling errors of direct poverty rate estimates have variance of the form ve / nit is inconsistent with making the same assumption for CPS direct estimates of log number poor or log poverty rate. Simple Taylor series approximations suggest that if ve / nit is the appropriate variance for poverty rate estimates, then the sampling error variance for log poverty rates will depend on the underlying true poverty rate p, and vice versa. (The sampling error variance for log poverty rates will be the same as that for log number poor, ignoring, as a crude approximation, variability in the denominator of the poverty rates.) In fact, considerations of the binomial distribution suggest that sampling error variances of poverty rates and log poverty rates could both depend on p (see Bell (1997b) for a little more discussion.) The form ve / nit of the sampling error variances was chosen not because it was believed to be exactly correct for any of the various data being modeled (poverty rates, log poverty rates, or log number poor), but because it is the simplest form that allows sampling error variance to depend inversely on sample size. Because of the need to estimate ve from the fitting of the CPS equation, it is doubtful that much more involved sampling error variance formulations could be effectively estimated. Since the Census Bureau now has direct estimates of county sampling error variances (Fay, 1997b), there is more information for exploring alternative sampling variance formulations, and that work has begun. (Fixed state effects can also be added to the poverty rate models, as discussed above.)
SAIPE and Bivariate Models for Log Poverty Rates
Models for log poverty rates are of the same form as those for poverty rates just discussed, except that the models are applied with the logarithms of all the rates involved. That is, yit and Ceni are defined to be the logarithms of the CPS and census poverty rates (defined above) and (x1it,. . ., x3it) are defined to be the logs of the rates given in (15). The yit are not defined for counties for which there are no poor children 5-17 in the CPS sample, so they must be dropped from the model fitting, as is done with the log number poor models.
As with the models discussed above, the assumptions about the covariance structure of (1) and (2) (for a SAIPE model of log poverty rates), or about the covariance structure of (9) and (10) (for a bivariate model), remain unchanged. The parameter values will change, of course: in particular, the sampling variances ci, which now refer to the log census poverty rates, can be approximated from those for the census poverty rates. Thus, if ![]() are the sampling variances in census estimates
are the sampling variances in census estimates ![]() of poverty rates pi, and ci are the corresponding sampling variances in the
of poverty rates pi, and ci are the corresponding sampling variances in the ![]() , from Taylor series linearization the two are approximately related by
, from Taylor series linearization the two are approximately related by
![]() .
.
D-Revised Models for Log Poverty Rates
The “D-Revised” models for log poverty rates are a hybrid: they use CPS and census log poverty rates for yit and Ceni, as defined above, but with regression variables as defined for the log number poor models in (8).3 Only the SAIPE form of this model was tried, and fixed state effects were not used. (Alternatives using the bivariate model form or fixed state effects, or both, could be investigated.) For the D-Revised model form there is one additional difference between (1) and (2): the census data appearing on the right-hand side of the equations are—analogous to the other regression variables—defined as log number poor children 5-17, whereas Cen90i appearing on the left-hand side is the log census poverty rate. With the data thus defined, the model fitting proceeds in the same fashion as for the other models discussed.
State Poverty Rate Models
Models for state poverty rates are discussed in detail in Fay and Train (1997). Here I provide only brief summary remarks relating their model to the forms just discussed. The model developed was of the form of (11), but with the coefficient (γi) on the census residuals assumed constant over states i:
|
3 |
“D-Revised” was the term originally used by the panel for the hybrid log rate-number model. |
![]()
The model error variance, ![]() , was also assumed constant over states. For states, the census sampling error variances ci are effectively 0. Thus, examining (12) and (13) for states, a bivariate model does indeed lead to the model form (16), with a constant γ and
, was also assumed constant over states. For states, the census sampling error variances ci are effectively 0. Thus, examining (12) and (13) for states, a bivariate model does indeed lead to the model form (16), with a constant γ and ![]() . In Fay and Train (1997), the equation (16) and corresponding census equation of form (10) were fitted separately. Because the census data have negligible sampling error variance, the census equation for states can be fitted by OLS. Fay and Train then fitted (16) by maximum likelihood to estimate β, γ, and
. In Fay and Train (1997), the equation (16) and corresponding census equation of form (10) were fitted separately. Because the census data have negligible sampling error variance, the census equation for states can be fitted by OLS. Fay and Train then fitted (16) by maximum likelihood to estimate β, γ, and ![]() , given previous estimates of the Var(eit).
, given previous estimates of the Var(eit).
The estimates of Var(eit) were developed by Mark Otto and myself (see Otto and Bell, 1995). These estimates used generalized variance functions fitted to direct estimates of state sampling error variances developed in Fay and Train (1995). In their later paper on the state modeling, Fay and Train (1997) refined the estimates of Var(eit) as their iterative estimation proceeded by updating the dependence of the Var(eit) on the poverty rate being estimated.
MODEL FITTING
Once the data for a given model have been defined, model fitting proceeds in the same fashion for all models. Thus, model fitting can be discussed in general terms, with one qualification: for models for log number poor or log poverty rates, counties with no CPS sample poor are omitted from the model fitting, as discussed above. Small numbers of other counties may also be eliminated due to no census sample poor or problems in defining the regression variables.
First, consider estimation of the regression parameters given estimates of the model variance parameters. Let y and Cen (similarly, Cen90 and Cen80) be vectors containing the county CPS and census data to be used for model fitting, and let Xt and X89 be the corresponding matrices of regression variables for their respective equations. The SAIPE model form given by (1) and (2) can be written in a rather obvious matrix-vector notation as

The error vectors wt, ![]() , et, and
, et, and ![]() are all assumed uncorrelated with each other,
are all assumed uncorrelated with each other,
and there are also no correlations among their elements (i.e., each has a diagonal covariance matrix). Thus, ![]() , where K is a diagonal matrix with elements 1/nit. Also,
, where K is a diagonal matrix with elements 1/nit. Also, ![]() , where C is a diagonal matrix with elements ci. Given
, where C is a diagonal matrix with elements ci. Given ![]() , ve, and the nit and ci (always assumed known), (17) can be fitted by weighted least squares to estimate the regression parameters (β, γ, η,
, ve, and the nit and ci (always assumed known), (17) can be fitted by weighted least squares to estimate the regression parameters (β, γ, η, ![]() ). In fact, since there is no correlation between the error terms in the equations for y and Cen90, these two equations can be fitted separately.
). In fact, since there is no correlation between the error terms in the equations for y and Cen90, these two equations can be fitted separately.
For the bivariate model, the corresponding equation to (17) is
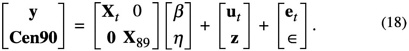
In (18) the vectors ut and z have, in general, nonzero correlations for observations corresponding to the same county. Thus, while ![]()
![]() , similar to the SAIPE model (17), one also needs to allow for the correlations between ut and z when estimating the regression parameters (β, η). This can be done by applying generalized least squares to (18). In fact, it is simpler to structure the equations for the bivariate model so that the CPS and census data are paired off (for those counties with CPS data available for model fitting), for which the covariance matrix for the resulting equation is block diagonal, with blocks no larger than 2 × 2. (For counties with only census data available for model fitting, the “block” is a scalar.) (This process is straightforward, but the notation is tedious and details are omitted here.)
, similar to the SAIPE model (17), one also needs to allow for the correlations between ut and z when estimating the regression parameters (β, η). This can be done by applying generalized least squares to (18). In fact, it is simpler to structure the equations for the bivariate model so that the CPS and census data are paired off (for those counties with CPS data available for model fitting), for which the covariance matrix for the resulting equation is block diagonal, with blocks no larger than 2 × 2. (For counties with only census data available for model fitting, the “block” is a scalar.) (This process is straightforward, but the notation is tedious and details are omitted here.)
Fixed state effects are easily added to (17) or (18) by simply augmenting the regression matrix and parameter vector as appropriate. For example, for the bivariate model (18), with 50 state contrast variables Mji and corresponding parameters ![]() added to each equation, the resulting model can be written
added to each equation, the resulting model can be written
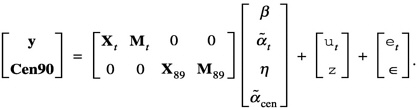
Finally, it is necessary to discuss how the covariance parameters are estimated and how this estimation is integrated with that for the regression parameters. Two approaches have been taken. One approach (implemented in SAS IML) was used in fitting models to produce the evaluations against the 1990
census. This approach used basically a method of moments approach (see Fisher, 1997).
The second approach (implemented in Splus) was used in fitting the models for producing the regression diagnostics. This approach uses Gaussian maximum likelihood. For bivariate form models, for given values of the model parameters (β, η, ![]() , ρ, ve), the Joint density of the data (the likelihood function) can be evaluated, and thus numerically maximized over the parameters to produce the maximum likelihood estimates (MLEs). This is done by iterating between GLS estimation of (β, η) for given values of (
, ρ, ve), the Joint density of the data (the likelihood function) can be evaluated, and thus numerically maximized over the parameters to produce the maximum likelihood estimates (MLEs). This is done by iterating between GLS estimation of (β, η) for given values of (![]() , ρ, ve) and maximization of the likelihood over (
, ρ, ve) and maximization of the likelihood over (![]() , ρ, ve), using the regression residuals yit −
, ρ, ve), using the regression residuals yit − ![]() β and Ceni −
β and Ceni − ![]() η as data. This approach can be called iterative GLS. Asymptotic inference (approximate standard errors, etc.) about (β, η) follows from standard GLS results by plugging in MLEs of (
η as data. This approach can be called iterative GLS. Asymptotic inference (approximate standard errors, etc.) about (β, η) follows from standard GLS results by plugging in MLEs of (![]() , ρ, ve), and inference about (
, ρ, ve), and inference about (![]() , ρ,ve) uses standard asymptotic results for MLEs (use of an approximate normal distribution with covariance matrix given by the inverse negative Hessian of the log-likelihood evaluated at the MLEs).
, ρ,ve) uses standard asymptotic results for MLEs (use of an approximate normal distribution with covariance matrix given by the inverse negative Hessian of the log-likelihood evaluated at the MLEs).
This second approach can also fit models of the SAIPE form. For these models, ρ = 0, so the CPS and census equations are independent. However, these two equations are linked by the common variance, ![]() , assumed for the model errors wit and z̃i. Thus, fitting the two equations jointly combines their information for the estimation of
, assumed for the model errors wit and z̃i. Thus, fitting the two equations jointly combines their information for the estimation of ![]() . Practically speaking, this makes little difference, as the information from the census data swamps that from the CPS data, so that essentially the same results would be obtained by fitting the census equation first to estimate
. Practically speaking, this makes little difference, as the information from the census data swamps that from the CPS data, so that essentially the same results would be obtained by fitting the census equation first to estimate ![]() and then treating
and then treating ![]() as known when estimating the CPS equation. This latter strategy was used in the first approach (implemented in SAS IML).
as known when estimating the CPS equation. This latter strategy was used in the first approach (implemented in SAS IML).
The SAS program differs from the Splus program in another related respect: in the SAS program the census equation is fitted only to data from the counties that also provide data for the CPS equation. The reasoning behind this decision was that the model error variance might differ for counties without a CPS sample (which are smaller, on average, than counties included in the CPS), and thus it may be appropriate to exclude them from the fitting of the census equation. As noted in the next section, an important role of the model error variance relates to how weights are assigned to the regression predictions and the direct CPS estimates in constructing the smoothed estimates. Since this calculation is irrelevant to counties without a CPS sample, it may be appropriate to avoid their influence on estimates of the model error variance. In the Splus bivariate model software, all the census data are used in the model fitting, along with as much CPS data as are available for the year and the poverty statistic being modeled. This approach assumes that the model applies equally well to counties with and without a CPS sample.
The two different model fitting approaches were adopted because some analysts use SAS and others use Splus and because the SAS code was developed for the original SAIPE model and could not be used to fit models of bivariate form,
necessitating development of a second program. Generalization of the Splus bivariate model software is a recent development, and there has not been time to make extensive comparisons of the two programs for models they can both fit. For the comparisons that have been made, the differences in results appear to be small.
SMOOTHED ESTIMATES
Smoothed estimates from an estimated 1993 SAIPE model form are determined from the CPS equation (1), treating Cen90i the same way as the other regression variables in xit. (For t = 1989, the same approach is applied to (4).) Recall that the true quantity of interest for county i is ![]() , and the direct CPS estimate is yit = Yit + eit. The estimate of Yit and its variance are
, and the direct CPS estimate is yit = Yit + eit. The estimate of Yit and its variance are
![]()
![]()

where
![]()
and ![]() is obtained from the weighted least squares results. From (19) the smoothed estimate Ŷit is a weighted average of the regression prediction
is obtained from the weighted least squares results. From (19) the smoothed estimate Ŷit is a weighted average of the regression prediction ![]() and the direct estimate yit. The first term in (20),
and the direct estimate yit. The first term in (20), ![]() , is the variance that would result if all model parameters were known. The second term in (20) accounts for additional error due to estimating the regression parameters (β, γ). One can also augment (20) to account for additional error due to estimating some or all of the variance parameters (
, is the variance that would result if all model parameters were known. The second term in (20) accounts for additional error due to estimating the regression parameters (β, γ). One can also augment (20) to account for additional error due to estimating some or all of the variance parameters (![]() and ve), using either the approach of Prasad and Rao (1990:47-59), or by simulation. These calculations have been done for some of the models, and this addition to the variance was found to be small. (Note that the models have a small number of variance parameters relative to the amount of data.)
and ve), using either the approach of Prasad and Rao (1990:47-59), or by simulation. These calculations have been done for some of the models, and this addition to the variance was found to be small. (Note that the models have a small number of variance parameters relative to the amount of data.)
For models with fixed state effects, smoothed estimates and their variances are obtained from expressions analogous to (19) and (20) by appropriately augmenting the regression variables and parameters with the state effect regression variables and parameters.
For counties without a CPS sample or that have a CPS sample with no poor children and are dropped from the fitting of log(number poor) or log(poverty
rate) models, the estimate Ŷit is defined to be just the regression prediction ![]()
![]() , which has variance
, which has variance
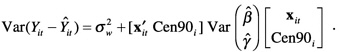
Smoothed estimates and their variances for the bivariate model are a little more complicated, but follow the same principles; they are discussed in Bell (1997a).
When log(numbers of poor) or log(poverty rates) are modeled, smoothed estimates on the original scale (of numbers of poor or of poverty rates, unlogged) can be obtained by exponentiating Ŷit. However, it is useful to use the following modified estimate, based on the mean of the lognormal distribution, to remove bias:
Prediction intervals on the original scale can be obtained by exponentiating prediction interval limits on the transformed (log) scale, yielding asymmetric intervals on the original scale.
When poverty rates are modeled, the resulting smoothed rate estimate for county i must be multiplied by the population estimate of total children 5-17 in county i (see (14) and discussion following) to convert it to a smoothed estimate of the number of poor children. This is also necessary for smoothed poverty rate estimates from the state model, and, similarly, when log(poverty rates) for counties are modeled, with smoothed rate estimates produced using (21). Prediction error variances in these cases could be taken to be those for the smoothed poverty rates multiplied by the square of the population estimates, though this ignores error in the 5-17 population estimates. Formal measures (variances) of error in state and county population estimates are not available, so there is no ready way to recognize this additional uncertainty. Treating error in the population estimates as ignorable is more tenable for states than it is for counties.
As a final step, smoothed county estimates of number of poor related children aged 5-17 are “raked” to agree with the corresponding smoothed estimates from the state model. Thus, the smoothed county estimates are aggregated to states, and then the individual county estimates are multiplied by the ratio of their state model estimate to the aggregated county estimates for that state. These ratios, or “raking factors,” one for each state for a given model, have been developed for the 1989 models. Deriving variances for the raked, smoothed estimates is complicated, but an approximate procedure (described in Fisher, 1997) has been implemented in conjunction with the SAS estimation software.
















