Promising Approaches for Helping Prospective Elementary Teachers Learn Mathematics for Teaching
The closing panel offered a broad array of perspectives—from mathematics to teaching to policy—on how teachers come to learn the mathematics they need to know to teach well. The moderator concluded the session by presenting an argument for why sites of teaching practice might provide opportunities for teacher learning and broadened the list of sites of practices beyond those considered in the Workshop.
PANELISTS
Looking at Textbooks
Richard Askey, University of Wisconsin-Madison
The Professional Growth of a Classroom Teacher
Carol Midgett, Southport Elementary School
The Importance of Mathematical Content
Alice Gill, American Federation of Teachers
NSF and Teacher Preparation Programs
James Lightbourne, National Science Foundation
Where Are We? Moderator's Summary
Joan Ferrini-Mundy, Mathematical Sciences Education Board
Looking at Textbooks
Richard Askey
INTRODUCTION
When considering what knowledge elementary school teachers need, the first book to read is the recent one by Liping Ma (1999). The answers given by many of the Chinese teachers she interviewed start to illustrate what teachers should know. There are even some suggestions about what we can do to help teachers develop this knowledge. One of the suggestions surprised me very much. Ma claimed that one of the main ways in which the Chinese teachers she interviewed developed their deep understanding of elementary mathematics was by serious study of their texts.
Here is an example of a problem that appears in a Chinese fifth-grade book and also in a Japanese elementary school text. The curves in Figure 1 are halves of
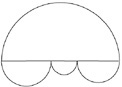
Figure 1. Comparing Circles
circles. The question is whether the length of the large half-circle is longer (along the circumference), shorter, or equal to the sum of the lengths of the three smaller half-circles.
This is a very nice problem, since it helps students to understand how the fact that the circumference of half of a circle is proportional to the diameter is important and not just a fact they have memorized and then used to compute the circumferences of different circles with different diameters. Having good multi-step problems seems to be a characteristic of a mathematics program that works. It is probably a necessary condition for a good mathematics program. Of course, as Ma says, much of the study comes from looking seriously at problems that do not need as much insight as this one does and developing different ways of solving them.
There seems to be a general feeling that long ago our textbooks only had procedures for students to follow, and reasoning was only introduced in high school geometry. A casual glance at old arithmetic books can give this impression, but a more careful reading of some of them shows this is false. Here are two illustrations from an arithmetic book by White (1870). More details will be given
here than were possible in my presentation, since the details are important and the relevant texts are not widely available. One can occasionally find old texts at used bookstores, especially those in small towns and in the country.
One of the problems used by Deborah Ball (1990) and again by Liping Ma (1999) in their work on the mathematical knowledge of elementary school teachers was to divide 1¾ by ½, and make up a story problem with this division being the operation leading to a solution. The topic of division of fractions is treated very well by White. The same general format is used for two special cases and the general case. In each case, a few word problems are given, some more complicated calculations are done with numbers, and then this is summarized by principles and/or rules. Then the text contains other problems for the student to do. A few examples of each from White's text will be given here.
2. A man divided 8/9 of his farm equally between 4 sons; what part of the farm did each receive?
4. If 10 oranges cost 5/8 of a dollar, what will 1 orange cost?
10. Divide 12/25 by 6.
This is worked out two ways, by dividing the numerator by 6 and by multiplying the denominator by 6. This is followed by nine problems for students to do, ending with dividing 6 2/3 by 10. The word problems give a good illustration of what is happening, and the calculation problems strengthen arithmetic skills. Then a general result is stated.
98. Principle. A fraction is divided by dividing its numerator or multiplying its denominator.
20. How many times is 2/5 of a cent contained in 4 cents? Solution. In four cents there are 20 fifths of a cent, and 2 fifths of a cent is contained in 20 fifths of a cent 10 times.
[I doubt if fractions of cents were used in 1870, but following the introduction of state sales taxes in the 1930s, a number of states used mills for sales taxes. In Missouri, where I grew up, there were one mill and five mill tokens, a mill being a tenth of a cent.]
22. If 5/8 of a yard of silk will make a vest, how many vests will 5 yards make? 7 yards? 10 yards?
26. Show that ![]()
33. What is the quotient of 125/(21/50)?
100. Rules. To divide an integer by a fraction,
-
Multiply the integer by the denominator of the fraction and divide the product by the numerator. Or,
-
Divide the integer by the numerator and multiply the quotient by the denominator.
37. How many times is 2/5 of an inch contained in 4/5 of an inch?
40. How many times is 1/3 contained in ¾? ¼ in 2/3? Suggestion: Change the fractions to twelfths.
46. What is the quotient of (12/13)/(8/11)?
57. If a family uses 4/9 of a barrel of flour in a month, how long will 2 1/3 barrels last?
60. If a man walks 3 3/10 miles in an hour, in how many hours will he walk 20 ¼ miles?
101. Principles.
-
The quotient of two fractions having a common denominator equals the quotient of their numerators.
-
The multiplying of both dividend and divisor by the same number does not change the value of the quotient.
102. Rules. To divide a fraction by a fraction.
-
Reduce the fractions to a common denominator and divide the numerator of the dividend by the numerator of the divisor. Or,
-
Invert the terms of the divisor and then multiply the numerators together and also the denominators. Or,
-
Multiply both the dividend and the divisor by the least common multiple of the denominators of the fractions and divide the resulting dividend by the resulting divisor.
Notes.
-
The third rule depends on the second principle; and since multiplying two fractions by their least common multiple changes them to integers, the new dividend and divisor are always integral.
-
It is not necessary that the pupil be made equally familiar with these three methods of dividing one fraction by another. He should thoroughly master one of them.
There is a lot of good mathematics contained in a few pages. I think this material could be used as Ma says the Chinese teachers she interviewed used their texts, to develop a deeper understanding of the mathematics they teach.
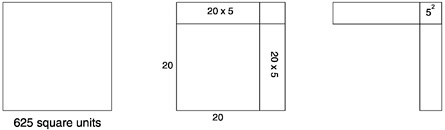
An even more impressive treatment is given for square roots. Section 14 is titled “Involution and Evolution.” “Involution” is defined to be the process of finding powers of numbers, and “evolution” is the process of finding roots of numbers. In a note after the definition of “evolution,” it says that “Evolution is the inverse of involution.”
The chapter starts with powers. The first, second, third, and fourth powers of 4 are illustrated, with the last written as 4 × 4 × 4 × 4 = 256. This section ends with “etc.,” so the student is to infer the general rule from this example. Many problems are given for the students to calculate, including fractions and decimals with numerical work expected to be done up to the fifth power.
Powers are then defined. The second power of a number is the product obtained by taking the number twice as a factor. An illustration of a 3 by 3 square is given, and the following comment is made. “It is also called the Square of the number, since the area of a geometrical square is represented by the product obtained by taking the number of linear units in one of its sides twice as a factor.” Similar comments are made about third powers, or cubes, including an illustration of a 3 by 3 by 3 cube.
Rule. To raise a number to a given power, multiply the number by itself as many times LESS ONE as there are units in the exponent of the given power. The last product will be the required power.
The next subsection gives a second way to find a square and a cube.
32. What is the square of 53?
53 = 50 + 3, and 532 = (50 + 3)2

In like manner, it may be shown that the square of any number, composed of tens and units, is equal to the square of the tens, plus twice the product of the tens by the units, plus the square of the units.
Problems are given, including squares of three digit numbers. Then cubes are introduced, starting with 53 again.
The cube of 53 = (50 + 3)3 = 503 + 3(502 × 3) + 3(50 × 32) + 33, as can be shown by multiplying 502 + 2(50 × 3) + 32 by 50 + 3.
This is used as background material for taking square roots and cube roots. The section on square roots starts by listing the squares of 1, 10, 100, and 1,000 and the squares of 9, 99, 999, and 9,999.
Then this section continues with:
A comparison of the above numbers with their squares shows that the square of a number contains twice as many orders as the number or twice as many orders less one.
This is followed with:
406. Hence, if a number be separated into periods of two orders each, beginning at the right, there will be as many orders in its square root as there are periods in the number.
The first problems deal with how many “periods” there are in the square root of 2809, then 36864, and larger numbers up to 14440000.
The procedure for evaluating a square root starts with marking off pairs of numbers, and taking the largest square root of the pair or single digit on the left hand side of the number. For 2809, the pairs can be denoted by 28‘09, although a dot above the right member of each pair is used in the book. The leftmost pair is 28, and 5 2 = 25 is the largest square less than or equal to 28. This 5 appears in the second spot, or the tens place, since the square root of a four digit number has two digits if it can be found exactly, and so is greater than or equal to 10 and is less than 100. It is still in this range if the square root cannot be found exactly. The next term is found by using the procedure for forming a square. This is done with numbers in White's book, but it is easier to use letters. The rule above for squaring can be written as
(10a + b)2 = 100a2 + 20ab + b2 = 100a2 + (20a + b)b.
The 5 found above is really 50, and the partial square root is 50 2 = 2500. The difference of 2809 and 2500 is 309. Multiply 50 by 2 to get 100, and see how many times this divides into 309. 3 is a possibility as the next digit, but that is not sure since you need to calculate (20a + b) × b = (2 × 50 + 3) × 3 = 300 + 9.
If the number whose square root is wanted were 2808, then 53 would be too large, the partial quotient of 3 would be too large, and 2 would have to be used instead. To continue, one just adds a decimal point, a bunch of zeros depending on how much accuracy is wanted, and continue. One problem asked was to find the square root of 586.7 to three decimal places.
As usual, Principles and Rules are then stated. These seem dogmatic, and if one has not read the text and worked the problems, these look like rules given to memorize without any reason why they hold. I hope the reader is convinced that this is not necessarily what happened, since the text contains much more than just rules to memorize. However, there is still more.
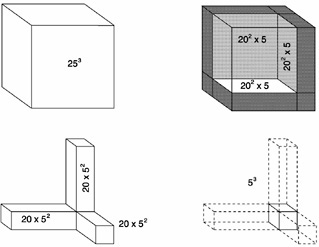
The next section, 411, is titled “Geometrical Explanation.” The method of taking powers and of using this to take square roots is illustrated by a series of pictures (see Figure 2).
The same is then done for cube roots. Here are the pictures that help explain how this method works (see Figure 3).
These explanations are excellent. Current books do not have explanations for this square root algorithm, since square root algorithms are no longer taught. If all that were taught was an algorithm without any reasons why it
works, then there would be no reason for teaching it. There are other ways to do an algorithm one does not understand, such as punch a button on a calculator. However, if important mathematics can be taught while learning an algorithm, that changes the picture.
What I would like is the method outlined above, with one picture added to it (Figure 4), to give a geometric picture for why (a + b) (c + d) = ac + ad + bc + bd.
I would also like a second method of taking square roots via the old Babylonian method that we now say comes from Newton's method. There is also a very nice pictorial way of explaining this method, which is usually not given.
Draw a square with area N, and mark off a length a which is approximately the square root of N. Let e denote the error made. Then
N = (a + e)2= a2 + 2ae + e2.
We cannot solve this equation without taking a square root, which is what we are trying to learn to do. However, e is small, so e2 is smaller. Drop it and solve the resulting linear equation for e. The resulting approximation is the old Babylonian method for extracting square roots. To see that you understand this method, work out the corresponding formula for cube roots.
What we get are algebra tiles, which seem to me to be a very restricted way of doing things that might hamper a more general picture one wants students to develop. My feeling about these tiles has been confirmed in discussions with a number of very good teachers who have had students who used algebra tiles in other programs and then had more trouble with symbolic manipulation than they should have. Drawing pictures is flexible. Algebra tiles also have the unfortunate tendency of reinforcing the mistaken view which many students have that x2 is greater than x.
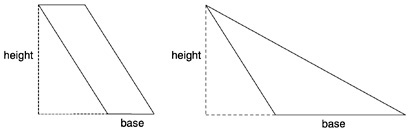
Let me contrast one topic as it is done in our textbooks and in a set from Singapore (Primary Mathematics Project Team, 1993-1995). This is the area of a triangle. In many of our textbooks, this is done in the following manner. First, the formula for the area of a rectangle is motivated in reasonable ways. Second, a formula for the area of a parallelogram is found by the construction shown in Figure 5.
There is one problem with this argument. It does not deal with the general case, since the parallelogram can look like
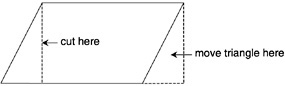
Figure 5. Finding the Area of a Parallelogram
Figure 6. Another Parallelogram
Figure 6. There are ways of dealing with this case, but in most of our textbooks this gap in the argument is not mentioned.
To find the area of a triangle, a parallelogram is cut in half by a line connecting opposite vertices. If the general case of a parallelogram has not been done, the general case of a triangle will also not have been done.
In a Singapore series of elementary school math books, area is introduced in the second half of third grade (Primary Mathematics Project Team, 1993-1995, 3B). Here, unit squares are used to build up more complicated figures, and halves of squares and half of a two by one rectangle are also used. They are combined into figures that are not too complicated. In the first half of fourth grade (Primary Mathematics Project Team, 1993-1995, 4A), areas and perimeters are considered again. One problem in a workbook has students compute areas and perimeters of five rectangles. They are asked to find two rectangles with the same area and two rectangles with the same perimeter. The teacher's manual (Primary Mathematics Project Team, 1994-1996, 4A) specifically points out that a figure that has a bigger area need not have a longer perimeter. More complicated figures are introduced, including a picture of a ship that was constructed with 4 by 3 postage stamps as the pieces and a couple of diagonal cuts made so that fractions of the rectangles have to be considered. It is only in the first half of fifth grade where a formula is introduced for the area of a triangle. Up to this point, all of the areas of triangles have been based on at most half integer multiples of the unit square. In fifth grade (Primary Mathematics Project Team, 1993-1995, 5A), this restriction is removed, and the general case of a triangle is considered.
First, there is an early section on areas of specific types of polygons. These are relatively simple ones whose vertices lie on the grid points so that the figure can be decomposed into subpieces each of which is made up of rectangles or halves of rectangles. For example, there is a triangle with vertices at the points (2,0), (0,3) and (4,4) on a 4 by 4 grid. (The points are not labeled with numbers but are here for ease of reference.) The student is asked to find the area of the 4 by 4 square with vertices (0,0), (4,0), (0,4) and (4,4) and of the three triangles that are in this square and outside of the given triangle. In the workbook, students are asked to find such areas without hints. A formula for the area of a triangle is not given in this section.
Later in the same book, there is a section on areas of triangles. It starts with three illustrations of triangles and associated rectangles. For all three triangles, the base is taken to be the horizontal segment. The first is a right triangle with vertices at (0,0), (6,0), and (0,5). The second triangle has vertices at (0,0), (6,0), and (4,6), and so is completely contained in the associated rectangle, which has the vertices on the edges of the rectangle and the base as one side. The third triangle has vertices (0,0), (4,0), and (7,6), and so lies outside of the rectangle with base 4 and height 6. Students are asked to find the area of each shaded triangle and its
related rectangle. They did harder problems earlier, so these problems should cause no difficulty. On the next page, arguments are given to show that the area of the triangle is half that of the related rectangle. For the right triangle, the same picture is repeated, since this argument works for all right triangles, not just those whose vertices lie on grid points. In the other two cases, new arguments are given (see Figure 7). In both cases, the triangle is decomposed into subparts that are moved to make a rectangle with the same base and half the height. These triangles are pictured with coordinates on the grid points, so it might seem that the general case is not considered. However, the arguments are completely general.
Four pages of problems follow in the text, and these are the type of problem Ma mentioned. Serious study of them can lead to alternative ways of solution and other insights. For example, the picture in Figure 8a suggests that another way of finding the area of a triangle is to decompose the triangle into two right triangles. Another figure ( Figure 8b) suggests a way of doing this when an obtuse angle occurs, and the perpendicular from a vertex to the opposite side does not hit the base.
Will the students pick up on this and learn more than a formula? Some will, and many more will if the teachers know what to look for and what questions to ask. The teacher's guide (Primary Mathematics Project Team, 1994-1996,
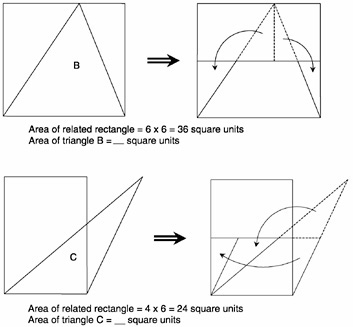
Figure 7. Areas of Triangles
Figure 8. Decomposing Triangles into Right Triangles
5A) has a number of useful suggestions about how to structure the 12 lessons suggested for this topic. At the start, the students are to cut out triangles, then cut them apart and reassemble them into related rectangles. The last suggestion is
Draw different triangles in different orientation with given base and height on the board. Get the student to find the area of each triangle using the formula. Bring to the pupils' attention that each side of the triangle can be regarded as a base. The base of a triangle need not be drawn horizontally all the time.
From Covering and Surrounding: Two-Dimensional Measurement Teacher's Edition by Lappan, Fey, Fitzgerald, Friel & Phillips. © 1998 by Connected Math. Used by Permission.
The last point is important, since students frequently only see pictures of triangles with the base horizontal.
Most U.S. books do not treat the general case. Here is the treatment from one book which at least mentioned the general case. The book (Lappan, Fey, Fitzgerald, Friel, & Phillips, 1998) is one of the sixth-grade volumes in the Connected Mathematics Program. The area of a parallelogram is done in the usual way, as outlined above. The remaining case is mentioned as shown in Figure 9.
Here is what the Teacher's Guide says about this problem.
23a. Answers will vary. This is particularly difficult because it is hard to see that the parallelogram can be cut into three pieces and reassembled to form a rectangle with the given base and height as side lengths. Some students may rename the base the height and then describe why the formula works for the new base and height.
That is all that is said. I cannot make sense of it. I do not know what three pieces the authors had in mind, nor do I know what parallelogram they had in mind when they wrote to rename the “height” as the base. What they probably meant in the last case was not renaming the “height ” but one of the two sides not parallel to the one used as the base. Some students will do this, but they need to be told that is not acceptable, since either of the two nonparallel sides could be the base and there needs to be a demonstration that the formula works in both cases.
There are reasonable ways to show that the area formula continues to hold in the case when the easy argument fails. One is to cut the parallelogram by lines parallel to the base to form smaller parallelograms where the simple argument works and then add up the areas. This requires the distributive law, which students should know and be able to use. Another way is to complete the picture drawn above by drawing another triangle to form a rectangle. Then move the two triangles together to form a rectangle with the same height. Its base is the length of the side of one of the triangles where the side is the one on the same line as the base. The remaining part of the original rectangle is a rectangle whose area is the same as the area of the given parallelogram, and the height and base of this rectangle are the same as the height and base of the parallelogram. To help teachers, these arguments would have been useful in the Teacher's Guide.
If we had teachers with mathematical knowledge shown by most of the Chinese teachers interviewed by Liping Ma, then we would not have to worry too much about what is in our manuals for teachers. However, we do not have many teachers with this knowledge base, so we have to provide for them.
Ball, D. ( 1990). The mathematical understandings that prospective teachers bring to teacher education. The Elementary School Journal, 90(4), 449-466.
Lappan, G., Fey, J. T., Fitzgerald, W. M., Friel, S. N., & Phillips, E. D. ( 1998). Covering and surrounding, teacher's edition (Connected Mathematics Series). White Plains, NY: Dale Seymour.
Ma, L. ( 1999). Knowing and teaching elementary mathematics: Teachers' understanding of fundamental mathematics in China and the United States. Mahwah, NJ: Lawrence Erlbaum.
Primary Mathematics Project Team. ( 1993-1995). Primary mathematics, 1A to 6B and associated workbooks (2nd ed.). Singapore: Federal Publications.
Primary Mathematics Project Team. ( 1994-1996). Primary mathematics teacher's guide, 1A to 6B (2nd ed.). Singapore: Federal Publications.
White, E. E. ( 1870). A complete arithmetic. Cincinnati, OH: Van Antwerp, Bragg and Co.
Carol Midgett
My comments about productive ways of helping prospective elementary mathematics teachers learn about mathematics content and the nature and practice of mathematics are framed in this way. First, I shall synthesize some promising approaches in which I have engaged. Second, I will note the promising approaches discussed this weekend.
Integrating the 1989 National Council of Teachers of Mathematics (NCTM) Curriculum and Evaluation Standards into practice had a profound influence on my teaching. The Standards deepened my personal knowledge of mathematics and enabled me to recognize and understand many more connections within the discipline of mathematics. For example, I came to more fully understand the connections between patterns and algebra. Although I had taught my students to recognize, create patterns using multiple media, extend and correct patterns, I failed to see the pervasive value of patterns in all strands of mathematics and their multiple foundations in algebra. The Standards also gave me a view of the development of mathematical ideas across the K-12 continuum and where my grade level contributed to that continuum. The 1989 NCTM Standards extended my understanding of the role of discourse in learning mathematics, both for myself and for my students. I came to realize that talking about mathematics enables one to examine and clarify conceptions and misconceptions and to benefit from the collective wisdom of the group. Discussion allows young children the same opportunities for stating ideas, examining conjectures, clarifying hypothesis, and understanding the “what and why” of mathematics.
One far-reaching impact of the '89 Standards on my instructional practice and development as a teacher leader came from my participating in the NCTM project to implement the geometry standards. Based upon my high school experience, my view of geometry was entirely from an Euclidean perspective. My experiences in the geometry project gave me a picture of the role of geometry in the field of mathematics as related to measurement and number. I began to see geometry as a way of viewing the world. With the rich experiences of the geometry project as the impetus, I established a math support group for K-8 teachers that began in 1991. This group of more than 70 teachers continues to meet monthly to discuss issues related to mathematics instruction
and to support each other's growth and understanding of mathematics. We have moved from generating activities to discussing the nature of significant mathematical tasks and how they should be taught to help students make sense of mathematics.
A second significant event in my personal journey came in 1989 when North Carolina implemented the first- and second-grade assessment. The contributions the K-2 assessment has made to my professional practice are documenting student learning to inform practice, informing students of their growth and development, and informing parents and administrators of what mathematical learning is occurring and needs to occur. Nine years ago, we began conducting student-led conferences. The preparation for, and presentation of, the conferences have led to children assuming responsibility for their own learning. They have helped parents understand the content of the state curriculum and how students need to understand mathematics as well as the procedures for applying that mathematically meaningfully. This vision of making sense of mathematics helps parents recognize the absolute need for mathematics instruction and products to look different from their own experience. The three-way student-led conferences have created a perfect triangle that includes cooperation and collaboration among student, teacher, and parent. Now the parents of my students are actively engaged in setting goals for their child's learning and readily accept their responsibilities to achieve them.
The third milestone in my growth and development is my involvement in the professional development system at the regional university, the University of North Carolina at Wilmington. To serve student interns, I was required to take two graduate-level courses. One helped me to understand the theory of learning-centered supervision and cognitive coaching. The second course engaged me in the practice of coaching for learning. Serving as a partnership teacher provides an excellent, ongoing opportunity for me to be involved in another learning community with preservice teachers and university faculty. The transfer of coaching practices extends to my young students. The art of reflection is no longer a dream but a reality for me and for my first-graders. It is a natural consequence of each instructional event. Reflective practice has increased the quality and quantity of learning among the members of our classroom community.
Another milestone came in 1995-96, when I participated in the National Board for Professional Teaching Standards (NBPTS) process leading to certification. It synthesized all that had gone before. The tasks required that I analyze my instructional practice and its impact on student learning. I had to provide evidence, as well as artifacts, proving that I thoughtfully planned, intentionally taught to a learning objective, and reflected upon the impact of my practice on student achievement. It was also necessary for me to articulate (in writing) this analysis to present a picture of my practice to a critical reviewer. Meeting National Board Standards has been both an affirmation and a challenge. It affirms that integrating curriculum, instruction, and assessment is valued as essential. It challenges me because I am no longer content to teach and move on! I must analyze my practice against the learning target and plan for re-teaching, re-directing, or extending the knowledge and skills of my students.
The most recent milestone in my professional development, which is really
just beginning, is the initiation of performance-based licensure in North Carolina. This too, is based on standards and provides an opportunity for me to nurture novice teachers and support their growth and development. This engagement in analyzing and reflecting on instruction creates an ever-spiraling learning curve. It also forces me to articulate what I am doing, why I am doing it, and its impact on learning. Working with novice teachers continues the experiences with university student interns. It enables me to make a value contribution to my profession. It helps me to guide others to routinely engage in reflective practice as an essential practice not an “if I have the time” activity. It allows me to help generate and perpetuate a community of learners.
The second aspect of my presentation today addresses the positive and promising approaches resulting from this Teacher Preparation Conference. As a practicing classroom teacher, I sometimes feel that top-down management has no view of the reality of the classroom. Therefore, it is most significant that we are gathered as a community of learners. The participants represent all the levels of educational practice from the classroom to the national policy level. It is a beautiful experience to know that a classroom teacher's words have similar or equal value to other members of the community assembled here. A second thing is the affirmation of knowing that we all grapple with essentially the same issues. We talk about the fundamentals of mathematics. It is as difficult for us to define and describe them here as it is for me at home in my classroom. We're also examining ways to structure and restructure tasks for the maximum mathematical learning potential. We are grappling with the complexities of teaching. We are struggling with how to communicate those complexities to preservice teachers and instruct them to become effective teachers. We are examining designs for preservice education that will give education majors an experience that parallels what we expect them to do when they assume responsibility for classroom instruction.
Everything that we've done has focused on learning and developing the knowledge and skills to teach for learning. We talk about the changes that each of us must make if we are to reform teacher preparation and the learning of mathematics in American classrooms pre-K-16. Just think, as teachers —and all of us are—we have unlimited possibilities and we have unending challenges. Whether we are assisting
-
six-year-olds in understanding mathematics,
-
preservice teachers to recognize the inadequacies of their own mathematics instruction,
-
planning professional development to extend the learning of veteran teachers,
-
structuring university classes to retool professors,
we are identifying the common practices that lead to learning and the structures that support their teaching. How exciting for a first-grade teacher to be part of a journey that has started us on the investigation of some promising possibilities! I am ready to accept the challenge to change and to lead that process with others.
Alice Gill
My work has primarily been with teachers who are already in service, but they're much like preservice teachers when it comes to professional development, except for two things. First, they have experience in real classrooms, under real conditions. Second, the kind of teaching for which they were prepared, and through which they learned, has been part of their daily practice for a long time, making it more entrenched. So, it's more difficult for these teachers to change, I think, than it might be to give preservice teachers a good foundation.
I cannot reflect on what we've done today without going back to yesterday and the conversation about mathematical content. As we go through all of the skills and processes teachers need to know, it's important that we keep in mind the mathematics behind it all. The big ideas about definitions, about understanding what a mathematical claim is and how it can be justified are critical in classrooms today. Teachers are picking up the language of the standards, but many really don't understand what it all means mathematically. Generalizations and language are highly important. You have to be very careful, not only when you pose problems but when you explain things to students. For example, when we talk to elementary teachers, just the definition of a “row” can lead to a discussion, because row has non-mathematical conceptions of a grid with rows and columns. Many teachers have never thought about that and, therefore, have not thought about the importance of connecting to the mathematics of coordinate geometry and teaching that in mathematics rows are horizontal and columns are vertical.
Many teachers don't understand (and this is because we haven't taught them) how to develop a concept, as opposed to just throwing something out for students to learn as “the way it is.” We know there are teachers who really don't even have a good grasp of the procedures and algorithms for mathematics in grades above the ones they expect to teach in elementary school. The sad thing is that the way our licensure system works and the way teachers in school districts are assigned, teachers may think they're going to teach first or second grade and end up in sixth or seventh because they hold a K-8 license. We can't let them be unprepared for whatever class they eventually may have to teach. So, teachers really need to know the mathematics and know it well. When Liping Ma said, “know the funda-
mental math deeply, profoundly,” that's exactly what teachers need.
A number of the processes and vehicles that we looked at today, I think, are very powerful, as long as you keep in mind where teachers are and what additional supports you may need to provide. Video is a wonderful tool to help teachers reflect, to step back and see what 's going on in a classroom—what effect, for example, one question has, as opposed to another one. I've used the Third International Mathematics and Science Study 's (TIMSS) eighth-grade geometry videos with elementary teachers to show the difference in the kinds of answers different kinds of questions provoke. Is it a question that has substance and requires students to think and articulate or begin to see a basic mathematical idea or does the question prompt students to just parrot something back that they don't understand? Is it just filling in a blank? Hopefully, we can move teachers to begin to first view videos of others, and then to video their own classrooms—perhaps privately at first—and examine their own practice from such perspectives. Later, they can share their own videos or exchange classroom visits with peers and talk about teaching and lessons without feeling personally threatened.
Analyzing student work is very important, but you can't analyze it until you know the math behind the work. Who are the people who facilitate groups when teachers get together? I always worry about that. You need a leader who really knows the math that they see on the students' papers in front of them, what the math could be, as well as what the math is.
Analyzing tasks is an important ability teachers should have, and I look at this from two perspectives: (1) what math is contained in this task, what can a teacher get to, and (2) how can we help teachers distinguish intellectual difficulty from “this is hard for kids” because we haven't taught it to them. When the mathematicians studied the TIMSS videos to analyze the lesson content, one of their conclusions was that U.S. lessons didn't have many intellectually difficult tasks, and they often don't. As researcher William Schmidt has observed, our curriculum does not really spiral, that is, increase the complexity of a topic as it appears in the curriculum over time, it just goes around in a circle. As teachers, we need to know how to move students from a simple problem or task to a more complex one so we are deepening their understanding and not just continuing at the same level.
According to the TIMSS study, there was little reasoning in U.S. lessons. Yet mathematical reasoning is at the heart of the discipline. This needs to be addressed in preservice programs. Teachers need to understand reasoning as it applies to lower grades, as well as the reasoning of formal proof. Some of the activities showcased here can be powerful tools for developing an understanding of how to focus on reasoning in the classroom. The work of Deborah Ball and Hyman Bass in this area holds great promise. Video provides opportunities to follow student thinking about a problem or procedure. The questions a teacher uses to draw out the student's thinking, uncover missing steps, or lead a student to see or articulate a fundamental mathematical idea can be made visible as it plays out in real time. Cases are also very useful for analysis. Why didn't these kids know a particular concept? What else could the teacher have done to help them understand? A case study can offer an opportunity to reflect on how to build a concept that the students missed. Navigating a mathematical discussion is certainly important because such discussions are going to go
on in classrooms. Teachers have to know what to take and run with, and what not to, and what kinds of questions to ask to move student thinking. All of that, of course, depends on knowing the mathematics behind what it is a teacher is doing.
One topic related to how teachers learn and know the mathematics they teach has not been mentioned in my sessions so far at this conference. There is a very urgent need in schools today for teachers to understand how to look at math standards. There are state standards, district standards, NCTM Standards, textbooks, and curriculum frameworks. There are many other resources that the teachers can use, and teachers have to figure out how to put all of these together. They're often doing that without being able to say, “Oh well, it's stated differently here, but that's really the same concept as (or maybe a subskill of) the statement over there.” They need to be able to look at mathematics from a larger perspective and from different viewpoints so that they don't think there are a thousand things to teach as little separate ideas. This is not a task for the general education people who talk about instructional planning. This is very specific to the discipline of mathematics. If teachers can't put the information all together and if they can't understand how one thing connects to another, they have a tough time, their students have a tough time, and they may well leave teaching very soon.
Carol Midgett talked about having been given a conceptual framework so that she could see where what she taught fit into the whole picture. It's very important to know, for example, that the concept of division is the same whether you're using whole numbers or fractions. This strategy came up in one of the workshops. We need to help teachers think about intervention with students who don't understand by making a connection to a basic concept that they already know. Many teachers wouldn't think of going back to whole number division because they haven't been prepared with an adequate conception of either division or fractions to know how to make the connection.
The development of excellent math teachers is a complex process. No single idea or tool will accomplish what is needed, including requiring deeper knowledge of mathematical content. However, that knowledge is the necessary foundation that makes powerful tools work. We have a big job, but it has to be done.
James Lightbourne
Improvement in the preparation of future teachers in both content knowledge and educational practice is a critical factor in improving mathematics education. The experiences in which we have engaged at this Workshop have highlighted the significance of preparing teachers in ways that enable them to gain a fundamental understanding of mathematics. Programs described by the speakers here provide promising avenues through which future teachers can gain this understanding of mathematics.
One observation about the activities at this Workshop is that they are all designed to promote student understanding of mathematics. Skills are important, but I think these students are best served for their roles as future teachers if they come to think about mathematics in the ways that a mathematician thinks about mathematics. As teachers, they will then have the understanding necessary to go beyond teaching mathematics as a bag of manipulations and tricks, routine drills that will not surprisingly be quickly forgotten. Rather, they will be able to provide their students with experiences to gain the insights and confidence necessary to learn and use mathematics.
The NSF Collaboratives for Excellence in Teacher Preparation (CETP) program has been one effort at NSF to promote achievement of significant and systemic improvement in the science, mathematics, and technology preparation of prospective kindergarten through grade 12 teachers. The program has particularly emphasized the importance of involving science and mathematics faculty and their departments in K-12 teacher preparation. Twenty-four projects have been awarded through the CETP program from 1992 through 1999 at funding levels of $500,000 to $1 million per year for up to five years. Information about the projects can be found at: http://www.her.nsf.gov/HER/DUE/awards/cetp/cetplist.htm.
The following brief descriptions from CETP project reports illustrate aspects of the projects and findings in evaluating the impact of the projects.
The Arizona Collaborative (ACEPT) developed a classroom observation instrument for evaluating reformed teaching K-20 classrooms across all science and mathematics disciplines. Findings indicate a strong correlation between the use of reformed teaching strategies and students ' achievement pre/post test gains. An instrument for assessing the effectiveness of ACEPT reforms
on student views about mathematics was administered to over 4,000 mathematics students at Arizona State University. Findings indicate shifts in elementary preservice students' mathematical methods toward increased perseverance and use of general problem solving approaches, for example, as well as changes in beliefs (e.g., difficult problems require multiple attempts). Success rates have remained high (at around 90%) in two mathematics preservice courses (Theory of Mathematics for Preservice Elementary Teachers and Methods of Teaching Secondary Mathematics) that have adopted a more rigorous and conceptually focused curriculum.
Evaluation of ACEPT reform in chemistry courses indicates that: 95% of students attend class compared with 60-70% prior to ACEPT. The dropout rate in reformed sections is 3-4% compared with 20-30% in non-reformed sections. Student performance on identical questions improved by 17% in reformed sections with comparable student characteristics (GPA, SAT, age). A physics concept test administered to students in the Fundamentals of Physical Science course at Arizona State University indicated that inquiry-oriented teaching leads to substantially improved understanding of physics concepts among non-science majors (including elementary education majors).
In addition to increasing the mathematics requirements for future teachers at the Collaborative institutions, the Virginia Collaborative (VCEPT) was instrumental in influencing changes in state policy regarding certification of elementary and middle schools teachers. Whereas previously the state did not require prospective elementary teachers to study any science or mathematics, new licensure requirements include 12 hours of mathematics and 12 hours of science for a K-6 license and 21 hours of mathematics for a middle school license to teach mathematics. Previously any teacher was certified to teach all subjects in middle school when certified to teach in any two of four areas: social studies, language arts, science, or mathematics. Students enrolled in a VCEPT course were asked to indicate the importance of various course characteristics in helping them to learn in the course. The three characteristics most often cited as being very important were active student learning, interesting and intellectually involving concepts, and assessment of student performance in different ways.
The Maryland Collaborative (MCTP) has developed an instrument to examine preservice students' attitudes and beliefs about the teaching of mathematics and science. MCTP undergraduate classes are taught by faculty in mathematics, science, and education who make efforts to focus on “developing understanding of a few central concepts and to make connections between the sciences and between mathematics and science.” The MCTP Research Group investigated whether prospective teachers enrolled in MCTP adopt more positive attitudes over time towards mathematics and science, and towards the teaching of these subjects over time as they participate in the MCTP program. In particular, the study considered whether preservice students' beliefs about the best ways to teach mathematics and science are compatible with the project's goals; use of constructivist instructional strategies, emphasis on connections between mathematics and science, and appropriate use of technology when teaching mathematics and science, and encouragement of students from diverse backgrounds to participate in challenging and meaningful learning. Findings indicate that MCTP teacher
candidates' beliefs about the nature of the two disciplines, and about how one ought to teach science and mathematics, are becoming more in line with beliefs advocated by current reform efforts in mathematics and science education. The significance of this result is particularly interesting since, during most of the three-year period when MCTP teacher candidates were surveyed, the majority of them were completing the MCTP-revised mathematics and science content courses, and had not yet begun to take the MCTP-revised pedagogy courses or student teaching.
The College Algebra in Context course at the Colorado CETP (Colorado State University) is a reform course that replaces breadth with depth, covering a few topics considered central to mathematics in great depth and maximizing the use of student-centered activities to encourage students to construct knowledge, explore the meaning behind mathematical concepts, employ multiple strategies in problem solving, and communicate mathematical ideas. A comparison of students in the reform college algebra class with students in a traditionally taught class indicated the students in the reform class scored significantly higher than traditionally taught students in three dimensions: conceptual understanding, ability to employ multiple approaches, and communication skills.
At San Francisco State University, one of the San Francisco Bay Area CETP institutions, Mathematics 301, a course required for future mathematics teachers, was revised to increase the hours and revise the materials and processes used during the class. Student achievement increased as measured by the increase in B's (from 27% to 48%) and decrease in C's (from 40% to 24%). Also at San Francisco State University, two capstone courses for secondary mathematics teachers involved problem solving, cooperative learning, the use of technology, and a variety of assessment techniques were introduced. Enrollment doubled in the revised courses.
In conclusion, effective preparation of future teachers requires a comprehensive effort on the part of colleges and universities and their faculty. The challenges cover a range of areas, including, for example:
-
faculty improving their courses and how they are taught;
-
institutions providing resources and incentives for faculty;
-
students having research experiences and early teaching experiences;
-
mathematics, education, and K-12 faculty communicating and working together;
-
teachers being supported in their novice years, and provided continued professional development.
Many effective practices have developed. However, their implementation remains perhaps the greatest challenge, requiring institutional and faculty commitment and priority for the preparation of their students as future teachers.
ACKNOWLEDGMENT
Appreciation is expressed to Dr. Joan Prival, NSF Division of Undergraduate Education, for providing the information about the CETP projects for this article.
Joan Ferrini-Mundy
The sessions in this part of the Workshop focused on helping teachers learn the content they need to teach well by considering sites of actual teaching practice as the vehicle for instruction. An earlier speaker pointed out that video provides the opportunity to actually focus on questions and answers as they arise, which can lead to additional opportunities to learn. Another speaker indicated that teachers are being charged to look at standards, national standards and state standards, to develop frameworks for their own teaching. This means teachers have to navigate and align these different standards across their own work trying to make a consistent message for their own classrooms. Other conversations suggested other promising sites of practice, and it seemed that a reasonable way to focus our discussion was to begin to make a list about tasks of teaching that serve as places where teachers have an opportunity to learn some mathematics. Such a list might include the following potential sites of practice:
-
Learning to use and adapt student curriculum materials and teachers ' guides
-
Critiquing and reviewing instructional materials
-
Studying cases of mathematics teaching
-
Analyzing cases of student thinking
-
Analyzing videotapes of teaching, including an analysis of questions and answers
-
Analyzing student work
-
Remodeling mathematical tasks and analyzing the nature of tasks
-
Managing classroom discussion
-
Implementing assessments
-
Looking at standards
As we think about this perspective on developing teacher knowledge, we might make some conjectures about why sites of practice seem promising as contexts through which teachers can learn mathematics, in particular the mathematics it takes to teach well. The discussion has highlighted different possibilities and reasons, conjectures that are still emerging in my own thinking as reasons why these sites of practice might be productive. One reason might be that such sites could be motivational for a prospective teacher. The opportunity to begin working with curriculum material that teachers might envision themselves using six
months later in a classroom could be a natural incentive. Likewise, viewing a real classroom on tape could be motivational and useful as a way to think about issues of practice and their relation to the content knowledge needed to effectively function as the teacher in the videotaped classroom.
Another factor is that sites of practice are instances of actual application. I think this connects back to something Hy Bass said yesterday, the notion that we teach a calculus course and include in that course applications that an engineer might find realistic. In the same way, sites of practice such as we have discussed offer the possibility for devising applications and problems of teaching that teachers might find productive as places to think more about mathematical questions.
Sites of practice might also be thought of as generative. As an individual, they cause me to think about, or to focus on, areas of mathematics that might not have seemed as productive or important in other settings. The complexity of a set of student answers can draw you into other kinds of mathematics that you might not have been choosing as a focus at the beginning.
Finally, sites of practice serve in an activating role. They cause you to think about mathematics you might not have thought of before and to draw on mathematics that you might have known but that might not have come to the surface without this sort of spark.
These reasons sites of practice might be promising are just a beginning that poses a tentative set of suggestions. It would seem feasible that the next steps are to add to, refine, and explicate the list, making the conjectures more robust. As next steps then, in an interactive mode, we should begin to propose arguments for why these might be reasonable conjectures, and we should begin to actually design experiences to help further the argument. One way to go forward is to actually try out certain kinds of ideas to get a better understanding about which elements of this list might be most useful in terms of making the case. We need to begin in a disciplined way, using what we know about doing research, the task of studying outcome as we build coherence and language, and grounded arguments about using sites of practice to help preservice students come to know the mathematics they will need to teach well.