(EXCERPTS FROM)
EXPLANATION OF THE UNIT ON WEIGHT
-
OVERVIEW
Students have experienced the measurement of weight such as at the time of physical health check-ups to measure their body weight. We should remind them of such experiences to introduce the concept of weight for the first time in this unit. Although weight is a quantity unable to be measured in a direct, visible way like length and size, have the students realize that they can use an arbitrary unit and find how many units there are to find weight just like in length and size. It should be done through actual measuring of concrete objects, then have them understand the usage of the units of weight such as “g” and “kg.”
Like a clock, a scale has graduations along the curve on its surface. Students sometimes have difficulty reading the measures. Also, the fact that weight cannot be determined by the object's size nor texture makes it hard for the students to understand weight. Thus, it is important to allow them to experience many occasions of actually measuring the weights and getting familiar with the concept.
-
GOALS
-
To understand the concept of weight.
-
To understand the units of weight, “g” and “kg.”
-
To be able to read a scale and measure various objects with a scale.
-
To understand the relationship between “g” and
-
To be able to add and subtract weight.
-
-
KEY POINTS OF INSTRUCTION
-
Concept and measurement of weight
Although this is the first unit of formal instruction on weight, children have had previous experience with weight in daily life and in various routine activities such as physical examinations.
Judging from outward appearance only, it is easier to estimate an object's length or volume than its weight. However, when determining weight, both indirect and direct approaches are possible: feeling the weight of the object in one's hands or placing it on a scale. It is also possible to numerically express an object's weight beginning with an arbitrary unit of measurement. A similar instructional method was outlined in the unit on Length and Measurement.
These basic ideas are important not only in order for students to understand the concept of weight, but also for them to understand its measurement. As in the instruction of length and volume, there are four steps for the instruction of weight:
-
Direct comparison;
-
Indirect comparison;
-
Measurement by an arbitrary unit;
-
Measurement by a universal unit.
Because weight is difficult to judge visually, it is important to focus on the necessity of a measuring tool. Students' subjective interpretations of weight (e.g., “heavy,” “light”) are replaced by the graduation indicated on measuring tools and visualized there. This leads to the introduction of a scale.
A scale is constructed to capture the force of gravity on an object 's mass with visual movement. One example is associating an object 's weight with the lengthening of a spring. Another example is converting the weight into rotational movement, observing the weight in relation to the number of degrees a scale's dial hand moves. This idea of measurement is much more difficult for students to learn compared to the measurement of length or volume. For example, it is easy to visually grasp the sense of an object's length by using a measuring tape, because the increments shown on the flexible tape are the same as those on a graduated ruler. But using a scale, an object's weight is indicated more abstractly—by the degree a dial hand has moved—so it is harder to get the sense of how much it weighs visually.
Because a balance scale makes it easier for children to understand the concept of weight and visualize the meaning of measurement, it is better to use a balance scale when first introducing the topic. However, because upperdish automatic scales are used more frequently in real life, it is also important that children learn how to use and read them accurately.
As part of their study of the automatic scale, students in this unit will assemble several bags of sand with amounts such as 1 kg, 2 kg, and 3 kg. This is so that students are exposed to both the physical experience and actual measurement of standard weight.
-
-
Introducing the unit of weight
There are three key points regarding the instruction of the weight unit.
-
Weight can be expressed using the number of standard units; it can be numerically stated and labeled.
-
It is more convenient to have two related units such as g and kg so that depending on the purpose one can determine the unit to use and can write the weight in simplest terms (e.g., 2 g rather than 0.002 kg).
-
1 kg is equivalent to 1000 times 1 g.
Because children are not particularly good at converting between these units, and converting is not encountered so often in daily life, it is extremely important to emphasize the relation 1 kg=1000g.
The minimum graduation of an upper-dish automatic scale with the capacity of 1 kg represents 5 g, and there are 200 of these increments shown on such a scale. It follows then, that if the minimum graduation were 1g there
-
-
were 1g there would be 1000 increments on the scale. This may be one way for students to imagine the relation of 1 kg and 1000 g.
Also, it is advisable to tell the students that the “k” in 1 kg means “one thousand times.” Teachers can remind students that a similar relationship was encountered previously with length (1 km=1000 m).
-
Sense of weight: Estimating standard quantity
Concerning the sense of weight, 1 kg and 1 g are the best standard quantities for students to become familiar with so they may begin to grasp the actual numeric amount certain objects weigh. Since there are various capacity levels for upper-dish automatic scales (e.g., 1 kg, 4 kg, 10 kg, etc.), depending on what the objects will actually weigh, it is also important to be capable of determining which scale to use.
For example, knowing roughly how much 1 kg weighs helps when estimating the weight of a 3-4 kg object since it is possible to guess that it would be 3 or 4 times heavier than 1 kg.
Another advantage of acquiring a sense of standard quantity is that, given a desired numeric amount and objects with an insufficient weight sum, students can estimate the additional amount needed to make up the difference. For this reason, teachers should provide an environment that includes many different objects weighing various standard amounts so that students have the opportunity to re-experience the weight of them at any time. For example, when assembling a bag of sand with the weight of 1 kg, teachers can keep an eye out for daily objects weighing 100 g or 500 g.
-
How to read graduations
It is harder for students to read graduations on a scale than to read graduations on a ruler, because a scale includes numbers such as 5, 50, 500; or 2, 20, 200; as well as 1, 10, 100 as the smallest graduations. However, it does not show numbers such as 3 or 70. Commenting on the contrast between the graduations on a scale and the ones on a ruler will lead to students' awareness about the structure of the base-10 system.
Be aware of the following points in order to use a scale correctly.
-
Put the scale on a level surface.
-
Before measuring, make sure that the hand points precisely at 0.
-
Check the maximum weight capacity of the scale, and do not put objects on it that seem heavier. (Before measuring, hold the objects and estimate their weight by hand.)
-
Place objects on the plate gently and take them away gently.
-
Face the dial straight on to read the graduation accurately.
It is also important to develop the students' ability to distinguish the characteristics of different scales and to choose a correct one according to their purpose. This can be done by having students actually use different scales to measure the weight of various objects existing around them.
Next, the following steps should be taken in order to read graduations.
-
Check the maximum capacity of the scale (e.g., the graduation of 1 kg).
-
Check the graduations of large increment numbers.
-
How many graduations can these large increments be divided into?
-
What is the sense of physical weight represented by one of these large increments?
-
Check the smallest graduations.
-
How many graduations are there between two larger increments?
-
What is the sense of physical weight represented by one of these smallest increments?
Students should read from the large graduation to smaller graduations as outlined above. Also, if the dial hand points between two graduations, they should choose the number that is closest to the hand.
-
-
The importance of manipulative activities
Unlike the study of length or volume in first and second grade, it is hard to understand the conservation and additivity of weight. Since weight cannot be sensed visibly, and because many students may think an object's weight changes when its physical position or shape changes, it is difficult to illustrate the concepts through simple verbal explanation. It is therefore imperative to engage students in activities such as weighing a toy after changing its position and weighing clay after tearing it, then connecting it, etc.
Hence, we deal with several manipulative activities in this unit. For each activity, teachers should show a model experiment and should make sure every child is involved and gets frequent opportunities to use the scales.
The following are examples of manipulative activities.
-
Have students go to a sandbox and put 1 kg sand (which they have to guess) in a plastic bag and measure it on a scale. Most children at this age have not yet developed a sense of 1 kg of weight, so have them try to make the 1 kg bag by adding or removing sand many times. As an expansion of this activity, teachers can have the students make bags with 2 kg, 3 kg, or 1.5 kg sand, which will enhance their interest and motivation in their study of weight.
-
Let students try to make 2 kg by putting everyday objects on a scale. (It could be 1.5 kg or 3 kg, etc.) Given this assignment, students will likely begin to put objects on a scale randomly and soon become aware that they can make 2 kg more quickly with heavier objects. This activity will also help them develop a method of estimating an object's weight before measuring. Some students may even record the weight of each object and add to make the total weight of 2 kg.
Furthermore, teachers can show students how they can determine the weight of fruits in a basket if they subtract the weight of the basket from the total weight. This will help them understand the meaning of conservation and additivity of weight.
-
A. Section One (2 hours):
Objectives for the first section:
To learn the concept of weight, the meaning of measurement, and the unit of weight [gram (g)].
|
Hour One and Two: Goal: To understand the concept of weight and the unit of weight, the gram (g). Materials: Dictionary or books A bucket with water Large springs Scale Scissors Compass (the type used to draw circles) Glue Pencil Wooden blocks 1-yen coins |
(Example of a proposal for teaching this section)
Topic 1:
“Which book is heavier? Which bucket is heavier?”
Activity: Present two kinds of books and two buckets of water.
Guidance: Let students compare the weights of both of the objects by holding one in one hand and another in another hand. Allow students to realize the importance of measurements of weights by letting them know that it is not necessarily possible to distinguish the weights of the objects just by holding them.
Topic 2:
“Which one is heavier? How can we compare the weight of the objects? ”
Activity: Present scissors, compass, and glue.
Guidance: Have students discuss the different ways to compare the weights of the objects. Even though students may suggest using a regular scale, suggest that they use a justice scale indicated in the textbook.

Important Notes:
-
How to introduce the concept of weights: Weight is a difficult concept for students to understand, compared with the concepts of length and volume, because (a) weight is hard to determine visually and (b) weight is not necessarily determined by the size and shape of the objects.
Therefore, it is important that more manipulative activities are introduced and that students measure the weights of objects by picking up the objects to feel their weights (direct comparison).
In other words, it is important for teachers to introduce them step-by-step to direct comparisons and indirect comparisons, leading to the use of universal units.
For the comparison of two objects, it is important to use objects that are tactually discernible in weight and objects that are not tactually discernible in weight, so that students can learn that they cannot measure the weight of the objects just by using their senses.
Editor's note: The Japanese teachers' manual includes—in a contrasting color of type, so as to be easily seen—the answers to each of the questions that appear in the children's text.
-
The order of guidance for teaching weight: It is important to include the following steps:
-
Direct comparison (by using hands and justice scale);
-
Indirect comparison (by using a regular scale);
-
Arbitrary units (by using wooden blocks);
-
Universal units (e.g., one gram).
-
-
Purpose of the unit:
The purpose of this unit is to remind students of the steps of measurement and weight, which are similar to those with the measurement of volume and length. Let the students realize the necessity of using arbitrary units and universal units.
Topic 3:
“Let's compare the objects using the justice scale.”
Activity: Present a justice scale.
Guidance: Be sure to check if students know that when comparing two objects on a justice scale, the heavier side will drop down, and the lighter side will rise, and that if the two weights are the same, the two sides will remain even.
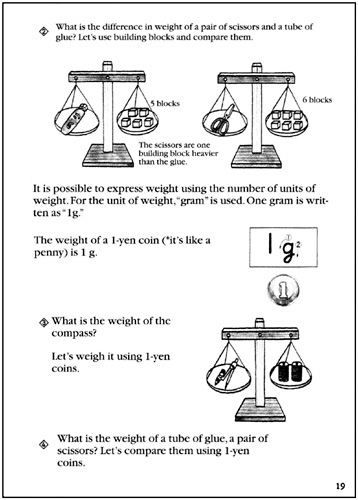
In the example on p. 18, the scissors is heaviest, and the compass and the glue have the same weight.
Topic 4:
“How much heavier are the scissors than the glue? Let's examine and find out by using wooden blocks.”
Activity: Continue to weigh using the justice scale. This deals with step two on p. 19.
Guidance: First, allow students to realize the difference in the weights of the glue and the scissors. Second, get them to remember how they can measure the length by the number of units (i.e., make a certain unit and count how many units equal a certain length). Third, suggest that they use wooden blocks as units of measurement. Each block should be the same weight.
The glue in the textbook illustration equals five wooden blocks, whereas the scissors equals six blocks. Therefore, the scissors is one block heavier than the glue.
It may also be a good idea to suggest other items such as nails or paper clips as a unit of measurement. Then explain to the students that there is a unit of weight, a gram (g), and one gram is equal to one coin of one yen. One gram is written as 1g.
Topic 5:
“What is the weight of the compass? Let's measure it by using oneyen coins.”
Activity: This deals with step three on p. 19.
Guidance: Let the students measure the weight of the compass by one-yen coins and finally represent the weight in terms of grams. Twenty one-yen coins equals twenty grams.
Topic 6:
“What are the weights of the glue and scissors, in terms of grams? Let's measure them using one-yen coins.”
Activity: This deals with step four on p. 19.
Guidance: Let the students measure the objects and then share their findings with the class.
B. Section Two (6 hours)
Objectives for the second section:
-
To learn how to read and use the units on a scale;
-
To learn the unit of weight, the kilogram, and that 1kg=1000g;
-
To learn how to select appropriate units and measuring devices depending on the objects;
-
To learn that weight has conservation and additivity.
|
Hour Three: Goal: To learn how to read units of a scale. Materials: Scale with a horizontal platform (two types: 1kg and 400g) Book (weight has to be less than 1kg) Enlarged drawing of the face of the scale |
(Example of a proposal for teaching this section)
Topic 1:
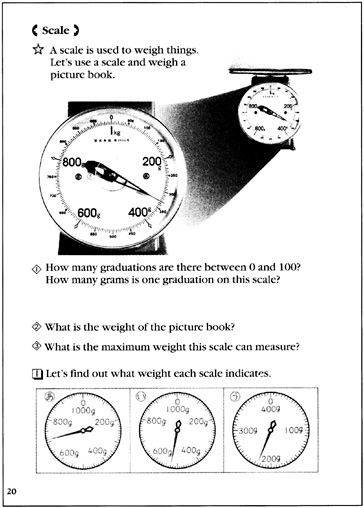
This deals with the asterisk and step one in the text on p. 20: “In order to measure weight we use a scale. How many lines are there between 0g and 100g, and how much does each line indicate in grams? ”
Activity: Present the 1kg scale.
Guidance: Let the students understand the unit system of a scale before measuring the weights. There are three points:
-
the largest units on the scale are 200g, 400g, 600g, 800g, and 1kg;
-
the smallest unit on the scale is 5g, with increments of 5g;
-
the smallest unit on the scale is the least discriminable unit on the scale.
Topic 2:
“What's the weight of the picture book in grams?”
Activity: This deals with step two on p. 20.
Guidance: Show the enlarged drawing of the face of the scale, and let the students see that the picture book weighs 330g. Also, let them realize that 330g is lighter than 400g, and is heavier than 300g.
Exercise: Reading units on a scale
Read the weight of the scales a, b, and c in the textbook, which is on p. 20 of the textbook.
Important Notes:
-
Guidance for teaching students how to read units on the scale:
In the beginning, students are usually unfamiliar with reading units on the scale. So introduce the following basic steps in teaching:
-
Let students read the large units on the scale, such as 200g or 1kg.
-
Let students read the intermediate level of units. Let students see how many intermediate units there are in one large unit. Let them say what one intermediate level is.
-
Let students read the smallest level of units.
By following these steps, students can learn how to read the units correctly.
In terms of reading units, students should learn first to read the larger units (100s). Then the intermediate units (10s). And then the smallest units (1s). Finally, to learn to put units together to equal the weight.
In addition, students can also read the unit as being some number of units away from the maximum unit (e.g., 30g away from 400g equal 370g).

|
Hour Four and Five: Goal: To learn the unit of weight, the kilogram, and that 1kg=1000g. Materials: Scale with a horizontal platform (two types: 1kg and 400g) Bookbag |
Topic 1:
“Let's measure the weight of the bookbags.”
Guidance: Let students talk about their bookbags and let them estimate the weight of their bookbag.
Teach them the units of weight (e.g., kg for heavy objects) and let them practice using the unit of kilogram.
Let students understand the relation between 1kg and 1000g.
Let students figure out what the bookbag in the textbook illustration weighs.
Topic 2:
“What is the maximum this scale (p. 21) would be able to measure?”
Activity: This deals with step three on p. 21.
Guidance: Let students know that the scale can measure up to 4kg. Let the students determine the minimum unit on the scale.
Topic 3:
“Let's list the points we need to be aware of when we measure weights. ”
Guidance: Let students know the right way of measuring weights and get them used to doing it.
-
Sense of the weight of one kilogram:
Let students measure the weight of a liter of milk or juice, or whatever liquid they can find. Let them acquire the sense of weight for 1 kg by holding one liter of water, which equals 1 kg.
Exercise one:
Let the students get the idea of the weight of 1kg.
“By holding a bag of sand that weighs 1kg, let's get an idea of the weight of 1kg.” In addition, hold different objects and estimate the weight of each of the objects. Then find the exact weight by using a scale.
Exercise two: Reading the unit on a scale:
-
Let the students learn how to read units in kilograms and in grams.
-
Get them familiar with reading the larger units first, and to figure out the weight by reading the smaller units.
Exercise three: Reading weight in grams (5200g), and in kilograms and grams (5kg 200g).
|
Hour Six: Goal: To learn how to select appropriate units and measuring devices depending on the objects. Materials: Body scale Spring scale Automatic balance scale Objects to be measured |
Topic 1:
This deals with steps one and two in the textbook. Step one: “What kind of objects do you measure with these scales??” Step two: “Lets' estimate the weight of the different objects and measure them with the scale.”
Activity: Show the three different scales on p. 22 in the textbook.
Guidance: Let the students realize that there are different scales for measuring different objects. Let them think of the kinds of objects they can use with the scales on p. 22 by thinking of the objects around them.
Let them realize that, before measuring weights, it is better to estimate the weight first, and then choose the right scale to measure the weight.

Supplementary problems
Let's find out the weight that each scale indicates:


|
Hour Seven: Goal: To learn conservation and additivity of the weight of an object. Materials: Automatic balance scale Pumpkins |
Topic 1:
“There are two pumpkins. One weighs 900g and the other weighs 800g. When you put the two pumpkins on one scale, what is the total weight? ”
Activity: (Step one): “Let's measure the weight.” “Add the weight of the two pumpkins and obtain the total weight of the pumpkins.”
Guidance: Draw a number line similar to this:
Obtain the total weight
Topic 2:
Activity: This deals with step two.
Guidance: Based on the results in step one, make an equation to obtain the total weight:
900g + 800g = 1700g
1700g = 1kg 700g
Topic 3:
“What is the difference between the two pumpkins in grams?”
Activity: This deals with step 2a.
Guidance: Make an equation and calculate it.
Topic 4:
The addition and subtraction of weights (problems 6 and 7 on p. 23).
-
Conservation of weights:
Suppose there is a kilogram clay ball. The weight of the clay won 't change regardless of the shape of the clay. The number of pieces one divides the clay into also does not change the total weight. This characteristic is called conservation of weights.
-
Additivity of weights:
Suppose we add 3g of clay and 2g of clay. It is 3+2=5, which means there is a total of 5g of clay. This characteristic is called the additivity of weights.
Because it is believed that there are children who have not yet acquired the concepts of the conservation and additivity of weights, it is important to let children discover the ideas by shaping, cutting, and weighing the clay.
|
Hour Eight: Goal: Summary of this unit and more exercises. |
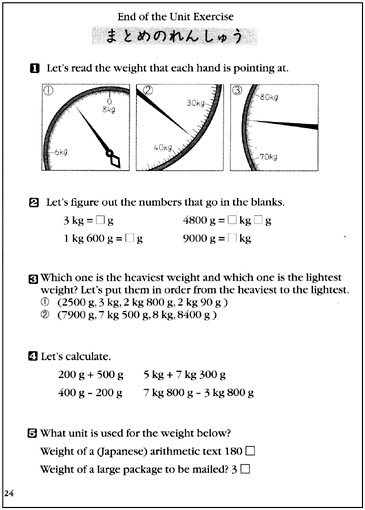
Exercise one: exercise for reading the units on the scale.
Exercise two: exercise for reading weight in kilograms and in grams.
Exercise three: ordering of weights, from heaviest to lightest.
Exercise four: addition and subtraction of weights.
Exercise five: exercise for selecting the appropriate units.
Supplementary Problems
-
Find out the numbers that fit in the blanks(□) and write the numbers down.
|
7kg = ☐g |
(7000) |
|
4000 g = ☐kg |
(4) |
|
2 kg800 g = ☐g |
(2800) |
|
8300 g = ☐kg ☐g |
(8;300) |
|
5 kg40 g = ☐g |
(5040) |
|
3050 g = ☐kg ☐g |
(3;50) |
-
What units are used for the weights mentioned below:
|
body weight |
1 tomato |
-
Calculate the problems.
500 g +700 g (1200g, 1 kg200g)
4 kg + 8 kg (12kg)
6 kg800 g + 9 kg600 g (16kg400 g)
1300 g − 800 g (500 g)
7 kg400 g − 3 kg (4 kg400 g)










