CHALLENGES TO OURSELVES AS PROFESSIONAL DEVELOPMENT DESIGNERS
How can we design learning professional development experiences that:
INCLUSIVE
Are inclusive and effective with teachers, regardless of their pedagogical views, knowledge, or skills.
PRODUCTIVE AND EFFICIENT
Have rapid, significant, and direct positive impact on the learning of teachers and their students—and on their ability to continue to learn from their own experiences.
MEASURABLE
Demonstrate a positive impact on students' understanding of mathematics which is measurable on a variety of instruments, including standardized tests.
OPEN TO CRITICAL EXAMINATION
Provide an environment that supports teachers questions themselves, each other's ideas, even the most highly regarded ideas of the mathematics teaching community.
TEACHER LEADERSHIP
Assumes that all teachers, regardless of their experience or pedagogical philosophy, should be given the opportunity to assume leadership roles.
WHY LEARN TO DISCUSS AND FACILITATE MATH CASES?
Mathematics
-
To deepen our own understanding of the mathematics
Children's Thinking about Mathematics
-
To experience the mathematics from our students' points of view
Mathematics Instruction
-
To make informed teaching decisions by examining the benefits and drawbacks of various strategies
Language
-
To understand the impact of oral, symbolic, visual, and written communication on the mathematics learning of all students
Case Discussion Roadmap Summary
Mathematics Case Methods Project
-
Opening inclusion activity
Purpose: to build trust and support open discussion; participants may pass.
-
Starter Problem
Purpose: to stimulate thinking about the mathematics and student thinking; participants work independently; solutions may be presented during the discussion, but are not shared prior to the discussion.
-
Read or quickly review the case
If possible, participants read the case before coming to the discussion and begin to think about issues to discuss.
-
Facts
Purpose: to build common background about the case; collected quickly popcorn style without comments.
-
Issues written in question format
Purpose: to generate questions that will stimulate deep discussion; focus on the mathematics, child's thinking, instruction and materials, or language; participants
generate issues in pairs.
-
Begin the discussion
The issues are read to the group; a volunteer chooses one of the issues and begins the discussion.
-
During the discussion
Participants build on and ask questions about each other's ideas; a few ideas are examined in depth; participants come to the board to make drawings or use materials to explain their ideas.
-
Closing inclusion activity
Purpose: to bring the group together for a brief reflection or appreciation of the experience; may be an oral or written reflection.
-
Process Check
Purpose: to allow participants to give feedback to each other on how well the group participated in the discussion; it is not an evaluation of the facilitator.
Six-Tenths or Four-Fifths of a Dollar?
The math experiences of the 30 students in my fourth-grade class vary widely. Esmarelda, a recent immigrant to the United States, is Limited English Proficient (LEP) and has never had formal schooling, Chris is a gifted student who enjoys calculations and problem solving. Michael participates in my class, then later in the day goes to the resource room for additional math help. There are also 3 children with special needs, 4 other LEP students, and 12 extremely economically disadvantaged students.
Often, it seems, I teach a lesson 4 or 5 times before I feel comfortable moving ahead Sometimes I worry that I'm beating a dead, horse. For those students who catch on quickly I try to plan enrichment activities or set up activity centers. This year—my third year of teaching—I've been trying to include more math journal writing before, during, and after lessons. I also try to use concrete materials before explaining a mathematical concept to the class.
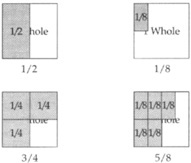
I recently introduced the class to fractions. They have learned how to identify fractions using diagrams such as the following:

Each student made a fraction kit that allowed them to show and identify various fractions. The denominators of the fractions in the kits were 1, 2, 4, 8, and 16.


My beginning lesson had focused on identifying and orally naming various fractions.
“Place your ‘whole' on the desk top,” I said. “Show me ¼ of a whole by placing ¼ on top of it.” The students responded by placing a “one-fourth” piece on the square representing 1 whole.
By the end of the lesson, they could successfully name and use the fraction kit to show unit fractions like ½ or 1/8 and nonunit fractions like ¾ or 5/8
The next lesson focused on equivalent fractions. I asked the students to figure out the answer to questions like how many eighths would be equal to ¼ or how many sixteenths would equal 3/8. They used their fraction-kit pieces to determine the answers. By the end of this lesson, students were very familiar with the relationship among the fraction pieces and could solve simple equivalency problems without using the pieces.
I was then ready to have students learn how to compare fractions that have different denominators and numerators. Prior to beginning, I asked them to write about fraction equivalency in their journals, so I could assess their understanding of previous lessons and know what information I needed to cover, I asked, them to answer this question:
Which would you rather have: 6/10 of a dollar or 4/5 of a dollar? Explain your reasons for choosing your answer.
After reflecting, the students picked up their pencils and wrote.
Cindy's journal read: “If I had 6/10, I would have 2 more than 4/5. I would choose 6/10 so I could have more money.”
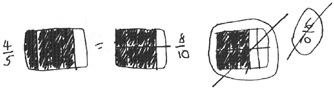
Chris wrote: “4/5 = 8/10, 8/10 is greater than 6/10. Of course, I'd take 4/5 of a dollar. Wouldn't you?” He included an illustration:
Esmarelda wrote: “No sé. 6/10 es mas grande.”
Nikki drew a picture to accompany her answer: “I want 6/10. It is bigger.”
Only 4 of the 30 students wrote 4/5. Their journals gave me some hints about how they were thinking about fractions, but I was not sure how to use this information to plan our future work. Since the students were familiar with the fraction kit, I wondered if they would have answered differently if the question had been, “Would you rattier have ¾ or 5/8 of a chocolate bar?”
Suggested Reading
Behr, M. J., T. R. Post and I. Wachsmuth. 1986. “Estimation and Children's Concept of Rational Number Size.” In Estimation and Mental Computation, edited by H. L. Schoen and M. J. Zweng, 103-111. Reston, VA: The National Council of Teachers of Mathematics.
Cuevas, G. 1990. “Increasing the Achievement and Participation of Language Minority Students in Mathematics Education.” In Teaching and Learning Mathematics in the 1990s, edited by T. J. Cooney and C. R. Hirsch, 159–165. Reston, VA: The National Council of Teachers of Mathematics.
PROCESS CHECK
Mathematics Case Methods Project
Rating Scale: 1 2 3 4 5
Strongly Disagree Strongly Agree
Feedback to the group:
-
___ Group members gave different points of view respectful consideration even when there was disagreement or the ideas were unpopular.
-
___ I felt I had opportunities to comment, whether or not I contributed during the discussion.
-
___ Members built on and contributed to each other's ideas. Members asked questions about each other's ideas.
-
___ The group gave a high priority to discussing the mathematics and student thinking.
Feedback to the facilitator:
-
What is one thing that worked well?
-
What is one thing that might be tried next time?









