11
Parameterization and Upscaling in Modeling Flow and Transport in the Unsaturated Zone of Yucca Mountain
Gudmundur S. Bodvarsson,1 Hui Hai Liu,1 C. Fredrik Ahlers,1 Yu-Shu Wu,1 and Eric Sonnenthal1
ABSTRACT
Parameterization and upscaling for unsaturated rocks are discussed with application to Yucca Mountain in Nevada, the potential site for a geological repository of high-level nuclear waste. A complex three-dimensional model of the unsaturated zone at Yucca mountain (UZ model) has been developed (Bodvarsson et al., 1997) utilizing all of the available data from the site, including those from numerous surface boreholes and underground tunnels. As the typical grid spacing used in the UZ model is on the order of tens of meters to more than 100 m, the parameterization for the model based on much smaller-scale in situ tests and core measurements must be carefully conducted. A methodology for doing this has been developed and used in the UZ model; this methodology is applicable to most other fractured unsaturated sites. The primary upscaling process used in the UZ model is a direct inversion of the observed data, including saturation, moisture tension, pneumatic, perched water, temperature, and geochemical data. The process starts with one-dimensional inversions and then proceeds to two- and three-dimensional inversions.
INTRODUCTION
The unsaturated zone at Yucca Mountain, Nevada, is being considered by the United States Department of Energy (DOE) as a potential site for the geologic disposal of high-level radioactive waste. The unsaturated zone consists of a series
|
1 |
Earth Sciences Division, Lawrence Berkeley National Laboratory |
of welded and unwelded volcanic tuff layers with different hydrological characteristics and degree of fracturing. The welded units are heavily fractured and characterized by fracture permeabilities that are many orders of magnitude higher than the corresponding matrix permeabilities. The unwelded or poorly welded units, on the other hand, have significant matrix permeabilities and fewer fractures. Prior to the site characterization activities at Yucca Mountain, little work had been performed in deep unsaturated fractured rocks. Most relevant previous research was performed in shallow unsaturated near-surface soils. Because of this, the site characterization activities at Yucca Mountain have been extremely challenging, with a need to develop relevant theories and hypotheses to explain the observed data from this extremely complex system.
The unsaturated zone at Yucca Mountain is about 600 m thick, and the area of characterization amounts to some 50 km2. Thus, a rock mass with a volume of 30 km3, including approximately 109 fractures and the corresponding matrix blocks, needs to be characterized. It is clear that only a small fraction of this volume and fractures can be characterized with an economical number of boreholes and underground tunnels. Furthermore, the available measurements of important flow and transport parameters are only possible on spatial scales much smaller than what is needed for a large site-scale model intended to represent global parameters, processes, and conditions. Typically, the grid size for a site-scale model is tens of meters, if not more than 100 m. This creates an enormous challenge in the development of the appropriate parameterization for a site-scale model by taking into account parameter measurements performed in laboratories and the corresponding measurement scales, in-situ dynamic and static observations and their scales, and in situ measurements and the scales they represent. All of this needs careful evaluation of the appropriate parameterization and upscaling practices that are required for the development of a robust, defensible flow and transport model of the unsaturated zone at Yucca Mountain.
In this chapter, we describe the methodologies we are using in the development of the flow and transport model (UZ model) of the unsaturated zone at Yucca Mountain. We will first briefly describe the available data and the basic elements of the conceptual model of the unsaturated zone flow and transport. Then, the development of the hydrological and transport parameters are discussed with reference to many relevant issues such as upscaling, applicability of conventional unsaturated flow theories to fractured rocks, fracture and fault parameters, and others. Parameter estimation and one-dimensional data inversion are described using the methodology we have developed over the last few years (Bodvarsson et al., 1997a; Bandurraga and Bodvarsson, 1997; Liu et al., 1998); this again considers upscaling and other processes. These inversion activities are then augmented by a three-dimensional numerical analysis that folds in and considers multidimensional flow and transport effects, the incorporation of thermal analysis, and the extremely important calibration of data associated with perched-water bodies. Finally, the geochemical data and analysis are described in terms of
available data, calibration activities, and their constraining value in the development of the UZ flow and transport model.
CONCEPTUAL MODEL
The evolution of the conceptual model of the unsaturated zone at Yucca Mountain is given in Chapter 2. Here we briefly describe the essential features of the conceptual model for water flow through Yucca Mountain. Plate 5 shows a schematic view of a simplified model for water flow through the mountain. Concentrated infiltration into the Tiva Canyon welded unit (TCw) takes place through narrow zones mostly on ridgetops, where exposed fractures are present (Flint et al., 1996). The infiltration is sporadic with major episodes estimated to occur every few years on average. Episodic fracture flow is believed to be prevalent in the Tiva Canyon, with travel time from the ground surface to the Paintbrush nonwelded unit (PTn) only on the order of one year. These episodic pulses are dampened in the PTn due to its porous medium-type characteristics, with high matrix porosity and permeability. The PTn consists of a series of nonwelded tuff layers with variable porosity and permeability that average about 40 percent and 300 md, respectively (Flint, 1998). Flow through this unit is believed to be primarily vertical (Wu et al., 1999a), although some lateral flow may occur due to its layering structure and associated heterogeneities, and also capillary redistribution. Water flow within the Topopah Springs unit (TSw) is dominated by fracture flow, estimated to range from 50-90 percent of the total flow (Wu et al., 1999a), depending on the fracture and matrix hydrological parameters of the subunits. In general, most of the subunits are heavily fractured with fracture spacings of 20-50 cm (Sweetkind and Williams-Stroud, 1996). However, only a small percentage of these fractures are believed to currently transmit liquid water through the mountain. Pruess (1999) and Pruess et al. (1997) estimated spacings of water flow paths (weeps) in the TSw to be on the order of 10 m, based on various hydrological and geochemical observations. Thus, one expects that there are hundreds of thousands of water flow paths of various sizes within the repository unit at Yucca Mountain.
The main tuff units below the repository are the Calico Hills (CHn) and Prow Pass, Crater Flat (CFu) units. Both of these units have vitric and zeolitic components that differ by the degree of hydrothermal alteration. The zeolitic rocks have low matrix permeabilities, on the order of microdarcies, and some fracture permeabilities. The current conceptual model, primarily based on perched water data, favors a small amount of water flow through the zeolitic units, with most of the water flowing laterally in perched water bodies and then vertically down through highly permeable faults (Wu et al., 1999b; Kwicklis et al., 1999; Flint et al., 1999). The vitric units, on the other hand, possess relatively high matrix permeability (0.1 to 10 Darcies), and therefore porous medium-type flow dominates. Fracture flow is believed to be limited in these units. A much more detailed
description of conceptual models for water flow at Yucca Mountain is given by Kwicklis et al. (1999).
HYDROLOGICAL PARAMETERS
Parameterization of the Hydraulic Property Distribution
An important aspect in characterizing a site is to use a number of parameters to represent heterogeneous hydraulic property distributions at the site. These parameters are determined or inferred from the relevant observed data. Heterogeneities at different scales are presented in fractures and matrix. A variety of approaches are available for constructing subsurface heterogeneous hydraulic property distributions, as reviewed by Koltermann and Gorelick (1996). A geology-based, deterministic approach, in which entire model layers are assigned uniform hydraulic properties, has been mainly used for characterizing the unsaturated zone of Yucca Mountain (e.g., Bodvarsson et al., 1997a). The reasons for this are as follows: first, it is generally believed that overall behavior of site-scale flow and transport processes are mainly determined by relatively large-scale heterogeneities associated with the geological structure of the mountain. Second, the complexity of a heterogeneity model needs to be consistent with the availability of relevant data. More complicated models introduce a larger degree of uncertainty in rock property estimations based on inverse modeling, when data are limited. Third, the adopted layered approach is also supported by field observations, such as matrix saturation distributions. For a given geological unit, measured matrix saturation distributions are similar in different boreholes, indicating that large-scale matrix flow behavior and effective fracture and matrix hydraulic parameters should be similar within a unit. Note that matrix saturation distributions are determined by both fracture and matrix properties through fracture-matrix interactions.
Matrix Parameters and Upscaling
Core-scale values for matrix permeability and van Genuchten (1980) parameters are available for each model layer from measurements in several boreholes (Flint, 1998). A practical upscaling approach has been developed to obtain the large-scale effective parameter values for model layers from these small-scale measurements.
It is well known that hydraulic parameters for porous media are generally scale-dependent. For example, large-scale effective permeability can be considerably larger than that measured at a small scale (Neuman, 1990, 1994). A variety of theories have been developed for upscaling parameters such as permeability (Neuman, 1990, Paleologos et al., 1996). However, these theories may not be directly applicable for the matrix in unsaturated fractured rocks due to fracture-matrix interaction. Large fractures can act as capillary barriers for flow between
matrix blocks separated by these fractures, even when the matrix is essentially saturated (capillary pressure is close to the air entry value). Therefore, the existence of fractures could reduce the effective permeability of the matrix continuum. Based on these considerations, the currently available relations for up-scaling porous medium permeability (Paleologos et al., 1996) are not used for determining effective permeability for model layers. Instead, a two-step approach is employed. We use geometric means of core measurements to determine effective permeabilities for model layers. Then, parameter calibration by data inversion, as discussed in a later section of this paper, is employed to further refine the permeability values.
In general, the upscaling of the water retention curve, characterized by van Genuchten parameters, is a more difficult task. Simply speaking, the main reason behind the upscaling is differences in liquid water distribution mechanisms at different scales. On the core-scale, the liquid water distribution is controlled by the capillary force. Small pores are always filled with liquid water before relatively large pores during a wetting process. At a larger scale, however, the water distribution mechanism is more complicated. As an extreme example, when subgrid fingering occurs for a large grid block, liquid water is distributed based on the fingering pattern that results from gravitational instability and heterogeneity, rather than pore size distribution. Obviously, these differences give rise to very different water retention curves at different scales, if the retention curve can be defined at large scales.
Compared with most natural soils, however, the matrix in these highly fractured rocks has a very small average pore size. In other words, capillary force plays a very important role in the water-flow process within the matrix. It is therefore reasonable to assume that matrix liquid water distribution within a site-scale grid block, similar to that at the core scale, is mainly controlled by capillary force under the steady-state flow condition. In this case, the upscaled retention curve can be simply obtained by averaging the retention curves measured from core samples for a given model layer. To further clarify this point, let us consider an ideal case, in which the capillary force is so strong that there is a uniform capillary pressure distribution within the grid-block while local retention curves are very different. Obviously, the retention curve for the grid block can be estimated as
(11.1)
where θblock is the average saturation of the grid block, P is the capillary pressure, N is the number of core samples within the block, ni and ![]() are core sample porosity and average porosity for the grid-block, respectively, and θi is the liquid water saturation for sample i at capillary pressure P. Although Equation 11.1 was developed for a grid block, it can be used for a model layer if uniform hydraulic property distributions are assumed within the model layer.
are core sample porosity and average porosity for the grid-block, respectively, and θi is the liquid water saturation for sample i at capillary pressure P. Although Equation 11.1 was developed for a grid block, it can be used for a model layer if uniform hydraulic property distributions are assumed within the model layer.
In summary, compared to other subsurface porous media, matrix in fractured rocks is unique in two aspects, the existence of fractures and the generally strong capillarity. These aspects make the currently available upscaling approaches for matrix permeability, developed from stochastic hydrology, not applicable. While the focus of this study is on the development of physically reasonable and practically workable approaches, further study on upscaling of unsaturated properties of matrix in fractured rocks, based on stochastic methodologies, is useful for refining the approaches developed in this study.
Analysis and Development of Fracture Hydrologic Parameters
The purpose of this section is to provide an overview for incorporating measured properties of fractured rock in a large-scale model to capture flow and transport in unsaturated rocks. A conceptual model of unsaturated flow in fractured rock must represent processes within individual fractures, in fracture networks, and the coupling between these systems and the rock matrix. The characterization of flow in fractured rock requires consideration of the orientation, connectivity, and aperture of fractures at different scales. In contrast to saturated systems, additional hydrologic parameters (van Genuchten parameters) are required that cannot be measured or calculated as satisfactorily as permeability or porosity. Furthermore, the equations describing unsaturated flow in fractures are usually loosely borrowed from soil physics, with little experimental work to support their applicability. Thus, we must use any calculated parameters with great caution, utilizing data inversion, to be discussed later on, to refine the values so that the overall system behavior is captured.
Considerable progress has been made recently in improving our understanding of unsaturated flow in fractures (Bodvarsson et al., 1997a). Glass et al. (1996) used lab-scale experiments to demonstrate that the main flow mechanism for a vertical unsaturated fracture is fingering as a result of gravitational instability and aperture heterogeneities, which is further supported by the numerical model studies of Pruess et al. (1997). Tokunaga and Wan (1997) showed that film water flow along the rough fracture surface could be important when the matrix potential is close to or larger than the air entry value. Faybishenko (1999) suggested that unsaturated fracture flow might be described using the nonlinear dynamics (chaos).
Figure 11-1 shows fractures at different scales. It is a very challenging task to develop an approach to describe large-scale fracture flow, which incorporates fracture flow mechanisms observed at smaller scale. While different approaches are available, we believe that a continuum approach is a suitable and robust approach for the large-scale fracture flow in the unsaturated zone of Yucca Mountain. This is mainly based on the following considerations. First, bomb-pulse 36Cl has been found at depth in Yucca Mountain at only a few locations that are associated with geological features (Fabryka-Martin et al., 1996), and there is no
FIGURE 11-1 Schematic of fractures at different scales.
correlation between these locations and enhanced matrix water saturation and potential, suggesting that the related fast-flow paths likely carry a small amount of water. Second, the existence of many dispersed flowing fractures, allowing the continuum approximation, is also supported by many field observations. For example, very similar matrix saturation distributions were observed from different deep boreholes. Calcite coatings, signatures of water flow history, are found in many fractures within the welded units. It may also be important to note that it is difficult, if not impossible, to construct and calibrate a discrete fracture-network model for a site-scale problem. However, we recognize the importance of detailed study on relations between small-scale (say, a single fracture scale) flow processes and those at large scales.
Commonly, there is a positive correlation between fracture permeability and the scale of the system. Measurements of air permeability done at Yucca Mountain over a wide range of scales allow for an examination of this scale dependence (Figure 11-2). Here we show the range in fracture permeability measurements within the welded zones of the Topopah Spring Tuff. Faults are the largest scale features and exhibit the highest permeability along their strike (lateral) for a measurement scale of approximately 500-700 m. Vertical permeability in faults, measured at a scale of some 100-200 meters, is about an order of magnitude less. Air permeability in rocks outside of faults is shown in the hatched and shaded boxes, and by the dashed arrow denoted “niche.” The upper permeability limit is similar for all measurement scales, except at the largest scale, with the lower permeability limit generally decreasing at the smaller scales. This relationship is fully expected, because the probability of intersecting a conductive fracture declines as the volume of the region probed diminishes. The unfractured rock matrix has a maximum permeability of about 10−16 m2 with a minimum value below the detection limit of about 5 × 10−19 m2, thus setting the lower bound for any larger-scale permeability measurement.
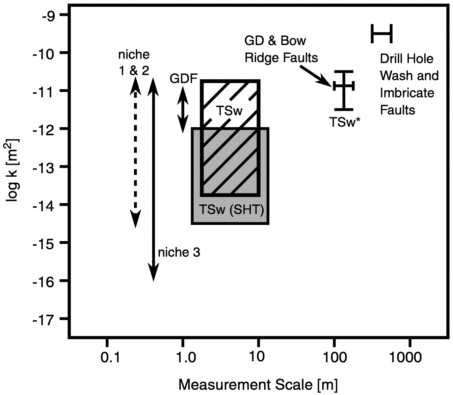
FIGURE 11-2 Schematic diagram showing range in measured air permeability as a function of the measurement scale. TSw* and GD and Bow Ridge faults refer to calibrated permeability based on matching to ambient pneumatic signal (Bandurraga and Bodvarsson, 1997). GDF refers to Ghost Dance Fault (air-k test; LeCain and Patterson, 1997). TSwSHT measurements refer to Single-Heater Test pretest characterization air-k tests (Tsang et al., 1999). TSw refers to in-situ tests in boreholes (LeCain, 1997).
Recently, a number of researchers (Neuman, 1990, 1994; Molz et al., 1997; Liu and Molz, 1997) have indicated that in many cases subsurface heterogeneities can be characterized by stochastic fractals. The air permeability data seem to support this reasoning. According to Neuman (1990, 1994), a fractal-based relation between effective permeability and measurement (support) scale can be given as
(11.2)
where k is the effective permeability, kg is the geometric mean, L is the measurement scale, and H is the Hurst coefficient. When the fractional Brownian motion
(fBm) is applicable for characterizing subsurface heterogeneities, previous studies showed that the H values range from 0.1-0.5, and the average value is about 0.25 (Neuman, 1990, 1994; Molz et al., 1997; Liu and Molz, 1997). Figure 11-3 also shows a curve determined from Equation 11.2 using H = 0.25 and log(kg) = −13.09, as compared with the average log(k) data. The curve is consistent with the overall trend of the air permeability scale-dependent behavior. One important implication of this result is that there may be some similarities between spatial variations of fracture permeability at different scales. The above discussion was used to demonstrate the complex scale-dependent behavior of fracture permeability. Different fracture permeability values should be used for modeling flow and transport at different scales. The permeability values for the site-scale model were determined by calibrating the model against field observations, including ambient pneumatic signals, while the small-scale (<10 m) measurements were employed as initial guesses for model calibration. A more detailed discussion is given in the section “Parameter Estimation/Data Inversion. ”
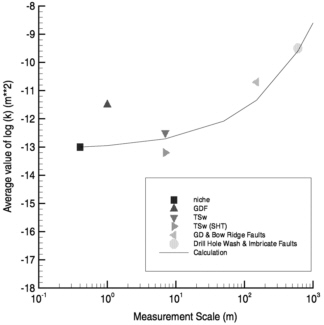
FIGURE 11-3 Comparison of the average log(k) data obtained from Figure 11-2 and the curve calculated from Equation 11.2.
Once the permeability (k) of the fracture system has been determined, the equivalent hydraulic fracture aperture (b) may be estimated using a relation such as the cubic law, as follows:
(11.3)
where f is the fracture frequency. Assuming a simplified form (Altman et al., 1996) of the Young-Laplace equation, values of α (Pa−1) may be calculated directly from the fracture aperture b,
(11.4)
where ρ is the density of water, g is the acceleration due to gravity, τ is the surface tension of water, and θ is the contact angle (here assumed to be zero). Although an estimate of α may be obtained in this way, it is preferable to consider a range of apertures determined from the spread of measured permeability and fracture frequencies, followed by curve-fitting using, for example, the method of van Genuchten (1980), as done for the Topopah Spring welded tuff (Sonnenthal et al., 1997).
The fracture parameters, developed above, are intended for the fracture continuum. However, it is very important to note that van Genuchten models were developed and have been successfully used for describing water flow in porous media without fingering flow. Unlike the rock matrix, unsaturated flow in fractures is mainly gravity-driven, giving rise to fingering flow at both a single fracture scale and a fracture network scale. In this case, the van Genuchten relations may not be valid. Recently, we developed an “active fracture model,” which is based on the hypothesis that not all connected fractures actively conduct liquid water in the unsaturated zone at Yucca Mountain because of fingering (Liu et al., 1998). In this model, van Genuchten relations are generalized by including a new parameter, which is used to characterize the degree of fingering in a connected fracture network. This additional parameter is estimated based on inverse modeling. A detailed description of the active fracture model and a procedure to determine values for the additional parameter are given in Liu et al. (1998).
TRANSPORT PARAMETERS
In this section, we discuss only parameters used to describe diffusion and dispersion processes. A discussion of reactive transport is given in a later section. In unsaturated fractured rock, transport processes occur in both fractures and rock matrix. Within the matrix, molecular diffusion is considered to be much more
important than the mechanical dispersion due to high saturation and low pore velocity. Measured diffusion coefficient values for rock matrix at the Yucca Mountain site are summarized by Robinson et al. (1995). The values for saturated rocks are of order of 10−10 m2/s. These lab-scale results can be directly used in the site-scale model, in which the matrix mechanical dispersion is ignored. Note that the diffusion process is generally not subject to upscaling.
Within the fracture continuum, diffusion can be ignored compared with dispersion. We expect the dispersivity for the fracture continuum to be very large, and it may be dependent on travel distance if a dispersivity can be defined for that continuum. However, a large-scale tracer test, which is needed to determine the dispersivity value for the site-scale model, is not considered to be a realistic task for the unsaturated zone of Yucca Mountain considering the temporal scale required for conducting the test. Since fracture dispersivity values from field observations are currently not available, in order to evaluate the importance of fracture dispersivity to the overall chemical transport behavior, we simulate tracer transport along a vertical column extracted from the three-dimensional model for the unsaturated zone of Yucca Mountain (Bodvarsson et al., 1997a). The flow is at steady state, and a constant concentration condition was used at the potential repository. Figure 11-4 shows simulated breakthrough curves at the water table for two different fracture dispersivity values (0 and 100 m). These breakthrough curves were obtained based on combined mass flux from fractures and matrix. A random walk particle method (Pan et al., 1999) is used such that numerical dispersion is essentially eliminated. These two breakthrough curves are very similar, indicating that the overall tracer transport behavior is not very sensitive to the fracture dispersivity value.
This insensitivity of the transport to fracture dispersivity is physically understandable. The large-scale dispersion results from subsurface heterogeneities. For a dual-continua system (matrix and fracture), the largest heterogeneity corresponds to property differences between the two continua. The importance of heterogeneities within each continuum becomes secondary. To further clarify this point, Figure 11-4 also shows a breakthrough curve with a matrix molecular diffusion coefficient value larger than that for the other two curves. A considerable change in the breakthrough curve is observed in this case. This is simply because mass transfer between fracture and matrix continua is directly related to the matrix molecular diffusion. Therefore, parameters to characterize mass transfer between fractures and matrix, such as matrix molecular diffusion coefficients and tortuosity, are the most important for chemical transport. In our current study, effective fracture/matrix interface area values are obtained from inverse modeling studies (see the section “Parameter Estimation/Data Inversion”). Note that this argument cannot be applied to the saturated fractured system, where flow and transport are generally characterized by a single (fracture) continuum while the matrix acts as a source/sink.
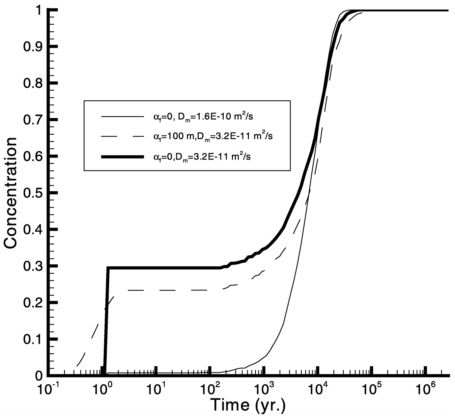
FIGURE 11-4 Breakthrough curves at the water table (αf is the dispersivity for fracture continuum, and Dm is the matrix molecular coefficient).
PARAMETER ESTIMATION/DATA INVERSION
Approach
In order to further refine parameters for the UZ model, determined based on the procedures given in the section “Hydrological Parameters, ” data from the site are inverted.
Data inversion involves using numerical models to predict conditions in the unsaturated zone and then comparing them to observations of these conditions from the field (e.g., saturation data and gas pressure data). Model parameters are adjusted (calibrated) so that the difference between the model predictions and the observed data is minimized. This procedure can be carried out by trial and error,
analyzing the results of each parameter adjustment by hand, or automatically using a program such as ITOUGH2 (Finsterle, 1999).
Data are inverted using a series of increasingly complex models. Three-dimensional modeling studies indicate that vertical flow of fluids and heat is predominant and therefore one-dimensional models are reasonable approximations for many units. In addition, one-dimensional models are used for initial parameter estimation, because of computational efficiency constraints. For the Yucca Mountain problem, we are trying to estimate approximately 210 parameters, which means that thousands of forward simulations are necessary when using an automated inversion program, such as ITOUGH2 (Finsterle, 1999). Moisture dispersion may limit the validity of the vertical percolation assumption. Perched water and lateral movement on top of low-permeability layers/lenses may also limit the validity of the vertical percolation assumption. However, we believe that the vertical percolation assumption is valid for Yucca Mountain from the surface to the bottom of the TSw. Below the TSw, where low-permeability/altered/zeolitized/perched water zones exist, the vertical percolation assumption may break down.
Using one-dimensional models, data from multiple boreholes are inverted simultaneously to estimate layer average properties. Saturation and moisture tension data inversion is used to estimate the matrix and fracture flow parameters, including permeability, a fracture-matrix interaction parameter, and unsaturated flow parameters (van Genuchten's α and m). Pneumatic pressure (barometric pumping response) data inversion is used to estimate fracture diffusivity, or alternatively either permeability or porosity; in our inversions, we choose permeability. Figure 11-5 shows the flow of one-dimensional inversions to multi-dimensional inversions that are used for estimating parameters for the UZ model.
Two-dimensional, cross-sectional models are used to refine parameter estimates. Two-dimensional models allow for lateral flow and therefore will provide a better estimate of properties of low-permeability/altered/zeolitized/perched water layers; then also allow for estimation of the properties of faults. In the two-dimensional models, faults are modeled perpendicular to the plane of the model. Again, saturation, water tension, and pneumatic pressure data are inverted.
Computational expense of using two-dimensional models versus one-dimensional models is increased for each forward simulation, but we are able to reduce the number of parameters that are being estimated because some of the parameters are reliably estimated by the one-dimensional inversions. Therefore, the overall computational expense of the automated two-dimensional model inversions does not increase substantially with respect to the automated one-dimensional model inversions.
Three-dimensional models are used for limited trial-and-error calibrations and verification of simulation results against many different data sets, including data sets used for one- and two-dimensional automated inversions. These will be

FIGURE 11-5 Flow chart showing inversion/calibration/verification approach. Parameter estimation progresses from one-dimensional inversion of saturation, water tension, and pneumatic pressure data, through two-dimensional inversion of fault and perched water data, to three-dimensional calibration/verification of all data.
discussed further in the section “Multidimensional Model Calibration and Sensitivity Analysis.”
One-Dimensional Data Inversion
Saturation and potential data are inverted first. In order to speed up the inversion process, an attempt is made to eliminate some of the parameters being estimated. The sensitivity of all the parameters is evaluated periodically throughout the inversion process, which takes an iterative approach, and only those parameters that exceed a sensitivity cut-off are included in the set of parameters being estimated for the next few iterations. This is a feature of the ITOUGH2 code (Finsterle, 1999) that is used for the automated inversions. The quality of the data must also be considered. ITOUGH2 allows the data to be weighted; better quality data (judged by number of measurements and/or measurement uncertainty) can be more heavily weighted. Even automated inversion requires some human intervention to ensure that calibration is not being trapped in local minima and that the estimated parameters are reasonable. This is especially important when a large number of parameters is being estimated with relatively sparse data, and when nonuniqueness is a problem, as is the case here. Figure 11-6 shows the match between the simulated and observed matrix saturation and
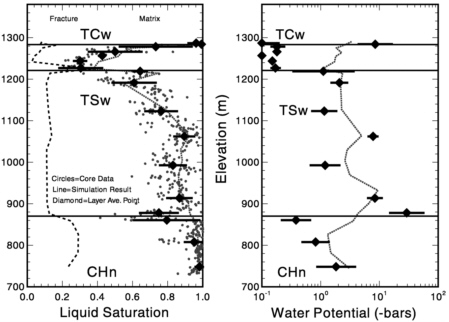
FIGURE 11-6 Calibrated simulation match to saturation and moisture tension data at borehole USW SD-9.
potential values for one of the boreholes used in the simultaneous inversion of several boreholes. Generally, the parameters best constrained by these matrix data are the matrix parameters (i.e., matrix permeability and unsaturated flow parameters).
Time-series pneumatic pressure data (subsurface response to barometric pumping) inversion is the second step in the one-dimensional inversion process. The simulated response to barometric pumping is mainly sensitive to fracture diffusivity, which is proportional to permeability divided by porosity. This is especially true in the densely welded, high-saturation rocks. Yucca Mountain fractures are assumed to be, on average, dry, so that gas-relative permeability of fractures may be assumed to be one or nearly one. Therefore the choice of gasrelative permeability parameters for the fractures is not crucial. Figure 11-7 shows the match between the simulated and observed pneumatic pressure values at one borehole used in the multiple borehole simultaneous inversion. Parameters estimated using inversion of pneumatic data are checked to see that they have not significantly changed saturation and moisture tension data matches.
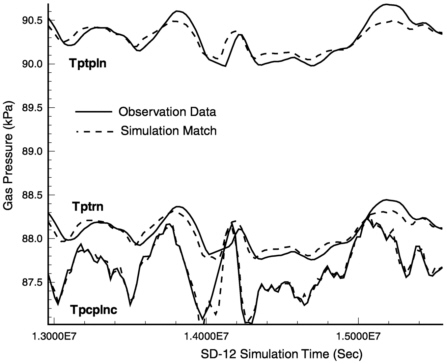
FIGURE 11-7 Calibrated simulation match to pneumatic pressure data at borehole USW SD-12.
Upscaling Issues
Inverting data using mountain-scale models inherently considers upscaling of rock parameters. Matrix parameters change little for many model layers during the inversion process. This is consistent with the previous discussion on the effect of fractures on the effective permeability of matrix in the section on hydrological parameters. Matrix permeability shows little increase, generally less than one-half an order of magnitude, with permeability even being reduced in some layers. Above the bottom of the TSw, where one-dimensional saturation and water potential inversions are reliable, matrix van Genuchten α also shows little variation. Fracture parameters, on the other hand, are expected to upscale because of the difference between the measurement scale and the connected mountain scale. Fracture permeability is measured on the 1- to 10-m air injection testing scale. In the TSw, the calibrated fracture permeability is one order of magnitude, or much larger than the average of the air injection measurements. This is because mountain-scale models and data consider larger fracture connectivity structures than those tested by air injection.
Parameter Uncertainty
ITOUGH2 quantitatively evaluates the uncertainty of the estimated parameters by comparing the match between the simulation and the data (saturation, water potential, etc.) for variations of each of the parameters. Matrix parameters typically have lower uncertainty than the fracture parameters because the saturation and water potential data are measured on the matrix. Where pneumatic data is used to calibrate fracture permeability, the uncertainty of the fracture permeability is much less than the uncertainty of the matrix permeability. This is because there are substantially more pneumatic data points than saturation and water potential data points.
Supplemental information and feedback from downstream users of the calibrated model parameters can also be used to qualitatively judge parameter uncertainty. Modeling of smaller-scale experiments performed at Yucca Mountain using the mountain-scale parameter sets provides invaluable insight into the multiscale applicability of the parameter sets.
MULTIDIMENSIONAL MODEL CALIBRATION AND SENSITIVITY ANALYSIS
Discussion
The three-dimensional nature of fluid flow, heat transfer, and chemical transport at Yucca Mountain makes it a challenge to conduct modeling analysis in such a complicated hydrological system. Even with a significant amount of field data collected from the Yucca Mountain site and good estimates of modeling parameters, as discussed above, a direct input of these parameters into a three-
dimensional model may produce physically inconsistent results, as compared with observations. In particular, the model results cannot match certain important observed phenomena well, such as perched water occurrence, temperature profiles, and geochemical data. This is primarily due to limitations in data collected on both spatial and temporal scales of the three-dimensional models, and also because the one-dimensional and two-dimensional simplification and analysis cannot fully capture the complexity of flow and transport processes in the highly heterogeneous fracture-matrix system. In addition, there exist considerable uncertainties associated with data collected from the site. Furthermore, numerical model results depend not only on input rock and fluid parameters, but also on the conceptual hydrogeological models, spatial and temporal scaling and grid discretization, and numerical modeling approaches selected. Therefore, three-dimensional model calibration and sensitivity studies are necessary to obtain a consistent set of modeling parameters using all the available, observed data in combination with inverse and direct (forward) modeling analyses.
The methodology presented in this section consists of the final stage of parameter estimation process, involving the use of one-dimensional and two-dimensional inversion results in a three-dimensional model to perform further calibration and sensitivity analyses. Direct modeling studies are used here to calibrate multidimensional models against field-measured liquid saturation, water potential, perched water, environmental isotopes, geochemical, and temperature data. During this calibration process some rock parameter adjustments may be made to provide a better match between model results and observed field data in order to reduce parameter uncertainties and to evaluate the differences that occur due to changes in dimensionality of the model. This section focuses on model calibration studies using perched water, temperature, and geochemical data.
Lateral Flow and Perched Water Occurrence
Perched water in the vicinity of the potential repository at Yucca Mountain has been observed in several boreholes during the site characterization study (Patterson, 1998; Striffler et al., 1996). The presence of perched water bodies in the unsaturated zone of Yucca Mountain has many implications for assessment of the potential repository. At the same time, it may provide invaluable insights into water movement, flow and transport pathways, or surface infiltration history of the mountain (Wu et al., 1999b). Perched water at Yucca Mountain has been found to be associated with the densely welded basal vitrophyre of the Topopah Spring Tuff or with zeolitic intervals of the Crater Flat and Calico Hills Formations. The presence of perched water indicates that the vertical percolation flux locally exceeds the saturated hydraulic conductivity at those perching layers and suggests that flow paths may not be vertical through the entire thickness of the unsaturated zone to the water table. Instead, water may be diverted laterally to a fault zone or another high-permeability channel that serves to focus flow down-
ward to the water table. As a result, substantial lateral flow may occur at perching layers, which leads to complex flow pathways of groundwater through the unsaturated zone fractured media.
Perched water is observed across Yucca Mountain within the lower TSw and the upper CHn hydrologic units, as indicated in a number of boreholes at Yucca Mountain, including UZ-14, SD-7, SD-9, SD-12, NRG-7a, G-2, and WT-24. The locations of these boreholes are shown in Plate 6 for a plan view. Also shown in the figure are the three-dimensional model domain of the UZ model and the horizontal grid.
The permeability of the zeolitic tuffs within CHn is generally very low (in microdarcies). This low value is converted to as low as 0.5 mm/yr or so of percolation flux in terms of flow capacity through the zeolitized tuffs. Recent studies (Flint et al., 1996) estimate an average net infiltration rate of 5 mm/yr over the UZ model domain. As a result, on average, about 90 percent of the water must bypass the low-permeability zeolitic units and travel through faults, other well-connected fractures, or high-permeability vitric formations to reach the saturated zone. This will affect radionuclide transport from the repository horizon to the water table, which directly impacts geologic repository performance. To capture these phenomena of lateral flow caused by water perching conditions, three-dimensional model calibrations are needed.
The genesis of perched water at Yucca Mountain is much debated among Yucca Mountain Project scientists, and several conceptual models have been discussed (Rousseau et al., 1998; Wu et al., 1999b). The permeability barrier conceptual model for perched-water occurrence has been used in unsaturated-zone flow modeling studies for the Yucca Mountain Project. In this conceptualization, perched-water bodies in the vicinity of the northern part of the model domain (near boreholes UZ-14, SD-9, NRG-7a, G-2, and WT-24) are assumed to lie along the base of the TSw, a zone of altered, more intensely fractured rock, underlain by low-permeability, zeolitized rock. The perched body in this northern area of the repository may be interconnected. The perched-water zones at boreholes SD-7 and SD-12 are considered to be localized, isolated bodies.
The perched-water numerical model used in this work is based on the three-dimensional UZ flow and transport model (Bodvarsson et al., 1997a). The UZ model domain, as shown in Plate 6, covers nearly 43 km2 and extends from Yucca Wash in the north to the approximate latitude of borehole G-3 in the south. In the east-west direction, the model extends from the Bow Ridge Fault to approximately 1 km west of the Solitario Canyon Fault. The land surface of the mountain (or the tuff/alluvium contact, in areas of significant alluvial cover) is taken as the top model boundary. The water table is treated as the bottom boundary. Both top and bottom boundaries of the models are treated as Dirichlet-type conditions, with specified constant (but areally distributed) gas pressures and constant liquid saturation. A spatially distributed infiltration map (Flint et al., 1996) was used as the top water recharge boundary of the three-dimensional
model. This map gives an average net infiltration rate of 4.9 mm/yr of water distributed over the site-scale model domain.
The simulation results presented in this section were obtained using the TOUGH2 code (Pruess, 1991), and the dual-permeability method was used to treat fracture and matrix interactions. The integral finite-difference model grid used consisted of 150,000 elements and 500,000 connections.
Many flow scenarios were investigated to calibrate the perched water model. The simulation results for these modeling scenarios were calibrated against the observed matrix liquid saturation and water potential data, and perching elevations. In general, it was found that the permeability barrier conceptual model of water perching could reproduce the moisture and perched-water conditions beneath Yucca Mountain. Plate 7 shows the extent of perched water, as predicted by the permeability barrier conceptual model. The simulation uses the calibrated perched-water parameters for fractures and matrix in several grid layers near the top of the CHn unit. In this figure, the blue isosurface reflects 100 percent liquid-saturation within fractures, indicating a perched-water body, while the green surface represents the top elevation of the CHn.
Plate 7 shows clearly that several perched bodies develop in the northern part of the model domain, located near the basal vitrophyre of the Topopah Spring Tuff above the top of the CHn unit. These perched bodies match the observed perching elevations from the boreholes in these areas.
The simulated percolation flux at the water table is shown in Plate 8. Comparing the fluxes and their distribution in Plate 8 with that of the surface infiltration map of Flint et al. (1996) indicates the occurrence of significant lateral flow or diversion. Significant lateral flow occurs mainly as water travels from the repository horizon to the water table in perched areas. A large amount of water, when travelling across the CHn, is diverted laterally to the east, along a dip, and intersects faults that focus flow downward to the water table.
The modeling study and sensitivity analysis of this work concludes that it is necessary to conduct three-dimensional model calibrations in order to describe perched water occurrences at Yucca Mountain. Several key factors were identified for creating a perched-water zone in a numerical model. These factors are (1) a water-perching geologic structure with low permeability zones and/or a capillary barrier underlain and surrounding perched-water zones, (2) weak capillary forces under high saturation condition within and near perched-water zones, and (3) sufficient water infiltration rates.
Heat Flow and Geothermal Conditions
In parameter estimation and model calibration using measured temperature data, the ambient geothermal condition at Yucca Mountain is assumed to be at a steady-state condition. The three-dimensional steady-state solution of fluid (water and air) and heat flow were used to match available temperature data mea-
sured at 26 boreholes located within the model domain (Wu et al., 1999a). The locations of some of these boreholes are also shown on Plate 6. The objective of the heat flow studies is to confirm if use of the parameters, derived from isothermal calibrations, can predict geothermal conditions at the mountain.
Unlike the above three-dimensional perched-water calibrations, which used a dual-permeability model, fracture-matrix interaction was treated using the effective continuum model (ECM) approach in this section. The ECM assumes a thermodynamic equilibrium between the fracture and the matrix, and adequately approximates steady-state heat transfer, which is dominated by heat conduction.
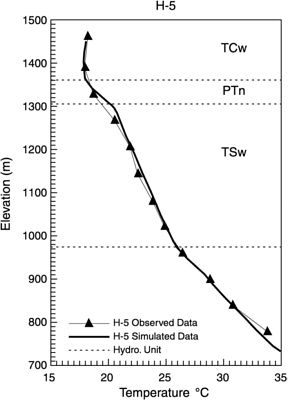
Measured temperature data (Sass et al., 1988; Rousseau, 1996) were compared with the three-dimensional simulation results for 26 boreholes within and near the study area. In general, temperature data from all the boreholes matched reasonably well with the three-dimensional model (Bodvarsson et al., 1997; Ahlers et al., 1995), in which surface and bottom temperatures were slightly adjusted. We present only one of the 26 comparisons conducted in the model calibration as demonstration examples. The selected borehole is H-5, and it is located in the middle of the model domain, shown in Plate 6. The simulated temperature profile is plotted in Figure 11-8. The simulated temperature profile matches the data very well, as was the case for all the other borehole data/simulation comparisons.
The three-dimensional temperature calibrations have helped us in constraining percolation fluxes and estimating geothermal conditions for thermal studies (Bodvarsson et al., 1997; Wu et al., 1999a).
Unsaturated Zone Geochemistry
The geochemistry of water (and gas) in the unsaturated zone can be used as an important constraint on net infiltration rates, percolation fluxes, and flow pathways, and as an indicator of the extent of fracture-matrix and water-rock interaction. Mineral paragenesis, distribution, and composition are also useful, yet complex, systems for quantifying flow and transport processes. In contrast to hydrologic parameters, such as water potential or saturation, and possibly temperature, large-scale attainment of steady-state chemical distributions is unlikely, because molecular diffusivity is several orders of magnitude smaller than water or thermal diffusivity. Therefore, climate changes can have a long-lasting effect on the geochemistry of the unsaturated zone, especially in an arid environment such as at Yucca Mountain. There, chemical patterns at depth seem to reflect periods of higher infiltration during the last glacial period, while those close to the surface are consistent with the modern climate (Sonnenthal and Bodvarsson, 1999).
Conservative Chemical Species
The sensitivity of natural conservative tracers such as Cl to infiltration rate is well known, e.g., the chloride mass-balance method. For such constituents the
flux is related to the precipitation rate and additions from other sources such as windblown dust. The extent of evapotranspiration in the shallow soil zone then controls the concentration in infiltrating water. In arid environments, with significant topographic and soil cover thickness variations, the infiltration rate can vary by orders of magnitude over short distances (Flint et al., 1996). Thus, it is expected that spatial distributions of a conservative tracer in the subsurface may also vary by a similar range. In contrast to directly using a method such as chloride mass balance and making assumptions as to the absence of diffusion and lateral flow, limiting the system to one-dimensional piston-flow, it is preferable to incorporate directly such tracers into the calibrated flow model.
An example using chloride as a conservative tracer in UZ flow and transport simulations of Yucca Mountain is presented in Figure 11-9. Chloride fluxes to the
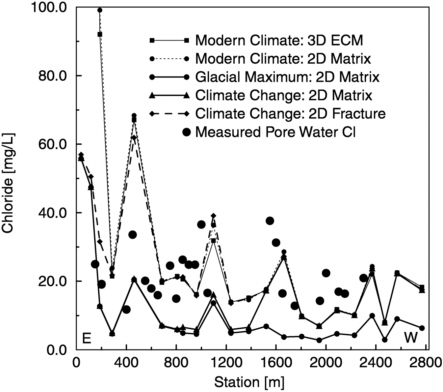
FIGURE 11-9 Prediction of chloride concentrations in pore waters prior to excavation of the ECRB, for two-dimensional dual permeability and three-dimensional ECM simulations, compared to data collected subsequently. The climate change simulation considered a glacial maximum infiltration rate, followed by 10,000 years of modern climate. From Flint et al. (1996).
surface were calculated using precipitation maps of the region (Bodvarsson et al., 2000) and assuming a uniform average effective concentration in precipitation (Fabryka-Martin et al., 1998). Combined with infiltration rates (Flint et al., 1996) the concentrations in infiltrating waters are generated. The simulations were performed as part of a prediction prior to the excavation of a tunnel at the potential repository level (Ritcey et al., 1998), and recent preliminary Cl results (Fabryka-Martin et al., 2000) confirm the trend of lower concentrations under areas of higher predicted net infiltration. Another outcome of the dual-permeability modeling is the remnant disequilibrium between fractures and matrix, resulting from the climate change that took place about 10,000 years ago. Under areas of lower infiltration, matrix pore waters are predicted to have retained their chloride concentrations from the last glacial period. These results are generally consistent with the 14C ages of some perched waters (up to 8,000 to 12,000 years; Yang et al., 1996), and the average 14C age of air at this level (~6,000 years; Yang et al., 1996); however, data from this particular zone will be needed for model validation.
The large-scale continuum model has proven remarkably effective in predicting the range in concentrations and their trends in the unsaturated zone (Sonnenthal and Bodvarsson, 1999). Looking a little closer though, it is clear from numerous chemical analyses of pore waters at Yucca Mountain (Fabryka-Martin et al., 1998), that variability is the norm at nearly every scale. The difficulty in the interpretation of this variability is due to the superposition of short-term transient flow processes (i.e., fast-path flow) on top of longer-term climate effects, the spatial variability induced at the surface, variability in local fracture-matrix interaction, and diffusion-limited fracture-matrix chemical equilibration. Small-scale variability could be due to tempered variations and differences in transport velocities and fracture-matrix interaction, even if over shorter time periods there is spatial redistribution in the PTn.
Reactive Geochemical Systems
Reactive geochemical systems range from the simplest sorption or exchange reactions involving trace ions, to those strongly coupled systems involving multicomponent water-gas-rock interaction with mineral precipitation and dissolution. Analysis of such systems through measurement and modeling yields otherwise unattainable information regarding transport processes at a variety of scales, both spatial and temporal.
Here we present a relatively simple example of a chemical species, strontium (Sr), that shows dominantly conservative behavior in the upper part of the unsaturated zone at Yucca Mountain and strong cation exchange behavior in lower zeolitized units. An important, and previously overlooked, aspect to the behavior of Sr in the unsaturated zone is its relatively high concentration in infiltrating waters, as a result of evapotranspiration, compared to the Sr added through
kinetically slow reactions with unzeolitized tuffaceous rocks and that lost to precipitation of calcite in fractures.
Results from a three-dimensional simulation (ECM assumption) at specific locations corresponding to boreholes that intersect perched water are shown in Figure 11-10. Sr is considered to be nearly conservative in unzeolitized rocks (kD = 0.02 m2/kg), and extremely reactive in zeolitized rocks (kD = 1000 m2/kg). Modeled values are compared to measured Sr concentrations in perched waters (Patterson et al., 1998). Concentrations in waters in unzeolitized rocks (UZ-14 and WT-24) are similar to (but generally higher than) the predicted concentrations (governed mainly by the extent of surface evapotranspiration). Perched waters that are in contact with zeolitized rocks have Sr concentrations one to two orders of magnitude lower. The mismatch between concentrations in the zeolitic units could be due to lateral flow or errors in geologic stratigraphy.
Abundant data on mineral distributions in fractures and their compositions (collected by the USGS and Los Alamos National Laboratory) have been used to infer flow pathways and long-term infiltration rates (Marshall et al., 1998; Vaniman and Chipera, 1996). These data are also important for inferring flow
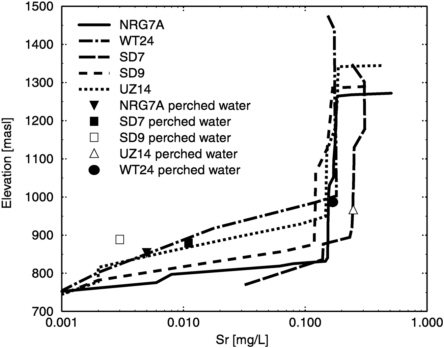
FIGURE 11-10 Modeled (three-dimensional ECM) and measured Sr concentrations (perched water) as a function of elevation.
processes within individual fractures (e.g., fracture mineralization occurs on the footwall of fractures only; Paces et al., 1998). Some of these data are now being evaluated using multicomponent reactive transport modeling for further calibration of the UZ flow and transport model, to assess relations between infiltration rates and mineral precipitation. Such studies reveal information on processes that have taken place over tens of thousands to millions of years, in contrast to other geochemical systems, such as nuclear fallout-generated 36Cl, which records transient processes that have occurred over the past 50 years.
Spatial and Temporal Variability and Uncertainties
The UZ flow and transport model plays an important role in better understanding of flow and transport processes at Yucca Mountain. However, the accuracy and reliability of the model predictions are critically dependent on the accuracy of estimated model properties. Past site investigations have shown that there exists a large variability of the flow and transport parameters over the large spatial and temporal scales of the mountain. Even though considerable progress has been made in this area, uncertainty associated with the UZ model input parameters will continue to be a key issue for future studies. The major uncertainties in model parameters are: (1) accuracy in estimated current, past, and future net infiltration rates over the mountain; (2) quantitative descriptions of the heterogeneity of welded and non-welded tuffs, their flow properties, and detailed spatial distributions within the mountain, especially below the repository; (3) insufficient field studies, especially for fracture properties; and (4) evidence of lateral diversion in the CHn units, where the zeolitic zones may play an important role in diverting moisture laterally. All of these uncertainties have been addressed to a certain extent in past studies; however, a comprehensive study is still needed to reduce these parameter uncertainties further by continuous field, laboratory, and modeling efforts.
SUMMARY AND CONCLUSIONS
The unsaturated zone flow and transport model of Yucca Mountain, Nevada, is a very complex three-dimensional, dual-permeability numerical model. The model considers all relevant geological, hydrological, and geochemical data from the unsaturated zone, and is calibrated to the extent possible using these data. A major challenge in development of the model is the parameterization and up-scaling of important fracture and matrix parameters used in the model. The following points represent our current understanding and beliefs regarding parameterization and upscaling in the UZ model.
-
Conventional upscaling methods cannot be used to upscale core-scale (matrix) permeabilities for unsaturated fractured rocks, because fractures may reduce effective matrix permeability at larger scales.
-
No upscaling of fracture permeability is needed, as pneumatic tests have been done at various scales. Fracture permeability data show typical increases with scale and can be represented as stochastic fractals. Other fracture parameters, such as the van Genuchten parameters and fracture porosity, can be derived from the fracture permeability data using the cubic law, but this may yield inaccurate results. For example, in-situ seepage, gas tracer, and thermal test data suggest fracture porosities that are orders of magnitude higher than derived values.
-
Matrix diffusion is more important than dispersion, and neither fracture diffusion or dispersion significantly affects transport at Yucca Mountain. The fracture/matrix interaction factor has large effects on flow and transport; the UZ model utilizes the newly developed “active” fracture concept.
-
The primary upscaling process used in the UZ model is a direct inversion of the observed data, including saturation, moisture tension, pneumatic, perched water, temperature, and geochemical data. A generic approach has been developed that starts with one-dimensional inversions, and then proceeds to two-dimensional and three-dimensional inversions.
-
The one-dimensional inversions are performed using saturation, moisture tension, and pneumatic data. The results obtained show that only limited upscaling is needed for most parameters, with the fracture and matrix a and matrix permeability being the most sensitive parameters.
-
Three-dimensional trial-and-error calibrations are performed primarily for the perched water, temperature, and geochemistry data. The perched water calibrations greatly alter the hydrological parameters below the repository region, but the temperature data match model results reasonably well using the current infiltration maps.
-
Three-dimensional model validation was performed with various chemical species, including Cl, 36Cl, and Sr. Cl modeling gives valuable constraints on infiltration/percolation fluxes and patterns, whereas 36Cl modeling yields the fast component of the flow. Sr reacts strongly in zeolitic rocks, and its modeling yields valuable information, including flow paths and fracture-matrix interaction.
ACKNOWLEDGMENTS
The authors thank Yvonne Tsang, Jianchun Liu, and Dan Hawkes (Lawrence Berkeley National Laboratory) for careful technical and editorial review of this paper. This work was supported by the Director, Office of Civilian Radioactive Waste Management, U.S. Department of Energy, through Memorandum Purchase Order EA9013MC5X between TRW Environmental Safety Systems and the Ernest Orlando Lawrence Berkeley National Laboratory (Berkeley Lab). The support is provided to Berkeley Lab through the U.S. Department of Energy Contract No. DE-AC03-76SF00098.
REFERENCES
Ahlers, C. F., T. M. Bandurraga, G. S. Bodvarsson, G. Chen, S. Finsterle, and Y. S. Wu, 1995. Summary of Model Calibration and Sensitivity Studies Using the LBNL/USGS Three-Dimensional Unsaturated Zone Site-Scale Model. Yucca Mountain Project Milestone 3GLM107M. Berkeley, Calif.: Lawrence Berkeley National Laboratory.
Altman, S. J., B. W. Arnold, R. W. Barnard, G. E. Barr, C. K. Ho, S. A. McKenna, and R. R. Eaton, 1996. Flow Calculations for Yucca Mountain Groundwater Travel Time (GWTT-95) . SAND96-0819. Albuquerque, N.M.: Sandia National Laboratories.
Bandurraga, T. M., and G. S. Bodvarsson, 1997. Calibrating matrix and fracture properties using inverse modeling (Chapter 6). In: The Site-Scale Unsaturated Zone Model of Yucca Mountain, Nevada, for the Viability Assessment. G. S. Bodvarsson, T. M. Bandurraga, and Y. S. Wu, eds. LBNL-40376, Lawrence Berkeley National Laboratory, Berkeley, Calif.
Bodvarsson, G. S., C. F. Ahlers, M. Cushey, F. H. Dove, S. A. Finsterle, C. B. Haukwa, J. Hinds, C. K. Ho, J. Houseworth, Q. Hu, H. H. Liu, M. Pendleton, E. L. Sonnenthal, A. J. Unger, J. S. Y. Wang, M. Wilson, and Y.-S. Wu, 2000. Unsaturated Zone Flow and Transport Model Process Model Report. Civilian Radioactive Waste Management System, Management and Operating Contractor, Las Vegas, Nev.
Bodvarsson, G. S., T. M. Bandurraga, and Y. S. Wu (eds.), 1997a. The Site-Scale Unsaturated Zone Model of Yucca Mountain, Nevada, for the Viability Assessment. Rep. LBNL-40376. Berkeley, Calif.: Lawrence Berkeley National Laboratory.
Bodvarsson, G. S., C. Shan, A. Htay, A. Ritcey, and Y. S. Wu, 1997b. Estimation of percolation flux from temperature data. Chapter 11. In: The Site-Scale Unsaturated Zone Model of Yucca Mountain, Nevada, for the Viability Assessment. G. S. Bodvarsson, T. M. Bandurraga, and Y. S. Wu, eds. Report LBNL-40376. Berkeley, Calif.: Lawrence Berkeley National Laboratory.
Fabryka-Matin, J. T., A. Meijer, B. Marshall, L. Neymark, J. Paces, J. Whelan, and A. Yang, 2000. Analysis of Geomechanical Data for the Unsaturated Zone. Civilian Radioactive Waste Management System, Management and Operating Contractor, Las Vegas, Nev.
Fabryka-Martin, J. T., A. V. Wolfsberg, J. L. Roach, S. T. Winters, L. E. Wolfsberg, 1998. Using Chloride to Trace Water Movement in the Unsaturated Zone at Yucca Mountain. In: Proceedings of the Eighth International Conference on High-Level Radioactive Waste Management. American Nuclear Society, May 11-14, 93-96.
Fabryka-Martin, J. T., P. R. Dixon, S. Levy, B. Liu, H. J. Turin, and A. V. Wolfsburg, 1996. Summary Report of Chlorine-36 Studies: Systematic Sampling for Chlorine-36 in the Exploratory Studies Facility. Los Alamos National Laboratory Milestone Report 3783AD. Los Alamos, N.M.: Los Alamos National Laboratory.
Faybishenko, B., 1999. Evidence of Chaotic Behavior in Flow Through Fractured Rocks, and How We Might Use Chaos Theory in Fractured Rock Hydrology. Proceedings of the International Symposium on Dynamics of Fluids in Fractured Rocks in Honor of Paul A. Witherspoon's 80th Birthday. Lawrence Berkeley National Laboratory Report LBNL-42718. Berkeley, Calif.: Lawrence Berkeley National Laboratory.
Finsterle, S., 1999. ITOUGH2 User's Guide. Report LBNL-40040. Berkeley, Calif.: Lawrence Berkeley National Laboratory.
Flint, A. L., J. A. Hevesi, and L. E. Flint, 1996. Conceptual and Numerical Model of Infiltration for the Yucca Mountain Area, Nevada. Milestone 3GU1623M. U.S. Geol. Surv. Water Res. Invest. Rep. Denver, Colo.: U.S. Geological Survey.
Flint, A. L., L. E. Flint, G. S. Bodvarsson, and E. M. Kwicklis, 1999. Evolution of the Conceptual Model of Vadose Zone Hydrology for Yucca Mountain. National Research Council, National Academy of Sciences, U.S. National Committee for Rock Mechanics. Presented at the “Conceptual Models of Flow and Transport in the Fractured Vadose Zone, ” March 18-19, 1999, Irvine, Calif.
Flint, L. E., 1998. Matrix properties of hydrogeologic units at Yucca Mountain, Nevada . U.S. Geological Survey Report 97-4243. Denver, Colo.: U.S. Geological Survey.
Glass, R. J., M. J. Nicholl, and V. C. Tidwel, 1996. Challenging and Improving Conceptual Models for Isothermal Flow in Unsaturated, Fractured Rocks Through Exploration of Small-Scale Processes . Rep. SAND95-1824. Albuquerque, N.M.: Sandia National Laboratories.
Koltermann, C. E., and S. M. Gorelick, 1996. Heterogeneity in sedimentary deposits: A review of structure imitating, process-imitating, and descriptive approaches. Water Resour. Res. 32: 2617-2658.
Kwicklis, E. M., G. S. Bodvarsson, and A. L. Flint, 1999. A Conceptual Model of the Unsaturated Zone Flow and Transport, Yucca Mountain, Nevada. U.S. Geol. Surv. Water Resour. Rep. Denver, Colo.: U.S. Geological Survey.
LeCain, G. D., 1997. Air-Injection Testing in Vertical Boreholes in Welded and Nonwelded Tuff, Yucca Mountain, Nevada. U.S. Geol. Surv. Water Resour. Invest. Rep. 96-4262. Denver, Colo.: U.S. Geological Survey.
LeCain, G., and G. Patterson, 1997. Technical Analysis and Interpretation, Air-Permeability and Hydrochemistry Data through January 31, 1997. Memo/Report to Robert Craig. Level 4 Yucca Mountain Milestone SPH35EM4 . Denver, Colo.: U.S. Geological Survey.
Liu, H. H., and F. J. Molz, 1997, Multifractal analyses of hydraulic conductivity distributions. Water Resour. Res. 33(11): 2483-2488.
Liu, H. H., C. Doughty, and G. S. Bodvarsson, 1998. An active fracture model for unsaturated flow and transport in fractured rocks. Water Resour. Res. 34(10): 2633-2646.
Marshall, B. D., J. B. Paces, L. A. Neymark, J. F. Whelan, Z. E. Peterman, 1998. Secondary minerals record past percolation flux at Yucca Mountain, Nevada. In: Proceedings of the Eighth Annual International Conference, High Level Radioactive Waste Management, May 11-14. Las Vegas, Nev.: American Nuclear Society.
Molz, F. J., H. H. Liu, and J. Szulga, 1997. Fractional Brownian motion and fractional Gaussian noise in subsurface hydrology: A review, presentation of fundamental properties, and extensions. Water Resour. Res. 33(10): 2273-2286.
Neuman, S. P., 1990. Universal scaling of hydraulic conductivities and dispersivities in geologic media. Water Resour. Res. 26(8): 1749-1758.
Neuman, S. P., 1994. Generalized scaling of permeabilities: Validation and effect of support scale. Geophy. Res. Lett. 30(21): 349-352.
Paces, J. B., B. D. Marshall, L. A. Neymark, J. F. Whelan, Z. E. Peterman, 1998. Inferences for Yucca Mountain unsaturated zone hydrology from secondary minerals. In: Proceedings of the Eighth Annual International Conference, High Level Radioactive Waste Management, May 11-14, 1998. Las Vegas, Nev.: American Nuclear Society, Pp. 36-39.
Paleologos, E. K., S. P. Neuman, and D. Tatakovsky, 1996. Effective hydraulic conductivity of bounded, strongly heterogeneous porous media. Water Resour. Res. 32: 1333-1341.
Pan, L., H. H. Liu, M. Cushey, and G. S. Bodvarsson, 1999. A New Random Walk Particle Tracker for Dual-Continua. LBNL-42928, Lawrence Berkeley National Laboratory, Calif.
Patterson, G., 1998. Occurrences of Perched Water in the Vicinity of the Exploratory Studies Facility North Ramp. Section 4.2.4 (including sections 4.2.4.1-4.2.4.5). In: J. P Rousseau, E. M. Kwicklis, and D. C. Gillies, eds. Hydrogeology of the Unsaturated Zone, North Ramp Area of the Exploratory Studies Facility, Yucca Mountain, Nevada. Yucca Mountain Project Milestone Report 3GUP667M. U.S. Geological Survey Water Resources Investigations Report 98-4050. Denver, Colo.: U.S. Geological Survey.
Patterson, G. L., Z. E. Peterman, and J. B. Paces, 1998. Hydrochemical evidence for the existence of perched water at USW WT-24, Yucca Mountain, Nevada. In: Proceedings of the Eighth Annual International Conference, High Level Radioactive Waste Management, May 11-14. Las Vegas, Nev.: American Nuclear Society, pp. 277-278.
Pruess K., 1991. TOUGH2: A General Purpose Numerical Simulator for Multiphase Fluid and Heat Flow. Lawrence Berkeley National Laboratory Report LBNL-29400. Berkeley, Calif.: Lawrence Berkeley National Laboratory.
Pruess, K., 1999. A mechanistic model for water seepage through thick unsaturated zones in fractured rocks of low matrix permeability. Water Resour. Res. 35(4): 1039-1051.
Pruess, K., B. Faybishenko, and G. S. Bodvarsson, 1997. Alternative Concepts and Approaches for Modeling Unsaturated Flow and Transport in Fractured Rocks. Chapter 24 of The Site-Scale Unsaturated Zone Model of Yucca Mountain, Nevada, for the Viability Assessment. G. S. Bodvarsson, T. M. Bandurraga, and Y. S. Wu, eds. Rep. LBNL-40376. Berkeley, Calif.: Lawrence Berkeley National Laboratory.
Ritcey, A. C., E. L. Sonnenthal, Y. S. Wu, C. Haukwa, and G. S. Bodvarsson, 1998. Final Prediction of Ambient Conditions along the East-West Cross Drift Using the 3-D UZ Site-Scale Model. Yucca Mountain Project Milstone SP22ABM4. Berkeley, Calif.: Lawrence Berkeley National Laboratory.
Robinson, B. A., A. V. Wolfsberg, G. A. Zyvoloski, and C. W. Gable, 1995. An Unsaturated Zone Flow and Transport Model of Yucca Mountain, Milestone 3468. Los Alamos, N.M.: Los Alamos National Laboratory.
Rousseau, J. P., 1996. Data Transmittal of Pneumatic Pressure Records from 10/24/94 through 3/31/96 for Boreholes UE-25 UZ#4, UE-25 UZ#5, USW NRG-6, USW NRG-7a, USW SD-12, and USW UZ-7a. U.S. Geological Survey Preliminary Data from Yucca Mountain, Nevada . Denver, Colo.: U.S. Geological Survey.
Rousseau, J. P., E. M. Kwicklis, and D. C. Gillies, eds., 1998. Hydrogeology of the Unsaturated Zone, North Ramp Area of the Exploratory Studies Facility, Yucca Mountain, Nevada. USGS-WRIR-98-4050 Yucca Mountain Project Milestone 3GUP667M (formerly 3GUP431M). Denver, Colo.: U.S. Geological Survey.
Sass J. H., A. H. Lachenbruch, W. W. Dudley Jr., S. S. Priest, and R. J. Munroe, 1988. Temperature, thermal conductivity, and heat flow near Yucca Mountain, Nevada: Some tectonic and hydrologic implications. USGS OFR-87-649. U.S. Geological Survey Open File Rep. 87-649. DE89 002697. Denver, Colo.: U.S. Geological Survey.
Sonnenthal, E. L., and G. S. Bodvarsson, 1999. Constraints on the hydrology of the unsaturated zone at Yucca Mountain, Nevada, from Three-Dimensional Models of Chloride and Strontium Geochemistry . Journal of Contaminant Hydrology 38(1-3): 107-156.
Sonnenthal, E. L., C. F. Ahlers, and G. S. Bodvarsson, 1997. Fracture and Fault Properties for the UZ Site-Scale Flow Model. In: G. S. Bodvarsson, T. M. Bandurraga, and Y. S. Wu, eds. The Site-Scale Unsaturated Zone Model of Yucca Mountain, Nevada, for the Viability Assessment. Chapter 7. Yucca Mountain Site Characterization. Lawrence Berkeley National Laboratory Report LBNL-40376. Berkeley, Calif.: Lawrence Berkeley National Laboratory.
Striffler, P., G. M. O'Brien, T. Oliver, and P. Burger, 1996 (Unpublished). Perched Water Characteristics and Occurrences, Yucca Mountain, Nevada . Yucca Mountain Milestone 3LGUS600M. Submitted for publication as a USGS Water Resources Investigation Report. Denver, Colo.: U.S. Geological Survey.
Sweetkind, D. S., and S. C. Williams-Stroud, 1996. Characteristics of Fractures at Yucca Mountain, Nevada. YMP Milestone 3GGF205M. Denver, Colo.: U.S. Geological Survey.
Tokunaga, T. K., and J. Wan, 1997. Water film flow along fracture surfaces of porous rock. Water Resour. Res. 33(6): 1287-1295.
Tsang, Y. W., J. A. Apps, J. T. Birkholzer, B. Freifeld, J. Peterson, M. Q. Hu, E. Sonnenthal, and N. Spycher, 1999. Single Heater Test Final TDIF Submittal and Final Report. Lawrence Berkeley National Laboratory Report LBNL-42537. Berkeley, Calif.: Lawrence Berkeley National Laboratory.
Van Genuchten, M., 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Amer. J 44(5): 892-898.
Vaniman, D. T., and S. J. Chipera, 1996. Paleotransport of lanthanides and strontium recorded in calcite compositions from Tuffs at Yucca Mountain, Nevada, USA. Geochimica et Cosmochimica Acta 60(22): 4417-4433.
Wu, Y. S., C. Haukwa, and G. S. Bodvarsson, 1999a. A site-scale model for fluid and heat flow in the unsaturated zone of Yucca Mountain, Nevada. Journal of Contaminant Hydrology 38(1-3): 185-217.
Wu, Y. S., A. C. Ritcey, and G. S. Bodvarsson, 1999b. A modeling study of perched water phenomena in the unsaturated zone at Yucca Mountain. Journal of Contaminant Hydrology 38(1-3): 157-184.
Yang, I. C., G. W. Rattray, and P. Yu, 1996. Interpretation of Chemical and Isotopic Data from Boreholes in the Unsaturated Zone at Yucca Mountain. U.S. Geol. Surv. Water Resour. Invest. Rep. 96-4058. Denver, Colo.: U.S. Geological Survey.