7
Free-Surface Films
Maria Ines Dragila1 and Stephen W. Wheatcraft2
ABSTRACT
A new transport mechanism is proposed to explain the anomalous fast transport observed at fractured vadose sites. Recent field observations have shown that fluid transport rates may be orders of magnitude greater than existing models can predict. This implies that a key transport mechanism is acting which is not being included in these models. It is imperative that the acting transport mechanism be identified because fractured vadose sites are being marked for potential toxic waste repositories.
A free-surface film may provide a mechanism by which fluids in the unsaturated zone are transported through air-filled fractures much more rapidly than plug flow or porous matrix transport. A rigorous mathematical model is developed to analyze the character of free surface films. The model shows free-surface films are chaotic. The chaotic character of the system is used to develop a hydrologic model for free-surface film transport in unsaturated fractures. This model is applied to the example of seepage from the matrix into a fracture and is shown to generate velocities of the order necessary to explain the fast transport rates observed in the field.
|
1 |
Department of Geological Sciences, University of Nevada, Reno; presently at Department of Crop and Soil Science, Oregon State University, Corvallis |
|
2 |
Department of Geological Sciences, University of Nevada, Reno |
INTRODUCTION
Recent field observations at fractured vadose study sites have determined that fluid transport rates through the earth's vadose zone may be orders of magnitude greater than existing models can predict. This implies that a key transport mechanism is acting which is not being included in these models. It is imperative that this transport mechanism be identified because fractured vadose sites are being identified for potential toxic waste repositories. Miscalculations regarding fluid transport could have a major impact on the future integrity of any repository.
A free-surface film may provide a mechanism by which fluids in the unsaturated zone are transported through air-filled fractures much more rapidly than plug flow or porous matrix transport. In fact, flow rates predicted by this particular mechanism are sufficient to explain recently observed behavior.
The vadose zone, also known as the unsaturated zone, is the region between the ground surface and water table. Porous media in this region are only partially saturated with fluid. Existing theory states that flow progresses only through filled and interconnected pores. Conceptual models for flow within the vadose zone are based on capillary theory, where the largest pore size to be saturated is determined by the local pressure head (matric potential). Natural extension to fractures of flow through porous media theory suggests that fluid will fill the smallest fracture apertures first, progressively filling larger apertures. In addition, the fracture will not conduct unless there is a connected fluid pathway. Flow through porous media, whether saturated or unsaturated, is a very slow process.
Models developed to date for flow through unsaturated fractures retain some of the basic maxims from porous media transport. An unsaturated fracture is one that sustains both an air phase and a fluid phase. Until recently it had been assumed that the fluid phase is confined to, and completely saturates, regions where the aperture is sufficiently small, as defined by the matric potential of the surrounding porous media. The larger aperture regions of the fracture are air-saturated. Dual-porosity models simply replace the fracture with a permeable medium of higher porosity than the surrounding matrix. Although the result is that flow is faster through the more permeable conduit, it is not sufficiently fast to explain the recently observed fast-flow phenomena. Cubic law models approximate the fracture aperture by a set of parallel plates, and the flow rate is calculated using what has come to be known as the cubic law, where flow rate is proportional to the cube of the fracture aperture (Figure 7-1) (Nitao et al., 1993). Further studies were performed to characterize the effect of aperture variability on tortuosity and the development of channels allowing for higher flow rates through regions of wider aperture (Tsang, 1984; Tsang and Tsang, 1987). Fractures sustaining this type of two-phase capillary saturation have also been shown to develop flow instabilities as the two saturated phases interact (Pruess and Tsang, 1990; Geller et al., 1996; Su et al., 1999). Instabilities have also been seen at the wetting front in fracture flow leading to fingering phenomena (Nicholl et
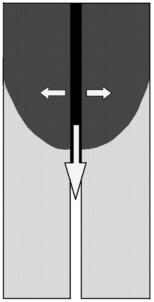
FIGURE 7-1 Parallel plate model for fracture flow with absorption into the matrix.
al., 1994). Although fingers are capable of generating faster flow than the remainder of the wetting front, they sustain capillary saturation and the flow rate is limited by the aperture geometry as defined by the cubic law.
Central to these models is the assumption that a continuous saturated path is required for fluid conduction. At high matrix saturations the entire fracture may fill and be capable of conducting fluid. However, at low capillary pressures, because pressure equilibrium is required between the fracture and matrix, the largest liquid-filled aperture in the fracture will be on the order of magnitude of the largest pore size that is liquid-filled in the surrounding porous medium. Fractures in arid regions, where the porous medium is at very low saturation and very low capillary pressures, are likely to be saturated only in sections where the aperture is very small, such as where two porous blocks touch. These saturated sections are most likely disconnected, in which case, a continuous fluid-filled conduit would not exist. These small sections of trapped water in the fracture are held against gravity by contact angle hysteresis. Using this scenario, and applying it to the arid conditions found in the Yucca Mountain area, Wang and Narasimhan (1985) hypothesized that flow in vadose zone fractures would be unlikely in arid regions. Their model is shown in Figure 7-2.
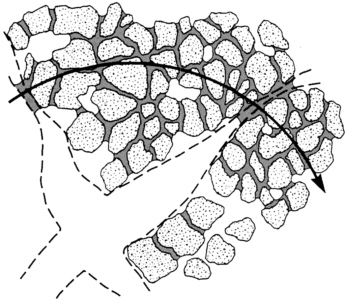
FIGURE 7-2 Model for unsaturated fracture showing flow only through capillary bridges between porous blocks. From Wang, J.S.Y., and T.N. Narasimhan, 1985. Hydrologic mechanism governing fluid flow in a partially saturated, fractured, porous medium. Water Resources Research 21(12): 1861-1874. Copyright from American Geophysical Union.
Because of this hypothesis, over the last two decades arid fractured vadose environments have been suggested as possible sites for placement of long-term nuclear waste repositories (Nitao and Buscheck, 1991). Since water is most likely the primary agent for movement of hazardous materials in the subsurface, the combination of an arid environment, a low permeability matrix, and fractures that possibly separate the matrix blocks and further delay transport, seemed ideal conditions for the isolation of toxic wastes. The sensitivity of the proposed use and the severe consequences of failure have significantly increased the importance of understanding the hydrologic behavior within an add fractured vadose zone.
Contrary to the prediction of models mentioned above, radionuclides have been detected in arid vadose regions at much greater distances from the source than expected. At the Exploratory Studies Facility (ESF), Yucca Mountain, Nevada, a bomb-pulse chlorine-36 signature was found hundreds of feet below surface, even though the bomb-pulse signal is less than 50 years old (Fabryka-Martin et al., 1998). This anomalous rapid transport rate is occurring in an add region where the vadose zone is highly unsaturated and fractured. Unfortunately,
porous matrix theory, dual-porosity models, and plug flow have not been able to predict such rapid movement of fluid in a region that is highly unsaturated and disconnectd from surface fractures that could transmit possible episodic flooding events.
Consequently, a new transport mechanism needs to be identified that is able to more accurately predict the large velocity flows observed within the fractured vadose zone. It is proposed that a free-surface film may be the mechanism by which fluids in unsaturated fractures are transported very rapidly through the vadose zone.
CONCEPTUAL MODEL FOR FREE-SURFACE FILM
The free-surface film model consists of a thin film of fluid flowing down the wall of an air-filled fracture in the vadose zone. The film is in contact with the porous matrix along one fracture wall and sustains an air phase between itself and the opposing fracture wall, as shown in Figure 7-3 (Dragila and Wheatcraft, 1997). The film flows under the influence of gravity, exclusive of capillary forces within the fracture. This mechanism can generate very rapid transport deep into the vadose zone. Transport velocities for a free-surface film can be up to four times that for an equivalently thick saturated plug (White, 1991). Furthermore,
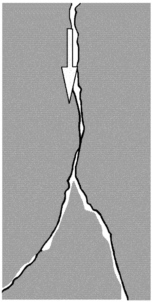
FIGURE 7-3 Model for flow in unsaturated fractures where fluid flows in the form of free surface films down the fracture walls while sustaining a continuous air phase.
velocities generated by wavy chaotic films may be two times higher still (Dragila and Wheatcraft, 1998).
The free-surface film model differs from the standard fracture flow models in that the fracture aperture does not directly control flow rate during transport by a free-surface film. Film flow can occur in small-aperture as well as large-aperture fractures. This characteristic eliminates the restrictions that constrain the standard fracture flow models.
Much experimental work has been done to study the behavior of flow in unsaturated fractures (Persoff and Pruess, 1985; Pruess and Tsang, 1990; Nicholl et al., 1994; Geller et al., 1996: Podgorney et al., 1998; Su et al., 1999). Most experimental and theoretical work on free-surface films is limited to the fields of mechanical and chemical engineering, where they have been studied in relation to many industrial operations, from wrinkle-free paint applications to solute transfer in chemical air strippers (Kapitza, 1965; Nakoryakov et al., 1977; Wasden and Dukler, 1992). The work by Tokunaga and Wan (1997) is the first reported experiment that specifically focuses on the characteristics of a free-surface film in a natural fracture.
The experiment presented by Tokunaga and Wan (1997) showed development of free-surface films on a fractured sample of Bishop Tuff. They established steady-state conditions in which flow delivered to the upper surface of their sample was quickly distributed to both the rock matrix and fracture surface while the matric potential was kept near saturation. Their experiment showed that these free-surface films can generate very high transport rates and velocity while sustaining subatmospheric pressures within the film (see section on Seepage Generated Film Flow below).
MATHEMATICAL MODEL
The mathematical model presented here was developed to understand the characteristics and transport capacity of film flow. Governing equations are mathematical expressions of fundamental laws that constrain the behavior of nature. In the case of fluid flow, these fundamental laws are conservation of mass (Equation 7.1), conservation of momentum (Equation 7.2), and conservation of energy (Equation 7.3):
(7.1)
(7.2)
(7.3)
The symbols used represent the following parameters: ρ is the fluid density; µ is the fluid dynamic viscosity; u is the velocity vector; t is the time variable; g is the constant of gravitational acceleration; p is the pressure; h is the enthalpy; T is the temperature; k is the thermal constant, and ![]() is a dissipation function. The momentum equations, also known as the Navier-Stokes equations, are fundamental and rigorous. They are also nonlinear, complex, nonunique, and difficult to solve. In order to solve the problem of a film of fluid flowing down an air-filled fracture, we have assumed the following simplified model: the fracture surface is vertical, smooth, and impermeable; the air phase is quiescent; and there is no mass transfer into the vapor phase. A sketch of the model is provided in Figure 7-4. A steady-state solution can be obtained by integrating the one-dimensional momentum equation and applying the appropriate boundary conditions. Nevertheless, a solution to the film-flow problem poses a particular difficulty. The free surface makes the thickness of the film a dynamic variable, and thus cannot be used as a boundary condition. This lack of boundary condition can be resolved by assuming that at steady state the free surface is flat and the film thickness constant (Nusselt, 1916). As will be shown later, although this assumption is incorrect, it provides a
is a dissipation function. The momentum equations, also known as the Navier-Stokes equations, are fundamental and rigorous. They are also nonlinear, complex, nonunique, and difficult to solve. In order to solve the problem of a film of fluid flowing down an air-filled fracture, we have assumed the following simplified model: the fracture surface is vertical, smooth, and impermeable; the air phase is quiescent; and there is no mass transfer into the vapor phase. A sketch of the model is provided in Figure 7-4. A steady-state solution can be obtained by integrating the one-dimensional momentum equation and applying the appropriate boundary conditions. Nevertheless, a solution to the film-flow problem poses a particular difficulty. The free surface makes the thickness of the film a dynamic variable, and thus cannot be used as a boundary condition. This lack of boundary condition can be resolved by assuming that at steady state the free surface is flat and the film thickness constant (Nusselt, 1916). As will be shown later, although this assumption is incorrect, it provides a
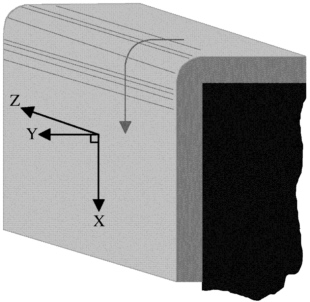
FIGURE 7-4 Geometry used for development of free-surface film mathematical model.
very useful solution. The steady-state solution to the velocity profile for a free-surface film flowing under the action of gravity along a vertical plane is
(7.4)
The mean velocity across the thickness of the film at steady-state is
(7.5)
where hN is the steady-state film thickness; uN is the steady-state velocity, and η is the kinematic viscosity (η = µ/ρ). The coordinate convention used throughout this paper is as follows: the x-coordinate points in the direction of flow, the y-coordinate points normal to the fracture wall, and the z-coordinate points parallel to the wall and normal to the direction of flow. The value for the steady-state film thickness, hN, can be obtained using the concept of conservation of mass. Once the film has attained a steady state, the flow rate per unit width can be expressed as
(7.6)
As this equation shows, film thickness is purely a function of the incoming, or source, flow rate. It is a dynamic variable.
To obtain the steady-state solution, we assumed that the film would sustain a flat free-surface film as it flows. However, these flat films are inherently unstable. Instability is commonly seen for a wide range of fluids and has been the advantage as well as the plague of many industrial applications (Dukler and Bergelin, 1952; Yih, 1963; Pumir et al., 1983). Chemical engineers use the naturally developing wavy surface to increase the two-phase contact area for systems such as heat exchangers and chemical air strippers. Conversely, in the field of industrial paints, wavy surfaces appearing in the form of wrinkles in paint coatings are to be avoided. Experimental observations indicate that films develop large-amplitude waves that have either a two-hump or one-hump structure. These solitary waves appear to ride over a thin fluid substrate. They travel faster than the mean film speed, can have amplitudes two to five times the substrate thickness, and appear to trap a recirculating region of fluid (Figure 7-5) (Wasden and Dukler, 1992).
A more rigorous mathematical model for the film-flow problem is presented below. It was developed in an attempt to understand the character of the wavy structure (Dragila, 1999). The following simplifying assumptions were made: the system is assumed to be two-dimensional; the fracture surface is vertical, smooth, and impermeable; the air phase is quiescent and there is no mass transfer into the
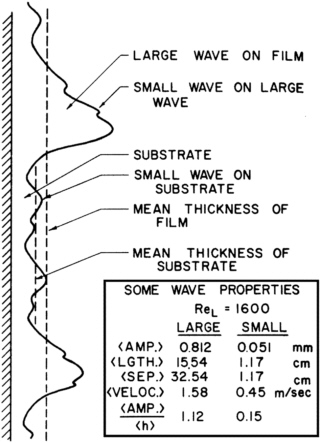
FIGURE 7-5 Schematic showing free-surface wave characteristics. From Chu and Dukler (1974).
vapor phase; the restorative force of surface tension due to the waviness of the surface is included in the fifth boundary condition; and the film is allowed to vary in thickness. The complete family of governing equations for this model follows. The x-momentum equation is
(7.7)
the y-momentum equation is
(7.8)
and the conservation of mass equation is
(7.9)
The first boundary condition is no slip at the wall,
at y = 0, u = 0; (7.10)
The second boundary condition is no slip at the wall and no matrix absorption,
at y = 0, v = 0; (7.11)
the third boundary condition is the kinematic condition at the free surface,
at y = h, v = ht + uhx, (7.12)
where the subscript signifies differentiation with respect to that variable; the fourth boundary condition is balance of shear stresses at the free surface,
(7.13)
and the fifth boundary condition is balance of normal stresses at the free surface, at y = h,
(7.14)
To solve this family of eight nonlinear partial differential equations, the model was further simplified. A boundary layer technique was used, as developed by Prandtl (1904), that takes advantage of the peculiar geometry of the flow system, where the scale of space and motion in one coordinate dimension is orders of magnitude greater than in the other dimension. Furthermore, the definition of the stream function was used, which reduces the number of unknowns at the cost of increasing the order of differentiation. Lastly, a coordinate system transformation was made into one that moves with the wave generated by the perturbation. Yu et al. (1995) used a similar approach to characterize the waviness of thicker films used in chemical air stripping equipment. This approach has led to development
of a family of ordinary differential equations in a coordinate system moving with the free-surface disturbance. The final set of equations is a family of six ordinary differential equations that can be used to study the evolution of perturbations with time:
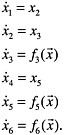
(7.15)
The components of the six-dimensional vector are:
(7.16)
where h is the film thickness and ai are the coefficients of the stream function expansion. The three functions in Equation 7.15, f3, f5, f6, are defined as follows:
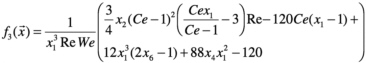
(7.17)
(7.18)
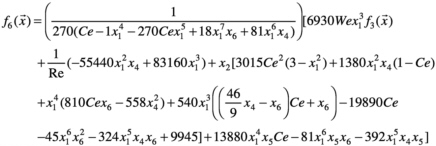
(7.19)
The ODEs in Equations 7.15 are dimensionless and apply to films of any thickness within the limitations of the boundary conditions and assumptions used. At
the two extremes are very thick films and very thin films. For very thick vertical films (greater than a millimeter), the Reynolds number is large and the flow dynamics are outside the bounds of Poiseuille-type flow and approach the domain of turbulent dynamics. Very thin films, less than a few microns, would require a different order of magnitude analysis in order to simplify the equations, and this would result in a different set of equations. All films within the valid thickness range are susceptible to shear stresses due to surface-tension gradients generated by surface active agents and temperature variability. This possible source of perturbation has not been included in the mathematical model, though it may be one source for generating unstable perturbations. The solution to the family of ODEs follows the development of a perturbation traveling at a given speed (celerity), Ce, and for a given Reynolds number, Re, and Weber number, We. Celerity is the wave speed normalized to the steady-state mean film speed, uN. The family of ODEs (Equations 7.16) can be solved for the film thickness, h (or x1), given a specific celerity and Reynolds number.
The solution to the family of ordinary differential equations above shows that the film-flow model has a distinctive chaotic behavior. Bifurcation of the solution appears with decreasing wave speed. Figure 7-6 shows phase diagrams for three celerity values indicating the solution at various stages of bifurcation and chaos for a sample film of Reynolds number 150 (dictating a film thickness of about 1/3 mm). For a celerity of 1.75 the behavior is sinusoidal. As the celerity is reduced below 1.748 the perturbation grows to a two-hump structure. Below a celerity of 1.73805 the behavior of the film thickness is chaotic. It exhibits a range of wave shapes including the characteristic single-hump solitary wave that has been experimentally observed. This analysis leads one to hypothesize that solitary waves that naturally form in free-surface films form as a result of a chaotic attractor natural to the system.
A very important result of this model is the link between the structure of the predicted chaotic disturbance and the shape of the naturally forming solitary wave. Since the attractor exists only for perturbations with celerity less than a specific value, we can hypothesize that the solitary waves forming on the free surface will travel at an approximate speed equal to the product of the transition celerity times the predicted steady-state film speed, uN. Analysis of the chaotic transitions as a function of film thickness allows determination of a general equation for the speed of the solitary wave (Equation 7.23). Experimental observations indicate that the amount of liquid in these waves at any point in time can be as high as 50 percent. Due to their high velocity, these waves are responsible for transporting as much as 90 percent of the liquid. This large amount of liquid moving in lumps has major implications when building models for transport into and by these films (Telles and Dukler, 1970). Figure 7-7 shows a photograph of the solitary waves and the underlying substrate (Kapitza, 1965). Experimental observations by Nakoryakov et al. (1977) indicate that the velocity profile within the thin substrate is parabolic. This observation allows us to use the parabolic
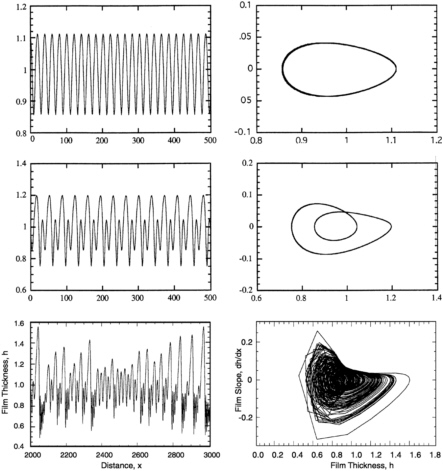
FIGURE 7-6 Phase diagrams for waves at various celerity values. From Yu (1995).
velocity profile solution derived from steady-state theory for the substrate. The development of solitary waves has implications for fracture flow related to transport rate, dispersion of contaminants, solute transfer between matrix and fluid, and sporadic flow behavior. Transport rate will be enhanced by the higher speed of the solitary waves. The existence of these waves has been attributed to increases of up to 500 percent in solute transfer between porous walls and fluid films (Striba and Hurt, 1955). Sporadic flow behavior may also be the result of the solitary waves, since contact with the opposite fracture wall during development of these waves could locally saturate the fracture and temporarily reduce the

FIGURE 7-7 Photographs of fluid films on vertical glass rod; flow is from left to right. From Kapitza (1965).
flow rate through the network. These observations indicate that these waves may have important implications for hydrologic systems.
HYDROLOGIC MODEL
The mathematical model has permitted determination of key characteristics of the chaotic film that were used to develop a more simplified hydrologic model for fluid transport. The following simple expressions account for the dual-mode transport by a chaotic film:
(7.20)
(7.21)
(7.22)
(7.23)
APPLICATIONS
The equations above can be used to analyze the impact that film development would have on transport through an unsaturated fracture. These are applied to the simple fracture model sketched in Figure 7-8. The model consists of a fracture with aperture variable in the z-direction, but no variability in the direction of flow, resembling a set of curtains. The fracture was allowed to sustain free-surface flow in the largest apertures and plug flow in the smallest saturated pathways. Figure 7-9 shows the transport distance after 1 second as predicted by the three models, free-surface films, saturated plug flow, and parallel plates. The mean aperture used for parallel plates was 0.31 mm. Film thickness was assumed to be that which “almost” saturates the conduit so as to properly compare it to the plug flow model. Both the plug flow and film flow models predict channeling of flow down the fracture; however, a more subdued behavior is predicted by the plug flow model.
One of the central interests in using these models is for determination of contaminant first arrivals. Equations 7.20-7.23 have been used in conjunction
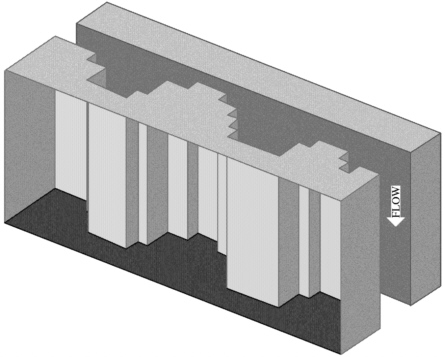
FIGURE 7-8 Fracture model; no aperture variability in flow direction.
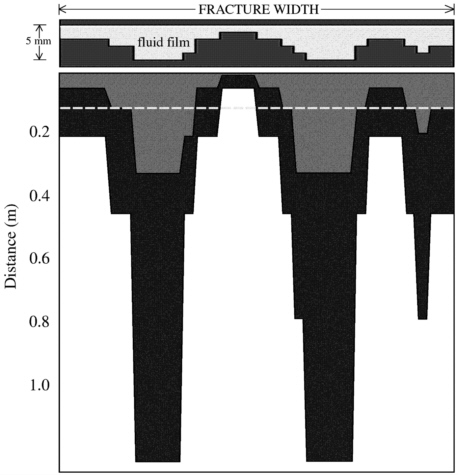
FIGURE 7-9 Top portion of figure shows cross-section of fracture aperture used for the calculations. Bottom portion of figure shows distance of contaminant first arrival for three models: free surface film model (dark grey), plug flow model (light grey), and parallel plate model (dashed line).
with the conservation of mass equation to generate the following predictive algorithm for determining the fastest velocities for a simple fracture model:
(7.24)
where Qsource is the source volumetric flow rate into the fracture; b the half aperture; W the total fracture width; wi the percent of fracture width having
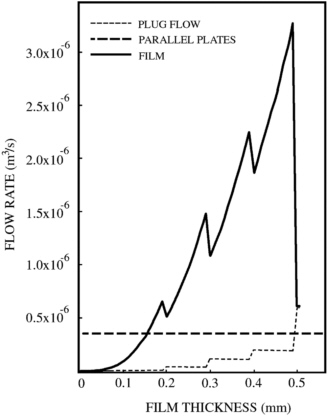
FIGURE 7-10 Flow capacity within a fracture for free-surface film model (solid line), plug model (dashed line), and parallel plate model (bold dashed line).
aperture 2bi; and wF the percent of fracture width exhibiting free-surface film flow. Width weights are calculated from the discretization of the model aperture, total width of the fracture, and total flow rate. This algorithm allows prediction of first arrival times from fracture statistics and knowledge of the incoming flow rate. It should be noted that this algorithm represents idealized conditions for a simple fracture model. This first-order equation will solve for the fast end of the transport envelope. It does not take into account matrix absorption, path tortuosity, or chaotic resaturation from wave growth, all of which serve to slow the transport rate.
Free-surface films in a fracture can also generate sharp local changes in flow rate by two mechanisms; resaturation of the conduit and desaturation into a film.
A dry fracture that receives a small amount of source flow rate will carry flow in the form of a free-surface film. If flow rate is increased, smaller-aperture sections of the fracture will become saturated, reducing the local capacity for flow. If the flow rate is increased to the point where the free-surface film touches the opposing fracture wall, the conduit will completely saturate and the flow rate will be correspondingly reduced. This behavior is shown in Figure 7-10, which was generated by using the simple fracture model in Figure 7-8. For comparison, the graph also shows curves for the cubic law model and the equivalent permeability model. Note that as the fracture completely saturates, the flow rate drops to the plug flow value. Sudden saturation events can occur due to increases in flow rate, changes in fracture aperture, and growth of chaotic waves.
Sudden episodic increases in flow rate may also be generated by the chaotic nature of the free surface. Flow rates that range between the film rate and the plug flow rate (the envelope between the two curves in Figure 7-9), are subject to unstable wave growth. If the wave grows sufficiently in amplitude to touch the opposing fracture wall, the system will locally saturate, resulting in a local reduction in flow that will force the fluid to back up the system or find another route. However, since the flow rate is within the specified range, fluid prefers (by energy argument) to sustain a free surface. Sudden changes in flow rate or air movement within the fracture could induce the fluid to desaturate and reform the free-surface film, which is the more efficient transport mode (Dragila and Wheatcraft, 1998). Local development of a film could drain fluid from higher in the fracture and generate sudden changes in flow rate. These peaks in transport rate would be short lived if the free surface once again became unstable. Duration of the episodic fast-flow events may be related to the time it takes for a solitary wave to form and grow. Observations of such spurious, short-lived events have been recently reported (Podgorney and Wood, 1999). A qualitative schematic of the expected behavior is shown in Figure 7-11.
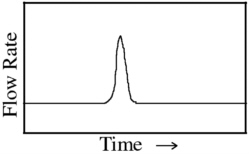
FIGURE 7-11 Conceptual schematic of changes in flow rate due to a chaotic fast-flow event within a fracture.
SEEPAGE GENERATED FILM FLOW
Free-surface films have been seen to form in fractures open to the surface such as expansion cracks in clay soils. Tokunaga and Wan (1997) showed development of a significant free-surface film along a vertically oriented fracture in a sample of Bishop tuff. Figure 7-12 shows the dramatic increase in the hydraulic conductivity of the system by the presence of the free-surface film. In a vadose environment these films could transport large fluxes down interconnected paths within the fracture system. But the observation of chlorine-36 at the ESF is hundreds of feet down from the surface, and fractures in this region may not be completely connected to the surface. A second likely method for generating free-surface films is by seepage into a fracture.
Flow through unsaturated porous material is dominated by capillary forces. Fluid moves only through the saturated-pore portions of the matrix. When matrix fluid encounters a wide-aperture air-filled fracture, the fluid stops moving until the hydrostatic pressure builds up sufficiently at the boundary. If the fracture is inclined from the horizontal, seepage from the fracture wall will flow down the wall and travel as a free-surface film to the terminus of the fracture. The algorithm
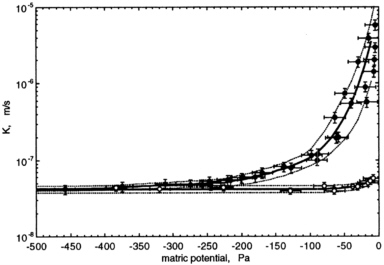
FIGURE 7-12 Hydraulic conductivity measurements on fractured tuff with fractures sealed (open circles) and with fluid allowed to flow down an unsealed fracture as a free-surface film. From Tokunaga, T. K., and J. Wan, 1997. Water film flow along fracture surfaces of porous rock. Water Resources Research 33(6): 1287-1295. Copyright by American Geophysical Union.
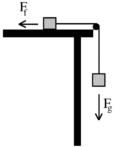
FIGURE 7-13 Sliding block conceptual model for seep generation at a fracture wall.
presented below was developed to model flux rate and flow velocity for free-surface films generated by seepage into a fracture. The rate at which the matrix feeds the seep is derived using an analogous model; a block of wood sliding at constant velocity on a table is tied to a second block that is hanging freely (Figure 7-13). The energy of the system is composed of the gain in energy of the hanging block and the loss of energy due to friction by the sliding block. Similarly, the energy equation for the seep needs to include the energy gradient provided by the gravitational field and the energy loss due to the frictional characteristic of the porous medium that is accounted for by the hydraulic conductivity. The flow equation for the source of the seep becomes
Q(x)source = KmatrixA(x)seepageface = KmatrixWx (7.25)
where K is the hydraulic conductivity of the porous matrix; A the cross-sectional area of the seepage face; W the lateral width of the seepage wall; and x the vertical distance over which seepage occurs. Although the source flow rate is determined by the hydraulic conductivity of the porous matrix, once the film starts to flow, the film thickness becomes a dynamic variable and different equations apply. The source of seepage is a distributed source, thus the film is being continuously fed, and as a result, continuously increasing in thickness and velocity. The film flow rate is a function of the source flow rate and the distance along the wall:
(7.26)
The Nusselt film thickness, Nusselt velocity, and mean film flux rate are now a function of location down the seepage wall and a function of matrix properties,
(7.27)
(7.28)
Since mass must be conserved, the flux carried by the film is equal to the flux exiting the seep. Thus, there is a direct relationship between film properties and seep matrix properties:
Q(x)film = WhN(x)ūN(x) = WxKmatrix. (7.29)
After the film exits the seep area, its thickness and velocity will no longer increase. Film flow rate per unit width below the active seep area can be found by solving Equation 7.29 for x = L, where L is the length of the seep:
Qfilm = hNuN = LKmatrix. (7.30)
Figure 7-14 shows the relationship between seep matrix hydraulic conductivity and maximum film velocity for a chaotic film. Since the fastest rates are generated by solitary waves, the values were calculated by combining Equations 7.23 and 7.30 to obtain the following relationship:
(7.31)
Using the range of velocity shown in the graph, the time it would take for a film to reach a depth of 100 m would be between 1 day and 35 years, depending on the saturated hydraulic conductivity of the matrix supporting the seep. The model above assumes a flat untextured surface, whereas a natural fracture is textured. Fracture surface topography could provide deeper pathways for development
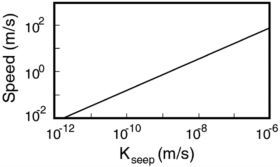
FIGURE 7-14 Graph of maximum film velocity predicted by chaotic film model as a function of seep matrix hydraulic conductivity.
of thicker films, providing faster conduits for the fluid. At higher seepmatric conductivity, the source flow rate would increase, resulting in thicker films. The general thickening of the film would allow lateral connection to higher-conductivity pathways. As the film progressively thickens, more and more of the flow is conducted through narrower and thicker film conduits. Noting that the predicted flow rate increases as the cube of the film thickness, deeper channels could carry a disproportionate percentage of the flow. With increasing film source flow rate, a power-law behavior may develop in the velocity profile of the film in response to possible power-law distributions in the topographic character of the natural fracture surface. It is clear that much more work needs to be done in this area.
A final comparison is made between the prediction of the algorithm above and an equivalent model using the TOUGH computer code commonly in use for fractured media transport. TOUGH is a multidimensional numerical model for simulating the transport in porous and fractured media. It assumes Darcy type flow, and fractures are modeled as porous conduits of higher permeability (Pruess and Wang, 1987). The model selected is a seepage area into a natural fracture generated by a horizontal capillary barrier. Figure 7-15 includes a schematic of the hydrologic model and shows the results of the TOUGH code model and film flow model.
Parameters used for the TOUGH model may be found in Ross et al. (1982) with some adjustment for a much longer fracture to avoid boundary problems. The cells were 1 cm square, and the fracture was a soil-filled conduit of high permeability, 10 cm in aperture and 2 m long with a seep area only 4 cm long. For the film model, flow rate used to feed the film was calculated using Equation 7.29 and the same seep permeability as used for the TOUGH model. Comparing results for the three time steps shown in Figure 7-15, it is evident that the two models address two different mechanisms in fluid flow. The mass of fluid contained in each time step in the two models is the same; however, the film redistributes the mass in a very different way than the TOUGH model. By a time of 1,000 seconds, the film has traveled 42 cm and is out of the seep area. In contrast, the TOUGH model moves the fluid laterally as well as downward due to capillary forces within the conduit.
CONCLUDING REMARKS
Free-surface films have a greater capacity for transporting fluids via unsaturated fractures than plug flow. They are minimally affected by fracture aperture characteristics and as a result do not suffer the capillary and geometric restrictions imposed on standard fracture flow models. Fractures connected to the surface can take advantage of episodic precipitation events. Fractures deeper in the vadose zone not exposed to the surface may generate seepage by creating a capillary barrier against the unsaturated porous matrix. This seepage may generate a free-surface film that will flow under the influence of gravity if the fracture
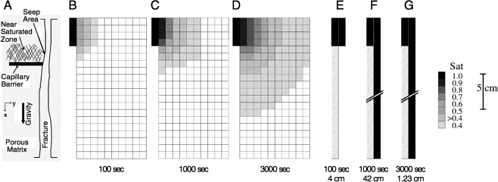
FIGURE 7-15 Comparison of results from TOUGH and free-surface film models for a seep into a fracture: (a) conceptual hydrologic model showing a seep forming from a near-saturation matrix above a capillary barrier; (b-d) results of the TOUGH model for three time steps; (e-g) results of the same problem using free-surface film model.
is inclined toward the vertical. Where the fracture system is not connected, free-surface film will transport fluid at very rapid speeds to the terminus of the fracture, where it is again reabsorbed into the matrix. By this mechanism, the fracture system becomes a short circuit to the porous matrix flow, transporting fluid rapidly across entire sections of unsaturated porous matrix. A series of fortuitously placed fractures could dramatically increase the transport rate of a contaminant.
Much work is still to be done in determining the mass exchange between film and matrix induced by the chaotic behavior of the free surface. Experimental studies have shown up to a 500 percent increase in solute transfer between matrix and fluid film when the film becomes wavy (chaotic) (Striba and Hurt, 1955). The assumption that pressure balance must be sustained across the film-matrix interface is still an open issue. Even though the free surface of the film would indicate that pressure in the film is atmospheric, tensiometer measurements in the Bishop Tuff experiment indicate that the free-surface film was subatmospheric. The hopscotch potential of a combined fracture-film transport mechanism suggests that dispersion of contaminants in a fractured vadose system may require a different approach than used in standard unsaturated porous transport.
The proposed free-surface film model represents one mechanism that may be responsible for the presence of bomb-pulse chlorine-36 at great depths at Yucca Mountain. In addition, it proposes explanations for interesting observed behavior such as episodic fast-flow events, erratic flow rate observations, and very rapid transport through air-filled fractures. Further research is required in order to comprehensively understand the extent to which this mechanism is operative in fractured vadose zones.
REFERENCES
Chu, K. J., and A. E. Dukler, 1974. Statistical characteristics of thin, wavy films: Part II. Studies of the substrate and its wave structure. AIChE Journal 20(4): 695-706.
Dragila, M. I., 1999. A New Theory for Transport in Unsaturated Fractures: Free-Surface Film Flows. Ph.D. Dissertation, University of Nevada, Reno.
Dragila, M. I., and S. W. Wheatcraft, 1997. Chaotic dynamics in unsaturated fracture flow. Abstract, Geological Society of America.
Dragila, M. I., and S. W. Wheatcraft, 1998. Non-linear characteristics of fluid flow in unsaturated fractures . Chapman Conference on Fractal Scaling, Non-linear Dynamics, and Chaos in Hydrologic Systems, Clemson, S.C., May 12-15.
Dukler, A. E., and O. P. Bergelin, 1952. Characteristics of flow in falling fluid films.Chemical Engineering Progress 48(11).
Fabryka-Martin, J. T., A. V. Wolfsberg, S. S. Levy, K. Campbell, P. Tseng, J. L. Roach, and L. E. Wolfsberg, 1998. Evaluation of flow and transport models of Yucca Mountain, based on chlorine-36 studies for FY98. Los Alamos National Laboratory, Yucca Mountain Project Milestone Report SP33DDM4.
Geller, J. T., G. Su, and K. Pruess, 1996. Preliminary studies of water seepage through rough-walled fractures . Lawrence Berkeley National Laboratory, LBNL-38810, UC-403.
Kapitza, P. L., 1965. Wave flow on thin layers of a viscous fluid (1943). In: Collected Works of P. L. Kapitza, D. Ter Haar, ed., Pergamon Press.
Nakoryakov, V. E., B. G. Pokusaev, S. V. Alekseenko, and V. V. Orlov, 1977. Instantaneous velocity profile in a wavy fluid film. Journal of Engineering Physics and Thermophysics 33(3): 1012-1016. Translated from Inzhenerno-Fizicheskii Zhurnal 33(3): 399-404.
Nitao, J. J., and T. A. Buscheck, 1991. Infiltration of a liquid front in an unsaturated, fractured porous medium. Water Resources Research 27(8): 2099-2112.
Nitao, J. J., T. A. Buscheck, and D. A. Chesnut, 1993. Implications of episodic nonequilibrium fracture-matrix flow on repository performance. Nuclear Technology 104: 385-402.
Nusselt, W., 1916. Die Oberflocaekondensation des Easserdampfer, ZVDI, 60: 541.
Persoff, P., and K. Pruess, 1985. Two-phase flow visualization and relative permeability measurement in natural rough-walled rock fractures. Water Resources Research 31(5): 1175-1186.
Podgorney, R. K., T. R. Wood, T. M. Stoops, R. G. Taylor, and J. M. Hubbell, 1998. Basalt outcrop infiltration tests to evaluate chaotic behavior of unsaturated flow in fractured rock. Data Summary Report, 1997 Field Season, Idaho National Laboratories.
Podgorney, R. K., and T. R. Wood, 1999. Observations of water movement in variably saturated fractured basalt and its possible implications on predictive modeling. In: Proceedings of the International Symposium on Dynamics of Fluids in Fractured Rocks, Concepts and Recent Advances, B. Faybishenko, ed. Lawrence Berkeley Laboratory, pp. 300-304.
Prandtl, L., 1904. Uber Flussigkeitsbewegung bei sehr kleiner Reibung. Proc. Third Internat. Math. Cong. Heidelberg [English translation in NACA Technical memo, 452].
Pruess, K., and J. S. Y. Wang, 1987. Numerical modeling of isothermal and nonisothermal flow in unsaturated fractured rock: A review. In: Flow and Transport Through Unsaturated Fractured Rock. D. D. Evans and T. J. Nicholson, eds. Geophys. Monogr. Ser. 42, American Geophysical Union , Washington, D.C., pp. 11-21.
Pruess, K., and Y. W. Tsang, 1990. On two-phase relative permeability and capillary pressure of rough-walled rock fractures. Water Resources Research 26(9): 1915-1926.
Pumir, A., P. Manneville, and Y. Pomeau, 1983. On solitary waves running down an inclined plane. Journal of Fluid Mechanics 135: 27-50.
Ross, B., J. W. Mercer, S. D. Thomas, B. H. Lester, 1982. Benchmark Problems for Respiratory Siting Models, NRC-Report, NUREG/CR-3097.
Striba, C., and D. M. Hurt, 1955. Turbulence in falling liquid films. AIChE J. 1: 178.
Su, G., J. T. Geller, K. Pruess, and F. Wen, 1999. Experimental studies of water seepage and intermittent flow in unsaturated, rough-walled fractures. Water Resources Research, 35(4): 1019-1038.
Telles, A. S., and A. E. Dukler, 1970. Statistical characteristics of thin, vertical, wavy liquid films. Ind. Eng. Chem. Fundam. 9(3): 412-421.
Tokunaga, T. K. and J. Wan, 1997. Water film flow along fracture surfaces of porous rock. Water Resources Research 33(6): 1287-1295.
Tsang, Y. W., 1984. The effect of tortuosity on fluid flow through a single fracture. Water Resources Research 20(9): 1209-1215.
Tsang, Y. W., and C. F. Tsang, 1987. Channel model of flow through fractured media. Water Resources Research 23(3): 467-480.
Wang, J. S. Y., and T. N. Narasimhan, 1985. Hydrologic mechanism governing fluid flow in a partially saturated, fractured, porous medium. Water Resources Research 21(12): 1861-1874.
Wasden, F. K., and A. E. Dukler, 1992. An experimental study of mass transfer from a wall into a wavy film . Chemical Engineering Science 47(17/18): 4323-4331.
White, F. M., 1991. Viscous Fluid Flow. 2nd ed., McGraw Hill, New York.
Yih, C.-S., 1963. Stability of liquid flow down an inclined plane. The Physics of Fluids 6(3).
Yu, L.-Q., 1995. Studies of wavy films in vertical gas-liquid annual flows. Ph.D. dissertation, University of Houston.
Yu, L.-Q., F. K. Wasden, A. E. Dukler, and V. Balakotaiah, 1995. Nonlinear evolution of waves on falling films at high Reynolds numbers . Physics of Fluids 7(8): 1886-1902.


























