1
Introduction
M. Suzanne Donovan and John D. Bransford
More than any other species, people are designed to be flexible learners and, from infancy, are active agents in acquiring knowledge and skills. People can invent, record, accumulate, and pass on organized bodies of knowledge that help them understand, shape, exploit, and ornament their environment. Much that each human being knows about the world is acquired informally, but mastery of the accumulated knowledge of generations requires intentional learning, often accomplished in a formal educational setting.
Decades of work in the cognitive and developmental sciences has provided the foundation for an emerging science of learning. This foundation offers conceptions of learning processes and the development of competent performance that can help teachers support their students in the acquisition of knowledge that is the province of formal education. The research literature was synthesized in the National Research Council report How People Learn: Brain, Mind, Experience, and School.1 In this volume, we focus on three fundamental and well-established principles of learning that are highlighted in How People Learn and are particularly important for teachers to understand and be able to incorporate in their teaching:
-
Students come to the classroom with preconceptions about how the world works. If their initial understanding is not engaged, they may fail to grasp the new concepts and information, or they may learn them for purposes of a test but revert to their preconceptions outside the classroom.
-
To develop competence in an area of inquiry, students must (a) have a deep foundation of factual knowledge, (b) understand facts and ideas in the context of a conceptual framework, and (c) organize knowledge in ways that facilitate retrieval and application.
-
A “metacognitive” approach to instruction can help students learn to take control of their own learning by defining learning goals and monitoring their progress in achieving them.
A FISH STORY
The images from a children’s story, Fish Is Fish,2 help convey the essence of the above principles. In the story, a young fish is very curious about the world outside the water. His good friend the frog, on returning from the land, tells the fish about it excitedly:
“I have been about the world—hopping here and there,” said the frog, “and I have seen extraordinary things.”
“Like what?” asked the fish.
“Birds,” said the frog mysteriously. “Birds!” And he told the fish about the birds, who had wings, and two legs, and many, many colors. As the frog talked, his friend saw the birds fly through his mind like large feathered fish.
The frog continues with descriptions of cows, which the fish imagines as black-and-white spotted fish with horns and udders, and humans, which the fish imagines as fish walking upright and dressed in clothing. Illustrations below from Leo Lionni’s Fish Is Fish © 1970. Copyright renewed 1998 by Leo Lionni. Used by permission of Random House Children’s Books, a division of Random House, Inc.

Principle #1: Engaging Prior Understandings
What Lionni’s story captures so effectively is a fundamental insight about learning: new understandings are constructed on a foundation of existing understandings and experiences. With research techniques that permit the study of learning in infancy and tools that allow for observation of activity in the brain, we understand as never before how actively humans engage in learning from the earliest days of life (see Box 1-1). The understandings children carry with them into the classroom, even before the start of formal schooling, will shape significantly how they make sense of what they are
|
BOX 1-1 Research studies have demonstrated that infants as young as 3 to 4 months of age develop understandings and expectations about the physical world. For example, they understand that objects need support to prevent them from falling to the ground, that stationary objects may be displaced when they come into contact with moving objects, and that objects at rest must be propelled into motion.3 In research by Needham and Baillargeon,4 infants were shown a table on which a box rested. A gloved hand reached out from a window beside the table and placed another box in one of two locations: on top of the first box (the possible event), and beyond the box—creating the impression that the box was suspended in midair. In this and similar studies, infants look reliably longer at the impossible events, suggesting an awareness and a set of expectations regarding what is and is not physically possible. 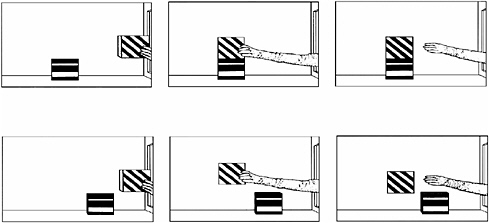 SOURCE: Needham and Baillargeon (1993). Reprinted with permission from Elsevier. |
|
BOX 1-2 Andrea DiSessa5 conducted a study in which he compared the performance of college physics students at a top technological university with that of elementary schoolchildren on a task involving momentum. He instructed both sets of students to play a computerized game that required them to direct a simulated object (a dynaturtle) so that it would hit a target, and to do so with minimum speed at impact. Participants were introduced to the game and given a hands-on trial that allowed them to apply a few taps with a wooden mallet to a ball on a table before they began. DiSessa found that both groups of students failed miserably at the task. Despite their training, college physics majors—just like the elementary school children—applied the force when the object was just below the target, failing to take momentum into account. Further investigation with one college student revealed that she knew the relevant physical properties and formulas and would have performed well on a written exam. Yet in the context of the game, she fell back on her untrained conceptions of how the physical world works. |
taught. Just as the fish constructed an image of a human as a modified fish, children use what they know to shape their new understandings.
While prior learning is a powerful support for further learning, it can also lead to the development of conceptions that can act as barriers to learning. For example, when told that the earth is round, children may look to reconcile this information with their experience with balls. It seems obvious that one would fall off a round object. Researchers have found that some children solve the paradox by envisioning the earth as a pancake, a “round” shape with a surface on which people could walk without falling off.6
How People Learn summarizes a number of studies demonstrating the active, preconception-driven learning that is evident in humans from infancy through adulthood.7 Preconceptions developed from everyday experiences are often difficult for teachers to change because they generally work well enough in day-to-day contexts. But they can impose serious constraints on understanding formal disciplines. College physics students who do well on classroom exams on the laws of motion, for example, often revert to their untrained, erroneous models outside the classroom. When they are confronted with tasks that require putting their knowledge to use, they fail to take momentum into account, just as do elementary students who have had no physics training (see Box 1-2). If students’ preconceptions are not addressed directly, they often memorize content (e.g., formulas in physics), yet still use their experience-based preconceptions to act in the world.
Principle #2: The Essential Role of Factual Knowledge and Conceptual Frameworks in Understanding
The Fish Is Fish story also draws attention to the kinds of knowledge, factual and conceptual, needed to support learning with understanding. The frog in the story provides information to the fish about humans, birds, and cows that is accurate and relevant, yet clearly insufficient. Feathers, legs, udders, and sport coats are surface features that distinguish each species. But if the fish (endowed now with human thinking capacity) is to understand how the land species are different from fish and different from each other, these surface features will not be of much help. Some additional, critical concepts are needed—for example, the concept of adaptation. Species that move through the medium of air rather than water have a different mobility challenge. And species that are warm-blooded, unlike those that are cold-blooded, must maintain their body temperature. It will take more explaining of course, but if the fish is to see a bird as something other than a fish with feathers and wings and a human as something other than an upright fish with clothing, then feathers and clothing must be seen as adaptations that help solve the problem of maintaining body temperature, and upright posture and wings must be seen as different solutions to the problem of mobility outside water.
Conceptual information such as a theory of adaptation represents a kind of knowledge that is unlikely to be induced from everyday experiences. It typically takes generations of inquiry to develop this sort of knowledge, and people usually need some help (e.g., interactions with “knowledgeable others”) to grasp such organizing concepts.8
Lionni’s fish, not understanding the described features of the land animals as adaptations to a terrestrial environment, leaps from the water to experience life on land for himself. Since he can neither breathe nor maneuver on land, the fish must be saved by the amphibious frog. The point is well illustrated: learning with understanding affects our ability to apply what is learned (see Box 1-3).
This concept of learning with understanding has two parts: (1) factual knowledge (e.g., about characteristics of different species) must be placed in a conceptual framework (about adaptation) to be well understood; and (2) concepts are given meaning by multiple representations that are rich in factual detail. Competent performance is built on neither factual nor conceptual understanding alone; the concepts take on meaning in the knowledge-rich contexts in which they are applied. In the context of Lionni’s story, the general concept of adaptation can be clarified when placed in the context of the specific features of humans, cows, and birds that make the abstract concept of adaptation meaningful.
|
BOX 1-3 In one of the most famous early studies comparing the effects of “learning a procedure” with “learning with understanding,” two groups of children practiced throwing darts at a target underwater.9 One group received an explanation of refraction of light, which causes the apparent location of the target to be deceptive. The other group only practiced dart throwing, without the explanation. Both groups did equally well on the practice task, which involved a target 12 inches under water. But the group that had been instructed about the abstract principle did much better when they had to transfer to a situation in which the target was under only 4 inches of water. Because they understood what they were doing, the group that had received instruction about the refraction of light could adjust their behavior to the new task. |
This essential link between the factual knowledge base and a conceptual framework can help illuminate a persistent debate in education: whether we need to emphasize “big ideas” more and facts less, or are producing graduates with a factual knowledge base that is unacceptably thin. While these concerns appear to be at odds, knowledge of facts and knowledge of important organizing ideas are mutually supportive. Studies of experts and novices—in chess, engineering, and many other domains—demonstrate that experts know considerably more relevant detail than novices in tasks within their domain and have better memory for these details (see Box 1-4). But the reason they remember more is that what novices see as separate pieces of information, experts see as organized sets of ideas.
Engineering experts, for example, can look briefly at a complex mass of circuitry and recognize it as an amplifier, and so can reproduce many of its circuits from memory using that one idea. Novices see each circuit separately, and thus remember far fewer in total. Important concepts, such as that of an amplifier, structure both what experts notice and what they are able to store in memory. Using concepts to organize information stored in memory allows for much more effective retrieval and application. Thus, the issue is not whether to emphasize facts or “big ideas” (conceptual knowledge); both are needed. Memory of factual knowledge is enhanced by conceptual knowledge, and conceptual knowledge is clarified as it is used to help organize constellations of important details. Teaching for understanding, then, requires that the core concepts such as adaptation that organize the knowledge of experts also organize instruction. This does not mean that that factual knowledge now typically taught, such as the characteristics of fish, birds, and mammals, must be replaced. Rather, that factual information is given new meaning and a new organization in memory because those features are seen as adaptive characteristics.
|
In one study, a chess master, a Class A player (good but not a master), and a novice were given 5 seconds to view a chess board position from the middle of a chess game (see below). After 5 seconds the board was covered, and each participant attempted to reconstruct the board position on another board. This procedure was repeated for multiple trials until everyone received a perfect score. On the first trial, the master player correctly placed many more pieces than the Class A player, who in turn placed more than the novice: 16, 8, and 4, respectively. (See data graphed below.) However, these results occurred only when the chess pieces were arranged in configurations that conformed to meaningful games of chess. When chess pieces were randomized and presented for 5 seconds, the recall of the chess master and Class A player was the same as that of the novice—they all placed 2 to 3 positions correctly. The apparent difference in memory capacity is due to a difference in pattern recognition. What the expert can remember as a single meaningful pattern, novices must remember as separate, unrelated items. 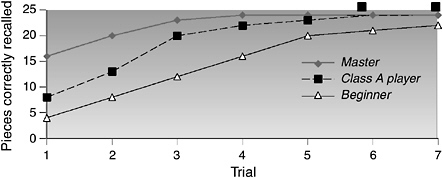 SOURCE: Chase and Simon (1973). Reprinted with permission from Elsevier. |
Principle #3: The Importance of Self-Monitoring
Hero though he is for saving the fish’s life, the frog in Lionni’s story gets poor marks as a teacher. But the burden of learning does not fall on the teacher alone. Even the best instructional efforts can be successful only if the student can make use of the opportunity to learn. Helping students become effective learners is at the heart of the third key principle: a “metacognitive” or self-monitoring approach can help students develop the ability to take control of their own learning, consciously define learning goals, and monitor their progress in achieving them. Some teachers introduce the idea of metacognition to their students by saying, “You are the owners and operators of your own brain, but it came without an instruction book. We need to learn how we learn.”
“Meta” is a prefix that can mean after, along with, or beyond. In the psychological literature, “metacognition” is used to refer to people’s knowledge about themselves as information processors. This includes knowledge about what we need to do in order to learn and remember information (e.g., most adults know that they need to rehearse an unfamiliar phone number to keep it active in short-term memory while they walk across the room to dial the phone). And it includes the ability to monitor our current understanding to make sure we understand (see Box 1-5). Other examples include monitoring the degree to which we have been helpful to a group working on a project.10
|
BOX 1-5 Read the following passage from a literary critic, and pay attention to the strategies you use to comprehend: If a serious literary critic were to write a favorable, full-length review of How Could I Tell Mother She Frightened My Boyfriends Away, Grace Plumbuster’s new story, his startled readers would assume that he had gone mad, or that Grace Plumbuster was his editor’s wife. Most good readers have to back up several times in order to grasp the meaning of this passage. In contrast, poor readers tend to simply read it all the way through without pausing and asking if the passage makes sense. Needless to say, when asked to paraphrase the passage they fall short. SOURCE: Whimbey and Whimbey (1975, p. 42). |
In Lionni’s story, the fish accepted the information about life on land rather passively. Had he been monitoring his understanding and actively comparing it with what he already knew, he might have noted that putting on a hat and jacket would be rather uncomfortable for a fish and would slow his swimming in the worst way. Had he been more engaged in figuring out what the frog meant, he might have asked why humans would make themselves uncomfortable and compromise their mobility. A good answer to his questions might have set the stage for learning about differences between humans and fish, and ultimately about the notion of adaptation. The concept of metacognition includes an awareness of the need to ask how new knowledge relates to or challenges what one already knows—questions that stimulate additional inquiry that helps guide further learning.11
The early work on metacognition was conducted with young children in laboratory contexts.12 In studies of “metamemory,” for example, young children might be shown a series of pictures (e.g., drum, tree, cup) and asked to remember them after 15 seconds of delay (with the pictures no longer visible). Adults who receive this task spontaneously rehearse during the 15-second interval. Many of the children did not. When they were explicitly told to rehearse, they would do so, and their memory was very good. But when the children took part in subsequent trials and were not reminded to rehearse, many failed to rehearse even though they were highly motivated to perform well in the memory test. These findings suggest that the children had not made the “metamemory” connection between their rehearsal strategies and their short-term memory abilities.13
Over time, research on metacognition (of which metamemory is considered a subset) moved from laboratory settings to the classroom. One of the most striking applications of a metacognitive approach to instruction was pioneered by Palincsar and Brown in the context of “reciprocal teaching.”14 Middle school students worked in groups (guided by a teacher) to help one another learn to read with understanding. A key to achieving this goal involves the ability to monitor one’s ongoing comprehension and to initiate strategies such as rereading or asking questions when one’s comprehension falters. (Box 1-5 illustrates this point.) When implemented appropriately, reciprocal teaching has been shown to have strong effects on improving students’ abilities to read with understanding in order to learn.
Appropriate kinds of self-monitoring and reflection have been demonstrated to support learning with understanding in a variety of areas. In one study,15 for example, students who were directed to engage in self-explanation as they solved mathematics problems developed deeper conceptual understanding than did students who solved those same problems but did not engage in self-explanation. This was true even though the common time limitation on both groups meant that the self-explaining students solved fewer problems in total.
Helping students become more metacognitive about their own thinking and learning is closely tied to teaching practices that emphasize self-assessment. The early work of Thorndike16 demonstrated that feedback is important for learning. However, there is a difference between responding to feedback that someone else provides and actively seeking feedback in order to assess one’s current levels of thinking and understanding. Providing support for self-assessment is an important component of effective teaching. This can include giving students opportunities to test their ideas by building things and seeing whether they work, performing experiments that seek to falsify hypotheses, and so forth. Support for self-assessment is also provided by opportunities for discussion where teachers and students can express different views and explore which ones appear to make the most sense. Such questioning models the kind of dialogue that effective learners internalize. Helping students explicitly understand that a major purpose of these activities is to support metacognitive learning is an important component of successful teaching strategies.17
Supporting students to become aware of and engaged in their own learning will serve them well in all learning endeavors. To be optimally effective, however, some metacognitive strategies need to be taught in the context of individual subject areas. For example, guiding one’s learning in a particular subject area requires awareness of the disciplinary standards for knowing. To illustrate, asking the question “What is the evidence for this claim?” is relevant whether one is studying history, science, or mathematics. However, what counts as evidence often differs. In mathematics, for example, formal proof is very important. In science, formal proofs are used when possible, but empirical observations and experimental data also play a major role. In history, multiple sources of evidence are sought and attention to the perspective from which an author writes and to the purpose of the writing is particularly important. Overall, knowledge of the discipline one is studying affects people’s abilities to monitor their own understanding and evaluate others’ claims effectively.
LEARNING ENVIRONMENTS AND THE DESIGN OF INSTRUCTION
The key principles of learning discussed above can be organized into a framework for thinking about teaching, learning, and the design of classroom and school environments. In How People Learn, four design characteristics are described that can be used as lenses to evaluate the effectiveness of teaching and learning environments. These lenses are not themselves research findings; rather, they are implications drawn from the research base:
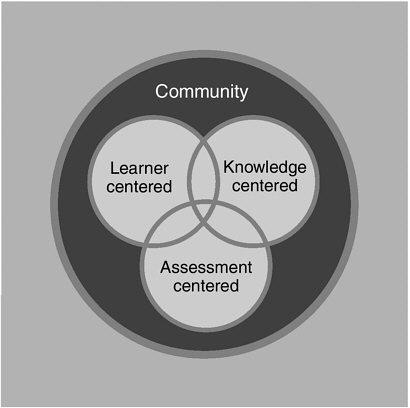
FIGURE 1-1 Perspectives on learning environments.
-
The learner-centered lens encourages attention to preconceptions, and begins instruction with what students think and know.
-
The knowledge-centered lens focuses on what is to be taught, why it is taught, and what mastery looks like.
-
The assessment-centered lens emphasizes the need to provide frequent opportunities to make students’ thinking and learning visible as a guide for both the teacher and the student in learning and instruction.
-
The community-centered lens encourages a culture of questioning, respect, and risk taking.
These aspects of the classroom environment are illustrated in Figure 1-1 and are discussed below.
Learner-Centered Classroom Environments
Instruction must begin with close attention to students’ ideas, knowledge, skills, and attitudes, which provide the foundation on which new learning builds. Sometimes, as in the case of Lionni’s fish, learners’ existing ideas lead to misconceptions. More important, however, those existing conceptions can also provide a path to new understandings. Lionni’s fish mistakenly projects the model of a fish onto humans, birds, and cows. But the fish does know a lot about being a fish, and that experience can provide a starting point for understanding adaptation. How do the scales and fins of a fish help it survive? How would clothing and feathers affect a fish? The fish’s existing knowledge and experience provide a route to understanding adaptation in other species. Similarly, the ideas and experiences of students provide a route to new understandings both about and beyond their experience.
Sometimes the experiences relevant to teaching would appear to be similar for all students: the ways in which forces act on a falling ball or feather, for example. But students in any classroom are likely to differ in how much they have been encouraged to observe, think about, or talk about a falling ball or feather. Differences may be larger still when the subject is a social rather than a natural phenomenon because the experiences themselves, as well as norms regarding reflection, expression, and interaction, differ for children from different families, communities, and cultures. Finally, students’ expectations regarding their own performances, including what it means to be intelligent, can differ in ways that affect their persistence in and engagement with learning.
Being learner-centered, then, involves paying attention to students’ backgrounds and cultural values, as well as to their abilities. To build effectively on what learners bring to the classroom, teachers must pay close attention to individual students’ starting points and to their progress on learning tasks. They must present students with “just-manageable difficulties”—challenging enough to maintain engagement and yet not so challenging as to lead to discouragement. They must find the strengths that will help students connect with the information being taught. Unless these connections are made explicitly, they often remain inert and so do not support subsequent learning.
Knowledge-Centered Classroom Environments
While the learner-centered aspects of the classroom environment focus on the student as the starting point, the knowledge-centered aspects focus on what is taught (subject matter), why it is taught (understanding), how the knowledge should be organized to support the development of exper-
tise (curriculum), and what competence or mastery looks like (learning goals). Several important questions arise when one adopts the knowledge-centered lens:
-
What is it important for students to know and be able to do?
-
What are the core concepts that organize our understanding of this subject matter, and what concrete cases and detailed knowledge will allow students to master those concepts effectively?
-
How will we know when students achieve mastery?18 This question overlaps the knowledge-centered and assessment-centered lenses.
An important point that emerges from the expert–novice literature is the need to emphasize connected knowledge that is organized around the foundational ideas of a discipline. Research on expertise shows that it is the organization of knowledge that underlies experts’ abilities to understand and solve problems.19 Bruner, one of the founding fathers of the new science of learning, has long argued the importance of this insight to education:20
The curriculum of a subject should be determined by the most fundamental understanding that can be achieved of the underlying principles that give structure to a subject. Teaching specific topics or skills without making clear their context in the broader fundamental structure of a field of knowledge is uneconomical…. An understanding of fundamental principles and ideas appears to be the main road to adequate transfer of training. To understand something as a specific instance of a more general case—which is what understanding a more fundamental structure means—is to have learned not only a specific thing but also a model for understanding other things like it that one may encounter.
Knowledge-centered and learner-centered environments intersect when educators take seriously the idea that students must be supported to develop expertise over time; it is not sufficient to simply provide them with expert models and expect them to learn. For example, intentionally organizing subject matter to allow students to follow a path of “progressive differentiation” (e.g., from qualitative understanding to more precise quantitative understanding of a particular phenomenon) involves a simultaneous focus on the structure of the knowledge to be mastered and the learning process of students.21
In a comparative study of the teaching of mathematics in China and the United States, Ma sought to understand why Chinese students outperform students from the United States in elementary mathematics, even though teachers in China often have less formal education. What she documents is
that Chinese teachers are far more likely to identify core mathematical concepts (such as decomposing a number in subtraction with regrouping), to plan instruction to support mastery of the skills and knowledge required for conceptual understanding, and to use those concepts to develop clear connections across topics (see Box 1-6).
If identifying a set of “enduring connected ideas” is critical to effective educational design, it is a task not just for teachers, but also for the developers of curricula, text books, and other instructional materials; universities and other teacher preparation institutions; and the public and private groups involved in developing subject matter standards for students and their teachers. There is some good work already in place, but much more needs to be done. Indeed, an American Association for the Advancement of Science review of middle school and high school science textbooks found that although a great deal of detailed and sophisticated material was presented, very little attention was given to the concepts that support an understanding of the discipline.22
Each of the chapters in this volume describes core ideas in a subject area that support conceptual understanding and that connect the particular topic discussed to the larger discipline: the concepts of historical evidence and perspective in history; the concepts of proportionality and dependence in mathematics; and the concepts of scientific evidence and modeling in science. Because textbooks sometimes focus primarily on facts and details and neglect organizing principles, creating a knowledge-centered classroom will often require that a teacher go beyond the textbook to help students see a structure to the knowledge, mainly by introducing them to essential concepts. These chapters provide examples of how this might be done.
Assessment-Centered Classroom Environments
Formative assessments—ongoing assessments designed to make students’ thinking visible to both teachers and students—are essential. Assessments are a central feature of both a learner-centered and a knowledge-centered classroom. They permit the teacher to grasp students’ preconceptions, which is critical to working with and building on those notions. Once the knowledge to be learned is well defined, assessment is required to monitor student progress (in mastering concepts as well as factual information), to understand where students are in the developmental path from informal to formal thinking, and to design instruction that is responsive to student progress.
An important feature of the assessment-centered classroom is assessment that supports learning by providing students with opportunities to revise and improve their thinking.23 Such assessments help students see their own progress over time and point to problems that need to be addressed in instruction. They may be quite informal. A physics teacher, for
example, reports showing students who are about to study structure a video clip of a bridge collapsing. He asks his students why they think the bridge collapsed. In giving their answers, the students reveal their preconceptions about structure. Differences in their answers provide puzzles that engage the students in self-questioning. As the students study structure, they can mark their changing understanding against their initial beliefs. Assessment in this sense provides a starting point for additional instruction rather than a summative ending. Formative assessments are often referred to as “classroom-based assessments” because, as compared with standardized assessments, they are most likely to occur in the context of the classrooms. However, many classroom-based assessments are summative rather than formative (they are used to provide grades at the end of a unit with no opportunities to revise). In addition, one can use standardized assessments in a formative manner (e.g., to help teachers identify areas where students need special help).
Ultimately, students need to develop metacognitive abilities—the habits of mind necessary to assess their own progress—rather than relying solely on external indicators. A number of studies show that achievement improves when students are encouraged to assess their own contributions and work.24 It is also important to help students assess the kinds of strategies they are using to learn and solve problems. For example, in quantitative courses such as physics, many students simply focus on formulas and fail to think first about the problem to be solved and its relation to key ideas in the discipline (e.g., Newton’s second law). When students are helped to do the latter, their performance on new problems greatly improves.25
The classroom interactions described in the following chapters provide many examples of formative assessment in action, though these interactions are often not referred to as assessments. Early activities or problems given to students are designed to make student thinking public and, therefore, observable by teachers. Work in groups and class discussions provide students with the opportunity to ask each other questions and revise their own thinking. In some cases, the formative assessments are formal; in elementary mathematics, for example, the number knowledge test allows teachers to quickly assess the current mastery level of a student in order to guide the choice of the subsequent instructional activities. But even when informal, the teaching described in those chapters involves frequent opportunities for both teachers and students to assess understanding and its progress over time.
Community-Centered Classroom Environments
A community-centered approach requires the development of norms for the classroom and school, as well as connections to the outside world,
|
BOX 1-6 A study by Ma27 compares the knowledge of elementary mathematics of teachers in the United States and in China. She gives the teachers the following scenario (p. 1): Look at these questions (52–25; 91–79 etc.). How would you approach these problems if you were teaching second grade? What would you say pupils would need to understand or be able to do before they could start learning subtraction with regrouping? The responses of teachers were wide-ranging, reflecting very different levels of understanding of the core mathematical concepts. Some teachers focused on the need for students to learn the procedure for subtraction with regrouping (p. 2): Whereas there is a number like 21–9, they would need to know that you cannot subtract 9 from 1, then in turn you have to borrow a 10 from the tens space, and when you borrow that 1, it equals 10, you cross out the 2 that you had, you turn it into a 10, you now have 11–9, you do that subtraction problem then you have the 1 left and you bring it down. Some teachers in both the United States and China saw the knowledge to be mastered as procedural, though the proportion who held this view was considerably higher in the United States. Many teachers in both countries believed students needed a conceptual understanding, but within this group there were considerable differences. Some teachers wanted children to think through what they were doing, while others wanted them to understand core mathematical concepts. The difference can be seen in the two explanations below. They have to understand what the number 64 means…. I would show that the number 64, and the number 5 tens and 14 ones, equal the 64. I would try to draw the comparison between that because when you are doing regrouping it is not so much knowing the facts, it is the regrouping part that has to be understood. The regrouping right from the beginning. This explanation is more conceptual than the first and helps students think more deeply about the subtraction problem. But it does not make clear to students the more fundamental concept of the place value system that allows the subtraction problems to be connected to other areas of mathematics. In the place value system, numbers are “composed” of tens. Students already have been taught to compose tens as 10 ones, and hundreds as 10 tens. A Chinese teacher explains as follows (p. 11): What is the rate for composing a higher value unit? The answer is simple: 10. Ask students how many ones there are in a 10, or ask them what the rate for composing a higher value unit is, their answers will be the same: 10. However, the effect of the two questions on their learning is not the |
|
same. When you remind students that 1 ten equals 10 ones, you tell them the fact that is used in the procedure. And, this somehow confines them to the fact. When you require them to think about the rate for composing a higher value unit, you lead them to a theory that explains the fact as well as the procedure. Such an understanding is more powerful than a specific fact. It can be applied to more situations. Once they realize that the rate of composing a higher value unit, 10 is the reason why we decompose a ten into 10 ones, they will apply it to other situations. You don’t need to remind them again that 1 hundred equals 10 tens when in the future they learn subtraction with three-digit numbers. They will be able to figure it out on their own. Emphasizing core concepts does not imply less of an emphasis on mastery of procedures or algorithms. Rather, it suggests that procedural knowledge and skills be organized around core concepts. Ma describes those Chinese teachers who emphasize core concepts as seeing the knowledge in “packages” in which the concepts and skills are related. While the packages differed somewhat from teacher to teacher, the knowledge “pieces” to be included were the same. She illustrates a knowledge package for subtraction with regrouping, which is reproduced below (p. 19). The two shaded elements in the knowledge package are considered critical. “Addition and subtraction within 20” is seen as the ability that anchors more complex problem solving with larger numbers. That ability is viewed as both conceptual and procedural. “Composing and decomposing a higher value unit” is the core concept that ties this set of problems to the mathematics students have done in the past and to all other areas of mathematics they will learn in the future. 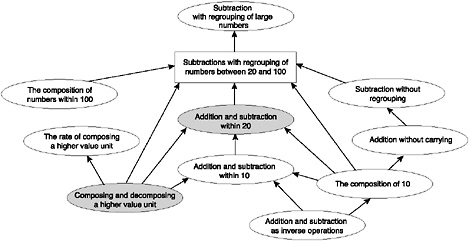 SOURCE: Ma (1999). Illustration reprinted with permission of Lawrence Erlbaum Associates. |
that support core learning values. Learning is influenced in fundamental ways by the context in which it takes place. Every community, including classrooms and schools, operates with a set of norms, a culture—explicit or implicit—that influences interactions among individuals. This culture, in turn, mediates learning. The principles of How People Learn have important implications for classroom culture. Consider the finding that new learning builds on existing conceptions, for example. If classroom norms encourage and reward students only for being “right,” we would expect students to hesitate when asked to reveal their unschooled thinking. And yet revealing preconceptions and changing ideas in the course of instruction is a critical component of effective learning and responsive teaching. A focus on student thinking requires classroom norms that encourage the expression of ideas (tentative and certain, partially and fully formed), as well as risk taking. It requires that mistakes be viewed not as revelations of inadequacy, but as helpful contributions in the search for understanding.28
Similarly, effective approaches to teaching metacognitive strategies rely on initial teacher modeling of the monitoring process, with a gradual shift to students. Through asking questions of other students, skills at monitoring understanding are honed, and through answering the questions of fellow students, understanding of what one has communicated effectively is strengthened. To those ends, classroom norms that encourage questioning and allow students to try the role of the questioner (sometimes reserved for teachers) are important.
While the chapters in this volume make few direct references to learning communities, they are filled with descriptions of interactions revealing classroom cultures that support learning with understanding. In these classrooms, students are encouraged to question; there is much discussion among students who work to solve problems in groups. Teachers ask many probing questions, and incorrect or naïve answers to questions are explored with interest, as are different strategies for analyzing a problem and reaching a solution.
PUTTING THE PRINCIPLES TO WORK IN THE CLASSROOM
Although the key findings from the research literature reviewed above have clear implications for practice, they are not at a level of specificity that would allow them to be immediately useful to teachers. While teachers may fully grasp the importance of working with students’ prior conceptions, they need to know the typical conceptions of students with respect to the topic about to be taught. For example, it may help science teachers to know that students harbor misconceptions that can be problematic, but those teachers will be in a much better position to teach a unit on light if they know
specifically what misconceptions students typically exhibit when learning about light.
Moreover, while teachers may be fully convinced that knowledge should be organized around important concepts, the concepts that help organize their particular topic may not be at all clear. History teachers may know that they are to teach certain eras, for example, but they often have little support in identifying core concepts that will allow students to understand the era more deeply than would be required to reproduce a set of facts. To make this observation is in no way to fault teachers. Indeed, as the group involved in this project engaged in the discussion, drafting, and review of various chapters of this volume, it became clear that the relevant core concepts in specific areas are not always obvious, transparent, or uncontested.
Finally, approaches to supporting metacognition can be quite difficult to carry out in classroom contexts. Some approaches to instruction reduce metacognition to its simplest form, such as making note of the subtitles in a text and what they signal about what is to come, or rereading for meaning. The more challenging tasks of metacognition are difficult to reduce to an instructional recipe: to help students develop the habits of mind to reflect spontaneously on their own thinking and problem solving, to encourage them to activate relevant background knowledge and monitor their understanding, and to support them in trying the lens through which those in a particular discipline view the world. The teacher–student interactions described in the chapters of this volume and the discipline-specific examples of supporting students in monitoring their thinking give texture to the instructional challenge that a list of metacognitive strategies could not.
INTENT AND ORGANIZATION OF THIS VOLUME
In the preface, we note that this volume is intended to take the work of How People Learn a next step in specificity: to provide examples of how its principles and findings might be incorporated in the teaching of a set of topics that frequently appear in the K–12 curriculum. The goal is to provide for teachers what we have argued above is critical to effective learning—the application of concepts (about learning) in enough different, concrete contexts to give them deeper meaning.
To this end, we invited contributions from a variety of researchers with extensive experience in teaching or partnering with teachers, whose work incorporates the ideas highlighted in How People Learn. The chapter authors were given leeway in the extent to which the three learning principles and the four classroom characteristics described above were treated explicitly or implicitly. Most of the authors chose to emphasize the three learning principles explicitly as they described their lessons and findings. The four design characteristics of the How People Learn framework (Figure 1-1) are implicitly
represented in the activities sketched in each of the chapters but often not discussed explicitly. Interested readers can map these discussions to the How People Learn framework if they desire.
The chapters that follow explore the application of core learning principles in three content areas and at three different grade levels. The text is organized into parts by discipline, and each part begins with a chapter that considers the learning principles in the context of the discipline generally. The chapters that follow then explore particular topics. While we began with a common description of our goal, we had no common model from which to work. One can point to excellent research papers on principles of learning, but the chapters in this volume are far more focused on teaching a particular topic. There are also examples of excellent curricula, but the goal of these chapters is to give far more attention to the principles of learning and their incorporation into teaching than is typical of curriculum materials. Thus the authors were charting new territory as they undertook this task, and each found a somewhat different path. As a result, the character of each of the three sections (history, mathematics, and science) differs considerably.
The history part contains three chapters (2 through 4). The first of these treats the principles of learning as they apply to the discipline of history in impressive depth. Elementary and middle school history are treated together at length in Chapter 3, a decision that permits the authors to demonstrate progression in the sophistication with which the same concepts can be discussed at different grade levels. Chapter 4 on high school history also focuses on the treatment of particular concepts that fall under the general topic of exploration and discovery. Because there is no agreed-upon sequence of topics in history during the K–12 years, using a single broad topic allows for a clearer focus on the nature of the investigations in which students might engage at different grade levels.
The mathematics part consists of four chapters. Chapter 5 presents an introduction to the principles as they apply to mathematics generally. The three chapters that follow treat important topics at the three different grade levels: whole number in elementary school (Chapter 6), rational number in middle school (Chapter 7), and functions in high school (Chapter 8). These three topics are routinely covered in K–12 curricula in this sequence and represent the major conceptual shifts required of students in mathematics.
Following the introductory Chapter 9, the science part treats three very different topics: light and shadow at the elementary school level (Chapter 10), gravity at the middle school level (Chapter 11), and genetics and evolution at the high school level (Chapter 12). The sequence of K–12 science topics in the United States is far less predictable than that of mathematics. The topics in this part of the volume were chosen at the three grade levels for the opportunities they provide to explore the learning principles of inter-
est, rather than for their common representation in a standard curricular sequence. Light as a topic might just as well appear in middle or high school as in elementary school, for example, and physics is generally taught either in middle school or high school.
The reader will find that the chapters in this volume differ a great deal from one to the next. In inviting contributions, we drew on the expertise and talents of individuals whose work has differed not only in topic, but in the aspects of learning investigated most deeply. For example, the introductory chapter in the history part (Chapter 2) gives more detailed treatment of the principles as they relate to the discipline of history than do the introductory chapters in the other two disciplines. This treatment reflects the research program undertaken by Peter J. Lee and his colleagues, which has systematically explored student conceptions about history and its core concepts. Annemarie Sullivan Palincsar, one of the authors of the elementary science chapter, has done extensive work on metacognition, and the chapter by Magnusson and Palincsar (Chapter 10) is particularly strong in its emphasis on supporting the development of metacognitive skills in students.
Mathematics chapter authors Sharon Griffin, Joan Moss, and Mindy Kalchman all worked closely with Robbie Case, whose untimely death prevented his intended participation in this volume. Case and his colleagues did extensive research on central conceptual structures in mathematics, making the treatment of core conceptual understandings a strength of these chapters. Chapters authored by teachers (Chapter 4 by Robert B. Bain and Chapter 11 by James Minstrell and Pamela Kraus) are particularly strong in the classroom experience they bring to student–teacher interactions and the familiarity with the challenges of teaching they communicate. And the chapters written by authors who have done extensive work on curriculum development (Chapter 5 by Karen C. Fuson, Mindy Kalchman, and John D. Bransford, Chapter 6 by Sharon Griffin, and Chapter 12 by James Stewart, Jennifer L. Cartier, and Cynthia M. Passmore) exhibit strengths in drawing connections among concepts across a topic area. The work of Rosalyn Ashby, Peter J. Lee, and Denis Shemilt in Chapter 3 looks at the development of the concepts of a discipline (in this case history) over the span of school years in more depth than does any other chapter.
These differences we take to be a varied set of strengths. We did not attempt to impose uniformity across chapters, since we believed that the authors could make their greatest individual contributions by emphasizing their specific areas of expertise. For this reason, we urge readers to cross the disciplines and take lessons from one that might be applied to others.
The major focus of the volume is student learning. It is clear that successful and sustainable changes in educational practice also require learning by others, including teachers, principals, superintendents, parents, and com-
munity members. For the present volume, however, student learning is the focus, and issues of adult learning are left for others to take up.
The willingness of the chapter authors to accept this task represents an outstanding contribution to the field. First, all the authors devoted considerable time to this effort—more than any of them had anticipated initially. Second, they did so knowing that some readers will disagree with virtually every teaching decision discussed in these chapters. But by making their thinking visible and inviting discussion, they are helping the field progress as a whole. The examples discussed in this volume are not offered as “the” way to teach, but as approaches to instruction that in some important respects are designed to incorporate the principles of learning highlighted in How People Learn and that can serve as valuable examples for further discussion.
In 1960, Nobel laureate Richard Feynman, who was well known as an extraordinary teacher, delivered a series of lectures in introductory physics that were recorded and preserved. Feynman’s focus was on the fundamental principles of physics, not the fundamental principles of learning. But his lessons apply nonetheless. He emphasized how little the fundamental principles of physics “as we now understand them” tell us about the complexity of the world despite the enormous importance of the insights they offer. Feynman offered an effective analogy for the relationship between understanding general principles identified through scientific efforts and understanding the far more complex set of behaviors for which those principles provide only a broad set of constraints:29
We can imagine that this complicated array of moving things which constitutes “the world” is something like a great chess game being played by the gods, and we are observers of the game. We do not know what the rules of the game are; all we are allowed to do is to watch the playing. Of course, if we watch long enough, we may eventually catch on to a few of the rules. The rules of the game are what we mean by fundamental physics. Even if we knew every rule, however, we might not be able to understand why a particular move is made in the game, merely because it is too complicated and our minds are limited. If you play chess you must know that it is easy to learn all the rules, and yet it is often very hard to select the best move or to understand why a player moves as he does…. Aside from not knowing all of the rules, what we really can explain in terms of those rules is very limited, because almost all situations are so enormously complicated that we cannot follow the plays of the game using the rules, much less tell what is going to happen next. (p. 24)
The individual chapters in this volume might be viewed as presentations of the strategies taken by individuals (or teams) who understand the rules of the teaching and learning “game” as we now understand them. Feynman’s metaphor is helpful in two respects. First, what each chapter offers goes well
beyond the science of learning and relies on creativity in strategy development. And yet what we know from research thus far is critical in defining the constraints on strategy development. Second, what we expect to learn from a well-played game (in this case, what we expect to learn from well-conceptualized instruction) is not how to reproduce it. Rather, we look for insights about playing/teaching well that can be brought to one’s own game. Even if we could replicate every move, this would be of little help. In an actual game, the best move must be identified in response to another party’s move. In just such a fashion, a teacher’s “game” must respond to the rather unpredictable “moves” of the students in the classroom whose learning is the target.
This, then, is not a “how to” book, but a discussion of strategies that incorporate the rules of the game as we currently understand them. The science of learning is a young, emerging one. We expect our understanding to evolve as we design new learning opportunities and observe the outcomes, as we study learning among children in different contexts and from different backgrounds, and as emerging research techniques and opportunities provide new insights. These chapters, then, might best be viewed as part of a conversation begun some years ago with the first How People Learn volume. By clarifying ideas through a set of rich examples, we hope to encourage the continuation of a productive dialogue well into the future.
NOTES
|
1. |
National Research Council, 2000. |
|
2. |
Lionni, 1970. |
|
3. |
National Research Council, 2000, p. 84. |
|
4. |
Needham and Baillargeon, 1993. |
|
5. |
diSessa, 1982. |
|
6. |
Vosniadou and Brewer, 1989. |
|
7. |
Carey and Gelman, 1991; Driver et al., 1994. |
|
8. |
Hanson, 1970. |
|
9. |
Judd, 1908; see a conceptual replication by Hendrickson and Schroeder, 1941. |
|
10. |
White and Fredrickson, 1998. |
|
11. |
Bransford and Schwartz, 1999. |
|
12. |
Brown, 1975; Flavell, 1973. |
|
13. |
Keeney et al., 1967. |
|
14. |
Palincsar and Brown, 1984. |
|
15. |
Aleven and Koedinger, 2002. |
|
16. |
Thorndike, 1913. |
|
17. |
Brown et al., 1983. |
|
18. |
Wood and Sellers, 1997. |
|
19. |
National Research Council, 2000, Chapter 2. |
|
20. |
Bruner, 1960, pp. 6, 25, 31. |
|
21. |
National Research Council, 2000. |
|
22. |
American Association for the Advancement of Science Project 2061 Website. http://www.project2061.org/curriculum.html. |
|
23. |
Barron et al., 1998; Black and William, 1989; Hunt and Minstrell, 1994; Vye et al., 1998. |
|
24. |
Lin and Lehman, 1999; National Research Council, 2000; White and Fredrickson, 1998. |
|
25. |
Leonard et al., 1996. |
|
26. |
National Research Council, 2003, pp. 78-79. |
|
27. |
Ma, 1999. |
|
28. |
Brown and Campione, 1994; Cobb et al., 1992. |
|
29. |
Feynman, 1995, p. 24. |
REFERENCES
Aleven, V., and Koedinger, K. (2002). An effective metacognitive strategy—Learning by doing and explaining with a computer-based cognitive tutor. Cognitive Science, 26, 147-179.
American Association for the Advancement of Science. (2004). About Project 2061. Available: http://www.project2061.org/about/default/htm. [August 11, 2004].
Barron, B.J., Schwartz, D.L., Vye, N.J., Moore, A., Petrosino, A., Zech, L., Bransford, J.D., and Cognition and Technology Group at Vanderbilt. (1998). Doing with understanding: Lessons from research on problem and project-based learning. Journal of Learning Sciences, 7(3 and 4), 271-312.
Black, P., and William, D. (1989). Assessment and classroom learning. Special Issue of Assessment in Education: Principles, Policy and Practice, 5(1), 7-75.
Bransford, J.D., and Schwartz, D.L. (1999). Rethinking transfer: A simple proposal with multiple implications. Review of Research in Education, 24(40), 61-100.
Brown, A.L. (1975). The development of memory: Knowing about knowing and knowing how to know. In H.W. Reese (Ed.), Advances in child development and behavior (p. 10). New York: Academic Press.
Brown, A.L., and Campione, J.C. (1994). Guided discovery in a community of learners. In K. McGilly (Ed.), Classroom lessons: Integrating cognitive theory and classroom practices. Cambridge, MA: MIT Press.
Brown, A.L., Bransford, J.D., Ferrara, R.A., and Campione J.C. (1983). Learning, remembering, and understanding. In J.H. Flavell and E.M Markman (Eds.), Handbook of child psychology: Cognitive development volume 3 (pp. 78-166). New York: Wiley.
Bruner, J. (1960). The process of education. Cambridge, MA: Harvard University Press.
Carey, S., and Gelman, R. (1991). The epigenesis of mind: Essays on biology and cognition. Mahwah, NJ: Lawrence Erlbaum Associates.
Chase, W.G., and Simon, H.A. (1973). Perception in chess. Cognitive Psychology, 4(1), 55-81.
Cobb P., Yackel, E., and Wood, T. (1992). A constructivist alternative to the representational view of mind in mathematics education. Journal for Research in Mathematics Education, 19, 99-114.
Cognition and Technology Group at Vanderbilt. (1996). Looking at technology in context: A framework for understanding technology and education research. In D.C. Berliner and R.C. Calfee (Eds.), The handbook of educational psychology (pp. 807-840). New York: Simon and Schuster-MacMillan.
diSessa, A. (1982). Unlearning Aristotelian physics: A study of knowledge-based learning. Cognitive Science, 6(2), 37-75.
Driver, R., Squires, A., Rushworth, P., and Wood-Robinson, V. (1994). Making sense out of secondary science. London, England: Routledge Press.
Feynman, R.P. (1995). Six easy pieces: Essentials of physics explained by its most brilliant teacher. Reading, MA: Perseus Books.
Flavell, J.H. (1973). Metacognitive aspects of problem-solving. In L.B. Resnick (Ed.), The nature of intelligence. Mahwah, NJ: Lawrence Erlbaum Associates.
Hanson, N.R. (1970). A picture theory of theory meaning. In R.G. Colodny (Ed.), The nature and function of scientific theories (pp. 233-274). Pittsburgh, PA: University of Pittsburgh Press.
Hendrickson, G., and Schroeder, W.H. (1941). Transfer training in learning to hit a submerged target. Journal of Educational Psychology, 32, 205-213.
Hunt, E., and Minstrell, J. (1994). A cognitive approach to the teaching of physics. In K. McGilly (Ed.), Classroom lessons: Integrating cognitive theory and classroom practice (pp. 51-74). Cambridge, MA: MIT Press.
Judd, C.H. (1908). The relation of special training to general intelligence. Educational Review, 36, 28-42.
Keeney, T.J., Cannizzo, S.R., and Flavell, J.H. (1967). Spontaneous and induced verbal rehearsal in a recall task. Child Development, 38, 953-966.
Leonard, W.J., Dufresne, R.J., and Mestre, J.P. (1996). Using qualitative problem solving strategies to highlight the role of conceptual knowledge in solving problems. American Journal of Physics, 64, 1495-1503.
Lin, X.D., and Lehman, J. (1999). Supporting learning of variable control in a computer-based biology environment: Effects of prompting college students to reflect on their own thinking. Journal of Research in Science Teaching, 36(7), 837-858.
Lionni, L. (1970). Fish is fish. New York: Scholastic Press.
Ma, L. (1999). Knowing and teaching elementary mathematics. Mahwah, NJ: Lawrence Erlbaum Associates.
National Research Council. (1999). How people learn: Brain, mind, experience, and school. Committee on Developments in the Science of Learning. J. D. Bransford, A.L. Brown, and R.R. Cocking (Eds.). Commission on Behavioral and Social Sciences and Education. Washington, DC: National Academy Press.
National Research Council. (2000). How people learn: Brain, mind, experience, and school, Expanded edition. Committee on Developments in the Science of Learning and Committee on Learning Research and Educational Practice. J.D. Bransford, A. Brown, and R.R. Cocking (Eds.). Commission on Behavioral and Social Sciences and Education. Washington, DC: National Academy Press.
National Research Council. (2003). Learning and instruction: A SERP research agenda. Panel on Learning and Instruction, Strategic Education Research Partnership. M.S. Donovan and J.W. Pellegrino (Eds.). Division of Behavioral and Social Sciences and Education. Washington, DC: The National Academies Press.
Needham, A., and Baillargeon, R. (1993). Intuitions about support in 4 1/2 month-old-infants. Cognition, 47(2), 121-148.
Palincsar, A.S., and Brown, A.L. (1984). Reciprocal teaching of comprehension monitoring activities. Cognition and Instruction, 1, 117-175.
Thorndike, E.L. (1913). Educational psychology (Vols. 1 and 2). New York: Columbia University Press.
Vosniadou, S., and Brewer, W.F. (1989). The concept of the Earth’s shape: A study of conceptual change in childhood. Unpublished manuscript. Champaign, IL: Center for the Study of Reading, University of Illinois.
Vye, N.J., Schwartz, D.L., Bransford, J.D., Barron, B.J., Zech, L., and Cognitive and Technology Group at Vanderbilt. (1998). SMART environments that support monitoring, reflection, and revision. In D. Hacker, J. Dunlosky, and A. Graessner (Eds.), Metacognition in educational theory and practice. Mahwah, NJ: Lawrence Erlbaum Associates.
Whimbey, A., and Whimbey, L.S. (1975). Intelligence can be taught. New York: Dutton.
White, B.Y., and Fredrickson, J.R. (1998). Inquiry, modeling, and metacognition: Making science accessible to all students. Cognition and Instruction, 16(1), 3-118.
Wood, T., and Sellers, P. (1997). Deepening the analysis: Longitudinal assessment of a problem-centered mathematics program. Journal for Research in Mathematics Education, 28, 163-186.


