6
Fostering the Development of Whole-Number Sense: Teaching Mathematics in the Primary Grades
Sharon Griffin
After 15 years of inquiry into children’s understanding and learning of whole numbers, I can sum up what I have learned very simply. To teach math, you need to know three things. You need to know where you are now (in terms of the knowledge children in your classroom have available to build upon). You need to know where you want to go (in terms of the knowledge you want all children in your classroom to acquire during the school year). Finally, you need to know what is the best way to get there (in terms of the learning opportunities you will provide to enable all children in your class to achieve your stated objectives). Although this sounds simple, each of these points is just the tip of a large iceberg. Each raises a question (e.g., Where are we now?) that I have come to believe is crucial for the design of effective mathematics instruction. Each also points to a body of knowledge (the iceberg) to which teachers must have access in order to answer that question. In this chapter, I explore each of these icebergs in turn in the context of helping children in the primary grades learn more about whole numbers.
Readers will recognize that the three things I believe teachers need to know to teach mathematics effectively are similar in many respects to the knowledge teachers need to implement the three How People Learn principles (see Chapter 1) in their classrooms. This overlap should not be surprising. Because teaching and learning are two sides of the same coin and
because effective teaching is defined primarily in terms of the learning it supports, we cannot talk about one without talking about the other. Thus when I address each of the three questions raised above, I will at the same time offer preschool and elementary mathematics teachers a set of resources they can use to implement the three principles of How People Learn in their classrooms and, in so doing, create classrooms that are student-centered, knowledge-centered, community-centered, and assessment-centered.
Addressing the three principles of How People Learn while exploring each question occurs quite naturally because the bodies of knowledge that underlie effective mathematics teaching provide a rich set of resources that teachers can use to implement these principles in their classrooms. Thus, when I explore question 1 (Where are we now?) and describe the number knowledge children typically have available to build upon at several specific age levels, I provide a tool (the Number Knowledge test) and a set of examples of age-level thinking that teachers can use to enact Principle 1—eliciting, building upon, and connecting student knowledge—in their classrooms. When I explore question 2 (Where do I want to go?) and describe the knowledge networks that appear to be central to children’s mathematics learning and achievement and the ways these networks are built in the normal course of development, I provide a framework that teachers can use to enact Principle 2—building learning paths and networks of knowledge—in their classrooms. Finally, when I explore question 3 (What is the best way to get there?) and describe elements of a mathematics program that has been effective in helping children acquire whole-number sense, I provide a set of learning tools, design principles, and examples of classroom practice that teachers can use to enact Principle 3—building resourceful, self-regulating mathematical thinkers and problem solvers—in their classrooms. Because the questions I have raised are interrelated, as are the principles themselves, teaching practices that may be effective in answering each question and in promoting each principle are not limited to specific sections of this chapter, but are noted throughout.
I have chosen to highlight the questions themselves in my introduction to this chapter because it was this set of questions that motivated my inquiry into children’s knowledge and learning in the first place. By asking this set of questions every time I sat down to design a math lesson for young children, I was able to push my thinking further and, over time, construct better answers and better lessons. If each math teacher asks this set of questions on a regular basis, each will be able to construct his or her own set of answers for the questions, enrich our knowledge base, and improve mathematics teaching and learning for at least one group of children. By doing so, each teacher will also embody the essence of what it means to be a resourceful, self-regulating mathematics teacher. The questions themselves are thus more important than the answers. But the reverse is also true:
although good questions can generate good answers, rich answers can also generate new and better questions.
I now turn to the answers I have found useful in my own work with young children. By addressing question 2 (Where do I want to go?) first, I hope to give readers a sense of the general direction in which we are heading before I turn to question 1 (Where are we now?) and provide a detailed description of the knowledge children generally have available to build upon at each age level between 4 and 8. While individual children differ a great deal in the rate at which they acquire number knowledge, teachers are charged with teaching a class of students grouped by age. It is therefore helpful in planning instruction to focus on the knowledge typical among children of a particular age, with the understanding that there will be considerable variation. In a subsequent section, I use what we have learned about children’s typical age-level understandings to return to the issue of the knowledge to be taught and to provide a more specific answer for question 2.
DECIDING WHAT KNOWLEDGE TO TEACH
All teachers are faced with a dizzying array of mathematics concepts and skills they are expected to teach to groups of students who come to their classrooms with differing levels of preparedness for learning. This is true even at the preschool level. For each grade level, the knowledge to be taught is prescribed in several documents—the national standards of the National Council of Teachers of Mathematics (NCTM), state and district frameworks, curriculum guides—that are not always or even often consistent. Deciding what knowledge to teach to a class as a whole or to any individual child in the class is no easy matter.
Many primary school teachers resolve this dilemma by selecting number sense as the one set of understandings they want all students in their classrooms to acquire. This makes sense in many respects. In the NCTM standards, number sense is the major learning objective in the standard (numbers and operations) to which primary school teachers are expected to devote the greatest amount of attention. Teachers also recognize that children’s ability to handle problems in other areas (e.g., algebra, geometry, measurement, and statistics) and to master the objectives listed for these standards is highly dependent on number sense. Moreover, number sense is given a privileged position on the report cards used in many schools, and teachers are regularly required to evaluate the extent to which their students “demonstrate number sense.” In one major respect, however, the choice of number sense as an instructional objective is problematic. Although most teachers and lay people alike can easily recognize number sense when they see it, defining what it is and how it can be taught is much more difficult.
Consider the responses two kindergarten children provide when asked the following question from the Number Knowledge test (described in full later in this chapter): “If you had four chocolates and someone gave you three more, how many would you have altogether?”
Alex responds by scrunching up his brow momentarily and saying, “seven.” When asked how he figured it out, he says, “Well, ‘four’ and ‘four’ is ‘eight’ [displaying four fingers on one hand and four on the other hand to demonstrate]. But we only need three more [taking away one finger from one hand to demonstrate]. So I went—‘seven,’ ‘eight.’ Seven is one less than eight. So the answer is seven.”
Sean responds by putting up four fingers on one hand and saying (under his breath), “Four. Then three more—‘five, six, seven.’” In a normal tone of voice, Sean says “seven.” When asked how he figured it out, Sean is able to articulate his strategy, saying, “I started at four and counted—‘five, six, seven’” (tapping the table three times as he counts up, to indicate the quantity added to the initial set).
It will be obvious to all kindergarten teachers that the responses of both children provide evidence of good number sense. The knowledge that lies behind that sense may be much less apparent, however. What knowledge do these children have that enables them to come up with the answer in the first place and to demonstrate number sense in the process? Scholars have studied children’s mathematical thinking and problem solving, tracing the typical progression of understanding or developmental pathway for acquiring number knowledge.1 This research suggests that the following understandings lie at the heart of the number sense that 5-year-olds such as Alex and Sean are able to demonstrate on this problem: (1) they know the counting sequence from “one” to “ten” and the position of each number word in the sequence (e.g., that “five” comes after “four” and “seven” comes before “eight”); (2) they know that “four” refers to a set of a particular size (e.g., it has one fewer than a set of five and one more than a set of 3), and thus there is no need to count up from “one” to get a sense of the size of this set; (3) they know that the word “more” in the problem means that the set of four chocolates will be increased by the precise amount (three chocolates) given in the problem; (4) they know that each counting number up in the counting sequence corresponds precisely to an increase of one unit in the size of a set; and (5) it therefore makes sense to count on from “four” and to say the next three numbers up in the sequence to figure out the answer (or, in Alex’s case, to retrieve the sum of four plus four from memory, arrive at “eight,” and move one number back in the sequence). This complex knowl-
edge network—called a central conceptual structure for whole number—is described in greater detail in a subsequent section.
The knowledge that Alex and Sean demonstrate is not limited to the understandings enumerated above. It includes computational fluency (e.g., ease and proficiency in counting) and awareness of the language of quantity (e.g., that “altogether” indicates the joining of two sets), which were acquired earlier and provided a base on which the children’s current knowledge was constructed. Sean and Alex also demonstrate impressive metacognitive skills (e.g., an ability to reflect on their own reasoning and to communicate it clearly in words) that not only provide evidence of number sense, but also contributed to its development.
Finally, children who demonstrate this set of competencies also show an ability to answer questions about the joining of two sets when the contexts vary considerably, as in the following problems: “If you take four steps and then you take three more, how far have you gone?” and “If you wait four hours and then you wait three more, how long have you waited?” In both of these problems, the quantities are represented in very different ways (as steps along a path, as positions on a dial), and the language used to describe the sum (“How far?” “How long?”) differs from that used to describe the sum of two groups of objects (“How many?”). The ability to apply number knowledge in a flexible fashion is another hallmark of number sense.
Each of the components of number sense mentioned thus far is described in greater detail in a subsequent section of this chapter. For now it is sufficient to point out that the network of knowledge the components represent—the central conceptual structure for whole number—has been found to be central to children’s mathematics learning and achievement in at least two ways. First, as mentioned above, it enables children to make sense of a broad range of quantitative problems in a variety of contexts (see Box 6-1 for a discussion of research that supports this claim). Second, it provides the base—the building block—on which children’s learning of more complex number concepts, such as those involving double-digit numbers, is built (see Box 6-2 for research support for this claim). Consequently, this network of knowledge is an important set of understandings that should be taught. In choosing number sense as a major learning goal, teachers demonstrate an intuitive understanding of the essential role of this knowledge network and the importance of teaching a core set of ideas that lie at the heart of learning and competency in the discipline (learning principle 2). Having a more explicit understanding of the factual, procedural, and conceptual understandings that are implicated and intertwined in this network will help teachers realize this goal for more children in their classrooms.
Once children have consolidated the set of understandings just described for the oral counting sequence from “one” to “ten,” they are ready to make sense of written numbers (i.e., numerals). Now, when they are exposed to
|
BOX 6-1 A central conceptual structure is a powerful organizing knowledge network that is extremely broad in its range of application and that plays a central role in enabling individuals to master the problems that the domain presents. The word “central” implies (1) that the structure is vital to successful performance on a range of tasks, ones that often transcend individual disciplinary boundaries; and (2) that future learning in these tasks is dependent on the structure, which often forms the initial core around which all subsequent learning is organized. To test the first of these claims, Griffin and Case selected two groups of kindergarten children who were at an age when children typically have acquired the central conceptual structure for whole number, but had not yet done so.2 All the children were attending schools in low-income, inner-city communities. In the first part of the kindergarten year, all the children were given a battery of developmental tests to assess their central conceptual understanding of whole number (Number Knowledge test) and their ability to solve problems in a range of other areas that incorporate number knowledge, including scientific reasoning (Balance Beam test), social reasoning (Birthday Party task), moral reasoning (Distributive Justice task), time telling (Time test), and money knowledge (Money test). On this test administration, no child in either group passed the Number Knowledge test, and fewer than 20 percent of the children passed any of the remaining tests. One group of children (the treatment group) was exposed to a mathematics program called Number Worlds that had been specifically designed to teach the central conceptual structure for whole number. The second group of children (a matched control group) received a variety of other forms of mathematics instruction for the same time period (about 10 weeks). The performance of these two groups on the second administra- |
the symbols that correspond to each number name and given opportunities to connect name to symbol, they will bring all the knowledge of what that name means with them, and it will accrue to the symbol. They will thus be able to read and write number symbols with meaning. To build a learning path that matches children’s observed progression of understanding, this would be a reasonable next step for teachers to take. Finally, with experience in using this knowledge network, children eventually become capable
|
tion of the same tests at the end of the kindergarten year is presented in the following table. The treatment group—those exposed to the Number Worlds curriculum—improved substantially in all test areas, far surpassing the performance of the control group. Because no child in the treatment group had received any training in any of the areas tested in this battery besides number knowledge, the strong post-training performance of the treatment group on these tasks can be attributed to the construction of the central conceptual structure for whole number, as demonstrated in the children’s (post-training) performance on the Number Knowledge test. Other factors that might have accounted for these findings, such as more individual attention and/or instructional time given to the treatment group, were carefully controlled in this study. Percentages of Children Passing the Second Administration of the Number Knowledge Test and Five Numerical Transfer Tests
|
||||||||||||||||||||||||
of applying their central conceptual understandings to two distinct quantitative variables (e.g., tens and ones, hours and minutes, dollars and cents) and of handling two quantitative variables in a coordinated fashion. This ability permits them to solve problems involving double-digit numbers and place value, for example, and introducing these concepts at this point in time (sometime around grade 2) would be a reasonable next step for teachers to
|
BOX 6-2 To test the second centrality claim—that future learning is dependent on the acquisition of the central conceptual structure for whole number—Griffin and Case conducted a follow-up study using the same sample of children as that in Box 6-1.3 Children in both the treatment and control groups had graduated to a variety of first-grade classrooms in a number of different schools. Those who had remained in the general geographic area were located 1 year later and given a range of assessments to obtain measures of their mathematics learning and achievement in grade 1. Their teachers, who were blind to the children’s status in the study, were also asked to rate each child in their classroom on a number of variables. The results, displayed in the following table, present an interesting portrait of the importance of the central conceptual structure (assessed by performance at the 6-year-old level of the Number Knowledge test) for children’s learning and achievement in grade 1. Recall that 87 percent of the treatment group had passed this level of the number knowledge test at the end of kindergarten compared with 25 percent of the control group. As the table indicates, most of the children in the control group (83 percent) had acquired this knowledge by the end of grade 1, but it appears to have been too late to enable many of them to master the grade 1 arithmetic tasks that require conceptual understanding (e.g., the Oral Arithmetic test; the Word Problems; test and teacher ratings of number sense, number meanings, and number use). On all of these measures, children who had acquired the central conceptual structure before the start of the school year did significantly better. On the more traditional measures of mathematics achievement (e.g., the Written Arithmetic test and teacher ratings of addition and subtraction) that rely more on procedural knowledge than conceptual understanding, the performance of children in the control group was stronger. It was still inferior, however, in absolute terms to the performance of children in the treatment group. Possibly the most interesting finding of all is the difference between the two groups on tests that tap knowledge not typically taught until grade 2 (e.g., the 8-year-old level of the Number Knowledge test and the 8-year-old level of the Word Problems test). On both of these tests, a number of children in the treatment group demonstrated that they had built upon their central conceptual structure for whole number during their first-grade experience and were beginning to construct the more elaborate understandings required to mentally solve double-digit arithmetic problems. Few children in the control group demonstrated this level of learning. |
|
Percentages of Children Passing the Number Knowledge Test and Measures of Arithmetic Learning and Achievement at the End of Grade 1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
take in building learning paths that are finely attuned to children’s observed development of number knowledge.
In this brief example, several developmental principles that should be considered in building learning paths and networks of knowledge (learning principle 2) for the domain of whole numbers have come to light. They can be summarized as follows:
-
Build upon children’s current knowledge. This developmental principle is so important that it was selected as the basis for one of the three primary learning principles (principle 1) of How People Learn.
-
Follow the natural developmental progression when selecting new knowledge to be taught. By selecting learning objectives that are a natural next step for children (as documented in cognitive developmental research and described in subsequent sections of this chapter), the teacher will be creating a learning path that is developmentally appropriate for children, one that fits the progression of understanding as identified by researchers. This in turn will make it easier for children to construct the knowledge network that is expected for their age level and, subsequently, to construct the higher-level knowledge networks that are typically built upon this base.
-
Make sure children consolidate one level of understanding before moving on to the next. For example, give them many opportunities to solve oral problems with real quantities before expecting them to use formal symbols.
-
Give children many opportunities to use number concepts in a broad range of contexts and to learn the language that is used in these contexts to describe quantity.
I turn now to question 1 and, in describing the knowledge children typically have available at several successive age levels, paint a portrait of the knowledge construction process uncovered by research—the step-by-step manner in which children construct knowledge of whole numbers between the ages of 4 and 8 and the ways individual children navigate this process as a result of their individual talent and experience. Although this is the subject matter of cognitive developmental psychology, it is highly relevant to teachers of young children who want to implement the developmental principles just described in their classrooms. Because young children do not reflect on their own thinking very often or very readily and because they are not skilled in explaining their reasoning, it is difficult for a teacher of young children to obtain a picture of the knowledge and thought processes each child has available to build upon. The results of cognitive developmental research and the tools that researchers use to elicit children’s understandings can thus supplement teachers’ own knowledge and expertise in important ways, and help teachers create learner-centered classrooms that build effectively on students’ current knowledge. Likewise, hav-
ing a rich picture of the step-by step manner in which children typically construct knowledge of whole numbers can help teachers create knowledge-centered classrooms and learning pathways that fit children’s spontaneous development.
BUILDING ON CHILDREN’S CURRENT UNDERSTANDINGS
What number knowledge do children have when they start preschool around the age of 4? As every preschool teacher knows, the answer varies widely from one child to the next. Although this variation does not disappear as children progress through the primary grades, teachers are still responsible for teaching a whole classroom of children, as well as every child within it, and for setting learning objectives for their grade level. It can be a great help to teachers, therefore, to have some idea of the range of understandings they can expect for children at their grade level and, equally important, to be aware of the mistakes, misunderstandings, and partial understandings that are also typical for children at this age level.
To obtain a portrait of these age-level understandings, we can consider the knowledge children typically demonstrate at each age level between ages 4 and 8 when asked the series of oral questions provided on the Number Knowledge test (see Box 6-3). The test is included here for discussion purposes, but teachers who wish to use it to determine their student’s current level of understanding can do so.
Before we start, a few features of the Number Knowledge test deserve mention. First, because this instrument has been called a test in the developmental research literature, the name has been preserved in this chapter. However, this instrument differs from school tests in many ways. It is administered individually, and the questions are presented orally. Although right and wrong answers are noted, children’s reasoning is equally important, and prompts to elicit this reasoning (e.g., How do you know? How did you figure that out?) are always provided on a subset of items on the test, especially when children’s thinking and/or strategy use is not obvious when they are solving the problems posed. For these reasons, the “test” is better thought of as a tool or as a set of questions teachers can use to elicit children’s conceptions about number and quantity and to gain a better understanding of the strategies children have available to solve number problems. When used at the beginning (and end) of the school year, it provides a good picture of children’s entering (and exit) knowledge. It also provides a model for the ongoing, formative assessments that are conducted throughout the school year in assessment-centered classrooms.
Second, as shown in Box 6-3, the test is divided into three levels, with a preliminary (warm-up) question. The numbers associated with each level
|
BOX 6-3 Preliminary Let’s see if you can count from 1 to 10. Go ahead. Level 0 (4-year-old level): Go to Level 1 if 3 or more correct. 1. Can you count these chips and tell me how many there are? (Place 3 counting chips in front of child in a row.) 2a. (Show stacks of chips, 5 vs. 2, same color.) Which pile has more? 2b. (Show stacks of chips, 3 vs. 7, same color.) Which pile has more? 3a. This time I’m going to ask you which pile has less. (Show stacks of chips, 2 vs. 6, same color.) Which pile has less? 3b. (Show stacks of chips, 8 vs. 3, same color.) Which pile has less? 4. I’m going to show you some counting chips (Show a line of 3 red and 4 yellow chips in a row, as follows: R Y R Y R Y Y). Count just the yellow chips and tell me how many there are. 5. (Pick up all chips from the previous question.) Here are some more counting chips (show mixed array [not in a row] of 7 yellow and 8 red chips.) Count just the red chips and tell me how many there are. Level 1 (6-year-old level): Go to Level 2 if 5 or more correct. 1. If you had 4 chocolates and someone gave you 3 more, how many chocolates would you have altogether? 2. What number comes right after 7? 3. What number comes two numbers after 7? 4a. Which is bigger: 5 or 4? 4b. Which is bigger: 7 or 9? 5a. This time, I’m going to ask you about smaller numbers. Which is smaller: 8 or 6? 5b. Which is smaller: 5 or 7? 6a. Which number is closer to 5:6 or 2? (Show visual array after asking the question.) |
|
6b. Which number is closer to 7:4 or 9? (Show visual array after asking the question.) 7. How much is 2 + 4? (OK to use fingers for counting.) 8. How much is 8 take away 6? (OK to use fingers for counting.) 9a. (Show visual array 8 5 2 6. Ask child to point to and name each numeral.) When you are counting, which of these numbers do you say first? 9b. When you are counting, which of these numbers do you say last? Level 2 (8-year-old level): Go to Level 3 if 5 or more correct. 1. What number comes 5 numbers after 49? 2. What number comes 4 numbers before 60? 3a. Which is bigger: 69 or 71? 3b. Which is bigger: 32 or 28? 4a. This time I’m going to ask you about smaller numbers. Which is smaller: 27 or 32? 4b. Which is smaller: 51 or 39? 5a. Which number is closer to 21:25 or 18? (Show visual array after asking the question.) 5b. Which number is closer to 28:31 or 24? (Show visual array after asking the question.) 6. How many numbers are there in between 2 and 6? (Accept either 3 or 4.) 7. How many numbers are there in between 7 and 9? (Accept either 1 or 2.) 8. (Show visual array 12 54.) How much is 12 + 54? 9. (Show visual array 47 21.) How much is 47 take away 21? |
(0, 1, 2) are drawn from the cognitive developmental tradition and are meant to suggest that the knowledge demonstrated at Level 0 is foundational for the knowledge demonstrated at Level 1, which represents a new, higher-order knowledge structure and a major reorganization of children’s thought. The knowledge demonstrated at Level 2 represents an even more sophisticated version of this knowledge structure. The ages associated with each level of the test represent the midpoint in the 2-year age period during which this knowledge is typically constructed and demonstrated. Thus, the 4-year-old level captures children’s thinking between the ages of 3 and 5 years, and the 6-year-old level captures children’s thinking between the ages of 5 and 7 years. Finally, the age norms given in the test are the age ranges within which children in developed societies (drawn primarily from middle-income homes) typically pass that level of the test. But even when the norm is accurate for a group of children, it is important to remember that the knowledge possessed by individual children can differ by as much as 2 years (e.g., from knowledge typical of a 3- and a 5-year-old among the group at age 4). The test thus provides a set of broad developmental milestones for the majority of U.S. children, although the extent to which these levels hold true for children from vastly different sociocultural groups remains to be determined. (Directions for administering and scoring the test are provided in Box 6-4.)
Understandings of 4-Year-Olds
By the age of 4 to 5, most children can accurately count a set of three chips that are placed in front of them (Level 0, #1) and tell how many there are. They typically do so by touching the chips in a systematic fashion, usually proceeding from left to right; by saying “one,” “two,” “three” as they do so; and by giving the last number said, “three,” as the answer. Fewer children (but still the majority) can also solve the more challenging counting problems at this level. They can count a set of four yellow chips that are intermixed with three red chips in a row (Level 0, #4) by counting just the yellow chips in the row or by physically moving the yellow chips into a separate space to make counting easier, and tell you how many there are. They can also count a set of eight red chips that are intermixed with seven white chips in a randomly distributed array (Level 0, #5), using one of the strategies just mentioned. Children who are successful with these items have learned to isolate the partial set to be counted, either mentally or physically, and to count items in this set in a systematic fashion, making sure that they know which chip they counted first and that they touch each chip only once when counting.
Children who are unsuccessful often fail to count systematically. They say the counting words and touch the chips, but these strategies are not
|
BOX 6-4 Administration: The Number Knowledge test is an oral test. It is administered individually, and it requires an oral response. Paper and pencil are not permitted. Use of a follow-up question—“How did you figure that out?”—for Questions 1, 3, and 7 at Level 1 and Questions 1, 2, and 8 at Level 2 provides additional insight into children’s reasoning and strategy use. Scoring: One point is assigned for each item passed at Levels 0, 1, and 2. For all two-part items, both (a) and (b) must be passed to earn a point. Props Needed: For Level 0:12 red and 8 yellow counting chips, at least 1/8” thick (other contrasting colors can be substituted). For Levels 1 and 2: visual displays (see samples below). Each image should be at least twice the size of the samples shown here. 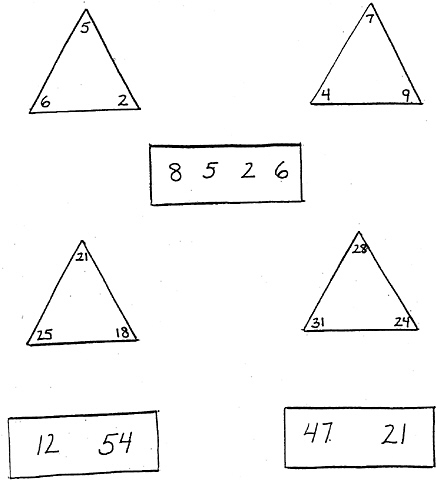 |
aligned, so they say more words than chips touched or skip some chips while counting, or (particularly on item #5) forget which chip they started with and count one or more chips twice. Children who make these errors are demonstrating some knowledge of counting. They are typically able to say the string of counting words in the correct sequence, and they know what must be done to figure out the answer to the question (e.g., touch the objects present while saying the words). What they do not yet understand is that the chips must be touched in a certain order and manner to coincide precisely with their recitation of the counting words. An even less sophisticated response is given by children who have not yet learned to say the counting words in the correct sequence and who may count the four red chips in item #4 by saying, “one,” “two,” “five,” seven.”
By the age of 4, most children can also compare two stacks of chips that differ in height in obvious, perceptually salient ways (Level 0, #2 and #3) and tell which pile has more or less. Children who can do this can solve the same problem when the question is phrased “Which pile is bigger (or smaller)?” and can solve similar problems involving comparisons of length (when the chips are aligned along a table) and of weight (when the chips are placed on a balance scale), provided the differences between the sets are visually obvious. Children who fail these items often look genuinely puzzled by the question, and either sit quietly waiting for further instruction or start to play with the chips by taking the stacks apart and moving the chips about. It appears that the words “more–less” (or “bigger–smaller,” “longer–shorter,” “heavier–lighter”) and the comparison process that underlies them have no meaning for these children, and they are uncertain how to respond.
Although most children of this age can handle these quantity comparisons easily, they fail to achieve more than a chance rate of success when the differences between the sets are not visually obvious, and counting is required to determine which set has more or less. Although 4-year-olds have acquired some fairly sophisticated counting skills (as suggested above), they tend not to use counting to make quantity judgments, instead relying almost exclusively on visual cues in answering this sort of question.
If 4-year-olds can do these things, what might that suggest about what they know? Using this test and other performance assessments, researchers have constructed hypotheses about children’s knowledge, which can be summarized as follows. By the age of 4, most children have constructed an initial counting schema (i.e., a well-organized knowledge network) that enables them to count verbally from one to five, use the one-to-one correspondence rule, and use the cardinality rule.4 By the same age, most have also constructed an initial quantity schema that gives them an intuitive understanding of relative amount (they can compare two groups of objects that differ in size and tell which has a lot or a little) and of the transformations
that change this amount (they know that one group will get bigger or smaller if objects are added to it or taken away). Most preschoolers can also use words to talk about these quantity relations and transformations.5 As suggested earlier, however, most preschoolers do not use these schemas in a coordinated or integrated fashion.6 It is as if they were stored in separate files in children’s minds.
Understandings of 5-Year-Olds
A major change takes place for children when they can begin to solve problems involving small (single-digit) numbers and quantities without having real objects available to count. For the typical child this happens some time during the kindergarten year, between ages 5 and 6. With this change, children behave as if they are using a “mental counting line” inside their heads and/or their fingers to keep track of how many items they have counted. When asked how many chocolates they would have if they had four and someone gave them three more (Level 1, #1), the majority of children aged 5 to 6 can figure out the answer. The most advanced children will say that they just knew the answer was seven because four and three makes seven. More typically, children in this age range will use their fingers and one of three counting strategies to solve the problem. They may use the count-on strategy (the most sophisticated counting strategy) by starting their count at “four,” often holding up four fingers to represent the first set, and then counting on “five,” “six,” “seven,” often putting up three additional fingers to represent the second set. Alternatively, they may use the less sophisticated count-up-from-one strategy by starting their count at “one,” putting up four fingers in sequence as they count up to four (to mark off the first set), and then continuing to count up to seven as they raise three additional fingers (to mark off the second set). Children who are unsure of this strategy will use it to put up seven fingers, counting as they do so, and will then use their noses or nods of their heads to count the fingers they have raised and thus determine that the answer to the question is seven.
Although it may take children 1 or 2 years to move from the least to the most sophisticated of these strategies, children using these approaches are in all cases demonstrating their awareness that the counting numbers refer to real-world quantities and can be used, in the absence of countable objects, to solve simple addition problems involving the joining of two sets. Children who respond to the same question by saying “I don’t know” or by taking a wild guess and saying “one hundred” appear to lack this awareness. In between these two extremes are children who make a common error and say the answer is “five,” thus demonstrating some understanding of addition (i.e., that the answer must be larger than four) but an incomplete understanding of how to use counting numbers to find the answer.
Kindergarten children use the same range of strategies to figure out what number comes two numbers after seven (Level 1, #3). Some use the count-on strategy to solve this problem and say, “seven [pause], eight, nine. The answer is nine.” Others count up from one to get the same answer. Two common errors that children make on this problem shed light on what successful children appear to know about the number sequence. The first error involves starting at seven, saying two counting words—“seven, eight”—and explaining that eight is the answer. The second error is to say that the answer is “eight and nine” and to repeat this answer when prompted with the question, “Well, which is it—eight or nine?” Both of these answers show an understanding of the order of counting words but a weak (or incomplete) understanding of the position of each word in the number sequence and what position entails in terms of quantity. Finally, children who say “I don’t know” to this question appear to lack either sufficient knowledge of the counting sequence or sufficient understanding of the term “after” to even attempt the problem.
At this age level, children are also able to tell which of two single-digit numbers is bigger or smaller (Level 1, #4 and #5). This is a large leap from the previous (4-year-old) level, at which children could compare quantities that were physically present as long as the differences between them were visible to the naked eye. This new competence implies the presence of a sophisticated set of understandings. Children who are successful with these items appear to know (1) that numbers indicate quantity and therefore (2) that numbers themselves have magnitude, (3) that the word “bigger” or “more” is sensible in this context, (4) that the numbers seven and nine occupy fixed positions in the counting sequence, (5) that seven comes before nine when one is counting up, (6) that numbers that come later in the sequence—are higher up—indicate larger quantities, and (7) that nine is therefore bigger (or more) than seven. Children who lack these understandings typically guess hesitantly. (Note that because children can get the right answer to these questions 50 percent of the time by guessing, they must pass both parts of each question to receive credit for these items on the test.)
Understandings of 6-Year-Olds
The last three items on Level 1 of the test are typically not passed until children are 6 years old, in first grade, and have had the benefit of some formal schooling. The addition problem “How much is two plus four?” and the subtraction problem “How much is eight take away six?” are particularly challenging because they are stated formally, in a decontextualized fashion, and because the quantity to be added or subtracted is larger than three, making it difficult for children to easily count up or back a few numbers to figure out the answer. The most sophisticated response children provide to
the addition question is to count on from the largest addend (intuitively using the commutative principle) and to say “four [pause], five, six.” Although many children use this strategy, many others start with the first addend in the stated problem (two); they then have the cumbersome job of counting on four more, making sure they count correctly at the same time they are keeping track of how many they have counted. It is not surprising that this strategy results in more errors in counting than does the first strategy.
Although some children make wild guesses in response to these questions, two other examples of a partial understanding are provided more frequently when children say, after pausing to think, that the answer is “five.” Although five appears to be a favorite number for many children, regardless of the context, it is also a reasonable answer for both of these questions. If it reflects an awareness that the answer to the addition problem must be bigger than four (the largest addend), and the answer to the subtraction problem must be smaller than eight (the first subtrahend), it suggests a partial understanding of addition and subtraction.
The final item at Level 1 (#9) presents children with a conflicting cue (i.e., four numerals presented in a random order—8, 5, 6, 2) and gives them a chance to show just how solid their understanding of the counting sequence is: “When you’re counting, which of these numbers do you say first (and last)?” Children can easily solve this problem if their experience with counting is extensive and their knowledge solid. If this is not the case, they are easily confused and give the first (or last) numeral listed in the display as their answer. As with all other items at this level of the test, the majority (about 60 percent) of children in developed societies acquire the knowledge needed for success sometime between the ages of 5 and 7.
Again we can ask what knowledge undergirds these performances. Scholars hypothesize that, around the age of 5 to 6, as children’s knowledge of counting and quantity becomes more elaborate and differentiated it also gradually becomes more integrated, eventually merging in a single knowledge network termed here as a central conceptual structure for whole number, or a mental counting line structure.7 This structure is illustrated in Figure 6-1. The figure can be thought of as a blueprint showing the important pieces of knowledge children have acquired (depicted by words or pictures in the figure) and the ways these pieces of knowledge are interrelated (depicted by arrows in the figure).
The top row of the figure illustrates children’s knowledge of the counting words and suggests that they can not only say those words in sequence, but also understand the position of each word in the sequence and tell what number comes next, after, or before any number from one to ten. The second row shows that children know they touch each object once and only once when counting. The third row shows that children know the precise
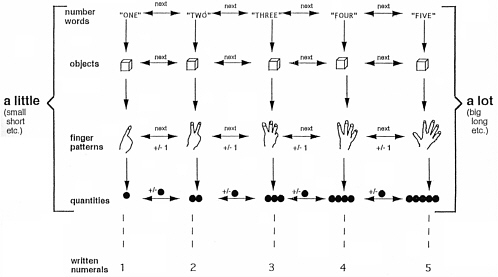
FIGURE 6-1 Mental counting line structure—a blueprint showing the important pieces of knowledge children have acquired (words or pictures) and the ways these pieces are interrelated (arrows).
finger patterns associated with each counting word; as indicated by the horizontal and vertical arrows that connect finger displays to each other and to the counting words, they also know that the finger display contains one more finger each time they count up by one and contains one less finger each time they count down by one. The fourth row suggests that children have acquired similar understandings with respect to objects (and other real-world quantities). The fifth row is connected to all the others with dotted lines to show that children acquire knowledge of the numerals that are associated with each counting word somewhat later, and this knowledge is not a vital component of the central conceptual structure. What is vital, however, are the brackets that contain the first four rows and connect the knowledge indicated within them (i.e., knowledge of counting) to several words used to make quantity judgments. These connectors show that children at this age can use their knowledge of counting to make precise judgments about relative amount.
With this higher-order knowledge structure, children come to realize that a question about addition or subtraction can be answered, in the absence of any concrete set of objects, simply by counting forward or backward along the counting string. They also come to realize that a simple
verbal statement about a transformation, such as “I have four things, and then I get three more,” has an automatic entailment with regard to quantity. One does not even need to see the objects involved or know anything else about them. These simple understandings actually mark a major revolution in children’s understanding, which changes the world of formal mathematics from something that can occur only “out there” to something that can occur inside their own heads and under their own control. As this change takes place, children begin to use their counting skills in a wide range of other contexts. In effect, children realize that counting is something one can do to determine the relative value of two objects on a wide variety of dimensions (e.g., width, height, weight, musical tonality).8
Around age 6 to 7, supported by their entry into formal schooling, children typically learn the written numerals (though this is taught to some children earlier). When this new understanding is linked to their central conceptual understanding of number, children understand that the numerals are symbols for number words, both as ordered “counting tags” and as indicators of set size (i.e., numerical cardinality).
Understandings of 7-Year-Olds
Around the age of 7 to 8, in grade 2, children are able to solve the same sorts of problems they could solve previously for single-digit numbers, but for double-digits numbers. When asked what number comes five numbers after forty-nine (Level 2, #1) or four numbers before sixty (Level 2, #2), the majority of second graders can figure out the answer. They do so by counting up from forty-nine (or down from sixty), often subvocally and, less frequently than at the previous stage, using their fingers to keep track of how many they have counted up (or down). When children make errors on these problems, they demonstrate the same sorts of partial understandings that were described earlier. That is, they may show a strong partial understanding of double-digit numbers by making a counting error (e.g., counting the number from which they start as the first number added or subtracted), or a weak understanding by saying, “I don’t know. That’s a big number. I haven’t learned them yet.” Between these two extremes are children who know intuitively that the answer to each problem must be in the fifties but are unsure how to count up or down.
At this age level, children can also tell which of two double-digit numbers is bigger or smaller (Level 2, #3 and #4). To do so, they must recognize that numbers in the tens place of each problem (e.g., sixty-nine versus seventy-one) have a much greater value than numbers in the ones place, and thus outweigh the value of even big numbers such as nine that occur in the units position. In short, children who succeed on these items recognize that any number in the seventies is automatically bigger than any number in the
sixties “because you have to go through all the numbers in the sixties before you even hit seventy.” A common error children make—which reveals an absence of this awareness—is to choose consistently on the basis of the value of the unit digits and to say, for example, that sixty-nine is bigger than seventy-one because nine is larger than one.
Finally, typically toward the end of this age period, children are able to figure out how many whole numbers are in between two and six (Level 2, #7) and in between seven and nine (Level 2, #8). These are complex single-digit problems that require the use of two mental counting lines, one with the numbers involved in the problem and one with the numbers involved in the solution. Children who are successful with the first item often start the solution process by looking fixedly ahead and saying “two” [pause] “six,” as if they were looking at an imaginary counting line and marking the numbers two and six on this line. They then proceed to count the numbers in between by nodding their heads; saying “three,” “four,” “five” (sometimes using their fingers to keep track of the second number line, in which “three” is one, “four” is two, and “five” is three); and providing “three” as the answer. This behavior suggests they are using one mental counting line as an operator to count the numbers on a second mental number line that shows the beginning and end points of the count. By contrast, children who are unsuccessful with this item often give “five” as the answer and explain this answer by saying that five is in between two and six. Although this answer demonstrates an understanding of the order of numbers in the counting sequence, it completely ignores the part of the question that asks, “How many numbers are there in between?” Other children look stunned when this question is posed, as if it is not a meaningful thing to ask, and respond “I don’t know,” suggesting that they have not yet come to understand that numbers have a fixed position in the counting sequence and can themselves be counted.
Understandings of 8-Year-Olds
The last two items at Level 2 are more complex than the previous items, and they are frequently not solved until children are 8 years old. Children succeed on the problem “How much is 12 plus 54?” most easily by reducing one of these numbers to a benchmark value, carrying the amount that was taken away in their heads, adding the new values, and then adding on the amount that was carried (e.g., “ten and fifty-four is sixty-four; add two; the answer is sixty-six”). Use of this strategy implies a good understanding of the additive composition of double-digit numbers and of the value of using benchmark numbers to make addition and subtraction easier.
Other children solve these problems more laboriously, with less sophisticated strategies. Some count on from fifty-four by ones until they have
marked twelve fingers, essentially ignoring the base-ten value of these numbers and treating them as units. Others try to line the numbers up in their heads into the typical vertical format used on worksheets in the classroom. They then add the numbers in the ones column—“two and four is six”—and the numbers in the tens column—“five and one is six”—and, with much mental effort, say that the answer is sixty-six. Children using this solution strategy are essentially performing two single-digit addition operations in succession and are not demonstrating a good understanding of the base-ten features of double-digit numbers. As with all the other test problems, there are always some children who take a wild guess and produce an answer that is not even in the ballpark or who look puzzled and say, more or less forlornly, “I don’t know. I haven’t learned that yet.”
Again we can ask what knowledge underlies these performances. Researchers have suggested that, around the age of 7 to 8 years, children’s central conceptual understandings become more elaborate and more differentiated, permitting them to represent two distinct quantitative dimensions, such as tens and ones, in a coordinated fashion. With this new structure, called a bidimensional central conceptual structure for number, children are able to understand place value (e.g., represent the tens dimension and the ones dimension in the base-ten number system and work with these dimensions in a coordinated fashion). They are also able to solve problems involving two quantitative dimensions across multiple contexts, including time (hours and minutes), money (dollars and cents), and math class (tens and ones).9
ACKNOWLEDGING TEACHERS’ CONCEPTIONS AND PARTIAL UNDERSTANDINGS
As illustrated in the foregoing discussion, the questions included on the Number Knowledge test can provide a rich picture of the number understandings, partial understandings, and problem-solving strategies that children in several age groups bring to instruction.
The test can serve another function as well, however, which is worth discussing in the present context: it can provide an opportunity for teachers to examine their own mathematical knowledge and to consider whether any of the partial understandings children demonstrate are ones they share as well. My own understanding of number has grown considerably over the past several years as a result of using this test with hundreds of children, listening to what they say, and examining how their explanations and understandings change as they grow older. Three insights in particular have influenced my teaching.
Insight #1: Math Is Not About Numbers, but About Quantity
It is easy to endorse the myth that math is about numbers because numbers, after all, are everywhere in math. What my work with children has taught me is that math is about quantity, and numbers express those quantities. As the age-level descriptions of children’s understandings suggest, numbers acquire meaning for children when they recognize that each number refers to a particular quantity (which may be represented in a variety of different ways) and when they realize that numbers provide a means of describing quantity and quantity transformations more precisely than is possible using everyday language such as “lots,” “little,” or “more.” This realization—that numbers are tools that can be used to describe, predict, and explain real-world quantities and quantity transactions—gives children a tremendous boost in mastering and using the number system. To help children construct this understanding, therefore, it is crucial to introduce numbers to children in the context of the quantities (e.g., objects, pictures of objects) and quantity representations (e.g., dot set patterns, number lines, thermometers, bar graphs, dials) that will give these numbers meaning as quantities.
Insight #2: Counting Words Is the Crucial Link Between the World of Quantity and the World of Formal Symbols
Numbers are expressed in our culture in two quite different ways: orally, as a set of counting words, and graphically, as a set of formal symbols. Because children start using the counting words so early—learning to say “one–two–three” almost as soon as they learn to talk—it may be tempting to think that they should abandon this early form of expression when they start their formal schooling and learn to use the graphic symbol system instead. But children have spent most of their preschool years using the counting words in the context of their real-world exploration and ever so slowly building up a network of meaning for each word. Why should they be deprived of this rich conceptual network when they start their school-based math instruction and be required, instead, to deal with a set of symbols that have no inherent meaning? Mathematics instruction that takes advantage of this prior knowledge and experience—rather than denying it or presenting math as distinct from these everyday experiences—is bound to be more accessible to children.
In my own work, I have found that the key to helping children acquire meanings for symbols is providing opportunities for them to connect the symbol system to the (more familiar) counting words. This is best accom-
plished when children have previously acquired a solid set of connections between the counting words themselves and the quantities to which they refer. Many third graders are still constructing this latter understanding (e.g., acquiring an awareness of the links between double-digit counting numbers and the quantities to which they refer). Thus, to enable children to use their current understandings to build new ones, it is crucial that they have ample opportunities to use the oral language system to make sense of quantitative problems and that they be introduced to the graphic equivalents of that system in this familiar context.
Insight #3: Acquiring an Understanding of Number Is a Lengthy, Step-by-Step Process
I used to think (or at least I liked to believe) that if I designed an especially elegant lesson that made the concept I was attempting to teach transparent for children, I could produce an “aha” experience and enable the children to grasp a connection that was previously unavailable to them. I now realize that this goal (or wish) is not only unrealistic, but also unobtainable if the concept to be learned is not within reach of the child’s current level of understanding. As the earlier age-level descriptions of children’s understanding suggest, the acquisition of number knowledge is, by its very nature, a step-by-step process, with each new understanding building systematically and incrementally on previous understandings. Although I still believe in the value of carefully designed, elegant lessons, my goals, while still ambitious, are more limited. Now, I hope that a lesson or series of lessons will enable a child to move up one level at a time in his or her understanding, to deepen and consolidate each new understanding before moving on to the next, and to gradually construct a set of understandings that are more sophisticated and “higher-level” than the ones available at the start. I now recognize that such a process takes time and that each child may move through the process at his or her own pace.
REVISITING QUESTION 2: DEFINING THE KNOWLEDGE THAT SHOULD BE TAUGHT
Now that we have a better idea of the knowledge children have available to work with at several age levels and the manner in which this knowledge is constructed, it is possible to paint a more specific portrait of the knowledge that should be taught in school, at each grade level from preschool through second grade, to ensure that each child acquires a well-developed whole-number sense. As suggested previously, the knowledge taught to each child should be based, at least in part, on his or her existing
understandings (Principle 1). However, because teachers are required to teach whole classrooms of children (as well as individuals), they need a set of general learning objectives for each grade level that will be appropriate for the range of children involved. Two sets of objectives are paramount for this purpose. The first is to ensure that all children in the class attain the developmental milestones—the central conceptual structures for whole number—described earlier; the second is to ensure that all children become familiar with the major ways in which number and quantity are represented and talked about so they can recognize and make sense of number problems they encounter across contexts.
The framework presented in the previous section leads to a clear set of learning goals for each grade level from prekindergarten through grade 2 that are within reach of the majority of children at that level and that teachers can use to “teach” the developmental milestones (i.e., to ensure that children who have not yet acquired these central conceptual understandings have an opportunity to do so). Using this framework, it can be suggested that a major goal for the preschool year is to ensure that children acquire a well-developed counting schema and a well-developed quantity schema. A major goal for the kindergarten year is to ensure that children acquire a well-consolidated central conceptual structure for single-digit numbers. A major goal for first grade is to help children link this structure to the formal symbol system and to construct the more elaborated knowledge network this entails. Finally, a major goal for second grade is to help children acquire the bidimensional central conceptual structure for double-digit numbers that underlies a solid understanding of the base-ten system.
These grade-level goals (see Box 6-5) not only specify knowledge networks to be taught at specific grade levels to foster the development of whole-number sense, but also form a “number sense” learning pathway—a sequence of learning objectives teachers can use to individualize instruction for children who are progressing at a rate that is faster or slower than that of the rest of the class. The second body of knowledge to be taught—knowledge of the major ways number and quantity are represented and talked about—can be defined most clearly in the context of the tools developed to teach it, as discussed in the following section.
HOW CAN THIS KNOWLEDGE BE TAUGHT?: THE CASE OF NUMBER WORLDS
During the past two decades, several innovative programs and approaches to mathematics teaching have been developed to teach whole-number concepts and to put the principles of How People Learn into curricular action.10 The program described here—Number Worlds—was designed specifically to teach the knowledge described above. It is also the one with which I am
most familiar. As codeveloper of this program, I was involved in its inception in 1988 under the name Rightstart. In the ensuing years, I have continued to participate in the program’s development, revising it annually to achieve a better fit with teachers’ needs and learning goals, conducting program evaluations to assess its effects on children’s learning and achievement, and ultimately producing the expanded set of prekindergarten–grade 2 programs now called Number Worlds.11 Like the other programs and approaches referred to above, Number Worlds was designed specifically to (1) build on children’s existing understandings (learning principle 1), (2) help children construct new knowledge, both factual and conceptual, that is organized so as to facilitate retrieval and application (learning principle 2), and (3) require and teach metacognitive strategies (learning principle 3). Like each of the other programs and approaches referred to above, Number Worlds provides a distinctive way of thinking about mathematics and mathematics teaching.
To maximize opportunities for all children to achieve the knowledge objectives of the Number Worlds program, a set of design principles drawn from the How People Learn research base was adopted and used to create each of the more than 200 activities included in the program. The principles that are most relevant to the present discussion are listed below. In the ensuing discussion, each design principle is described more fully and illustrated with one or more activities from the Number Worlds program:
-
Activities should expose children to the major ways number is represented and talked about in developed societies.
-
Activities should provide opportunities to link the “world of quantity” with the “world of counting numbers” and the “world of formal symbols.”
-
Activities should provide visual and spatial analogs of number representations that children can actively explore in a hands-on fashion.
-
Activities should be affectively engaging and capture children’s imagination so knowledge constructed is embedded not only in their minds, but also in their hopes, fears, and passions.
-
Activities should provide opportunities for children to acquire computational fluency as well as conceptual understanding.
-
Activities should encourage or require the use of metacognitive processes (e.g., problem solving, communication, reasoning) that will facilitate knowledge construction.
Design Principle 1: Exposing Children to Major Forms of Number Representation
Number is represented in our culture in five major ways: through objects, dot set patterns, segments on a line, segments on a scale (or bar graph),
|
BOX 6-5
|
and segments or points on a dial. Children who are familiar with these forms of representation and the language used to talk about number in these contexts have a much easier time making sense of the number problems they encounter inside and outside of school. The Number Worlds program provides one example of how these forms of representation can be taught. In so doing, it illustrates what a knowledge-centered classroom might look like in the area of elementary mathematics.
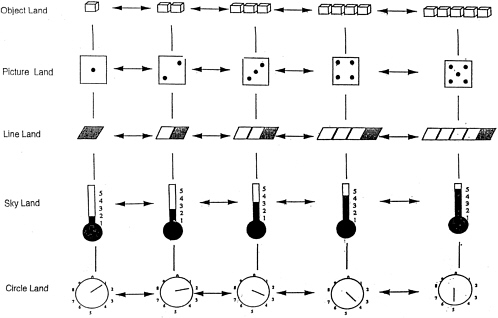
At each grade level in this program, children explore five different lands. Learning activities developed for each land share a particular form of number representation while simultaneously addressing specific knowledge goals (i.e., the developmental milestones) for each grade level. The five forms of representation and the lands in which they appear are illustrated in Figure 6-2. As the figure suggests, the first land to which children are exposed is Object Land, where numbers are represented by the bundling of several
|
||||||||||||
objects, such as pennies or fingers, into groups. This is the first way in which numbers were represented historically and the first that children learn naturally.12 In Object Land, children first work with real objects (e.g., “How many crackers will you have left after you eat one? After you eat one more?”) and then move on to working with pictures of objects (e.g., “Are there enough hats so that each clown will have one? How many more do you need? How do you know?”).
The second land to which children are introduced is Picture Land, where numbers are represented as stylized, semiabstract dot set patterns that are equivalent to mathematical sets. These patterns provide a link between the world of movable objects and the world of abstract symbols. Unlike the real objects they represent, dot set pictures cannot be placed physically in one-to-one correspondence for easier comparison. Instead, a child must make a mental correspondence between two sets, for example by noticing that the
pattern for five is the same as that for four, except that the five pattern has one extra dot in the center. As children engage in Picture Land activities (e.g., by playing an assortment of card and dice games similar in format to War, Fish, and Concentration), they gradually come to think of these patterns as forming the same sort of ordered series as do the number words themselves. Numerals, another way of representing numbers, are also part of Picture Land, and are used extensively in the activity props that are provided at all grade levels and, by the children themselves, in the upper levels of the program. Tally marks are used as well in this land to record and compare quantities.
A third way to represent numbers is as segments along a line—for example, the lines that are found on board games such as Chutes and Ladders. The language that is used for numbers in this context is the language of distance. In Line Land, children come to understand (by playing games on a Human Game Mat and on an assortment of smaller number line game boards) that a number such as “four” can refer not only to a particular place on a line, but also to a number of moves along the line. One can talk about going four numbers forward from the number four on one’s fourth turn. Perhaps the most important transition that children must make as they move from the world of small countable objects to that of abstract numbers and numerical operations is to treat the physical addition or subtraction of objects as equivalent to movement forward or backward along a line. All children eventually make this correspondence; until they do, however, they are unable to move from physical to mental operations with any insight.
Yet another way to represent numbers is with bar graphs and scales, such as thermometers. In Sky Land (a name chosen as a child-friendly substitute for the word “scale,” as in “reach for the sky”), this sort of representation is always used in a vertical direction, such that bigger numbers are higher up. These forms of representation make a convenient context for introducing children to the use of numbers as a measure, as a way to keep track of continuous quantity in standard units. Systems for measuring continuous quantity have the same long history as do systems for enumerating discrete objects, and it is important to develop children’s intuitions for the properties of the former systems from the outset.13
Dials are the final representation of number included in Number Worlds. Sundials and clocks are more sophisticated ways of representing numbers since they incorporate the cyclic quality—a path that repeats itself—possessed by certain real-world dimensions, such as time and the natural rhythm of the seasons. In Circle Land, children develop spatial intuitions (e.g., by playing games on a skating rink configuration that requires them to chart progress within and across revolutions to determine a winner) that become the foundation for understanding many concepts in mathematics dealing with circular motion (e.g., pie charts, time, and number bases).
Although the five forms of number representation have been introduced in a fixed order here, from easiest to most difficult, an important goal of the Number Worlds program is to help children appreciate the equivalence of these forms of representation and of the language used to talk about number in these contexts. To this end, children are encouraged to explore all lands and all number representations early in the school year by beginning with activities in each land that target lower-level knowledge objectives (labeled Level 1 activities) and by proceeding throughout the year to activities in each land that target higher-level knowledge objectives (labeled Level 3 activities). By moving back and forth across lands throughout the year, children gradually come to appreciate, for example, that “nine” is bigger than “seven” by a precise amount and that this difference holds whether these numbers are represented as groups of objects, as positions along a path, or as points on a scale. They also come to appreciate that this difference is the same whether it is talked about as “more” in one context, as “farther along” in another, or as “higher up” in a third. For adults, these various manifestations of the whole-number counting system are easily seen to be equivalent. To very young children, they are quite different, so different that they might appear to be from different “worlds.” Helping children construct an organized knowledge network in which these ideas are interconnected (learning principle 2) is thus a major goal of Number Worlds.
Design Principle 2: Providing Opportunities to Link the “World of Quantity” with the “World of Counting Numbers” and the “World of Formal Symbols”
Although every activity created for the Number Worlds program provides opportunities to link the “world of quantity” with the “world of counting numbers” and the “world of formal symbols”—or to link two of these worlds—the three activities described in this section illustrate this principle nicely, at the simplest level. Readers should note that the remaining design principles are also illustrated in these examples, but to preserve the focus are not highlighted in this section.
Plus Pup
Plus Pup is an Object Land activity that is used in both the preschool and kindergarten programs to provide opportunities for children to (1) count a set of objects and identify how many there are, and (2) recognize that when one object is added, the size of the set is increased by one (see Figure 6-3). To play this game, the teacher and children put a certain number of cookies into a lunch bag to bring to school, carefully counting the cookies as they do so, and being sure they remember how many cookies they placed

FIGURE 6-3 Plus Pup—an Object Land activity used to provide opportunities for children to understand addition problems.
inside the bag. Next, the teacher (or a child volunteer) takes a little walk (as if going to school) and encounters Plus Pup along the way (by picking up the Plus Pup card). As the icon on the card suggests, Plus Pup gives the cookie carrier one more cookie. The bag is opened up slightly to receive a real cookie and is then promptly closed. The challenge children confront is this: How many cookies are in the bag now? How can we figure this out?
If the teacher is patient and allows children to explore these questions as genuine problems, a range of solution strategies are often provided as children play and replay the game with different quantities of cookies. The first and most obvious solution children suggest (and implement) is to open the bag, take the cookies out, and count them. This provides opportunities for the teacher to draw children’s attention to the quantity transaction that has occurred to produce this amount. For example, the teacher may say, “We have five cookies now. How do we know how many Plus Pup gave us? How can we figure this out?” If no answers are forthcoming, the teacher can prompt the children by asking, “Does anyone remember how many cookies we had at the start?”—thus leading them to make sense of the quantity transaction that has occurred (i.e., the initial amount, the amount added, the end total) by describing the entire process in their own words.
As children replay this game, they gradually come to realize that they can use the counting numbers themselves, with or without their fingers, to solve this sort of problem, and that dumping the cookies out of the bag to count them is unnecessary. When children begin to offer this solution strategy, the teacher can shift the focus of her questions to ask, “Who can predict how many cookies are in the bag now? How do you know?” After predictions and explanations (or proofs) have been offered, the children can be allowed to examine the contents of the bag “to confirm or verify their pre-
dictions.” Although preschoolers are often unfamiliar with these scientific terms when first introduced, it is not long before they understand the meaning of the terms in this context and use these words themselves, feeling very pleased with the air of sophistication this language bestows on their own mathematical activity. By encouraging problem solving and communication, this activity, like all activities in the program, makes children’s thinking visible, and in so doing provides the basis for ongoing assessment that is the hallmark of assessment-centered classrooms.
The rationale that was created for this activity is as follows: “In this activity, a giving pup icon is used to give children a meaningful mental image of the addition operation. This image will serve as a conceptual bridge and help children build strong connections between an increase in quantity in the real world and the +1 symbol that describes this increase in the world of formal mathematics” (Object Land: Lesson #7). Although children are not expected to make explicit use of the +1 symbol in either the preschool or kindergarten program, it is available for those who are ready to take advantage of it. To our delight, children who have been exposed to this activity in their preschool or kindergarten year spontaneously remember Plus Pup when they encounter more complex addition problems later on, providing evidence they have indeed internalized the set of connections (among name, icon, and formal symbol) to which they were exposed earlier and are able to use this knowledge network to help them make sense of novel addition problems.
Minus Mouse
Once children have become familiar with Plus Pup and what Plus Pup does, they are introduced to Minus Mouse (see Figure 6-4). The format of

FIGURE 6-4 Minus Mouse—an Object Land activity used to provide opportunities for children to understand subtraction problems.
this activity is identical to that of the former except, of course, that whereas Plus Pup will add one cookie to the bag, Minus Mouse will take one away. The challenge children are asked to deal with in this activity is this: “How many cookies will we have left?” How can we figure this out? The similarly in format between these two activities and the repetition that results proves not to be the deterrent to children that adults might expect. Most young children prefer the comfort of the familiar to the excitement of the novel. Indeed, they appear to thrive on the opportunities this similarity provides for them to anticipate what might happen and, with confidence, make predictions about those outcomes.
Plus Pup Meets Minus Mouse
Once children have become familiar with Minus Mouse and reasonably adept at solving the problems this activity presents for a range of single-digit quantities, the teacher makes the problem more complex by including both Plus Pup and Minus Mouse in the same activity. This time, when the cookie carrier walks to school, he or she draws a card from a face-down pack and either Plus Pup or Minus Mouse will surface. The challenge this time is to interpret the icon with its associated symbol, to determine the action that should be performed (adding one more cookie to the bag or taking one away), and to figure out how to solve the problem of how many cookies are in the bag now and how we can figure this out. Children who have become reasonably competent at counting on (from the initial amount) to solve Plus Pup problems and counting back (from the initial amount) to solve Minus Mouse problems will now have to employ these strategies in a much more flexible fashion. They will also have to pay much closer attention to the meaning of the icon and its associated symbol and what this entails in terms of the quantity transaction to be performed. Both of these challenges pose bigger problems for children than adults might expect; thus, by providing opportunities for children to confront and resolve these challenges, this activity scaffolds the development of whole-number sense.
All three of the above activities can provide multiple opportunities for teachers to assess each child’s current level of understanding as reflected in the solutions constructed (or not constructed) for each of the problems posed, the explanations provided, and the strategies employed (e.g., emptying the cookies out of the bag to determine how many or using the counting numbers instead, with or without fingers, to solve the problem). These informal assessments, in turn, can help teachers determine the quantity of cookies that would provide an appropriate starting place for the next round of each activity and the sorts of questions that should be posed to individual children to help them advance their knowledge. By using assessment in this formative fashion—to create learning opportunities that are finely attuned to
children’s current understandings and that help them construct new knowledge at the next level up—teachers are creating classrooms that are, at one and the same time, learner-centered, knowledge-centered, and assessment-centered.
Design Principle 3: Providing Visual and Spatial Analogs of Number Representations That Children Can Actively Explore in a Hands-On Fashion
Because the central conceptual understandings that the program was designed to teach involve the coordination of spatial and numeric concepts, it was deemed important to provide several opportunities for children to explore the number system in a variety of spatial contexts, to scaffold this coordination. The spatial contexts that were created for the Number Worlds program often take the form of game boards on which number is depicted as a position on a line, scale, or dial and on which quantity is depicted as segments on these line, scale, and dial representations. By using a pawn to represent “self” as player and by moving through these contexts to solve problems posed by the game, children gain a vivid sense of the relationship between movement along a line, scale, or dial and increases and decreases in quantity. This experience is illustrated in the following activities.
The Skating Party Game
This game is played in Circle Land at the kindergarten level. It was designed to help children realize that a dial (or a circular path) is another device for representing quantity, and that the same relationships that apply between numbers and movement on a number line apply also to numbers and movement in this context (see Figure 6-5). In this game, a dial is represented as a circular path. By including 10 segments on this path, numbered 0 to 9, this prop provides opportunities for children to acquire an intuitive understanding of the cyclical nature of the base-ten number system. This understanding is explicitly fostered and built upon in activities children encounter later on, at higher levels of the program. The explicit learning objectives that were developed for the Skating Party game are as follows: (1) identify or compute set size, and associate set size with a position on a dial (i.e., a circular path); (2) associate increasing a quantity with moving around a dial; and (3) compare positions on a dial to identify which have more, less, or the same amount, and use this knowledge to solve a problem.
These objectives are achieved as children engage in game play and respond to questions that are posed by the teacher (or by a child serving as group leader). With four children sharing one game board, children start
FIGURE 6-5 Skating Party game board—a Circle Land activity used to provide a hands-on representation for children to explore the relationship between movement and increases and decreases in quantity.
game play by placing their pawns at the starting gate. They then take turns rolling a die, counting the dots, and moving their pawns that many spaces around the dial. Each time they complete a revolution around the dial, they collect an Award card. At the end of the game, children count and compare their Award cards, and the child with the most cards is the first winner, followed by the child with the second most, who is the second winner, and so on. In one variation of this game, the Award cards collected by each group of four children are computed and compared, and a group winner is declared.
Questions are posed at several points in game play, and the sorts of questions that are put to individual children are most productive if they are finely tuned to each child’s current level of understanding (learning principle 1). For example, when all children have their pawns on the board, they can be asked, “Who is farther around? Who has gone the least distance? How much farther do you need to go to win an Award card?” These questions are always followed by “How do you know?” or “How did you figure that out?” Plenty of time needs to be allowed for children to come up with answers that make sense to them and for them to share their answers with each other. When children are counting their Award cards, they can be asked, “How many times did you go around the rink? Who has the most Award cards? How come that child went around the rink more times than this child if everyone had the same number of turns?” The last question is the most challenging of this set, and beginning players often attribute going
around the rink more times to skating faster (rather than to rolling a lot of high numbers).
Eventually children will make this connection, and they can be encouraged to do so by being asked to pay close attention to movement around the rink the next time they play. For example, the teacher might say, “Did that child really skate faster? Let’s watch next time we play and see.” In encouraging children to construct their own answers to the question by reflecting on their own activity, teachers are encouraging the use of metacognitive processes and allowing children to take charge of their own learning (learning principle 3).
In a follow-up activity, the teacher adds another level of complexity to this game by providing an illustrated set of skating cards that show either “+1, You skate well”; “–1, You stumbled”; or “0,” blank symbol and image (see Figures 6-6a and 6-6b). In this version of the game, children play as before, but in addition, they draw a skating card from the face-down deck after every turn and follow the instructions on the card to move one space forward or backward around the rink, or to stay where they are. This version of the game provides opportunities for children to meet an additional learning objective—identifying how many there will be if a set is increased or decreased by one (or by two in a challenge activity). This objective, in turn, is met most easily if the teacher scaffolds children’s learning by providing opportunities for them to talk about the quantity transactions they are performing. For example, when a child draws a card, the teacher can ask, “Where are you now? What does that card tell you to do? How far around the rink will you be after you do that? Is that closer to the finish line
FIGURE 6-6 An illustrated set of skating cards used in the Circle Land Skating Party game.
FIGURE 6-7 Neighborhood Number Line game board—used to help children understand the base-ten number system.
or farther away from it? How do you know?” By answering and discussing these questions and by confirming or disconfirming their thoughts and predictions with real actions, children gradually build up a solid intuitive understanding of the links among the world of quantity (in spatial contexts), the world of counting numbers, and the world of formal symbols.
Rosemary’s Magic Shoes
This game provides an illustration of a spatial context developed for Line Land in the second-grade program to help children build an understanding of the base-ten number system. The prop itself—the Neighborhood Number Line—comprises 10 blocks of houses, each containing 10 houses that attach with Velcro to create a linear neighborhood of 100 houses that is 15 feet long when fully assembled (see Figure 6-7). This prop is used extensively in the first-grade program as well, to teach several concepts implicit in the 1–100 number sequence. The character created for this game, a professional monster-tracker called Rosemary, has a pair of magic shoes that allows her to leap over 10 houses in a single bound. For Rosemary’s shoes to work, however, she first must tell them how many times to jump 10 houses and how many times to walk past 1 house.
To play this game, children take turns picking a number tile that indicates a house where the presence of a monster has been suspected. Using Rosemary’s magic shoes, they then move to the house as quickly and efficiently as possible; check for monsters (by drawing a card from a face-down deck that indicates the monsters’ presence or absence); and, if indicated, place a sticker on the house to show that it is a “monster-free zone.” In later
versions of this game, children are required to keep a written record of Rosemary’s movements, using the formal symbol system to do so. In all versions of this game, they are required to watch each player carefully to see if the oral directions given (e.g., “Magic shoes, jump over 5 blocks and walk to the eighth house”) were followed precisely, to consider whether other ways of getting to the same house (#58) might have been more efficient, and to share their thinking with the class.
With exposure to this game, children gradually come to realize that they can leap over 10 houses (i.e., count up or down by tens) from any number in the sequence, not just from the decade markers (e.g., 10, 20, 30). They also come to realize that they need not always move in a forward direction (e.g., count up) to reach a particular number, that it might be more efficient to move to the closest tens marker and go back a few steps (e.g., jump over 6 blocks and walk back two steps to get to house #58). With these realizations and opportunities to put them into practice, children gain fluency in computing the distance between any two numbers in the 1-100 sequence and in moving fluently from one location (or number) to the next, using benchmark values to do so. They also gain an appreciation of the relative value of numbers in this sequence (e.g., that 92 is a long way away from 9) and can recognize immediately that the sum of 9 + 2 could not possibly be 92, an error that is not uncommon for this age group. The knowledge gains that have just been described—the acquisition of procedural fluency, factual knowledge, and conceptual understanding—appear to be greatly facilitated by the provision of spatial analogs of the number system that children can actively explore in a hands-on fashion (design principle 3 as set forth in this chapter), coupled with opportunities to explain their thinking, to communicate with their peers, and to reflect on their own activity (learning principle 3).
Design Principle 4: Engaging Children’s Emotions and Capturing Their Imagination So Knowledge Constructed Is Embedded Not Only in Their Minds, but Also in Their Hopes, Fears, and Passions
Each of the activities described thus far has been engaging for children and has captured their imagination. The one described in this section possibly achieves this purpose to a greater extent than most others. It also provides an example of how the Number Worlds program addresses a major learning goal for first grade: helping children link their central conceptual structure for whole number to the formal symbol system.

FIGURE 6-8 Dragon Quest game board—a Picture Land activity that uses numerals and operation signs to achieve the game’s goals.
Dragon Quest
Dragon Quest was developed for Picture Land in the first-grade program (see Figure 6-8). Although the game is played on a line and children can use objects to solve the problems posed by the game, the major representation of number that children must work with in this game to achieve the game’s goals are numerals and operation signs. For this reason, this game is classified as a Picture Land activity. Children are introduced to Phase 1 of this activity by being told a story about a fire-breathing dragon that has been terrorizing the village where the children live. The children playing the game are heroes who have been chosen to seek out the dragon and put out his fire. To extinguish this dragon’s fire (as opposed to that of other, more powerful dragons they will encounter in later phases), a hero will need at least 10 pails of water. If a hero enters the dragon’s area with less than 10 pails of water, he or she will become the dragon’s prisoner and can be rescued only by one of the other players.
To play the game, children take turns rolling a die and moving their playing piece along the colored game board. If they land on a well pile (indicated by a star), they can pick a card from the face-down deck of cards that illustrate, with images and symbols (e.g., + 4), a certain number of pails of water. Children are encouraged to add up their pails of water as they receive them and are allowed to use a variety of strategies to do so, ranging from mental math (which is encouraged) to the use of tokens to keep track of the quantity accumulated. The first child to reach the dragon’s lair with at least 10 pails of water can put out the dragon’s fire and free any teammates who have become prisoners.
Needless to say, this game is successful in capturing children’s imagination and inducing them to engage in the increasing series of challenges posed by later versions. As they do so, most children acquire increasingly sophisticated number competencies. For example, they become capable of performing a series of successive addition and subtraction operations in
their heads when spill cards (e.g., – 4) are added to the set of cards in the well pile. When they encounter more-powerful dragons whose fire can be extinguished only with 20 buckets of water, they become capable of performing these operations with larger sets of numbers and with higher numbers. When they are required to submit formal proof to the mayor of the village that they have amassed sufficient pails of water to put out the dragon’s fire before they are allowed to do so, they become capable of writing a series of formal expressions to record the number of pails received and spilled over the course of the game. In such contexts, children have ample opportunity to use the formal symbol system in increasingly efficient ways to make sense of quantitative problems they encounter in the course of their own activity.
Design Principle 5: Providing Opportunities for Children to Acquire Computational Fluency As Well As Conceptual Understanding
Although opportunities to acquire computational fluency as well as conceptual understanding are built into every Number Worlds activity, computational fluency is given special attention in the activities developed for the Warm-Up period of each lesson. In the prekindergarten and kindergarten programs, these activities typically take the form of count-up and count-down games that are played in each land, with a prop appropriate for that land. This makes it possible for children to acquire fluency in counting and, at the same time, to acquire a conceptual understanding of the changes in quantity that are associated with each successive number up (or down) in the counting sequence. This is illustrated in an activity, developed for Sky Land, that is always introduced after children have become reasonably fluent in the count-up activity that uses the same prop.
Sky Land Blastoff
In this activity, children view a large, specially designed thermometer with a moveable red ribbon that is set to 5 (or 10, 15, or 20, depending on children’s competence) (see Figure 6-9). Children pretend to be on a rocket ship and count down while the teacher (or a child volunteer) moves the red ribbon on the thermometer to correspond with each number counted. When the counting reaches “1,” all the children jump up and call “Blastoff!” The sequence of counting is repeated if a counting mistake is made or if anyone jumps up too soon or too late. The rationale that motivated this activity is as follows: “Seeing the level of red liquid in a thermometer drop while counting down will give children a good foundation for subtraction by allowing

FIGURE 6-9 A specially designed thermometer for the Sky Land Blastoff activity—to provide an understanding of the changes in quantity associated with each successive number (up) or down in the counting sequence.
them to see that a quantity decreases in scale height with each successive number down in the sequence. This will also lay a foundation for measurement” (Sky Land: Activity #2).
This activity is repeated frequently over the course of the school year, with the starting point being adjusted over time to accommodate children’s growing ability. Children benefit immensely from opportunities to perform (or lead) the count-down themselves and/or to move the thermometer ribbon while another child (or the rest of the class) does the counting. When children become reasonably fluent in basic counting and in serial counting (i.e., children take turns saying the next number down), the teacher adds a level of complexity by asking them to predict where the ribbon will be if it is on 12, for example, and they count down (or up) two numbers, or if it is on 12 and the temperature drops (or rises) by 2 degrees. Another form of complexity is added over the course of the school year when children are asked to demonstrate another way (e.g., finger displays, position on a human game mat) to represent the quantity depicted on the thermometer and the way this quantity changes as they count down. By systematically increasing the complexity of these activities, teachers expose children to a learning path that is finely attuned to their growing understanding (learning principle 1) and that allows them to gradually construct an important network of conceptual and procedural knowledge (learning principle 2).
In the programs for first and second grade, higher-level computation skills (e.g., fluent use of strategies and procedures to solve mental arithmetic
problems) are fostered in the Warm-Up activities. In Guess My Number, for example, the teacher or a child picks a number card and, keeping it hidden, generates two clues that the rest of the class can use to guess the number (e.g., it is bigger than 25 and smaller than 29). Guessers are allowed to ask one question, if needed, to refine their prediction (e.g., “Is it an odd number?” “Is it closer to 25 or to 29?”).
Generating good clues is, of course, more difficult than solving the problem because doing so requires a refined sense of the neighborhood of numbers surrounding the target number, as well as their relationship to this number. In spite of the challenges involved, children derive sufficient enjoyment from this activity to persevere through the early stages and to acquire a more refined number sense, as well as greater computational fluency, in the process. In one lovely example, a first-grade student provided the following clues for the number he had drawn: “It is bigger than 8 and it is 1 more than 90 smaller than 100.” The children in the class were stymied by these clues until the teacher unwittingly exclaimed, “Oh, I see, you’re using the neighborhood number line,” at which point all children followed suit, counted down 9 blocks of houses, and arrived at a correct prediction, “9.”
Design Principle 6: Encouraging the Use of Metacognitive Processes (e.g., Problem Solving, Communication, Reasoning) That Will Facilitate Knowledge Construction
In addition to opportunities for problem solving, communication, and reasoning that are built into the activities themselves (as illustrated in the examples provided in this chapter), three additional supports for these processes are included in the Number Worlds program. The first is a set of question cards developed for specific stages of each small-group game. The questions (e.g., “How many buckets of water do you have now?”) were designed to draw children’s attention to the quantity displays they create during game play (e.g., buckets of water collected and spilled) and the changes in quantity they enact (e.g., collecting four more buckets), and to prompt them to think about these quantities and describe them, performing any computations necessary to answer the question. Follow-up questions that are also included (e.g., “How did you figure that out?”) prompt children to reflect on their own reasoning and to put it into words, using the language of mathematics to do so. Although the question cards are typically used by the teacher (or a teacher’s aide) at first, children can gradually take over this function and, in the process, take greater control over their own learning (learning principle 3). This transition is facilitated by giving one child in the group the official role of Question Poser each time the game is
played. By giving children important roles in the learning process (e.g., Question-Poser, Facilitator, Discussion Leader, Reporter) and by allowing them to be teachers as well as learners, teachers can create the sort of community-centered classroom that is described in Chapters 1 and 5.
The second support is a set of dialogue prompts included in the teacher’s guide, which provides a more general set of questions (e.g., “Who has gone the farthest? How do you know?”) than those provided with the game. Although both sets of questions are highly useful in prompting children to use metacognitive processes to make mathematical sense of their own activity, they provide no guidance on how a teacher should respond to the answers children provide. Scaffolding good math talk is still a significant challenge for most primary and elementary teachers. Having a better understanding of the sorts of answers children give at different age levels, as well as increased opportunities to listen to children explain their thinking, can be helpful in building the expertise and experience needed for the exceedingly difficult task of constructing follow-up questions for children’s answers that will push their mathematical thinking to higher levels.
The third support for metacognitive processes that is built into the Number Worlds program is a Wrap-Up period that is provided at the end of each lesson. In Wrap-Up, the child who has been assigned the role of Reporter for the small-group problem-solving portion of the lesson (e.g., game play) describes the mathematical activity his or her group did that day and what they learned. The Reporter then takes questions from the rest of the class, and any member of the Reporter’s team can assist in providing answers. It is during this portion of the lesson that the most significant learning occurs because children have an opportunity to reflect on aspects of the number system they may have noticed during game play, explain these concepts to their peers, and acquire a more explicit understanding of the concepts in the process. Over time, Wrap-Up comes to occupy as much time in the math lesson as all the preceding activities (i.e., the Warm-Up activities and small-group problem-solving activities) put together.
With practice in using this format, teachers become increasingly skilled at asking good questions to get the conversation going and, immediately thereafter, at taking a back seat in the discussion so that children have ample opportunity to provide the richest answers they are capable of generating at that point in time. (Some wonderful examples of skilled teachers asking good questions in elementary mathematics classrooms are available in the video and CD-ROM products of the Institute for Learning [www.instituteforlearning.org].) This takes patience, a willingness to turn control of the discussion over to the children, and faith that they have something important to say. Even at the kindergarten level, children appear to be better equipped to rise to this challenge than many teachers, who, having been taught that they should assume the leadership role in the class,
often feel that they should dominate the discussion. Teachers who can rise to this challenge have found that their faith is amply rewarded by the sophistication of the explanations children provide, even at the kindergarten level; by the opportunities this occasion provides for assessing children’s growth and current understandings; and by the learning and achievement gains children demonstrate on standard measures.
WHAT SORTS OF LEARNING DOES THIS APPROACH MAKE POSSIBLE?
The Number Worlds program was developed to address three major learning goals: to enable children to acquire (1) conceptual knowledge of number as well as procedural knowledge (e.g., computational fluency); (2) number sense (e.g., an ability to use benchmark values, an ability to solve problems in a range of contexts); and (3) an interest in and positive attitude toward mathematics. Program evaluation for the most part has focused on assessing the extent to which children who have been exposed to the program have been able to demonstrate gains on any of these fronts. The results of several evaluation studies are summarized below.
The Number Worlds program has now been tried in several different communities in Canada and in the United States. For research purposes, the groups of students followed have always been drawn from schools serving low-income, predominantly inner-city communities. This decision was based on the assumption that if the program works for children known to be at risk for school failure, there is a good chance that it will work as well, or even better, for those from more affluent communities. Several different forms of evaluation have been conducted.
In the first form of evaluation, children who had participated in the kindergarten level of the program (formerly called Rightstart) were compared with matched controls who had taken part in a math readiness program of a different sort. On tests of mathematical knowledge, on a set of more general developmental measures, and on a set of experimental measures of learning potential, children who had participated in the Number Worlds program consistently outperformed those in the control groups (see Box 6-1 for findings from one of these studies).14 In a second type of evaluation, children who had taken part in the kindergarten level of the program (and who had graduated into a variety of more traditional first-grade classrooms) were followed up 1 year later and evaluated on an assortment of mathematical and scientific tests, using a double-blind procedure. Once again, those who had participated in the Number Worlds program in kindergarten were found to be superior on virtually all measures, including teacher evaluations of “general number sense” (see Box 6-2).15
The expansion of the Number Worlds program to include curricula for first and second grades permitted a third form of evaluation—a longitudinal study in which children were tracked over a 3-year period. At the beginning of the study and the end of each year, children who had participated in the Number Worlds program were compared with two other groups: (1) a second low-socioeconomic-status group that had originally been tested as having superior achievement in mathematics, and (2) a mixed-socioeconomic-status (largely middle-class) group that had also demonstrated a higher level of performance at the outset and attended an acclaimed magnet school with a special mathematics coordinator and an enriched mathematics program. These three groups are represented in the figure of Box 6-6, and the differences between the magnet school students and the students in the low-socioeconomic-status groups can be seen in the different start positions of the lines on the graph. Over the course of this study, which extended from the beginning of kindergarten to the end of second grade, children who had taken part in the Number Worlds program caught up with, and gradually outstripped, the magnet school group on the major measure used throughout this study—the Number Knowledge test (see Box 6-6). On this measure, as well as on a variety of other mathematics tests (e.g., measures of number sense), the Number Worlds group outperformed the second low-socioeconomic-status group from the end of kindergarten onward. On tests of procedural knowledge administered at the end of first grade, they also compared very favorably with groups from China and Japan that were tested on the same measures.16
These findings provide clear evidence that a program based on the principles of How People Learn (i.e., the Number Worlds program) works for the population of children most in need of effective school-based instruction—those living in poverty. In a variety of studies, the program enabled children from diverse cultural backgrounds to start their formal learning of arithmetic on an equal footing with their more-advantaged peers. It also enabled them to keep pace with their more-advantaged peers (and even outperform them on some measures) as they progressed through the first few years of formal schooling and to acquire the higher-level mathematics concepts that are central for continued progress in this area. In addition to the mathematics learning and achievement demonstrated in these studies, two other findings are worthy of note: both teachers and children who have used the Number Worlds program consistently report a positive attitude toward the teaching and learning of math. For teachers, this often represents a dramatic change in attitude. Math is now seen as fun, as well as useful, and both teachers and children are eager to do more of it.
|
BOX 6-6 As the figure below shows, the magnet school group began kindergarten with substantially higher scores on the Number Knowledge test than those of children in the Number Worlds and control groups. The gap indicated a developmental lag that exceeded one year, and for many children in the Number Worlds group was closer to 2 years. By the end of the kindergarten year, however, the Number Worlds children had narrowed this gap to a small fraction of its initial size. By the end of the second grade, the Number Worlds children actually outperformed the magnet school group. In contrast, the initial gap between the control group and the magnet school group did not narrow over time. The control group children did make steady progress over the 3 years; however, they were never able to catch up. 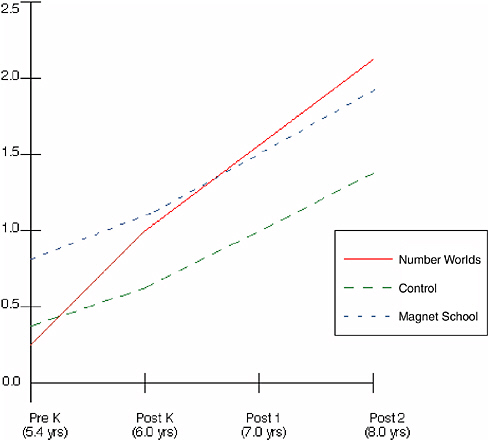 Mean developmental level scores on Number Knowledge test at four time periods. |
SUMMARY AND CONCLUSION
It was suggested at the beginning of this chapter that the teaching of whole-number concepts could be improved if each math teacher asked three questions on a regular basis: (1) Where am I now? (in terms of the knowledge children in their classrooms have available to build upon); (2) Where do I want to go? (in terms of the knowledge they want all children in their classrooms to acquire during the school year); and (3) What is the best way to get there? (in terms of the learning opportunities they will provide to enable all children in their class to reach the chosen objectives). The challenges these questions pose for primary and elementary teachers who have not been exposed in their professional training to the knowledge base needed to construct good answers were also acknowledged. Exposing teachers to this knowledge base is a major goal of the present volume. In this chapter, I have attempted to show how the three learning principles that lie at the heart of this knowledge base—and that are closely linked to the three questions posed above—can be used to improve the teaching and learning of whole numbers.
To illustrate learning Principle 1 (eliciting and building upon student knowledge), I have drawn from the cognitive developmental literature and described the number knowledge children typically demonstrate at each age level between ages 4 and 8 when asked a series of questions on an assessment tool—the Number Knowledge Test—that was created to elicit this knowledge. To address learning Principle 2 (building learning paths and networks of knowledge), I have again used the cognitive developmental literature to identify knowledge networks that lie at the heart of number sense (and that should be taught) and to suggest learning paths that are consistent with the goals for mathematics education provided in the NCTM standards.17 To illustrate learning Principle 3 (building resourceful, self-regulating mathematics thinkers and problem solvers), I have drawn from a mathematics program called Number Worlds that was specifically developed to teach the knowledge networks identified for Principle 2 and that relied heavily on the findings of How People Learn to achieve this goal. Other programs that have also been developed to teach number sense and to put the principles of How People Learn into action have been noted in this chapter, and teachers are encouraged to explore these resources to obtain a richer picture of how Principle 3 can be realized in mathematics classrooms.
In closing, I would like to acknowledge that it is not an easy task to develop a practice that embodies the three learning principles outlined herein. Doing so requires continuous effort over a long period of time, and even when this task has been accomplished, teaching in the manner described in this chapter is hard work. Teachers can take comfort in the fact the these efforts will pay off in terms of children’s mathematics learning and achievement; in the positive attitude toward mathematics that students will acquire
and carry with them throughout their lives; and in the sense of accomplishment a teacher can derive from the fruits of these efforts. The well-deserved professional pride that this can engender, as well as the accomplishments of children themselves, will provide ample rewards for these efforts.
ACKNOWLEDGMENTS
The development of the Number Worlds program and the research that is described in this chapter were made possible by the generous support of the James S. McDonnell Foundation. The author gratefully acknowledges this support, as well as the contributions of all the teachers and children who have used the program in various stages of development, and who have helped shape its final form.
NOTES
REFERENCES
Ball, D.L. (1993). With an eye on the mathematical horizon: Dilemmas of teaching elementary school mathematics. Elementary School Journal, 93(4), 373-397.
Carpenter, T., and Fennema, E. (1992). Cognitively guided instruction: Building on the knowledge of students and teachers. International Journal of Research in Education, 17(5), 457-470.
Case, R., and Griffin, S. (1990). Child cognitive development: The role of central conceptual structures in the development of scientific and social thought. In E.A. Hauert (Ed.), Developmental psychology: Cognitive, perceptuo-motor, and neurological perspectives (pp. 193-230). North-Holland, The Netherlands: Elsevier.
Cobb, P., Yackel, E., and Wood, T. (1988). A constructivist approach to second grade mathematics. In E. von Glasserfeld (Ed.), Constructivism in mathematics education. Dordecht, The Netherlands: D. Reidel.
Dehaene, S., and Cohen, L. (1995). Towards an anatomical and functional model of number processing. Mathematical Cognition, 1, 83-120.
Damerow, P., Englund, R.K., and Nissen, H.J. (1995). The first representations of number and the development of the number concept. In R. Damerow (Ed.), Abstraction and representation: Essays on the cultural evolution of thinking (pp. 275-297). Book Series: Boston studies in the philosophy of science, vol. 175. Dordrecht, The Netherlands: Kluwer Academic.
Fuson, K. (1997). Snapshots across two years in the life of an urban Latino classroom. In J. Hiebert (Ed.), Making sense: Teaching and learning mathematics with understanding. Portsmouth, NH: Heinemann.
Gelman, R. (1978). Children’s counting: What does and does not develop. In R.S. Siegler (Ed.), Children’s thinking: What develops (pp. 213-242). Mahwah, NJ: Lawrence Erlbaum Associates.
Griffin, S. (1997). Number worlds: Grade one level. Durham, NH: Number Worlds Alliance.
Griffin, S. (1998). Number worlds: Grade two level. Durham, NH: Number Worlds Alliance.
Griffin, S. (2000). Number worlds: Preschool level. Durham, NH: Number Worlds Alliance.
Griffin, S. (in press). Evaluation of a program to teach number sense to children at risk for school failure. Journal for Research in Mathematics Education.
Griffin, S., and Case, R. (1996a). Evaluating the breadth and depth of training effects when central conceptual structures are taught. Society for Research in Child Development Monographs, 59, 90-113.
Griffin, S., and Case, R. (1996b). Number worlds: Kindergarten level. Durham, NH: Number Worlds Alliance.
Griffin, S., and Case, R. (1997). Re-thinking the primary school math curriculum: An approach based on cognitive science. Issues in Education, 3(1), 1-49.
Griffin, S., Case, R., and Sandieson, R. (1992). Synchrony and asynchrony in the acquisition of children’s everyday mathematical knowledge. In R. Case (Ed.), The mind’s staircase: Exploring the conceptual underpinnings of children’s thought and knowledge (pp. 75-97). Mahwah, NJ: Lawrence Erlbaum Associates.
Griffin, S., Case, R., and Siegler, R. (1994). Rightstart: Providing the central conceptual prerequisites for first formal learning of arithmetic to students at-risk for school failure. In K. McGilly (Ed.), Classroom lessons: Integrating cognitive theory and classroom practice (pp. 24-49). Cambridge, MA: Bradford Books MIT Press.
Griffin, S., Case, R., and Capodilupo, A. (1995). Teaching for understanding: The importance of central conceptual structures in the elementary mathematics curriculum. In A. McKeough, I. Lupert, and A. Marini (Eds.), Teaching for transfer: Fostering generalization in learning (pp. 121-151). Mahwah, NJ: Lawrence Erlbaum Associates.
Hiebert, J, (1997). Making sense: Teaching and learning mathematics with understanding. Portsmouth, NH: Heinemann.
Lampert, M. (1986). Knowing, doing, and teaching multiplication. Cognition and Instruction 3(4), 305-342.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics.
Schifter, D., and Fosnot, C. (1993). Reconstructing mathematics education. New York: Teachers College Press.
Schmandt-Basserat, D. (1978). The earliest precursor of writing. Scientific American, 238(June), 40-49.
Siegler, R.S., and Robinson, M. (1982). The development of numerical understanding. In H.W. Reese and R. Kail (Eds.), Advances in child development and behavior. New York: Academic Press.
Starkey, P. (1992). The early development of numerical reasoning. Cognition and Instruction, 43, 93-126.