1
Introduction
The National Research Council’s Committee on Programs for Advanced Study of Mathematics and Science in American High Schools (parent committee) formed the mathematics panel to provide advice on the effectiveness of and potential improvements to programs for the advanced study of mathematics in U.S. high schools.1 In accordance with its charge (see Appendix A) the panel focused its work on the Advanced Placement (AP) and International Baccalaureate (IB) programs.
A member of the parent committee chaired the panel. This individual also served as the panel’s liaison to the committee and consolidated the panel’s findings and recommendations into this report. The five other panel members represent university and high school mathematics faculty with a wide range of teaching experiences and a diversity of perspectives on mathematics education (for biographical sketches, see Appendix B).
In conducting this study, the panel examined two AP courses—Calculus AB and Calculus BC—and three of the four mathematics courses offered by the International Baccalaureate Organisation (IBO)—Mathematical Methods Standard Level (SL),2 Mathematics Higher Level (HL), and Further Mathematics SL.3 The panel’s analysis was informed primarily by a range of program materials, such as published mission statements, course outlines, teacher guides, sample syllabi, released examinations, and scoring rubrics provided by the College Board and the IBO; scholarly research related to the teaching
|
1 |
The mathematics panel is one of four panels convened by the parent committee. Each panel represented one of the four disciplines that were the focus of the committee’s study: biology, chemistry, physics, and mathematics. The reports of the other panels and the report of the full committee are available at www.nap.edu/catalog/10129.html [4/23/02]. |
|
2 |
It is the hours of contact time, not necessarily the level of course difficulty, that determines whether a course is designated as SL or HL. |
|
3 |
The panel did not review Mathematical Studies SL because it is a basic rather than an advanced course. |
and learning of mathematics; and the combined experience and expertise of the panel members (College Entrance Examination Board, 1987, 1989, 1992, 1993, 1994, 1995, 1996a, 1996b, 1997a, 1997b, 1998a, 1998b, 1999a, 1999b, 1999c, 1999d, IBO, 1993, 1997, 1998a, 1998b, 1998c, 1998d, 1999a, 1999b, 1999c, 1999d, 1999e, 1999f, 1999g.,1999h, 1999i, 1999j, 1999k,.1999l; 1999m; Kennedy, 1997). The panel also considered two College Board studies addressing AP student achievement in college (Morgan and Ramist, 1998; Willingham and Morris, 1986) and several studies that examined the subsequent performance of IB students in college.4 The panel found surprisingly few other data on AP and IB on which to base its evaluation.5
For example, little is known, except anecdotally, about how either program is implemented in U.S. high schools, including the instructional strategies and resources used in individual classrooms, the structure of the syllabi in different schools, the quantity and quality of the facilities available, the preparation of teachers who teach the courses, and the ways in which students are prepared prior to enrolling in AP calculus or advanced IB mathematics courses. Information about the AP and IB assessments is also limited. The IBO currently conducts no systematic research addressing the validity,6 reliability,7 or comparability8 of its assessments across administrations. The senior examiners, not psychometricians, make determinations about the degree to which each administration is a valid and reliable measure of student achievement. The College Board, on the other hand, has gathered considerable data to demonstrate the reliability and comparability of student scores from one administration to the next and from one student to another. However, neither program has a strong program of validity research, and
|
4 |
Downloaded from www.rvcschools.org in August 2000. |
|
5 |
Although few data currently exist, the panel notes that both programs have circulated requests for proposals to conduct research on the ways in which their respective programs are implemented in schools and classrooms and the effects of these different implementations on student learning and achievement. No data from any of these studies were available at the time this report was prepared. |
|
6 |
Validity addresses what a test is measuring and what meaning can be drawn from the test scores and the actions that follow. It should be clear that what is being validated is not the test itself, but each inference drawn from the test score for each specific use to which the test results are put. |
|
7 |
Reliability generally refers to the stability of results. For example, the term denotes the likelihood that a particular student or group of students would earn the same score if they took the same test again or took a different form of the same test. Reliability also encompasses the consistency with which students perform on different questions or sections of a test that measure the same underlying concept, for example, energy transfer. |
|
8 |
Comparability generally means that the same inferences can be supported accurately by test scores earned by different students, in different years, on different forms of the test. That is, a particular score, such as a 4 on an AP examination, represents the same level of achievement over time and across administrations. |
neither has gathered data to document that the test items on its examinations measure the skills and cognitive processes they purport to measure. To fully analyze or evaluate the AP and IB assessments, it is necessary to know, for example, that test items intended to measure problem solving do in fact tap those skills and do not just elicit memorized solutions or procedures.
Further, little evidence is available for evaluating the long-term effects of the AP and IB programs. For instance, the panel could not find systematic data on how students who participate in AP and IB fare in college mathematics relative to other students. Nor could the panel find studies that examined the effects on postsecondary mathematics programs of the ever-increasing numbers of students who are entering college with credit or advanced standing in mathematics. While the College Board and a few colleges that receive IB students have conducted some isolated studies addressing how AP or IB students perform in college (see, for example, Morgan and Ramist, 1998), the inferences that can accurately be drawn from the findings of these studies are ambiguous (see Chapter 10 of the parent committee’s report).
Because empirical evidence about the programs’ quality and effectiveness is lacking, the panel focused its analysis on what the programs say they do, using available program materials. This report details the panel’s findings about the programs based on its analysis of these materials, its advice to the committee regarding the major issues under its charge, and the types of evidence that are needed to enable more complete appraisal of the AP and IB mathematics programs—evidence that is urgently needed.
Before proceeding to report its findings and recommendations, the panel wishes to commend the College Board and the IBO for the ways in which they have responded to changes in the teaching of mathematics: AP by changing its syllabus and introducing technology; IB by introducing portfolio projects and technology. Both organizations have undertaken these changes in a balanced, reasoned way, with input from a wide range of communities. Considering that they are large organizations affecting thousands of students, teachers, universities, and colleges, both AP and IB have made significant and forward-looking changes remarkably successfully. The panel additionally commends the College Board for helping to bring together college faculty and high school teachers in collaborative efforts to improve the teaching of calculus across the secondary and postsecondary levels. These efforts have paid off in more coherent syllabi that are better aligned with what is known about the ways in which students learn mathematics.
While the IBO’s collaborations with IB teachers are an important aspect of the development of IB programs and assessments, collaborations outside of the IBO network, for example, with professional disciplinary societies or colleges and universities, currently are not part of the approach taken to program development. As the IB program becomes more prominent in the
United States, the panel encourages the IBO to expand its collaboration efforts to include more members of the U.S. mathematics community. These types of collaborative efforts can increase public awareness of the program and its relationship to the calculus typically taught in U.S. high schools, colleges, and universities.
The remainder of this report is organized into five chapters. Chapter 2 provides an overview of the AP and IB programs in mathematics. Chapters 3 and 4 present, respectively, the panel’s analyses of curriculum and assessment and of teacher preparation and professional development in the two programs. The impact of the programs is examined in Chapter 5. Throughout these four chapters, the panel’s key findings are presented in italic type. Finally, the panel’s recommendations are given in Chapter 6.
2
Overview of the AP and IB Programs in Mathematics
Although the Advanced Placement (AP) and International Baccalaureate (IB) programs serve similar populations of highly motivated high school students, the College Board and the International Baccalaureate Organisation (IBO) developed their programs for different purposes. These different purposes affect how the individual courses are developed, structured, and implemented; how student learning is assessed; and how assessment results are used. They also affect how teachers who are assigned to teach AP and IB courses are prepared and supported by the programs and what types of school resources must be allocated for the programs.
Detailed information about the history, mission, goals, and growth of the AP and IB programs is available from the College Board and the IBO (see the organizations’ Web sites9). This report includes only information directly relevant to the panel’s analysis, findings, and recommendations. A more complete discussion of the AP and IB programs can be found in the parent committee’s report (Chapters 3 and 4, respectively).
THE ADVANCED PLACEMENT PROGRAM
Since its inception in the 1950s, the goal of the AP program has been to offer interested, motivated, and well-prepared students the opportunity to tackle college-level material and to earn college credit while they are still in high school. To this end, AP courses are designed to be equivalent to college courses in the corresponding subject area. Standardized, nationally administered, comprehensive achievement examinations that are offered annually in May provide a vehicle for students to demonstrate mastery of the
college-level material and to earn college credit or advanced placement in upper-level college courses with qualifying scores.10
The AP mathematics program consists of statistics11 and two levels of calculus—AB and BC.12 Both AB and BC concentrate on calculus of a function of a single variable. Consistent with the purpose of the program, AP courses are designed by a development committee comprised of university faculty, mathematicians, and master calculus teachers to be equivalent to many introductory college calculus courses with respect to the range and depth of topics covered, the kinds of textbooks used, the kinds work done by students, and the time and effort required of students (College Entrance Examination Board [CEEB], 1999a). This approach ensures that students have a smooth transition to college, but also means that any shortcomings in college calculus are likely to be transferred to advanced high school students.
AP courses are designed to represent generic introductory-level college courses. The determination of the content to include in AP calculus courses is based on information gathered from responses to an annual survey of college and university departments that offer general calculus courses in their institutions. It should be noted that the response rate to the survey is rather low (30–40 percent), calling into question the consistency of survey results with actual course syllabi in individual schools and in different types of institutions.
Each year the College Board publishes the Advanced Placement Program Course Description: Calculus, AB and BC (often referred to as the Acorn Book). This booklet includes a topical outline for the two calculus courses,13 sample examinations, and information about how previous AP mathematics examinations have been graded (see, for example, CEEB, 1992,
|
10 |
The College Board allows colleges and universities to establish their own criteria for awarding credit or advanced placement. See Chapter 2 of the parent committee’s full report for additional information on this issue. |
|
11 |
Far more AP students enroll in AP calculus courses and take the related examinations than is the case for the statistics course, although the number of statistics students has been growing steadily since the course was first offered in the fall of 1997. To date, the College Board has identified 22,749 students who have taken both the AP Statistics and the AP calculus examinations; 54 percent took both examinations in the same year, 29 percent took the calculus examination first, and 17 percent took the statistics examination first (Gloria Dion, personal communication). Students who took both examinations earned slightly higher calculus grades than statistics grades. |
|
12 |
The AB curriculum is generally regarded as equivalent to one semester or two quarters of college calculus, whereas the BC curriculum is considered the equivalent of one year or three quarters of college calculus. |
|
13 |
The College Board publishes a separate guide for AP Statistics and for each of its other AP courses. |
1996b, 1999b). Although the booklet is published annually, changes from year to year are usually small, and sometimes there are no changes.14
There are no AP calculus curricula in the true sense of the word; there are only topic outlines. The topic outlines are intended to indicate the scope of the courses, but they do not necessarily suggest the order in which the topics are to be taught, nor do they specify any particular pedagogy.15 Teachers are free to determine the order in which topics are introduced, and they are also encouraged to enrich their courses with additional topics as appropriate. Thus as implemented, the curricula for AP courses can vary from school to school in both sequence and emphasis. The resulting curricula are often more a function of the decisions made by individual teachers than decisions made by a centralized curriculum development group.
The topical outline for AP Calculus BC includes all of the topics from AP Calculus AB plus additional topics (see Appendixes C and D, respectively, for the AB and BC topic outlines for May 2000/May 2001). AB and BC students are expected to understand topics common to both courses at the same conceptual level. Both AB and BC calculus are designed to be taught over one school year.16 Decisions about which AP calculus course an individual student should select are generally based on both the school’s offerings and the individual’s abilities, achievements, and mastery of the prerequisite material.
The International Baccalaureate Diploma Programme
The IB Diploma Programme, created in 1968, was originally designed to serve a geographically mobile population, primarily children of diplomats, who relocate frequently but do not want to lose the continuity of their educational experiences. Thus, the program incorporates elements of several national systems without being based on any particular one. IB courses do not reflect the content and structure of college courses but rather what is believed by the program developers to be the full range of content knowledge and skills that should be mastered by well-prepared students prior to
study at the university level. Thus the courses are developed not to replicate college courses but to reflect an international conception of a well-designed college preparatory program of study among a small group of master teachers and discipline experts who design the courses using both their expertise and information gathered systematically from IB teachers in every IB school. A curriculum review committee with international membership is responsible for articulating, implementing, and maintaining the vision in each subject area. The mathematics committee is also responsible for specifying the presumed knowledge and skills (prerequisites) for each of the four IB mathematics courses.
The IB mathematics curriculum is substantially broader than the AP calculus curricula. IB offerings include four mathematics courses: Mathematical Studies Standard Level (SL), Mathematical Methods SL, Mathematics Higher Level (HL), and Further Mathematics SL. Each course has been designed to meet the needs of a particular group of students, and schools and teachers are encouraged to exercise care in selecting the appropriate course for each student.17 Courses that are designated as SL require a minimum of 150 hours of teacher contact time, while those designated as HL require a minimum of 240 hours of teacher contact time. As noted earlier, it is the hours of contact time, not necessarily the level of course difficulty, that determines whether a course is designated as SL or HL (IBO, 1993). For example, Further Mathematics SL is the most advanced mathematics course in the IB program. Both SL and HL courses include a common core of compulsory topics (105 hours for the SL courses and 195 hours for the HL courses), as well as one or more optional topics that are selected by individual teachers for their classes (45 hours for both HL and SL courses). Because the IB program has an international mission, this flexibility in curriculum enables schools to satisfy higher education entrance requirements in many countries.
The IB Mathematics HL course is taught over two years and includes as core material a substantial amount of calculus, roughly equivalent to the AP Calculus AB course, as well as substantial treatment of probability, algebra and trigonometry, complex numbers, mathematical induction, vectors, and matrices. In addition, the HL curriculum has optional units, one of which is taught in addition to the common core. There are units on abstract algebra, graphs and trees, statistics, analysis and approximation, and Euclidean geometry and conic sections. With the analysis and approximation option, the calculus coverage becomes roughly equivalent to that of AP Calculus BC.
With the statistics option, the statistics coverage becomes roughly equivalent to the purely mathematical parts of AP Statistics (note, however, that AP Statistics devotes substantial attention to the nonmathematical aspects of statistics).
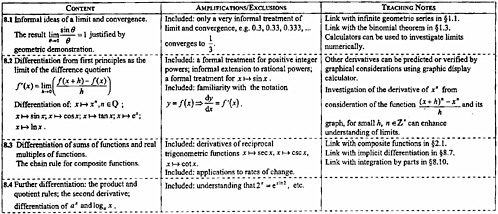
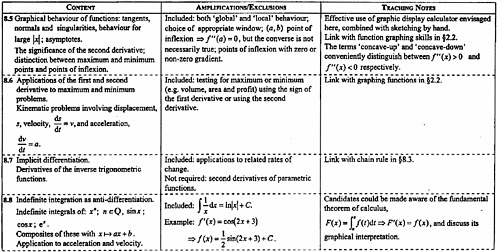
The IB program guides for the mathematics courses present the common aims and objectives for all Group 5 (mathematics) courses (see Box 2-1). The guides also provide a syllabus outline for each course (see Boxes 2-2 through 2-4). In addition to the syllabus outline, IB teachers are provided with a detailed syllabus that defines more explicitly what will be covered on the final examinations. The detailed syllabi include estimated teaching hours for each topic, but do not recommend a sequence for the presentation of topics (see Appendix E for an example of a detailed syllabus). IB mathematics program guides provide general guidance on instruction and offer specific suggestions regarding instructional strategies. The teaching notes also include suggestions for linking content to help students see connections, such as linking the study of the second derivative in the further calculus option to the study of exponents and logarithms in the core content. Teachers use the guides as the basis for determining the structure of their own curriculum. Thus as implemented, the curricula for IB courses, like those for AP courses, can vary from school to school in sequence and emphasis. Little is known about the nature of these variations and their effects on student learning and achievement.
Finding: The AP and IB programs are both designed to meet the educational needs of highly motivated and well-prepared students, but the origins, goals, purposes, missions, organizations, and structures of the two programs are very different. These differences contribute to variations in the educational expectations, opportunities, and experiences of students and teachers participating in the two programs.
AP AND IB TEST DEVELOPMENT
AP Program
AP calculus examinations are designed by a development committee comprised of high school teachers and university faculty in consultation with statisticians and psychometricians who attempt to create examinations that meet accepted standards for technical quality (American Educational Research Association/American Psychological Association/National Council on Measurement in Education, 1999). The development process incorporates the judgments of both disciplinary and psychometric experts. The AP calculus examinations are timed, with about 50 percent of the total time devoted to multiple-choice questions and the rest to free-response problem-
|
BOX 2-1 International Baccalaureate Mathematics Common Aims and Objectives AIMS
OBJECTIVES Having followed any one of the programmes in group 5 (mathematics), candidates will be expected to:
SOURCE: Adapted from IBO (1997, 1998a). |
|
BOX 2-2 Syllabus Outline Mathematical Methods—SL The mathematical methods SL programme consists of the study of six core topics and one option.
Five assignments, based on different areas of the syllabus, representing the following three activities:
SOURCE: Adapted from IBO (1997). |
||||||||||||||||||||||||||||||||||||||||||
|
BOX 2-3 Syllabus Outline Mathematics—HL The mathematical methods SL programme consists of the study of eight core topics and one option.
Five assignments, based on different areas of the syllabus, representing the following three activities:
SOURCE: Adapted from IBO (1998a). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
BOX 2-4 Syllabus Outline Further Mathematics—SL The mathematical methods SL programme consists of the study of six core topics and one option.
Three assignments, based on different areas of the syllabus, representing at least two of the following four activities:
SOURCE: Adapted from IBO (1997). |
|||||||||||||||||||||||||||
solving questions.18 The development committees are responsible for deciding the general content of the examination and the ability level to be tested.
Content specifications for AP calculus examinations are determined at the same time the topic outlines for the courses are developed. Examinations are constructed using the topic percentages from the AP course descriptions as a guideline for the distribution of questions. The development committee helps write and review test questions, as well as materials (including the AP course descriptions) that are distributed to schools. They work closely with College Board and Educational Testing Service (ETS) content specialists and psychometricians to ensure that the examination scores will mean the same thing from year to year and from student to student (CEEB, 1999a).
For optimal measurement, the development committee endeavors to design a multiple-choice section such that the average raw score is between 40 and 60 percent of the maximum possible raw score. Questions at varying levels of difficulty are included. Some previously administered questions are included to link the current form of the examination to previous forms, thus maintaining comparability from year to year and examination to examination. The committees write, select, review, and refine free-response questions. One important aspect of test development is determining which item type and format are best for assessing a given topic or skill area. AP development committee members work with AP content experts and ETS statisticians in making this determination (CEEB, 1999a). However, the College Board has not conducted any systematic research to determine whether particular test items actually measure the cognitive processes they purport to measure.
IB Program
IB mathematics assessments have two components—external and internal. The external assessment consists of a written examination that is administered internationally over a period of two days in May of each year (in November for split-session schools). The examinations test knowledge of both the core and optional topics. The internal assessment is a portfolio that represents the teacher’s formative assessment of students’ practical work judged against established assessment criteria.19 This component is conducted by teachers within the school environment and is moderated externally by the IBO. The Mathematical Methods SL portfolio consists of five assignments, based on different areas of the syllabus, representing the following three activities: mathematical investigation, extended closed-problem solving, and mathematical modeling. The Mathematics HL and Further Math-
ematics SL courses add mathematical research to the list of activities from which students and teachers can draw portfolio activities.
The course guide, which includes a detailed description of the content, skills, and understanding students are expected to master during the course, serves as the test blueprint. Amplifications and exclusions are provided for each topic. They provide more explicit information on specific subtopics and help define what is and is not required in terms of preparing students for the examination (see, for example, IBO, 1997, 1998b, 1998c, 1998d).
New questions are written for each external examination. Unlike the College Board, the IBO does not develop its examinations in consultation with psychometricians. Rather, it relies on the expertise of its senior examining team to prepare a different form of the examination that is approximately of the same level of difficulty as previous examinations. Test items are not field tested prior to administration, and reliability is not calculated. Items are not repeated from one administration to another. After each examination session, a sample of candidate responses is closely scrutinized to determine whether they are in line with expectations for each question. In addition, the IBO solicits comments from teachers about the suitability of the examination papers in achieving the examination’s objectives. Information gained in this manner is used in the preparation of future examinations. Like the College Board, the IBO does not conduct systematic research to determine whether particular test items actually measure the cognitive processes they are intended to measure.
3
Analysis of AP and IB Curricula and Assessments
To evaluate the appropriateness of the Advanced Placement (AP) calculus and International Baccalaureate (IB) mathematics programs for advanced high school students, the panel considered the degree to which the curricula and assessments of each emphasize four areas listed below. These areas represent the kind of mathematical learning the panel believes advanced mathematics students should experience in their high school calculus course:
-
Technical skill, including flexibility with symbolic manipulation, graphical representation, numerical approximation, and function notation
-
Conceptual understanding, including, for example, the derivative as a rate of change
-
Theory, including precise definitions, carefully reasoned mathematical arguments, and mathematical rigor
-
Applications and modeling, including situations in which students must set up the model (for example, choose a formula that represents a real situation)
CURRICULUM
AP Program
In the panel’s opinion, the topics on the AP syllabi are appropriate and well connected. A strength of the AP curricula and examinations is their focus on reasoning that integrates graphical, algebraic, numerical, and modeling viewpoints. In its current formulation, AP calculus pays careful attention to the central concept of function and to connections among the common ways (numerical, graphical, analytical, and verbal) of representing functions. There is likewise careful attention to developing the main concepts of differentiation and integration, including several interpretations of and applica-
tions for each. However, because AP calculus courses are designed to be general-purpose courses, the applications to real-world problems and situations tend to be limited to those that are most manageable, both conceptually and technically. There are relatively few applications requiring deeper investigation that might prove more memorable and provide better opportunities for interpretation and modeling.
The panel views the content of the AP courses as sufficient, given the assumption that the preparatory coursework provides a solid foundation for calculus. There is considerable anecdotal evidence, however, that students intending to take calculus are rushed through prerequisite courses without learning the material well enough. Mathematical sophistication takes time and should not be confused with knowledge of a catalog of mathematical facts and techniques. Additionally, because the AP examinations create the focus for the curriculum, and they do so quite effectively, material not on the AP assessments tends not to be taught either in calculus or in the prerequisite courses.
Further, particularly able AP students could profit from an AP course enriched by modeling activities and more attention to proof. In this sense, the panel sees the AP calculus programs as minimal rather than maximal courses for advanced study. Teachers should be encouraged to challenge their students with problems that may go beyond the scope of the syllabi, teaching a course that is more demanding than the tests. Doing so would result in students having a richer learning experience. For the preparation of mathematicians, the panel views the slight attention paid to proof by the AP courses as a deficiency.
IB Program
The panel found that a broad factual base of information is provided by the IB curricula for Mathematical Methods Standard Level (SL) and Mathematics Higher Level (HL). The curricula encompass an introduction to elementary calculus (similar to the AP program’s Calculus AB course) and additional areas of study selected by the teacher from among available options. However, the small number of hours suggested for study of each topic (50 hours for the introduction to calculus for Mathematics HL and 20 hours for Mathematical Methods SL) leads to the concern that students study each topic only at a procedural level. As compared with the AP program, the panel views the calculus portions of the IB curricula as “very traditional.” For example, question #6 on the Mathematics HL exam, Paper 1, November 1999, reads:
The area between the graph of y = ex and the x axis from x = 0 to x = k (k > 0) is rotated through 360° about the x axis. Find, in terms of k and e, the volume of the solid generated.
The panel views the branching away from calculus as a positive aspect of the IB program. Mathematics HL coupled with Further Mathematics SL requires students to show competence in elementary calculus, as well as an introductory understanding of probability, matrices and vectors, abstract algebra, graphs and trees, statistics, analysis and approximation, and either mathematical foundations or mathematical proof. While it would be wonderful for students to have an understanding of all these topics, the panel is concerned that the breadth of the curricula may force somewhat superficial coverage. The panel believes that a more beneficial alternative would be to help students develop a deeper and richer understanding of one or two of the mathematical topics and their applications.
The advanced options present teachers with an enormous challenge in trying to cover advanced material in a highly limited time frame. The abstract algebra option of Mathematics HL provides an example. In this option, both the extent and depth of the study of the subject are quite limited, necessarily so in view of the time available and the prior mathematical experience of the candidates. Therefore, the study of abstract algebra is confined to basic definitions and a few elementary properties. The focus is formal; no significant applications of groups are given. The difficult part of learning about groups is not the formal definitions and elementary properties but understanding why the ideas are important. The panel believes it is more useful for students to study deeply topics that are closer to the high school curriculum, such as the study of solutions of polynomial equations (with emphasis on 3rd- and 4th-order equations), the use of transformations in plane geometry, or elementary number theory. Students with these topics in their background will be better prepared to appreciate later the significance of group theory.
The IB curricula provide a strong foundation in the key concepts of college preparatory mathematics. The syllabi and the assessments, however, do not appear to promote the relationships among the mathematical concepts learned. The syllabus for Further Mathematics SL states: “At this level, less emphasis should be put on departmentalizing the various topics and more emphasis should be given to the links between topics. For example, the knowledge of complex numbers, recurrence relations and Newton’s method could be brought together in a brief introduction to fractals.” However, the assessment materials do not support this linkage but are strictly departmentalized. Waiting until the final year of advanced study to emphasize the links among topics with the portfolio assessment is too little, too late.
Finding: The AP curricula are largely sound. The recently revised syllabi with more emphasis on conceptual understanding have significantly improved
the program, although further change in this direction is desirable. The panel also believes the focus on reasoning should be increased.
Finding: The IB curricula are largely sound. The portfolio requirement, with its emphasis on applications of mathematics, is likely to introduce a focus on modeling that will benefit IB students. However, the calculus sections of the syllabi do not place enough emphasis on conceptual understanding. The panel also has some concern that the breadth of the curricula, although an attractive feature of the program, could lead to superficial learning.
Finding: AP and IB curricula are designed to prepare students for successful performance on end-of-course examinations. The content and structure of the examinations, therefore, have a profound effect on what is taught and how it is taught in AP and IB classrooms.
ASSESSMENTS
Research indicates that the problems students solve as part of their classes have a significant effect on the strength of the background they acquire. Since the types of problems that are on the end-of-course assessments largely determine the structure and content of classroom and homework problems, evaluation of the effectiveness of the programs must include an evaluation of the problems on the examinations.
AP Program
On the basis of the four areas of emphasis described above, the panel believes the AP examinations should include questions that emphasize the following:
-
Complex problems that may require significant technical skills
-
Problems that probe students’ conceptual understanding and take into account what research tells us about common misconceptions
-
Problems that require mathematical reasoning, clear exposition, and the ability to write precise mathematical statements
-
Problems in which students must construct a mathematical model from a verbal description
The panel reviewed 5 years of publicly released AP Calculus AB and AP Calculus BC examinations, related course descriptions, teachers’ guides, and scoring rubrics (College Entrance Examination Board [CEEB], 1989, 1993,
1997a, 1998a, 1999b, 1999d). This review focused primarily on the examinations that were administered after 1998, when the revised AP calculus courses were fully implemented. The following findings with regard to the AP calculus examinations (both AB and BC) emerged from the panel’s review.
Technical Skill
The goals of the AP program explicitly support the development of strong computational skills, both by hand and using technology. There is a reasonable balance of symbolic and graphical problems on AP calculus examinations. However, there are not many numerical problems, and more would be an improvement. The division of the examinations into two parts—one that allows the use of a graphing calculator and one that does not—is useful, ensuring that students acquire skills with both symbols and numerical approximations.
The need to cover in one 13/4-hour multiple-choice test all of the material from two semesters of calculus makes the tests broad with limited depth; thus, for example, only a modest amount of time is available for solving each problem. As a result, the chain rule is tested at a superficial level, and only routine integration-by-parts questions are given. Seldom do Taylor series questions go beyond the basics, for example, rarely to a composite series such as the first five terms of sin (x2)ex.
Student achievement on the examinations confirms that the goals for technical skills are not being met at a high level. The College Board’s analysis of grades earned on the 1998 AB examination indicated that fewer than 15 percent of the students who earned a 3 obtained a score above 23 out of 45 on the multiple-choice questions.20 Most of these multiple-choice questions tested very basic calculus knowledge. The panel speculates that the underlying reason students could not answer these questions was poor algebra skills rather than a lack of understanding of the necessary calculus. For example, on the 1998 AB exam, 75 percent of students who earned a grade of 3 were able to evaluate the integral in question #3, ![]() , but only 38 percent were successful when they had to separate the fraction and then integrate in question #7,
, but only 38 percent were successful when they had to separate the fraction and then integrate in question #7, ![]() .
.
It also appears that AP students taking the examination had not had enough practice solving nonstandard problems. For instance, on the 1998 AB exam, 75 percent of the students were able to differentiate the “harder” implicit function in question #6:
If then when x2 + xy = 10, ![]() .
.
However, only 36 percent were able to figure out that the second derivative of a linear function is zero and then integrate in question #11: If f is a linear function and a < x < b, then ![]() .
.
Question #3 of the free-response section of the 1998 AB examination was a problem about motion in which information was given in a graph and table, rather than the more usual formula. The score on this question (average 2.9 out of 9) was much lower than the scores on the two multiple-choice questions in which the position was given by a formula (questions #14 and #24, with 94 percent and 52 percent correct, respectively). This result suggests that although students had learned how to answer questions like #14 and #24, they had not fully understood the concept. The panel includes these data to illustrate its contention that some AP students can do very well on AP calculus examinations without understanding the underlying concepts. Further analysis of this kind is necessary and should be part of a systematic program of validity research.
Conceptual Understanding
In recent changes to the syllabi for AP calculus, the emphasis on calculus as a collection of techniques has decreased, and the emphasis on conceptual understanding of fundamental principles has increased. The panel applauds this change. The current syllabi and examinations acknowledge the importance of techniques but do not allow them to overwhelm the course.
AP assessment items emphasize the major concepts of calculus (e.g., functions, derivative, integral, the Fundamental Theorem). Furthermore, the items incorporate current perspectives on learning by emphasizing multiple representations (i.e., the rule of four) and by placing some items in real-world contexts. However, there are missed opportunities to include questions that address common student misconceptions identified by educational research (for example, in understanding the derivative, slope fields, and functions). In addition, the test does not place enough emphasis on ensuring that students are fluent with the symbolic language.
AP examination problems also sometimes reinforce the idea that mathematics is essentially procedural. The questions may be divided into so many parts that they become exercises in following instructions rather than in
choosing a strategy to solve a problem. For example, in 1998, the following problem was given on the AP Calculus BC exam:
A particle moves along the curve defined by the equation y = x3 – 3x. The x-coordinate of the particle, x(t), satisfies the equation
for t ≥ 0 with initial condition x(0) = –4.
(a) Find x(t) in terms of t.
(b) Find ![]() in terms of t.
in terms of t.
(c) Find the location and speed of the particle at time t = 4.
Note that parts (a) and (b) of this problem lead the student to the solution of part (c). Thus, solving this problem successfully involves executing each step correctly and seeing the connections among them. But suppose parts (a) and (b) were omitted. The problem would then take on a very different character: it would test whether a student can find a path to the solution rather than execute steps. The most talented students—those in BC Calculus—should have more practice with problems in which they must design a method or solution.
Theory and Proof
Theoretical questions do not appear explicitly on AP examinations; there is little emphasis on proof in the AP syllabi. In the last decade, however, the emphasis on conceptual understanding has increased in the examinations. For example, in the 1998 syllabi, the movement away from a “laundry list” of topics encouraged students to think about the key ideas rather than memorize problem types. The panel applauds this change. Indeed, further change in this direction would be welcome. The panel recommends the inclusion of one or two items that assess students’ understanding of the definition of the derivative. By this we mean including problems that assess understanding of the meaning of the definition of the derivative, not the ability to compute using the definition.
Applications and Modeling
The AP program does not make a sufficient attempt to connect calculus with other fields in a realistic way. There is a tendency to use applications of rather ritualistic and formulaic kinds and of limited difficulty. The test con-
centrates on a few prescribed applications (e.g., calculation of volumes) or gives applications that consist largely of interpretation of symbols or computations in a new context. Its problems have a “whiff” of application, but they are often jarringly unreal at a deeper level. For example, question #5 of the free-response section of the 1995 AB examination states:
… [W]ater is draining from a conical tank with height 12 feet and diameter 8 feet into a cylindrical tank that has a base area 400π square feet. The depth h, in feet, of the water in the conical tank is changing at the rate of h – 12 feet per minute.
And question #1 on the 1995 BC examination reads:
A particle moves in the xy plane so that its position at any time t, 0 ≤ t ≤ π, is given by ![]() and y(t) = 3 sin t.
and y(t) = 3 sin t.
It is difficult to imagine mechanisms that would make liquid or particles behave as described in these problems. In their attempt to make mathematics seem real, items of this sort may in fact contribute to the sense of many students that mathematics is disconnected from reality.
There is also a paucity of problems requiring substantial background development or technical facility for their solution. For example, there are no modeling problems in which students have to construct a function in an unfamiliar context. Students whose encounter with calculus does not include substantial applications and difficult problems are not likely to regard calculus as the immensely useful problem-solving and explanatory tool it in fact is. The panel notes that the portfolio component of the IB program does require students to perform mathematical investigations, extended closed-problem solving, and mathematical modeling.
The panel is concerned that the need to standardize AP has led to a course with the rough edges smoothed out as much as possible. However, a real appreciation of the subject may require experiencing those rough spots. This is the analog of laboratory work for science courses.
In conclusion:
-
The AP examinations are closely aligned with the topics included in the related “Course Description for the AP Calculus Program.”
-
Students who do well on the AP examinations can be considered fluent in the basic operations and key ideas of calculus.
-
The AP examinations are light in their expectations of technical skill (severity of symbolic calculations) and theory (precision in argument).
-
The AP examinations do not place enough emphasis on critical thinking, communication, and reasoning.
-
The problems on the AP examinations do not appear to be sufficiently difficult to fully assess important skills and conceptual understanding.
-
The AP examinations should include questions that ask students to interpret/explain their results.
-
The word problems used on the AP examinations are limited in scope. The examinations try for a veneer of reality by including problems that appear to be taken from real-life situations (e.g., water draining and particles moving), but better applications are needed.
-
The types of problems included on the AP examinations are somewhat formulaic and predictable from year to year. This creates a situation that encourages teachers to teach problem types rather than focusing on the development of students’ problem-solving skills and mathematical thinking. Research shows that when teachers know what problem types to expect on an examination, their students tend to focus on lower-level problem-solving behaviors.
-
It is the consensus of the panel that the AP examinations would be greatly improved and would encourage better teaching practices if they included fewer predictable problems and more challenging and interesting problems.
Finding: The AP examinations have improved under the current syllabi. The effort to promote conceptual understanding by asking nonstandard questions and requiring verbal explanations is excellent. For example, the fact that there is now a wider variety of applications of integration (and not from a prescribed list) encourages students to think about the meaning of an integral. The inclusion of graphing problems involving a parameter focuses attention on the behavior of a family of functions. The variety of representations of a function—by a graph and a table as well as by a formula—promotes a better understanding of the concept of function. However, the examination is still predictable enough for many students to do respectably well by mastering question types rather than concepts. The examination does not include enough problems that focus on conceptual understanding. More problems are needed that involve multiple steps, test technical skills in the context of applied problems, ask for interpretation and explanation of results, include substantial realistic applications of calculus, and test reasoning or theoretical understanding.
The panel acknowledges that including problems such as these on AP examinations, while providing important information about student learning and understanding, could increase testing time and add complexity to the scoring process. A careful analysis of the pros and cons of changing the AP examinations along the lines suggested above should therefore be conducted.
One possible solution to this dilemma might be to use multiple measures of student achievement that are administered over a period of time to compute a final AP grade, rather than to maintain exclusive reliance on a single 3-hour examination for determining what students have learned over 5 years of mathematics instruction.
IB Program
In conducting its analysis of the IB assessments, the panel reviewed the May and November 1999 examination papers for Mathematical Methods SL and Mathematics HL, the Group 5 Mathematics Guide (1993), and the 1998 updated course descriptions for Mathematical Methods SL and Mathematics HL, all published by the IBO (International Baccalaureate Organisation, 1999a, 1999b, 1999c, 1999d, 1999e, 1999f, 1999g, 1999h, 1999i, 1999j, 1999k). The panel’s analysis of the IB examinations suggests that considerable conceptual understanding is required for students to do well. However, the current level of emphasis on procedural knowledge does not appear to be appropriate given emerging research on the relative importance of conceptual knowledge. It appears that opportunities are missed throughout the examinations to connect procedural knowledge with conceptual knowledge. The panel is concerned that the procedural aspects of the IB examinations could lead to superficial instruction in the mathematics. The mathematical investigations, extended closed-problem solving, mathematical modeling, and mathematical research options for the internal portfolio assignments are a large step in the right direction to mitigate this problem.
Technical Skill
The overall technical level of the IB examinations is high compared with typical U.S. high school expectations. Some IB examination questions demand levels of technical accomplishment that the AP Calculus BC examination does not attempt. For example, the May 1999 examination for Mathematics HL, Paper 2, contains the following question 8, part (ii):
-
Using the trapezium rule and Simpson’s rule with 6 subintervals, evaluate the integral
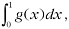
where g(x) is given at seven points by the following table.
|
x |
x0 = 0 |
x1 = 1/6 |
x2 = 2/6 |
x3 = 3/6 |
x4 = 4/6 |
x5 = 5/6 |
x6 = 1 |
|
g(x) |
1 |
0.97260 |
0.89483 |
0.77880 |
0.64118 |
0.49935 |
0.36789 |
-
Find the error estimate for Simpson’s rule in terms of g(4)(x).
-
When |g(4)(x)| ≤ 6, determine the number of subintervals required to use Simpson’s rule to obtain a value for the above integral, which is correct to five decimal places.
Items in Further Mathematics SL frequently require a high level of computational skill. Research on learning suggests that procedural fluency also influences students’ ability to utilize their mathematical knowledge. As a result, although the panel calls for an increase in conceptual focus, we do not advocate a decrease in the level of computational skill required.
Unlike the AP examinations, all IB examinations allow the use of calculators. The calculators must be of a preapproved type, which include graphing calculators, but not those with a computer algebra system. Although the IB examinations require substantial skill with symbol manipulations, they do not require much graphical and numerical skill. Few problems are primarily graphical or numerical. The numerical problems that appear more often concern numerical algorithms rather than use of numerical data.
The algebraic skills required for success on the IB examinations are impressive. The examinations often involve the use of parameters, which increases the difficulty of the resulting algebra. Most computations in the questions in Part 1 require two steps. For example, on the May 1999 examination for Mathematics HL, Paper 1, questions #6 and #12 are the following problems:
6. Find the value of a for which the following system of equations does not have a unique solution.
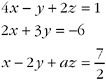
12. Given f(x)=x2 + x(2 – k) + k2, find the range of values of k for which f(x) > 0 for all real values of x.
The calculus included on the IB examinations is basic and focuses primarily on techniques. The functions do not appear to be chosen to simplify the computations. For example, in question #14 on the May 1999 examination for Mathematics HL, Paper 1, students were given ![]() and asked to find the interval where g″(t) > 0. However, the Subject Report coauthored later by the chief examiner and two deputy chief examiners states, “the errors resulting from messy answers [for g′(t)] were sad.” (IBO, 1999m). The
and asked to find the interval where g″(t) > 0. However, the Subject Report coauthored later by the chief examiner and two deputy chief examiners states, “the errors resulting from messy answers [for g′(t)] were sad.” (IBO, 1999m). The
fact that substitutions for integration and techniques for solving differential equations were given explicitly to the students greatly—and in the panel’s opinion, inappropriately—reduced the level of technical calculus skill required. Problems such as the following appear to be typical:
Using the substitution ![]() , or otherwise, find the integral
, or otherwise, find the integral ![]() .
.
Conceptual Understanding
Few questions on the IB examinations are focused explicitly on conceptual understanding. Many problems could be done procedurally if the teachers had taught this way or if students had done enough practice problems. However, there is such a broad range of topics on the examinations that it would be difficult for students to do well without understanding mathematical concepts.
The IB examinations test conceptual understanding indirectly. Many questions require a significant level of understanding to be solved in a practical manner. For example, consider question #16 from the May 1999 Mathematics HL exam, Paper 1:
Given that (1 + x)5 (1 + ax)6 =1 + bx + 10x2 + … + a6x11, find the values of a, b∈ Z*.
It is unreasonable for a student to multiply out the two expressions on the left to solve this problem; in practice, the student needs to understand which terms of the binomial expansions contribute to the unknown terms on the right. Problems requiring this level of conceptual understanding are not uncommon.
Very few IB examination problems require interpretation. Some IB questions also lead the student too much. In such cases, the student often does not need to decide what to do, as this is specified by the question; the “question” revolves around whether the student can perform the appropriate procedure accurately. (The integration problem on substitution given above is of this type.)
Theory and Proof
Few problems on the IB examinations involve anything resembling theory. Paper 2 of Mathematics or Further Mathematics may include problems on induction, as well as some problems requiring students to “prove” a simple
statement (for example, to show that cos x + cos 2x is periodic and even). However, many of these “proofs” involve only one step or a computation.
Applications and Modeling
The questions on the 1999 IB examinations for Mathematical Methods SL and Mathematics HL make almost no attempt to connect calculus with the real world (although the graph theory and statistics questions do feature quasirealistic settings). However, there is an emphasis on mathematical models in the portfolio section, which was initiated in 2000.
There were no problems on the 1999 IB examinations for Mathematics Methods SL and Mathematics HL in which students needed to develop a mathematical model. The statistical problems on the examinations were stated in an applied context, but the students were never required to decide what statistical technique was appropriate for that setting. Some problems had unrealistic modeling settings; others had settings that were never involved in the solution. For example, question #20 on the May 1999 examination for Mathematics HL, Paper 1, reads:
A particle moves along a straight line. When it is a distance s from a fixed point, where s > 1, the velocity v is given by ![]() . Find the acceleration when s = 2.
. Find the acceleration when s = 2.
In conclusion:
-
Including more conceptually focused prompts could strengthen IB test items. This shift in focus would increase the likelihood that instruction would assist students in both overcoming common misconceptions and acquiring a deeper understanding of the mathematical ideas.
-
Some IB questions are too focused on procedure. For example, almost all the integrals to be done by substitution have the substitution given explicitly. This has the effect of making the substitution problems “plug and chug.” Instead, students could be asked to (1) decide that the integral should be done by substitution and (2) be able to select an effective substitution.
-
The IB examination could be improved by including more conceptually focused prompts in items designed to assess students’ techniques for computing solutions.
-
The IB examinations could include prompts that demonstrate the ability to use computational procedures in solving complex problems.
The panel acknowledges that including problems such as these on IB examinations, while providing important information about student learning and understanding, could increase testing time. However, some IB testing
time might be recaptured and used more effectively if the IBO eliminated the easy prompts that are included to make students feel more comfortable in the testing situation and replaced them with the types of items described above. A careful analysis of the pros and cons of including more complex problems on the IB examinations should be conducted before a decision is made about how to accomplish this task.
Finding: The IB examinations benefit from being more varied than the AP examinations. However, a few examination questions are at too low a level as they ask students to perform algorithms specified in the problem. The examinations should include more problems that focus on conceptual understanding, and do not include enough problems that test whether students know which algorithm to apply (e.g., integration by substitution), test technical skills in the context of applied problems, ask for interpretation and explanation of results, and include substantial realistic applications.
Examination Practices
Beyond their impact on curriculum and pedagogy, AP and IB examinations play a critical role in student learning. Students who do not take the examination at the end of an AP or IB course are less likely to have a college-level experience. Virtually all of the students in IB mathematics courses take the end-of-course examination. Although the panel was unable to obtain precise figures, the director of the North American IBO office estimated that more than 90 percent of IB students take the examination. In contrast, College Board data suggest that nearly 40 percent of the students who enroll in AP calculus courses do not take the exam. It is unclear why this is so. Some students may decide not to take the examination because they expect not to do well. Others may not take it for financial reasons or because they plan to matriculate at a college where the score will not count. Since schools pay the College Board in June only for the examinations that are taken, many schools allow students to opt out at the last minute. It also is possible that because schools are under increased scrutiny for quality and AP examinations may be misused as a measure of quality, weaker students in AP courses may be discouraged from taking the examinations, thereby eliminating potentially low scores from the school’s analysis (see Chapter 10 of the parent committee’s report for further discussion of this issue).
Finding: Students who do not take the examination at the conclusion of an AP or IB course miss the opportunity to pull the material together for themselves. They also have a negative effect on the experience of other students by making the course appear to be less serious.
COMPARISON OF AP AND IB SYLLABI AND EXAMINATIONS
Comparison of the AP and IB syllabi and examinations led the panel to make the following observations:
-
Students who take AP Calculus AB or BC and AP statistics will likely know more calculus and more statistics but may know less precalculus (particularly vectors) than a student who completes an IB mathematics program.
-
Students who take IB mathematics will likely know more statistics than those who take AP Calculus AB or BC without AP statistics. The IB program provides more variety in topics than the AP program and appears to provide more quality assurance in the areas of algebra and trigonometry. As yet, however, there are no data on this point.
-
Both AP and IB examinations have little emphasis on modeling. However, the IB examinations reflect even less of an attempt than the AP examinations to connect to the real world.
-
The AP calculus examinations are still fairly predictable, even after the recent revisions to the syllabi. The IB examinations appear to be less consistent in style and content than the AP examinations, leading the panel to wonder whether IB questions are required to undergo less psychometric screening than AP questions. This situation has advantages and disadvantages. There is less predictability in the IB examination in any given year, and some innovative questions are included, such as question #3 on the November 1999 examination for Mathematics HL, Paper 2. Others, such as the question involving
 , benefit from not having been constructed primarily so they would be easy to grade. However, some IB problems suffer from apparently not having had the level of revision typical of AP questions. (An example is question #8 on the May 1999 Mathematics HL exam, Paper 1, whose correct answer, 4/5, can be obtained by the most obvious wrong method—confusing P(A|S), which is given, with P(S|A), which is the answer.)
, benefit from not having been constructed primarily so they would be easy to grade. However, some IB problems suffer from apparently not having had the level of revision typical of AP questions. (An example is question #8 on the May 1999 Mathematics HL exam, Paper 1, whose correct answer, 4/5, can be obtained by the most obvious wrong method—confusing P(A|S), which is given, with P(S|A), which is the answer.)
Finding: The problems on the AP and IB assessments are too predictable. This encourages teachers to focus on helping students recognize and solve particular problem types. A less predictable examination would encourage instruction focused on the development of students’ critical thinking and problem-solving abilities.
4
Teacher Preparation and Professional Development
The College Board publishes teachers’ guides and sponsors professional development activities for new and experienced teachers; however, it does not specify in its program materials the instructional strategies to be used by teachers. The International Baccalaureate (IB) mathematics program guides provide general guidance on instruction and also offer specific suggestions about instructional strategies. Teaching notes for each topic in the syllabus for each mathematics course provide suggestions for teachers while stating “it is not mandatory that these suggestions be followed” (International Baccalaureate Organisation [IBO], 1997, p. 8). The teaching notes also include suggestions for linking content to help students see connections, such as linking the study of the second derivative in the Further Calculus option to the study of exponents and logarithms in the core content (IBO, 1997, p. 23).
Neither program describes the professional qualifications required for teachers of its courses, nor do they provide guidance to schools and districts about the level of instructional resources that should be made available to teachers of advanced mathematics. Such resources include, for example, technology, class time, time for collaborative planning and reflection on professional practice, and opportunities for professional development (see below). The panel notes that this lack of specificity is intentional on the part of the IBO. Because IB is an international program offered in many countries with varying resources, the IBO prefers to let schools determine what resources they can make available in the context of their unique situations. The IBO believes specifying necessary resources would create an insur-mountable barrier for schools in poor nations or in poor school districts wishing to offer IB. As part of the process used to authorize schools to offer
IB, the IBO ascertains what resources the schools have and how they will be used to offer a quality program.21
Both the Adanced Placement (AP) and IB mathematics programs are expanding rapidly, and there is little reason to expect this growth to taper off in the near future. A natural consequence of this growth is an increased demand for well-qualified and well-prepared teachers to staff AP and IB mathematics classrooms. This increased demand comes at a time when there is already a shortage of qualified teachers who are prepared to teach advanced mathematics—a shortage that will be exacerbated by the large number of retirements expected during the next 10 years and a growing turnover rate among U.S. mathematics teachers. The teacher shortage is particularly notable in rural and inner-city schools (National Commission on Mathematics and Science Teaching for the 21st Century, 2000). Current professional development models will be insufficient to ensure adequate numbers of well-prepared and well-qualified AP and IB teachers.
This panel is united in asserting that professional development for teachers of mathematics, as for all teachers, must be a planned, collaborative, ongoing, and relevant process. It is not sufficient to offer one-time workshops, regardless of their length, nor is it prudent to assume that good teachers do not need ongoing support from professional communities. Burton et al. (2000) report that many AP teachers feel isolated and unsupported after leaving AP workshops and returning to their home school districts. AP and IB teachers need opportunities to experiment with new ideas about teaching and learning and to receive feedback about their teaching. Of paramount importance is the need for time to reflect on teaching and learning, both individually and with colleagues.
We draw support for these observations from the work of Liping Ma, a mathematics educator, whose 1999 book Knowing and Teaching Elementary Mathematics: Teachers’ Understanding of Fundamental Mathematics in China and the United States, sheds light on ways in which professional development for U.S. mathematics teachers can be improved. According to Ma, teachers in China report that their profound understanding of fundamental mathematics was often developed after becoming teachers. The main factors that contribute to Chinese teachers’ development of their profound understanding of fundamental mathematics include the following:
-
Learning from colleagues
-
Learning mathematics from their students
-
Learning mathematics by doing problems
-
Teaching round-by-round (teaching grades 1–6, or 1–3, 4–5, which develops an understanding of how mathematical concepts build upon each other through the grades)
-
Studying teaching materials intensively
Other important differences between U.S. and Chinese teachers include the following:
-
Chinese teachers spend more time preparing than teaching a lesson.
-
Chinese teachers are organized into “teaching research groups.”
-
Chinese teachers learn a great deal of mathematics from their colleagues. They are assigned mentors, with whom they have regular conversations about mathematics.
Teaching materials used by Chinese teachers generally consist of a framework, manuals, and a text. The framework outlines the concepts to be taught, and the manual provides the mathematics background for the corresponding textbook. The manual contains a section-by-section discussion of each topic in the textbook, focusing on the following:
-
What is the concept connected with the topic?
-
What are the important points in teaching the topic?
-
What are the difficult points in teaching the topic?
With Ma’s work in mind, the panel encourages the College Board, the IBO, and individual schools and school districts that offer AP and IB courses to plan, support, and provide professional development activities for AP and IB mathematics teachers that focus on increasing teachers’ subject matter knowledge, knowledge of how students learn mathematics, discipline-specific pedagogical knowledge, mastery of new topics or new approaches to the AP or IB syllabi, opportunities to generate and contribute new knowledge to the profession, and access to collegial communities of AP/IB teachers and to opportunities for collaborative work with college faculty.
AP and IB calculus teachers are often the best in their schools, and many compare favorably with teachers at any level. However, AP and IB teachers still need ongoing opportunities and incentives for professional development both to promote their understanding of the underlying mathematical content and to provide information about exemplary strategies for teaching the courses. These support systems might take one or more of the forms discussed below.
Workshops Prior to Teaching AB/IB. Both AP and IB teachers are offered optional workshops before beginning to teach an AP or IB course,
as well as workshops that cover advanced topics for more experienced teachers.22,23 However, a review of selected workshop materials suggests that some of these workshops may be as much administrative as mathematical in nature. The panel’s vision for an effective workshop is a format in which teachers are provided an opportunity to deepen their understanding of mathematics, as well as develop their pedagogical expertise.
Teachers’ Manuals/Background Information. The College Board and the IBO publish and distribute teachers’ manuals (Kennedy, 1997; IBO, 1998b, 1998c, 1998d). However, the panel does not find these materials to be optimally designed to promote the type of instruction emphasized in this report. The panel recommends that manuals be produced in collaboration with high school AP and IB teachers, mathematicians, and mathematics education researchers. The documents should be organized around major mathematical ideas of the AP and IB mathematics courses. We recommend that these manuals include sample questions and answers; text on the mathematical context in which a mathematical idea is situated; and the theoretical underpinnings, the common student misconceptions, and the process by which students acquire understanding. (Note that a new AP Calculus Teachers’ Guide was released in 2000, but the panel did not have the opportunity to review it.)
Mentoring Support: Colleagues and the Internet. An essential ingredient in ongoing teacher development is helping every teacher become part of a comfortable and reliable support group. Teachers, especially novice teachers, need a way to have their questions answered. They must feel comfortable sharing their inexperience with content and pedagogy with colleagues who can offer solutions and support. The best support group is usually departmental colleagues, but teachers of calculus are often the only
members of their departments who are assigned to teach this subject. Additionally, new teachers often express trepidation about professing their ignorance or inexperience regarding either mathematical content or pedagogical strategies for fear that doing so may compromise their academic position in the school or their assignment as an AP or IB teacher. When school colleagues cannot provide appropriate support, district or regional professional groups are an alternative. The College Board, through its regional offices, and the IBO are uniquely positioned to take a leadership role in helping to develop and support these professional communities of teachers.
In recent years, teachers have found an alternative on the Internet. The AP calculus and AP Statistics discussion groups on the Swarthmore College Web site have been highly successful in supporting beginning teachers. The online discussions have helped teachers deepen their understanding of the course content and improve their instructional techniques, particularly with regard to technology.24
In both discussion groups, more experienced high school teachers offer new teachers suggestions for instruction, help clarify content issues, and suggest references and resources to improve instruction. In addition to secondary teachers helping each other, the discussion groups have regular contributions from university faculty. The AP statistics discussion group is characterized by high-level support offered to high school teachers by leading statisticians. For example, the last two presidents of the American Statistical Association regularly offer background information at a fairly deep level to teachers on the topics in the AP curricula. Their responses to teachers’ questions reveal an understanding and recognition of both the teachers’ level of understanding of the content and the difficulties of teaching statistics. Some panel members note that this level of supportive response is not always true of the AP calculus discussion group. Some teachers who teach both statistics and calculus suggest that while they feel very comfortable asking questions in the statistics group, they hesitate to ask questions in the calculus group. This is the case in part because university mathematicians who participate in the discussions sometimes provide abrupt and condescending responses to questions. It is not uncommon for teachers to feel denigrated by the response, which ends their participation in the discussion.
School-Based Support for Teachers of Advanced High School Mathematics. Instruction for advanced students can be greatly improved by a coordinated effort among the staff teaching at all levels at a school. At a minimum, staff development is needed for precalculus and calculus teach-
|
24 |
The Swarthmore Web site is The Math Forum, http://forum.swarthmore.edu [4/23/02]. Both the College Board and the IBO also sponsor online discussion groups for mathematics teachers. |
ers. To address the development of mathematical stamina and persistence in students, staff development should include all teachers, from algebra to calculus.
Part of staff development involves providing a stronger foundation in content knowledge for all teachers. All mathematics teachers need to understand calculus so that students can begin working on its underpinnings in algebra. More important, however, staff development involves ongoing professional contact among colleagues at a school. School districts need to create working environments in which teachers have time to meet and discuss, reflect on, and refine instructional practices. School districts should also create mechanisms for teachers to participate in more structured professional development during contract hours. Currently, most teachers are required to participate in these activities, such as AP or IB teacher workshops, before or after school or during the summer, as suitable substitute teachers are not always available or affordable.
The need for more on-site staff development is particularly acute in schools that offer AP. The AP examinations help focus instruction but because they are so effective the materials that are not on the tests tend not to get taught in the prerequisite courses. These courses generally contain both students who eventually take AP calculus and those who do not. Thus, accommodations are made in prerequisite courses to ensure that all students are prepared to some extent for AP calculus. The AP calculus examinations have therefore become a 3-hour test that measures 5 years of instruction. To the extent that the test is superficial the previous 5 years of instruction will also be superficial. Staff development opportunities are needed for the staff to reclaim some ownership of the instructional output at a school.
Finding: Neither the College Board nor the IBO explicitly articulates in its published materials what it considers to be excellent teaching in mathematics.
Finding: The availability of high-quality professional development activities and the establishment of support networks for AP and IB mathematics teachers are crucial to promoting and maintaining excellence in these programs.
Finding: Adequate preparation of teachers for courses leading to calculus or other advanced study options is a critical factor in enabling students to succeed in the advanced courses.
Finding: U.S. teachers have few opportunities to deepen their understanding of mathematics during the school year, and opportunities during the summer, while useful, tend to be disconnected from everyday teaching.
5
Impact of the AP and IB Programs
Enrollment in Advanced Placement (AP) mathematics courses in the United States far outstrips enrollment in International Baccalaureate (IB) mathematics courses at all levels (see Table 5-1). Consequently, AP calculus has had and continues to exert a far greater influence than the IB courses on the secondary and collegiate mathematics courses offered in the United States. We therefore focus here on the impact of AP.
AP’S IMPACT ON MATHEMATICS IN GRADES 8–12
For most students, goals such as proficiency in problem solving, proof, and application may be more important than calculus. But realizing these goals takes time—time that is not available in a rushed curriculum. As we focus on the AP program and make suggestions for its improvement, we also must ask whether those suggestions will improve mathematics for all. On balance, the effect of AP calculus is probably to improve student achievement in mathematics. However, this is not the case for all students.
Because calculus requires 4 years of preparation, the AP calculus program has repercussions throughout the high school mathematics curriculum and even into the middle-school curriculum. Thus, the question of impact may be more important in mathematics than in the sciences. In some schools, the emphasis on preparing a classroom of students for AP calculus governs the curriculum for all other students. This impact has both positive and negative aspects. On the positive side, calculus helps counteract pressures to make high school mathematics easier. For example, such pressures have led to efforts by some programs to get more students to continue in mathematics by making Algebra II a less challenging course. The need to get students ready for the AP courses helps counter such pressures.
On the negative side, precalculus courses are condensed in some schools so that three semesters can be set aside to cover AP calculus (especially if the school plans to offer AP Calculus BC). This practice may send otherwise
TABLE 5-1 Comparison of Participation in AP and IB Mathematics Courses Based on Number of Examinations Administered
strong students to college with an inadequate background in algebra and trigonometry, which they will need for the study of science and engineering, as well as further mathematics. In addition, to complete 4 full years of mathematics prior to enrolling in AP calculus, students must either take a mathematics course over the summer or start algebra in grade 8.25 In the United States, few students take algebra before the ninth grade.26 Thus, the desire to have as many students as possible ready to take calculus by their senior year can lead to condensing the mathematics sequence in a fashion that creates long-term problems for some students. For example, students may choose to “double up” and take two mathematics courses in one year—usually geometry and Algebra II. Other students elect to go to summer school to learn geometry or Algebra II. Because they are compressed, summer courses often do not provide a solid background upon which to build higher-level concepts. High school teachers are aware of the dangers of shortchanging precalculus but are often powerless to resist the pressure from students and parents who believe that calculus on students’ transcripts will boost their chances for admission to college.
The idea that a large proportion of high school students should reach the level of calculus has led to many schools offering, and a significant number of students taking, non-AP and non-IB calculus courses—calculus
that is not at the college level.27 Many of these students also lack the necessary algebra and precalculus skills for successful calculus learning. Thus, students in these courses, as well as the less-prepared students in AP calculus courses, would be better served by strengthening their precalculus background and starting calculus in college. A solid background in precalculus is an essential tool for later study in the sciences and quantitative social sciences. The panel sees some merit in developing an AP-level precalculus course for these students (the panel notes that many colleges give credit for precalculus courses). Such a course would be more beneficial to these students than taking a less demanding calculus course or taking AP without adequate preparation, as it would help prepare them for the kind of thinking a good calculus course should require. This would be the ideal course in which to hold students accountable for remembering their mathematical knowledge acquired from algebra and applying it to precalculus. It would encourage the development of students’ ability to solve more difficult problems. A strong precalculus course would have the effect of reducing the amount of remediation (currently unacceptably large) that goes on in AP calculus and allowing the exploration of more difficult problems within that course.
Finding: The adequacy of the preparation students receive before taking calculus has an effect on whether they can understand calculus or merely do calculus. Without understanding, students cannot apply what they know and do not remember the calculus they have learned.
Finding: Many teachers and schools are under great pressure to compress algebra and trigonometry so they can prepare as many students as possible for calculus. Sometimes students spend too little time mastering the prerequisite knowledge and skills. The performance of many calculus students is undermined by the fact that they do not learn precalculus thoroughly or learn to solve problems and think mathematically. Thus, the rush to calculus may curtail their future options to pursue mathematics, science, and engineering. It is important to realize that it is not the structure or curriculum
|
27 |
In September 1986, the Mathematical Association of America (MAA) and the National Council of Teachers of Mathematics (NCTM) released a joint statement advocating that calculus courses taken in high school be at the college level, in other words, at the level of AP or IB. The statement was published in Calculus for a New Century (Steen, 1988). The MAA/NCTM statement includes the recommendation “that students who enroll in a calculus course in secondary school should have demonstrated mastery of algebra, geometry, trigonometry, and coordinate geometry. This means that students should have at least four full years of mathematical preparation beginning with the first course in algebra.” The panel supports this recommendation. The full text of the statement is in Appendix F. |
of the AP calculus courses that causes this problem but the way in which the program is used.
Finding: There are not enough checks in the system to ensure that students have the prerequisite algebra, trigonometry, and precalculus skills necessary for success in calculus and courses beyond.
Finding: The courses that precede calculus are often designed to help students make a smooth transition to an AP course. The topics and speed of prerequisite courses are determined by what is needed for AP. Even schools that do not offer AP calculus usually teach from books and curricula that are used in other schools to prepare students for this course. Thus, the AP curriculum influences many more courses and many more students than those who take the AP examinations.
IMPACT OF AP AND IB ON COLLEGE CALCULUS PROGRAMS
Although the intent of AP courses is to give students a head start on college-level work, many students take high school calculus and then repeat calculus in college. This group includes students who score well on the AP assessment but retake the course in college in the hope of receiving an A, students who take the AP course but do not take the examination, and students who take non-AP calculus courses. Although there are no data on the numbers of students in each category, anecdotally the result is college calculus classes in which only a few students have not had some calculus before. Students who have not had any calculus may feel at a disadvantage in this situation, although the data do not always support their concerns. It is interesting to note that many students who have had calculus in high school and repeat the course in college are also at a disadvantage because they do not devote sufficient attention to their college course, perhaps wrongly believing that they know calculus more deeply than they actually do.
ACCEPTANCE OF STUDENTS’ AP AND IB TEST RESULTS BY COLLEGES AND UNIVERSITIES
Students’ scores on AP calculus examinations are widely accepted by college and university mathematics departments for placement and/or credit. The amount of credit and final placement in advanced courses are dependent on which AP examination a student takes (AB or BC), the score that he/ she earns, and the college or university where the student seeks credit or advanced placement. Research conducted by the College Board and others
(see for example, University of California at Los Angeles, 2000) supports accepting scores of 4 or 5 for credit and/or placement. In one study, researchers administered the same calculus problems to AP calculus students who earned a score of 4 or 5 on the AP examination and students who completed a college calculus course. This study revealed that AP students who scored a 4 or 5 on the AP examination performed on these questions as well as or better than most of their college counterparts who received honor grades in the comparable college courses (College Entrance Examination Board [CEEB], 1999a).
The panel agrees with departmental policies that accept scores of 4 or 5 on an AP calculus examination as evidence that students have mastered knowledge and skills equivalent to those presented in an introductory college calculus course. Through legislative mandate, however, some publicly funded colleges are required to award credit or placement for scores of 3, and the panel is not convinced that such scores reflect sufficient mastery of the subject to warrant credit or placement. Students who earn a score of 3 or lower on an AP examination or 5 on an IB examination can present problems for colleges in terms of placement in introductory courses. The panel suggests that credit or placement should be awarded to students who earn a score of 3 on the AP examination on an individual basis and should be supported by additional evidence beyond examination performance.28
Scores earned on IB mathematics examinations are treated similarly to scores earned on AP calculus examinations. It should be noted, however, that the different levels at which IB courses and examinations can be taken and the variety of optional topics that are included in different classrooms add further considerations for awarding of credit and/or placement, as it is more difficult for a university mathematics department to know exactly what an IB student has learned.
The calculus portion of IB Mathematics HL, including the Approximation and Analysis option, is generally considered to be at least the equivalent of AP Calculus BC. The calculus portion of Mathematical Methods SL by itself is less than a full AP Calculus AB course. However, the majority of Mathematical Methods SL teachers in the United States teach a full calculus class that is equivalent to an AB Calculus course, even though this additional material is not required for the IB examination. Students who earn scores of 6 or 7 are usually regarded as having passed the equivalent of a college-level course. The exact course for which credit and further placement are awarded depends on the IB course and examination for which the student submits a score. Since many fewer students take IB than AP, acceptance of the IB score
is often based on analogy with AP, rather than on an evaluation of the particular strengths of the IB course. There is likely to be less topic-by-topic correspondence between IB courses and college courses than is the case for AP because of differences in the ways in which the IB and AP courses have been developed. However, research and experience appear to indicate that students who have been successful in the IB curriculum are as well prepared for further mathematics as those who have taken AP.29
Neither advanced placement nor acceleration is a goal of the IB program. The International Baccalaureate Organisation does not actively encourage colleges and universities to accept IB examination results for college credit and/or advanced placement in upper-level mathematics courses. Rather, the acceptance of these credits resulted through analogy to AP (conference notes, speech by Paul Campbell, Director of Operations, Internatonal Baccalaureate North America). Acceptance occurred slowly as parents, teachers, and students, on an individual basis at first, demonstrated to college registrars and mathematics departments that IB courses were equivalent to AP courses in rigor and content. It was this comparison that led to the acceptance of IB examination scores. Thus, understanding the use of IB examination scores for purposes of college credit and placement also requires understanding how AP gained widespread acceptance.
The College Board has done an admirable job in helping to establish and maintain communication between college and high school mathematics faculties so they can stay abreast of each other’s interests and concerns. Members of the AP test development committee, which is responsible for the AP calculus program, are drawn from both college and high school faculty. Every year a group of several hundred college and high school faculty meet for a week or more in early June to grade the free-response questions of that year’s AP examination. This provides an excellent opportunity for informal exchanges on mathematics and teaching and allows the College Board to monitor the reactions of college and high school faculty, as well as student responses to questions on the examination.30
|
29 |
We compare the preparation level of good IB students with that of good AP students because college and university faculty have had much more extensive experience with AP calculus than with IB mathematics. The panel is not implying that AP is the standard to be met. |
|
30 |
The College Board views its experiences with the revision of the AP calculus program as a potential model for ways in which to approach the redesign of other AP courses (Breland and Oltman, 2001). A detailed historical perspective on the communications among the College Board, mathematicians, teachers, and professional mathematics organizations that led to the creation of the new AP calculus courses was written by Dan Kennedy of the Baylor School and can be found on the College Board’s Web site: www.collegeboard.com [4/23/02]. |
Finding: Most college and university placement and credit practices that are based on student performance on AP calculus or IB mathematics examinations are reasonable.
UNINTENDED USES OF AP AND IB ENROLLMENT FIGURES AND EXAMINATION RESULTS
The media and others sometimes use AP and IB scores inappropriately as measures of quality for factors that are not related to the intended purposes of the courses or examinations. For example, some members of the media have proposed using the number of AP and IB courses offered in schools as a tool to rate and rank the schools against each other, possibly leading some schools to offer more AP or IB courses than they are able to support adequately with existing resources. Some schools use the results of AP or IB examinations to evaluate teachers, the consequence of which may be to discourage potentially low-scoring students from taking the courses or the examinations. It is not uncommon for selective colleges to view the existence of AP or IB courses on an applicant’s transcript as an important part of their evaluation of the student’s intellectual and academic motivations. Without any measure of the quality of the student’s achievement in such courses,31 however, this emphasis on the number of AP or IB courses on a transcript leads many students to enroll in the courses without a commitment to mastering the material. AP and IB enrollments are increasingly used as a policy lever, as a method of raising the standards and expectations for all students. This leads to negative consequences for students for whom advanced courses in general, and AP and IB mathematics in particular, may not be appropriate.
Finding: Data on the number of AP and IB courses offered by schools and the results of the examinations are sometimes used in ways for which they were not intended, thus creating situations that can be detrimental to student learning.
6
Recommendations
PREPARATION OF STUDENTS
1. All calculus taught in high school should be at the college level.
2. All students who enroll in Advanced Placement (AP) calculus should have had at least 4 years of college preparatory mathematics prior to AP calculus. The structure of International Baccalaureate (IB) mathematics courses is different, and this recommendation is not as applicable to them.
3. Strategies must be developed to ensure that students who enroll in calculus have an adequate background in algebra and trigonometry for subsequent work in mathematics and science.
PROFESSIONAL DEVELOPMENT
4. The professional development opportunities available to AP and IB teachers should be improved and expanded.
5. The College Board and the International Baccalaureate Organisation should ensure that adequate professional development opportunities are available to all AP and IB teachers.
6. Schools that choose to offer AP and IB programs must find ways to encourage all teachers to take part in professional development, perhaps by providing time during the school day rather than on nights and weekends.
7. The College Board should consider developing procedures to certify AP calculus teachers.
ASSESSMENT
8. The AP and IB examinations should vary more from year to year. If teachers expect that major ideas will be assessed rather than
specific problem types, it is likely that instruction will encourage the development of students’ critical thinking and problem-solving abilities. The AP and IB examinations must strike a balance between judging students’ conceptual understanding by asking unfamiliar probing questions and alarming teachers and students with a strange and unfamiliar test.
9. Both the AP and IB programs should maintain and increase their focus on conceptual understanding in their assessments.
10. To assess computational and procedural knowledge, students should be asked questions that demonstrate their ability to use these procedures in solving more complex problems.
11. All students enrolled in AP and IB courses ordinarily should take the relevant external examinations as part of the course requirements.32
12. AP and IB examinations should contain more emphasis on realistic applications, including those in which students have to set up the mathematical model.
|
32 |
The panel recognizes that policies must be developed to ensure that students without the financial means to take the tests are not penalized by this requirement. The panel notes that the College Board is investigating ways to increase the numbers of students who take the AP examination at the conclusion of an AP course. For more information, see the report of the Commission on the Future of the Advanced Placement Program, which is available at www.collegeboard.com [4/23/02]. |
References
American Educational Research Association, American Psychological Association, and National Council on Measurement in Education. (1999). Standards for educational and psychological testing. Washington, DC: American Educational Research Association.
Breland, H.M., & Oltman, P.K. (2001). An analysis of Advanced Placement (AP) examinations in economics and comparative government and politics (College Board Research Report 2001-4; ETS RR-01-17). New York: College Entrance Examination Board.
Burton, N.W., Bruschi, B., Kindig, L., & Courtney, R. (2000). Draft interim report of advanced placement research project—Documentation and evaluation of advanced placement summer institutes: Advanced placement new teacher needs study. New York: College Entrance Examination Board.
Campbell, P. (2000). International baccalaureate program. Presentation to the Committee on Programs for Advanced Study of Mathematics and Science in American High Schools, March 26, Irvine, CA.
College Entrance Examination Board. (1987). Advanced placement course description: Mathematics: Calculus AB, Calculus BC—May 1988 [acorn book]. New York: Author.
College Entrance Examination Board. (1989). Released exams: The entire 1988 AP calculus AB examination and key. New York: Author.
College Entrance Examination Board. (1992). Advanced placement course description: Mathematics: Calculus AB, calculus BC—May 1993, May 1994 [acorn book]. New York: Author.
College Entrance Examination Board. (1993). Released exams: 1993 AP calculus AB: Free-response scoring guide with multiple-choice section. New York: Author.
College Entrance Examination Board. (1994). College and university guide to the advanced placement program. New York: Author.
College Entrance Examination Board. (1995). AP mathematics: Calculus AB & BC– Free-response questions 1995. New York: Author.
College Entrance Examination Board. (1996a). AP calculus 1995 free-response questions. New York: Author.
College Entrance Examination Board. (1996b). Advanced placement course description: Mathematics: Calculus AB, calculus BC—May 1997 [acorn book]. New York: Author.
College Entrance Examination Board. (1997a). AP calculus 1996 free-response questions. New York: Author.
College Entrance Examination Board. (1997b). Advanced placement course description: Calculus: Calculus AB, calculus BC—May 1998, May 1999 [acorn book]. New York: Author.
College Entrance Examination Board. (1998a). Released exams: 1997 AP calculus AB and calculus BC. New York: Author.
College Entrance Examination Board. (1998b). Released exams: 1997 AP statistics. New York: Author.
College Entrance Examination Board. (1999a). Advanced placement technical manual 2000. New York: Author.
College Entrance Examination Board. (1999b). Released exams: 1998 AP calculus AB and calculus BC. New York: Author.
College Entrance Examination Board. (1999c). Advanced placement program course description: Statistics—May 1999, May 2000 [acorn book]. New York: Author.
College Entrance Examination Board. (1999d). 5-year set of free-response questions, calculus AB, calculus BC: 1995-1999. New York: Author.
Commission on the Future of the Advanced Placement Program. (2001). Access to excellence: A report of the Commission on the Future of the Advanced Placement Program. New York: College Entrance Examination Board.
Council of Chief State School Officers. (1999). State indicators of science and mathematics 1999: State trends and new indicators from the 1997–1998 school year. Washington, DC: Author
International Baccalaureate Organisation. (1993). Group 5 mathematics guide—For examination from May 1995 onwards—Edition 1.2. Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1997). Mathematical methods standard level. Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1998a). IB mathematics HL diploma programme guide 1998. Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1998b). Teacher support material: Further mathematics SL—The portfolio. Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1998c). Teacher support material: Mathematics HL—The portfolio. Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1998d). Teacher support material: Mathematical methods SL—The portfolio. Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1999a). Further mathematics SL specimen papers and markschemes (for the programme with first examinations in May 2000)—SPEC/540/S(1-2) and specimen/540/S(1-2)M. Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1999b). International baccalaureate mathematical methods standard level May 1999 exam—M99/520/S(1-2). Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1999c). International baccalaureate mathematical methods standard level November 1999 exam—N99/520/S(1-2). Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1999d). International baccalaureate mathematics higher level May 1999 exam—M99/510/H(1-2). Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1999e). International baccalaureate mathematics higher level November 1999 exam—N99/510/H(1-2). Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1999f). Markscheme May 1999 mathematical methods standard level—M99/520/S(1-2)M. Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1999g). Markscheme May 1999 mathematics higher level—M99/510/H(1-2)M. Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1999h). Markscheme November 1999 mathematical methods standard level—N99/520/S(1-2)M. Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1999i). Markscheme November 1999 mathematics higher level—N99/510/H(1-2)M. Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1999j). Mathematical methods SL specimen papers and markschemes (for the programme with first examinations in May 2000—SPEC/520/S(1-2) and Specimen/520/S(1-2)M. Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1999k). Mathematics HL specimen papers and markschemes (for the programme with first examinations in May 2000—SPEC/510/H(1-2) and Specimen/510/H(1-2)M. Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1999l). Subject reports—May 1999: Mathematical methods. Geneva, Switzerland: Author.
International Baccalaureate Organisation. (1999m). Subject reports—May 1999: Mathematics higher level. Geneva, Switzerland: Author.
Kennedy, D. (1997). Teacher’s guide: AP calculus. New York: College Entrance Examination Board.
Ma, L. (1999). Knowing and teaching elementary mathematics: Teachers’ understanding of fundamental mathematics in China and the United States. Mahwah, NJ: Earlbaum.
Morgan, R., & Ramist, L. (1998). Advanced placement student in college: An investigation of course grades at 21 colleges. Unpublished Statistical Report No. SR-98-13. Princeton, NJ: Educational Testing Service.
National Commission on Mathematics and Science Teaching for the 21st Century. (2000). Before it’s too late: A report to the nation from the National Commission on Mathematics and Science Teaching for the 21st Century. Jessup, MD: Education Publications Center.
National Research Council. (2000). How people learn: Brain, mind, experience, and school: expanded edition. Committee on Developments in the Science of Learning. J.D. Bransford, A.L. Brown, and R.R. Cocking (Eds.). Committee on Behavioral and Social Sciences and Education. Washington, DC: National Academy Press.
Steen, L.A. (Ed.). (1988). Calculus for a new century: A pump, not a filter. Washington, DC: Mathematical Association of America.
University of California at Los Angeles, Department of Mathematics. (2000). Performance of AP and non AP UCLA mathematics students on selected calculus placement problems. Unpublished manuscript. Los Angeles: Author.
Watkins, A.E., Roberts, R.A., Olsen, C.R., & Scheaffer, R. L. (1997). Teacher’s guide: AP statistics. New York: College Entrance Examination Board.
Willingham, W.W., & Morris, M. (1986). Four years later: A longitudinal study of advanced placement students in college (College Board Report No. 86-2; ETS RR No. 85-46). New York: College Entrance Examination Board.
Appendix A
Charge to the Content Panels from the Parent Committee
Charge to the Parent Committee and Content Panels: The charge to the committee is to consider the effectiveness of, and potential improvements to, programs for advanced study of mathematics and science in American high schools. In response to the charge, the committee will consider the two most widely recognized programs for advanced study: the Advanced Placement (AP) and the International Baccalaureate (IB) programs. In addition, the committee will identify and examine other appropriate curricular and instructional alternatives to IB and AP. Emphasis will be placed on the mathematics, physics, chemistry, and biology programs of study.
Charge to Content Panels: The content panels are asked to evaluate the AP and IB curricular, instructional, and assessment materials for their specific disciplines.
Below is a list of questions that the content panels will use to examine the curriculum, laboratory experiences, and student assessments for their specific subject areas. The content panels will use these questions to issue a report to the committee about the effectiveness of the AP and IB programs for educating able high school students in their respective disciplines. In answering these questions, the content panels should keep in mind the committee’s charge and study questions.
The panels should focus on the following specific issues in advising the committee:
I. CURRICULAR AND CONCEPTUAL FRAMEWORKS FOR LEARNING
Research on cognition suggests that learning and understanding are facilitated when students: (1) have a strong foundation of background knowledge, (2) are taught and understand facts and ideas in the context of a conceptual framework, and (3) learn how to organize information to facili-
tate retrieval and application in new contexts (see, e.g., National Research Council [NRC], 2000).
-
To what degree do the AP and IB programs incorporate current knowledge about cognition and learning in mathematics and science in their curricula, instructions, and assessments?
-
To what degree is the factual base of information that is provided by the AP and IB curricula and related laboratory experiences adequate for advanced high school study in your discipline?
-
Based on your evaluation of the materials that you received, to what extent do the AP and IB curricula and assessments balance breadth of coverage with in-depth study of important topics in the subject area? In your opinion, is this balance an appropriate one for advanced high school learners?
-
Are there key concepts (big ideas) of your discipline around which factual information and ideas should be organized to promote conceptual understanding in advanced study courses (e.g., Newton’s laws in physics)? To what degree are the AP and IB curricula and related laboratory experiences organized around these identified key concepts?
-
To what degree do the AP and IB curricula and related laboratory experiences provide opportunities for students to apply their knowledge to a range of problems and in a variety of contexts?
-
To what extent do the AP and IB curricula and related laboratory experiences encourage students and teachers to make connections among the various disciplines in science and mathematics?
II. THE ROLE OF ASSESSMENT
Research and experience indicate that assessments of student learning play a key role in determining what and how teachers teach and what and how students learn.
-
Based on your evaluation of the IB and AP final assessments and accompanying scoring guides and rubrics, evaluate to what degree these assessments measure or emphasize:
-
students’ mastery of content knowledge;
-
students’ understanding and application of concepts; and
-
students’ ability to apply what they have learned to other courses and in other situations.
-
-
To what degree do the AP and IB final assessments assess student mastery of your disciplinary subject at a level that is consistent with expectations for similar courses that are taught at the college level?
III. TEACHING
Research and experience indicate that learning is facilitated when teachers use a variety of techniques that are purposefully selected to achieve particular learning goals.
-
How effectively do the AP and IB curricula and assessments encourage teachers to use a variety of teaching techniques (e.g., lecture, discussion, laboratory experience and independent investigation)?
-
What preparation is needed to effectively teach advanced mathematics and science courses such as AP and IB?
IV. EMPHASES
The NRC’s National Science Education Standards and the National Council of Teachers of Mathematics’ Standards 2000 propose that the emphases of science and mathematics education should change in particular ways (see supplemental materials).
-
To what degree do the AP and IB programs reflect the recommendations in these documents?
V. PREPARATION FOR FURTHER STUDY
Advanced study at the high school level is often viewed as preparation for continued study at the college level or as a substitute for introductory-level college courses.
-
To what extent do the AP and IB curricula, assessments, and related laboratory experiences in your discipline serve as adequate and appropriate bases for success in college courses beyond the introductory level?
-
To what degree do the AP and IB programs in your discipline reflect changes in knowledge or approaches that are emerging (or have recently occurred) in your discipline?
-
How might coordination between secondary schools and institutions of higher education be enhanced to optimize student learning and continued interest in the discipline?
Appendix B
Biographical Sketches of Mathematics Content Panel Members
Harold Boger is currently a mathematics specialist for District G in the Los Angeles Unified School District. Previously he taught at Crenshaw High School. In addition to teaching AP calculus and AP statistics, he served as the chairman of the mathematics department and taught geometry, algebra with transformations, and the second and third levels of an integrated mathematics program. Mr. Boger’s thirteen years of outstanding teaching led to his selection as a visiting lecturer at the University of California at Los Angeles as part of the prestigious Visiting High School Teacher Program. He received his B.S. in Applied Mathematics and M.A.Ed. from the University of California at Los Angeles.
Marilyn P. Carlson is an associate professor in the department of mathematics at Arizona State University. Her research area is mathematics education with primary area of focus on cognitive aspects of knowing and learning major conceptual strands of first semester calculus. A National Science Foundation (NSF) CAREER Award is supporting her current development of concept assessment instruments for precalculus and beginning calculus and curricular materials for first semester calculus. She has recently been involved in developing two new Ph.D. programs in research in undergraduate mathematics education at Arizona State University. She is the coordinator for the MAA Special Interest Group, Research in Undergraduate Mathematics Education, and has been active in various professional organizations, including PME, PME-NA, National Council of Teachers of Mathematics (NCTM), Mathematical Association of America (MAA) and Association for Research in Undergraduate Mathematics Education (ARUME). Dr. Carlson received her Ph.D. in mathematics education from the University of Kansas.
Roger E. Howe has been a professor of mathematics at Yale University for over twenty-five years. He has been a visiting scholar at numerous universities, both in the United States and abroad. Recently, Dr. Howe was a Phi Beta Kappa visiting scholar. Dr. Howe is a member of the American Mathematical
Society (AMS), MAA, NCTM, the Connecticut Academy of Science and Engineering, the American Academy of Arts and Sciences, and the National Academy of Sciences (NAS). He is a former member of the Mathematical Sciences Education Board (MSEB). He serves on the board of directors of the Connecticut Academy for Education in Mathematics, Sciences and Technology, and was chairman of the AMS Review Group for revision of the NCTM Standards. He currently serves as chair of the AMS Committee on Education. Dr. Howe received his Ph.D. in mathematics from the University of California at Berkeley.
Daniel J. Teague teaches mathematics at The North Carolina School of Science and Mathematics in Durham, North Carolina. His twenty-five years of teaching at both the secondary and undergraduate levels have been recognized by awards such as the Tandy Technology Scholar Outstanding Teacher Award and the Presidential Award for Excellence in Mathematics Teaching. Dr. Teague’s previous National Research Council (NRC) experience includes appointments to the MSEB and the U.S. Commission on Mathematics Instruction. He received his Ph.D. in Mathematics Education from North Carolina State University where he completed his doctoral work in international comparisons of calculus education.
Alan C. Tucker is a professor with the Department of Applied Mathematics and Statistics at the State University of New York at Stony Brook. He has served the department for over 30 years, previously as the department chair and currently as associate department chair and undergraduate program director. Dr. Tucker currently heads the NSF-funded Long Island Consortium for Interconnected Learning, which explores the teaching and learning of mathematically based subjects through instruction, curricula, technology, and interdepartmental coordination. He has previously served the NRC with appointments to MSEB’s Undergraduate Math Advisory Board and the U.S. Commission on Mathematics Instruction. Dr. Tucker received his Ph.D. in Mathematics from Stanford University.
Deborah Hughes Hallett (committee liaison and chair) is a professor of mathematics at the University of Arizona; from 1991 to 1998 she was a Professor of Practice in the Teaching of Mathematics at Harvard University. She was a principal investigator for the NSF–funded Bridge Calculus Consortium. She has served on committees for the Graduate Record Examination and the Massachusetts state mathematics framework review process, and on the Mathematics and Science Teacher Education Program (MASTEP) Advisory Board, an NSF-funded program to improve teacher training in California. Dr. Hughes Hallett served on NRC’s Committee on Information Technology in Undergraduate Education. A Fulbright Scholar, she received M.A. degrees from both Harvard University and the University of Cambridge, England.
Appendix C
Topical Outline for AP Calculus AB
This outline of topics is intended to indicate the scope of the course, but it is not necessarily the order in which the topics are to be taught. Teachers may find that topics are best taught in different orders. (See the Teacher’s Guide—AP Calculus [Kennedy, 1997] for sample syllabi.) Although the examination is based on the topics listed in the topical outline, teachers may wish to enrich their courses with additional topics.
I. Functions, Graphs, and Limits
Analysis of graphs. With the aid of technology, graphs of functions are often easy to produce. The emphasis is on the interplay between the geometric and analytic information and on the use of calculus both to predict and to explain the observed local and global behavior of a function.
Limits of functions (including one-sided limits).
-
An intuitive understanding of the limiting process.
-
Calculating limits using algebra.
-
Estimating limits from graphs or tables of data.
Asymptotic and unbounded behavior.
-
Understanding asymptotes in terms of graphical behavior.
-
Describing asymptotic behavior in terms of limits involving infinity.
-
Comparing relative magnitudes of functions and their rates of change. (For example, contrasting exponential growth, polynomial growth, and logarithmic growth.)
Continuity as a property of functions.
-
An intuitive understanding of continuity. (Close values of the domain lead to close values of the range.)
-
Understanding continuity in terms of limits.
-
Geometric understanding of graphs of continuous functions (Intermediate Value Theorem and Extreme Value Theorem).
II. Derivatives
Concept of the derivative.
-
Derivative presented graphically, numerically, and analytically.
-
Derivative interpreted as an instantaneous rate of change.
-
Derivative defined as the limit of the difference quotient.
-
Relationship between differentiability and continuity.
Derivative at a point.
-
Slope of a curve at a point. Examples are emphasized, including points at which there are vertical tangents and points at which there are no tangents.
-
Tangent line to a curve at a point and local linear approximation.
-
Instantaneous rate of change as the limit of average rate of change.
-
Approximate rate of change from graphs and tables of values.
Derivative as a function.
-
Corresponding characteristics of graphs of f and f′.
-
Relationship between the increasing and decreasing behavior of f and the sign of f′.
-
The Mean Value Theorem and its geometric consequences.
-
Equations involving derivatives. Verbal descriptions are translated into equations involving derivatives and vice versa.
Second derivatives.
-
Corresponding characteristics of the graphs of f, f′, and f″.
-
Relationship between the concavity of f and the sign of f″.
-
Points of inflection as places where concavity changes.
Applications of derivatives.
-
Analysis of curves, including the notions of monotonicity and concavity.
-
Optimization, both absolute (global) and relative (local) extrema.
-
Modeling rates of change, including related rates problems.
-
Use of implicit differentiation to find the derivative of an inverse function.
-
Interpretation of the derivative as a rate of change in varied applied contexts, including velocity, speed, and acceleration.
Computation of derivatives.
-
Knowledge of derivatives of basic functions, including power, exponential, logarithmic, trigonometric, and inverse trigonometric functions.
-
Basic rules for the derivative of sums, products, and quotients of functions.
-
Chain rule and implicit differentiation.
III. Integrals
Interpretations and properties of definite integrals.
-
Computation of Riemann sums using left, right, and midpoint evaluation points.
-
Definite integral as a limit of Riemann sums over equal subdivisions.
-
Definite integral of the rate of change of a quantity over an interval interpreted as the change of the quantity over the interval:
-
Basic properties of definite integrals. (Examples include additivity and linearity.)
Applications of integrals. Appropriate integrals are used in a variety of applications to model physical, social, or economic situations. Although only a sampling of applications can be included in any specific course, students should be able to adapt their knowledge and techniques to solve other similar application problems. Whatever applications are chosen, the emphasis is on using the integral of a rate of change to give accumulated change or using the method of setting up an approximating Riemann sum and representing its limit as a definite integral. To provide a common foundation, specific applications should include finding the area of a region, the volume of a solid with known cross sections, the average value of a function, and the distance traveled by a particle along a line.
Fundamental theorem of calculus.
-
Use of the Fundamental Theorem to evaluate definite integrals.
-
Use of the Fundamental Theorem to represent a particular antiderivative, and the analytical and graphical analysis of functions so defined.
Techniques of antidifferentiation.
-
Antiderivatives following directly from derivatives of basic functions.
-
Antiderivatives by substitution of variables (including change of limits for definite integrals).
Applications of antidifferentiation.
-
Finding specific antiderivatives using initial conditions, including applications to motion along a line.
-
Solving separable differential equations and using them in modeling. In particular, studying the equation y′ = ky and exponential growth.
Numerical approximations to definite integrals. Use of Riemann and trapezoidal sums to approximate definite integrals of functions represented algebraically, goemetrically, and by tables of values.
SOURCE: College Entrance Examination Board (1999, pp. 6–9).
Appendix D
Topical Outline for AP Calculus BC
The topic outline for Calculus BC includes all Calculus AB topics. Additional topics are found in paragraphs that are marked with a plus sign (+) or an asterisk (*). The additional topics can be taught anywhere in the course that the instructor wishes. Some topics will naturally fit immediately after their Calculus AB counterparts. Other topics may fit best after the completion of the Calculus AB topical outline. (See the Teacher’s Guide—AP Calculus [Kennedy, 1997] for sample syllabi.) Although the examination is based on the topics listed in the topical outline, teachers may wish to enrich their courses with additional topics.
I. Functions, Graphs, and Limits
Analysis of graphs. With the aid of technology, graphs of functions are often easy to produce. The emphasis is on the interplay between the geometric and analytic information and on the use of calculus both to predict and to explain the observed local and global behavior of a function.
Limits of functions (including one-sided limits).
• An intuitive understanding of the limiting process.
• Calculating limits using algebra.
• Estimating limits from graphs or tables of data.
Asymptotic and unbounded behavior.
• Understanding asymptotes in terms of graphical behavior.
• Describing asymptotic behavior in terms of limits involving infinity.
• Comparing relative magnitudes of functions and their rates of change. (For example, contrasting exponential growth, polynomial growth, and logarithmic growth.)
Continuity as a property of functions.
• An intuitive understanding of continuity. (Close values of the domain lead to close values of the range.)
• Understanding continuity in terms of limits.
• Geometric understanding of graphs of continuous functions (Intermediate Value Theorem and Extreme Value Theorem).
*Parametric, polar, and vector functions. The analysis of planar curves includes those given in parametric form, polar form, and vector form.
II. Derivatives
Concept of the derivative.
• Derivative presented geometrically, numerically, and analytically.
• Derivative interpreted as an instantaneous rate of change.
• Derivative defined as the limit of the difference quotient.
• Relationship between differentiability and continuity.
Derivative at a point.
• Slope of a curve at a point. Examples are emphasized, including points at which there are vertical tangents and points at which there are no tangents.
• Tangent line to a curve at a point and local linear approximation.
• Instantaneous rate of change as the limit of average rate of change.
• Approximate rate of change from graphs and tables of values.
Derivative as a function.
• Corresponding characteristics of graphs of f and f′.
• Relationship between the increasing and decreasing behavior of f and the sign of f′.
• The Mean Value Theorem and its geometric consequences.
• Equations involving derivatives. Verbal descriptions are translated into equations involving derivatives and vice versa.
Second derivatives.
• Corresponding characteristics of the graphs of f, f′, and f″.
• Relationship between the concavity of f and the sign of f″.
• Points of inflection as places where concavity changes.
Applications of derivatives.
• Analysis of curves, including the notions of monotonicity and concavity.
+ Analysis of planar curves given in parametric form, polar form, and vector form, including velocity and acceleration vectors.
• Optimization, both absolute (global) and relative (local) extrema.
• Modeling rates of change, including related rates problems.
• Use of implicit differentiation to find the derivative of an inverse function.
• Interpretation of the derivative as a rate of change in varied applied contexts, including velocity, speed, and acceleration.
+ Geometric interpretation of differential equations via slope fields and the relationship between slope fields and derivatives of implicitly defined functions.
+ Numerical solution of differential equations using Euler’s method.
+ L’Hôpital’s Rule and its use in determining convergence of improper integrals and series.
Computation of derivatives.
• Knowledge of derivatives of basic functions, including power, exponential, logarithmic, trigonometric, and inverse trigonometric functions.
• Basic rules for the derivative of sums, products, and quotients of functions.
• Chain rule and implicit differentiation.
+ Derivatives of parametric, polar, and vector functions.
III. Integrals
Interpretations and properties of definite integrals.
• Computation of Riemann sums using left, right, and midpoint evaluation points.
• Definite integral as a limit of Riemann sums over equal subdivisions.
• Definite integral of the rate of change of a quantity over an interval interpreted as the change of the quantity over the interval:
• Basic properties of definite integrals. (Examples include additivity and linearity.)
*Applications of integrals. Appropriate integrals are used in a variety of applications to model physical, social, or economic situations. Although only a sampling of applications can be included in any specific course, students should be able to adapt their knowledge and techniques to solve other similar application problems. Whatever applications are chosen, the emphasis is on using the integral of a rate of change to give accumulated change or
using the method of setting up an approximating Riemann sum and representing its limit as a definite integral. To provide a common foundation, specific applications should include finding the area of a region (including a region bounded by polar curves), the volume of a solid with known cross sections, the average value of a function, the distance traveled by a particle along a line, and the length of a curve (including a curve given in parametric form).
Fundamental theorem of calculus.
• Use of the Fundamental Theorem to evaluate definite integrals.
• Use of the Fundamental Theorem to represent a particular antiderivative, and the analytical and graphical analysis of functions so defined. Techniques of antidifferentiation.
• Antiderivatives following directly from derivatives of basic functions.
+ Antiderivatives by substitution of variables (including change of limits for definite integrals), parts, and simple partial fractions (nonrepeating linear factors only).
+ Improper integrals (as limits of definite integrals).
Applications of antidifferentiation.
• Finding specific antiderivatives using initial conditions, including applications to motion along a line.
• Solving separable differential equations and using them in modeling. In particular, studying the equation y′ = ky and exponential growth.
+ Solving logistic differential equations and using them in modeling.
Numerical approximations to definite integrals. Use of Riemann and trapezoidal sums to approximate definite integrals of functions represented algebraically, geometrically, and by tables of values.
*IV. Polynomial Approximations and Series
*Concept of series. A series is defined as a sequence of partial sums, and convergence is defined in terms of the limit of the sequence of partial sums. Technology can be used to explore convergence or divergence.
*Series of constants.
+ Motivating examples, including decimal expansion.
+ Geometric series with applications.
+ The harmonic series.
+ Alternating series with error bound.
+ Terms of series as areas of rectangles and their relationship to improper integrals, including the integral test and its use in testing the convergence of p-series.
+ The ratio test for convergence and divergence.
+ Comparing series to test for convergence or divergence.
*Taylor series.
+ Taylor polynomial approximation with graphical demonstration of convergence. (For example, viewing graphs of various Taylor polynomials of the sine function approximating the sine curve.)
+ Maclaurin series and the general Taylor series centered at x = a.
+ Maclaurin series for the functions ex, sin x, cos x, and 1 / (1 – x).
+ Formal manipulation of Taylor series and shortcuts to computing Taylor series, including substitution, differentiation, antidifferentiation, and the formation of new series from known series.
+ Functions defined by power series.
+ Radius and interval of convergence of power series.
+ Lagrange error bound for Taylor polynomials.
SOURCE: College Entrance Examination Board (1999a, 1999c, pp. 9–14).
Appendix F
Text of a Letter Endorsed by the Governing Boards of the Mathematical Association of America and the National Council of Teachers of Mathematics Concerning Calculus in the Secondary Schools33
TO: Secondary School Mathematics Teachers
FROM: The Mathematical Association of America
The National Council of Teachers of Mathematics
DATE: September, 1986
RE: Calculus in the Secondary School
Dear Colleague:
A single variable calculus course is now well established in the 12th grade at many secondary schools, and the number of students enrolling is increasing substantially each year. In this letter, we would like to discuss two problems that have emerged.
The first problem concerns the relationship between the calculus course offered in high school and the succeeding calculus courses in college. The
Mathematical Association of America (MAA) and the National Council of Teachers of Mathematics (NCTM) recommend that the calculus course offered in the 12th grade should be treated as a college-level course. The expectation should be that a substantial majority of the students taking the course will master the material and will not then repeat the subject upon entrance to college. Too many students now view their 12th grade calculus course as an introduction to calculus with the expectation of repeating the material in college. This causes an undesirable attitude on the part of the student both in secondary school and in college. In secondary school all too often a student may feel “I don’t have to study this subject too seriously, because I have already seen most of the ideas.” Such students typically have considerable difficulty later on as they proceed further into the subject matter.
MAA and NCTM recommend that all students taking calculus in secondary school who are performing satisfactorily in the course should expect to place out of the comparable college calculus course. Therefore, to verify appropriate placement upon entrance to college, students should either take one of the Advanced Placement (AP) Calculus Examinations of the College Board, or take a locally-administered college placement examination in calculus. Satisfactory performance on an AP examination carries with it college credit at most universities.
The second problem concerns preparation for the calculus course. MAA and NCTM recommend that students who enroll in a calculus course in secondary school should have demonstrated mastery of algebra, geometry, trigonometry, and coordinate geometry. This means that students should have at least four full years of mathematical preparation beginning with the first course in algebra. The advanced topics in algebra, trigonometry, analytic geometry, complex numbers, and elementary functions studied in depth during the fourth year of preparation are critically important for students’ latter courses in mathematics.
It is important to note that at present many well-prepared students take calculus in the 12th grade, place out of the comparable course in college, and do well in succeeding college courses. Currently, the two most common methods for preparing students for a college-level calculus course in the 12th grade are to begin the first algebra course in the 8th grade or to require students to take second year algebra and geometry concurrently. Students beginning with algebra in the 9th grade, who take only one mathematics course each year in secondary school, should not expect to take calculus in the 12th grade. Instead, they should use the 12th grade to prepare themselves fully for calculus as freshmen in college.
We offer these recommendations in an attempt to strengthen the calculus program in secondary schools. They are not meant to discourage the