Biographical Memoirs: Volume 79 (2001)

September 30, 1913–January 30, 1998

BY HYMAN BASS, HENRI CARTAN, PETER FREYD, ALEX HELLER, AND SAUNDERS MAC LANE

SAMUEL EILENBERG DIED IN New York, January 30, 1998, after a two-year illness brought on by a stroke. He left no surviving family, except for his wide family of friends, students, and colleagues, and the rich legacy of his life’s work, in both mathematics and as an art collector.

“Sammy”, as he has long been called by all who had the good fortune to know him, was one of the great architects of twentieth-century mathematics and definitively reshaped the ways we think about topology. The ideas that accomplished this were so fundamental and supple that they took on a life of their own, giving birth first to homological algebra and in turn to category theory, structures that now permeate much of contemporary mathematics.

Born in Warsaw, Poland, Sammy studied in the Polish school of topology. At his father’s urging, he fled Europe in 1939. On his arrival in Princeton, Oswald Veblen and Solomon Lefschetz helped him (as they had helped other refugees) find a position at the University of Michigan, where Ray Wilder was building up a group in topology. Wilder made Michigan a center of topology, bringing in such figures as

Norman Steenrod, Raoul Bott, Hans Samelson, and others. Saunders Mac Lane’s invited lecture there on group extensions precipitated the long and fruitful Eilenberg-Mac Lane collaboration.

In 1947 Sammy came to the Columbia University mathematics department, which he twice chaired and where he remained till his retirement. In 1982 he was named a University professor, the highest faculty distinction that the university confers.

Sammy traveled and collaborated widely. For fifteen years he was a member of Bourbaki. His collaboration with Steenrod produced the book Foundations of Algebraic Topology, that with Henri Cartan the book Homological Algebra, both of them epoch-making works. The Eilenberg-Mac Lane collaboration gave birth to category theory, a field that both men nurtured and followed throughout their ensuing careers. Sammy later brought these ideas to bear in a multivolume work on automata theory. A joint work on topology with Eldon Dyer may see posthumous publication soon.

Among his many honors Sammy won the Wolf Prize (shared in 1986 with Atle Selberg), was awarded several honorary degrees (including one from the University of Pennsylvania), and was elected to membership in the National Academy of Sciences of the USA. On the occasion of the honorary degree at the University of Pennsylvania in 1985, he was cited as “our greatest mathematical stylist”.

The aesthetic principles that guided Sammy’s mathematical work also found expression in his passion for art collecting. Over the years Sammy gathered one of the world’s most important collections of Southeast Asian art. His fame among certain art collectors overshadows his mathematical reputation. In a gesture characteristically marked by its generosity and elegance, Sammy in 1987 donated much of his collection to the Metropolitan Museum of Art in New York, which

in turn was thus motivated to contribute substantially to the endowment of the Eilenberg Visiting Professorship in Mathematics at Columbia University.

—Hyman Bass

Samuel Eilenberg died in New York on January 30, 1998, after spending two years in a state of precarious health. I would like to write here of the mathematician and especially of the friend that I gradually discovered in the course of a close collaboration that lasted at least five years and that taught me many things.

I met Sammy for the first time at the end of December 1947: he had come to greet me at LaGuardia Airport in New York, a city buried under snow, where airplanes had been unable either to take off or to land for two days. This was my first visit to the United States; it was to last five months. Of course, Eilenberg was not unknown to me, because since the end of the war I had begun to be interested in algebraic topology. Notably I had studied the article in the 1944 Annals of Mathematics in which Eilenberg set forth his theory of singular homology (one of those theories which immediately takes on a definitive shape). I had, for my part, reflected on the “Künneth formula”, which gives the Betti numbers and the torsion coefficients of the product of two simplicial complexes. In fact, that formula amounts to a calculation of the homology groups of the tensor product of two graded differential groups as a function of the homology groups of each of them. The solution involves

not only the tensor product of the homology groups of the factors but also a new functor of these groups, the functor Tor. At the time of my first meeting with Sammy, I was quite happy with telling that to him.

This was the point of departure for our collaboration, by means of postal mail at first. Then Sammy came to spend the year 1950–51 in Paris. He took part in my seminar at the École Normale, devoted that year to cohomology of groups, spectral sequences, and sheaf theory. Sammy gave two lectures on spectral sequences. Armand Borel and Jean-Pierre Serre took an active part in this seminar also.

Independently of the seminar, Sammy and I had work sessions with the aim of writing an article that would develop some of the new ideas born out of the Künneth formula. We went from discovery to discovery, Sammy having an extraordinary gift for formulating at each moment the conclusions that would emerge from the discussion. And it was always he who wrote everything up as we went along in precise and concise English. After the notion of satellites of a functor came that of derived functors, with their axiomatic characterization. Gradually the theory included several existing theories (cohomology of groups, cohomology of Lie algebras, in the sense of Chevalley and Eilenberg, cohomology of associative algebras). Then came the concept of hyperhomology.

Of course, this work together took several years. Sammy made several trips to my country houses (in Die and in Dolomieu). Outside of our work hours he participated in our family life.

Sammy knew how to put his friends to work. I think I remember that he persuaded Steenrod to contribute the preface of our book, where the evolution of the ideas is explained perfectly. He arranged also for other colleagues to collaborate in the writing of the chapter devoted to finite

groups. Our initial project of a mere article for a journal was transformed; it became a book that we would propose to a publisher and for which it would be necessary to find a title that captured its content. We finally agreed on the term Homological Algebra. The text was given to Princeton University Press in 1953. I do not know why the book appeared only in 1956.

For fifteen years Sammy was also an active member of the Bourbaki group. It was, I think, in 1949 that André Weil, who was living in the United States, made contact with him in order to have him collaborate on a draft for use by Bourbaki, entitled “SEAW Report on Homotopy Groups and Fiber Spaces”. It is therefore very natural that Eilenberg was invited to the Congress that Bourbaki held in October 1950. He was immediately appreciated and became a member of the group under the name “Sammy”. It is necessary to say that he mastered the French language perfectly, which he had learned when he was living in his native Poland.

The collaboration of Sammy with Bourbaki lasted until 1966. He took part in the summer meetings, which lasted two weeks. He knew admirably how to present his point of view, and he often made us agree to it.

The above gives only a faint idea of Samuel Eilenberg’s mathematical activity. The list made in 1974 of his publications comprises, besides 4 books, 111 articles; the first 37 articles are before his emigration from Poland to the United States in 1939, and almost all are written in French. He was not yet twenty years old when he began to publish. The celebrated articles written with S.Mac Lane extended from 1942 to 1954. The list of his other collaborators is long: N.E.Steenrod, J.A.Zilber, T.Nakayama, T.Ganea, J.C. Moore, G.M.Kelly, to cite only the main ones. Starting in 1966, Sammy became actively interested in the theory of automata, which led him to write a book entitled Automata,

Languages, and Machines, published in 1974 by Academic Press.

I have not mentioned a magnificent collection of sculptures in bronze, silver, or stone, patiently collected in India, Pakistan, Indonesia, Cambodia,…, some of which dated to the third century B.C. In 1967 he gave a great part of his collection to the Metropolitan Museum in New York.

In 1982 Eilenberg retired from Columbia University, where he had taught since 1947. In 1986 his mathematical work was recognized by the award of the Wolf Prize in Mathematics, which he shared with Atle Selberg.

The last time I saw Sammy was when the Université de Louvain-la-Neuve organized a conference in his honor. Our meeting there was not without emotion. He was for me a friend whose kindness, humor, and faithfulness cannot be forgotten.

Samuel Eilenberg, who made decisive contributions to topology and other areas of mathematics, died on Friday, January 30, 1998, in New York City. He had been a leading member of the department of mathematics at Columbia University since 1947. His mathematical books, ideas and papers had a major influence.

Eilenberg was born in Poland in 1913. At the University of Warsaw he was a student of Borsuk in the active school of Polish topology. His thesis, concerned with the topology of the plane, was published in Fundamenta Mathematica in 1936. Its results were well received in Poland and in the

USA. In 1938 he published in the same journal another influential paper on the action of the fundamental group on the higher homotopy groups of a space. Algebra was not foreign to his topology!

Early in 1939 Sammy’s father told him, “Sammy, it doesn’t look good here in Poland. Get out.” He did, arriving in New York on April 23, 1939, and going at once to Princeton. At that university Oswald Veblen and Solomon Lefschetz efficiently welcomed refugee mathematicians and found them suitable positions at American universities. Sammy’s work in topology was well known, so a position for him was found at the University of Michigan. There Ray Wilder had an active group of topologists, including Norman Steenrod, then a recent Princeton Ph.D. Sammy immediately fitted in, did collaborative research (for example, with Wilder, O.G.Harrold, and Deane Montgomery). His 1940 paper in the Annals of Mathematics formulated and codified the ideas of the “obstructions” recently introduced by Hassler Whitney. He also argued with Lefschetz. Finding the Lefschetz book (1942) obscure in its treatment of singular homology, he provided an elegant and definitive treatment in the Annals (1944).

Sammy’s idea was to dig deep and deeper till he got to the bottom of each issue. This I learned when I lectured at Ann Arbor about group extensions. I had calculated an example of group extensions for an interesting factor group involving a prime number p. When I told Sammy this result, he immediately saw that it answered a question of Steenrod about the regular cycles of the p-adic solenoid (inside a solid torus, wrap another one p times around, and so on, ad infinitum). So Sammy and I stayed up all night to find out the reason for this unexpected appearance of group extensions. We found out more: it rested on a “universal coefficient theorem” which gave cohomology with any coeffi-

cient group G in terms of homology and an exact sequence involving Ext, the group of group extensions. Thus Sammy insisted on understanding this unexpected connection between algebra and topology. There was more there: the connection involved mapping topology into algebra, so we were forced to invent functors, natural transformations, and categories to describe this. All told, this led to our fifteen joint papers.

They all involved the maxim: Dig deeper and find out. For example, Hurewicz and Heinz Hopf had observed that the fundamental group of a space had effects on the higher homology and cohomology groups. Sammy, with his knowledge of his singular homology theory, had just the needed tools to understand this, which resulted in our discovery of the cohomology of groups. Sammy saw that this idea went further, so he started Gerhard Hochschild on his study of the cohomology of algebras and then went on to write, with Henri Cartan, that very influential book on homological algebra, which caught the interest of many algebraists and provided the first book presentation of the important French technique of spectral sequences.

Sammy applied his maxim in other connections. With Joe Zilber he developed the category of simplicial sets as a new type of space—using his singular simplices with face and degeneration operations. With Calvin Elgot he wrote about recursion, a topic in logic. By himself he wrote two volumes on Automata, Languages, and Machines. And with Eldon Dyer he prepared two volumes (not yet published) on General and Categorical Topology.

Algebraic topology was decisively influenced by Eilenberg’s earlier 1952 work with Norman Steenrod, entitled Foundations of Algebraic Topology. At that time there were many different and confusing versions of homology theory, some singular, some cellular. This book used categories to show

that they all could be described conceptually as presenting homology functors from the category of pairs of spaces to groups or to rings, satisfying suitable axioms such as “excision”. Thanks to Sammy’s insight and his enthusiasm, this text drastically changed the teaching of topology.

At Columbia University Sammy took vigorous steps to build up the department. He trained many graduate students. For example, his students and postdocs in category theory included Harry Applegate, Mike Barr, Jonathan Beck, David Buchsbaum, Peter Freyd, Alex Heller, Daniel Kan, Bill Lawvere, Fred Linton, Steve Schanuel, Myles Tierney, and others. He was an inspiring teacher.

Early in 1996 Sammy was felled by a stroke. It became hard for him to talk. In May 1997 I was able to visit him; he was lively and passed on to me a not clearly understood proposal. He was then able to spend some time in his apartment on Riverside Drive. I think his message then to me was the same maxim: Keep on pressing those mathematical ideas. This is well illustrated by his life. His ideas—singular homology, categories, simplicial sets, generic acyclicity, obstructions, automata, and the rest—will live on.

Our fifteen joint research papers have been collected in the volume Eilenberg/Mac Lane, Collected Works, Academic Press, Inc., New York, 1988.

Next, I comment on Eilenberg’s contributions to the sources of homological algebra. The startling idea that homology theory for topological spaces could be used for algebraic objects first arose with the discovery of the cohomology groups of a group. Hurewicz had considered spaces which are aspherical (any image of a higher-dimensional sphere can be deformed into a point) and had shown that the fundamental group p₁ determines the homotopy type of the space—and hence its homology and cohomology groups. Hopf had then found explicit formulas for the ho-

mology (Betti) groups of such a space. Then Eilenberg-Mac Lane exhibited the n^th cohomology group Hⁿ(X, A) of such a space with coefficients in an abelian group A as a functor of π₁ and A—the n^th cohomology Hⁿ(π₁, A) of the group π₁ with coefficients in the π₁-module A. In particular H¹ was simply the group of “crossed homomorphisms” f:π₁→A satisfying

and taken modulo the “principal” such—those f given as f(x)=xa–a for some a in A. The elements of Hⁿ(π₁, A) were functions f(x₁,…, x_n) of n elements x_i satisfying a suitable equation, modulo trivial solutions. In other words, the cohomology of π₁ was given as the cohomology of a certain chain complex, the so-called “bar resolution”. In the terminology subsequently refined by Cartan-Eilenberg, Hⁿ(π₁, —) was the (n–1)^st “derived” functor of H¹(π₁, —). In other words, old functors lead to new ones.

Eilenberg very quickly saw that such cohomological methods would apply to any algebraic situation. He explained this in the 1949 paper [2]. In 1948 he wrote with Chevalley a paper on the cohomology theory of Lie algebras, and about the same time he encouraged Gerhard Hochschild, then one of Chevalley’s Ph.D. students, to introduce cohomology groups for associative algebras. In each of these cases the cohomology groups in question were the derived functors of naturally occurring Hom functors. Classical questions of algebraic topology also entered by way of the Künneth formulas. These formulas originally were stated to give the Betti numbers and torsion coefficients of a product of two spaces X and Y. This really involved the tensor product of homology groups, and in the famous Eilenberg-Steenrod book it appears in the following short exact sequence:

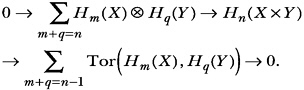
Here “exact” means that at each point the image of the incoming arrow is the kernel of the outgoing arrow. Also, Tor(A,B) is a functor of abelian groups, as is ; in fact, Tor turns out to be the first derived functor of ! The definitions of these terms do suffice for the topological task in question: elements of finite order in the groups A and B give elements in Tor. I clearly recall an occasion when I tried to explain to Professor Künneth at Erlangen University that this abstract language did indeed produce his original numerical Künneth formulas. As stated, Tor is the first derived functor of ; it turns out for modules that there are also higher derived functors Tor_n(A, B) for each n. The construction of these higher torsion products and their description by generators and relations were examined by Eilenberg-Mac Lane; these products provided new examples of higher derived functors of modules. For abelian groups A and B, Tor_n(A, B)=0 when n>1.

Now return to the functor Ext (A, B), the group of abelian group extensions E of B by A, so that E appears in a short exact sequence of abelian groups:

It turns our that the functor Ext (A, —) is the first derived functor of Hom (A, —) and thus that there are higher derived functors Ext_n(A, —). They vanish for abelian groups A, but not generally for modules. The work of the Japanese mathematician Yoneda showed that an element of Ext_n(A, B)

could be represented as a long exact sequence of modules (with n intermediate terms):

All these various examples of the construction of new functors as “derived” functors of given ones were at hand for Eilenberg. He saw how they could be used to determine a homological “dimension” for algebraic objects, and he established the connection with the Hilbert notion of a syzygy in a 1956 paper [3]. This provided the background for the influential Cartan-Eilenberg book [1] on homological algebra. This text emphasized how the derived functors for a module M could be calculated from any “resolution” of M by free modules, a long exact sequence

with all X_j free. One simply applies the functor to the resolution with the M term dropped and then takes the homology or cohomology of the resulting complex. This effectively generalized the computation from specific “bar resolutions” used to define the cohomology of a group. The ideas of homological algebra were presented in two pioneering books by Cartan-Eilenberg [1] and Mac Lane [4]. The Cartan-Eilenberg treatise had a widespread and decisive influence in algebra. This again illustrates the genius of Eilenberg: If essentially the same idea crops up in different places, follow it out and find out where it lives.

When I met Samuel Eilenberg in 1947, he was introduced as Sammy. He was always referred to as Sammy. It would be wrong to speak of him otherwise. I was then a student; I promptly became his student. I would like to record what drew me then to Sammy and continued over the years to do so—namely, what I perceived as his radical insistence on lucidity, order, and understanding as opposed to trophy hunting, and his idea of how that understanding was to be achieved.

Perhaps I should illustrate this by a partial (in both senses) account of his mathematical career. At the end of the 1930s algebraic topology had amassed a stock of problems which its then available tools were unable to attack. Sammy was prominent among a small group of mathematicians—among them, for example, J.H.C.Whitehead, Hassler Whitney, Saunders Mac Lane, and Norman Steenrod—who dedicated themselves to building a more adequate armamentarium. Their success in doing this was attested to by the fact that by the end of the 1960s most of those problems had been solved (inordinately many of them by J.F.Adams).

Sammy’s contributions appeared for the most part in a series of collaborations. With Mac Lane he developed the theory of cohomology of groups, thus providing a proper setting for the remarkable theorem of Hopf on the homology of highly connected spaces. This led them to the study of the Eilenberg-Mac Lane spaces and thus to a deeper understanding of the relations between homotopy and homology. Their most fateful invention perhaps was that of category

theory, responding, no doubt, to the exigencies of algebraic topology but destined to radiate across most of mathematics.

In collaboration with Steenrod, Sammy drained the Pontine Marshes of homology theory, turning an ugly morass of variously motivated constructions into a simple and elegant system of axioms applied, for the first time, to functors. This was a radical innovation. Heretofore homology theories had been procedures for computing; henceforth they would be mathematical objects in their own right. What was especially remarkable was that in order to achieve this, Sammy and Steenrod undertook to raise the logical level of the things that might be so regarded.

The algebraic structures of the new algebraic topology were proving themselves useful in other parts of mathematics: in algebra, representation theory, algebraic geometry, and even in number theory. Together with Henri Cartan, Sammy systematized these structures under the rubric of Homological Algebra, once more raising the level of discourse by introducing such notions as derived functors. I am tempted to insert a parenthesis here. This latest innovation brought its authors into conflict with the “establishment” by putting in question the very notion of definition, raising a fundamental question of the relation between category theory and set theory that has yet to be put definitively to rest. Since homological algebra has proved indispensable, the honors lie, I think, with Cartan and Eilenberg. In any case, the field proliferated so rapidly that Grothendieck, only a few years later, was said to have spoken of their book as “le diplodocus”, regarding it apparently as palaeontology.

The roots of homological algebra lay nevertheless in algebraic topology, and Sammy, in collaboration with John Moore, returned to these. They introduced such novelties as differential graded homological algebra and relative homological algebra to provide homes for the new techniques intro-

duced not only by Sammy and his collaborators but also by a new generation including Serre, Grothendieck, and Adams. Notable among them are the so-called Eilenberg-Moore spectral sequences, which deal with pullbacks of fibrations and with associated fiber bundles.

Unfortunately neither Sammy nor his last collaborator, Eldon Dyer, lived to complete their ultimate project of refounding algebraic topology in the correct—which is to say, homotopical—setting. Perhaps this project was too ambitious. I learned from Eldon how much agony accompanied even such choices as that of the correct definition of a topological space. Some part of their book may yet survive, and others are already continuing their project piecemeal.

As I perceived it, then, Sammy considered that the highest value in mathematics was to be found, not in specious depth nor in the overcoming of overwhelming difficulty, but rather in providing the definitive clarity that would illuminate its underlying order. This was to be accomplished by elucidating the true structure of the objects of mathematics. Let me hasten to say that this was in no sense an ontological quest: the true structure was intrinsic to mathematics and was to be discerned only by doing more mathematics. Sammy had no patience for metaphysical argument. He was not a Platonist; equally, he was not a non-Platonist. It might be more to the point to make a different distinction: Sammy’s mathematical aesthetic was classical rather than romantic.

Category theory was one of Sammy’s principal tools in his search for mathematical reality. Category theory also developed into a mathematical subject with its own honorable history and practitioners, beginning with Mac Lane and including, notably, F.W.Lawvere, Sammy’s most remarkable student, who saw it as a foundation for all of mathematics and justified this intuition with such innovations as

categorical semantics and topos theory. Sammy did not, I think, want to be reckoned a member of this school. I believe, in fact, that he would have rejected the idea that mathematics needed a foundation. Category theory was for him only a tool—in fact, a powerful one—for expanding our understanding. It was his willingness to search for this understanding at an ever higher level that really set him apart and that made him, in my estimation, the author of a revolution in mathematics as notable as that initiated by Cantor’s invention of set theory. Like Cantor, Sammy has changed the way we think about mathematics.

Thirty years ago I found myself a neighbor of Arthur Upham Pope, the master of ancient Persian art. He had retired in his nineties to an estate in the center of the city of Shiraz in southern Iran, where I lived, briefly, across the street. I found an excuse for what has to be called an audience, and I mentioned that I was a friend of Samuel Eilenberg.

“I don’t know him,” he said. “I know of him, of course. How do you know him?”

“We work in the same area of mathematics.”

“You’re talking about a different Eilenberg. I meant the dealer in Indian art.”

“Actually, it’s the same person. He’s both a mathematician and a collector of Indian art.”

“Don’t be silly, young man. The Eilenberg I mean is not a collector of Indian art, he’s the dealer in Indian art. I know

him well. He established the historicity of one of the Persian kings. He certainly is not a mathematician.”

End of audience.

In later years even Arthur Upham Pope would have known. In the art world, Eilenberg became universally known as “Professor”. Indeed, if one walked with him in London or Zürich or even Philadelphia and one heard “Professor!”, it was always Eilenberg who was being hailed, and it was always the art world hailing him.

If you heard “Sammy!”, you knew it was a mathematician.

It was complicated, explaining that name. For a person who knew him first through his works, it was hard to conceive of him as “Sammy”. And upon meeting him for the first time, it was even harder: He was in charge of entire fields of mathematics—indeed, he had created a number of them. Whenever he was in a room, he was in charge of the room, and it did not matter whose room it was. Sammy? The name did not fit.

But he had to have a name like Sammy. I said it was hard to explain. Here was one of the most aggressive people one might ever meet. He would challenge almost anything. If a person mentioned something about the weather, he would challenge it: once in California I heard him insist that it was not weather; it was climate. But somehow it was almost always clear: it was all right to challenge him right back. Aggressive and challenging, but not at all pompous. One cannot be pompous with a name like Sammy.

Sammy kept his two worlds, mathematics and art, at something of a distance. But both worlds seemed to agree on one thing, the very one that Arthur Upham Pope had insisted upon: Sammy was the dealer.

Without question, Sammy loved playing the role of dealer. In the days when mathematicians were in demand and jobs were easy to come by, Sammy loved to tell about the math

market he was going to create. The trade would be in mathematician futures: “This one’s done only two lemmas and one proposition in the last year; the most recent theorem was two years ago; better sell this one at a loss.” With his big cigar (expensive) and his big gold ring (in fact, a valuable Indian artifact), he could enter his dealer mode at a moment’s notice. One always wondered just how many young mathematicians’ careers were in his hands.

But his two worlds, mathematics and art, perceived this role of dealer quite differently. In mathematics we understood that it was a role he loved playing, but that he was only playing. His being a mathematician was what counted, and he would have been the same mathematician whether or not he played the dealer, indeed, whether or not he played—and he did—high-stakes poker. This was not so clear in his other world.

It was usually frustrating trying to explain to others how Sammy was perceived by his fellow mathematicians. Sammy had an unprintable way of saying that mathematics required both intelligence and aggression. But imagine not knowing how his mathematics—when he had finished—would totally belie that aggression. Imagine not knowing how remarkably well-behaved his mathematics always was. Imagine not knowing how his mathematics, when he had finished, always seemed preordained and how it seemed no more aggressive than, say, the sun rising at its appointed sunrise time.

Forty years ago Sammy hoped to turn the study of Indian bronzes into an equally well-behaved subject. He had already acquired a reputation for being the best detector of fakes in the business, and he believed he could axiomatize the process. He even had a provisional list of axioms, and it was truly an elegant list.

A few years later we found ourselves at a small French-style bistro in La Jolla, California. We had been out of touch:

there had been an argument about mathematical ethics, but somehow we had resolved it; the dinner was something of a celebration of the resolution. I asked him about his book on bronzes.

“The axioms failed.”

“What does that mean?”

“It means that I’ve been taken. I bought a fake.”

He had suspected it only after the work had been in his bedroom for a few weeks. He had the pleasure, at least, of investigating until he found out who the master faker was and tracking him down in his studio, not to berate him, but to congratulate him.

After that, Sammy made a point of not building bridges between his two worlds. I recall just one exception. He moved from a conversation about sculpture to one about mathematics. Sculptors, he said, learn early to create from the inside out: what finally is to be seen on the surface is the result of a lot of work in conceptualizing the interior. But there are others for whom the interior is the result of a lot of work on getting the surface right. “And,” Sammy asked, “isn’t that the case for my mathematics?”

Style is only one part of his mathematics—as, of course, he knew—but there are, indeed, wonderful stories about Sammy, attending only to what seemed the most superficial of stylistic choices, restructuring entire subjects on the spot.

Many have witnessed this triumph of style over substance, particularly with students. But the most dramatic example had a stellar cast. D.C.Spencer gave a colloquium at Columbia in the spring of 1962, and Sammy decided it was time to demonstrate his get-rid-of-subscripts rule: “If you define it right, you won’t need a subscript.” Spencer, with the greatest of charm—it was for good reason that he was already affectionately known as “Uncle Don” —followed Sammy’s orders and proceeded to restructure his subject while standing

there at the board. One by one, the subscripts disappeared, each disappearance preceded by a Sammy-dictated redefinition. He had virtually no idea of the intended meanings of any of the symbols. He was operating entirely on the surface, looking only at the shape of the syntax.

The process went on for several minutes, until Sammy took on the one proposition on the board. “So now what does that say?”

“Sammy, I don’t know. You’re the one making all the definitions.”

So Sammy applied his definitions, and one by one the subscripts continued to disappear, until finally the proposition itself disappeared: it became the assertion that a thing was equal—behold—to itself.

“My mother’s father had the town brewery and he had one child, a daughter. He went to the head of the town yeshiva and asked for the best student,” Sammy told me one day. “So my future father became a brewer instead of a rabbi.”

Sammy regarded prewar Poland with some affection. He felt that he had been well nurtured by the Polish community of mathematicians, and he told me of his pleasure on being received by Stefan Banach himself, a process of being welcomed to the holy of holies, the café in which Banach spent his time during the annual Polish mathematical conferences. By the time Sammy came to the U.S. in his mid-twenties he was a well-known topologist.

When I questioned him on his attitude about prewar Poland, he answered that one must “watch the derivative”: Don’t judge just by how good things are, but by how fast they’re becoming better.

Sammy’s view of Poland since the war was more complicated. It was particularly complicated by what he viewed as its treatment of category theory as a fringe subject.

In the late 1950s Sammy began to concentrate his mathematical activities, both research and teaching, on category theory. He and Mac Lane had invented the subject, but to them it was always an applied subject, not an end in itself. Categories were defined in order to define functors, which in turn were defined in order to define natural transformations, which were defined finally in order to prove theorems that could not be proved before. In this view, category theory belonged in the mainstream of mathematics.

There was another view, the “categories-as-fringe” view. It said that categories were defined in order to state theorems that could not be stated before, that they were not tools but objects of nature worthy of study in their own right. Sammy believed that this counterview was a direct challenge to his role as the chief dealer for category theory. He had watched many of his inventions become standard mathematics— singular homology, obstruction theory, homological algebra— and he had no intention of leaving the future of category theory to others.

Today the language of category theory has permeated a good part of mathematics and is treated with some respect. It was not ever so. There were years before the words “category” and “functor” could be pronounced unapologetically in diverse mathematical company. One of my fonder memories comes from sitting next to Sammy in the early 1960s when Frank Adarns gave one of his first lectures on how every functor on finite-dimensional vector spaces gives rise to a natural transformation on the K-functor. Frank used that construction to obtain what are now called the Adams operations, and he used those to count how many independent vector fields there could be on a sphere. It was not until then that it became permissible to say “functor” without a little snort.

In those years, Sammy was a one-man employment agency

for a fresh generation of mathematicians who viewed categories not just as a language but as a potentially central mathematical subject. For the next thirty-five years he went to just about every category theory conference, and, much more important, he used his masterly expository skills to convey categorical ideas to other mathematicians. Sammy’s efforts succeeded for the language of category theory, and he never abandoned his efforts for the theory itself. He was confident that the categorical view would eventually be the standard mathematical view, with or without his salesmanship. Its inevitability would be based not on Sammy’s skills as a dealer but on the theorems whose proofs required category theory. That was obvious to Sammy. He wanted to make it obvious to everyone else.

Sammy visited the University of Chicago for a topology meeting while he was department chair at Columbia. I was then a graduate student, working with Irving Kaplansky on topics in homological algebra. So I was already familiar with some of Sammy’s work when I first met him and we discussed mathematics. Homological algebra was insinuating itself into commutative algebra and algebraic geometry through the pioneering work of Maurice Auslander and David Buchsbaum (Sammy’s student) and J.-P.Serre. Kaplansky was introducing many of my cohorts to this work.

When I graduated in 1959, in a now distant time of affluent mathematical opportunity, I contemplated a year at the Institute for Advanced Study. But Sammy, while I accompa-

nied him to an art dealer in downtown Chicago (an errand whose significance I only later appreciated), persuaded me that it would be better first to launch my professional career as a regular faculty member, doing both research and teaching. That might now seem a difficult case to make, but it fit with my own disposition, and, in any case, Sammy had a charismatic charm and warm humor that were hard to resist.

Sammy’s mentoring made me virtually his student. Columbia’s was a small and intimate department, with such figures as Harish-Chandra, Serge Lang, Paul Smith, Ellis Kolchin, Dick Kadison, Edgar Lorch, Masatake Kuranishi, Lipman Bers, Joan Birman, and, briefly, Heisuke Hironaka, Steve Smale, Wilfried Schmid, and many others. The department featured some strong personalities, but Sammy, along with Lipman Bers when he arrived somewhat later, set the tone and style of the department. Research in topology, algebraic geometry, complex analysis, number theory, and the then budding category theory were quite active there. Though a faculty member, I functioned much like a student, learning about both mathematics and the intellectual culture of our discipline.

Over the years my appreciation deepened for the way Sammy worked and thought about mathematics. Though quite accomplished at compution and geometric reasoning, Sammy was preeminently a formalist. He fit squarely into the tradition of Hilbert, E.Artin, E.Noether, and Bourbaki; he was a champion of the axiomatic unification that so dominated the early postwar mathematics. His philosophy was that the aims of mathematics are to find and articulate with clarity and economy the underlying principles that govern mathematical phenomena. Complexity and opaqueness were, for him, signs of insufficient understanding. He sought not just theorems, but ways to make the truth transparent, natural, inevitable for the “right thinking” person.

It was this “right thinking”, not just facts, that Sammy tried to teach and that, in many domains, he succeeded in teaching to a whole generation of mathematicians.

In some ways Sammy seemed to have a sense of the structure of mathematical thinking that almost transcended specific subject matter. I remember the uncanny sensation of this on more than one occasion when sitting next to him in department colloquia. The speaker was exposing a topic with which I knew that Sammy was not particularly familiar. Yet a half to two thirds of the way through the lecture, Sammy would accurately begin to tell me the kinds of things the speaker was going to say next.

Though his mathematical ideas may seem to have a kind of crystalline austerity, Sammy was a warm, robust, and very animated human being. For him mathematics was a social activity, whence his many collaborations. He liked to do mathematics on his feet, often prancing while he explained his thoughts. When something connected, one could read it in his impish smile and the sparkle in his eyes.

He was engaged with the world in many ways, a sophisticated and wise man who took a refined pleasure in life. His was a most satisfying and inspiring influence on my own professional life. After his stroke, it was painful to see Sammy, frail and gaunt and deprived of speech when his still active mind had so much yet to say. Yet he bravely showed the same good humor and dignity that marked his whole life. He leaves us with much to treasure, even while we miss him.

Kuo-Tsai Chen (1950)

Alex Heller (1950)

David Buchsbaum (1954)

Ramaiyengar Sridharan (1954)

Kalathoor Varadarajan (1954)

F.William Lawvere (1963)

Harry Applegate (1965)

Estelle Goldberg (1965)

Myles Tierney (1965)

George A.Hutchinson (1967)

Jonathan M.Beck (1967)

Stephen C.Johnson (1968)

Albert Feuer (1974)

Chang-San Wu (1974)

Martin Golumbic (1975)

Alan Littleford (1979)

[1] H.CARTAN and S.EILENBERG, Homological algebra, Princeton Univ. Press, Princeton, NJ, 1956.

[2] S.EILENBERG, Topological methods in abstract algebra: Cohomology theory of groups, Bull. Amer. Math. Soc. 55 (1949), 3–37.

[3] ———, Homological dimension and syzygies, Ann. Math. (2) 64 (1956), 328–336.

[4] S.MAC LANE, Homology, Springer-Verlag, Berlin, 1963.

Transformations continues en circonference et la topologie du plan, Fund. Math. XXVI (1936), 62–112.

On the relation between the fundamental group of a space and the higher homotopy groups, Fund. Math. XXXII (1939), 167–175.

With Mac Lane, S., Group extensions and homology, Ann. Math. 43 (1942), 758–831.

With Mac Lane, S., Natural isomorphisms in group theory, Proc. Nat. Acad. Sci. U. S. A. 28 (1942), 537–543.

With Wilder, R.L., Uniform local connectedness and contractibility, Amer. J. Math. 64 (1942), 613–622

With Harrold, O.G., Jr., Continua of finite linear measure I, Amer. J. Math. 65 (1943), 137–146.

Singular homology theory, Ann. Math. 45 (1944), 407–447.

With Mac Lane, S., General thory of natural equivalences, Trans. Amer. Math. Soc. 58 (1945), 231–294.

With Mac Lane, S., Relations between homology and homotopy groups of spaces, Ann. Math. 46 (1945), 480–509; 51 (1950), 514–573.

With Montgomery, D., Fixed point theorems for multi-valued transformations, Amer. J. Math. 68 (1946), 214–222.

Homology of spaces with operators, Trans. Amer. Math. Soc. 61 (1947), 378–417.

With Mac Lane, S., Cohomology theory in abstract groups, I, Ann. Math. 48 (1947), 51–78.

With Mac Lane, S., Cohomology and Galois theory, I: Normality of algebras and Teichmüller’s cocycle, Trans. Amer. Math. Soc. 64 (1948), 1–20.

With Mac Lane, S., Homology of spaces with operators, II, Trans. Amer. Math. Soc. 65 (1949), 49–99.

With Zilber, J.A., Semi-simplicial complexes and singular homology, Ann. Math. 51 (1950), 499–513.

With Steenrod, N.E., Foundations of Algebraic Topology. Princeton Univ. Press, Princeton, NJ, 1952.

With Mac Lane, S., Acyclic models, Amer. J. Math. 75 (1953), 189– 199.

With Mac Lane, S., On the groups H(Π,n), I, Ann. Math. 58 (1953), 55–106, 60 (1954), 49–139 and 513–557.

With Mac Lane, S., On the homology theory of abelian groups, Canad. J. Math. 7 (1955), 43–53.

With Cartan, E., Homological Algebra, Princeton, Univ. Press, Princeton, NJ, 1956.

With Ganea, T., On the Lusternik-Schnirelmann category of abstract groups, Ann. Math. 65 (1957), 517–518.

With Moore, J., Adjoint functors and triples, Illinois J. Math. 9 (1965), 381–398.

With Kelly, G.M., Closed categories. In Proceedings, Conference on Cat egorical Algebra, La Jolla, 1965, pp. 421–562. Springer-Verlag, New York, 1966.

Automata, Languages, and Machines (2 vols.). Academic Press, New York, 1974–76.

With Dyer, E., General and Categorical Topology (Vols. A & B), Cambridge Univ. Press, 2000.